Аналитическая теория чисел. L-функция Дирихле
Содержание
Введение
§1. Характеры Дирихле и L-функции Дирихле
§2. Функция θ(x ,χ), её функциональное уравнение
§3. Аналитическое продолжение L-функции Дирихле на комплексную плоскость
§4. Функциональное уравнение для L-функции Дирихле. Тривиальные нули L-функции Дирихле
§5. Нетривиальные нули L-функции Дирихле
5.1 Теорема Вейерштрасса о разложении в произведение целых функций
5.2 О бесконечности целых нетривиальных нулей L-функции Дирихле 12
§6. Обобщенная гипотеза Римана
Библиографический список
Введение
Теория L-функций Дирихле развилась в одно из важнейших вспомогательных средств аналитической теории чисел. Большую роль в приложениях играет исследование нулей L-функций Дирихле.
В аналитической теории чисел L-функция Дирихле играет такую же роль, как и ζ-функция при решении задач теории чисел, а именно задач, связанных с распределением простых чисел в арифметических прогрессиях и в задачах, связанных с оценками арифметических сумм.
Предметом исследования данной курсовой работы является распределение значений L-функций Дирихле, результаты Гурвица о выводе функционального уравнения для L-функции Дирихле и как следствие, показать, что L-функции Дирихле в критической полосе имеют бесконечное число нулей. Эти функции ввел в 1837 г. Густав Дирихле при исследовании вопроса о распределении простых чисел в арифметических прогрессиях. Основные результаты были получены в 1922 году А. Гурвицем.
В данной курсовой работе изложение материала отражает основные свойства L-функций Дирихле и соответствует результатам, полеченным Гурвицем касающимся L-функций Дирихле.
В заключении данной работы приводится гипотеза о распределении нулей дзета-функции, сформулированная Бернхардом Риманом в 1859 году. Гипотеза Римана входит в список семи «проблем тысячелетия».
§1. Характеры Дирихле и L-функции Дирихле
Прежде всего определим характеры по модулю k, равному степени простого числа, и докажем их основные свойства. Характеры по произвольному модулю к определим затем через характеры по модулю, равному степени простого числа; при этом основные свойства последних сохранятся.
Пусть k=ра, где р> 2 — простое число, α≥1. Как известно, по модулю k существуют первообразные корни, и пусть g — наименьший из них. Через ind n будем обозначать индекс числа п, (п, к) = 1, по модулю k при основании g, т. е. число γ = γ(п) = ind n такое, что
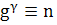(mod
k).
Определение 1.1. Характером по модулю k= ра, р>2 — простое, α≥ 1, называется конечнозначная мультипликативная периодическая функция χ(n), областью определения которой является множество целых чисел п, и такая, что
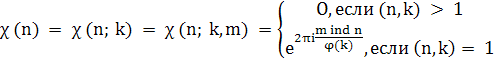
где т — целое число.
Из определения
характера видно, что функция
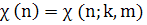зависит
от параметра т,
является
периодической по т
с
периодом φ(k),
т. е. существует, вообще говоря, φ(k)
характеров по модулю k,
которые
получаются, если брать т
равным
0, 1, ..., φ(k)
- 1.
Пусть теперь k = 2α, α≥ 3. Как известно, для любого нечетного числа п существует система индексов γ>0> = γ>0>(п) и γ>1> = γ>1>(n) по модулю k, т. е. такие числа γ>0> и γ>1 >, что
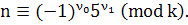
Таким образом, числа γ>0> и γ>1 >определяются с точностью до слагаемых, кратных соответственно 2 и 2α-2.
Определение
1.2. Характером
по модулю к = 2α,
α≥1,
называется
функция
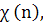областью
определения которой является множество
целых чисел п, определенная одной из
следующих формул:
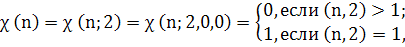
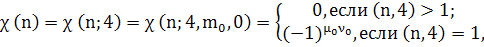
Где m>0> , m>1> целые числа.
Из определения
1.2. видно, что функция
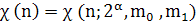зависит
от параметров т>0>
и
m>1>является
периодической по m>0>
и m>1>,
с периодами соответственно 2 и 2α-2
т. е. существует, вообще говоря, φ(k),
=< φ(kα)
характеров по модулю k
= 2α,
которые получаются, если брать m>0>
, равным 0, 1, а m>1>
равным 0, 1, ..., 2α-2
- 1.
Ввиду того, что индекс числа или система индексов числа периодические с периодом, равным модулю функции, аддитивные, т. е. индекс произведения (соответственно система индексов произведения) равняется сумме индексов сомножителей (соответственно сумме систем индексов сомножителей), получаем следующие свойства характера χ (п):
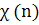по модулю
k—
периодическая
с периодом k
функция, т. е.
;
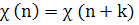2.
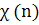—мультипликативная
функция, т. е.
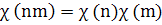
Очевидно также, что
χ(1) = 1.
L-ряды Дирихле — функции комплексного переменного, подобные дзета-функции Римана, введены Дирихле при исследовании вопроса о распределении простых чисел в арифметических прогрессиях. Везде ниже под L-рядом будем понимать L-ряд Дирихле.
Пусть k — натуральное число и χ — какой-либо характер по модулю k.
Определение 1.3. L-функцией называется ряд Дирихле вида:
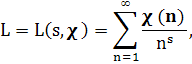
Ввиду того, что|χ(n)|≤1, следует аналитичность L(s, χ) в полуплоскости Re s>l. Для L(s, χ) имеет место аналог формулы Эйлера (эйлеровское произведение).
Лемма 1.1. При Re s > 1 справедливо равенство
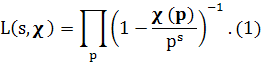
Доказательство. При X > 1 рассмотрим функцию
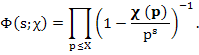
Так как Re s > 1, то
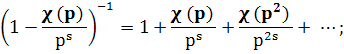
следовательно,
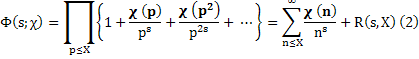
(воспользовались мультипликативностью χ(n) и однозначностью разложения натуральных чисел на простые сомножители). Далее,
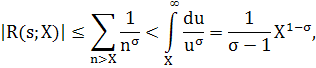
где σ=Re s>l. Переходя в (2) к пределу Х→+∞, получим утверждение леммы.
Из (1) находим
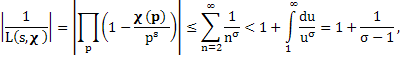
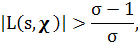
т. е. L(s, χ)≠0 при Re s>l. Если характер χ по модулю k является главным, то L(s, χ) лишь простым множителем отличается от дзета-функции ζ(s).
Лемма 1.2. Пусть χ(n) = χ> 0>(n) по модулю k. Тогда при Re s> 1
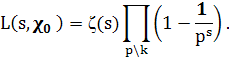
Доказательство леммы следует из (6) и определения главного характера χ>0>(n).
Следствие. L(s, χ) — аналитическая функция во всей s-плоскости, за исключением точки s = 1, где она имеет простой полюс с вычетом, равным
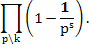
Если характер χ(n) является производным, a χ>1>(n) — примитивный характер по модулю k>1>, k>t>\k, отвечающий χ(n), то L(s, χ)лишь простым множителем отличается от L(s, χ>1>).
Лемма 1.3. Пусть χ>1>— примитивный характер по модулю k>1> и χ — индуцированный χ>1 >производный характер по модулю k, k>t> ≠ k. Тогда при Re s > 1
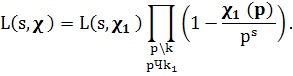
Доказательство леммы следует из (1) и свойств χ>1 >и χ.
Функцию L(s, χ) можно продолжить в полуплоскость Re s > 1
Лемма 1.4. Пусть χ≠χ>0>, тогда при Re s>0 справедливо равенство
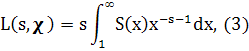
Где
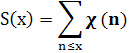
Доказательство. Пусть N ≥1, Re s>l. Применяя преобразование Абеля, будем иметь
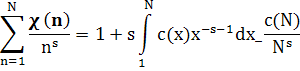
Где
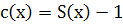
Переходя к пределу N → +∞, получим (8) при Re s>l. Но |S(x)|≤φ(k); поэтому интеграл в (3) сходится в полуплоскости Re s > 0 и определяет там аналитическую функцию, что и требовалось доказать.
§2. Функция θ(x ,χ), её функциональное уравнение
Функциональное уравнение будет получено для L(s, χ)с примитивным характером χ; тем самым и в силу леммы 3 L(s, χ) будет продолжена на всю s-плоскость при любом χ. Вид функционального уравнения зависит от того, четным или нечетным является характер χ, т. е. χ(-1)=+1 или χ(-1)=–1
Прежде чем вывести функциональное уравнение для L(s, χ) и продолжить L(s, χ) на всю s-плоскость, докажем вспомогательное утверждение, аналогичное функциональному уравнению для θ(х) (см. лемму 3, IV).
Лемма 2.1. Пусть χ — примитивный характер по модулю k. Для четного характера χ определим функцию θ (x, χ) равенством
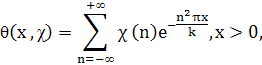
а для нечетного характера х определим функцию θ>1>(x, χ) равенством
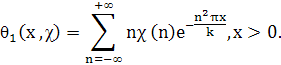
Тогда для введенных функций θ (x, χ) и θ>1>(x, χ) справедливы следующие соотношения (функциональные уравнения):
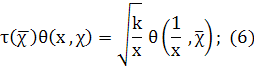
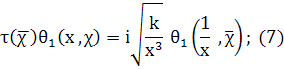
где τ(χ) — сумма Гаусса.
Доказательство. Воспользуемся доказанным в лемме 3, IV равенством
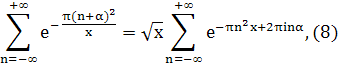
где x > 0, α — вещественное.
Имеем
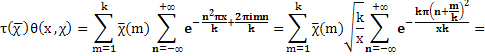
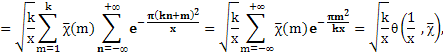
что доказывает равенство (6).
Чтобы доказать равенство (7), продифференцируем почленно (8) и заменим x на х/к, α на m/k (указанные ряды можно почленно дифференцировать, так как получающиеся после этого ряды равномерно сходятся). Получим
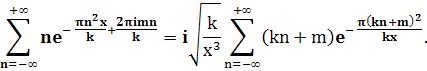
Отсюда, как и выше, выводим
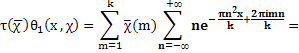
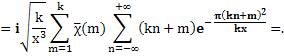
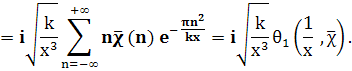
Лемма доказана.
§3. Аналитическое продолжение L-функции Дирихле на комплексную плоскость
Получим аналитическое продолжение функции L(s, χ) в область Re s >0.
Лемма 3.1.Пусть χ(n) – неглавный характер по модулю m,
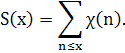
Тогда при Re s > 1 справедливо равенство
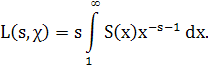
Доказательство. Пусть N≥1, Re s >1 . Применяя частное суммирование, будем иметь
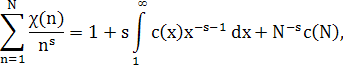
Где c(x)=S(x)-1.
Так как |c(x)|≤x
, то, переходя к пределу N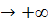
,
получим
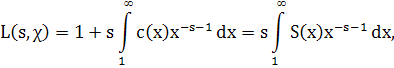
Что и требовалось доказать.
§4. Функциональное уравнение для L-функции Дирихле. Тривиальные нули L-функции Дирихле
Теорема 4.1. (функциональное уравнение). Пусть χ— примитивный характер по модулю k,
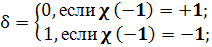
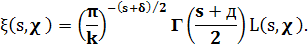
Тогда справедливо равенство
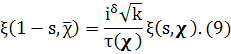
Доказательство, по—существу, повторяет вывод функционального уравнения для дзета-функции (теорема 1, IV).
Предположим, что χ(-1)=+1. Имеем
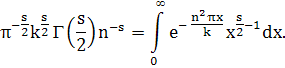
Умножая последнее равенство на χ (п) и суммируя по п, при Re s > 1 получим
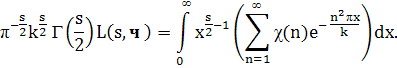
Ввиду того, что χ — четный характер, имеем
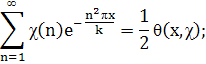
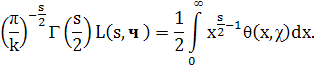
Разбивая последний интеграл на два, производя в одном из них замену переменной интегрирования (х → 1/х) и пользуясь (6), найдем
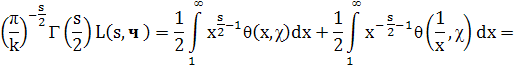
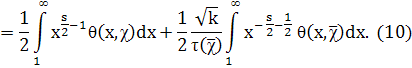
Правая часть
этого равенства является аналитической
функцией при любом s
и,
следовательно, дает аналитическое
продолжение L(s,
χ)
на
всю s-плоскость.
Так как Г(s/2)≠0,
то L(s,
χ) — регулярная всюду функция. Далее,
при замене s
на 1 — s
и χ на
,
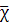правая часть (10) умножается на
,
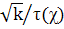так
как χ(—
1)=1 и, следовательно, τ(χ)
τ()=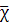
τ(χ)
=
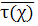k.
Отсюда
получаем утверждение теоремы при δ = 0.
Предположим, что χ(—1) = —1. Имеем
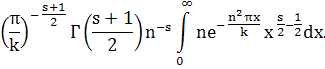
Следовательно, при Re s > 1
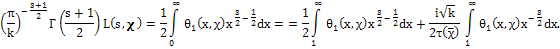
Последнее
равенство дает регулярное продолжение
L(s,
χ)
на всю s-плоскость;
правая часть его при замене s
на 1 — s
и χ на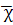
,
умножается на i
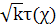ввиду
того, что
τ(χ)
τ()=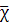
—k.
Отсюда получаем утверждение теоремы при δ = 1. Теорема доказана.
Следствие.
L(s,
χ)
—
целая
функция; если χ
(—1) = +1, то
единственными нулями L(s,
χ)
при Re
s
≤ 0
являются
полюсы Г
,
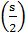т. е. точки
s
= 0,
—2, —4, ...;
если χ
(—1) = —1, то
единственными нулями L(s,
χ)
при
Re
s
≤ 0
являются
полюсы Г
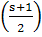т. е.
точки s
= —1, —3, —5, .. .
дирихле тривиальный вейерштрасс риман
§5. Нетривиальные нули L-функции Дирихле
Тривиальные нули L-функции Дирихле
ξ(s,
χ) — целая
функция; если χ
(—1) = +1, то
единственными нулями L(s,
χ)
при
Re
s≤0
являются
полюсы
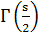,т.
е. точки
s
=0,
—2. —4, ...; если χ (—1) = —1, то единственными
нулями L(s,
χ)
при
Re
s≤0
являются
полюсы
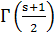т.е. точки
s
= —1,-3, -5, .. .
5.1 Теорема Вейерштрасса о разложении в произведение целых функций
Теорема 5.1. Пусть a>1>, ..., а>п>, ... — бесконечная последовательность комплексных чисел, причем
0< |a>1>| ≤ |a>1>| ≤...≤|а>n>|<...
И lim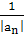
= 0.
Тогда существует целая функция G(s), которая имеет своими нулями только числа а>п> (если среди а>п> есть равные, то нуль G(s) будет иметь соответствующую кратность).
Следствие 5.1. Пусть последовательность чисел a>1>, ..., а>п>, ... удовлетворяет условиям теоремы 5.1., и, кроме того, существует целое число р > 0 такое, что сходится ряд
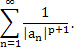
Тогда функция G>1>(s),
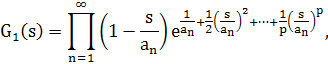
удовлетворяет теореме5. 1.
Теорема 5.2. Каждая целая функция G(s) может быть представлена в виде
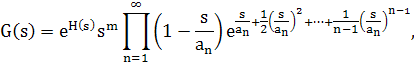
где H(s) — целая функция, а числа 0, a>1> ,a>2>, ..., а…,-— нули G(s), расположенные в порядке возрастания их модулей. Если, кроме того, последовательность а>n> , п = 1,2,..., удовлетворяет условиям следствия 5.1., то
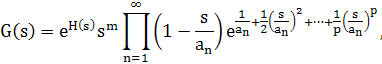
Доказательство. Нули G(s) не могут иметь предельной точки, т. е. их можно расположить в порядке возрастания модулей. По теореме 5.1. построим целую функцию G>1> (s), имеющую своими нулями нули G(s). Полагая
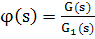при s≠a>n>,
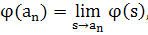
видим, что φ(s) — целая функция, нигде не равная нулю, т. е. и логарифм φ(s) — целая функция. Но тогда φ(s) = eH(s), где H(s) — целая функция. Так же доказывается второе утверждение теоремы. Теорема доказана.
Теорема 5.3. Пусть G(s)— целая функция конечного порядка α и G(0)≠0, s>n> — последовательность всех нулей G(s), причем 0 < |s>1>| ≤ |s>2>| ≤ ... ≤|s>n>|≤ ... Тогда последовательность s>n> имеет конечный показатель сходимости β≤α,
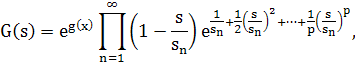
Где p≥0— наименьшее целое число, для которого
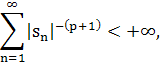
g(s)—
многочлен
степени g
≤α и α =
max
(g,
β) Если, кроме
того, для любого с >
0 найдется
бесконечная последовательность r>1>,
r>2>,
...,
r>n>,
..., r>n>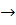
+∞, такая,
что
max
|G(s)|>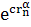
,
|s| = r>n>
, n = 1, 2, …,
то α=β
и ряд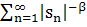
расходится.
5.2 О бесконечности целых нетривиальных нулей L-функции Дирихле
Из следствия
к теореме 4.1 видно, что функция L(s,
χ),
χ
—
примитивный характер, имеет в полуплоскости
Re
s
< 0
лишь действительные нули; эти нули
являются полюсами
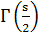или
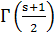называются тривиальными; тривиальным
также называется нуль s
= 0. Кроме тривиальных функция L(s,
χ)
имеет
подобно дзета-функции бесконечно много
нетривиальных нулей, лежащих в полосе
(критическая полоса) 0 ≤ Re
s
≤ 1.
Теорема 5.1.
Пусть
χ
—
примитивный
характер. Тогда функция ξ(s,
χ)
является целой функцией первого порядка,
имеющей бесконечно много нулей ρ>n>
таких,
что 0≤Re
ρ>n>
≤ 1, ρ>n>
≠0, причем
ряд
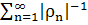расходится,
а ряд
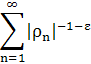
сходится при любом ε > 0. Нули ξ(s, χ) являются нетривиальными нулями L(s, χ).
Доказательство. При Re ≥1/2
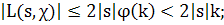
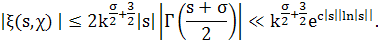
Последняя оценка |ξ(s, χ)| в силу функционального уравнения (9) из §4 и равенства
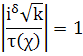
справедлива также при Re s<l/2; кроме того ξ(0, χ)≠ 0. Поскольку In Г(s) ~ s ln s при s -> +∞, по теореме 5.3 получаем первое утверждение теоремы. Так как L(s, χ)≠0 при Re s>l, то из
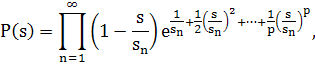
следует, что ξ(s, χ) ≠0 при Re s < 0, т. о. нули ξ(s, χ) являются нетривиальными нулями L(s, χ),лежащими в полосе 0≤Re s≤l. Теорема доказана.
§6. Обобщенная гипотеза Римана
Функция ζ(s) определена для всех комплексных s≠1 , и имеет нули для отрицательных целых s = —2, —4, —6 .... Из функционального уравнения
,
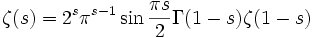и явного выражения
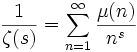
при Re
s
>1
следует, что все остальные нули, т.е.
нетривиальные, расположены в полосе
0≤Re
s
≤ 1 симметрично относительно критической
линии
.
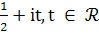Гипотеза Римана утверждает, что:
Все нетривиальные
нули дзета-функции имеют действительную
часть, равную
.
Обобщённая гипотеза Римана состоит из того же самого утверждения для обобщений дзета-функций, то есть L-функций Дирихле
Библиографический список
А.Л. Карацуба, Основы аналитической теории чисел // 2-е над.— М.: Наука. Главная редакция физико-математической литературы, 1983. -240 с.
С.М. Воронин, А.А. Карацуба, Дзета-функция Римана // М.: Физматлит. 1994. -376с.