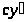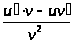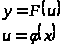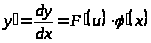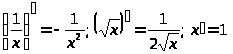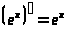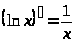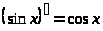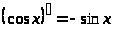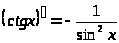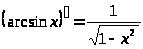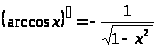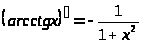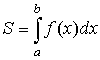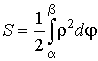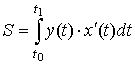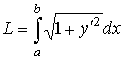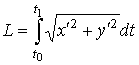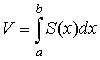Математический анализ. Практикум
Математический анализ.
Практикум.
Для студентов ВУЗов по специальности:
«Государственное и муниципальное управление»
Т.З. Павлова
Колпашево 2008
Глава 1. Введение в анализ
1.1 Функции. Общие свойства
1.2 Теория пределов
1.3 Непрерывность функции
Глава 2. Дифференциальное исчисление
2.1 Определение производной
2.2 Основные правила дифференцирования
2.3 Производные высших порядков
2.4 Исследование функций
2.4.1 План полного исследования функции
2.4.2 Примеры исследования функции
2.4.3. Наибольшее и наименьшее значение функции на отрезке
2.5 Правило Лопиталя
Глава 3. Интегрально исчисление
3.1 Неопределенный интеграл
3.1.1 Определения и свойства
3.1.2 Таблица интегралов
3.1.3 Основные методы интегрирования
3.2 Определенный интеграл
3.2.1 Понятие определенного интеграла и его свойства
3.2.2 Методы вычисления определенного интеграла
3.2.3 Приложения определенного интеграла
Глава 4. Функции нескольких переменных
4.1 Основные понятия
4.2 Пределы и непрерывность функций нескольких переменных
4.3 Производные и дифференциалы функций нескольких переменных
4.3.1 Частные производные первого порядка
4.3.2 Частные производные второго порядка
4.3.3 Полный дифференциал и его применение к приближенным вычислениям
4.3.4 Дифференцирование неявной функции
Глава 5. Классические методы оптимизации
5.2 Глобальный экстремум (наибольшее и наименьшее значение функции)
Глава 6. Модель потребительского выбора
6.1 Функция полезности.
6.2 Линии безразличия
6.3 Бюджетное множество
6.4 Теория потребительского спроса
Задания для домашней контрольной работы
Литература
Глава 1. Введение в анализ
1.1 Функции. Общие свойства
Числовая функция определена на
множестве D действительных чисел, если
каждому значению переменной
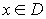 поставлено
в соответствие некоторое вполне
определенное действительное значение
переменной y, где D – область определения
функции.
поставлено
в соответствие некоторое вполне
определенное действительное значение
переменной y, где D – область определения
функции.
Аналитическое представление функции:
в явном виде:
 ;
;
в неявном виде:
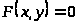 ;
;
в параметрической форме: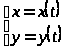
разными формулами в области
определения
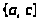 :
:

Свойства.
Четная функция:
 .
Например, функция
.
Например, функция
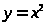 – четная, т.к.
– четная, т.к.
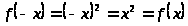 .
.
Нечетная функция:
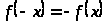 .
Например, функция
.
Например, функция
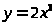 – нечетная, т.к.
– нечетная, т.к.
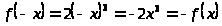 .
.
Периодическая функция:
 ,
где T – период функции,
,
где T – период функции,
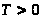 .
Например, тригонометрические функции.
.
Например, тригонометрические функции.
Монотонная функция. Если для
любых
 из области определения
из области определения
 – функция возрастающая,
– функция возрастающая,
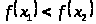 – убывающая. Например,
– убывающая. Например,
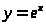 – возрастающая, а
– возрастающая, а
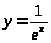 –
убывающая.
–
убывающая.
Ограниченная функция. Если
существует такое число M,
что
 .
Например, функции
.
Например, функции
 и
и
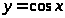 ,
т.к.
,
т.к.
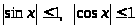 .
.
Пример 1. Найти область определения функций.



 + 2 – 3 +
+ 2 – 3 +

1.2 Теория пределов
Определение 1.
Пределом функции
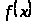 при
при
 называется число b, если для любого
называется число b, если для любого
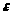 (
(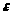 – сколь угодно малое положительное
число) можно найти такое значение
аргумента
– сколь угодно малое положительное
число) можно найти такое значение
аргумента
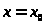 ,
начиная с которого выполняется неравенство
,
начиная с которого выполняется неравенство
 .
.
Обозначение:
 .
.
Определение 2.
Пределом функции
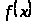 при
при
 называется число b, если для любого
называется число b, если для любого
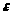 (
(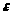 - сколь угодно малое положительное
число) существует такое положительное
число
- сколь угодно малое положительное
число) существует такое положительное
число
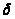 ,
что для всех значений x, удовлетворяющих
неравенству
,
что для всех значений x, удовлетворяющих
неравенству
 выполняется неравенство
выполняется неравенство
 .
.
Обозначение:
 .
.
Определение 3.
Функция
 называется бесконечно малой при
называется бесконечно малой при
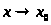 или
или
 ,
если
,
если
 или
или
 .
.
Свойства.
Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Произведение бесконечно малой величины на ограниченную функцию (постоянную, другую бесконечно малую величину) есть величина бесконечно малая.
Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Определение 4.
Функция
 называется бесконечно большой при
называется бесконечно большой при
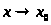 ,
если
,
если
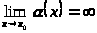 .
.
Свойства.
Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Теорема. (Связь
между бесконечно малой величиной и
бесконечно большой величиной.) Если
функция
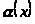 бесконечно малая при
бесконечно малая при
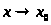 (
( ),
то функция
),
то функция
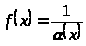 является бесконечно большой величиной
при
является бесконечно большой величиной
при
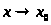 (
( ).
И, обратно, если функция
).
И, обратно, если функция
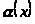 бесконечно большая при
бесконечно большая при
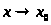 (
( ),
то функция
),
то функция
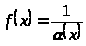 является бесконечно малой величиной
при
является бесконечно малой величиной
при
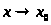 (
( ).
).
Теоремы о пределах.
Функция не может иметь более одного предела.
Предел алгебраической суммы нескольких функций равен алгебраической сумме пределов этих функций:
 .
.
Предел произведения нескольких функций равен произведению пределов этих функций:
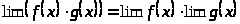
Предел степени равен степени предела:
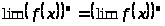
Предел частного равен частному пределов, если предел делителя существует:
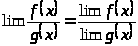 .
.
Первый замечательный предел.
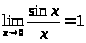 .
.
Следствия:

Второй замечательный предел:

Следствия:
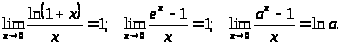
Эквивалентные бесконечно малые
величины при
 :
:
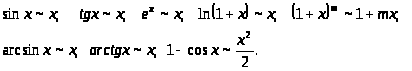
Вычисление пределов.
При вычислении пределов используют основные теоремы о пределах, свойства непрерывных функций и правила, вытекающие из этих теорем и свойств.
Правило 1. Чтобы
найти предел в точке
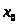 функции, непрерывной в этой точке, надо
в функцию, стоящую под знаком предела,
вместо аргумента x
подставить его предельное значение
функции, непрерывной в этой точке, надо
в функцию, стоящую под знаком предела,
вместо аргумента x
подставить его предельное значение
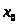 .
.
Пример 2. Найти

Правило 2. Если
при отыскании предела дроби предел
знаменателя равен нулю, а предел числителя
отличен от нуля, то предел такой функции
равен
 .
.
Пример 3. Найти
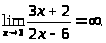
Правило 3. Если
при отыскании предела дроби предел
знаменателя равен
 ,
а предел числителя отличен от нуля, то
предел такой функции равен нулю.
,
а предел числителя отличен от нуля, то
предел такой функции равен нулю.
Пример 4. Найти
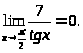
Часто подстановка предельного значения аргумента приводит к неопределенным выражениям вида
 .
.
Нахождение предела функции в этих случаях называется раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразование данного выражения. Для раскрытия неопределенностей используют различные приемы.
Правило 4.
Неопределенность вида
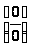 раскрывается путем преобразования
подпредельной функции т.о., чтобы в
числителе и знаменателе выделить
множитель, предел которого равен нулю,
и, сократив на него дробь, найти предел
частного. Для этого числитель и знаменатель
либо раскладывают на множители, либо
домножают на сопряженные числителю и
знаменателю выражения.
раскрывается путем преобразования
подпредельной функции т.о., чтобы в
числителе и знаменателе выделить
множитель, предел которого равен нулю,
и, сократив на него дробь, найти предел
частного. Для этого числитель и знаменатель
либо раскладывают на множители, либо
домножают на сопряженные числителю и
знаменателю выражения.
Пример 5.
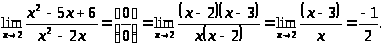
Пример 6.
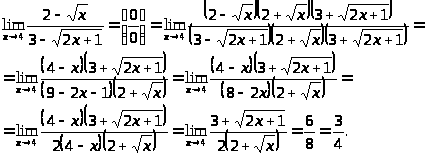
Правило 5. Если
подпредельное выражение содержит
тригонометрические функции, тогда,
чтобы раскрыть неопределенность вида
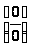 используют первый замечательный предел.
используют первый замечательный предел.
Пример 7.

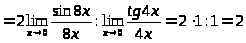 .
.
Пример 8.
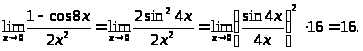
Правило 6. Чтобы
раскрыть неопределенность вида
 при
при
 ,
числитель и знаменатель подпредельной
дроби необходимо разделить на высшую
степень аргумента и находить далее
предел частного.
,
числитель и знаменатель подпредельной
дроби необходимо разделить на высшую
степень аргумента и находить далее
предел частного.
Возможны результаты:
искомый предел равен отношению коэффициентов при старших степенях аргумента числителя и знаменателя, если эти степени одинаковы;
предел равен бесконечности, если степень аргумента числителя выше степени аргумента знаменателя;
предел равен нулю, если степень аргумента числителя ниже степени аргумента знаменателя.
Пример 9.
а)

т.к.
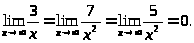
Степени равны, значит, предел
равен отношению коэффициентов при
старших степенях, т.е.
 .
.
б)
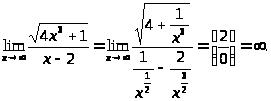
Степень числителя
 ,
знаменателя – 1, значит, предел равен
,
знаменателя – 1, значит, предел равен

в)
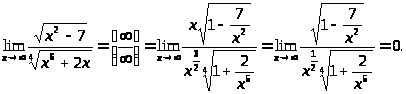
Степень числителя 1, знаменателя
–
 ,
значит, предел равен 0.
,
значит, предел равен 0.
Правило 7. Чтобы
раскрыть неопределенность вида
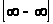 ,
числитель и знаменатель подпредельной
дроби необходимо домножить на сопряженное
выражение.
,
числитель и знаменатель подпредельной
дроби необходимо домножить на сопряженное
выражение.
Пример 10.


Правило 8. Чтобы
раскрыть неопределенность вида
 используют второй замечательный предел
и его следствия.
используют второй замечательный предел
и его следствия.
Можно доказать, что

Пример 11.

Пример 12.

Пример 13.
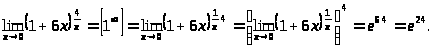
Правило 9. При раскрытии неопределенностей, подпредельная функция которых содержит б.м.в., необходимо заменить пределы этих б.м. на пределы б.м., эквивалентных им.
Пример 14.
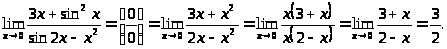
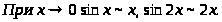
Пример 15.
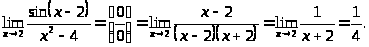

Правило 10. Правило Лопиталя (см. 2.6).
1.3 Непрерывность функции
Функция
 непрерывна в точке
непрерывна в точке
 ,
если предел функции при стремлении
аргумента к a, существует и равен значению
функции в этой точке.
,
если предел функции при стремлении
аргумента к a, существует и равен значению
функции в этой точке.
Эквивалентные условия:
 ;
;


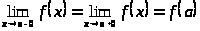
Классификация точек разрыва:
разрыв I рода
- устранимый – односторонние пределы существуют и равны;
- неустранимый (скачок) – односторонние пределы не равны;
разрыв II рода: предел функции в точке не существует.
Пример 16. Установить характер
разрыва функции
 в точке
в точке
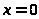 или доказать непрерывность функции в
этой точке.
или доказать непрерывность функции в
этой точке.
а)
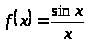
при
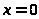 функция не определена, следовательно,
она не непрерывна в этой точке. Т.к.
функция не определена, следовательно,
она не непрерывна в этой точке. Т.к.
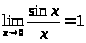 и,
соответственно,
и,
соответственно,
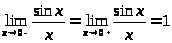 ,
то
,
то
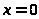 – точка устранимого разрыва первого
рода.
– точка устранимого разрыва первого
рода.
б)
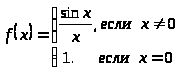
по сравнению с заданием (а) функция
доопределена в точке
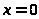 так, что
так, что
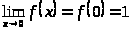 ,
значит, данная функция непрерывна в
данной точке.
,
значит, данная функция непрерывна в
данной точке.
в)

При
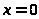 функция не определена;
функция не определена;
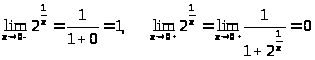 .
.
Т.к. один из односторонних пределов
бесконечен, то
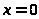 – точка разрыва второго рода.
– точка разрыва второго рода.
Глава 2. Дифференциальное исчисление
2.1 Определение производной
Определение производной
Производная
 или
или
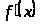 от данной функции
от данной функции
 есть предел отношения приращения функции
к соответствующему приращению аргумента,
когда приращение аргумента стремится
к нулю:
есть предел отношения приращения функции
к соответствующему приращению аргумента,
когда приращение аргумента стремится
к нулю:
 или
или
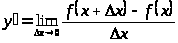 .
.
Механический смысл производной – скорость изменения функции. Геометрический смысл производной – тангенс угла наклона касательной к графику функции:
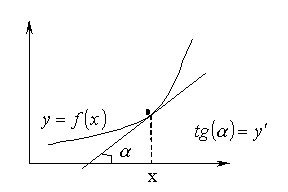
2.2 Основные правила дифференцирования
|
Наименование |
Функция |
Производная |
|
Умножение на постоянный множитель |
|
|
|
Алгебраическая сумма двух функций |
|
|
|
Произведение двух функций |
|
|
|
Частное двух функций |
|
|
|
Сложная функция |
|
|
Производные основных элементарных функций
|
№ п/п |
Наименование функции |
Функция и её производная |
|
1 |
константа |
|
|
2 |
степенная функция частные случаи |
|
|
3 |
показательная функция частный случай |
|
|
4 |
логарифмическая функция частный случай |
|
|
5 |
тригонометрические функции |
|
|
6 |
обратные тригонометрические функции |
|
Пример 17
а)

б)
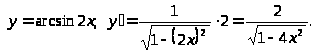
в)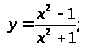

2.3 Производные высших порядков
Производная второго порядка
функции

Производная второго порядка
функции
 :
:

Пример 18.
а) Найти производную второго
порядка функции
 .
.
Решение. Найдем сначала производную
первого порядка
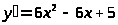 .
.
От производной первого порядка
возьмем еще раз производную
 .
.
Пример 19. Найти производную
третьего порядка функции
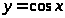 .
.
Решение.
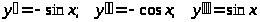 .
.
2.4 Исследование функций
2.4.1 План полного исследования функции:
План полного исследования функции:
Элементарное исследование:
- найти область определения и область значений;
- выяснить общие свойства: четность (нечетность), периодичность;
- найти точки пересечения с осями координат;
- определить участки знакопостоянства.
2. Асимптоты:
- найти вертикальные асимптоты
 ,
если
,
если
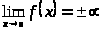 ;
;
- найти наклонные асимптоты:
 .
.
Если
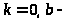 любое число, то
любое число, то
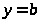 –
горизонтальные асимптоты.
–
горизонтальные асимптоты.
3. Исследование с помощью
 :
:
- найти критические точки, те.
точки в которых
 или не существует;
или не существует;
- определить интервалы возрастания,
те. промежутки, на которых
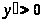 и
убывания функции –
и
убывания функции –
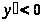 ;
;
- определить экстремумы: точки,
при переходе через которые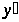 меняет знак с «+» на «–», являются точками
максимума, с «–» на «+» – минимума.
меняет знак с «+» на «–», являются точками
максимума, с «–» на «+» – минимума.
4. Исследование с помощью
 :
:
- найти точки, в которых
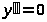 или не существует;
или не существует;
- найти участки выпуклости, т.е.
промежутки, на которых
 и вогнутости –
и вогнутости –
 ;
;
- найти точки перегиба, т.е. точки
при переходе через которые
 меняет знак.
меняет знак.
5. Построение графика функции.
Рекомендации по применению плана исследования функции:
Отдельные элементы исследования наносятся на график постепенно, по мере их нахождения.
Если появляются затруднения с построением графика функции, то находятся значения функции в некоторых дополнительных точках.
Целью исследования является описание характера поведения функции. Поэтому строится не точный график, а его приближение, на котором четко обозначены найденные элементы (экстремумы, точки перегиба, асимптоты и т.д.).
Строго придерживаться приведенного плана необязательно; важно не упустить характерные элементы поведения функции.
2.4.2 Примеры исследования функции:
20.
 .
.
1)

2) Функция нечетная:
 .
.
3) Асимптоты.
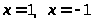 – вертикальные асимптоты, т.к.
– вертикальные асимптоты, т.к.

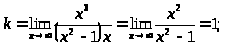

Наклонная асимптота
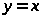 .
.
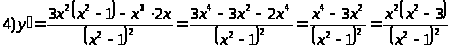
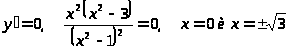
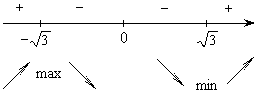
5)
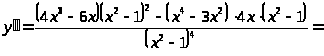


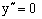

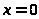 – точка перегиба.
– точка перегиба.
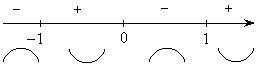
Схематичный график данной функции:

21.
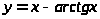
1)

2) Функция нечетная:

3) Асимптоты: Вертикальных асимптот нет.
Наклонные:
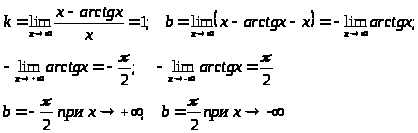
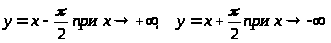 –
наклонные асимптоты
–
наклонные асимптоты
4)
 – функция возрастает.
– функция возрастает.
5)
 ,
,
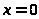 – точка перегиба.
– точка перегиба.
Схематичный график данной функции:

22.
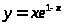
1)
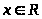
2) Функция общего вида
3) Асимптоты
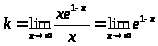
 – наклонных асимптот нет
– наклонных асимптот нет
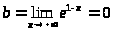
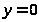 – горизонтальная асимптота при
– горизонтальная асимптота при

4)
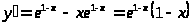

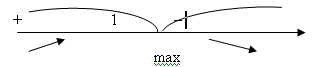

 – точка перегиба
– точка перегиба
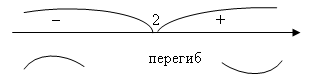
Схематичный график данной функции:
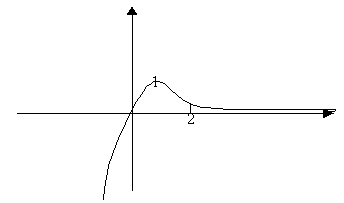
23.

1)
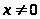
2) Асимптоты.
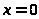 – вертикальная асимптота, т.к.
– вертикальная асимптота, т.к.
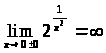
 – наклонных асимптот нет
– наклонных асимптот нет
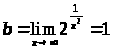 ,
,
 – горизонтальная асимптота
– горизонтальная асимптота
Схематичный график данной функции:
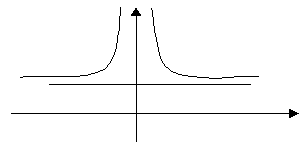
24.
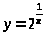
1)
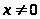
2) Асимптоты
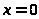 – вертикальная асимптота при
– вертикальная асимптота при
 ,
т.к.
,
т.к.
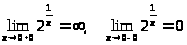
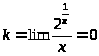 – наклонных асимптот нет
– наклонных асимптот нет
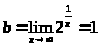 ,
,
 – горизонтальная асимптота
– горизонтальная асимптота
3)
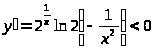 – функция убывает на каждом из промежутков.
– функция убывает на каждом из промежутков.
Схематичный график данной функции:
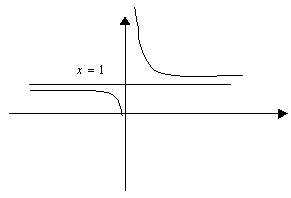
2.4.3 Наибольшее и наименьшее значение функции на отрезке
Чтобы найти наибольшее и наименьшее значение функции на отрезке можно воспользоваться схемой:
Найти
производную функции
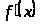 .
.
Найти
критические точки функции, в которых
 или не существует.
или не существует.
Найти
значение функции в критических точках,
принадлежащих заданному отрезку и на
его концах и выбрать из них наибольшее
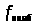 и наименьшее
и наименьшее
 .
.
Пример. Найти наименьшее и наибольшее значение функции на данном отрезке.
25.
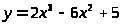 на промежутке
на промежутке
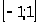
1)

2)
 – критические точки
– критические точки
3)
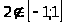 ,
,
 –
–

 –
–
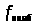
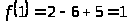
26.
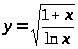 на промежутке
на промежутке
 .
.

Производная не существует при
 ,
но 1 не принадлежит данному промежутку.
Функция
,
но 1 не принадлежит данному промежутку.
Функция
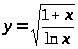 убывает на промежутке
убывает на промежутке
 ,
значит, наибольшего значения нет, а
наименьшее значение
,
значит, наибольшего значения нет, а
наименьшее значение
 .
.
2.5 Правило Лопиталя
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Т.е. при раскрытии неопределенностей
вида
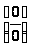 или
или
 можно использовать формулу:
можно использовать формулу:
 .
.
Примеры.
27.
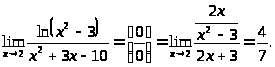
28.
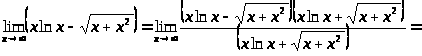

Глава 3. Интегрально исчисление
3.1 Неопределенный интеграл
3.1.1 Определения и свойства
Определение 1. Функция
 называется первообразной для
называется первообразной для
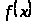 ,
если
,
если
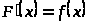 .
.
Определение 2. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.
Обозначение:
 ,
где c
- произвольная постоянная.
,
где c
- произвольная постоянная.
Свойства неопределенного интеграла
Производная неопределенного
интеграла:
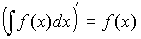
Дифференциал неопределенного
интеграла:

Неопределенный интеграл от
дифференциала:
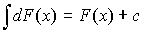
Неопределенный интеграл от суммы (разности) двух функций:
 ;
;
Вынесение постоянного множителя за знак неопределенного интеграла:
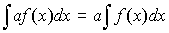
3.1.2 Таблица интегралов

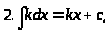

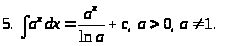
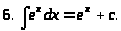
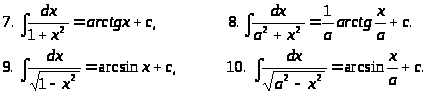

3.1.3 Основные методы интегрирования
Использование свойств неопределенного интеграла.
Пример 29.

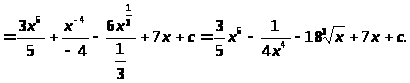
Подведение под знак дифференциала.
Пример 30.

Метод замены переменной:
а) замена
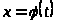 в интеграле
в интеграле
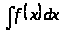 :
:
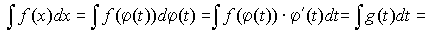
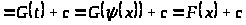 ,
,
где
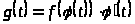 - функция, интегрируемая легче, чем
исходная;
- функция, интегрируемая легче, чем
исходная;
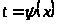 -
функция, обратная функции
-
функция, обратная функции
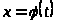 ;
;
 -
первообразная функции
-
первообразная функции
 .
.
Пример 31.
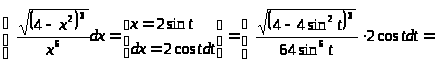
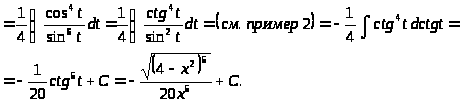
б) замена
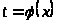 в интеграле вида:
в интеграле вида:
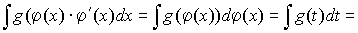
 ;
;
Пример 32.
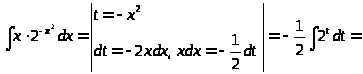
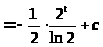
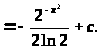
Пример 33.

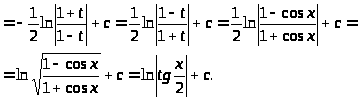
Метод интегрирования по частям:

Пример 34.


Пример 35.
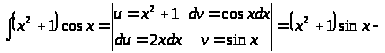

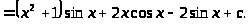
Возьмем отдельно интеграл
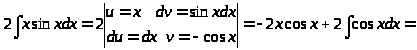

Вернемся к нашему интегралу:


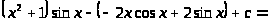
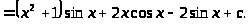
3.2 Определенный интеграл
3.2.1 Понятие определенного интеграла и его свойства
Определение. Пусть
на некотором интервале
 задана непрерывная функция
задана непрерывная функция
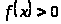 .
Построим ее график.
.
Построим ее график.
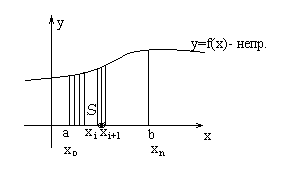
Фигура, ограниченная сверху
кривой
 ,
слева и справа прямыми
,
слева и справа прямыми
 и снизу отрезком оси абсцисс между
точками a
и b,
называется криволинейной трапецией.
и снизу отрезком оси абсцисс между
точками a
и b,
называется криволинейной трапецией.
S – область – криволинейная трапеция.
Разделим интервал точками
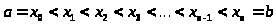 и получим:
и получим:

Интегральная сумма:
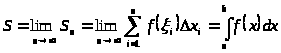

Определение. Определенным интегралом называется предел интегральной суммы.
Свойства определенного интеграла:
Постоянный множитель можно выносить за знак интеграла:
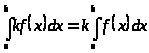
Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов этих функций:

Если отрезок интегрирования
разбит на части, то интеграл на всем
отрезке равен сумме интегралов для
каждой из возникших частей, т.е. при
любых a,
b,
c
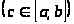 :
:
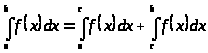
Если
на отрезке

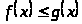 ,
то и
,
то и


Пределы интегрирования можно менять местами, при этом меняется знак интеграла:
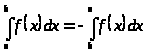
Интеграл в точке равен 0:
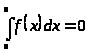
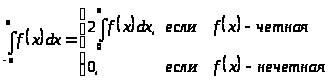
(“о среднем”) Пусть y = f(x) –
функция, интегрируемая на [a,b]. Тогда
 ,
где
,
где
 ,
f(c) – среднее
значение f(x) на
[a,b]:
,
f(c) – среднее
значение f(x) на
[a,b]:

Формула Ньютона-Лейбница
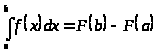 ,
,
где F(x) – первообразная для f(x).
3.2.2 Методы вычисления определенного интеграла.
Непосредственное интегрирование
Пример 35.
а)

б)
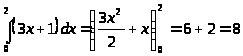
в)
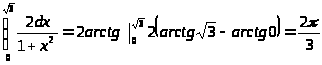
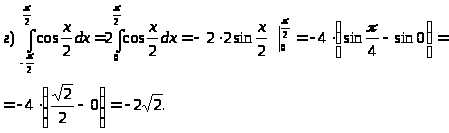
д)
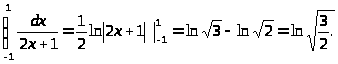
2. Замена переменных под знаком определенного интеграла.
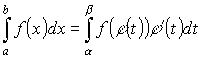

Пример 36.
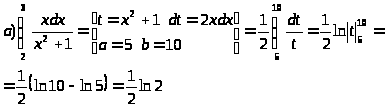
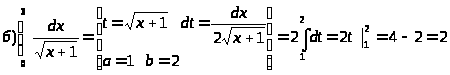
Интегрирование по частям в определенном интеграле.
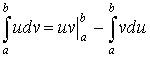
Пример 37.
а)
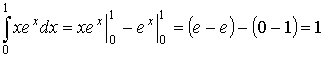
б)
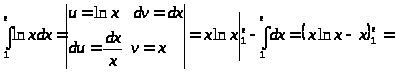
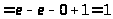
в)
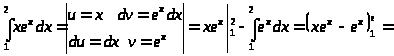



д)
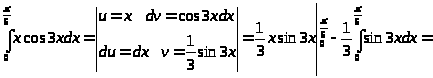
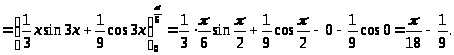
3.2.3 Приложения определенного интеграла
|
Характеристика |
Вид функции |
Формула |
|
площадь криволинейной трапеции |
в декартовых координатах |
|
|
площадь криволинейного сектора |
в полярных координатах |
|
|
площадь криволинейной трапеции |
в параметрической форме |
|
|
длина дуги кривой |
в декартовых координатах |
|
|
длина дуги кривой |
в полярных координатах |
|
|
длина дуги кривой |
в параметрической форме |
|
|
объём тела вращения |
в декартовых координатах |
|
|
объём тела с заданным поперечным сечением |
|
|
Пример 38. Вычислить площадь
фигуры, ограниченной линиями:
 и
и
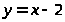 .
.
Решение: Найдем
точки пересечения графиков данных
функций. Для этого приравняем функции
и решим уравнение

Итак, точки пересечения
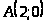 и
и
 .
.

Площадь фигуры найдем, используя формулу
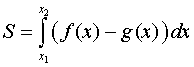 .
.
В нашем случае
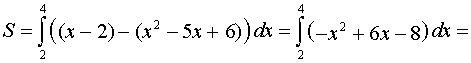
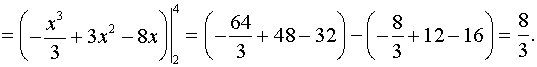
Ответ: площадь равна
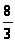 (квадратных единиц).
(квадратных единиц).
Глава 4. Функции нескольких переменных
4.1 Основные понятия
Определение. Если каждой паре
независимых друг от друга чисел
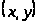 из некоторого множества по какому-либо
правилу ставится в соответствие одно
или несколько значений переменной z,
то переменная z
называется функцией двух переменных.
из некоторого множества по какому-либо
правилу ставится в соответствие одно
или несколько значений переменной z,
то переменная z
называется функцией двух переменных.
Определение. Областью определения
функции z
называется совокупность пар
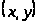 ,
при которых функция z
существует.
,
при которых функция z
существует.
Область определения функции
двух переменных
 представляет собой некоторое множество
точек на координатной плоскости Oxy.
Координата z
называется аппликатой, и тогда сама
функция изображается в виде некоторой
поверхности в пространстве E3.
Например:
представляет собой некоторое множество
точек на координатной плоскости Oxy.
Координата z
называется аппликатой, и тогда сама
функция изображается в виде некоторой
поверхности в пространстве E3.
Например:
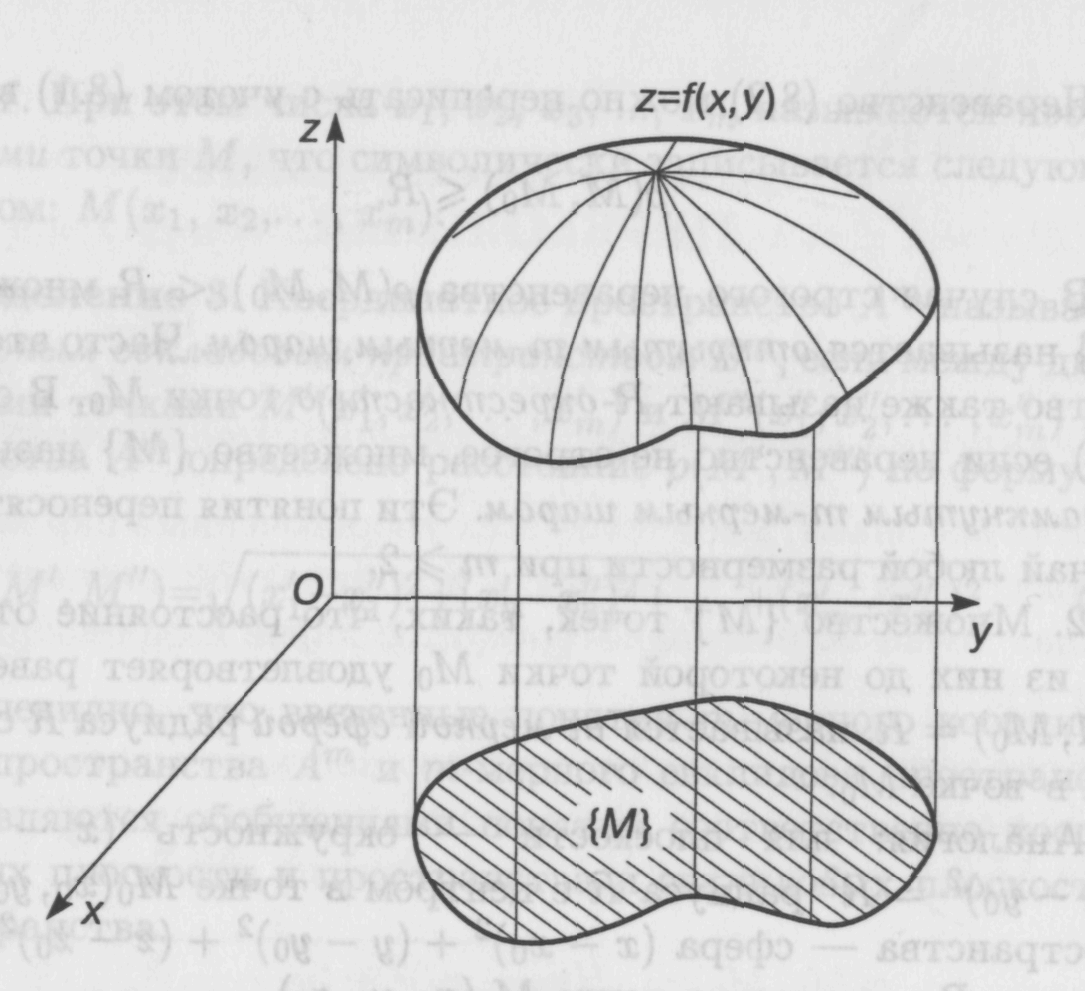
Рис.1
Пример 39. Найти область определения функции.
а)
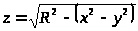
Выражение, стоящее в правой части
имеет смысл только при
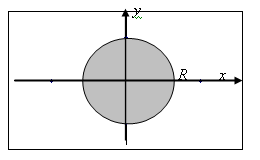
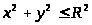 .
Значит, область определения данной
функции есть совокупность всех точек,
лежащих внутри и на границе круга радиуса
R с
центром в начале координат.
.
Значит, область определения данной
функции есть совокупность всех точек,
лежащих внутри и на границе круга радиуса
R с
центром в начале координат.
б)
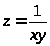 .
.
Область определения данной
функции – все точки плоскости
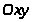 ,
кроме точек прямых
,
кроме точек прямых
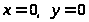 ,
т.е. осей координат.
,
т.е. осей координат.
Определение. Линии уровня функции
 – это семейство кривых на координатной
плоскости
– это семейство кривых на координатной
плоскости
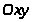 ,
описываемое уравнениями вида
,
описываемое уравнениями вида

 .
.
Пример 40. Найти линии уровня
функции
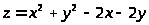 .
.
Решение. Линии уровня данной
функции – это семейство кривых на
плоскости
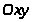 ,
описываемое уравнением
,
описываемое уравнением
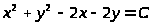 ,
или
,
или
 .
.
Последнее уравнение описывает
семейство окружностей с центром в точке
О>1>(1, 1) радиуса
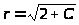 .
Поверхность вращения (параболоид),
описываемая данной функцией, становится
«круче» по мере ее удаления от оси,
которая задается уравнениями x
= 1, y
= 1. (Рис. 4)
.
Поверхность вращения (параболоид),
описываемая данной функцией, становится
«круче» по мере ее удаления от оси,
которая задается уравнениями x
= 1, y
= 1. (Рис. 4)
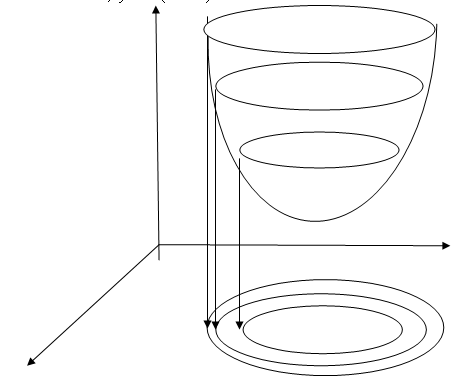
Рис.4
4.2 Пределы и непрерывность функций нескольких переменных.
1. Пределы.
Определение. Число A
называется пределом функции
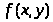 при стремлении точки
при стремлении точки
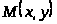 к точке
к точке
 ,
если для каждого сколь угодно малого
числа
,
если для каждого сколь угодно малого
числа
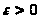 найдется такое число
найдется такое число
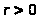 ,
что для любой точки
,
что для любой точки
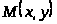 верно условие
верно условие
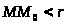 ,
также верно условие
,
также верно условие
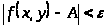 .
Записывают:
.
Записывают:
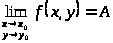 .
.
Пример 41. Найти пределы:
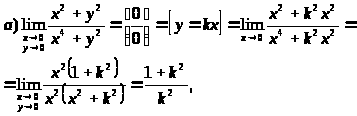
т.е. предел зависит от
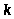 ,
а, значит, он не существует.
,
а, значит, он не существует.
2. Непрерывность.
Определение. Пусть точка
 принадлежит области определения функции
принадлежит области определения функции
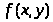 .
Тогда функция
.
Тогда функция
 называется непрерывной в точке
называется непрерывной в точке
 ,
если
,
если
 (1)
(1)
причем точка
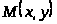 стремится к точке
стремится к точке
 произвольным образом.
произвольным образом.
Если в какой-либо точке условие
(1) не выполняется, то эта точка называется
точкой разрыва функции
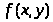 .
Это может быть в следующих случаях:
.
Это может быть в следующих случаях:
Функция
 не определена в точке
не определена в точке
 .
.
Не существует предел
 .
.
Этот предел существует, но он
не равен
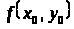 .
.
Пример 42. Определить, является
ли данная функция
 непрерывной
в точке
непрерывной
в точке
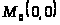 ,
если
,
если
 .
.
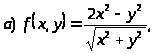

Получили, что
 значит, данная функция непрерывна в
точке
значит, данная функция непрерывна в
точке
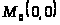 .
.
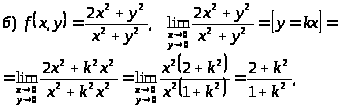
предел зависит от k, т.е. он в данной точке не существует, а значит, функция имеет в этой точке разрыв.
4.3 Производные и дифференциалы функций нескольких переменных
4.3.1 Частные производные первого порядка
Частная производная функции
 по
аргументу x
является обыкновенной производной
функции одной переменной x
при фиксированном значении переменной
y и
обозначается:
по
аргументу x
является обыкновенной производной
функции одной переменной x
при фиксированном значении переменной
y и
обозначается:

Частная производная функции
 по
аргументу y
является обыкновенной производной
функции одной переменной y
при фиксированном значении переменной
x и
обозначается:
по
аргументу y
является обыкновенной производной
функции одной переменной y
при фиксированном значении переменной
x и
обозначается:

Пример 43. Найти частные производные функций.
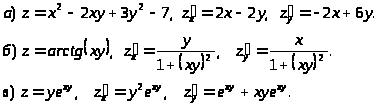
4.3.2 Частные производные второго порядка
Частные производные второго
порядка – это частные производные от
частных производных первого порядка.
Для функции двух переменных вида
 возможны четыре вида частных производных
второго порядка:
возможны четыре вида частных производных
второго порядка:
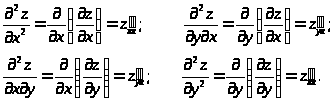
Частные производные второго порядка, в которых дифференцирование производится по разным переменным, называют смешанными производными. Смешанные производные второго порядка дважды дифференцируемой функции равны.
Пример 44. Найти частные производные второго порядка.
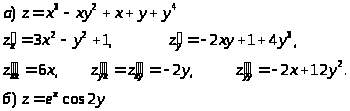
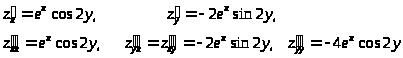
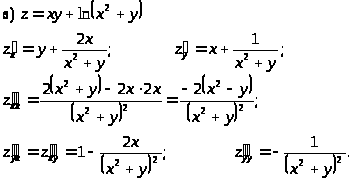
4.3.3 Полный дифференциал и его применение к приближенным вычислениям.
Определение. Дифференциал первого
порядка функции двух переменных
 находится по формуле
находится по формуле
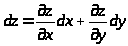 .
.
Пример 45. Найти полный дифференциал
для функции
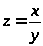 .
.
Решение. Найдем частные производные:
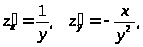
тогда
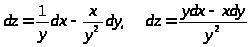 .
.
При малых приращениях аргументов
x и
y
функция
 получает
приращение
получает
приращение
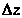 ,
приблизительно равное dz,
т.е.
,
приблизительно равное dz,
т.е.
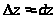 .
.
Формула для нахождения приближенного
значения функции
 в точке
в точке
 ,
если известно ее точное значение в точке
,
если известно ее точное значение в точке
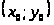 :
:
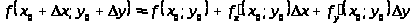 .
.
Пример 46. Найти
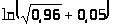 .
.
Решение. Пусть
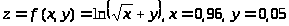 ,
,
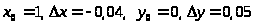 .
.
Тогда используем формулу
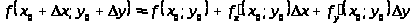 .
.
Получим:
 .
.

Ответ.
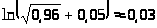 .
.
Пример 47. Вычислить приближенно
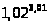 .
.
Решение. Рассмотрим функцию
 .
Имеем
.
Имеем

Ответ.
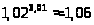 .
.
Пример 48. Вычислить приближенно
 .
.
Решение. Рассмотрим функцию
 .
Получим:
.
Получим:

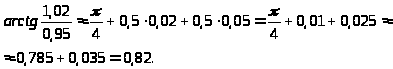
Ответ.
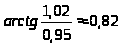 .
.
4.3.4 Дифференцирование неявной функции
Определение. Функция
 называется неявной, если она задается
уравнением
называется неявной, если она задается
уравнением
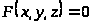 ,
не разрешимым относительно z.
,
не разрешимым относительно z.
Частные производные такой функции находятся по формулам:
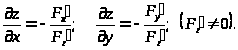
Пример 49. Найти частные производные
функции z,
заданной уравнением
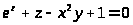 .
.
Решение.
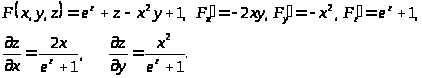
Определение. Функция
 называется
неявной, если она задается уравнением
называется
неявной, если она задается уравнением
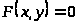 ,
не разрешимым относительно y.
,
не разрешимым относительно y.
Производная такой функции находится по формуле:
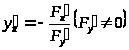 .
.
Пример 50. Найти производные данных функций.
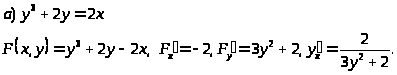

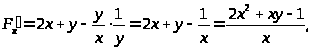
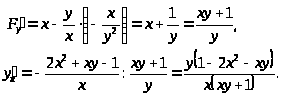
Глава 5. Классические методы оптимизации
5.1 Локальный экстремум функции нескольких переменных
Определение 1. Функция
 имеет максимум в точке
имеет максимум в точке
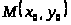 ,
если
,
если
 для всех точек
для всех точек
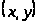 достаточно близких к точке
достаточно близких к точке
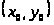 и отличных от нее.
и отличных от нее.
Определение 2. Функция
 имеет минимум в точке
имеет минимум в точке
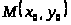 ,
если
,
если
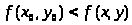 для всех точек
для всех точек
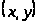 достаточно близких к точке
достаточно близких к точке
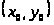 и отличных от нее.
и отличных от нее.
Необходимое условие экстремума.
Если функция
 достигает
экстремума в точке
достигает
экстремума в точке
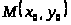 ,
то частные производные от функции
,
то частные производные от функции
 обращаются в нуль или не существуют в
этой точке.
обращаются в нуль или не существуют в
этой точке.
Точки, в которых частные производные обращаются в нуль или не существуют, называются критическими.
Достаточный признак экстремума.
Пусть функция
 определена
в некоторой окрестности критической
точки
определена
в некоторой окрестности критической
точки
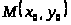 и имеет в этой точке непрерывные частные
производные второго порядка
и имеет в этой точке непрерывные частные
производные второго порядка

Тогда
1)
 имеет локальный максимум в точке
имеет локальный максимум в точке
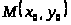 ,
если
,
если
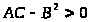 и
и
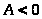 ;
;
2)
 имеет локальный минимум в точке
имеет локальный минимум в точке
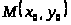 ,
если
,
если
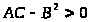 и
и
 ;
;
3)
 не имеет локального экстремума в точке
не имеет локального экстремума в точке
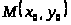 ,
если
,
если
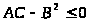 ;
;
Схема исследования на экстремум функции двух переменных.
Найти частные производные
функции
 :
: и
и
 .
.
Решить систему уравнений
 ,
,
 и найти критические точки функции.
и найти критические точки функции.
Найти частные производные второго порядка, вычислить их значения в критических точках и с помощью достаточного условия сделать вывод о наличии экстремумов.
Найти экстремумы функции.
Пример 51. Найти экстремумы функции
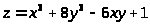 .
.
Решение.
Найдем частные производные
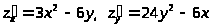 .
.
Решим систему уравнений


Найдем частные производные
второго порядка и их значения в
критических точках:
 .
В точке
.
В точке
 получим:
получим:
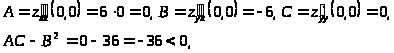
значит, в точке
 экстремума нет. В точке
экстремума нет. В точке
 получим:
получим:

значит, в точке
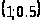 минимум.
минимум.
 .
.
Ответ.

5.2 Глобальный экстремум (наибольшее и наименьшее значение функции)
Наибольшее и наименьшее значения функции нескольких переменных, непрерывной на некотором замкнутом множестве, достигаются или в точках экстремума, или на границе множества.
Схема нахождения наибольшего и наименьшего значений.
Найти критические точки, лежащие внутри области, вычислить значение функции в этих точках.
Исследовать функцию на границе области; если граница состоит из нескольких различных линий, то исследование необходимо провести для каждого участка отдельно.
Сравнить полученные значения функции и выбрать наибольшее и наименьшее.
Пример 52. Найти наибольшее и
наименьшее значения функции
 в прямоугольнике
в прямоугольнике
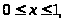
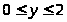 .
.
Решение. 1) Найдем критические
точки функции, для этого найдем частные
производные:
 ,
и решим систему уравнений:
,
и решим систему уравнений:
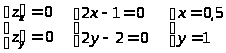
Получили критическую точку A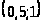 .
Полученная точка лежит внутри заданной
области,
.
Полученная точка лежит внутри заданной
области,

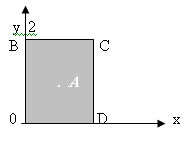
Границу области составляют
четыре отрезка:
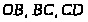 и
и .
найдем наибольшее и наименьшее значение
функции на каждом отрезке.
.
найдем наибольшее и наименьшее значение
функции на каждом отрезке.

Сравним полученные результаты
и получим, что
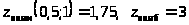 в точках
в точках
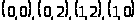 .
.
Глава 6. Модель потребительского выбора
Будем полагать, что имеется n
различных товаров. Тогда некоторый
набор товаров будем обозначать через
n-мерный
вектор
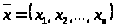 ,
где
,
где
 – количество i-того
товара
– количество i-того
товара .
Множество всех наборов товаров X
называется пространством.
.
Множество всех наборов товаров X
называется пространством.
Выбор индивида-потребителя
характеризуется отношением предпочтения:
считается, что потребитель может сказать
о любых двух наборах, какой более
желателен, или он не видит между ними
разницы. Отношение предпочтения
транзитивно: если набор
 предпочтительнее набора
предпочтительнее набора
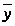 ,
а набор
,
а набор
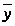 предпочтительнее набора
предпочтительнее набора
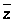 ,
то набор
,
то набор
 предпочтительнее набора
предпочтительнее набора
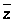 .
Будем полагать, что поведение потребителя
полностью описывается аксиомой
индивида-потребителя: каждый
индивид-потребитель принимает решение
о потреблении, покупках и т.п., исходя
из своей системы предпочтений.
.
Будем полагать, что поведение потребителя
полностью описывается аксиомой
индивида-потребителя: каждый
индивид-потребитель принимает решение
о потреблении, покупках и т.п., исходя
из своей системы предпочтений.
6.1 Функция полезности
На множестве потребительских
наборов X
определена функция
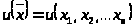 ,
значение которой на потребительском
наборе
,
значение которой на потребительском
наборе
 равно потребительской оценке индивида
для этого набора. Функция
равно потребительской оценке индивида
для этого набора. Функция
 называется функцией полезности
потребителя или функцией потребительского
предпочтения. Т.е. каждый потребитель
имеет свою функцию полезности. Но все
множество потребителей можно разделить
на определенные классы потребителей
(по возрасту, имущественному положению
и т.п.) и каждому классу приписать
некоторую, может быть, осредненную
функцию полезности.
называется функцией полезности
потребителя или функцией потребительского
предпочтения. Т.е. каждый потребитель
имеет свою функцию полезности. Но все
множество потребителей можно разделить
на определенные классы потребителей
(по возрасту, имущественному положению
и т.п.) и каждому классу приписать
некоторую, может быть, осредненную
функцию полезности.
Т.о., функция
 является потребительской оценкой или
уровнем удовлетворения потребностей
индивида при приобретении данного
набора
является потребительской оценкой или
уровнем удовлетворения потребностей
индивида при приобретении данного
набора
 .
Если набор
.
Если набор
 предпочтительнее набора
предпочтительнее набора
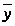 для данного индивида, то
для данного индивида, то
 .
.
Свойства функции полезности.
1.

Первые частные производные
функции полезности называются предельными
полезностями продуктов. Из этого свойства
следует, что возрастание потребления
одного продукта при неизменном потреблении
других продуктов приводит к росту
потребительской оценки. Вектор
 является градиентом функции
является градиентом функции
 ,
он показывает направление наибольшего
роста функции. Для функции
,
он показывает направление наибольшего
роста функции. Для функции
 ее градиент представляет собой вектор
предельных полезностей продуктов.
ее градиент представляет собой вектор
предельных полезностей продуктов.
2.

Т.е. предельная полезность любого товара уменьшается с ростом потребления.
3.
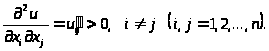
Т.е. предельная полезность каждого продукта увеличивается с ростом количества другого продукта.
Некоторые виды функций полезности.
Неоклассическая:
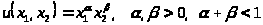 .
.
Квадратическая:
 ,
где матрица
,
где матрица
 отрицательно
определена и
отрицательно
определена и
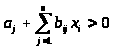 для
для
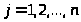 .
.
Логарифмическая функция:
 .
.
6.2 Линии безразличия
В прикладных задачах и моделях
потребительского выбора часто используется
частный случай набора из двух товаров,
т.е. когда функция полезности зависит
от двух переменных. Линия безразличия
– это линия, соединяющая потребительские
наборы, имеющие один и тот же уровень
удовлетворения потребностей индивида.
По сути своей линии безразличия
представляют собой линии уровня функции
 .
Уравнения линий безразличия:
.
Уравнения линий безразличия:
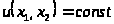 .
.
Основные свойства линий безразличия.
Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются.
Линии безразличия убывают.
Линии безразличия выпуклы вниз.
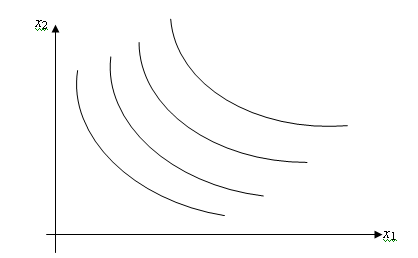
Из свойства 2 следует важное
приближенное равенство
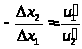 .
.
Это соотношение показывает, на
сколько индивид должен увеличить
(уменьшить) потребление второго продукта
при уменьшении (увеличении) потребления
первого продукта на одну единицу без
изменения уровня удовлетворения своих
потребностей. Отношение
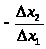 называется нормой замены первого
продукта вторым, а величина
называется нормой замены первого
продукта вторым, а величина
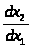 – предельной нормой замены первого
продукта вторым.
– предельной нормой замены первого
продукта вторым.
Пример 53. Если предельная полезность первого товара равна 6, а второго – 2, то при уменьшении потребления первого товара на единицу нужно увеличить потребление второго товара на 3 единицы при том же уровне удовлетворения потребностей.
6.3 Бюджетное множество
Пусть
 – вектор цен на набор из n
продуктов
– вектор цен на набор из n
продуктов
 ;
I –
доход индивида, который он готов потратить
на приобретение набора продуктов
;
I –
доход индивида, который он готов потратить
на приобретение набора продуктов
 .
Множество наборов товаров стоимостью
не более I
при данных ценах
.
Множество наборов товаров стоимостью
не более I
при данных ценах
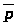 называется бюджетным множеством B.
При этом множество наборов стоимостью
I
называется границей G
бюджетного множества B.
Т.о. множество B
ограничено границей G
и естественными ограничениями
называется бюджетным множеством B.
При этом множество наборов стоимостью
I
называется границей G
бюджетного множества B.
Т.о. множество B
ограничено границей G
и естественными ограничениями
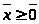 .
.
Бюджетное множество описывается системой неравенств:
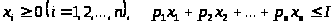 .
.

Рис. 1
Для случая набора из двух товаров
бюджетное множество B
(рис. 1) представляет собой треугольник
в системе координат
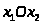 ,
ограниченный осями координат и прямой
,
ограниченный осями координат и прямой
 .
.
6.4 Теория потребительского спроса
В теории потребления полагается,
что потребитель всегда стремится
максимизировать свою полезность и
единственным ограничением для него
является ограниченность дохода I,
который он может потратить на покупку
набора товаров. В общем виде задача
потребительского выбора (задача
рационального поведения потребителя
на рынке) формулируется следующим
образом: найти потребительский набор
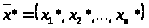 ,
который максимизирует его функцию
полезности при заданном бюджетном
ограничении. Математическая модель
этой задачи:
,
который максимизирует его функцию
полезности при заданном бюджетном
ограничении. Математическая модель
этой задачи:
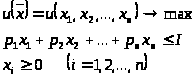
В случае набора из двух товаров:
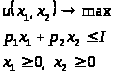
Геометрически решение этой задачи – это точка касания границы бюджетного множества G и линии безразличия.
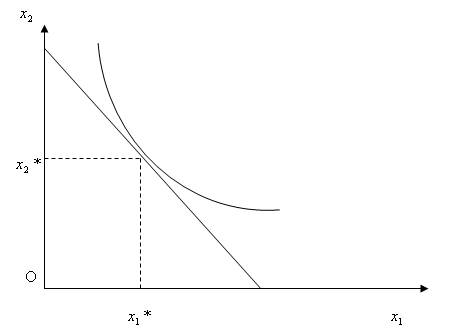
Решение этой задачи сводится к решению системы уравнений:
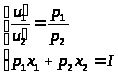 (1)
(1)
Решение этой системы
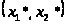 является решением задачи потребительского
выбора.
является решением задачи потребительского
выбора.
Решение задачи потребительского
выбора
 называется точкой спроса. Эта точка
спроса зависит от цен
называется точкой спроса. Эта точка
спроса зависит от цен
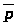 и дохода I.
Т.е. точка спроса является функцией
спроса. В свою очередь функция спроса
– это набор n
функций, каждая из которых зависит от
и дохода I.
Т.е. точка спроса является функцией
спроса. В свою очередь функция спроса
– это набор n
функций, каждая из которых зависит от
 аргумента:
аргумента:
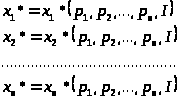
Эти функции называются функциями спроса соответствующих товаров.
Пример 54. Для набора из двух
товаров на рынке, известных ценах на
них
 и
и
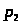 и дохода I
найти функции спроса, если функция
полезности имеет вид
и дохода I
найти функции спроса, если функция
полезности имеет вид
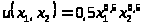 .
.
Решение. Продифференцируем функцию полезности:
 .
.
Подставим полученные выражения в (1) и получим систему уравнений:
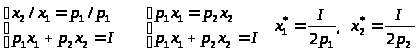
В данном случае расход на каждый товар составит половину дохода потребителя, а количество приобретенного товара равно затраченной на него сумме, поделенной на цену товара.
Пример 55. Пусть функция полезности
для первого товара
 ,
второго
,
второго
 ,
,
цена первого товара
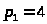 ,
цена второго
,
цена второго
 .
Доход
.
Доход
 .
Какое количество товара должен приобрести
потребитель, чтобы максимизировать
полезность?
.
Какое количество товара должен приобрести
потребитель, чтобы максимизировать
полезность?
Решение. Найдем производные функций полезности, подставим в систему (1) и решим ее:
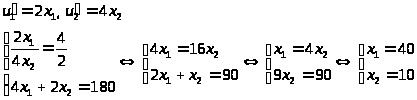
Этот набор товаров является оптимальным для потребителя с точки зрения максимизации полезности.
Задания для домашней контрольной работы
Контрольная работа должна быть выполнена в соответствии с вариантом, выбираемым по последней цифре номера зачетной книжки в отдельной тетради. Каждая задача должна содержать условие, подробное решение и вывод.
1. Введение в математический анализ
Задача 1. Найти область определения функции.
1.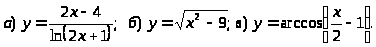
2.

3.

4.

5.

6.
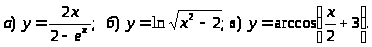
7.

8.
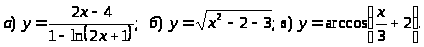
9.
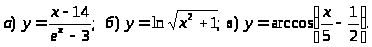
10.
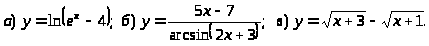
Задача 2. Найти пределы функций.
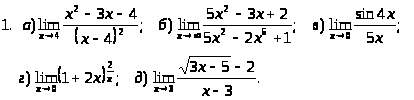
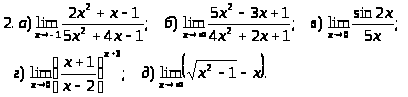

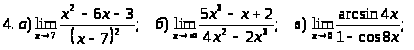
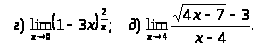
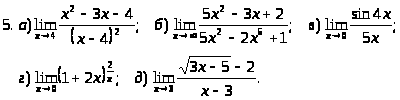
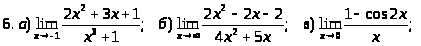
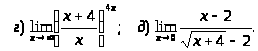


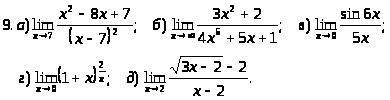
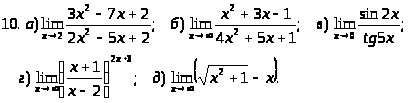 .
.
Задача 3. Найти точки разрыва функции и определить их тип.
1.
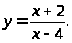 2.
2.
 3.
3.

4.
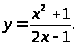 5.
5.
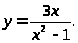 6.
6.
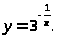
7.
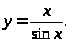 8.
8.
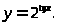 9.
9.
 10.
10.
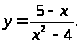
Глава 2. Дифференциальное исчисление функции одной переменной
Задача 4. Найти производные данных функций.
а)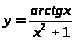 ;
б)
;
б)
 в) y
=
в) y
=
 ;
;
г) y =
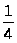 x6
+
x6
+
 +
+
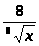 +
5; д)
y = x tg x + ln sin x + e3x;
+
5; д)
y = x tg x + ln sin x + e3x;
е) y = 2 x - arcsin x.
а)
 ;
б) y
=
;
б) y
=
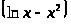
 ;
в) y
=
;
в) y
=
 ;
г) y
=
;
г) y
=
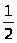 x2
–
x2
– +
3; д) y
= e
cos
+
3; д) y
= e
cos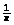 ;
е) y
=
;
е) y
=
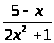 .
.
а) y
=
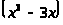 lnx;
б) y
=
lnx;
б) y
=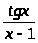 ;
в) y
= ln
;
в) y
= ln
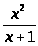 ;
;
г) y
=
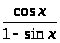 ;
д) y
=
;
д) y
=
 x7
+
x7
+
 +
1; е) y
= 2
+
1; е) y
= 2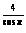 .
.
а) y
=
 ;
б) y
= (e5x
– 1)6; в) y
=
;
б) y
= (e5x
– 1)6; в) y
=
 ;
г) y
=
;
г) y
=
 ;
д) y
=
;
д) y
=
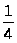 x8
+
x8
+ +
+
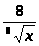 +
5; е) y
= 3 x
- arcsin
x.
+
5; е) y
= 3 x
- arcsin
x.
а) y
= 2x3
-
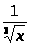 +
ex;
б) y
=
+
ex;
б) y
=
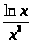 ;
в) y
=
;
в) y
=
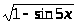 ;
;
г) y
=
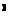
 ;
д) y
= 2 cos
;
д) y
= 2 cos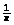 ;
е) y
=
;
е) y
=
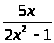 .
.
а) y
=
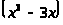 lnx;
б) y
=
lnx;
б) y
=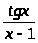 ;
в) y
= ln
;
в) y
= ln
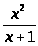 ;
;
г) y
=
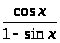 ;
д) y
=
;
д) y
=
 x7
+
x7
+
 +
1; е) y
= 2
+
1; е) y
= 2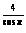 .
.
а)
 ;
б) y
=
;
б) y
=
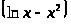
 ;
в)y
=
;
в)y
=
 ;
г)y
= x2
+ x
sin
x
+
;
г)y
= x2
+ x
sin
x
+
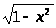 ;
д) y
= e
cos
;
д) y
= e
cos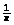 ;
е) y
=
;
е) y
=
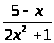 .
.
а) y
=
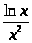 ;
б) y
= (3x
– 4)6; в) y
= sin
tg
;
б) y
= (3x
– 4)6; в) y
= sin
tg
 ;
;
г) y = 3x4
–
 – 9
– 9 +
9; д)
y =
+
9; д)
y =
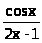 ;
;
е)
y = x2
+ arcsin x - x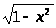 .
.
а) ;
б)
;
б) ;
в) y
=
;
в) y
=
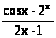 ;
г) y
= 5 sin3x;
д) y
=
;
г) y
= 5 sin3x;
д) y
=
 x3
–
x3
–
 – 6
– 6 +
3; е) y
= 4x
4
+
3; е) y
= 4x
4 + ln
+ ln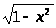 .
.
а)
 б)
y
=
б)
y
=
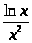 ;
в) y
= (3x
– 4)6; г) y
=
;
в) y
= (3x
– 4)6; г) y
=
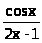 ;
д) y
= x2
- x
;
д) y
= x2
- x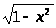 ;
е) y
= e
sin3x
+ 2.
;
е) y
= e
sin3x
+ 2.
Задача 5. Исследовать функцию и построить ее график.
1. а)
 б)
б)
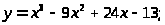 в)
в)
 .
.
2. а) б)
б)
 в)
в)
 .
.
3. а)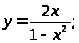 б)
б)
 в)
в)
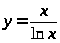 .
.
4.
 б)
б)
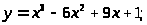 в)
в)
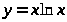
5. а)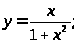 б)
б)
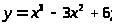 в)
в)
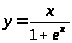 .
.
6. а)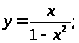 б)
б)
 в)
в)
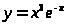 .
.
7. а)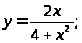 б)
б)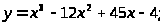 в)
в)
 .
.
8. а)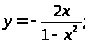 б)
б)
 в)
в)
 .
.
9. а)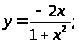 б)
б)
 в)
в)
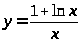 .
.
10. а) б)
б)
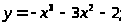 в)
в)
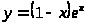 .
.
Задача 6. Найти наибольшее и наименьшее значение функции на заданном отрезке.
1.
 .
.
2.
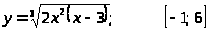 .
.
3.
 .
.
4.
 .
.
5.
 .
.
6.
 .
.
7.
 .
.
8.
 .
.
9.
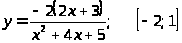 .
.
10.
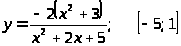 .
.
Глава 3. Интегральное исчисление
Задача 7. Найти неопределенные интегралы.
а)
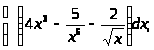 б)
б) ;
;
в)
 ;
г)
;
г)
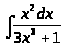 .
.
а)
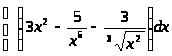 ;б)
;б)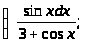 в)
в)
 г)
г)
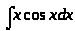 .
.
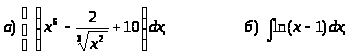

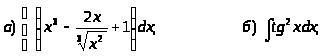
 г)
г)
а) ;
б)
;
б) ;
в)
;
в)
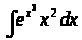 ;
г)
;
г) .
.
а)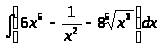 ;
б)
;
б)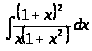 ;
в)
;
в) ;
г)
;
г)
а)
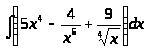 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
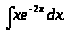
а)
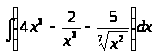 ;
б)
;
б)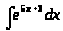 ;
в)
;
в) ;
г)
;
г)
 .
.
а)
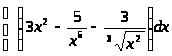 ;
б)
;
б)
 в)
в)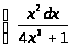 ;
г)
;
г)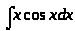 .
.
а)
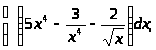 б)
б)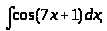 в)
в)
 ;
г)
;
г)
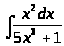 .
.
Задача 8. Вычислить определенные интегралы.
1.
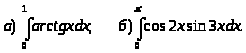
2.
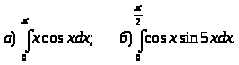
3.

4.
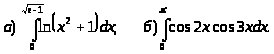
5.
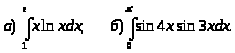
6.
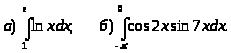
7.
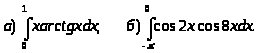 .
.
8.

9.
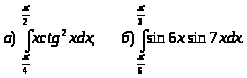
10.
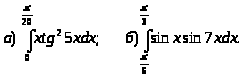
Задача 9. Найти несобственные интегралы или доказать, что они расходятся.
1.
 .
.
2.
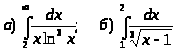 .
.
3.
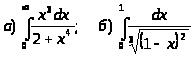 .
.
4.
 .
.
5.
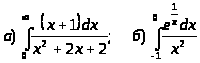 .
.
6.
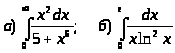 .
.
7.
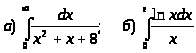 .
.
8.
 .
.
9.
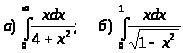 .
.
10.
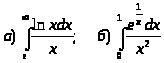 .
.
Задача 10. Найти площадь области, ограниченной кривыми
1.
 .2.
.2.
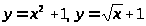 .
.
3.
 4.
4.

5.
 6.
6.
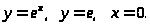
7.
 ,
,
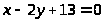 .8.
.8. .
.
9.
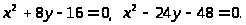
10.
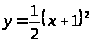 ,
,
 .
.
Глава 4. Дифференциальное исчисление функции нескольких переменных.
Задача 11. Найти область определения функции (показать на чертеже).
1.

2.
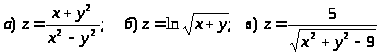 .
.
3.
 .
.
4.

5.
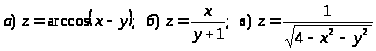 .
.
6.
 .
.
7.
 .
.
8.
 .
.
9.
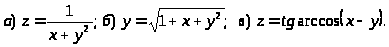 .
.
10.

Задача 12. Исследовать на непрерывность функции при
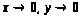 и
и
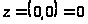 .
.
1.
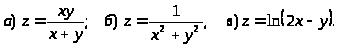
2.

3.
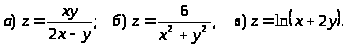
4.
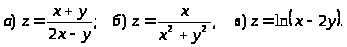
5.
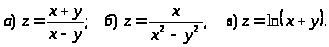
6.
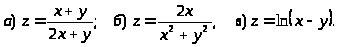
7.
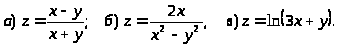
8.

9.

10.
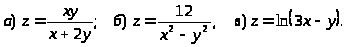
Задача 13. Найти производную неявно заданной функции.
1.
 .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
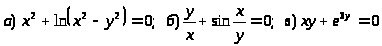 .
.
6.
 .
.
7.
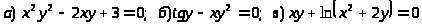 .
.
8.
 .
.
9.
 .
.
10.
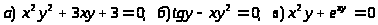 .
.
Задача 14. Вычислить приближенно
1. а)
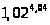 ;б)
;б)
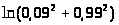 ;
в)
;
в)

2. а)
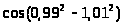 ;
б)
;
б)
 ;
в)
;
в)
 .
.
3. а)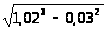 ;
б)
;
б)
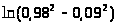 ;
в)
;
в)
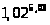 .
.
4. а)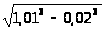 ;
б)
;
б)
 ;
в)
;
в)
 .
.
5. а) ;
б)
;
б)
 ;
в)
;
в)
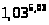 .
.
6. а) ;
б)
;
б)
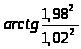 ;
в)
;
в)
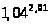 .
.
7. а) ;
б)
;
б)
 ;
в)
;
в)
 .
.
8. а)
 ;б)
;б)
 ;
в)
;
в)
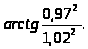
9. а)
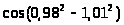 ;
б)
;
б)
 ;
в)
;
в)
 .
.
10. а)
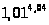 ;б)
;б)
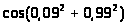 ;
в)
;
в)
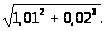
Задача 15. Исследовать функцию на экстремумы.
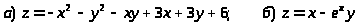 .
.
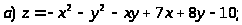
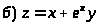 .
.

 .
.
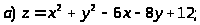
 .
.
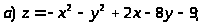
 .
.

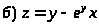 .
.
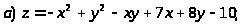
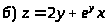 .
.
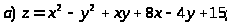
 .
.
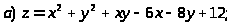
 .
.
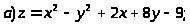
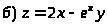 .
.
Задача 16. Найти наибольшее и
наименьшее значение функции
 в данной замкнутой области.
в данной замкнутой области.
1.
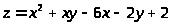 в прямоугольнике
в прямоугольнике

2.
 в треугольнике, ограниченном осями
координат и прямой
в треугольнике, ограниченном осями
координат и прямой

3.
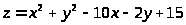 в прямоугольнике
в прямоугольнике
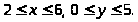
4.
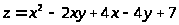 в области, ограниченной параболой
в области, ограниченной параболой
 и осью абсцисс.
и осью абсцисс.
5.
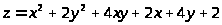 в квадрате
в квадрате

6.
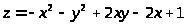 в треугольнике, ограниченном осями
координат и прямой
в треугольнике, ограниченном осями
координат и прямой

7.
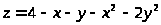 в треугольнике, ограниченном осями
координат и прямой
в треугольнике, ограниченном осями
координат и прямой

8.
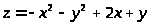 в треугольнике, ограниченном осями
координат и прямой
в треугольнике, ограниченном осями
координат и прямой
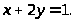
9.
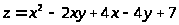 в области, ограниченной параболой
в области, ограниченной параболой
 и осью абсцисс.
и осью абсцисс.
10.
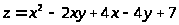 в области, ограниченной параболой
в области, ограниченной параболой
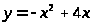 и осью абсцисс.
и осью абсцисс.
Литература
Основная
М.С. Красс, Б.П. Чупрынов. Основы математики и ее приложение в экономическом образовании: Учебник. – 4-е изд., исп. – М.: Дело, 2003.
М.С. Красс, Б.П. Чупрынов. Математика для экономических специальностей: Учебник. – 4-е изд., исп. – М.: Дело, 2003.
М.С. Красс, Б.П. Чупрынов. Математика для экономического бакалавриата. Учебник. – 4-е изд., исп. – М.: Дело, 2005.
Высшая математика для экономистов. Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера, - 2-е изд., перераб. и доп. – М: ЮНИТИ, 2003.
Кремер Н.Ш, Путко Б.А., Тришин И.М., Фридман М.Н.. Высшая математика для экономических специальностей. Учебник и Практикум (части I и II) / Под ред. проф. Н.Ш. Кремера, - 2-е изд., перераб. и доп. – М: Высшее образование, 2007. – 893с. – (Основы наук)
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М. высшая школа. 1999.
Дополнительная
И.И. Баврин, В.Л. Матросов. Высшая математика. «Гуманитарный издательский центр Владос», 2002.
И.А. Зайцев. Высшая математика. «Высшая школа», 1998.
А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. Математика в экономике / в двух частях/. М. Финансы и статистика. 1999.
1