Численные методы (работа 3)

ЛЕКЦИЯ №5

МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

СНУ

Пусть дана система вида:

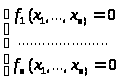(5.1)

f'(x)=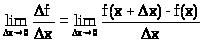 - производная

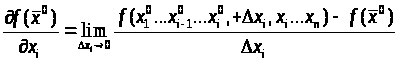
Частная производная 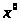- вектор (все значения).

МЕТОД НЬЮТОНА

Дана система вида (5.1), где f_>i> один раз непрерывно дифиринцируемые функции, т.е. существуют все частные первые производные этих функций.

Строим последовательность приближений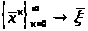 сходящуюся к точному решению системы .

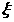Пусть 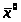- некоторое начальное приближение к решению, а 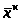- катое приближение к решению. Построим зависимость, позволяющую на основании 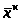построить .

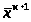Точное приближение

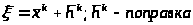
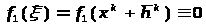
ξ-корень обращает уравнение в верное равенство(тождество).

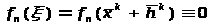(5.2)

Разложим функции f_>i> из системы (5.2) в ряд Тейлора в окрестности точки х^к до линейных составляющих.

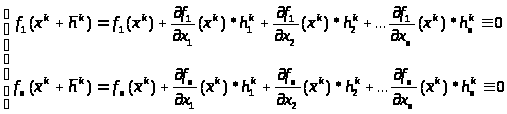(5.3)

Система (5.3) представляет собой систему линейных алгебраических уравнений для поиска компонента вектора поправки h^k.

Перепишем систему (5.3) в виде:

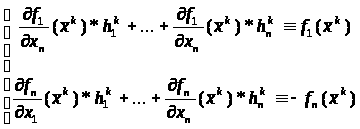(5.4)

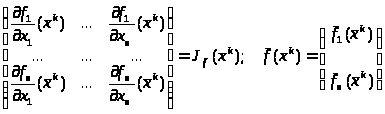
Сокращаем запись системы (5.4) : 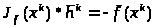(5.5)

Решим систему (5.5) методом обратной матрицы. Определитель Якобиана в точке х^к не равен 0.

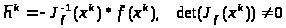
Получили связь последующего приближения с предыдущим.

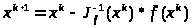(5.6)

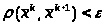условие окончания вычислений. (5.7)

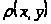- расстояние между векторами (метрика).

МЕТОД ИТЕРАЦИЙ

Пусть дана система вида (5.1). Преобразуем ее к виду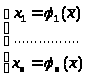 (5.8)

Система (5.8) в векторном виде 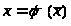(5.9)

Необходимо найти неподвижную точку систему

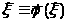
Очевидно, что эта точка ξ – решение системы (5.1)

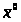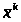Пусть дано -некоторое начальное приближение к ξ и на k-том шаге получено приближение . Тогда последующее приближение :

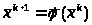(5.10)

Условие окончания совпадает с (5.7)

Всегда ли метод сходится?

Пусть М- матрица, составлена из элементов m_>ij>

M=[m_>ij>], где m_>ij>=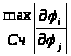

Определение нормы матрицы А: 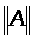-число удовлетворяющее свойствам.

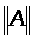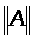1) ≥0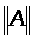, =0≡0

2) 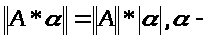число

3)

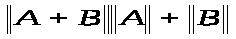
4)

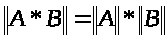
Способы задания нормы матрицы:

1) =

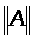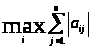
2) =

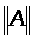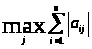
3) =

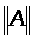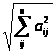
Достаточное условие сходимости метода итераций:

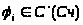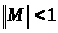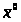
Если , i=1,n , на Сч и 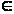Сч, то процесс итераций сходится независимо от выбора начального приближения.

МЕТОД ЗЕЙДЕЛЯ

Пусть дана система вида (5.1), преобразуем ее к виду (5.8). Как и в методе итераций строим последовательность приближений 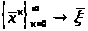к неподвижной точке.

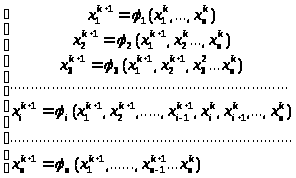
ускорение сходимости за счет подстановки предыдущего приближения.

Достаточное условие совпадает с достаточными условиями сходимости метода итераций.

Условие окончания получения приближений совпадает с (5.7).

ЛЕКЦИЯ № 6, 7

ПРИБЛИЖЕНИЕ ФУНКЦИИ

Общая постановка задачи.

Пусть () – некоторая функция, которая может быть известно, частично известной и неизвестной. Эту функцию необходимо заменить некоторой «хорошей» функцией (), которая будет достаточно близкой ().

Постановка задачи интерполяции.

Для того чтобы конкретизировать постановку задачи приближения функции необходимо ответить на следующие вопросы:

что известно о () (способ задания, степень гладкости);

к какому классу, семейству функций должна принадлежать ();

что понимаем под близостью () и () каков критерий согласия;

Часто приближение функции называют аппроксимацией

Постановка задачи интерполяции.

Пусть () задана на некотором разбиении отрезка [a;b] точками х_>i>_> >,

i=0,n , где a = х_>0><х_>1><…<x_>n>= b

интерполяция – вычисление () в точке [a;b], x  x_>i>, i = 0,n

экстраполяция – вычисление функции () в точке Х[a;b];

Определение интерполяции ввел в 1656 году Джон Уолесс, а в 1655 году ввел символ .

Для полиномиальной интерполяции () имеет вид ()=а_>0>+а_>1>х+а_>2>х²+…+а_>n>xⁿ.

Для того, чтобы считать () к () вводится ограничение (_>i>)= (_>i>), i=0,n ;

Т.е значения этих функций в точке х_>i> должны совпадать. Точки х_>i>_> > будем называть узлами интерполяции

Интерполяционный многочлен Лагранжа

Необходимо определить коэффициенты полинома степени n(их будет n+1), построения аппроксимации функции, заданной в n+1 узле. Используя ограничения на (): (_>i>)= (_>i>)=y, i=0,n , составим систему:

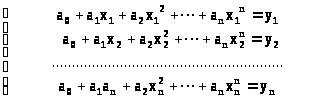_> >_> >_> >(6_>.>1)

Выпишем определитель этой системы

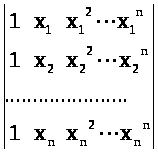
Определитель

Вандермонда

При условии: x_>0>x_>j>_> >при_> > ij определитель системы (6.1) отличен от нуля, следовательно, система имеет единственное решение.

Вывод:

если задано разбиение в виде n+1различной точки, то всегда существует функция в виде полинома n-ой степени, которая проходит через все точки графика (),определенной на этом разбиении.

Посторонние приближения_> >функции при помощи полиномов указанным способом весьма трудоемко и обладает большой вычислительной погрешностью, поэтому его использование для большого числа узлов интерполяции нецелесообразно.

Лагранж предложил строить интерполяционные полиномы в виде:

P_>n>(x)=∑ C_>i> l_>i>(x) (6.2)

C_>i>_>=>y_>i>_>=>(_>i>), l_>i>(x)=полиномы n-ой степени, которые удовлетворяют условию:

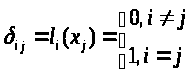
Для полинома узлы интерполяции x_>j>, j=0,n , j≠I являются корнями, причем действительными и попарно различными (все имеют кратность 1)

Тогда полином l_>i>_> >может быть записан в виде:

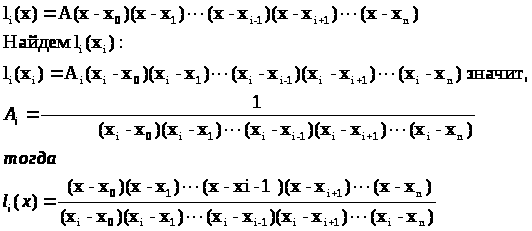(6.3)

Общий вид полинома Лагранжа:

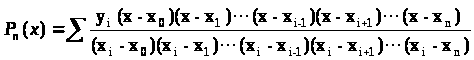(6.4)

Встает вопрос о точности, о приближения функции. Вводится понятие остаточного члена многочлена Лагранжа ; для того, чтобы оценить аппроксимации () в некоторой точке x [a;b]

Функцию () представим в виде ()= P_>n>(x)+R_>n>(x), где R_>n>(x)- остаточный член многочлена Лагранжа в процессе длительного и трудоемкого вывода для R_>n>(x) получена следующая формула:

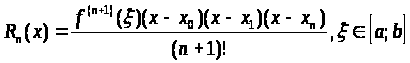(6.5)

Строится система вложенных отрезков

⁽ⁿ⁺¹⁾ -производная (n+1)-го порядка

Пусть

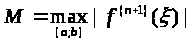
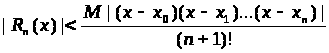(6.6)

Если ()-полином n-ой степени, то производная (n+1)-го порядка равна 0, тогда R_>n>(x)≡0 и мы получаем точную аппроксимацию.

Теорема:

Многочлен Лагранжа вида (6.4) для таблично заданной функции единственен.

Доказательство:

Пусть Q_>n>(x)- многочлен Лагранжа, построенный для этой же функции () по тем же узлам интерполяции. Q_>n>(x) P_>n>(x) Q_>n>(x_>i>)=y_>i>=P_>n>(x_>i>),

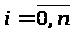
Рассмотрим многочлен L_>n>(x)= Q_>n>(x)-R_>n>(x)-это многочлен n-ой степени, для которого точки x_>i>_> >, i=0,n являются корнями. Это противоречит основной теореме алгебры, которая говорит о том, что полином n-ой степени имеет ровно n корней . А L_>n>(x) имеет n+1 корней . Противоречие доказывает теорему.

Интерполяционная схема Эйткина

Поскольку при большом числе узлов интерполяции вычисление значения полинома Лагранжа по формуле (6.4) громоздко, необходимо получить рекуррентную формулу.

Пусть ()- непрерывна, узлы выбраны на отрезке [a;b] таким образом, что:

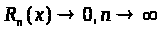
Введем функцию

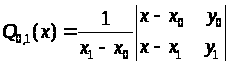
x_>i>-узлы интерполяции;

y_>i=>()

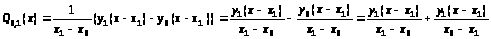
Полином Лагранжа: P_>n> (x) см. (6.4)

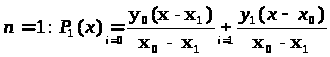
Таким образом, функция Q_>0,1> (x) представляет собой полином Лагранжа l-ой степени, построенной по узлам x_>0 >,x_>1 > введем функцию вида_> >

_>>

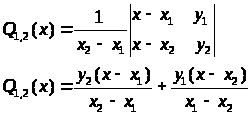Функция Q_>1,2> (x)- интерполяционный полином Лагранжа, построенный по узлам _> >x_>1 >,x_>2>.

Введем теперь функцию

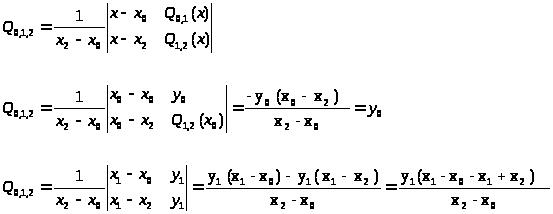
Аналогично:

Q_>0,1,2> (x_>2>)= у_>2 >

В силу единственности полинома Лагранжа, построенного по узлам _> >x_>0>, x_>1> ,x_>2 >

функция Q_>0,1,2> (x) представляет собой интерполяционный полином Лагранжа 2-ой степени, построенный по узлам x_>0>, x_>1> ,x_>2 >. _> >

Введем функцию:

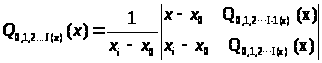(7.1)

Функция представляющая собой полином Лагранжа 2-ой степени, построенного по узлам x_>0>, x_>1,…>x_>i>.

Формула _> >(7.1) позволяет рекуррентно вычислять полином Лагранжа любой степени.

Т.к. (7.1) представляет собой альтернативную форму записи интерполяционного полинома, точность приближения функции также может быть оценена по формуле (6.5)

(7.1)-интерполяционная схема Эйткина.

КОНЕЧНЫЕ РАЗНОСТИ

Пусть функция () задана на системе равноотстоящих узлов x_>i>=x_>0>+ih,

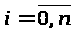
где h-шаг сетки, y_>i>=(_>i>).

Конечной разностью первого порядка в точке x_>0 >называется ∆y_>0>=y_>1>-y_>0>

Конечной разностью первого порядка в точке x_>i>: ∆y_>i>=y_>i>_>+1>-y_>0>-y_>i>

Конечной разностью второго порядка в точке x_>0> : ∆²y_>0>=∆y_>1>-∆y_>0>

Конечной разностью второго порядка в точке x_>i>: ∆²y_>i>=∆y_>i>_>+1>-∆y_>i>

Общая формула для конечной разности k-того порядка в точке x_>i>:

∆^ky_>i>=∆^k-1y_>i>_>+1>-∆^ky_> >(7.2)

Заметим: ∆⁰y_>i>= y_>i>

Формула (7.2) позволяет вычислять рекуррентно конечные разности

Связь конечных разностей и производных

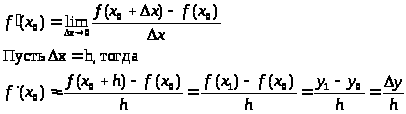
чем меньше h, тем точность выше

Аналогично можем получить связь

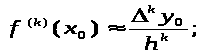
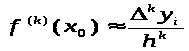; (7.3)

Свойства конечных разностей

В связи с производными вида (7.3) конечные разности обладают свойствами:

постоянные, равны нулю;

постоянный множитель у функции выносится за знак

суммы 2-х функций равны сумме каждой функции

полинома n-ой степени, n-го порядка постоянны и равны

∆ⁿy=hⁿa_>n>n!

a_>n>-коэффициент при xⁿ полинома R_>n>(x)

Верно и обратное утверждение: все конечные разности n-го порядка некоторой функции постоянны и одинаковы, конечные разности n +1-го порядка равны 0, а конечные разности n-1-го порядка различны, то функция представляет собой полином n-ой степени.

Распространение ошибки в исходных данных при вычислении конечные разности

Любые измерения несут в себе погрешность (ошибка округления, точность измерения приборов)

Пусть значения функции определены в узлах x_>0>, 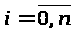и в некоторой точке x_>k>_> >значение некоторой точке x_>k>_> >значение функции найдено с ошибкой ε, т.е ỹ_>k>+ ε

Составим таблицу конечных разностей

x_>k>_>-2 >y_>k>_>-2 > ∆y_>k>_>-2 >∆²y_>k>_>-2 >∆³y_>k>_>-3 >+_> >ε

x_>k>_>-1 >y_>k>_>-1 > ∆y_>k>_>-1 >+_> >ε_> >∆²y_>k>_>-2 >+_> >ε_> >∆³y_>k>_>-2 >-3_> >ε

x_>k>_> >y_>k>+ε ∆y_>k>_>-1 >-_> >ε_> >∆²y_>k>_>-1 >-_> >2_> >ε_> >∆³y_>k>_>-1 >+_> >3_> >ε

x_>k>_>+1> y_>k>_>+1 >∆y_>k>_>+1 >∆²y_>k>+_> >ε_> > ∆³y_>k>-_> >ε

x_>k>_>+2> y_>k>_>+2 > ∆²y_>k>_>+1>

Как видно из таблицы конечных разностей при увеличении порядка конечных разностей ошибка в исходных данных распространяется и растет.

Такое взаимодействие ошибок называют шумом, если это ошибки округлений - то шумом округлений.

Если ошибки округлений достаточно большие, то может происходить следующее явление: при увеличении порядка конечных разностей они могут уменьшаться и→0, но, дойдя до некоторого малого значения, опять могут начать расти из-за шума округлений.

Столбец в таблице конечных разностей, в которой все конечные разности ≈0, называют «практическим постоянным»; при этом конечные разности высших порядков не используют.

Для интерполяции целесообразно использовать многочлен такой степени, которая совпадает с порядком «практической постоянной» конечных разностей.

ЛЕКЦИЯ №8

ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ДЛЯРАВНООТСТОЯЩИХ УЗЛОВ

Дана функция y=(),заданная на сетке равноотстоящих узлов:

y_>i>=(_>i>), x_>i>=x_>0>+ih_>i>,

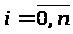
Строим интерполяционный полином с целью упрощения записи полинома (интерполяционного) и представления его в виде, позволяющем оценивать влияние каждого из компонентов на значение аппроксимации, запишем его так:

N_>n>(x)=-a_>0>+a_>1>(x-x_>0>)+a_>2>(x-x_>0>)(x-x_>1>)+…+a_>n>(x-x_>0>)…(x-x_>n-1>) (8.1)

Необходимо посчитать его коэффициенты a_>i>. Будем находить из условия

N_>n>(x_>i>)=y_>i>

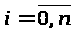
i=0: N_>n>(x_>0>)=y_>0>=a_>0>+a_>1>0+…+a_>n>0 a_>0>= y_>0>

i=1: N_>n>(x_>1>)=y_>1>= y_>0>+a_>1>(x_>1>-x_>0>) + a_>2>0+…+a_>n>0

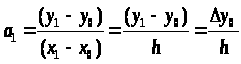
x_>1>=x_>0>+1h=x_>1>-x_>0>=h

i=2: N_>n>(x_>2>)=y_>2>= y_>0>+∆y_>0>/h(x_>2>-x_>0>) (x_>2>-x_>1>) + a_>3>0+…+a_>n>0

x_>2>-x_>0>=2h

x_>2>-x_>1>=h

y_>2>= y_>0>+∆y_>0>2+a_>2>2h²

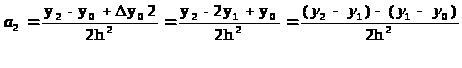
i=k: 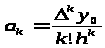(8.2)

Запишем теперь, используя (8.2), полином (8.1) в виде:

N_>n>(x)= y_>0>+∆y_>0>/h(x-x_>0>)+…+ ∆ⁿ y_>0> /n!hⁿ(x-x_>0>)(x-x_>1>)… (x-x_>n-1>) (8.3)

Полином (8.3) 1-ый интерполяционный многочлен Ньютона. Он наиболее приспособлен для вычисления значения функции в точках, близких к x_>0>

С целью упрощения записи полинома введем переменную

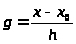
x=x_>0>+gh

Если g-целое, то будет совпадать с номером узла

x_>0 >– базовый узел полинома (8.3)

x_>i>=x_>0>+gh- x_>0>-ih=h(g-i);

N_>n>(g)= y_>0>+∆y_>0>g+…+ ∆ⁿ y_>0> /n!g(g-1)(g-2)(g-n+1) (8.4)

Полином Ньютона в силу единственности существования интерполяционного полинома Лагранжа является одной из форм записи полинома Лагранжа, поэтому для полинома (8.3) справедливо, что формула остаточного члена полинома Лагранжа

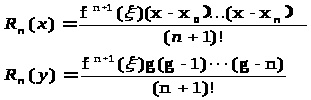
Для вычисления функции в точках находящихся в середине сетки узлов интерполяции либо в ее конце, т. е близкие к x_>n>, применяют два подхода

строят формулы для вычисления функции в точках х, близких к середине сетки интерполяции

формулы для точек х, близких к х_>n> (упорядочивание узлов интерполяции).

Соответственно получаются формулы Стирлинга , Бесселя, Гаусса, и 2-ой интерполяционный многочлен Ньютона .

Второй путь: в качестве узла х_>0> для заданной точки х берут тот узел, который наиболее близок к х, узел х_>1> выбирают как самый близкий из оставшихся узлов к х.

Т.е последовательность 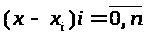упорядочившаяся по возрастанию.

Для вычисления значения функции в точке х используется 1-ый интерполяционный многочлен Ньютона.

х0 х1 х2 х3 х4 х5 х6

Преобразуем узлы:

х_>0>′=x_>3;>

x_>1>′=x_>4> ;

x_>2>′=x_>2> ;

x_>3>′=x_>5 >;

Разделенные разности

Пусть функция (),задана на системе неравно отстоящих узлов.

Разделенной разностью 1-го порядка назовем выражение:

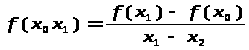
Разделенной разностью 2-го порядка:

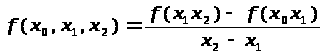
Разделенной разностью k-го порядка:

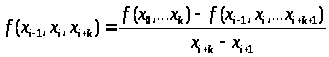_> >(8.6)

|x-x_>0>|,

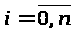
Свойства разделенной разности:

на сетке равноотстоящих узлов разделенной разности совпадают конечными разностями

разделенные разности понижают степень многочлена

разделенные разности n-го порядка постоянны и равны

Интерполяционная формула Ньютона для не равноотстоящих узлов

Пусть функция (), задана на сетке не равноотстоящих узлов x_>i>, 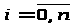.Запишем следующие разделенные разности:

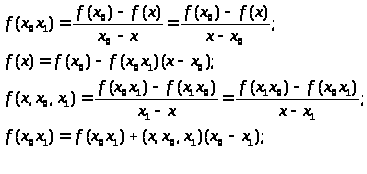
Выполним такие действия n-1 раз, получим:

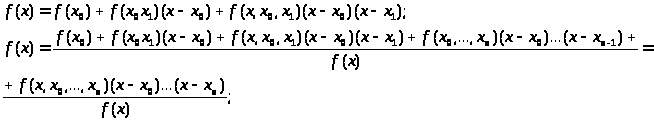Полином Ньютона:

N_>n>(x)= ⁰()

R_>n>(x)= (,_>0,…>_>n>)(x-x_>0>)… (x-x_>n>) (8.8)

То ()= N_>n>(x)+ R_>n>(x)

N_>n>(x) ≈ ()

R_>n>(x) = () - N_>n>(x)

Если () имеет (n+1)-ую производную, то остаточный член может быть преобразован к виду остаточного члена (8.9) полинома Лагранжа.

При вычислении полинома в точке х узлы интерполяции лучше переименовать так, чтобы х_>0> был самым близким к х, а все остальные узлы тем более удаленные по увеличению расстояния к х.