Основы математического анализа
1. Множества и операции над множествами
Напомним основные обозначения, понятия, относящиеся к множествам, которых будем придерживаться дальше.
Начнем с основного понятия, которое встречается практически в каждом разделе математики - это понятие множества.
Множество - это совокупность, набор элементов, объединенных общими свойствами.
Множества
обозначаются заглавными латинскими
буквами
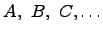 ,
а элементы множества строчными латинскими
буквами
,
а элементы множества строчными латинскими
буквами
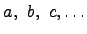 .
.
Запись
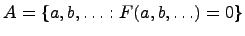 означает,
что есть множество
означает,
что есть множество
 с
элементами
с
элементами
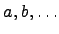 ,
которые связаны между собой какой-то
функцией
,
которые связаны между собой какой-то
функцией
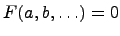 .
.
Замечание. Элементы в множество входят по одному разу, т.е. без повторений.
Основные операции:
Принадлежность элемента множеству:
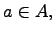
где
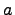 --
элемент и
--
элемент и
 --
множество (элемент
--
множество (элемент
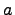 принадлежит
множеству
принадлежит
множеству
 ).
).
Непринадлежность элемента множеству:
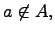
где
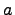 --
элемент и
--
элемент и
 --
множество (элемент
--
множество (элемент
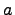 не
принадлежит множеству
не
принадлежит множеству
 ).
).
Объединение
множеств:
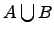 .
.
Объединением
двух множеств
 и
и
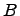 называется
множество
называется
множество
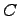 ,
которое состоит из элементов множеств
,
которое состоит из элементов множеств
 и
и
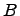 ,
т.е.
,
т.е.
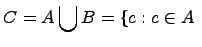 или
или
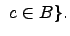
Пересечение
множеств:
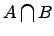 .
.
Пересечением
двух множеств
 и
и
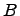 называется
множество
называется
множество
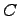 ,
которое состоит из общих элементов
множеств
,
которое состоит из общих элементов
множеств
 и
и
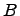 ,
т.е.
,
т.е.
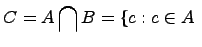 и
и
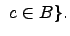
Разность
множеств:
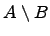 .
.
Разностью
двух множеств
 и
и
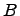 ,
например, множество
,
например, множество
 минус
множество
минус
множество
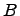 ,
называется множество
,
называется множество
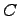 ,
которое состоит из элементов множества
,
которое состоит из элементов множества
 ,
которых нет в множестве
,
которых нет в множестве
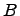 ,
т.е.
,
т.е.
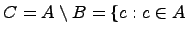 и
и
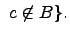
Симметрическая разность множеств:
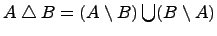 .
.
Симметрической
разностью двух множеств
 и
и
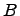 называется
множество
называется
множество
 ,
которое состоит из не общих элементов
множеств
,
которое состоит из не общих элементов
множеств
 и
и
 ,
т.е.
,
т.е.
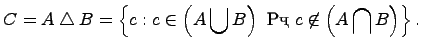
Дополнение
множества:
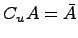 .
.
Если
предположим, что множество
 является
подмножеством некоторого универсального
множества
является
подмножеством некоторого универсального
множества
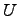 ,
тогда определяется операция дополнения:
,
тогда определяется операция дополнения:
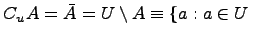 и
и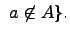
Вхождение
одного множества в другое множество:
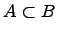 .
.
Если любой
элемент множества
 является
элементом множества
является
элементом множества
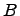 ,
то говорят, что множество
,
то говорят, что множество
 есть
подмножество множества
есть
подмножество множества
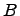 (множество
(множество
 входит
в множество
входит
в множество
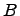 ).
).
Не вхождение
одного множества в другое множество:
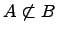 .
.
Если существует
элемент множества
 ,
который не является элементом множества
,
который не является элементом множества
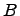 ,
то говорят, что множество
,
то говорят, что множество
 не
подмножество множества
не
подмножество множества
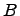 (множество
(множество
 не
входит в множество
не
входит в множество
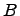 ).
).
2. Первая и вторая теорема Вейерштрасса
Теорема (первая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она ограничена на нем. Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk , сходящуюся к x0∈[a;b] . Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈N найдется точка xn∈[a;b] , что f(xn)>n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn) точек сегмента [a;b], для которых выполнено свойство f(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n... Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk) , которая сходится к точке x0∈[a;b] : limk→∞xnk=x0 (1) Рассмотрим соответствующую последовательность (f(xnk)) . С одной стороны f(xnk)>nk и поэтому limk→∞f(xnk)=+∞ (2), С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметь limk→∞f(xnk)=f(x0) (3) Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.
Замечание 1 Таким образом, если f непрерывна на [a;b], то ее множество значений ограничено и поэтому существует конечные верхняя и нижняя грань функции. c=infx∈[a;b]f(x),d=supx∈[a;b]f(x), но открыт вопрос о достижении функции своих граней. Замечание 2 Если слово сегмент в условии теоремы заменить словом интервал или полуинтервал, то теорема может и нарушиться. Пример, y=tgx,tgx∈C((−2π;2π)) , но функция не ограничена на этом интервале.
Теорема (вторая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения). Доказательство: Пусть f(x)∈C([a;b]) , c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой теореме Вейерштрасса c,d∈R . Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точки x1,x2∈[a;b] , чтоf(x1)=c,f(x2)=d. Докажем, например, существование точки x2.
По определению верхней грани имеем (∀x∈[a;b])(f(x)=d) . Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0 . Далее введем вспомогательную функцию ϕ(x)=1d−f(x). ϕ(x)на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x)на [a;b] ограничена. Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M) , отсюда имеем f(x)≤d−1M<d . Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, что f(x2)=d.
Аналогично доказывается существование точки x1∈[a;b] , такой что f(x1)=c.
Следствие Если f непрерывна и непостоянна на [a;b], то образ этого отрезка [a;b] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок. Доказательство: В самом деле образом отрезка [a;b] при отображении f будет отрезок [с;d], где c=inf[a;b]f(x)=min[a;b]f(x), а d=sup[a;b]f(x)=max[a;b]f(x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.
3. Теорема Ферма и Ролля
Пусть функция f(x) имеет на множестве E точку экстремума x₀?E, причём множество E содержит некоторую β- окрестность, что E=(x- β;x+ β) точки x. Тогда либо f(x) имеет в точке x производную, равную 0, то есть f´(x)=0 , либо производная в точке x не существует. Теорема Ролля Если функция f(x) непрерывна на отрезке (a;b), дифференцируема во всех внутренних точках этого отрезка и на концах x=a и x=b обращается в нуль, [f(a)=f(b)=0], то внутри отрезка (a;b) существует п окрпйней мере одна тоска x=c, a<c<b, в которой производная f´(x) обращается в нуль, т.е. f´(c)=0
Метод математической индукции
Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.
Метод математической индукции состоит в следующем:
Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:
P(1) является истинным предложением (утверждением);
P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).
Таким образом метод математической индукции предполагает два этапа:
Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).
Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).
Замечание 1. В некоторых случаях метод математической индукции используется в следующей форме:
Пусть m - натуральное число, m > 1 и P(n) - предложение, зависящее от n, n ≥ m.
Если
P(m) справедливо;
P(n) будучи истинным предложением, влечет истинность предложения P(n + 1) для любого натурального n, n ≥ m, тогда P(n) - истинное предложение для любого натурального n, n ≥ m.
В дальнейшем рассмотрим примеры применения метода математической индукции.
Пример 1. Доказать следующие равенства

g) формула бинома Ньютона:
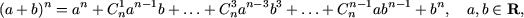
где n N.
Решение.
a) При n = 1 равенство
примет вид
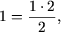 1=1,
следовательно, P(1)
истинно. Предположим, что данное равенство
справедливо, то есть, имеет место
1=1,
следовательно, P(1)
истинно. Предположим, что данное равенство
справедливо, то есть, имеет место
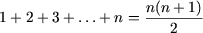 .
.
Следует проверить (доказать), что P(n + 1), то есть
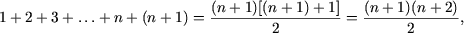
истинно. Поскольку (используется предположение индукции)
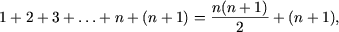
получим
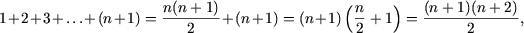
то есть, P(n + 1) - истинное утверждение.
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Замечание
2. Этот пример можно было
решить и иначе. Действительно, сумма 1
+ 2 + 3 + ... + n есть
сумма первых n
членов арифметической прогрессии с
первым членом a>1>
= 1 и разностью d =
1. В силу известной формулы
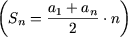 ,
получим
,
получим
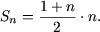
b) При n = 1 равенство примет вид: 2·1 - 1 = 12 или 1=1, то есть, P(1) истинно. Допустим, что имеет место равенство
1 + 3 + 5 + ... + (2n - 1) = n2
и докажем, что имеет место P(n + 1):
1 + 3 + 5 + ... + (2n - 1) + (2(n + 1) - 1) = (n + 1)2
или
1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = (n + 1)2.
Используя предположение индукции, получим
1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = n2 + (2n + 1) = (n + 1)2.
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При
n = 1 равенство
истинно:
 1=1.
Допустим, что истинно равенство
1=1.
Допустим, что истинно равенство
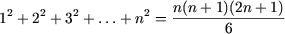
и покажем, что
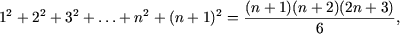
то есть истинность P(n) влечет истинность P(n + 1). Действительно,
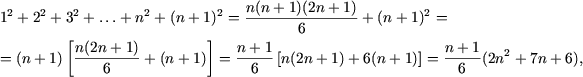
и, так как 2n2 + 7n + 6 = (2n + 3)(n + 2), получим
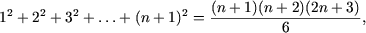
и, следовательно, исходное равенство справедливо для любого натурального n.
d) При
n = 1 равенство
справедливо:
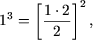 1=1.
Допустим, что имеет место
1=1.
Допустим, что имеет место
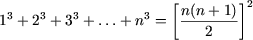
и докажем, что
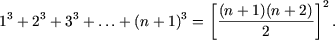
Действительно,
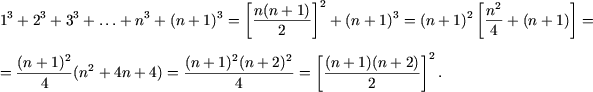
e)
Утверждение P(1)
справедливо:
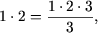 2=2.
Допустим, что равенство
2=2.
Допустим, что равенство
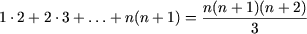
справедливо, и докажем, что оно влечет равенство
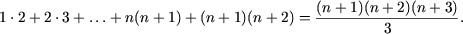
Действительно,
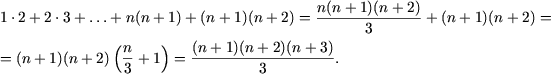
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1)
справедливо:
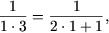 1/>3>
= 1/>3>.
Пусть имеет место равенство P(n):
1/>3>
= 1/>3>.
Пусть имеет место равенство P(n):
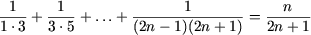 .
.
Покажем, что последнее равенство влечет следующее:
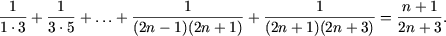
Действительно, учитывая, что P(n) имеет место, получим
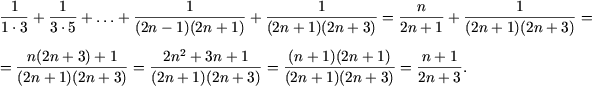
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
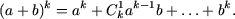
Тогда
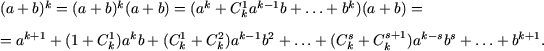
Используя
равенство
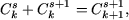 получим
получим
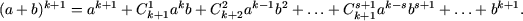
Пример 2. Доказать неравенства
a) неравенство Бернулли: (1 + )n ≥ 1 + n, > -1, n N.
b) x>1>
+ x>2>
+ ... + x>n>
≥ n,
если x>1>x>2>·
... ·x>n>
= 1 и x>i>
> 0,
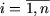 .
.
c) неравенство Коши относительно среднего арифемтического и среднего геометрического
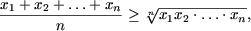 где x>i>
> 0,
где x>i>
> 0,
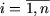 ,
n
≥ 2.
,
n
≥ 2.
d) sin2n + cos2n ≤ 1, n N.
e)
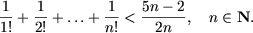
f) 2n > n3, n N, n ≥ 10.
Решение. a) При n = 1 получаем истинное неравенство
1 + ≥ 1 + .
Предположим, что имеет место неравенство
(1 + )n ≥ 1 + n (1)
и покажем, что тогда имеет место и
≥
≥
≥
≥,
≥≥
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
b) При n = 1 получим x>1> = 1 и, следовательно, x>1> ≥ 1 то есть P(1) - справедливое утверждение. Предположим, что P(n) истинно, то есть, если adica, x>1>,x>2>,...,x>n> - n положительных чисел, произведение которых равно единице, x>1>x>2>·...·x>n> = 1, и x>1> + x>2> + ... + x>n> ≥ n.
Покажем, что это предложение влечет истинность следующего: если x>1>,x>2>,...,x>n>,x>n>>+1> - (n + 1) положительных чисел, таких, что x>1>x>2>·...·x>n>·x>n>>+1> = 1, тогда x>1> + x>2> + ... + x>n> + x>n>> + 1> ≥ n + 1.
Рассмотрим следующие два случая:
1) x>1> = x>2> = ... = x>n> = x>n>>+1> = 1. Тогда сумма этих чисел равна (n + 1), и требуемое неравество выполняется;
2) хотя бы одно число отлично от единицы, пусть, например, больше единицы. Тогда, поскольку x>1>x>2>· ... ·x>n>·x>n>> + 1> = 1, существует еще хотя бы одно число, отличное от единицы (точнее, меньше единицы). Пусть x>n>> + 1> > 1 и x>n> < 1. Рассмотрим n положительных чисел
x>1>,x>2>,...,x>n>>-1>,(x>n>·x>n>>+1>).
Произведение этих чисел равно единице, и, согласно гипотезе,
x>1> + x>2> + ... + x>n>>-1> + x>n>x>n>> + 1> ≥ n.
Последнее неравенство переписывается следующим образом:
x>1> + x>2> + ... + x>n>>-1> + x>n>x>n>>+1> + x>n> + x>n>>+1> ≥ n + x>n> + x>n>>+1>
или
x>1> + x>2> + ... + x>n>>-1> + x>n> + x>n>>+1> ≥ n + x>n> + x>n>>+1> - x>n>x>n>>+1>.
Поскольку
(1 - x>n>)(x>n>>+1> - 1) > 0,
n + x>n> + x>n>>+1> - x>n>x>n>>+1> = n + 1 + x>n>>+1>(1 - x>n>) - 1 + x>n> = = n + 1 + x>n>>+1>(1 - x>n>) - (1 - x>n>) = n + 1 + (1 - x>n>)(x>n>>+1> - 1) ≥ n + 1.
Следовательно,
x>1> + x>2> + ... + x>n> + x>n>>+1> ≥ n+1,
то есть, если P(n) справедливо, то и P(n + 1) справедливо. Неравенство доказано.
Замечание 4. Знак равенства имеет место тогда и только тогда, когда x>1> = x>2> = ... = x>n> = 1.
c) Пусть x>1>,x>2>,...,x>n> - произвольные положительные числа. Рассмотрим следующие n положительных чисел:
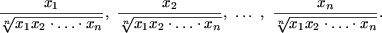
Поскольку их произведение равно единице:
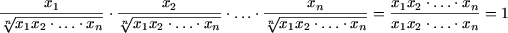
согласно ранее доказанному неравенству b), следует, что
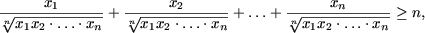
откуда
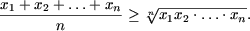
Замечание 5. Равенство выполняется если и только если x>1> = x>2> = ... = x>n>.
≤
≤
≤≤≤
e) При
n = 1 утверждение
справедливо:
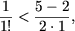 1 < 3/>2>.
1 < 3/>2>.
Допустим,
что
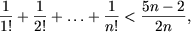 и
докажем, что
и
докажем, что
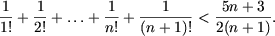
Поскольку
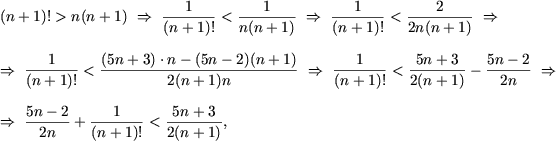
учитывая P(n), получим
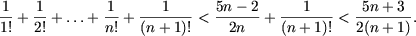
f) Учитывая замечание 1, проверим P(10): 210 > 103, 1024 > 1000, следовательно, для n = 10 утверждение справедливо. Предположим, что 2n > n3 (n > 10) и докажем P(n + 1), то есть 2n+1 > (n + 1)3.
Поскольку
при n > 10 имеем
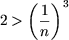 или
или
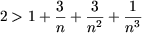 ,
следует, что
,
следует, что
2n3 > n3 + 3n2 + 3n + 1 или n3 > 3n2 + 3n + 1.
Учитывая неравенство (2n > n3), получим
2n+1 = 2n·2 = 2n + 2n > n3 + n3 > n3 + 3n2 + 3n + 1 = (n + 1)3.
Таким образом, согласно методу математической индукции, для любого ≥
a) n(2n2 - 3n + 1) делится на 6,
b) 62n-2 + 3n+1 + 3n-1 делится на 11.
Решение. a) P(1) - истинное утверждение (0 делится на 6). Пусть P(n) справедливо, то есть n(2n2 - 3n + 1) = n(n - 1)(2n - 1) делится на 6. Покажем, что тогда имеет место P(n + 1), то есть, (n + 1)n(2n + 1) делится на 6. Действительно, поскольку
n(n + 1)(2n + 1) = n(n - 1 + 2)(2n - 1 + 2) = (n(n - 1) + 2n)(2n - 1 + 2) =
= n(n - 1)(2n - 1) + 2n(n - 1) + 2n(2n + 1) = n(n - 1)(2n - 1) + 2n·3n =
= n(n - 1)(2n - 1) + 6n2
и, как n(n - 1)(2n - 1), так и 6n2 делятся на 6, тогда и их сумма n(n + 1)(2n + 1) делится 6.
Таким образом, P(n + 1) - справедливое утверждение, и, следовательно, n(2n2 - 3n + 1) делится на 6 для любого n N.
b) Проверим P(1): 60 + 32 + 30 = 11, следовательно, P(1) - справедливое утверждение. Следует доказать, что если 62n-2 + 3n+1 + 3n-1 делится на 11 (P(n)), тогда и 62n + 3n+2 + 3n также делится на 11 (P(n + 1)). Действительно, поскольку
62n + 3n+2 + 3n = 62n-2+2 + 3n+1+1 + 3n-1+1 =
= 62·62n-2 + 3·3n+1 + 3·3n-1 = 3·(62n-2 + 3n+1 + 3n-1) + 33·62n-2
и, как 62n-2 + 3n+1 + 3n-1, так и 33·62n-2 делятся на 11, тогда и их сумма 62n + 3n+2 + 3n делится на 11. Утверждение доказано.
Несобственные интегралы
Пусть функция
f(x)
определена на полуинтервале (a,
b]
и >
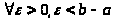 >,
>
>,
>
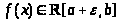 >;
кроме того
>;
кроме того
>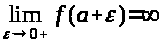 >
>
Определение: Несобственным интегралом 1рода от f(x) на (a, b] называется предел:
>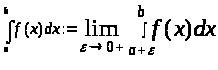 >
>
если этот предел существует. В этом случае говорят, что несобственный интеграл сходится.
Пример:
>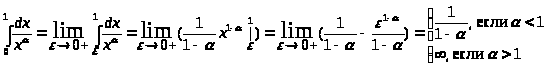 >
>
Если = 1, то
>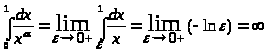 >
>
Следовательно, при < 1 интеграл
>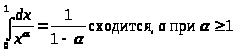 >
>
> >
>
Аналогично определяется несобственный интеграл, если
>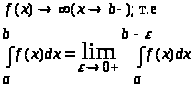 >
>
Определение несобственного интеграла 2 рода:
Пусть >
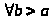 >:
>
>:
>
 >
и существует предел:
>
и существует предел:
>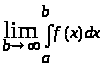 >
>
Тогда этот предел называется несобственным интегралом 2 рода, т.е.
> >
>
Пример:
>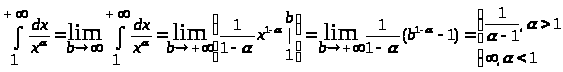 >
>
Если = 1, то
>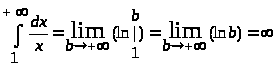 >
>
Следовательно, несобственный интеграл
>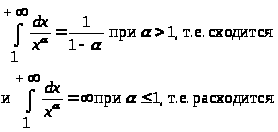 >
>
Для исследования сходимости и расходимости несобственных интегралов применяется признак сравнения:
Пусть функция
f(x)
и g(x)
удовлетворяют неравенству: >
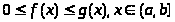 >и
несобственный интеграл >
>и
несобственный интеграл >
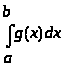 >
сходится. Тогда сходится и несобственный
интеграл >
>
сходится. Тогда сходится и несобственный
интеграл >
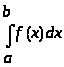 >.
>.
Доказательство:
В силу сходимости >
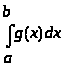 >
по критерию Коши для функции >
>
по критерию Коши для функции >
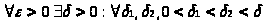 >,
выполняется неравенство >
>,
выполняется неравенство >
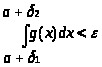 >.
Но тогда, ввиду неравенств: >
>.
Но тогда, ввиду неравенств: >
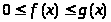 >
аналогично неравенство будет справедливо
и для функции f(x),
т.е.
>
аналогично неравенство будет справедливо
и для функции f(x),
т.е.
>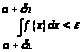 >
>
Следовательно, по критерию Коши существует предел:
>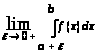 >,
>,
т.е. этот интеграл сходится.
Замечание1: Аналогичный признак сравнения справедлив и для несобственных интегралов 2 рода.
Замечание2:
Отрицанием признака сравнения будет
следующее утверждение: если несобственный
интеграл >
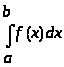 >
расходится, то расходится и несобственный
интеграл
>
расходится, то расходится и несобственный
интеграл
>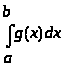 >.
>.
Эйлеровы интегралы () и (, ).
Определим функцию () равенством:
>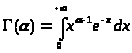 >.
>.
Покажем, что интеграл сходится при > 0. Представим этот интеграл в виде суммы двух интегралов:
>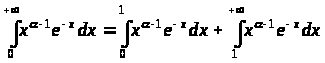 >
>
и докажем сходимость каждого из этих интегралов при > 0.
Обозначим
>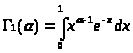 >
и >
>
и >
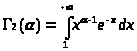 >.
>.
Если x(0,
1], то: >
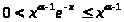 >.
Так как интеграл >
>.
Так как интеграл >
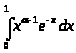 >,
как это было доказано выше сходится при
1 - <
1, т.е. при >0,
то по признаку сравнения интеграл >
>,
как это было доказано выше сходится при
1 - <
1, т.е. при >0,
то по признаку сравнения интеграл >
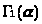 >
сходится при >0.
Если x[1,
+ >
>
сходится при >0.
Если x[1,
+ >
 >)
, то для некоторой константы c>0
выполняется неравенство: >
>)
, то для некоторой константы c>0
выполняется неравенство: >
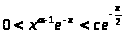 >.
>.
Заметим, что
>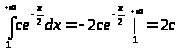 >,
>,
т.е. этот интеграл сходится при любых R. Следовательно, функция Эйлера () = >1>() + >2>() определена для всех >0.
Далее, определим функцию
(,
)
= >
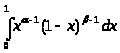 >
>
и докажем, что эта функция определена для любых >0 и >0.
Обозначим:
>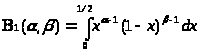 >
и >
>
и >
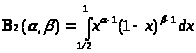 >.
>.
Если x(0,
1/2], то >
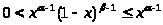 >.
Интеграл >
>.
Интеграл >
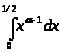 >
сходится по признаку сравнения 1 - <1,
т.е. при >0
и при любых значениях .
Заметим, что, если в интеграле >2>(,
)
сделать замену t
= 1 – x,
то мы >1>(,
),
который, как мы выяснили, сходится при
>0
и при любых .
>
сходится по признаку сравнения 1 - <1,
т.е. при >0
и при любых значениях .
Заметим, что, если в интеграле >2>(,
)
сделать замену t
= 1 – x,
то мы >1>(,
),
который, как мы выяснили, сходится при
>0
и при любых .
Следовательно, функция Эйлера (, ) = >1>(, ) + >2>(, ) определена для любых >0 и >0. Отметим (без доказательства) следующие свойства интегралов Эйлера:
(1) = 1
( + 1) = (), >0
(n + 1) = n!, nN
()(1 - ) =>
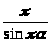 >,
0<<1
>,
0<<1(1/2) = >
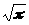 >
>(, ) = >
 >
>
Пример:
Вычислить интеграл вероятности
> >.
>.
В силу чётности
функции >
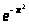 >
интеграл вероятности можно представить
в виде:
>
интеграл вероятности можно представить
в виде:
>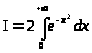 >.
>.
Сделав в этом интеграле замену t = x2 , получим следующий интеграл:
>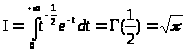 >
>