Старший и верхний центральный показатели линейной системы
1
М ИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ
ИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ
БЕЛАРУСЬ
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
Математический факультет
Кафедра дифференциальных уравнений
Допущена к защите
Зав. кафедрой
СТАРШИЙ И ВЕРХНИЙ ЦЕНТРАЛЬНЫЙ ПОКАЗАТЕЛИ ЛИНЕЙНОЙ СИСТЕМЫ
Дипломная работа
Исполнитель:
студентка группы М-51 Абраменко Т. Ф.
Научный руководитель:
доцент кафедры дифференциальных
уравнений, к. ф.-м. н. Зверева Т.Е.
Рецензент:
доцент кафедры ВМ и
программирования, к. ф.-м. н. Смородин В.С.
Гомель 2003
Содержание

ВВЕДЕНИЕ
1 НЕОБХОДИМЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
2 СООТНОШЕНИЕ
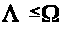
3 СТАРШИЙ И ВЕРХНИЙ ЦЕНТРАЛЬНЫЙ ПОКАЗАТЕЛИ ДЛЯ ДИАГОНАЛЬНОЙ СИСТЕМЫ
3.1 Старший и верхний центральный показатели для диагональной системы с произвольными коэффициентами
3.2 Старший и верхний центральный показатели для диагональной системы с постоянными коэффициентами
4 СТАРШИЙ И ВЕРХНИЙ
ЦЕНТРАЛЬНЫЙ ПОКАЗАТЕЛИ НЕКОТОРОЙ
ЛИНЕЙНОЙ ОДНОРОДНОЙ ДИАГОНАЛЬНОЙ
СИСТЕМЫ. СЛУЧАЙ
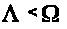
4.1 Старший показатель некоторой линейной однородной диагональной системы
4.2 Верхний центральный показатель некоторой линейной однородной диагональной системы
5 ОСНОВНЫЕ СВОЙСТВА ВЕРХНЕГО ЦЕНТРАЛЬНОГО ПОКАЗАТЕЛЯ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
В данной дипломной работе проводится изучение таких понятий, как верхний центральный показатель системы, характеристические показатели Ляпунова; рассматриваются различные соотношения между старшим и верхним центральным показателями линейных систем, то есть рассматриваются случаи, когда старший показатель Ляпунова строго меньше, равен верхнему центральному показателю.
В дипломной работе проводится
исследование конкретной линейной
однородной диагональной системы:
вычисляются характеристические
показатели системы, находятся спектр
системы, старший показатель системы, а
также верхний центральный показатель
этой же системы, устанавливается
соотношение
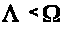 На конкретном примере выясняется, что
роль оценки сверху показателей решений
возмущенных систем
На конкретном примере выясняется, что
роль оценки сверху показателей решений
возмущенных систем
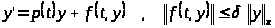
играет число
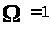 ,
а не
,
а не
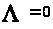 .
.
1. НЕОБХОДИМЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение 1.1
[1,с.123]. Наибольший из частичных пределов
a
функции
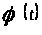 при
при
 называется ее верхним пределом:
называется ее верхним пределом:
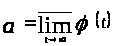 .
.
Определение 1.2
[1,с.125]. Число (или символ
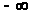 или
или
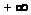 ),
определяемое формулой
),
определяемое формулой
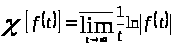 .
.
будем называть характеристическим показателем Ляпунова (или характерисическим показателем).
Для показательной функции
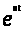 , очевидно, имеем
, очевидно, имеем
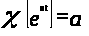 .
.
Лемма 1.1 [1,с.132].
Характеристический показатель
конечномерной матрицы
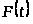 совпадает с характеристическим
показателем ее нормы, то есть
совпадает с характеристическим
показателем ее нормы, то есть
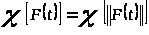 .
.
Для вектор-столбца
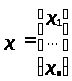
будем использовать одну из норм [1,с.20]:
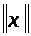 =
=
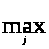
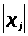 ;
;
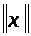 =
=
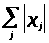 ;
;
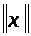 =
=
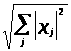 .
.
Свойства характеристического показателя функции [1,с.126,128]:
1)

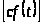 =
=

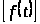 ,
,
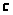
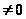 ;
;
2)

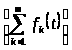
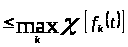 .
.
Замечание 1.1 [1,с.130]. Если линейная комбинация функций
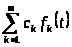 ,
,
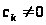 ,
,
где
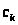 постоянны, содержит лишь одну функцию
с наибольшим характеристическим
показателем, то
постоянны, содержит лишь одну функцию
с наибольшим характеристическим
показателем, то

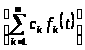 =
=
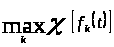 .
.
Определение 1.3 [1,с.142]. Система ненулевых вектор-функций
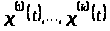
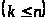
обладает свойством несжимаемости, если характеристичесий показатель любой существенной их линейной комбинации
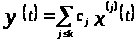 ,
,
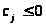 ,
,
где
 постоянны, совпадает с наибольшим из
характеристических показателей
комбинируемых вектор-функций, то есть
для всякой комбинации y
имеем
постоянны, совпадает с наибольшим из
характеристических показателей
комбинируемых вектор-функций, то есть
для всякой комбинации y
имеем

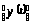 =
=
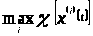 .
.
Определение 1.4
[1,с.137]. Множество всех собственных
характеристических показателей (то
есть отличных от
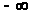 и
и
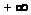 )
решений дифференциальной системы будем
называть ее спектром.
)
решений дифференциальной системы будем
называть ее спектром.
Теорема 1.1 [1,с.143]. Фундаментальная система линейной системы

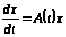 ,
,
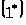
где
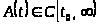 и
и
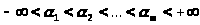
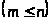 ─
спектр системы
─
спектр системы
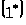 ,
является нормальной тогда и только
тогда, когда она обладает свойством
несжимаемости.
,
является нормальной тогда и только
тогда, когда она обладает свойством
несжимаемости.
Замечание 1.2 [1,с.142]. Совокупность вектор-функций с различными характеристическими показателями, очевидно, обладает свойством несжимаемости.
Следствие 1.1 [1,с.145]. Всякая нормальная фундаментальная система реализует весь спектр линейной системы.
Определение1.5 [2,с.71]. Наибольший верхний показатель
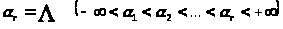
системы
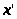
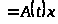
будем называть старшим показателем.
Определение 1.6
[2,с.7]. Пусть
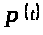 ─
функция. Тогда верхнее среднее значение
функции
─
функция. Тогда верхнее среднее значение
функции
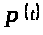 есть:
есть:
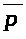 =
=
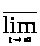
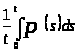 .
.
Рассмотрим какое-либо семейство кусочно непрерывных и равномерно ограниченных функций:
=
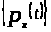 ,
,
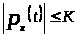 ,
,
зависящие от параметра
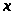 непрерывна в том смысле, что из
непрерывна в том смысле, что из
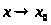 следует
следует
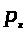
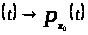 равномерно, по крайней мере, на каждом
конечном отрезке
равномерно, по крайней мере, на каждом
конечном отрезке
 .
.
Определение 1.7 [
2,с.103]. Ограниченная измеримая функция
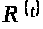 называется верхней или C-функцией
для семейства ,
если все функции этого семейства
равномерно не превосходят в интегральном
смысле функции
называется верхней или C-функцией
для семейства ,
если все функции этого семейства
равномерно не превосходят в интегральном
смысле функции
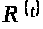 :
:
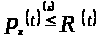 ,
,
то есть, если
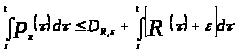 ,
,
где
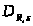 ─
константа, общая для всех
─
константа, общая для всех
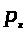 и
и
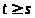 ,
но, вообще говоря, зависящая от выбора
,
но, вообще говоря, зависящая от выбора
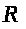 и
и
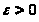 .
.
Определение 1.8 [2, с.103]. Совокупность всех верхних функций назовем верхним классом или C-классом семейства , и обозначим через
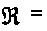
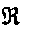 ().
().
Определение 1.9 [2,с.103]. Число
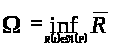
назовем верхним центральным или
C-числом
семейства .
Оно обозначается также через
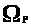 >
>или
>
>или
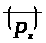 .
.
Утверждение 1.1
[2, с. 104]. Если существует такая C-функция
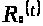 ,
что
,
что
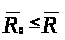
для всех
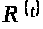 ,
то эта функция одна образует верхний
класс и C-число
совпадает с
,
то эта функция одна образует верхний
класс и C-число
совпадает с
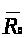 :
:
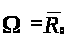 .
.
Замечание 1.3 [2,с.102]. Для упрощения записи введем обозначение
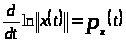
Определение 1.10 [2,с.115]. Центральное число семейства будем называть центральным показателем системы
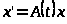 .
.
Определение 1.11 [2,с.106].
Разобьем полуось
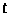 точками 0,T,2T,…
на промежутки
точками 0,T,2T,…
на промежутки
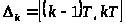 .
.
Пусть
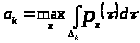 .
.
Найдем
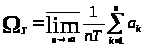 .
.
Замечание 1.4 [2,с.106]. Число
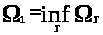
совпадает с
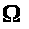 и знак
и знак
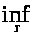 можно
заменить на
можно
заменить на
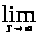 , то есть
, то есть
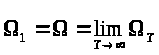 .
.
Определение 1.12 [2,с.107].
Пусть
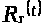 ─ любая ограниченная кусочно непрерывная
функция, для которой
─ любая ограниченная кусочно непрерывная
функция, для которой
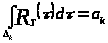
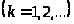 .
.
Замечание 1.5 [2,с.107].
Такие функции существуют: достаточно
положить
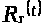 на
на
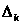 равной одной из тех функций
равной одной из тех функций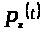 ,
для которых достигается максимальное
значение
,
для которых достигается максимальное
значение
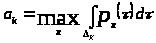 .
.
Утверждение 1.2 [2,с.537].
Верхнее среднее значение любой
ограниченной кусочно непрерывной
функции, а в частности функции
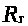 ,
где
,
где
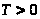 произвольное, равно
произвольное, равно
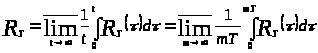 .
.
Утверждение 1.3 [2,с.114]. Пусть
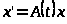 ,
,
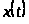 ─
ее решение и
─
ее решение и
=
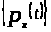 ─
─
семейство кусочно непрерывных и равномерно ограниченных функций, где
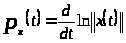 .
.
Тогда старший показатель этой
системы равен наибольшему из верхних
средних значений функций
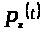 семейства ,
то есть
семейства ,
то есть
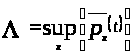 .
.
2. СООТНОШЕНИЕ
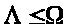 .
.
Рассмотрим какое-либо семейство кусочно непрерывных и равномерно ограниченных функций:
=
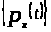 ,
,
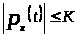 ,
,
зависящее от параметра
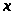 непрерывно в том смысле, что из
непрерывно в том смысле, что из
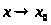 следует
следует
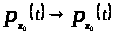 равномерно, по крайней мере, на каждом
конечном отрезке
равномерно, по крайней мере, на каждом
конечном отрезке
 .
.
Для доказательства соотношения
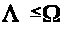 нам потребуется доказать несколько
утверждений и следствий.
нам потребуется доказать несколько
утверждений и следствий.
Утверждение 1.
Если семейство сужается, то его верхний класс может только расшириться, а верхнее число уменьшиться, то есть из
’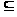
следует
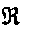 (’)
(’)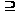
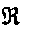 ()
()
и
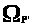 >
>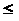
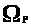 >>.>
>>.>
Доказательство.
Всякая верхняя функция
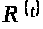 для семейства
является верхней и для ’,
так как ’
для семейства
является верхней и для ’,
так как ’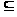 .
Значит,
.
Значит,
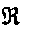 ()
()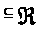 (’).
(’).
По определению 1.9

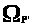
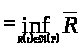 .
.
Из того, что
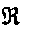 ()
()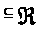 (’)
(’)
следует
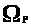 >
> >.
>.
А значит,
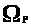
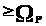 .
.
Утверждение 1 доказано.
Утверждение 2.
Если семейство ’
состоит из одной функции
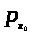
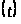 ,
то есть ’=
,
то есть ’=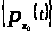 ,
то верхнее среднее значение функции
,
то верхнее среднее значение функции
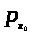
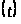 совпадает с верхним центральным числом
семейства ’,
то есть
совпадает с верхним центральным числом
семейства ’,
то есть
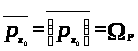
Доказательство.
Для доказательства равенства
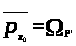
докажем два неравенства:
1)
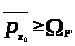 ;
;
2)
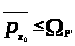 >.>
>.>
Из определения 1.7 следует, что
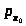
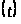 является верхней функцией, то есть
является верхней функцией, то есть
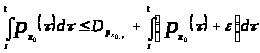 ,
,
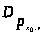 =
0;
=
0;
итак,
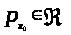 (’).
(’).
Следовательно,
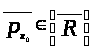 .
.
Пусть
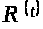 ─
любая верхняя функция семейства ’:
─
любая верхняя функция семейства ’:
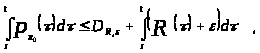
для любой
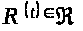 (’).
(’).
Тогда по определению 1.6
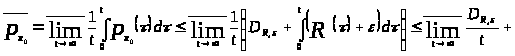
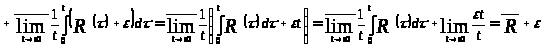 .
.
Так как
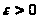 ─
любое, то
─
любое, то
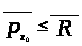
для любой функции
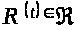 ().
().
Следовательно,
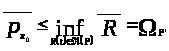 >.>
>.>
Тем самым утверждение 2 доказано.
Следствие 1.(из утверждений 1 и 2)
Пусть
=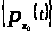 ─
семейство кусочно непрерывных функций
и равномерно ограниченных функций.
Тогда если семейство ’
состоит из одной функции
─
семейство кусочно непрерывных функций
и равномерно ограниченных функций.
Тогда если семейство ’
состоит из одной функции
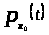 ,
то есть ’=
,
то есть ’=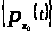 , и ’
, и ’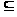
, то верхнее среднее значение функции
, то верхнее среднее значение функции
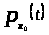 не превосходит верхнего центрального
числа семейства ,
то есть
не превосходит верхнего центрального
числа семейства ,
то есть
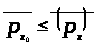 .
.
Доказательство.
Так как ’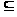 ,
то из утверждения 1 следует, что
,
то из утверждения 1 следует, что
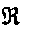 (’)
(’)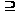
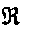 ()
()
и
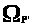
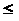
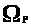 >
.>
>
.>
Так как ’
состоит из одной функции, то есть ’=
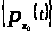 ,
то из утверждения 2 следует, что
,
то из утверждения 2 следует, что
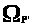
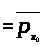 .
.
Следовательно,

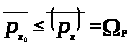 >,>
>,>
то есть
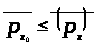 .
.
Следствие 1 доказано.
Следствие 2.(из следствия 1)
Пусть
=
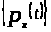 ─
семейство кусочно непрерывных и
равномерно ограниченных функций. Тогда
─
семейство кусочно непрерывных и
равномерно ограниченных функций. Тогда
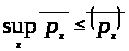 .
.
Доказательство.
Из следствия 1 вытекает, что для
любого
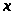 выполняется
выполняется
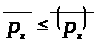 .
.
Следовательно,
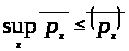 .
.
Следствие 2 доказано.
Воспользуемся доказательством следствия 2 для доказательства следующего утверждения.
Утверждение 3.
Пусть
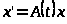 ─
─
некоторая линейная система дифференциальных уравнений и
=
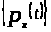 ─
─
семейство кусочно непрерывных и равномерно ограниченных функций, где
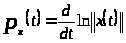 .
.
Тогда старший показатель Ляпунова
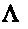 не превосходит верхнего центрального
числа
не превосходит верхнего центрального
числа
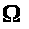 семейства ,
то есть
семейства ,
то есть
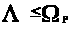 >.>
>.>
Доказательство.
Так как
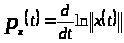 ,
,
то
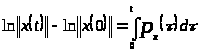 .
.
Выразим из последнего равенства
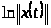 :
:
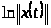
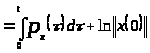 ,
,

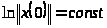 .
.
Тогда из определения 1.2 следует, что
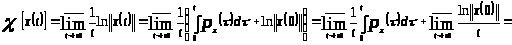
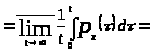 [определение
1.6]
[определение
1.6]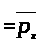 ,
,
то есть
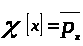 .
.
Из этого следует, что
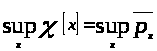 .
.
Так как по определению 1.5
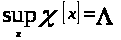 ,
,
то
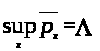 .
.
Тогда из следствия 2 получаем, что
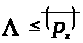 .
.
Так как по определению 1.9
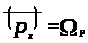 >,>
>,>
то
 .
.
(утверждение 3 доказано)
3 СТАРШИЙ И ВЕРХНИЙ ЦЕНТРАЛЬНЫЙ ПОКАЗАТЕЛИ ДЛЯ ДИАГОНАЛЬНОЙ СИСТЕМЫ
3.1 Старший и верхний центральный показатели для диагональной системы с произвольными коэффициентами
Исследуем случай, когда матрица
системы с произвольными коэффициентами
является диагональной. Найдем для нее
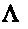 и
и
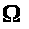 .
.
Рассмотрим диагональную систему
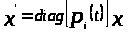 ,
,
где
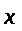 ─
вектор-функция размерности
─
вектор-функция размерности
 .
Она имеет матрицу Коши
.
Она имеет матрицу Коши
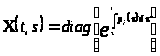 ,
,
то есть
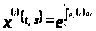 ,
,
с нормой
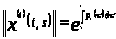 ,
где
,
где
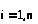 .
.
По определению 1.2 найдем для
каждой функции
 ее характеристический показатель
Ляпунова, используя определение 1.6:
ее характеристический показатель
Ляпунова, используя определение 1.6:
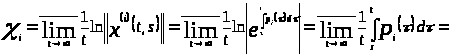
 .
.
Получаем, что
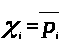 .
.
Из утверждения 1.3 и определения 1.5 вытекает, что
 ,
,
так как матрица конечномерная.
По определению 1.9
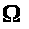 >>>
>>>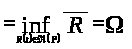 ,>
,>
где
 ().
().
3.2 Старший и верхний центральный
показатели для диагональной системы с
постоянными коэффициентами. Случай
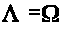 .
.
Исследуем случай, когда матрица
системы с постоянными коэффициентами
является диагональной. Найдем для нее
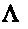 и
и
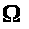 .
.
Рассмотрим диагональную систему
 ,
,
где
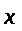 ─
вектор-функция размерности
─
вектор-функция размерности
 ,
,
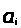 ─
некоторые числа,
─
некоторые числа,
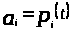 .
.
Она имеет матрицу Коши
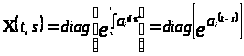 ,
,
то есть
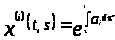 ,
,
с нормой
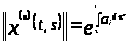 .
.
Рассмотрим следующую лемму.
Лемма*.
Пусть
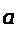 ─
некоторое число. Тогда
─
некоторое число. Тогда
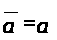 .
.
Доказательство.
По определению 1.6
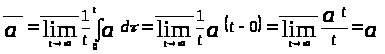 .
.
Имеем,
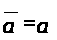 .
Что и требовалось доказать.
.
Что и требовалось доказать.
На основании предыдущего пункта заметим, что
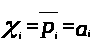 .
.
Тогда
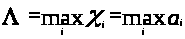 .
.
Теперь покажем, что
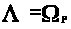 .
.
Пусть
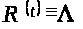 .
.
Так как для любого
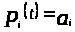
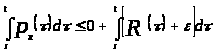 ,
,
то по определению 1.7
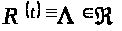 ().
().
Тогда по определению 1.9 и лемме*
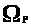 >
>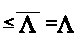 .>
.>
Так как
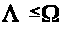 выполняется
всегда, то
выполняется
всегда, то
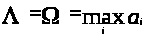 .
.
Следовательно, для диагональной системы с постоянными коэффициентами всегда
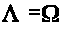 .
.
4 ВЫЧИСЛЕНИЕ СТАРШЕГО И ВЕРХНЕГО
ЦЕНТРАЛЬНОГО ПОКАЗАТЕЛЕЙ ДЛЯ ЗАДАННОЙ
СИСТЕМЫ. СЛУЧАЙ
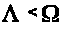 .
.
4.1 Вычисление старшего показателя системы.
Рассмотрим систему
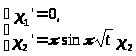 (1)
(1)
Решим ее.
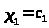 ,
,
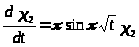 ,
,
получили уравнение с разделяющимися переменными.
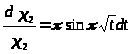 ,
,
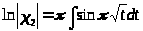 ,
,
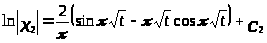 ,
,
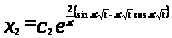 .
.
Общее решение системы (1) имеет вид:
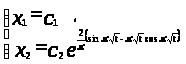
Возьмем 1)
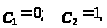
2)
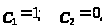
тогда получим два решения системы:
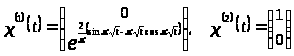 .
.
Составим матрицу решений системы (1).
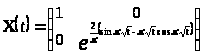 .
.
Проверим ее на фундаментальность:
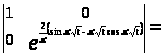
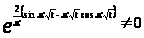 .
.
Следовательно [1,с.70], матрица
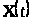 фундаментальна.
фундаментальна.
Перейдем к вычислению показателей
решений
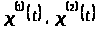 .
.
По определению [1,с.20] вычислим норму:
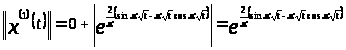 ;
;
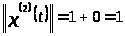 .
.
По определению 1.2 вычислим характеристические показатели, используя лемму 1.1:
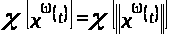 ,
,
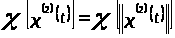 .
.
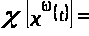
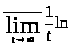
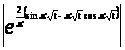
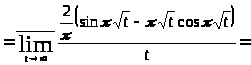
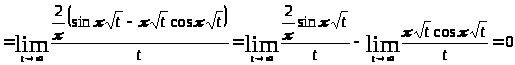 ,
,
так как функции
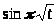 и
и
 ограниченные.
ограниченные.
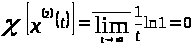 .
.
Проверим на несжимаемость систему
вектор-функций
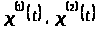 ,
используя определение 1.3.
,
используя определение 1.3.
Составим линейную комбинацию
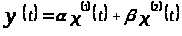 ,
где
,
где
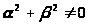 ,
,
и рассмотрим три случая: 1)
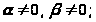
2)
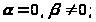

3)
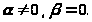
В первом случае
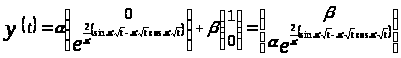 .
.
Во втором случае
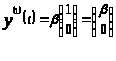 .
.
В третьем случае
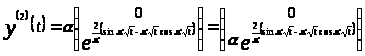 .
.
Найдем нормы
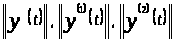 :
:
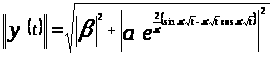 ;
;
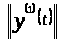
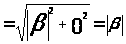 ;
;
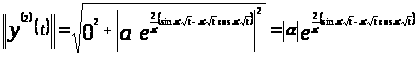 .
.
Итак,
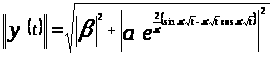 ,
,
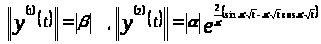 .
.
В силу определения 1.2:
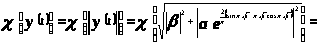
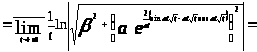
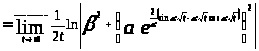 .
.
Так как
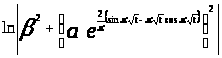
 ─ ограниченная величина, то
─ ограниченная величина, то
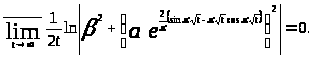
А значит,
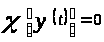 .
.
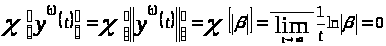 ;
;
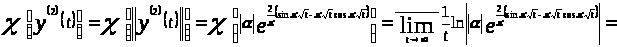
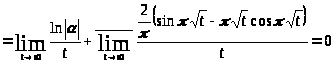 ;
;
По определению 1.3 следует, что
характеристический показатель линейной
комбинации
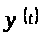 совпадает с наибольшим из характеристических
показателей комбинируемых решений, то
есть
совпадает с наибольшим из характеристических
показателей комбинируемых решений, то
есть
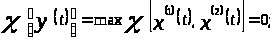

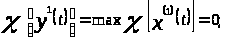
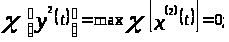
А это означает, что система (1)
обладает свойством несжимаемости. Тогда
по теореме 1.1 наша фундаментальная
система нормальная. По следствию 1.1
вытекает, что
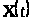 реализует весь спектр линейной системы.
Значит, спектр системы состоит из одного
числа:
реализует весь спектр линейной системы.
Значит, спектр системы состоит из одного
числа:
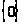 .
.
По определению 1.5 старший показатель системы (1) равен нулю, то есть
 .
.
4.2 Вычисление верхнего центрального показателя системы
По-прежнему рассматриваем систему (1):
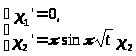 .
.
Применительно к нашей системе
семейство кусочно непрерывных и
равномерно ограниченных функций
состоит из двух функций
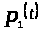 и
и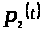 ,
то есть
,
то есть
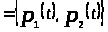 ,
,
где
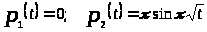
Для вычисления верхнего
центрального показателя
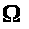 нам понадобится функция
нам понадобится функция
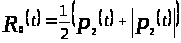 .
.
Докажем, что функция
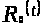 является верхней для семейства .
является верхней для семейства .
Доказательство:
По определению 1.7
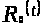 ─
верхняя функция для семейства ,
если
─
верхняя функция для семейства ,
если
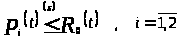 .
.
Докажем, что
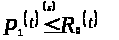 .
.
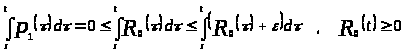 .
.
Следовательно,
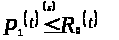 .
.
Докажем, что 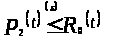 .
.
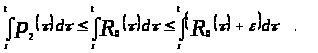
Следовательно,
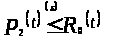 ,
,
то есть для любого
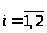
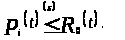
Тогда по определению верхней функции
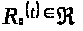 ()
.
()
.
Вычислим
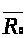 .
.
По определению 1.6 верхнего среднего значения функции

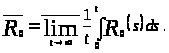
Для всякого
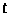 найдется такое
найдется такое
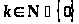 ,
что
,
что
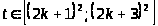 .
.
Тогда
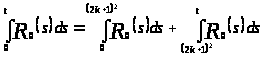 .
.
Вычислим отдельно
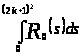 .
.
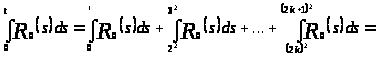
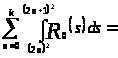
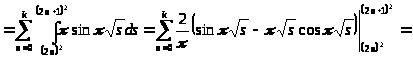
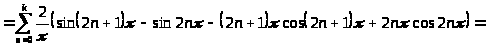
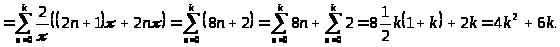
Итак,
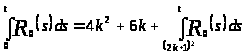 .
.
Оценим сверху 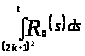 .
.
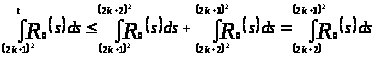 .
(*)
.
(*)
Учитывая (*) и оценивая
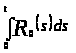 сверху,
получаем
сверху,
получаем
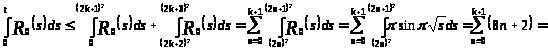
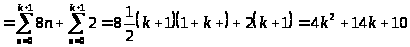 .
.
Тогда (при
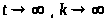 )
)
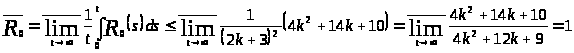 ,
,
то есть
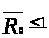 .
.
Оценивая
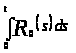 снизу,
получаем
снизу,
получаем
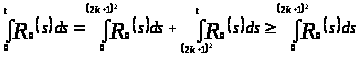 ,
,
где
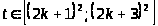 .
.
Тогда
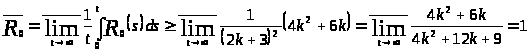 ,
,
то есть
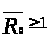 .
.
Следовательно,
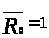 .
.
Теперь изобразим функции
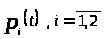 ,
и
,
и
 на графике.
на графике.
График функции
 :
:
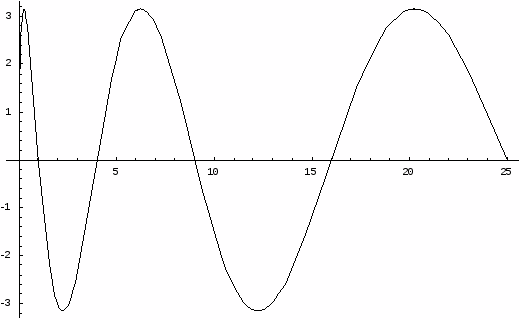





График функции
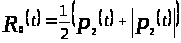 :
:
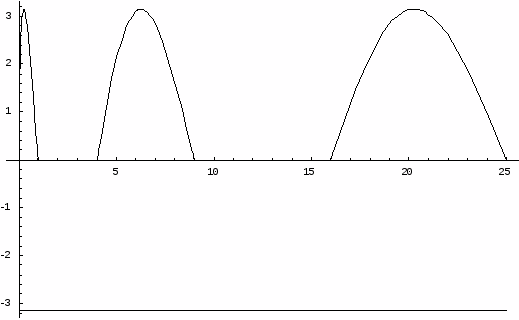


Очевидно, что на отрезках
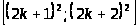
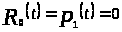 ,
,
а на отрезках
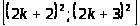
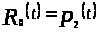 для любого
для любого
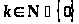 .
.
Теперь покажем, что верхний
центральный показатель
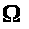 совпадает с
совпадает с
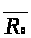 ,
то есть
,
то есть
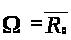 .
.
Докажем следующим образом:
1.Введем функцию
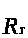 .
.
Разобьем ось
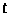 на промежутки
на промежутки
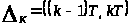 точками
точками
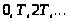
Используя определение 1.12, положим
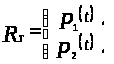 если
если
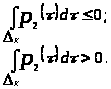
Оценим
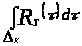 .
.
Возможны три случая:
если
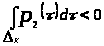 ,
то
,
то
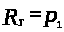 ;
значит,
;
значит,
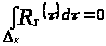 .
.
2) если
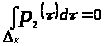 ,
то
,
то
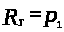 ;
значит,
;
значит,
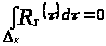 .
.
если
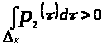 ,
то
,
то
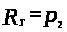 ;
значит,
;
значит,
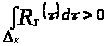 .
.
Таким образом,
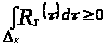 .
.
2.Докажем, что
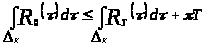 .
.
Очевидно, что
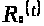 ─
функция ограниченная и
─
функция ограниченная и
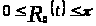 .
.
Отсюда следует, что
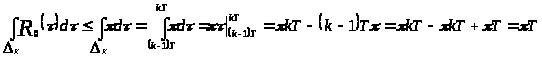 ,
,
то есть
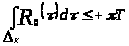 ,
,
Так как
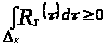 ,
,
то
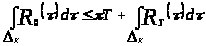 .
.
3.Докажем, что
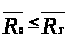 для любого
для любого
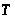 .
.
По определению 1.6 вычислим
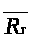 ,
используя утверждение 1.2:
,
используя утверждение 1.2:
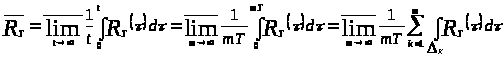 .
.
По определению 1.6 вычислим
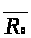 ,
используя утверждение 1.2:
,
используя утверждение 1.2:
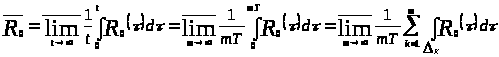 .
.
Теперь рассмотрим все возможные
случаи расположений отрезков
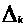 по отношению к отрезкам
по отношению к отрезкам
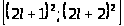 и
и
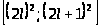 .
.
I. Если
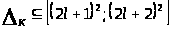 ,
где
,
где
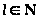 ,
то
,
то
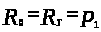 ,
,
следовательно,
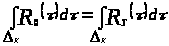 ;
;
II. если
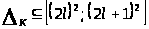 ,
где
,
где
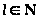 ,
то
,
то
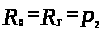 ,
,
следовательно,
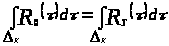 ;
;

III. если
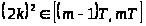 ,
,
то
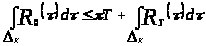 ;
;
IV. если
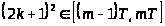 ,
,
то
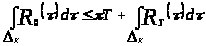 ;
;
Для каждого
 найдется такое
найдется такое
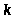 ,
что выполняется
,
что выполняется
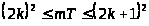 .
.
Тогда
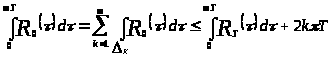 ;
;
Для каждого
 найдется такое
найдется такое
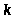 ,
что выполняется
,
что выполняется
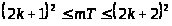 .
.
Тогда
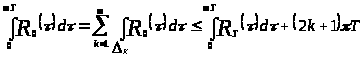 .
.
Из вышеперечисленных случаев 1) и 2) следует, что
 , (**)
, (**)
для любого
 такого, что
такого, что
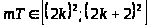 ,
,
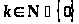 .
.
Учитывая неравенство (**), перейдем
к непосредственному доказательству
неравенства
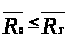 :
:
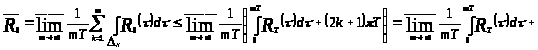
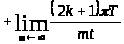 .
.
Теперь оценим выражение
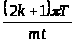 .
.
Очевидно, выполняется следующее неравенство:
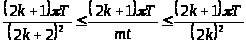 .
.
Перейдем к пределам:
 ,
,
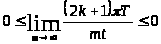 .
.
Следовательно,
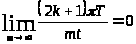 .
.
Значит,
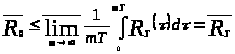 ,
,
то есть для любого
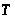
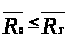 .
.
По определению 1.11
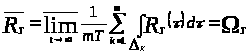 .
.
Таким образом,
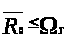 для любого
для любого
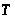 .
.
По замечанию 1.4 получаем, что
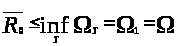 .
.
Следовательно,
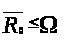 .
.
Так как мы доказали, что
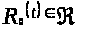 (),
то есть
(),
то есть  -
верхняя функция для семейства ,
то, опираясь на определение 1.9, получаем,
что
-
верхняя функция для семейства ,
то, опираясь на определение 1.9, получаем,
что
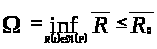 ,
,
то есть
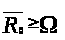 .
.
А значит,
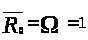 .
.
Итак, в этом разделе был рассмотрен случай
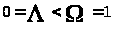 .
.
5. ОСНОВНЫЕ СВОЙСТВА ВЕРХНЕГО ЦЕНТРАЛЬНОГО ПОКАЗАТЕЛЯ
Р.Э. Виноград ввел[5] понятие
верхнего центрального показателя
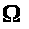 системы
системы
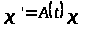 .
(1)
.
(1)
Переход от невозмущенной системы (1) к возмущенной системе
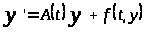
сопровождается изменением
показателей. Верхний центральный
показатель
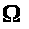 системы (1) и характеризует это изменение
в определенном классе возмущений. Имеет
место теорема Р.Э. Винограда.
системы (1) и характеризует это изменение
в определенном классе возмущений. Имеет
место теорема Р.Э. Винограда.
Теорема [2,с.164-166;3]. Для любого
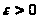 можно указать
можно указать
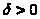 ,
что при любых непрерывных возмущениях
,
что при любых непрерывных возмущениях
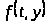 ,
,
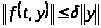 ,
,
будут выполняться неравенства
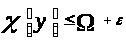 .
.
В.В. Миллионщиковым доказано, что последняя оценка неулучшаема, а именно
Теорема [4]. Для любого
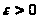 найдется возмущение
найдется возмущение
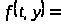 Q>>>
Q>>>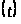 >
>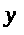 ,
||Q>>>
,
||Q>>>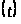 >||
>||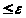 ,
,
такое, что система
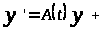 Q>>>
Q>>>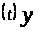 >
>
имеет решение
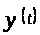 ,
для которой
,
для которой
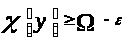 .
.
Значит, для рассмотренной в
дипломной работе системы наиболее
быстро растущими решениями «руководит»
показатель
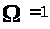 ,
а не показатель
,
а не показатель
 .
.
ЗАКЛЮЧЕНИЕ
В данной дипломной работе
рассматриваются соотношения между
старшим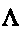 и
верхним центральным
и
верхним центральным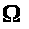 показателями
линейной системы
показателями
линейной системы
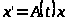
с кусочно непрерывными ограниченными коэффициентами.
Показано, что существует два
различных случая отношений между старшим
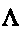 и верхним центральным
и верхним центральным
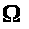 показателями
линейных систем:
показателями
линейных систем:
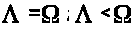 .
На примере заданной линейной однородной
диагональной системы дифференциальных
уравнений подробно рассмотрены вычисления
характеристического показателя Ляпунова,
спектра, старшего и верхнего центрального
показателей.
.
На примере заданной линейной однородной
диагональной системы дифференциальных
уравнений подробно рассмотрены вычисления
характеристического показателя Ляпунова,
спектра, старшего и верхнего центрального
показателей.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Б.П. Демидович, Лекции по математической теории устойчивости.-
Москва, «Наука», 1967г.
2. Б.Ф. Былов, Р.Э. Виноград, Д.М. Гробман, В.В. Немыцкий, Теория
показателей Ляпунова и ее приложения к вопросам устойчивости.- Москва, «Наука», 1966г.
3. Р.Э. Виноград, Оценка скачка старшего характеристического
показателя при малых возмущениях.-Докл. АН СССР, 1957г., т.114, №3, с.459-461.
4. В.М. Миллионщиков, Доказательство достижимости центральных показателей линейных систем.- Сиб. мат.ж., 1969г., т.10, №1, с.99-104.
5. Р.Э. Виноград, О центральном характеристическом показателе системы дифференциальных уравнений.- Матем.сб., 1957г., т.42(84), С.207-222.