Логарифмические уравнения
1
Введение
Логарифмы были придуманы для ускорения и упрощения вычислений. Идея логарифма, т. е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития. Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632) Первым опубликовал работу Непер в 1614г. под названием «Описание удивительной таблицы логарифмов», теория логарифмов Непера была дана в достаточно полном объёме, способ вычисления логарифмов дан наиболее простой, поэтому заслуги Непера в изобретении логарифмов больше, чем у Бюрги. Бюрги работал над таблицами одновременно с Непером, но долгое время держал их в секрете и опубликовал лишь в 1620г. Идеей логарифма Непер овладел около1594г. хотя таблицы опубликовал через 20 лет. Вначале он называл свои логарифмы «искусственными числами» и уже потом предложил эти «искусственные числа» называть одним словом «логарифм», который в переводе с греческого- «соотнесённые числа», взятые одно из арифметической прогресси, а другое из специально подобранной к ней геометрической прогресси. Первые таблицы на русском языке были изданы в1703г. при участии замечательного педагога 18в. Л. Ф Магницкого. В развитии теории логарифмов большое значение имели работы петербургского академика Леонарда Эйлера. Он первым стал рассматривать логарифмирование как действие, обратное возведению в степень, он ввёл в употребление термины «основание логарифма» и «мантисса» Бригс составил таблицы логарифмов с основанием 10. Десятичные таблицы более удобны для практического употребления, теория их проще, чем у логарифмов Непера. Поэтому десятичные логарифмы иногда называют бригсовыми. Термин «характеристика» ввёл Бригс.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Логарифмические уравнения и неравенства
1. Логарифмические уравнения
Уравнение, содержащее неизвестное под знаком логарифма или в его основании, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
log>a> x = b. (1)
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab.
Пример 1. Решить уравнения:
a)
log>2>
x
= 3, b) log>3>
x
= -1, c)
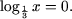
Решение.
Используя утверждение 1, получим a) x
= 23
или x
= 8; b) x
= 3-1
или x
= 1/>3>;
c)
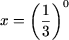 или
x
= 1.
или
x
= 1.
Приведем основные свойства логарифма.
Р1. Основное логарифмическое тождество:
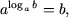
где a > 0, a ≠ 1 и b > 0.
Р2. Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:
log>a> N>1>·N>2> = log>a> N>1> + log>a> N>2> (a > 0, a ≠ 1, N>1> > 0, N>2> > 0).
Замечание. Если N>1>·N>2> > 0, тогда свойство P2 примет вид
log>a> N>1>·N>2> = log>a> |N>1>| + log>a> |N>2>| (a > 0, a ≠ 1, N>1>·N>2> > 0).
Р3. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя
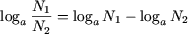 (a
> 0, a
≠ 1, N>1>
> 0, N>2>
> 0).
(a
> 0, a
≠ 1, N>1>
> 0, N>2>
> 0).
Замечание.
Если
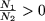 ,
(что равносильно N>1>N>2>
> 0) тогда свойство P3
примет вид
,
(что равносильно N>1>N>2>
> 0) тогда свойство P3
примет вид
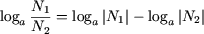 (a
> 0, a
≠ 1, N>1>N>2>
> 0).
(a
> 0, a
≠ 1, N>1>N>2>
> 0).
P4. Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:
log>a> N k = k log>a> N (a > 0, a ≠ 1, N > 0).
Замечание. Если k - четное число (k = 2s), то
log>a> N 2s = 2s log>a> |N| (a > 0, a ≠ 1, N ≠ 0).
P5. Формула перехода к другому основанию:
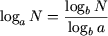 (a
> 0, a
≠ 1, b
> 0, b
≠ 1, N
> 0),
(a
> 0, a
≠ 1, b
> 0, b
≠ 1, N
> 0),
в частности, если N = b, получим
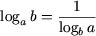 (a
> 0, a
≠ 1, b
> 0, b
≠ 1). (2)
(a
> 0, a
≠ 1, b
> 0, b
≠ 1). (2)
Используя свойства P4 и P5, легко получить следующие свойства
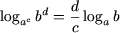 (a
> 0, a
≠ 1, b
> 0, c
≠ 0), (3)
(a
> 0, a
≠ 1, b
> 0, c
≠ 0), (3)
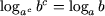 (a
> 0, a
≠ 1, b
> 0, c
≠ 0), (4)
(a
> 0, a
≠ 1, b
> 0, c
≠ 0), (4)
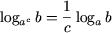 (a
> 0, a
≠ 1, b
> 0, c
≠ 0), (5)
(a
> 0, a
≠ 1, b
> 0, c
≠ 0), (5)
и, если в (5) c - четное число (c = 2n), имеет место
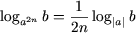 (b
> 0, a
≠ 0, |a|
≠ 1). (6)
(b
> 0, a
≠ 0, |a|
≠ 1). (6)
Перечислим и основные свойства логарифмической функции f(x) = log>a> x:
Область определения логарифмической функции есть множество положительных чисел.
Область значений логарифмической функции - множество действительных чисел.
При a > 1 логарифмическая функция строго возрастает (0 < x>1> < x>2> log>a> x>1> < log>a> x>2>), а при 0 < a < 1, - строго убывает (0 < x>1> < x>2> log>a> x>1> > log>a> x>2>).
log>a> 1 = 0 и log>a> a = 1 (a > 0, a ≠ 1).
Если a > 1, то логарифмическая функция отрицательна при x (0;1) и положительна при x (1;+∞), а если 0 < a < 1, то логарифмическая функция положительна при x (0;1) и отрицательна при x (1;+∞).
Если a > 1, то логарифмическая функция выпукла вверх, а если a (0;1) - выпукла вниз.
Следующие утверждения (см., например, [1]) используются при решении логарифмических уравнений.
Утверждение 2. Уравнение log>a> f(x) = log>a> g(x) (a > 0, a ≠ 1) равносильно одной из систем (очевидно, выбирается та система, неравенство которой решается проще)
|
|
f(x) = g(x), |
|
|
f(x) = g(x), |
|
f(x) > 0, |
g(x) > 0. |
Утверждение 3. Уравнение log>h>>(>>x>>)> f(x) = log>h>>(>>x>>)> g(x) равносильно одной из систем
|
|
f(x) = g(x), |
|
|
f(x) = g(x), |
|
h(x) > 0, |
h(x) > 0, |
|||
|
h(x) ≠ 1, |
h(x) ≠ 1, |
|||
|
f(x) > 0, |
g(x) > 0. |
Нужно подчеркнуть, что в процессе решения логарифмических уравнений часто используются преобразования, которые изменяют область допустимых значений (ОДЗ) исходного уравнения. Следовательно, могут появиться "чужие" решения или могут быть потеряны решения. Например, уравнения
f(x) = g(x) и log>a> f(x) = log>a> g(x)
или
log>a> [f(x)·g(x)] = b и log>a> f(x) + log>a> g(x) = b
вообще говоря, неравносильны (ОДЗ уравнений справа уже).
Следовательно, при решении логарифмических уравнений полезно использовать равносильные преобразования. В противном случае, проверка полученных решений является составной частью решения. Более того, необходимо учитывать и преобразования, которые могут привести к потере корней.
2. Использование определения логарифма
Пример 1. Решить уравнения
|
a) log>2>(5 + 3log>2>(x - 3)) = 3, |
c) log>(>>x>> - 2)>9 = 2, |
|
b)
|
d) log>2>>x>> + 1>(2x2 - 8x + 15) = 2. |
Решение. a) Логарифмом положительного числа b по основанию a (a > 0, a ≠ 1) называется степень, в которую нужно возвести число a, чтобы получить b. Таким образом, log>a>b = c, b = ac и, следовательно,
5 + 3log>2>(x - 3) = 23
или
3log>2>(x - 3) = 8 - 5, log>2>(x - 3) = 1.
Опять используя определение, получим
x - 3 = 21, x = 5.
Проверка полученного корня является неотъемлемой частью решения этого уравнения:
log>2>(5 + 3log>2>(5 - 3)) = log>2>(5 + 3log>2>2) = log>2>(5 + 3) = log>2>8 = 3.
Получим истинное равенство 3 = 3 и, следовательно, x = 5 есть решение исходного уравнения.
b) Аналогично примеру a), получим уравнение
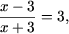
откуда следует линейное уравнение x - 3 = 3(x + 3) с решением x = -6. Сделаем проверку и убедимся, что x = -6 является корнем исходного уравнения.
c) Аналогично примеру a), получим уравнение
(x - 2)2 = 9.
Возведя в квадрат, получим квадратное уравнение x2 - 4x - 5 = 0 с решениями x>1> = -1 и x>2> = 5. После проверки остается лишь x = 5.
d) Используя определение логарифма, получим уравнение
(2x2 - 8x + 15) = (2x + 1)2
или, после элементарных преобразований,
x2 + 6x-7 = 0,
откуда x>1> = -7 и x>2> = 1. После проверки остается x = 1.
3. Использование свойств логарифма
Пример 3. Решить уравнения
|
a) log>3>x + log>3>(x + 3) = log>3>(x + 24), |
|
b) log>4>(x2 - 4x + 1) - log>4>(x2 - 6x + 5) = -1/>2> |
|
c) log>2>x + log>3>x = 1 |
Решение. a) ОДЗ уравнения есть множество x (0;+) которое определяется из системы неравенств (условия существования логарифмов уравнения)
|
|
x > 0, |
|
x+3 > 0, |
|
|
x+24 > 0. |
Используя свойство P2 и утверждение 1, получим
|
|
|
||||||||||||||
|
|
|
x = 4. |
b) Используя свойство P3, получим следствие исходного уравнения
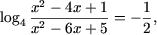
откуда, используя определение логарифма, получим
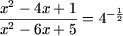
или
x2 - 4x + 1 = 1/>2>(x2 - 6x + 5),
откуда получаем уравнение
x2 - 2x - 3 = 0
с решениями x>1> = -1 и x = 3. После проверки остается лишь x = -1.
c) ОДЗ уравнения: x (0;+). Используя свойство P5, получим уравнение
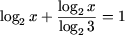
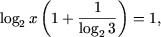
log>2>x(1 + log>3>2) = 1,
откуда
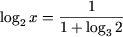 или
или
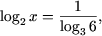 или log>2>x
= log>6>3.
Следовательно,
или log>2>x
= log>6>3.
Следовательно,
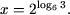
Логарифмические неравенства
Неравенство, содержащее неизвестное под знаком логарифма или в его основании называется логарифмическим неравенством. В процессе решения логарифмических неравенств часто используются следующие утверждения относительно равносильности неравенств и учитываются свойства монотонности логарифмической функции.
Утверждение 1. Если a > 1, то неравенство log>a> f(x) > log>a> g(x) равносильно системе неравенств
|
|
f(x) > g(x), |
|
g(x) > 0. |
Утверждение 2. Если 0 < a < 1, то неравенство log>a> f(x) > log>a> g(x) равносильно системе неравенств
|
|
f(x) < g(x), |
|
f(x) > 0. |
Утверждение 3. Неравенство log>h>>(>>x>>)> f(x) > log>h>>(>>x>>)> g(x) равносильно совокупности систем неравенств
|
|
|
h(x) > 1, |
|
f(x) > g(x) > 0, |
||
|
|
0 < h(x) < 1, |
|
|
0 < f(x) < g(x). |
Подчеркнем, что в неравенстве log>a> f(x) > log>a> g(x) вместо знака > может фигурировать любой из знаков ≥ , < , ≤ . В этом случае утверждения 1-3 соответственно преобразуются.
Пример 1. Решить неравенства
|
a) log>3>(x2 - x) ≥ log>3>(x + 8); |
|
|
b)
|
|
|
c)
|
Решение. a) Используя утверждение 1 , получим
|
log>3>(x2
- x)
≥ log>3>(x
+ 8)
|
x2 - x ≥ x + 8, |
|
x2 - 2x - 8 ≥ 0, |
|
|
x+8 > 0, |
x > -8, |
|
|
|
x ≤ -2, |
|
|
x ≥ 4, |
x
|
||
|
x > -8, |
b) Основание логарифма число между нулем и единицей, поэтому, используя утверждение 2, получим
|
|
|
|
|
|
|
|
c) Запишем 0 = log>2>1 и, используя утверждение 1, получим
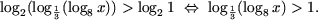
Запишем
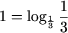 и,
используя утверждение 2, получим
и,
используя утверждение 2, получим
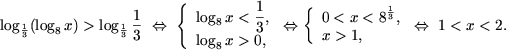
Показательные уравнения и неравенства
Показательные уравнения
Показательным называется уравнение, в котором неизвестное содержится только в показателе степени при постоянных основаниях.
Простейшим показательным уравнением является уравнение вида
Это уравнение равносильно алгебраическому уравнению
Пример 1. Решить уравнение
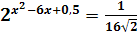 .
.
Представим правую часть уравнения в виде степени с основанием 2:
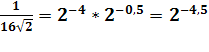 .
.
Перейдем теперь к равносильному алгебраическому уравнению:
Если
после введения новой переменной
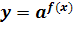 показательное уравнение сводится к
алгебраическому, дробно-рациональному
или другому уравнению от переменной y,
то сначала находят корни этого уравнения,
а потом выражают x
через
y,
используя
решение простейшего показательного
уравнения.
показательное уравнение сводится к
алгебраическому, дробно-рациональному
или другому уравнению от переменной y,
то сначала находят корни этого уравнения,
а потом выражают x
через
y,
используя
решение простейшего показательного
уравнения.
Показательные неравенства
Показательными называются неравенства, в которых неизвестное содержится в показателе степени.
При решении показательных неравенств используются следующие утверждения:
A.1. Если a > 1, неравенство
a f(x) > a g(x)
равносильно неравенству
f(x) > g(x).
Аналогично, a f(x) < a g(x) ; f(x) < g(x).
A.2. Если 0 < a < 1, неравенство
a f(x) > a g(x)
равносильно неравенству
f(x) < g(x).
Аналогично, a f(x) < a g(x) ; f(x) > g(x).
A.3. Неравенство
|
[h(x)] f(x) > [h(x)] g(x) |
(1) |
равносильно совокупности систем неравенств
|
|
|
h(x) > 1, |
|
f(x) > g(x), |
||
|
|
0 < h(x) < 1, |
|
|
f(x) < g(x). |
Замечание.. Если знак неравенства (1) нестрогий, дополнительно рассматривается и случай
|
|
h(x) = 1, |
|
x D(f); D(g), |
где D(f) (D(g)) означает область определения функции f (g).
A.4. Если b ≥ 0, неравенство
af(x) < b
не имеет решений (следует из свойств показательной функции).
A.5.
Если b
≤ 0, множеством решений неравенства
af(x)
> b
является x
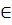 D(f).
D(f).
A.6. Если a > 1, b > 0, неравенство
af(x) > b
равносильно неравенству
f(x) > log>a>b.
Аналогично, a f(x) < b ; f(x) < log>a>b.
A.7. Если 0 < a < 1, b > 0, неравенство
a f(x) > b
равносильно неравенству
f(x) < log>a>b.
Аналогично, a f(x) < b ; f(x) > log>a>b.
Упражнение 1. Решить неравенства:
|
a)
|
|
|
b) (0.3)|2x-3| < (0.3)|3x+4|, |
|
|
c)
|
|
Решение. a) Так как 2 > 1, используя утверждение A.1, получаем равносильное неравенство
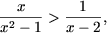
которое решается методом интервалов,
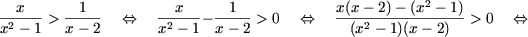
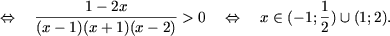
b) Так как 0 < 0.3 < 1 используя утверждение A.2, получаем равносильное неравенство
|2x-3| > |3x+4|,
которое решается, используя свойства модуля (|a| > |b| (a-b)(a+b) > 0):
|2x-3|
> |3x+4|
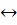 ((2x-3)-(3x+4))
((2x-3)+(3x+4))
> 0
((2x-3)-(3x+4))
((2x-3)+(3x+4))
> 0
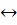 (-x-7)(5x+1)
> 0
(-x-7)(5x+1)
> 0
Решив последнее
неравенство методом интервалов, получим
x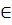 (-7;-1/>5>).
(-7;-1/>5>).
c) Используя утверждение A.3, получим
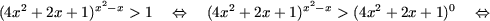
|
|
|
|
|
Заключение
Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XX век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.
Список литературы
Курош А.Г. «Курс высшей алгебры» Москва 1975
Штейн Е.А. «Большая школьная энциклопедия» том 1; Москва 2004
М. Д. Аксенова. «Энциклопедия для детей». Том 11. Математика. – Аванта+, 1998.
Цыпкин А. Г. Под ред. С. А. Степанова. «Справочник по математике для средней школы». – М.: Наука, 1980
Г. Корн и Т. Корн. «Справочник по математике для научных работников и инженеров». – М.: Наука, 1970
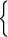
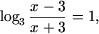
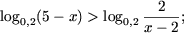
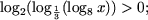
 [4;+∞).
[4;+∞).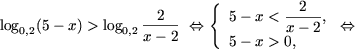
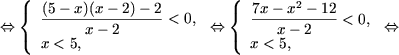
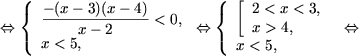
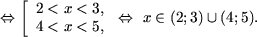
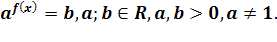
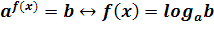
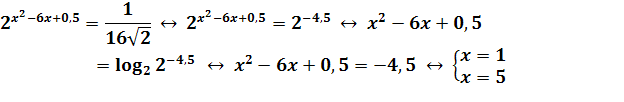
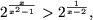
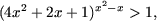
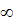 ;
-1>2>)
(1;+
;
-1>2>)
(1;+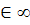
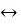 x
(-
x
(-