История математических констант - числа "пи" и "е"

Введение

Числа много тысячелетий назад вошли в жизнь и быт людей. Человек их использует не только при счёте и вычислениях, он придумал различные игры с числами и шарады. Некоторые числа наделил сверхъестественными свойствами, например, такие как 13, 666. Среди бесконечного множества действительных чисел существуют ещё особенные, и не только для математиков, числа  и е. Эти числа имеют свои собственные обозначения, так как их нельзя записать точно с помощью цифр. Числа 3,14 и 2,7 лишь одни из приближённых значений чисел π и е. Эти числа являются иррациональными и трансцендентными, для их точного определения не хватило бы и триллиона десятичных знаков.

"Математиками изучены последовательности цифр е и , и выяснено, что все цифры в этом числе встречаются с одинаковой частотой". Эти числа могут заворожить своей непокорностью, в особенности . "Этому числу удавалось в течении тысячелетий держать в плену мысли и чувства не только математиков и астрономов, но и философов и художников". Тратились годы для вычисления нескольких десятичных знаков числа .

История числа 

"Письменная история числа  начинается с египетского папируса, датируемого примерно 2000 годом до нашей эры, но оно было известно еще древним людям. Число  обратило на себя внимание людей ещё в те времена, когда они не умели письменно излагать ни своих знаний, ни своих переживаний, ни своих воспоминаний. С тех пор как первые натуральные числа 1,2,3,4,… стали неразлучными спутниками человеческой мысли, помогая оценивать количества предметов либо их длины, площади или объёмы, люди познакомились с числом . Тогда оно ещё не обозначалось одной из букв греческого алфавита и его роль играло число 3. Нетрудно понять, почему числу  уделяли так много внимания. Выражая величину отношения между длиной окружности и её диаметром, оно появилось во всех расчётах связанных с площадью круга или длиной окружности". Но уже в глубокой древности математики довольно быстро и не без удивления обнаружили, что число 3 не совсем точно выражает то, что теперь известно как число пи. Безусловно, к такому выводу могли прийти только после того, как к ряду натуральных чисел добавились дробные или рациональные числа. Так египтяне получили результат: 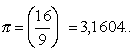В дальнейшем Архимед, используя метод верхних и нижних приближений, получает следующие границы числа пи. 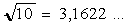Индусы в V-VI веках пользовались числом , китайцы - числом

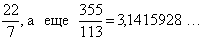
"Обозначение числа  происходит от греческого слова ("окружность"). Впервые это обозначение использовал в 1706 году английский математик У. Джонс, но общепринятым оно стало после того, как его (начиная с 1736 года) стал систематически употреблять Леонард Эйлер". В конце 18 века И. Ламберт и А. Лежандр установили, что  иррациональное число, а в 1882 году Ф. Лидерман доказал, что оно трансцендентное, т.е. не может удовлетворять никакому алгебраическому уравнению с целыми коэффициентами.

На протяжении всего существования числа , вплоть до наших дней, велась своеобразная "погоня" за десятичными знаками числа p. Леонардо Фибоначи около 1220 года определил три первых точных десятичных знаков числа . В 16 веке Андриан Антонис определил 6 таких знаков. Франсуа Виет (подобно Архимеду), вычисляя периметры вписанного и описанного 322216-угольников, получил 9 точных десятичных знаков. Андриан Ван Ромен таким же способом получил 15 десятичных знаков, вычисляя периметры 1073741824-угольников. Лудольф Ван Кёлен, вычисляя периметры 32512254720-угольников, получил 20 точных десятичных знаков. Авраам Шарп получил 72 точных десятичных знаков числа . В 1844 году З. Дазе вычисляет 200 знаков после запятой числа , в 1847 году Т. Клаузен получает 248 знаков, в1853 Рихтер вычисляет 330 знаков, в том же 1853 году 440 знаков получает З. Дазе и в этом же году У. Шенкс получает 513 знаков. "С появлением ЭВМ количество верных знаков десятичных знаков резко возрастает:

1949 год - 2037 десятичных знаков (Джон фон Нейман, ENIAC), 1958 год - 10000 десятичных знаков (Ф. Женюи, IBM-704), 1961 год - 100000 десятичных знаков (Д. Шенкс, IBM-7090), 1973 год - 10000000 десятичных знаков (Ж. Гийу, М. Буйе, CDC-7600), 1986 год - 29360000 десятичных знаков (Д. Бейли, Cray-2), 1987 год - 134217000 десятичных знаков (Я. Канада, NEC SX2), 1989 год - 1011196691 десятичных знаков (Д. Гудновски и Г. Гудновски, Cray-2+IBM-3040)"

При вычислении верных десятичных знаков числа  пользовались различными способами, некоторые, как и Архимед вычисляли периметры вписанных и описанных n-угольников, но позднее стали прибегать к помощи рядов.

Так Лейбниц вычислял с помощью ряда:

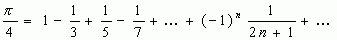
Шарп применил ряд:

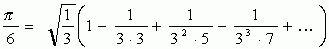
Л. Эйлер с помощью ряда:

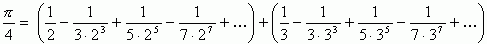
З. Дазе использовал ряд.

Джон Валлис (1616-1703) нашёл бесконечное произведение, с помощью которого можно вычислить число пи:

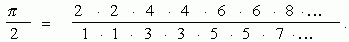
Определение числа 

Теорема: Отношение длины окружности к её диаметру одинаково для всех окружностей.

Доказательство.

Обозначим через L - длину окружности, через d - её диаметр, то формулировка теоремы запишется следующим образом: 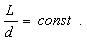Рассмотрим правильный n-угольник, вписанный в окружность радиуса r со стороной а_>n> и периметром Р_>n>, то 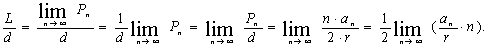Докажем, что отношение одинаково для всех окружностей. Рассмотрим две произвольные окружности с вписанными в них правильными n-угольниками. Из подобия треугольников АОВ и А_>1>О_>1>В_>1> следует, что 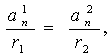т.к. окружности брали произвольные, то это равенство будет справедливо для всех окружностей. Итак,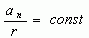 для всех окружностей, следовательно 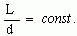Это отношение длины окружности к её диаметру принято обозначать греческой буквой "".

Определение: Числом  называется отношение длины окружности к её диаметру.

История числа е

Число 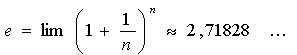появилось сравнительно недавно. Его иногда называют "неперовым числом" в честь изобретателя логарифмов шотландского математика Джона Непера (1550-1617), однако необоснованно, так как нет твёрдых оснований для утверждения, что Непер имел о числе е чёткое представление" [10]. Впервые обозначение "е" ввёл Леонард Эйлер (1707-1783). Он также вычислил точные 23 десятичные знака этого числа, использовав представление числа е в виде бесконечного числового ряда: 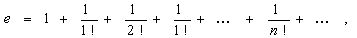полученное Даниилом Бернули (1700-1782). "В 1873 году Эрмит доказал трансцендентность числа е.Л. Эйлер получил замечательный результат, связывающий числа е, , и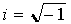: 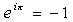. Ему принадлежит и заслуга определения функции 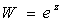для комплексных значений z, что положило начало математическому анализу в комплексной области - теории функций комплексного переменного" [10]. Эйлером были получены следующие формулы: 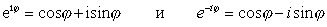Рассматривают логарифмы по основанию е, называемые натуральными и обозначаются Lnx.

Способы определения

Число e может быть определено несколькими способами.

Через предел:

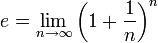(второй замечательный предел) .

Как сумма ряда:

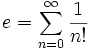или .

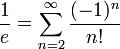Как единственное число a, для которого выполняется

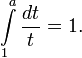
Как единственное положительное число a, для которого верно

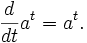
Свойства

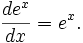Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения 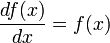является функция 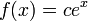, где c - произвольная константа.

Число e иррационально и даже трансцендентно. Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e - нормальное число, то есть вероятность появления разных цифр в его записи одинакова.

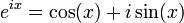, см. формула Эйлера, в частности

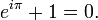
Ещё одна формула, связывающая числа е и π, т. н. "интеграл Пуассона" или "интеграл Гаусса"

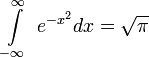
Для любого комплексного числа z верны следующие равенства:

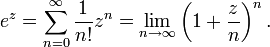
Число e разлагается в бесконечную цепную дробь следующим образом:

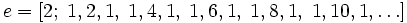, то есть

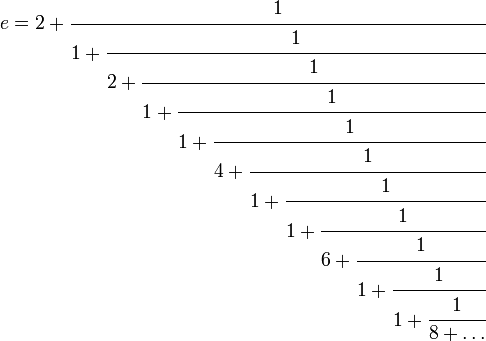
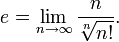
Представление Каталана:

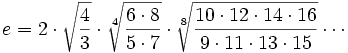
История

Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы "Описание удивительной таблицы логарифмов" (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен

.

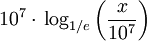Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).

Предполагается, что автором таблицы был английский математик Отред.

Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:

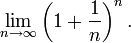
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690-1691 годы.

Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа "Механика, или Наука о движении, изложенная аналитически" 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.

Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential ("показательный", "экспоненциальный"). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой "свободной" буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler) [источник не указан 334 дня] .

Мнемоника

Приблизительное значение зашифровано в: "Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли" (нужно выписать подряд цифры, выражающие число букв в словах следующего стишка, и поставить запятую после первого знака)

Запомнить как 2,7 и повторяющиеся 18, 28, 18, 28.

Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: "Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой"

Цифры 45, 90 и 45 можно запоминать как "год победы над фашистской Германией, затем дважды этот год и снова он"

Правила e связывается с президентом США Эндрю Джексоном: 2 - столько раз избирался, 7 - он был седьмым президентом США, 1828 - год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем - опять-таки равнобедренный прямоугольный треугольник.

С точностью до трёх знаков после запятой через "число дьявола": нужно разделить 666 на число, составленное из цифр 6 − 4, 6 − 2, 6 − 1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки):

.

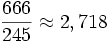Запоминание e как .

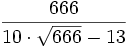Грубое (с точностью до 0,001), но красивое приближение полагает e равным 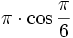. Совсем грубое (с точностью 0,01) приближение даётся выражением .

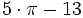"Правило Боинга": 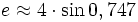даёт неплохую точность 0,0005.

Стишки:

Два и семь, восемнадцать,

Двадцать восемь, восемнадцать,

Двадцать восемь, сорок пять,

Девяносто, сорок пять.

Доказательство иррациональности

Предположим, что рационально. Тогда 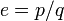, где 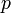- целое, а 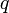- натуральное и больше 1, т.к. - не целое. Следовательно

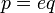
Умножая обе части уравнения на 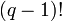, получаем

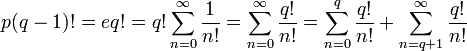
Переносим 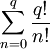в левую часть:

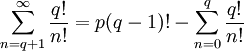
Все слагаемые правой части целые, следовательно:

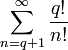- целое

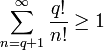
Но с другой стороны

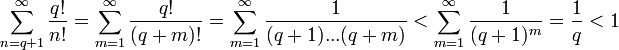
Получаем противоречие.

Интересные факты

В IPO компании Google в 2004 году было объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долларов. Заявленное число представляет собой первые 10 цифр известной математической константы.

В языках программирования символу e в экспоненциальной записи чисел соответствует число 10, а не Эйлерово число. Это связано с историей создания.

Ссылки:

История числа e (англ.)

e for 2.71828… (англ.) (история и правило Джексона)

Горобец, Борис Соломонович. Мировые константы в основных законах физики и физиологии // Наука и жизнь. - 2004. - № 2. - статья с примерами физического смысла констант π и e.

Числа с собственными именами

Если мы вспомним, что число е = 2,718281828., то увидим, что основание логарифмов Бюрги отличается от числа е только начиная с четвертого десятичного знака. Иоганн Кеплер, понимавший огромное значение таблиц Бюрги для вычислений, настойчиво рекомендовал ему опубликовать свой метод ко всеобщему сведению, но Бюрги медлил, и получилось так, что в печати раньше появились таблицы логарифмов другого автора. Таблицы Бюрги были изданы в 1620 г., а на 6 лет раньше (в 1614 г.) Джон Непер опубликовал составленные им таблицы под названием "Описание удивительной таблицы логарифмов". Шотландский барон Джон Непер (1550-1617) тоже не был специалистом-математиком. Он делил свои интересы между многими отраслями знания, причем главным образом занимался вопросами, имевшими непосредственное приложение к жизни. Так, он изобрел несколько сельскохозяйственных машин, а также некоторые военные приборы. В области математики Непер интересовался главным образом вопросами вычислительного характера, отыскивая способы для облегчения счета. Так, в сочинении "Рабдология", изданном в год его смерти, он описывает свой прибор, который в наше время носит название "неперовы палочки" и служит хорошим методическим пособием в школе. Этот прибор состоит из десяти основных палочек, на которых помещена таблица умножения. Левая палочка неподвижна, а все остальные могут менять свои места. В каждом квадратике таблицы проведены диагонали, причем в нижней части квадратика помещаются единицы частных произведений таблицы умножения, а в верхней - десятки. При помощи прибора Непера можно производить умножение и деление чисел, причем умножение заменяется сложением, а деление вычитанием. Если, например, нужно умножить число 684 на 4, то для этого ставим рядом палочки, имеющие сверху числа 6, 8 и 4, и обращаем внимание на клетки этих палочек, стоящие в одной строке с 4.

Список литературы

1. Бохан К.А. и др. Курс математического анализа т. II. - М.: Просвещение 1972.

2. Кымпан Ф. История числа . - М.: Наука, Гл. ред. физ.-мат. лит., 1987.

3. Райк А.Е. Очерки по истории математики в древности. - Саранск, 1987.

4. Фихтенгольц Г.М. Основы математического анализа т. I, II. - М.: Государственное издательство технико-теоретической литературы, 1956.

5. Болтянский В. Экспонента. // Квант, 1984 №3.

6. Звонкин А. Что такое  // Квант, 1978 №11.

7. Кузьмин Е., Ширшов А. О числе е. // Квант, 1979 №8.

8. Калейдоскоп Число . // Квант, 1996 №6.