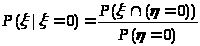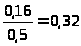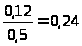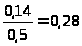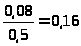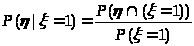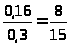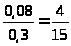Теория вероятности (работа 3)

Контрольная работа

по дисциплине: Теория вероятностей

2009г.

Контрольная работа № 1

Вариант 1.

Задача № 1.

Условие:

Из 10 изделий, среди которых 4 бракованные, извлекают 3. Найти вероятность того, что среди них одно бракованное.

Решение:

Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 10 деталей вынуть три, т.е. числу сочетаний из 10 элементов по 3:

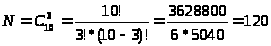
По условию задачи из трех извлеченных изделий одно бракованное, а два годные. Таким образом m_>A>:

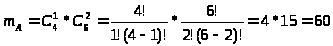
Найдем вероятность события, при котором из 3 извлеченных наугад деталей одна окажется бракованной:

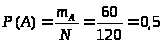
Ответ: вероятность события, при котором из 3 извлеченных наугад деталей одна окажется бракованной равна 0,5

Задача № 2

Условие:

Известны вероятности независимых событий А, В и С:

Р (А) = 0,5; Р (В) = 0,4; Р (С) = 0,6.

Определить вероятность того, что а) произойдет по крайней мере одно из этих событий, б) произойдет не более 2 событий.

Решение:

а) Для того чтобы найти вероятность того, что произойдет хотя бы 1 событие, найдем вероятность того, что ни одно событие не произойдет (обозначим эту вероятность P_>0>). Так как события независимы по условию, вероятность P_>0> равна произведению вероятностей того, что не произойдет каждое отдельное событие.

Таким образом, вероятность того, что не произойдет:

событие А: А_>0> = 1 - 0,5 = 0,5

событие В: В_>0> = 1 - 0,4 = 0,6

событие С: С_>0> = 1 - 0,6 - 0,4

Воспользуемся правилом умножения вероятностей и получим вероятность того, что ни одно событие не произойдет:

P_>0>= А_>0>*В_>0>*С_>0> =_> >0,5*0,6*0,4 = 0,12

Ситуация, при которой не произойдет ни одно событие, и ситуация, при которой произойдет хотя бы одно событие, образуют полную систему событий. Сумма вероятностей этих событий равна единице. Поэтому искомая вероятность P удовлетворяет уравнению:

P + P_>0> = 1, откуда следует, что

P = 1 - P_>0> = 1 - 0,12 = 0,88.

б) Для того, чтобы найти вероятность того, что произойдет не более 2 событий, найдем вероятность того, что произойдут все три события, и обозначим как Р_>1>:

Р_>1> = А*В*С = 0,5*0,4,*0,6 = 0,12

Ситуация, при которой произойдут все 3 события, и ситуация, при которой произойдет не более 2 событий (от 0 до 2), составляют полную систему событий. Сумма вероятностей этих событий равна единице. Поэтому искомая вероятность P удовлетворяет уравнению:

P + Р_>1> = 1, откуда следует, что

P = 1 - Р_>1> = 1 - 0,12 = 0,88.

Ответ:

а) вероятность того, что произойдет по крайней мере одно событие, равна 0,88

б) вероятность того, что произойдет не более двух событий, равна 0,88

Задача № 3

Условие:

Вероятности попадания в цель: первого стрелка - 0,6; второго - 0,7; третьего - 0,8. Найти вероятность хотя бы одного попадания в цель при одновременном выстреле всех трех.

Решение:

Для того чтобы найти вероятность попадания в цель хотя бы 1 стрелка, найдем вероятность того, что ни один из стрелков не попадет в цель (обозначим эту вероятность через P_>0>). Так как попадания различных стрелков в цель следует считать независимыми событиями, вероятность P_>0> равна произведению вероятностей того, что промажет каждый из стрелков.

Событие, состоящее в том, что некоторый стрелок попадет в цель, и событие, состоящее в том, что он промажет, составляют полную систему событий. Сумма вероятностей двух этих событии равна единице.

Таким образом, вероятность того, что

А) промажет 1 стрелок равна: 1 - 0,6 = 0,4

Б) промажет 2 стрелок равна: 1 - 0,7 = 0,3

В) промажет 3 стрелок равна: 1 - 0,8 = 0,2

Воспользуемся правилом умножения вероятностей и получим вероятность того, что промажут все трое стрелков:

P_>0>= 0,4*0,3*0,2 = 0,024

Событие, состоящее в том, что не попадет в цель ни один из стрелков, и событие, состоящее в том, что попадет хотя бы один, образуют полную систему событий. Сумма вероятностей этих событий равна единице. Поэтому искомая вероятность P удовлетворяет уравнению:

P + P_>0> = 1, откуда следует, что

P = 1 - P_>0> = 1 - 0,024 = 0,976

Ответ: вероятность попадания в цель хотя бы одного стрелка при одновременном выстреле всех трех равна 0,976 (или 97,6%)

Задача № 4

Условие:

Известно, что 80% продукции стандартно. Упрощенный контроль признает годной стандартную продукцию с вероятностью 0,9 и нестандартную с вероятностью 0,3. Найти вероятность того, что признанное годным изделие - стандартно.

Решение:

1) Найдем вероятность того, что стандартная продукция будет признана годной:

Р1 = 0,8*0,9 = 0,72 (72% продукции)

2) Найдем вероятность того, что нестандартная продукция будет признана годной:

Р2 = 0,2*0,3 = 0,06 (6% продукции)

3) Таким образом, упрощенный контроль признает годной Р1 + Р2 = 0,82 (82% продукции)

4) Найдем вероятность того, что признанное годным изделие - стандартно:

0,8*0,82 = 0,656

Ответ: вероятность того, что признанное годным изделие - стандартно, равна 0,656.

Задача № 5

Условие:

Имеется 4 радиолокатора. Вероятность обнаружить цель для первого - 0,86; для второго - 0,9; для третьего - 0,92; для четвертого - 0,95. Включен один из них. Какова вероятность обнаружить цель?

Решение:

Обозначим через А событие - цель обнаружена, а возможные события (гипотезы) обнаружения цели 1-м, 2-м, 3-м или 4-м локаторами - через, соответственно, В_>1>, В_>2>, В_>3> и В_>4>.

По условию задачи включен один из четырех локаторов, следовательно, вероятность обнаружения цели:

Р (В_>1>) = Р (В_>2>) = Р (В_>3>) = Р (В_>4>) = 1\4.

Соответствующие условные вероятности (по условию задачи) обнаружения цели равны:

Р (A|В_>1>) = 0,86; Р (A|В_>2>) = 0,9; Р (A|В_>3>) = 0,92; Р (A|В_>4>) = 0,95.

Таким образом, согласно формуле полной вероятности, искомая вероятность обнаружения цели равна:

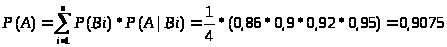
Ответ: вероятность обнаружения цели равна 0,9075

Контрольная работа № 2

Вариант 1.

Задача № 1.

Условие:

Известна вероятность события А: р (А) = 0,3. Дискретная случайная величина  - число появлений А в трех опытах. Построить ряд распределения случайной величины ; найти ее математическое ожидание m_>> и дисперсию D_>>.

Решение:

1) Вычислим вероятности р (х_>i>) по формуле Бернулли:

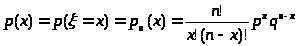, где, р = 0,3; q = 1 - р = 0,7; n = 3; х = .

Таким образом, получим ряд распределения случайной величины :

Значения 	0	1	2	3
Вероятности р (х>i>)	0,343	0,441	0,189	0,027

Графически ряд распределения случайной величины  выглядит следующим образом:

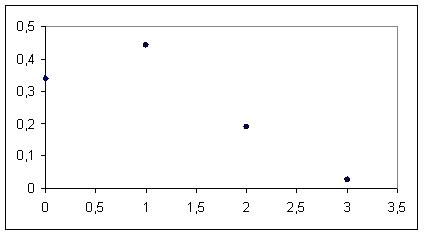
2) Найдем математическое ожидание m_>>:

Математическим ожиданием m_>>_> >дискретной случайной величины 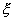_> >называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е.

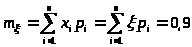
3) Найдем дисперсию D_>>:

Дисперсией D_>> дискретной случайной величины 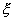_> >называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.:

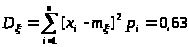
Ответ:

Ряд распределения случайной величины :

Значения 	0	1	2	3
Вероятности р (х>i>)	0,343	0,441	0,189	0,027

математическое ожидание m_>> = 0,9;

дисперсия D_>> = 0,63

Задача № 2

Условие:

Распределение дискретной случайной величины  содержит неизвестные значения х_>1> и х_>2> (х_>1> < х_>2>):

x>i>	х>1>	х>2>
р>i>	0,4	0,6

Известны числовые характеристики случайной величины: М_>> = 3,6; D_>> = 0,24. Требуется определить значения х_>1> и х_>2>.

Решение:

Поскольку

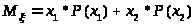, 0,4х_>1> + 0,6х_>2> = 3,6

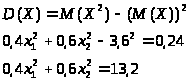
Для того, чтобы найти х_>1 >и х_>2>, необходимо решить систему уравнений:

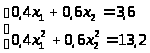
Выразим из первого уравнения х_>1 >и подставим во второе:

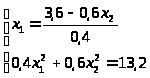
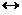
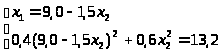
Решаем второе уравнение:

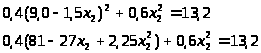
Умножим всю строку на 5:

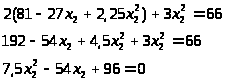
Умножим всю строку на 2:

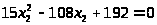
Разделим на 3:

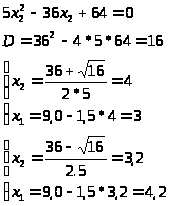
Учитывая условие х_>1> < х_>2>, получаем, что подходит только 1 вариант.

Ответ: х_>1> = 3, х_>2> = 4

Задача № 3

Условие

Плотность вероятности непрерывной случайной величины  задана следующим выражением:

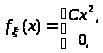
если 0 < x <1,при других х

Найти постоянную С, функцию распределения F (x), математическое ожидание М_>> и дисперсию D_>> случайной величины .

Решение:

Свойство плотности распределения:

,

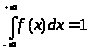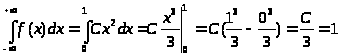
Получаем, что С = 3.

,

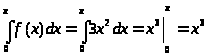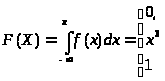
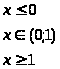
Математическое ожидание:

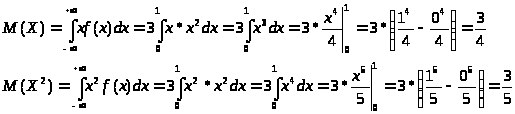
Дисперсия:

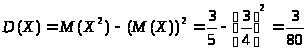
Ответ: С = 3, М = ¾, D = 3/80

Задача № 4.

Условие:

Случайная величина  имеет нормальное распределение с математическим ожиданием a = 56 и среднеквадратичным отклонением  = 8. Найти интервал, симметричный относительно математического ожидания, вероятность попадания в который равна Р = 0,95

Решение:

Поскольку, по условию задачи, случайная величина  имеет нормальное распределение, а также известна вероятность Р = 0,95, то является возможным использование правила трех сигм, а именно данной его части:

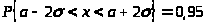
Подставив имеющиеся по условию задачи данные, получим следующий интервал, симметричный относительно математического ожидания:.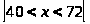

Ответ: .

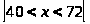Задача № 5.

Условие:

Известно распределение системы двух дискретных величин (, ).

 	1	2	3	4
0	0,16	0,12	0,14	0,08
1	0,08	0,10	0,09	0,08
2	0,06	0,04	0,03	0,02

Определить частные, условные (при  = 1,  = 0) распределения и числовые характеристики системы случайных величин m_>>, D_>>, m_>>, D_>>, K_>>_>,>_>>, r_>>_>,>_>>; а также найти вероятность попадания двумерной случайной величины (, ) в область

.

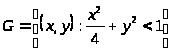Решение:

Частное распределение для  получается суммированием вероятностей в столбцах:

Р ( = 1) = Р ( = 1,  = 0) + Р ( = 1,  = 1) + Р ( = 1,  = 2) = 0,16 + 0,08 + 0,06 = 0,3

Р ( = 2) = Р ( = 2,  = 0) + Р ( = 2,  = 1) + Р ( = 2,  = 2) = 0,12 + 0,10 + 0,04 = 0,26

Р ( = 3) = Р ( = 3,  = 0) + Р ( = 3,  = 1) + Р ( = 3,  = 2) = 0,14 + 0,09 + 0,03 = 0,26

Р ( = 4) = Р ( = 4,  = 0) + Р ( = 4,  = 1) + Р ( = 4,  = 2) = 0,08 + 0,08 + 0,02 = 0,18

Частное распределение для  получается суммированием вероятностей в строках:

Р ( = 0) = Р ( = 0,  = 1) + Р ( = 0,  = 2) + Р ( = 0,  = 3) + Р ( = 0,  = 4) = 0,16 + 0,12 + 0,14 + 0,08 = 0,5

Р ( = 1) = Р ( = 1,  = 1) + Р ( = 1,  = 2) + Р ( = 1,  = 3) + Р ( = 1,  = 4) = 0,08 + 0,10 + 0,09 + 0,08 = 0,35

Р ( = 2) = Р ( = 2,  = 1) + Р ( = 2,  = 2) + Р ( = 2,  = 3) + Р ( = 2,  = 4) = 0,06 + 0,04 + 0,03 + 0,02 = 0,15

Полученные данные можно представить в виде таблицы:

 	1	2	3	4
0	0,16	0,12	0,14	0,08	0,5
1	0,08	0,10	0,09	0,08	0,35
3	0,06	0,04	0,03	0,02	0,15
	0,3	0,26	0,26	0,18

Вычислим математическое ожидание m_>>:

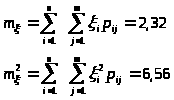
Вычислим математическое ожидание m_>>:

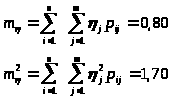
Вычислим дисперсию D_>>:

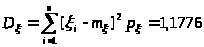
Вычислим дисперсию D_>>:

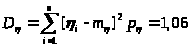
Условное распределение /=0:

	1	2	3	4

Условное распределение /=1:

	0	1	3

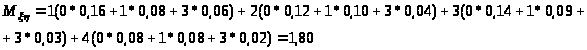
Вычислим ковариацию K_>>_>,>_>>:

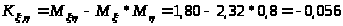
Вычислим коэффициент корреляции r_>>_>,>_>>:

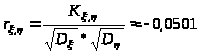
Вероятность попадания двумерной случайной величины (, ) в область:

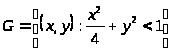- эллипс.

 	1	2	3	4
0	0,16	0,12	0,14	0,08
1	0,08	0,10	0,09	0,08
2	0,06	0,04	0,03	0,02

К необходимому условию подходят только точки (1; 0) и (2;)

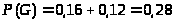
Ответ: m_>>_> >= 2,32, D_>>_> >= 1,1776, m_>> = 0,80, D_>> =1,06, K_>>_>,>_>> = - 0,056, r_>>_>,>_>> = - 0,0501.

Вероятность попадания двумерной случайной величины (, ) в область:

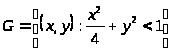= 0,028 (2,8%).