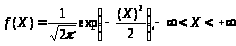Теория вероятностей и математическая статистика (работа 3)
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ЧАСТЬ I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
1. Случайные и достоверные события. Алгебра событий. Классическое и статистическое определение вероятности.
2. Общее определение вероятности: аксиомы Колмогорова.
3. Теоремы сложения. Условная вероятность и независимость.
4. Теоремы умножения. Формула полной вероятности и формула Бейеса.
5. Случайные величины- дискретные и непрерывные. Функция распределения и ее свойства.
6. Плотность вероятности распределения непрерывной случайной величины.
7. Числовые характеристики случайных величин (и их вероятностный смысл): математическое ожидание; дисперсия и среднее квадратическое отклонение; мода и медиана; коэффициент вариации; асимметрия, эксцесс.
8. Модельные законы распределения.
Биномиальное распределение и его числовые характеристики. Схема Бернулли-схема формирования биномиальной случайной величины. Формула Бернулли. Теорема Пуассона и теоремы Муавра-Лапласа.
Гипергеометрическое распределение и его числовые характеристики. Урновая схема- схема формирования гипергеометрического распределения.
Распределение Пуассона и его числовые характеристики.
Равномерное и показательное распределения. Числовые характеристики.
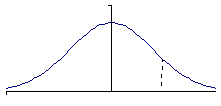
Нормальное распределение. Правило 3 сигм.
9.. Предельные теоремы: Закон больших чисел; центральная предельная теорема.
10. Зависимость случайных величин: ковариация и корреляция.
ЧАСТЬ II. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
1. Первичная обработка данных. Генеральная совокупность и выборка. Полигон и гистограмма. 2. Выборочные оценки числовых характеристик.
3. Теория оценивания. Точечные оценки и их свойства: несмещенность; состоятельность;
эффективность. Метод моментов.
4. Оценки максимального правдоподобия и их свойства.
5. Доверительные интервалы для средней и дисперсии нормальной генеральной совокупности. 6. Доверительные интервалы для неизвестной вероятности.
7. Проверка гипотез. Общая схема проверки гипотез. Ошибки 1-го и 2-го рода. F,T- критерии. 8.2-критерий.
9. Схема дисперсионного анализа.
10. Регрессионный анализ.
Таблица выбора заданий по вариантам для выполнения контрольной работы по курсу «Теория вероятностей и математическая статистика» Номер варианта соответствует последней цифре в № зачетки
|
№ варианта |
задание 1 |
задание 5 |
задание 8 |
задание 9 |
задание12 |
|
1 |
1 |
10 |
1 |
5 |
8 |
|
2 |
2 |
9 |
3 |
1 |
2 |
|
3 |
4 |
3 |
5 |
8 |
7 |
|
4 |
3 |
6 |
1 |
2 |
6 |
|
5 |
5 |
4 |
6 |
10 |
9 |
|
6 |
7 |
8 |
1 |
2 |
5 |
|
7 |
8 |
7 |
2 |
3 |
3 |
|
8 |
6 |
6 |
5 |
2 |
2 |
|
9 |
9 |
4 |
6 |
7 |
10 |
|
10 |
10 |
5 |
2 |
10 |
9 |
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ ДЛЯ ЗАОЧНОГО ОТДЕЛЕНИЯ
При выполнении контрольных работ (далее К.Р.) необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
Каждая К.Р. выполняется в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной не менее 2 см для замечаний рецензента.
Внешнее оформление К.Р.: на обложке тетради должны быть ясно написаны фамилия студента, его инициалы; название дисциплины; номер контрольной работы; вариант; название учебного заведения; проставлена дата ее выполнения и подпись студента.
В работу должны быть включены все задачи, указанные в задании, строго по соответствующему варианту. В случае не выполнения этого требования ставится «незачет».
Перед решением каждой задачи надо полностью выписать ее условие.
К.р. представляется не позднее установленных сроков. В случае не выполнения этого требования проверка К.Р. производится в неустановленные сроки (после сессии).
Если К.Р. «не зачтена», то ее необходимо переделать в соответствии с указаниями, данными в рецензии, и с надписью «повторная», сдать на проверку, приложив рецензию к работе.
Вносить исправления в сам текст работы после ее рецензирования запрещается.
К.Р. с оценкой «зачет» обязательно представляется на экзамене (зачете).
!!! Экзамен (зачет) начинается с проверки знаний студента по выполненной К.Р.. Если при этом обнаруживается не самостоятельность выполнения К.Р. и непонимания студентом смысла проведенных операций, то экзаменатор ставит «незачет», аннулируя предварительный «зачет» К.Р., а в ведомость оценку «неудовлетворительно» по данной дисциплине.
КОНТРОЛЬНАЯ РАБОТА
ЗАДАНИЕ 1. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ
Брошена стандартная игральная кость. Какова вероятность того, что выпадет а) два; б)меньше пяти.
В ящике находится 90 красных и 15 черных шаров. Наудачу извлекается один шар. Какова вероятность, что он а) красный, б) белый, в) черный.
Брошена стандартная игральная кость. Какова вероятность того, что выпадет а) три; б) меньше трех.
Случайным образом выбирается число из множества 12,20,32,41,53,64,72,86. Какова вероятность, что а) оно четно; б) четное и делится на 2.
Студент знает 20 вопросов из 30. Какова вероятность того, что предложенный вопрос студент а) знает б) не знает.
Из колоды в 36 карт случайным образом достается одна. Какова вероятность того, что а) эта туз; б) дама черви или король черви.
Из слова " вероятность " наугад выбирается одна буква. Какова вероятность, что это будет а) буква "В"; б) согласная буква.
В лотерее 1000 билетов, из них на 1 билет, попадает выигрыш 500 руб., на 10 билетов по 50 руб. и на 60 билетов по 10 руб. Некто покупает 1 билет. Какова вероятность, что он выиграет а) 50 рублей; б) не менее 50 рублей.
В магазин поступило 150 цветных телевизоров, среди которых 50 фирмы Самсунг. Некто случайным образом покупает телевизор. Какова вероятность, что он от фирмы Самсунг.
Набирая номер телефона, забыли последнюю цифру. Какова вероятность того, что набирая ее случайным образом, правильно наберем номер. Как изменится эта вероятность, если дополнительно известно, что это четная цифра.
ЗАДАНИЕ 2. СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ
Для определения доли бракованных изделий были взяты случайным образом 200 изделий. При проверке оказалось, что среди них 5 бракованных. Какова вероятность, что произведенная деталь является а) бракованной б) стандартной.
Обследование показало, что из 1000 зашедших в магазин потенциальных покупателей, действительно приобрело товар 190. Какова вероятность того, что зашедший в магазин человек а) приобретет товар б) не приобретет товар.
Стрелок произвел 100 выстрелов по мишени, причем поразил мишень 57 раз. Какова вероятность, что стрелок поразит мишень.
Из 500 телевизоров 490 проработало без поломок 10 000 часов и более. Какова вероятность, что произведенный по данной технологии телевизор проработает не менее 10 000 часов без поломок.
За последние 100 дней курс доллара повышался 25 раз. Какова вероятность, что на следующих торгах курс доллара повысится.
Статистика показала, что из последних 1000 новорожденных 560-мальчики. Какова вероятность того, что следующий новорожденный будет мальчик.
Из 1000 случайно отобранных семей у 350 доходы были выше 1000 у.е. Какова вероятность, что отдельная семья имеет доход выше 1000 у.е.
При аттестации 100 сотрудников неаттестованными оказались 8. Какова вероятность пройти аттестацию у данной категории сотрудников.
Относительная частота появления бракованных изделий на автоматической срочной линии составляет 0,02. Сколько проверялось изделий, если известно, что бракованных было 8?
Из 1000 проверенных изделий оказалось, что 130 из них - "подделки". Какова вероятность, что приобретенный товар является "подделкой"?
ЗАДАНИЕ 3. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ
Технологический процесс контролируется тремя независимо работающими приборами, вероятности отказа которых 0,1;0,1;0,2 соответственно. Определите вероятность выхода из строя хотя бы одного прибора.
Вероятность того, что на торговую площадку в течении минуты придет одно сообщению равна 0,3, то, что два равна 0,15, то, что три сообщения - 0,05. Какова вероятность того, что в течении следующей минуты придет от одного до трех сообщений включительно.
Вероятность того, что индекс N ценной бумаги А возрастет равна 0,4, а для ценной бумаги В эта вероятность равна 0,3. Вероятность того, что индекс N возрастет одновременно для обоих ценных бумаг равна 0,15. Какова вероятность того, что а) индекс N возрастет хотя бы для одной ценной бумаги; б) индекс N не возрастет ни у одной ценной бумаги.
Вероятность того, что студент изучает английский равна 0,8, а немецкий 0,3. Вероятность того, что студент изучает оба языка равна 0,2. Найти вероятность того, что случайно взятый студент а) изучает хотя бы один язык; б) не изучает ни одного.
Вероятность того, что станок А выйдет из строя в течении смены равна 0,1, а для станка В-0,05. Вероятность того, что оба станка выйдут из строя в течении смены - 0,01. Найти вероятность того, что в течении смены а) выйдет из строя хотя бы один станок; б) не выйдут из строя оба станка.
Рабочий обслуживает три станка, вероятности отказа станков в течении смены р>1>=0,4; р>2>=0,25; р>3>=0,15 соответственно. Найти вероятность того, что в течении смены откажут ровно два станка.
В условиях предыдущей задачи положить p>1>=0,45; p>2>=0,1, p>3>=0,35.
Для сигнализации об аварии установлено два независимо работающих датчика, вероятности отказа которых p>1>=0,2 и p>2>=0,1. Найти вероятность того, что при отказе сработает ровно один датчик.
В урне находится n=10 красных и m=20 белых шара. Из урны без возвращения вынимают три шара. Какова вероятность того, что среди них два белых. При решении использовать теоремы сложения и умножения.
В условиях предыдущей задачи положить n=20, m=40.
ЗАДАНИЕ 4. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ И ФОРМУЛА БЕЙЕСА
В магазин поступили телевизоры с двух заводов в соотношении 30% с завода №1 и 70% с завода №2. Продукция завода №1 содержит 5% телевизоров со скрытым дефектом, а завода №2-10%. Найти вероятность того, что купленный телевизор содержит скрытый дефект.
Пусть мы находимся в условиях предыдущей задачи. Известно, что купленный телевизор оказался со скрытым дефектом. Требуется найти вероятность того, что он произведен на заводе №2.
В урне 1 содержится 3 белых и 3 черных шара, а в урне №2 содержится 5 белых и 1 черный шар. Из случайно выбранной урны достается один шар. Какова вероятность того, что это белый шар?
В условиях предыдущей задачи, стало известно, что вынутый шар оказался белый. Какова вероятность того, что случайно выбрана была урна №2.
Известно, что 5% всех мужчин и 3% всех женщин - дальтоники. В группе из 100 человек 60 мужчин и 40 женщин. Найти вероятность того, что случайно выбранный человек - дальтоник.
Пусть мы находимся в условиях предыдущей задачи и предположим, что выбранный человек - дальтоник. Какова вероятность, что это женщина.
Вероятность того, что "хороший" эксперт оценит неправильно ценную бумагу равна 0,05, эта вероятность для "среднего" эксперта 0,15. В конторе работает 5 "хороших" и 3 "средних" эксперта. Для оценки ценной бумаги случайным образом выбран эксперт. Найти вероятность того, что ценная бумага будет оценена неправильно.
Пусть мы находимся в условиях предыдущей задачи. И пусть известно, что ценная бумага оценена неправильно. Какова вероятность того, что ошибку допустил "хороший" эксперт.
Два цеха штампуют однотипные детали. Первый цех дает 5% брака, второй - 4%. Для контроля отобрано 20 деталей с первого цеха и 10 деталей со второго. Эти детали смешаны в одну партию, и из нее на удачу извлекают одну деталь. Какова вероятность того, что она бракованная?
В условиях предыдущей задачи стало известно, что деталь оказалась бракованная. Какова вероятность того, что она из цеха №1.
ЗАДАНИЕ 5. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
В следующих задача дискретная случайная величина задана законом распределения. Требуется построить функцию распределения, найти математическое ожидание, моду, дисперсию, среднее квадратичесоке отклонение, коэффициент вариации, коэффициент асимметрии.
|
1. |
х |
0 |
1 |
4 |
|
|
p |
0.3 |
0.6 |
0.1 |
|
2. |
х |
-1 |
1 |
2 |
|
p |
0.25 |
0.25 |
0.5 |
|
3. |
x |
-1 |
0 |
4 |
|
p |
0.1 |
0.3 |
0.6 |
|
4. |
x |
-2 |
0 |
2 |
|
p |
0.1 |
0.3 |
0.6 |
|
5. |
x |
-5 |
0 |
5 |
|
p |
0.1 |
0.6 |
0.3 |
|
6. |
X |
-1 |
0 |
2 |
|
P |
0.2 |
0.2 |
0.6 |
|
7. |
X |
0 |
1 |
6 |
|
P |
0.5 |
0.4 |
0.1 |
|
8. |
X |
-3 |
0 |
3 |
|
P |
0.4 |
0.2 |
0.4 |
|
9. |
X |
-2 |
0 |
5 |
|
P |
0.5 |
0.1 |
0.4 |
|
10. |
X |
-1 |
0 |
1 |
|
P |
0.4 |
0.2 |
0.4 |
В следующих задачах непрерывная случайная величина Х задана плотностью распределения вероятности:
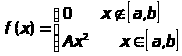
Требуется вычислить константу А и математическое ожидание Х. Найти вероятность Р(с<x<d) и изобразить это решение на графике плотности распределения.
11. a=0, b=3, c=1, d=2. 16. a=3, b=8, c=0, d=5.
12. a=0, b=2, c=1, d=3. 17. a=3, b=10, c=1, d=2.
13. a=1, b=5, c=2, d=3. 18. a=4, b=8, c=1, d=5.
14. a=1, b=7, c=5, d=10. 19. a=5, b=10, c=0, d=7.
15. a=1, b=10, c=5, d=7. 20. a=5, b=8, c=7, d=8.
ЗАДАНИЕ 6. СХЕМА БЕРНУЛЛИ
Вероятность рождения мальчика равна 0,52. Случайная величина Х- число родившихся мальчиков среди 1000 новорожденных. Найти числовые характеристики Х и вероятности
а)
Р (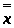 =520)
б) Р(510
=520)
б) Р(510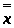 530).
530).
2.Вероятность
того, что клиенту страховой компании
понадобится страховка равна 0,01. Случайная
величина Х- число клиентов, которые
обратятся в страховую компанию за
страховкой из 10000 застраховавшихся.
Найти числовые характеристики Х и
вероятности а) Р(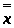 =100)
б)Р(90
=100)
б)Р(90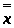 110).
110).
3. Вероятность того, что зашедший в магазин посетитель приобретет товар равна 0,35. Случайная величина Х- число посетителей, которые приобрели товар из 1000 вошедших в магазин. Найти числовые характеристики Х и вероятности
а) Р(Х=350) б) Р(320Х380).
4. По предварительным опросам известно, что 40% опрошенных готовы проголосовать на выборах мэра города за №. Найти вероятность того, что из 50000 жителей, имеющих право проголосовать, за № отдадут голоса а) ровно 20000 человек; б) от 15000 до 25000 человек.
5. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,1. Найти вероятность, что среди 500 деталей окажется бракованными а) ровно 50; б) от 40 до 60.
6. Вероятность нарушения герметичности банки консервов 0,001. Найти вероятность того, что среди 20000 банок с нарушениями окажутся а) ровно 20; б) от 15 до 25.
7. Всхожесть семян данного растения составляет 80%. Найти вероятность того, что среди 200 посаженных семян взойдет а) ровно 160; б) от 140 до 180.
8. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка будет повреждена равна 0,003. Найти вероятность того, что магазин получит поврежденными: а) ровно 3 бутылки; б) более 5 бутылок.
9. Книга издается тиражом 10000 экземпляров. Технология изготовления предполагает, что вероятность того, что в книге будет иметься дефект брошюровки равна 0,0003. Найти среднее число книг с дефектом брошюровки. Найти вероятность того, что число книг с дефектом брошюровки будет: а) хотя бы одна; б) более 4.
10. Устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течении часа равна 0,005. Найти числовые характеристики Х- числа элементов отказавших в течении часа. Найти вероятность того, что в течении часа откажет а) хотя бы один элемент; б) от 4 до 6 элементов.
ЗАДАНИЕ 7. РАСПРЕДЕЛЕНИЕ ПУАССОНА. РАВНОМЕРНОЕ И ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЯ
Число сообщений Х, поступающих на пульт диспетчера в течении часа, подчиняется закону Пуассона с параметром =5(сообщений в час). Найти числовые характеристики Х и вероятности следующих событий:
а) Р(Х=0); б) Р(Х>3).
В порт в среднем приходит 2,5 судна в день. Предполагается, что Х- число судов зашедших в порт в течении суток, имеет распределение Пуассона. Найдите числовые характеристики Х и вероятности следующих событий:
а) Р(Х1); б) Р(х3).
Интервалы времени между приходами в порт судов распределены по показательному закону с интенсивностью =5 (часов). Найти числовые характеристики Х- время между приходами двух судов. Вычислить: а)
Р(Х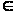 (1,2));
б) Р(Х
(1,2));
б) Р(Х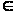 (4,6))
(4,6))
Время между двумя сообщениями, поступающими на торговую площадку (с.в.Х), имеет показательное распределение с параметрами =0,5 (часа). Найти числовые характеристики Х и следующие вероятности а)
Р(Х<0,2); б) Р(0,3<X<0,7).
С.в. Х - время безотказной работы элемента имеет показательное распределение, причем известно, что среднее время безотказной работы элемента рано 1,5 суток. Найти числовые характеристики Х и следующие вероятности:
а) Р(Х<1); б) Р(1,4<Х<1,6).
Случайная величина Х- время обслуживания клиентов в мастерской имеет показательное распределение с функцией распределения F(х)=1-е-3х(отсчет времени берется в часах). Найти числовые характеристики Х и следующие вероятности
а) Р(Х<0,5) б) Р(0,2<X<0,4).
Автобусы некоторого маршрута имеют интервал движения 10 мин. С.в. Х - время, в течении которого пассажиру придется ждать автобус, имеет равномерное распределение. Найти числовые характеристики Х и вероятность того, что пассажир будет ждать автобус более 3 минут.
С.в. Х - имеет равномерное распределение на отрезке [2,6]. Найти функцию распределения и плотность распределения вероятности, числовые характеристики Х и вероятность Р(Х
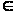 (3,4)).
(3,4)).Шкала лабораторных весов имеет цену деления 1 грамм. При взвешивании вес округляется в ближайшую сторону. Какова вероятность, что абсолютная ошибка определения массы: а) будет заключена между DX и 2DX? б) будет менее 0,2 грамма.
Минутная стрелка часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в настоящий момент часы покажут время, которое отличается от истинного не более чем на 15 секунд.
ЗАДАНИЕ 8. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. ПРАВИЛО 3-Х СИГМ
Автомат штампует детали. Контролируемый размер является случайной величиной Х, имеющей нормальное распределение с параметром а=50,
 =0,02.
Выписать функцию распределения и
плотность распределения с.в. Х. Деталь
считается годной, если ее размеры
попадают в интервал от 49,96 до 50,04. Найдите
процент бракованных деталей.
=0,02.
Выписать функцию распределения и
плотность распределения с.в. Х. Деталь
считается годной, если ее размеры
попадают в интервал от 49,96 до 50,04. Найдите
процент бракованных деталей.Жирность молока коров в область (в %) есть нормально распределенная с.в. с математическим ожиданием равным 4% и среднеквадратическим отклонением 0,03. Вычислить вероятность того, что в наудачу взятой пробе жирность молока будет: а) более 4%; б) менее 4%; в) от 3,95 до 4,05%. Выписать плотность распределения данной с.в.
Продолжительность работы прибора есть нормально распределенная с.в. с параметрами а=1000 ч. и
 2=900
ч. Найти вероятность того, что
продолжительность горения лампы
составляет: а) более 1000 ч. б) менее 1000 ч.
в) от 940 ч. до 1060 ч. Выписать плотность
распределения данной с.в. и изобразить
решение п. в) на графике плотности.
2=900
ч. Найти вероятность того, что
продолжительность горения лампы
составляет: а) более 1000 ч. б) менее 1000 ч.
в) от 940 ч. до 1060 ч. Выписать плотность
распределения данной с.в. и изобразить
решение п. в) на графике плотности.Рост людей призывного возраста предполагается нормально распределенным со средним 170 см. и средним квадратическим отклонением 7 см. Определить процент лиц, имеющих рост а) более 170 см. б) менее 170 см. в) от 170 до 180 см. Решение п. в) изобразить схематично на графике плотности распределения.
Изменение индекса ценной бумаги на фондовой бирже может быть смоделировано как нормально распределенная случайная величина с параметрами а=1 и
 2=0,01.
Найти вероятность того, что на следующих
торгах индекс ценной бумаги будет а)
более 1 б) менее 1 в) от 0,98 до 1,02. Выписать
функцию распределения и плотность
распределения данной с.в.
2=0,01.
Найти вероятность того, что на следующих
торгах индекс ценной бумаги будет а)
более 1 б) менее 1 в) от 0,98 до 1,02. Выписать
функцию распределения и плотность
распределения данной с.в.Средний процент выполнения плана предприятиями отрасли составляет 103%, среднее квадратическое отклонение 2%. Предполагая, что выполнение плана предприятиями подчиняется нормальному закону, определить процент предприятий, выполняющих план: а) более 103% б) менее 103% в) от 99% до 107%. Решение п. в) схематично изобразить на графике плотности распределения.
Диаметр деталей, изготовленных цехом, является с.в., имеющей нормальное распределение с математическим ожиданием равным а=5 см. и дисперсией 0,0004. В каких границах можно практически гарантировать диаметр деталей. Если данная с.в. выйдет за эти границы, то объясните ситуацию. Подсчитайте процент деталей, заключенных в пределах от 4,96 до 5,04.
На автомате изготовляют заклепки. Диаметр заклепок можно считать нормально распределенной с.в. со средним 3 мм и среднем квадратическим отклонением 0,1. Какие размеры диаметра головок заклепки можно гарантировать с вероятностью: а) 0,95; б) 0,9973.
Контролируемый размер детали представляет собой нормально распределенную с.в. с параметрами МХ=150 мм
 (Х)=2
мм. а) Найти вероятность брака, если
допустимые размеры должны быть 1503
мм. б) Какую точность контролируемого
размера можно гарантировать с вероятностью
0,97. в) За какие границы практически не
выйдет контролируемый размер детали.
Если он выйдет за эти границы, то
постарайтесь объяснить ситуацию.
(Х)=2
мм. а) Найти вероятность брака, если
допустимые размеры должны быть 1503
мм. б) Какую точность контролируемого
размера можно гарантировать с вероятностью
0,97. в) За какие границы практически не
выйдет контролируемый размер детали.
Если он выйдет за эти границы, то
постарайтесь объяснить ситуацию.Вес отдельной коробки конфет представляет собой нормально распределенную с.в. со средним 500 гр. и средним квадратическим отклонением 10 гр. а) Найти процент коробок, вес которых более 500 гр. б) Найти процент коробок, вес которых заключен в пределах 50015 гр.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ЗАДАНИЕ 9. ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ ПО НЕСГРУППИРОВАННЫМ НАБЛЮДЕНИЯМ
1-10. В следующих задачах дана выборка. Требуется:
а) Построить статистический ряд распределения частот и полигон частот;
б) Вариационный ряд;
в) Найти "хорошие" оценки математического ожидания и дисперсии;
г) Найти выборочные моду, медиану, коэффициент вариации, коэффициент асимметрии.
0,1,1,3,1,2,2,0,1,0.
1,5,1,2,1,3,2,3,1,2.
10,8,10,11,9,10,8,9,10,10.
50,45,45,55,45,50,40,45,50,45.
20,22,20,24,20,22,20,20,25,22.
-1,1,0,1,1,2,-1,1,2,1.
9,5,5,7,5,7,3,5,9,7.
15,12,8,15,10,15,8,12,15,12.
10,20,20,5,15,20,5,10,20,5.
0,-1,2,-2,0,0,-1,2,-1,-2.
ЗАДАНИЕ 10. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
25 рабочих контролировались в течении месяца по признаку - процент выполнения норм выработки за месяц. По выборочным данным были рассчитаны
 =102,3%
- средний процент выработки и дисперсия
S2=16.
Найти 95% доверительный интервал для
генеральной средней, если известно,
что признак имеет нормальное распределение.
=102,3%
- средний процент выработки и дисперсия
S2=16.
Найти 95% доверительный интервал для
генеральной средней, если известно,
что признак имеет нормальное распределение.Используя данные задачи 1, определите, каким должен быть минимальный размер выборки для того, чтобы оценить среднюю месячную норму выработки с 95% надежностью и с максимальной ошибкой (точностью) не более 0,5(%).
Из большой партии электроламп случайным образом взята выборка из 100 ламп. Средняя продолжительность горения лампы, оцененная по выборке оказалась равной 1200 ч. Из предыдущих проверок известно, что данный признак имеет нормальное распределение с дисперсией 2=2500. Найти 97% доверительный интервал для генеральной средней.
Используя данные задачи 3, определите, каким должен быть минимальный размер выборки для того, чтобы оценить среднюю продолжительность горения лампы с 99% надежностью и с точностью не более 100 (ч).
Произведено 15 замеров контролируемого признака детали, изготовляемой станком-автоматом. По выборочным данным найдено S2=20 мкм. Найти точность работы станка с надежностью 0,95. Предполагается, что контролируемый признак имеет нормальное распределение.
По предварительному опросу населения большого города, в котором участвовало 900 жителей, за мероприятие Х, готовы проголосовать 400 человек из опрошенных жителей. Найти 90% доверительный интервал, в котором находится истинный процент готовых проголосовать за мероприятие Х.
Используя данные задачи 6, определите, каким должен быть минимальный размер выборки для того, чтобы оценить истинный процент "за" с 95% надежностью и с точностью не более 2%.
Недельные доходы фирмы подчинены нормальному закону распределения. По 25-еженедельным наблюдениям за доходами фирмы найдено S2=1200. Найдите 95% доверительный интервал для среднего квадратического отклонения недельных доходов.
Средний привес 16 поросят, которым давали в пищу добавку А, составил 30 кг, а S2=1,5. Считая, что данный признак имеет нормальное распределение, найдите 90% доверительный интервал для генеральной средней.
Среди 400 деталей, изготовленных станком-автоматом, 20 оказалось нестандартных. Найдите доверительный интервал, покрывающий с надежностью 0,98 неизвестную вероятность "брака".
ЗАДАНИЕ 11. ПРОВЕРКА ГИПОТЕЗ. F, T - КРИТЕРИИ
1-5. Для сравнения организации работы на двух однотипных
предприятиях,
были взяты выборочные данные объемами
n>1>
и n>2>
соответственно по признаку - объемы
выпущенной продукции в у.е. Оценки
дисперсии
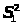 и
и
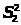 даны ниже. Можно ли считать, что предприятия
работают одинаково точно. Уровень
значимости выбрать самостоятельно.
даны ниже. Можно ли считать, что предприятия
работают одинаково точно. Уровень
значимости выбрать самостоятельно.
1.
n>1>=10,
n>2>=15;
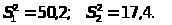
2.
n>1>=16,
n>2>=9;
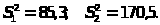
3.
n>1>=12,
n>2>=17;
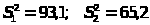
4.
n>1>=8,
n>2>=17;

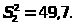

5.
n>1>=11,
n>2>=9;
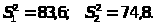
6-10.
Для сравнения производительности работы
двух однотипных отделов торговли, были
взяты две соответствующие выборки
объемами n>1>
и n>2>
соответственно, по которым подсчитаны
выборочные характеристики:

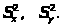 Проверьте гипотезу о том, что
производительность отделов одинакова.
Уровень значимости выбрать самостоятельно.
Проверьте гипотезу о том, что
производительность отделов одинакова.
Уровень значимости выбрать самостоятельно.
6.
n>1>=15,
n>2>=20;
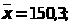
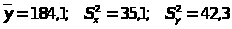



7.
n>1>=20,
n>2>=16;


8.
n>1>=12,
n>2>=8;
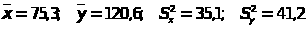


9.
n>1>=9,
n>2>=14;




10.
n>1>=8,
n>2>=20;
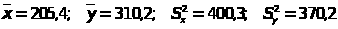
ЗАДАНИЕ 12.Критерий Пирсона
1-3. Ниже приведены данные о фактических объемах сбыта (в у.е.) в пяти районах. Согласуются ли эти результаты с предположением о том, что сбыт продукции в этих районах одинаков. Уровень значимости выбрать самостоятельно.
|
1. |
Район |
1 |
2 |
3 |
4 |
5 |
|
Объем сбыта |
75 |
90 |
85 |
70 |
80 |
|
2. |
Район |
1 |
2 |
3 |
4 |
5 |
|
Объем сбыта |
85 |
120 |
140 |
70 |
85 |
|
3. |
Район |
1 |
2 |
3 |
4 |
5 |
|
Объем сбыта |
50 |
65 |
70 |
80 |
35 |
4-10. В следующих задачах для приведенных сгруппированных данных проверить гипотезу о том, что они получены из нормальной генеральной совокупности. Уровень значимости выбрать самостоятельно.
|
4. |
Границы интервала |
0-6 |
6-12 |
12-18 |
18-24 |
24-30 |
30-36 |
36-42 |
|
Частота |
2 |
9 |
19 |
35 |
24 |
13 |
6 |
|
5. |
Граница интервала |
0-4 |
4-8 |
8-12 |
12-16 |
16-20 |
20-24 |
|
Частота |
7 |
16 |
55 |
22 |
4 |
2 |
|
6. |
Граница интервала |
10-14 |
14-18 |
18-22 |
22-26 |
26-30 |
30-34 |
|
Частота |
10 |
31 |
65 |
25 |
8 |
3 |
|
7. |
Граница интервала |
1-5 |
5-9 |
9-13 |
13-17 |
17-21 |
21-25 |
25-29 |
|
Частота |
3 |
29 |
56 |
81 |
67 |
19 |
8 |
|
8. |
Граница интервала |
14-16 |
16-18 |
18-20 |
20-22 |
22-24 |
24-26 |
|
Частота |
12 |
20 |
78 |
45 |
10 |
3 |
|
9. |
Граница интервала |
7-9 |
9-11 |
11-13 |
13-15 |
15-17 |
17-19 |
19-21 |
|
Частота |
2 |
35 |
97 |
86 |
45 |
26 |
4 |
|
10. |
Граница интервала |
30-32 |
32-34 |
34-36 |
36-38 |
38-40 |
40-42 |
42-44 |
|
Частота |
19 |
43 |
101 |
95 |
40 |
13 |
3 |
ЗАДАНИЕ 13. ИсслЕДОВАНИЕ ЗАВИСИМОСТЕЙ
В
следующих задачах следует построить
уравнение регрессии вида
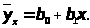 Сделать вывод о возможности использования
линию регрессии в дальнейших прогнозах.
Сделать вывод о возможности использования
линию регрессии в дальнейших прогнозах.
1. Данные о выпуске продукции (Y) и энерговооруженности (X) на 6 предприятиях.
-
X>i>
2
3
5
6
6
7
Y>i>
2,5
5,5
10
10
11,5
13,5
2. Данные об удельной величине спроса товаров (Y) и среднедушевого дохода (Х).
|
X>i> |
1 |
2 |
3 |
4 |
6 |
6 |
|
Y>i> |
3,5 |
6,1 |
7,5 |
7,8 |
8,2 |
8,1 |
3. Данные об объеме валового продукта (Y) и затратами на капитальные вложения (Х) по 6 предприятиям.
|
X>i> |
1 |
1 |
2 |
4 |
6 |
8 |
|
Y>i> |
4,5 |
5,1 |
10,3 |
18,1 |
19,2 |
19,8 |
4. Данные об объеме выпуска продукции (Y) и ее себестоимости.
|
X>i> |
2 |
2 |
3 |
4 |
5 |
6 |
|
Y>i> |
8,5 |
9,1 |
11,2 |
12,8 |
15,1 |
17,3 |
5. Данные о долговечности элемента (Y) и величине эксплуатационного напряжения (Х).
|
X>i> |
6 |
7 |
7 |
8 |
9 |
9 |
|
Y>i> |
40,1 |
45,4 |
46,2 |
53,2 |
59,5 |
60,2 |
6. Данные об урожайности (Y) и количестве весенних осадках (Х).
|
X>i> |
1 |
2 |
2 |
3 |
4 |
5 |
|
Y>i> |
0,8 |
3,5 |
4,2 |
7,1 |
9,8 |
13,1 |
7. Данные об урожайности (Y) и механовооруженности (Х)
|
X>i> |
1 |
1 |
2 |
2 |
3 |
5 |
|
Y>i> |
4,2 |
3,9 |
4,8 |
5,1 |
6,2 |
7,7 |
8. Данные о зависимости стоимости сооружения (Y) и срока ее эксплуатации (Х).
|
X>i> |
1 |
2 |
3 |
3 |
4 |
6 |
|
Y>i> |
0,7 |
4,2 |
7,3 |
7,1 |
10,3 |
15,6 |
9. Данные об изменении массы просят (Y) и возраста (Х).
|
X>i> |
4 |
5 |
7 |
7 |
8 |
10 |
|
Y>i> |
12,6 |
14,2 |
16,3 |
15,9 |
17,4 |
18,8 |
10. Данные о производительности труда (Y) и фондовооруженности (Х).
|
X>i> |
2 |
4 |
6 |
6 |
7 |
8 |
|
Y>i> |
0,8 |
5,2 |
8,7 |
9,2 |
11 |
13,2 |
IV. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Пример_1. Студент знает 15 вопросов из 25. Наудачу ему задается вопрос. Найти вероятность того, что он его знает.
Решение: Мы находимся в классической схеме. Действительно, если представить эксперимент
в виде урновой схемы - в урне 25 пронумерованных шаров из которой достается один шар- то ясно, что все исходы равновозможные и их конечное число. Далее A={студент знает предложенный вопрос}, m=15- число исходов благоприятствующих А, n=25- общее число исходов. Тогда
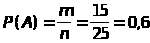 .
.
Пример 2. Из колоды в 36 карт, достается одна. Найти вероятность того, что она "красная".
Решение: Обозначим А={наудачу вынутая карта- "красная"}; m=18- число исходов благоприятствующих А, т.к. в колоде из 36 карт, 18 "красных" карт; n=36- общее число исходов. Тогда по классическому определению вероятности
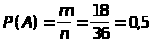 .
.
Пример 3.Стрелок произвел 100 выстрелов по мишени, причем поразил мишень в 45 случаях. Найти вероятность того, что стрелок поразит мишень.
Решение: Подсчитаем относительною частоту события А={стрелок поразит мишень при одном выстреле}.
 .
.
Таким образом искомая вероятность Р(А)=0,45.
Пример 4. Вероятность того, что событие А произойдет в опыте равна 0,75; вероятность того, что событие В произойдет в опыте- 0,4. Вероятность того, что оба события произойдут в опыте равна 0,25. Найти вероятность того, что хотя бы одно событие произойдет в опыте.
Решение: Обозначим А={событие А произошло в опыте}, В={событие В произошло в опыте}
Тогда АВ={события А и В произошли в опыте одновременно}.
Р(А)=0,75; Р(В)=0,4; Р(АВ)=0,25.
Используя теорему о сумме двух совместных событий получим
Р(А+В)=Р(А)+Р(В)-Р(АВ)=0,75+0,4-0,25=0,9.
Пример 5. Деталь проходит три операции обработки. Вероятность появления брака во время первой операции равна 0,02, второй- 0,01, третьей- 0,03. Найти вероятность: а) выхода стандартной детали, считая появление брака во время отдельных операций независимыми событиями; б) выхода бракованной детали.
Решение: а) введем события А={на выходе появилась стандартная деталь}, А>i>={i-я операция обработки прошла без брака}, i=1,2,3. Тогда А=А>1>А>2>А>3. >По условию задачи Р(А>1>)=0,98; Р(А>2>)=0,99; Р(А>3>)=0,97.Используя теорему умножения для независимых событий, получаем.
Р(А)=Р(А>1>А>2>А>3>)=Р(А>1>)Р(А>2>)Р(А>3>)=0,980,990,97=0,9411.
б) ={на
выходе появилась бракованная деталь}.Тогда
={на
выходе появилась бракованная деталь}.Тогда
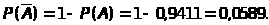
Пример_6. Партия деталей содержит 70% деталей первого завода и 30% деталей второго завода. Вероятность того, что деталь с первого завода проработает без отказа более 1000 часов (надежность) равна 0,95 , а для деталей со второго завода эта вероятность равна 0,9.
а) Найти вероятность того, что случайно взятая из партии деталь проработает без отказа более 1000 часов.
б) Деталь прошла испытание и проработала безотказно 1000 часов. Найти вероятность того, что она с первого завода.
Решение: Введем события А={деталь проработает без отказа более 1000 часов}.H>i>={взятая деталь с завода i} , i=1,2 по условию задачи P(H>1>)=0,7 ; P(H>2>)=0,3 ; P(A/H>1>)=0,95 ; P(A/H>2>)=0,9.
По формуле полной вероятности
P(A)= P(H>1>) P(A/H>1>)+ P(H>2>) P(A/H>2>)=0,70,95+0,30,9=0,935.
Таким образом, партия деталей (большое количество) будет содержать где-то 93,5% деталей с заданной надежностью. б) Сохраним обозначения п. а). по формуле Бейеса
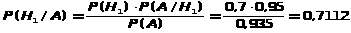 .
.
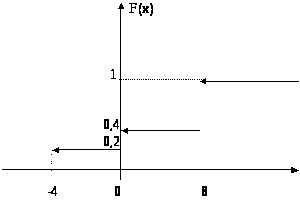
Пример 7. Найти числовые характеристики с.в. Х , построить функцию распределения если:
-
Х
-4
0
8
Р
0,2
р
0,6
Решение: р=1-(0,2+0,6)=0,2. График ф.р.
МХ=-40,2+00,2+80,6=4, DX=MX2-(MX)2=(-4)20,2+020,2+820,6-(4)2=25,6.
Среднее квадратическое отклонение
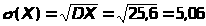 ,
,
коэффициент вариации
 .
.
Мода(Х)=8, т.к. 8 имеет наибольшую вероятность, равную 0,6. Коэффициент асимметрии
 .
.
Пример 8. Вероятность того, что в данный день торговая база уложится в норму расходов на транспорт, равна 0,8. Какова вероятность того, что за три рабочих дня база уложится в норму 2 раза. Найти числовые характеристики с.в. Х- число дней, когда база укладывается в норму транспортных расходов в течение трех рассматриваемых дней.
Решение: Можно считать, что мы находимся в схеме Бернулли, а следовательно с.в. Х имеет биномиальное распределение. По условию задачи n=3 , p=0,8.
Тогда
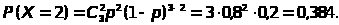 Основные
числовые характеристики с.в. Х равны:
а) математическое ожидание MX=
np=30,8=2,4;
б) дисперсия DX=
npq=30,80,2=0,48;
q=1-p=0,2,
Основные
числовые характеристики с.в. Х равны:
а) математическое ожидание MX=
np=30,8=2,4;
б) дисперсия DX=
npq=30,80,2=0,48;
q=1-p=0,2,
 0,7;
0,7;
в) коэффициент вариации
 ;
;
г) коэффициент асимметрии
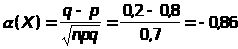 ;
;
д) коэффициент эксцесса
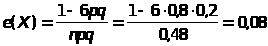 ;
;
е) Мода (наивероятнейшее число) находится из неравенства
np-qМода(Х)<np+p , т.е. 30,8-0,2Мода(Х)<30,8+0,8
2,2Мода(Х)<3,2Мода(Х)=3.
Пример 9. В условиях предыдущего примера, найти вероятность того, что из 100 рабочих дней торговая база уложится в норму транспортных расходов:
а) ровно 80 раз; б) от 75 до 85 дней включительно.
Решение: а) в нашем случае n=100; p=0,8; q=0,2.
Воспользоваться точной формулой для вычисления Р(Х=80) практически невозможно, поэтому воспользуемся приближенной. Так как npq=1000,80,2=16>9,то применим локальную теорему Муавра- Лапласа.
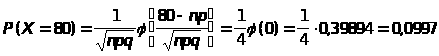 ,
,
(0)- найдено по таблице 3 приложения-плотности нормального распределения N(0,1);
б) воспользуемся интегральной теоремой Муавра- Лапласа.
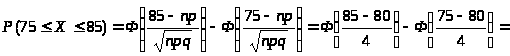
=2Ф(1,25)=20,39435=0,7887
здесь Ф(Х)- функция Лапласа, значение которой найдено по таблице.
Пример 10. Вероятность того, что наборщик ошибется при наборе знака равна 0,0001. Найти вероятность того, что набирая 30000 знаков, наборщик допустит:
а) ровно 3 ошибки; б) от 2 до 4 ошибок включительно.
Решение: Можно считать, что мы находимся в схеме Бернулли с параметрами n=30000, p=0,0001. Тогда npq=300000,00010,99993<9, поэтому для вычисления отдельных вероятностей воспользуемся теоремой Пуассона:
 ,
,
=np, k=0,1,2,...
а)пользуясь таблицей, получим
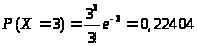 ,
=np=3.
,
=np=3.
б)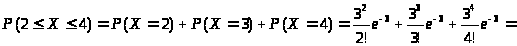
=0,22404+0,22404+0,16803=0,61611.
Пример 11. С.в. Х имеет распределение Пуассона со средним равным 1,5. Найти числовые характеристики Х. Вычислить вероятности: а) Р(Х=0); б) Р(Х1); в) Р(Х>7).
Решение: Для с.в. имеющей распределение Пуассона с параметром известно, что МХ=. Следовательно, из условия задачи (МХ=1,5) находим, что =1,5.Числовые характеристики Х равны
МХ==1,5 ; DХ==1,5; среднее квадратическое отклонение
 .
.
Коэффициент вариации
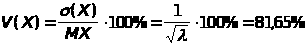 .
.
Коэффициент асимметрии
 .
.
Коэффициент эксцесса
 .
.
Моду с.в. Х найдем по таблице: Мода(Х)=1, т.к. Х=1 имеет наибольшую вероятность.а) По таблице находим Р(Х=0)=0,22313; б)
Р(Х1)=1-Р(Х=0)=0,77687;
в) Р(Х>7)=0,00017.Эта вероятность найдена по таблице 2 приложения, она настолько мала, что можно считать, что больше 7 событий практически не происходят.
Пример 12. Из урны содержащей четыре белых и шесть черных шаров, наудачу извлекают три шара. Какова вероятность, что среди них два черных шара. Найдите числовые характеристики с.в. Х- число черных шаров из вынутых трех шаров.
Решение: Мы находимся в схеме формирования с.в. Х имеющей гипергеометрическое распределение с параметрами (N,p,n):
 ,
,
k=0,1,2,..., q=1-p. В нашем случае: N=6+4=10 - общее число шаров в урне; n=3 - число шаров, которые достаются из урны; Np=6 - количество черных шаров, p=6/N=6/10=0,6 (p связано с черными шарами, т.к. Х- тоже связано с черными шарами);
Nq=4 - число белых шаров, q=0,4. Итак:
 .
.
Числовые характеристики с.в. Х равны MX=np=30,6=1,8 ;
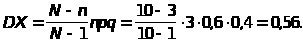
Среднее квадратическое отклонение

Коэффициент вариации
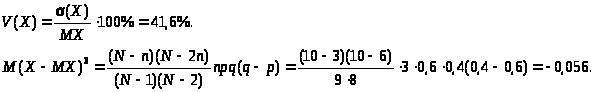
Коэффициент асимметрии
 .
.
Пример 13. С.в. Х имеет показательное распределение с параметром =2. Найти числовые характеристики с.в. Х и вычислить Р(1<X<3).
Решение: Числовые характеристики с.в. Х вычисляются по формулам:
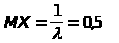

-математическое ожидание;
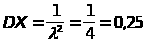 -дисперсия;
-дисперсия;
 -
-
среднее квадратическое отклонение;
V(X)=100% -коэффициент вариации
всегда равен 100% ; Медиана
(Х)=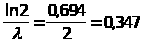 .
.
График плотности с.в. Х имеет вид изображенный на рис.1. Из этого графика видно, что локальный максимум плотности находится в точке О.
Следовательно Мода(Х)=0.
Коэффициент асимметрии (Х)=2 (всегда 2).
Коэффициент эксцесса е(Х)=6 (всегда 6).
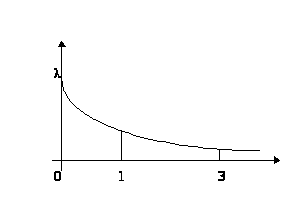
рис.1

Пример
14. С.в.
Х имеет нормальное распределение с
параметрами а=150, 2=36.
С.в.
Х имеет нормальное распределение с
параметрами а=150, 2=36.
а) Выпишите плотность с.в. Х и изобразите эскиз графика плотности.
б) Найти числовые характеристики с.в. Х.
в) Найти границы за которые практически не выходит с.в. Х.
г) Вычислить Р(135<X<165).
Решение: а) Выпишем плотность с.в. Х:
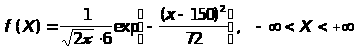
 ,
,
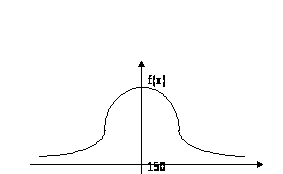
б) Найдем числовые характеристики Х.
МХ=Мода( )=Медиана(
)=Медиана( )=а=150
)=а=150
D(X)=2=36(x)=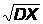 ==6
==6
Коэффициенты асимметрии и эксцесса равны 0. Коэффициент вариации
 ,
,
в) используя правило 3 сигм, можно утверждать, что с.в. Х практически (с вероятностью 0,9973) не выйдет за границы интервала а-
3<X<a+3, т.е. 150-36<X<150+ 36132<X<168;
г)
Р(135<X<165)=Ф
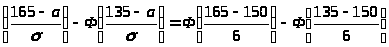 =
=
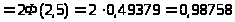 ,
,
здесь Ф()-функция Лапласа, значение которой найдено по таблице. Отметим свойство функции Ф(х):Ф(-х)=-Ф(х) поэтому Ф(-2,5)=- Ф(2,5)=-0,49379.
Пример 15. Найдите выборочные числовые характеристики по выборке: 3,5,6,3,3,6,3,7,5,5,3.
Решение: Построим статистический ряд частот:
-
Варианты х>i>
3
5
6
7
Частота n>i>
5
3
2
1
Объем выборки
n=n>1>+n>2>+n>3>+n>4>=5+3+2+1=11.
 ;
;
S2= ,
,
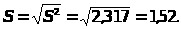
Оценки
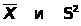 являются "хорошими" для математического
ожидания и дисперсии, т.к. выборка
является малой, а
являются "хорошими" для математического
ожидания и дисперсии, т.к. выборка
является малой, а
 Мода(Х)=3,
т.к. значение 3 встречается большее число
раз (пять). Построим вариационный ряд:
3,3,3,3,3,5,5,5,6,6,7.Т.к. n-нечетно
(n=11),
то на месте (n+1)/2=6
в вариационном ряде стоит медиана:
Медиана(Х)=5.
Мода(Х)=3,
т.к. значение 3 встречается большее число
раз (пять). Построим вариационный ряд:
3,3,3,3,3,5,5,5,6,6,7.Т.к. n-нечетно
(n=11),
то на месте (n+1)/2=6
в вариационном ряде стоит медиана:
Медиана(Х)=5.
Коэффициент асимметрии
(х)=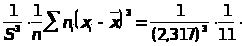
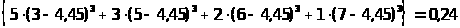 .
.
Пример
16.
По выборочным данным найти
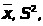 моду,
медиану. Построить гистограмму.
моду,
медиану. Построить гистограмму.
-
Интервал
Частота n>i>
5-11
18
11-17
25
17-23
14
23-29
8
29-35
2
Решение: Построим гистограмму частот

Для удобства
|
Интервал |
Середина интервала |
Частота n>i> |
Накопленная частота |
|
|
вычислений |
5-11 |
8 |
18 |
18 |
|
составим |
11-17 |
14 |
25 |
43 |
|
таблицу. |
17-23 |
20 |
14 |
57 |
|
23-29 |
26 |
8 |
65 |
|
|
29-35 |
32 |
2 |
67 |
|
|
=67 |
При вычислении

=

Медиана
оценивается по формуле Медиана= L+i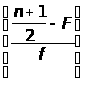
Здесь L- нижняя граница интервала, в котором находится медиана (медианный интервал);
i- величина медианного интервала; n- объем выборки; f- частота медианного интервала;
F- накопленная частота интервала, предшествующему медианному.
В нашем случае n=67, следовательно, медиана равна члену, стоящему на (n+1)/2=34-м месте в вариационном ряду. По накопленным частотам заключаем, что этот член находится в интервале (11,17). Следовательно, медианный интервал (11,17). Тогда L=11, i=6, (n+1)/2=34, f=25, F=18 и, следовательно
Медиана
= 11+6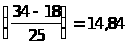 .
.
Мода
находится по формуле Мода= L+i
где L- нижняя граница модального интервала, i- величина модального интервала
f>мо>, f>мо-1>, f>мо+1> частота модального, предшествующего модальному и следующего за модальным интервала. В нашем случае модальный интервал [11,17], т.к. имеет наибольшую частоту. Тогда L=11, i=6,
f>мо>=25,
f>мо-1>=18,
f>мо+1>=14;
Мода =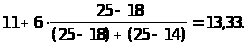
Пример
17. Найти
97,5% доверительный интервал для неизвестного
параметра а нормально распределенного
признака, если известно =7,3.
По выборке объема n=64
найдено
 .
.
Решение Требуемый доверительный интервал равен
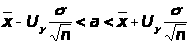 ,
,
где надежность =0,975 позволяет найти U>> из уравнения 2Ф(U>>)=0,975. Из таблицы 4 приложения находим U>>=2,24. Тогда
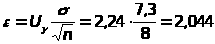 ;
;
120,3-2,044<a<120,3+2,044;118,256<a<122,344.
Пример 18. В условиях предыдущего примера, определите минимальный объем выборки, чтобы с надежностью =0,975 точность оценки была не больше 0,5.
Решение: Точность оценки зависит от выражения
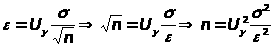
Подставляя U>>=2,24 ; 2=7,32=53,29 ; 2=0,52=0,25 ,получим
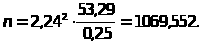

Таким образом, минимальный объем выборки должен составлять 1070 измерений.
Пример
19. По
выборке объема n=25
найдены
 .
Считая, что наблюдаемый признак имеет
нормальное распределение найдите
доверительный интервал с надежностью
0,9.
.
Считая, что наблюдаемый признак имеет
нормальное распределение найдите
доверительный интервал с надежностью
0,9.
Решение. Искомый доверительный интервал равен
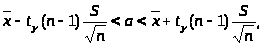
где
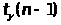 находится
по таблице 5 приложения:
находится
по таблице 5 приложения:
Здесь =1-=0,1; К=n-1=25-1=24, тогда t>0,1>(24)=1,711. Итак,
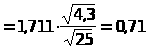 ;
16,3-0,71<a<16,3+0,71;
15,59<a<17,01.
;
16,3-0,71<a<16,3+0,71;
15,59<a<17,01.
Пример 20 Признак имеет нормальное распределение. По выборке объема n=30 найдена оценка дисперсии S2 =1,5. Найдите 95% доверительный интервал для дисперсии.
Решение: Доверительный интервал определяется так
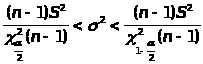 ,
,
Здесь
=1-0,95=0,05;
 тогда из таблицы 7 приложения находим
тогда из таблицы 7 приложения находим
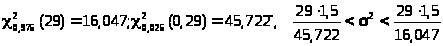 ,
0,95<2<2,7.
,
0,95<2<2,7.
Пример 21. Произведено 529 испытаний, в которых события А наблюдалось 70 раз. Найдите 93% доверительный интеграл для вероятности р события А.
Решение. Искомый доверительный интервал находится так: р>1><p<p>2>, где

 ,
,
здесь =0,93, U>> находится из уравнения Ф(U>>)=/2=0,465 по таблице 4 функции Лапласа находим U>>=1,811. Вычислим

Итак: 0,1323-0,0267<p<0,1323+0,0267; 0,1056<p<0,159.
Пример
22.
Необходимо проверить точность работы
двух агрегатов А и В по контролируемому
признаку. Для этого были взяты две
выборки n>A>=9,
n>B>=12 соответственно, по которым найдено
соответственно, по которым найдено
 .
Требуется проверить гипотезу о том, что
точность работы агрегатов одинакова,
если известна, что контролируемый
признак имеет нормальное распределение.
.
Требуется проверить гипотезу о том, что
точность работы агрегатов одинакова,
если известна, что контролируемый
признак имеет нормальное распределение.
Решение: Проверку проведем по F-критерию:
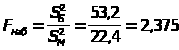 ,
,
здесь

m>1>=n>A>-1=9-1=8, т.к. А имеет большую дисперсию, m>2>=n>В>-1=12-1=11. По таблице, находим при =0,1 F>кр>=F(/2=0,05;8;11)=2,95. Т.к. F>наб.><F>кр.>, то нет основания считать, что точность работы агрегатов разная.
Пример 23. Нужно проверить влияние двух различных кормовых добавок на увеличение веса свиней. Для этого 10 свиней кормили с добавкой А, а других 8 с добавкой В. По выборочным данным вычислим

Решение Уровень значимости возьмем =0,1.Первый этап. Проверим гипотезу о равенстве дисперсии
 .
.
Т.к. F>наб><F>кр>, то гипотезу о равенстве дисперсий принимаем. Второй этап. Проверим гипотезу о равенстве увеличения веса для двух добавок (Н>0>:МХ=МУ).
Используем t – критерий:
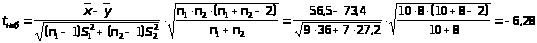 .
.
Выберем =0,05. Найдем для k=n>1>+n>2>-2=10+8-2=16 степеней свободы по таблице 5 приложения t>кр>=t(0,05;16)=2,12. Т.к.t>наб>>t>кр>, то различия признаются существенными. Следовательно добавка В дает больший привес в весе.
Пример 24. Фактический сбыт в шести районах характеризуется таблицей (выборкой).
|
Район |
1 |
2 |
3 |
4 |
5 |
6 |
|
Объем сбыта |
90 |
130 |
110 |
85 |
75 |
110 |
Согласуются ли эти результаты с предложением о том, что сбыт продукции в этих районах одинаков?
Решение: Выберем уровень значимости =0,05. Если гипотеза Н>0>: сбыт одинаков - верна, то теоретически объем сбыта в 600 у.е. (90+130+110+85+75+110=600) должен распределиться одинаково по шести районам, т.е. по 100 у.е. на каждый район. Дальнейшие вычисления сведем в таблицу.
|
Район |
|
|
|
|
|
1 2 3 4 5 6 |
90 130 110 85 75 110 |
100 100 100 100 100 100 |
100 900 100 225 625 100 |
1 9 1 2,25 6,25 1 |
|
|
20,5 |
Таким образом:

Т.к.
мы не оценивали ни один параметр, то по
числу степеней свободы k=6-1=5
и уровню значимости =0,05
по таблице 7 приложения находим
 , то различие в сбыте по районам признается
значимым и не может быть объяснено
действием случайного фактора.
, то различие в сбыте по районам признается
значимым и не может быть объяснено
действием случайного фактора.
Пример_25. Проверить гипотезу о нормальном распределении выборки:
|
Интервал |
10-12 |
12-14 |
14-16 |
16-18 |
18-20 |
20-22 |
22-24 |
|
Частота |
2 |
4 |
8 |
12 |
16 |
10 |
3 |
Решение: Для проверки гипотезы будем использовать критерий Пирсона. Уровень значимости выберем =0,1. Т.к. нормальное распределение определяется двумя параметрами а и 2, то оценим их по выборке, объем которой равен: n=2+4+8+12+16+10+3=55.
Итак:

Для
удобства вычисления статистики
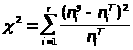 будем промежуточные результаты вносить
в таблицу. Объединим крайние интервалы
с соседними, так, чтобы выполнилось
условие
будем промежуточные результаты вносить
в таблицу. Объединим крайние интервалы
с соседними, так, чтобы выполнилось
условие

|
I |
II |
III |
IV |
V |
VI |
|
№ интервала |
Интервал |
|
P>i> |
|
|
|
1 2 3 4 5 |
-;14 14;16 16;18 18;20 20;+ |
6 8 12 16 13 |
0,0959 0,1686 0,2576 0,2484 0,2295 |
5,274 9,273 14,168 13,662 12,623 |
0,010 0,175 0,332 0,400 0,011 |
|
|
n=55 |
1 |
0,928 |
Здесь Р>i>- вероятность того, что с.в. Х попадает в соответствующий интервал >i> при условии, что она имеет нормальное распределение с параметрами а=17,84; 2=8,53 (=2,92). Например, используя таблицу 4 приложения, находим:

Значения в V столбце вычисляются так:
 и
т.д.
и
т.д.
Значения в VI столбце вычисляются так:
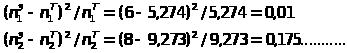
Тогда
сумма VI
столбца даст значение
 Теперь найдем
Теперь найдем
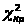 по таблице 7 приложения при уровне
значимости =0,1.
Т.к. после объединения интервалов у нас
осталось r=5-
интервалов и по выборке мы оценили два
(S=2)
параметра а и ,
то для нахождения
по таблице 7 приложения при уровне
значимости =0,1.
Т.к. после объединения интервалов у нас
осталось r=5-
интервалов и по выборке мы оценили два
(S=2)
параметра а и ,
то для нахождения
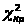 параметр число степеней свободы будет
равен k=r-s-1=5-2-1=2.
Тогда
параметр число степеней свободы будет
равен k=r-s-1=5-2-1=2.
Тогда
 Так
как
Так
как
 (т.е. 0,928<4,61), то гипотезу о нормальном
распределении можно принять.
(т.е. 0,928<4,61), то гипотезу о нормальном
распределении можно принять.
Пример_26.
Построить линию регрессии в виде
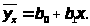 Можно ли использовать ее в дальнейших
прогнозах?
Можно ли использовать ее в дальнейших
прогнозах?
|
x>i> |
4 |
5 |
8 |
8 |
10 |
12 |
|
y>i> |
0,5 |
4,2 |
12,7 |
13,6 |
19,2 |
24,8 |
Решение:
Выборочное уравнение линейной регрессии
Y
на X
имеет вид
 , где
, где
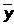 -условная
средняя (при фиксированным х);
-условная
средняя (при фиксированным х);
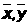 -выборочные
средние;
-выборочные
средние;
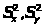 -несмещенные
оценки дисперсии; r>B>-
выборочный коэффициент корреляции:
-несмещенные
оценки дисперсии; r>B>-
выборочный коэффициент корреляции:
 .
.
n=6, т.к. наблюдалось 6 точек вида (x>i>;y>i>);
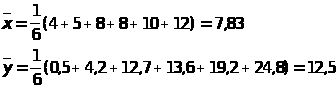
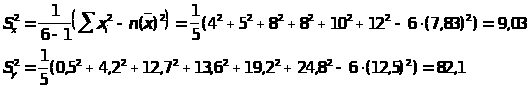
S>x>=3
; S>y>=9,06
; =40,5+54,2+812,7+813,6+1019,2+1224,8=723
=40,5+54,2+812,7+813,6+1019,2+1224,8=723
r>B>=(723-67,8312,5)/(639,06)=0,832.
Уравнение регрессии:
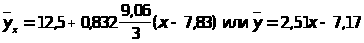 .
.
Проверим гипотезу о значимости коэффициента корреляции, т.е. H>0>:r=0, H>1>:r0.
Вычислим статистику критерия:

По уровню значимости =0,05 и числу степеней свободы k=n-2=6-2=4 из таблицы находим двухстороннюю критическую область t>кр>=2,776. Так как t>наб>>t>кр> , то гипотезу о равенстве нулю коэффициента корреляции отвергаем, т.е. считаем, что r0.
Найдем,
коэффициент детерминации
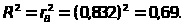 Так
как R2<0,75
(0,75-шаблонное значение), то уравнением
регрессии пользоваться не рекомендуется.
В дальнейшем, т.к. зависимость между X
и Y
существует (r0),
следует либо изменить вид зависимости,
либо увеличить число наблюдений и
провести анализ зависимости снова.
Так
как R2<0,75
(0,75-шаблонное значение), то уравнением
регрессии пользоваться не рекомендуется.
В дальнейшем, т.к. зависимость между X
и Y
существует (r0),
следует либо изменить вид зависимости,
либо увеличить число наблюдений и
провести анализ зависимости снова.
Таблица 1. Плотность стандартного нормального распределения
|
|
|
|||||||||
|
|
||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
0,39894 |
0,39892 |
0,39886 |
0,39876 |
0,39862 |
0,39844 |
0,39822 |
0,39797 |
0,39767 |
0,39733 |
|
0,1 |
0,39695 |
0,39654 |
0,39608 |
0,39559 |
0,39505 |
0,39448 |
0,39387 |
0,39322 |
0,39253 |
0,39181 |
|
0,2 |
0,39104 |
0,39024 |
0,38940 |
0,38853 |
0,38762 |
0,38667 |
0,38568 |
0,38466 |
0,38361 |
0,38251 |
|
0,3 |
0,38139 |
0,38023 |
0,37903 |
0,37780 |
0,37654 |
0,37524 |
0,37391 |
0,37255 |
0,37115 |
0,36973 |
|
0,4 |
0,36827 |
0,36678 |
0,36526 |
0,36371 |
0,36213 |
0,36053 |
0,35889 |
0,35723 |
0,35553 |
0,35381 |
|
0,5 |
0,35207 |
0,35029 |
0,34849 |
0,34667 |
0,34482 |
0,34294 |
0,34105 |
0,33912 |
0,33718 |
0,33521 |
|
0,6 |
0,33322 |
0,33121 |
0,32918 |
0,32713 |
0,32506 |
0,32297 |
0,32086 |
0,31874 |
0,31659 |
0,31443 |
|
0,7 |
0,31225 |
0,31006 |
0,30785 |
0,30563 |
0,30339 |
0,30114 |
0,29887 |
0,29659 |
0,29431 |
0,29200 |
|
0,8 |
0,28969 |
0,28737 |
0,28504 |
0,28269 |
0,28034 |
0,27798 |
0,27562 |
0,27324 |
0,27086 |
0,26848 |
|
0,9 |
0,26609 |
0,26369 |
0,26129 |
0,25888 |
0,25647 |
0,25406 |
0,25164 |
0,24923 |
0,24681 |
0,24439 |
|
1 |
0,24197 |
0,23955 |
0,23713 |
0,23471 |
0,23230 |
0,22988 |
0,22747 |
0,22506 |
0,22265 |
0,22025 |
|
1,1 |
0,21785 |
0,21546 |
0,21307 |
0,21069 |
0,20831 |
0,20594 |
0,20357 |
0,20121 |
0,19886 |
0,19652 |
|
1,2 |
0,19419 |
0,19186 |
0,18954 |
0,18724 |
0,18494 |
0,18265 |
0,18037 |
0,17810 |
0,17585 |
0,17360 |
|
1,3 |
0,17137 |
0,16915 |
0,16694 |
0,16474 |
0,16256 |
0,16038 |
0,15822 |
0,15608 |
0,15395 |
0,15183 |
|
1,4 |
0,14973 |
0,14764 |
0,14556 |
0,14350 |
0,14146 |
0,13943 |
0,13742 |
0,13542 |
0,13344 |
0,13147 |
|
1,5 |
0,12952 |
0,12758 |
0,12566 |
0,12376 |
0,12188 |
0,12001 |
0,11816 |
0,11632 |
0,11450 |
0,11270 |
|
1,6 |
0,11092 |
0,10915 |
0,10741 |
0,10567 |
0,10396 |
0,10226 |
0,10059 |
0,09893 |
0,09728 |
0,09566 |
|
1,7 |
0,09405 |
0,09246 |
0,09089 |
0,08933 |
0,08780 |
0,08628 |
0,08478 |
0,08329 |
0,08183 |
0,08038 |
|
1,8 |
0,07895 |
0,07754 |
0,07614 |
0,07477 |
0,07341 |
0,07206 |
0,07074 |
0,06943 |
0,06814 |
0,06687 |
|
1,9 |
0,06562 |
0,06438 |
0,06316 |
0,06195 |
0,06077 |
0,05959 |
0,05844 |
0,05730 |
0,05618 |
0,05508 |
|
2 |
0,05399 |
0,05292 |
0,05186 |
0,05082 |
0,04980 |
0,04879 |
0,04780 |
0,04682 |
0,04586 |
0,04491 |
|
2,1 |
0,04398 |
0,04307 |
0,04217 |
0,04128 |
0,04041 |
0,03955 |
0,03871 |
0,03788 |
0,03706 |
0,03626 |
|
2,2 |
0,03547 |
0,03470 |
0,03394 |
0,03319 |
0,03246 |
0,03174 |
0,03103 |
0,03034 |
0,02965 |
0,02898 |
|
2,3 |
0,02833 |
0,02768 |
0,02705 |
0,02643 |
0,02582 |
0,02522 |
0,02463 |
0,02406 |
0,02349 |
0,02294 |
|
2,4 |
0,02239 |
0,02186 |
0,02134 |
0,02083 |
0,02033 |
0,01984 |
0,01936 |
0,01888 |
0,01842 |
0,01797 |
|
2,5 |
0,01753 |
0,01709 |
0,01667 |
0,01625 |
0,01585 |
0,01545 |
0,01506 |
0,01468 |
0,01431 |
0,01394 |
|
2,6 |
0,01358 |
0,01323 |
0,01289 |
0,01256 |
0,01223 |
0,01191 |
0,01160 |
0,01130 |
0,01100 |
0,01071 |
|
2,7 |
0,01042 |
0,01014 |
0,00987 |
0,00961 |
0,00935 |
0,00909 |
0,00885 |
0,00861 |
0,00837 |
0,00814 |
|
2,8 |
0,00792 |
0,00770 |
0,00748 |
0,00727 |
0,00707 |
0,00687 |
0,00668 |
0,00649 |
0,00631 |
0,00613 |
|
2,9 |
0,00595 |
0,00578 |
0,00562 |
0,00545 |
0,00530 |
0,00514 |
0,00499 |
0,00485 |
0,00470 |
0,00457 |
|
3 |
0,00443 |
0,00430 |
0,00417 |
0,00405 |
0,00393 |
0,00381 |
0,00370 |
0,00358 |
0,00348 |
0,00337 |
|
3,1 |
0,00327 |
0,00317 |
0,00307 |
0,00298 |
0,00288 |
0,00279 |
0,00271 |
0,00262 |
0,00254 |
0,00246 |
|
3,2 |
0,00238 |
0,00231 |
0,00224 |
0,00216 |
0,00210 |
0,00203 |
0,00196 |
0,00190 |
0,00184 |
0,00178 |
|
3,3 |
0,00172 |
0,00167 |
0,00161 |
0,00156 |
0,00151 |
0,00146 |
0,00141 |
0,00136 |
0,00132 |
0,00127 |
|
3,4 |
0,00123 |
0,00119 |
0,00115 |
0,00111 |
0,00107 |
0,00104 |
0,00100 |
0,00097 |
0,00094 |
0,00090 |
|
3,5 |
0,00087 |
0,00084 |
0,00081 |
0,00079 |
0,00076 |
0,00073 |
0,00071 |
0,00068 |
0,00066 |
0,00063 |
|
3,6 |
0,00061 |
0,00059 |
0,00057 |
0,00055 |
0,00053 |
0,00051 |
0,00049 |
0,00047 |
0,00046 |
0,00044 |
|
3,7 |
0,00042 |
0,00041 |
0,00039 |
0,00038 |
0,00037 |
0,00035 |
0,00034 |
0,00033 |
0,00031 |
0,00030 |
|
3,8 |
0,00029 |
0,00028 |
0,00027 |
0,00026 |
0,00025 |
0,00024 |
0,00023 |
0,00022 |
0,00021 |
0,00021 |
Таблица 4. Функция Лапласа.
|
( заштрихованная площадь под кривой равна значению функции Лапласа ) |
||||||||||
|
|
||||||||||
|
о |
x |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0,0 |
0,00000 |
0,00399 |
0,00798 |
0,01197 |
0,01595 |
0,01994 |
0,02392 |
0,02790 |
0,03188 |
0,03586 |
|
0,1 |
0,03983 |
0,04380 |
0,04776 |
0,05172 |
0,05567 |
0,05962 |
0,06356 |
0,06749 |
0,07142 |
0,07535 |
|
0,2 |
0,07926 |
0,08317 |
0,08706 |
0,09095 |
0,09483 |
0,09871 |
0,10257 |
0,10642 |
0,11026 |
0,11409 |
|
0,3 |
0,11791 |
0,12172 |
0,12552 |
0,12930 |
0,13307 |
0,13683 |
0,14058 |
0,14431 |
0,14803 |
0,15173 |
|
0,4 |
0,15542 |
0,15910 |
0,16276 |
0,16640 |
0,17003 |
0,17364 |
0,17724 |
0,18082 |
0,18439 |
0,18793 |
|
0,5 |
0,19146 |
0,19497 |
0,19847 |
0,20194 |
0,20540 |
0,20884 |
0,21226 |
0,21566 |
0,21904 |
0,22240 |
|
0,6 |
0,22575 |
0,22907 |
0,23237 |
0,23565 |
0,23891 |
0,24215 |
0,24537 |
0,24857 |
0,25175 |
0,25490 |
|
0,7 |
0,25804 |
0,26115 |
0,26424 |
0,26730 |
0,27035 |
0,27337 |
0,27637 |
0,27935 |
0,28230 |
0,28524 |
|
0,8 |
0,28814 |
0,29103 |
0,29389 |
0,29673 |
0,29955 |
0,30234 |
0,30511 |
0,30785 |
0,31057 |
0,31327 |
|
0,9 |
0,31594 |
0,31859 |
0,32121 |
0,32381 |
0,32639 |
0,32894 |
0,33147 |
0,33398 |
0,33646 |
0,33891 |
|
1,0 |
0,34134 |
0,34375 |
0,34614 |
0,34849 |
0,35083 |
0,35314 |
0,35543 |
0,35769 |
0,35993 |
0,36214 |
|
1,1 |
0,36433 |
0,36650 |
0,36864 |
0,37076 |
0,37286 |
0,37493 |
0,37698 |
0,37900 |
0,38100 |
0,38298 |
|
1,2 |
0,38493 |
0,38686 |
0,38877 |
0,39065 |
0,39251 |
0,39435 |
0,39617 |
0,39796 |
0,39973 |
0,40147 |
|
1,3 |
0,40320 |
0,40490 |
0,40658 |
0,40824 |
0,40988 |
0,41149 |
0,41308 |
0,41466 |
0,41621 |
0,41774 |
|
1,4 |
0,41924 |
0,42073 |
0,42220 |
0,42364 |
0,42507 |
0,42647 |
0,42785 |
0,42922 |
0,43056 |
0,43189 |
|
1,5 |
0,43319 |
0,43448 |
0,43574 |
0,43699 |
0,43822 |
0,43943 |
0,44062 |
0,44179 |
0,44295 |
0,44408 |
|
1,6 |
0,44520 |
0,44630 |
0,44738 |
0,44845 |
0,44950 |
0,45053 |
0,45154 |
0,45254 |
0,45352 |
0,45449 |
|
1,7 |
0,45543 |
0,45637 |
0,45728 |
0,45818 |
0,45907 |
0,45994 |
0,46080 |
0,46164 |
0,46246 |
0,46327 |
|
1,8 |
0,46407 |
0,46485 |
0,46562 |
0,46638 |
0,46712 |
0,46784 |
0,46856 |
0,46926 |
0,46995 |
0,47062 |
|
1,9 |
0,47128 |
0,47193 |
0,47257 |
0,47320 |
0,47381 |
0,47441 |
0,47500 |
0,47558 |
0,47615 |
0,47670 |
|
2,0 |
0,47725 |
0,47778 |
0,47831 |
0,47882 |
0,47932 |
0,47982 |
0,48030 |
0,48077 |
0,48124 |
0,48169 |
|
2,1 |
0,48214 |
0,48257 |
0,48300 |
0,48341 |
0,48382 |
0,48422 |
0,48461 |
0,48500 |
0,48537 |
0,48574 |
|
2,2 |
0,48610 |
0,48645 |
0,48679 |
0,48713 |
0,48745 |
0,48778 |
0,48809 |
0,48840 |
0,48870 |
0,48899 |
|
2,3 |
0,48928 |
0,48956 |
0,48983 |
0,49010 |
0,49036 |
0,49061 |
0,49086 |
0,49111 |
0,49134 |
0,49158 |
|
2,4 |
0,49180 |
0,49202 |
0,49224 |
0,49245 |
0,49266 |
0,49286 |
0,49305 |
0,49324 |
0,49343 |
0,49361 |
|
2,5 |
0,49379 |
0,49396 |
0,49413 |
0,49430 |
0,49446 |
0,49461 |
0,49477 |
0,49492 |
0,49506 |
0,49520 |
|
2,6 |
0,49534 |
0,49547 |
0,49560 |
0,49573 |
0,49585 |
0,49598 |
0,49609 |
0,49621 |
0,49632 |
0,49643 |
|
2,7 |
0,49653 |
0,49664 |
0,49674 |
0,49683 |
0,49693 |
0,49702 |
0,49711 |
0,49720 |
0,49728 |
0,49736 |
|
2,8 |
0,49744 |
0,49752 |
0,49760 |
0,49767 |
0,49774 |
0,49781 |
0,49788 |
0,49795 |
0,49801 |
0,49807 |
|
2,9 |
0,49813 |
0,49819 |
0,49825 |
0,49831 |
0,49836 |
0,49841 |
0,49846 |
0,49851 |
0,49856 |
0,49861 |
|
3,0 |
0,49865 |
0,49869 |
0,49874 |
0,49878 |
0,49882 |
0,49886 |
0,49889 |
0,49893 |
0,49896 |
0,49900 |
|
3,1 |
0,49903 |
0,49906 |
0,49910 |
0,49913 |
0,49916 |
0,49918 |
0,49921 |
0,49924 |
0,49926 |
0,49929 |
|
3,2 |
0,49931 |
0,49934 |
0,49936 |
0,49938 |
0,49940 |
0,49942 |
0,49944 |
0,49946 |
0,49948 |
0,49950 |
|
3,3 |
0,49952 |
0,49953 |
0,49955 |
0,49957 |
0,49958 |
0,49960 |
0,49961 |
0,49962 |
0,49964 |
0,49965 |
|
3,4 |
0,49966 |
0,49968 |
0,49969 |
0,49970 |
0,49971 |
0,49972 |
0,49973 |
0,49974 |
0,49975 |
0,49976 |
|
3,5 |
0,49977 |
0,49978 |
0,49978 |
0,49979 |
0,49980 |
0,49981 |
0,49981 |
0,49982 |
0,49983 |
0,49983 |
|
3,6 |
0,49984 |
0,49985 |
0,49985 |
0,49986 |
0,49986 |
0,49987 |
0,49987 |
0,49988 |
0,49988 |
0,49989 |
|
3,7 |
0,49989 |
0,49990 |
0,49990 |
0,49990 |
0,49991 |
0,49991 |
0,49992 |
0,49992 |
0,49992 |
0,49992 |
|
3,8 |
0,49993 |
0,49993 |
0,49993 |
0,49994 |
0,49994 |
0,49994 |
0,49994 |
0,49995 |
0,49995 |
0,49995 |
|
4,0 |
0,49997 |
0,49997 |
0,49997 |
0,49997 |
0,49997 |
0,49997 |
0,49998 |
0,49998 |
0,49998 |
0,49998 |
|
4,5 |
0,50000 |
0,50000 |
0,50000 |
0,50000 |
0,50000 |
0,50000 |
0,50000 |
0,50000 |
0,50000 |
0,50000 |
Таблица 3. Распределение Стьюдента.
|
Таблица 5. Распределение Стьюдента ( t-распределение). |
|
||||||||
|
(k-степени свободы, - заданная вероятность ) |
|||||||||
|
k |
|
||||||||
|
0,10 |
0,05 |
0,025 |
0,020 |
0,010 |
0,005 |
0,003 |
0,002 |
0,001 |
|
|
1 |
6,314 |
12,706 |
25,452 |
31,821 |
63,656 |
127,321 |
212,193 |
318,289 |
636,578 |
|
2 |
2,920 |
4,303 |
6,205 |
6,965 |
9,925 |
14,089 |
18,217 |
22,328 |
31,600 |
|
3 |
2,353 |
3,182 |
4,177 |
4,541 |
5,841 |
7,453 |
8,891 |
10,214 |
12,924 |
|
4 |
2,132 |
2,776 |
3,495 |
3,747 |
4,604 |
5,598 |
6,435 |
7,173 |
8,610 |
|
5 |
2,015 |
2,571 |
3,163 |
3,365 |
4,032 |
4,773 |
5,376 |
5,894 |
6,869 |
|
6 |
1,943 |
2,447 |
2,969 |
3,143 |
3,707 |
4,317 |
4,800 |
5,208 |
5,959 |
|
7 |
1,895 |
2,365 |
2,841 |
2,998 |
3,499 |
4,029 |
4,442 |
4,785 |
5,408 |
|
8 |
1,860 |
2,306 |
2,752 |
2,896 |
3,355 |
3,833 |
4,199 |
4,501 |
5,041 |
|
9 |
1,833 |
2,262 |
2,685 |
2,821 |
3,250 |
3,690 |
4,024 |
4,297 |
4,781 |
|
10 |
1,812 |
2,228 |
2,634 |
2,764 |
3,169 |
3,581 |
3,892 |
4,144 |
4,587 |
|
11 |
1,796 |
2,201 |
2,593 |
2,718 |
3,106 |
3,497 |
3,789 |
4,025 |
4,437 |
|
12 |
1,782 |
2,179 |
2,560 |
2,681 |
3,055 |
3,428 |
3,707 |
3,930 |
4,318 |
|
13 |
1,771 |
2,160 |
2,533 |
2,650 |
3,012 |
3,372 |
3,639 |
3,852 |
4,221 |
|
14 |
1,761 |
2,145 |
2,510 |
2,624 |
2,977 |
3,326 |
3,583 |
3,787 |
4,140 |
|
15 |
1,753 |
2,131 |
2,490 |
2,602 |
2,947 |
3,286 |
3,535 |
3,733 |
4,073 |
|
16 |
1,746 |
2,120 |
2,473 |
2,583 |
2,921 |
3,252 |
3,494 |
3,686 |
4,015 |
|
17 |
1,740 |
2,110 |
2,458 |
2,567 |
2,898 |
3,222 |
3,459 |
3,646 |
3,965 |
|
18 |
1,734 |
2,101 |
2,445 |
2,552 |
2,878 |
3,197 |
3,428 |
3,610 |
3,922 |
|
19 |
1,729 |
2,093 |
2,433 |
2,539 |
2,861 |
3,174 |
3,401 |
3,579 |
3,883 |
|
20 |
1,725 |
2,086 |
2,423 |
2,528 |
2,845 |
3,153 |
3,376 |
3,552 |
3,850 |
|
21 |
1,721 |
2,080 |
2,414 |
2,518 |
2,831 |
3,135 |
3,355 |
3,527 |
3,819 |
|
22 |
1,717 |
2,074 |
2,405 |
2,508 |
2,819 |
3,119 |
3,335 |
3,505 |
3,792 |
|
23 |
1,714 |
2,069 |
2,398 |
2,500 |
2,807 |
3,104 |
3,318 |
3,485 |
3,768 |
|
24 |
1,711 |
2,064 |
2,391 |
2,492 |
2,797 |
3,091 |
3,302 |
3,467 |
3,745 |
|
25 |
1,708 |
2,060 |
2,385 |
2,485 |
2,787 |
3,078 |
3,287 |
3,450 |
3,725 |
|
26 |
1,706 |
2,056 |
2,379 |
2,479 |
2,779 |
3,067 |
3,274 |
3,435 |
3,707 |
|
27 |
1,703 |
2,052 |
2,373 |
2,473 |
2,771 |
3,057 |
3,261 |
3,421 |
3,689 |
|
28 |
1,701 |
2,048 |
2,368 |
2,467 |
2,763 |
3,047 |
3,250 |
3,408 |
3,674 |
|
29 |
1,699 |
2,045 |
2,364 |
2,462 |
2,756 |
3,038 |
3,239 |
3,396 |
3,660 |
|
30 |
1,697 |
2,042 |
2,360 |
2,457 |
2,750 |
3,030 |
3,230 |
3,385 |
3,646 |
|
40 |
1,684 |
2,021 |
2,329 |
2,423 |
2,704 |
2,971 |
3,160 |
3,307 |
3,551 |
|
50 |
1,676 |
2,009 |
2,311 |
2,403 |
2,678 |
2,937 |
3,120 |
3,261 |
3,496 |
|
60 |
1,671 |
2,000 |
2,299 |
2,390 |
2,660 |
2,915 |
3,094 |
3,232 |
3,460 |
|
100 |
1,660 |
1,984 |
2,276 |
2,364 |
2,626 |
2,871 |
3,042 |
3,174 |
3,390 |
|
S |
1,645 |
1,960 |
2,241 |
2,326 |
2,576 |
2,807 |
2,968 |
3,090 |
3,291 |
Таблица 4. Распределение Пирсона
|
|
||||||||
|
k-число степеней свободы |
||||||||
|
(В таблицах по заданным находятся >> ) |
||||||||
|
k |
|
|||||||
|
0,99 |
0,975 |
0,95 |
0,9 |
0,01 |
0,025 |
0,05 |
0,1 |
|
|
1 |
0,00016 |
0,00098 |
0,00393 |
0,01579 |
6,63489 |
5,02390 |
3,84146 |
2,70554 |
|
2 |
0,0201 |
0,0506 |
0,1026 |
0,2107 |
9,2104 |
7,3778 |
5,9915 |
4,6052 |
|
3 |
0,1148 |
0,2158 |
0,3518 |
0,5844 |
11,3449 |
9,3484 |
7,8147 |
6,2514 |
|
4 |
0,297 |
0,484 |
0,711 |
1,064 |
13,277 |
11,143 |
9,488 |
7,779 |
|
5 |
0,554 |
0,831 |
1,145 |
1,610 |
15,086 |
12,832 |
11,070 |
9,236 |
|
6 |
0,872 |
1,237 |
1,635 |
2,204 |
16,812 |
14,449 |
12,592 |
10,645 |
|
7 |
1,239 |
1,690 |
2,167 |
2,833 |
18,475 |
16,013 |
14,067 |
12,017 |
|
8 |
1,647 |
2,180 |
2,733 |
3,490 |
20,090 |
17,535 |
15,507 |
13,362 |
|
9 |
2,088 |
2,700 |
3,325 |
4,168 |
21,666 |
19,023 |
16,919 |
14,684 |
|
10 |
2,558 |
3,247 |
3,940 |
4,865 |
23,209 |
20,483 |
18,307 |
15,987 |
|
11 |
3,053 |
3,816 |
4,575 |
5,578 |
24,725 |
21,920 |
19,675 |
17,275 |
|
12 |
3,571 |
4,404 |
5,226 |
6,304 |
26,217 |
23,337 |
21,026 |
18,549 |
|
13 |
4,107 |
5,009 |
5,892 |
7,041 |
27,688 |
24,736 |
22,362 |
19,812 |
|
14 |
4,660 |
5,629 |
6,571 |
7,790 |
29,141 |
26,119 |
23,685 |
21,064 |
|
15 |
5,229 |
6,262 |
7,261 |
8,547 |
30,578 |
27,488 |
24,996 |
22,307 |
|
16 |
5,812 |
6,908 |
7,962 |
9,312 |
32,000 |
28,845 |
26,296 |
23,542 |
|
17 |
6,408 |
7,564 |
8,672 |
10,085 |
33,409 |
30,191 |
27,587 |
24,769 |
|
18 |
7,015 |
8,231 |
9,390 |
10,865 |
34,805 |
31,526 |
28,869 |
25,989 |
|
19 |
7,633 |
8,907 |
10,117 |
11,651 |
36,191 |
32,852 |
30,144 |
27,204 |
|
20 |
8,260 |
9,591 |
10,851 |
12,443 |
37,566 |
34,170 |
31,410 |
28,412 |
|
21 |
8,897 |
10,283 |
11,591 |
13,240 |
38,932 |
35,479 |
32,671 |
29,615 |
|
22 |
9,542 |
10,982 |
12,338 |
14,041 |
40,289 |
36,781 |
33,924 |
30,813 |
|
23 |
10,196 |
11,689 |
13,091 |
14,848 |
41,638 |
38,076 |
35,172 |
32,007 |
|
24 |
10,856 |
12,401 |
13,848 |
15,659 |
42,980 |
39,364 |
36,415 |
33,196 |
|
25 |
11,524 |
13,120 |
14,611 |
16,473 |
44,314 |
40,646 |
37,652 |
34,382 |
|
26 |
12,198 |
13,844 |
15,379 |
17,292 |
45,642 |
41,923 |
38,885 |
35,563 |
|
27 |
12,878 |
14,573 |
16,151 |
18,114 |
46,963 |
43,195 |
40,113 |
36,741 |
|
28 |
13,565 |
15,308 |
16,928 |
18,939 |
48,278 |
44,461 |
41,337 |
37,916 |
|
29 |
14,256 |
16,047 |
17,708 |
19,768 |
49,588 |
45,722 |
42,557 |
39,087 |
|
30 |
14,953 |
16,791 |
18,493 |
20,599 |
50,892 |
46,979 |
43,773 |
40,256 |
|
31 |
15,655 |
17,539 |
19,281 |
21,434 |
52,191 |
48,232 |
44,985 |
41,422 |
|
32 |
16,362 |
18,291 |
20,072 |
22,271 |
53,486 |
49,480 |
46,194 |
42,585 |
|
33 |
17,073 |
19,047 |
20,867 |
23,110 |
54,775 |
50,725 |
47,400 |
43,745 |
|
34 |
17,789 |
19,806 |
21,664 |
23,952 |
56,061 |
51,966 |
48,602 |
44,903 |
|
37 |
19,960 |
22,106 |
24,075 |
26,492 |
59,893 |
55,668 |
52,192 |
48,363 |
|
40 |
22,164 |
24,433 |
26,509 |
29,051 |
63,691 |
59,342 |
55,758 |
51,805 |
ЛИТЕРАТУРА
1. Айвазян С.А. Прикладная статистика: Основы моделирования и первичная обработка данных. - М: Финансы и статистика., 1983г.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М., 1999г.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., 1999г.
4. Ковалев Е.А. Вероятность и статистика. Тольятти, 2003г.
5. Ковалев Е.А. Задачник по теории вероятностей. Тольятти, 2002г.
6. Кремер Н.Ш. Теория вероятностей и математическая статистика. М., Юнита, 2001 г.