Ряды
Ряды
Фун 2 числовых аргументов.
Пусть имеется Е (х>1>;у>1>) – элементы принадлеж точке Е
Сущ закон или правило по которому каж точке (x>i>;y>i>) ставится в соот-е число W>i> или любой точке (x>i>;y>i>) или паре чисел ставится в соот-е z>i> след-но z>i>=F(х;у), где Е-обл опред-я F(х;у).
Если рассмот-ть точку (х>i>;у>i>) и нашли соот-е значения z>i>=F(х>i>;у>i>).
Пусть точка (х>0>;у>0>)ÎЕ дельта окрест-ю точки (х>0>;у>0>) наз множество точек (х;у) удовлетвор-х нерав-у
Ö[(х-х>0>)+(y-y>0>)] <d.
Точка (х>0>;у>0>) наз внутренней точкой множества Е, если сущ-ет некоторая окрест этой точки, которая вместе с точкой Î этому множеству.
Точка (х>0>;у>0>) наз граничной точкой множ-ва Е, если в любой ее окрест-и сущ точка кроме самой этой точки, которая Î множ Е.
Совокупность всех граничных точек множ-а Е наз границей множ-а Е.
Множ-во, все точки которого внутренние, наз открытыми, т.е. безграничным.
Точка (х>0>;у>0>)Î множ-ву Е наз изолированной точкой, если сущ-ет окрест этой точки в которой кроме этой точки нет ни одной точки из множества Е.
Фун 2 переменных.
Опр: Если каж паре (х;у) значений 2, не завис др от друга, переменных величин х и у, из некоторой обл их знач-я D, соот-ет опр-е знач-е величины z, то мы говорим, что z есть фун 2 независимых пременных х и у, определ-ся в обл D.
Геом. Смысл: Геометрическое место точек Р, коор-ты которых удовлет-т ур-ю z=f(х;у), где коор-ы точки Р х и у, z=f(х;у), наз графиком фун 2 переменных. Графиком фун 2 переменных яв-ся поверхность, проектирующая на плоскость Оху в обл опред-я фун. Каж перпендик-р к плоскости Оху пересекает поверхность z=f(х;у) не более чем в одной точке. Фун z=f(х;у) опред-ся в обл G.
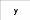

Обл опред-я фун 2 переменных – это совокупность пар (х;у) значений х и у при котором определяется фун-я z=f(х;у).
Совокупность точек на плоскости также наз-ся обл определения.
Предел фун 2 переменных.
Опр: Число А наз пределом фун z=f(х;у)при х®х>0>, у®у>0>, М(х;у)®М>0>. lim>х>>®>>х0 (у>>®>>у0)>f(х;у)=A
Если для любого e>0 сущ-ет d окрест-ть точки (х>0>;у>0>) такая, что при всех (х;у)Îd окрест-ти будет выполн нерав-во Ö[(х-х>0>)2+(y-y>0>)2] <d. êА-f(х;у)ê<e, A-e<f(х;у)<A+e.
Основные теоремы о пределах:
1)lim Xn=a, lim Yn=b => lim (Xn±Yn)=a±b (n®¥)
Док-во: lim Xn=a => Xn=a+a>n>; lim Yn=b => Yn=b+b>n>;
Xn ± Yn = (a + a>n>) ± (b + b>n>) = (a ± b) + (a >n>± b>n>) => lim(Xn±Yn)=a±b (n®¥).
2)limXnYn = lim Xn * lim Yn (n®¥).
3)lim Xn=a, lim Yn=b (n®¥) => lim Xn/Yn =
(lim Xn)/(lim Yn) = a/b.
Док-во: Xn/Yn – a/b = (a+a>n>)/(b+b>n>) – a/b = (ab+a>n>b–ab–ab>n>)/b(b+b>n>) =(ba>n>-ab>n>)/b(b+b>n>)=g>n >=> Xn/Yn=a/b+g>n> => $ lim Xn/Yn = a/b = (lim Xn)/(lim Yn) (n®¥).
Все св-ва и правила вычисл-я такие же как для 1 переменной.
Непрерывность фун в точке.
Опр: Пусть точка М>0>(х>0>;у>0>) Î обл опр-я фун-и f(х;у). Фун-я z=f(х;у) наз непрерывной в точке М>0>(х>0>;у>0>), если имеет место равенство lim>х>>®>>х0(у>>®>>у0)>f(х;у)=f(х>0>;у>0>) или lim>D>>х>>®>>0(>>D>>у>>®>>0)>f(х>0>+Dх;у>0>+Dу)= f(х>0>;у>0>), где х=х>0>+Dх и у=у>0>+Dу, причем точка М(х;у) стремиться к точке М>0>(х>0>;у>0>) произвольным образом, оставаясь в области определения фун-и.
Условия:1)f(х;у) – опред ф-ия; 2) Сущ-ют конечные пределы со всех сторон; 3)Эти пределы равны между собой; 4)Конечные пределы со всех сторон =f(x>0>;у>0>).
Если (х>0>;у>0>) точка разрыва и выполняется условие 2, то (х>0>;у>0>)–1 род.
Если (х>0>;у>0>)–1 род и выполняется условие 3, то разрыв устранимый.
Если (х>0>;у>0>) точка разрыва и не выполняется условие 2, то (х>0>;у>0>) – 2 рода.
Св-ва непрерывности в точке: 1)Если фун f>1>(х;у) и f>2>(х;у) непрерывны в точке (х>0>;у>0>), то сумма (разность) f(х;у)=f>1>(х;у)±f>2>(х;у), произведение f(х;у)=f>1>(х;у)*f>2>(х;у), а также отношение этих функций f(х;у)=f>1>(х;у)/f>2>(х;у), есть непрер-я фун в точке х>0>;у>0>.
Док-во (суммы): По определению получаем, что lim>х>>®>>х0(у>>®>>у0)>f>1>(х;у)=f>1>(х>0>;у>0>), lim>х>>®>>х0(у>>®>>у0)>f>2>(х;у)=f>2>(х>0>;у>0>) на основании св-ва: limXn=a, limYn=b => lim(Xn±Yn)=a±b (n®¥), можем написать: lim>х>>®>>х0(у>>®>>у0)>f(х;у)=lim>х>>®>>х0(у>>®>>у0)>[f>1>(х;у)+f>2>(х;у)]=
=lim>х>>®>>х0(у>>®>>у0)>f>1>(х;у)+lim>х>>®>>х0(у>>®>>у0)>f>2>(х;у)=
=f>1>(х>0>;у>0>)+f>2>(х>0>;у>0>)=f(х>0>;у>0>). Итак сумма есть непрерывная функция.· 2)Всякая непрерывная фун непрерывна в каждой точке, в которой она определена. 3) Если фун z=j(m) непрерывна в точке m=х>0>;у>0>, а фун y=f(z) непрерывна в соот-й точке z>0>=j(х>0>;у>0>), то фун y=f(j(х;у)) непрер-а в точке (х>0>;у>0>).
Если фун непрерывна в каждой точке некоторого интервала (а,в), где а<в, то говорят, что фун непреывна на этом интервале.
Если фун непрерывна в каждой точке некоторого интервала (а,в) и непрерывна на концах интервала, то говорят, что f(x;у) непрерывна на замкнутом интервале или отрезке (а,в).
Точки разрыва.
Если в некоторой точке N(х>0>;у>0>) не выполняется условие lim>х>>®>>х0(у>>®>>у0)>f(х;у)= f(х>0>;у>0>), то точка N(х>0>;у>0>) наз точкой разрыва фун z=f(х;у).
Условие lim>D>>х>>®>>0(>>D>>у>>®>>0)>f(х>0>+Dх;у>0>+Dу)=f(х>0>;у>0>) может не выпол-ся в след-х случаях: 1)z=f(х;у) определена во всех точках некоторой окрестности точки N(х>0>;у>0>), за исключением самой точки N(х>0>;у>0>); 2)фун z=f(х;у) определена во всех точках некоторой окрестности точки N(х>0>;у>0>), но не сущ-ет предела lim>х>>®>>х0(у>>®>>у0)>f(х;у); 3)фун z=f(х;у) определена во всех точках некоторой окрестности точки N(х>0>;у>0>) и сущ-ет предел lim>х>>®>>х0(у>>®>>у0)>f(х;у), но lim>х>>®>>х0(у>>®>>у0)>f(х;у)¹f(х>0>;у>0>).
Классификация точек разрыва:
Если (х>0>;у>0>) точка разрыва и сущ-ют конечные пределы со всех сторон, то (х>0>;у>0>) – 1 род.
Если (х>0>;у>0>) – 1 род, сущ-ют конечные пределы со всех сторон и эти пределы равны между собой, то разрыв устранимый.
Если (х>0>;у>0>) точка разрыва и не сущ-ют конечные пределы со всех сторон, то (х>0>;у>0>) – 2 рода.
Непрерывность фун нескольких (или 2) переменных в замкнутой области.
Опр: Фун-я, непрерывная в каж точке некоторой замкнутой области, наз непрерывной в этой замкнутой области.
Св-ва: 1)Если фун f(x;y…) определена и непрерывна в замкнутой и ограниченной области D, то в обл D найдется по крайней мере одна точка N(х>0>;у>0>…) такая, что для всех др точек обл будет выплн-ся соот-е f(х>0>;у>0>…)³f(х;у) и по крайней мере одна точка `N(`х>0>;`у>0>…) такая, что для всех др точек обл будет выпол соот-е f(`х>0>;`у>0>…)£f(х;у…). Фориулируется так: Непрерывная фун в замкнутой огранич обл D достигает по крайней мере один раз наиболь значения М и наимень значения m. 2)Если фун f(x;y…) непрерывна в замкнутой и ограниченной обл D и если M и m – наиб и наим значения фун f(x;y…) в обл, то для любого числа m, удовл усл m<m<М, найдется в обл такая точка N*(x*;y*…), что будет выполн рав-во f(x*>0>;y*>0>…)=m. Следствие из св2: Если фун f(x;y…) непрерывна в замкнутой огран обл и принимает как положит, так и отрицательные значения, то внутри области найдутся точки, в которых функция f(x;y…) обращается в нуль.
Частное приращ-е, произв-ные, диф-лы фун-и.
Пусть имеем функцию z=f(х;у). Дадим независимой переменной х приращение ∆х, тогда z получит приращение, кот. наз. частным приращением z по x. ∆>x>z=f(x+∆x,y)-f(x,y) Аналогично частное приращение по y ∆>y>z=f(x,y+∆y)-f(x,y).
Частные производные. Опр: Частной производной по x от функции z=f(x,y) наз. предел отношения частного приращения ∆>x>z к приращ-ю ∆x при ∆x®0.
∂z/∂x=lim>(∆x>>®>>0)>∆>x>z/∆x=lim>(∆x>>®>>0)>(f(x+∆x,y)-f(x,y))/∆x. Аналогично частная производная по y.
∂z/∂y=lim>(∆y>>®>>0)> ∆>y>z/∆y=lim>(∆y>>®>>0)>(f(x,y+∆y)-f(x,y))/∆y.
Част диф-л фун: d>x>z(x;y)=[(¶z/¶x)*Dx] и d>у>z(x;y)=[(¶z/¶у)*Dу].
Полное приращ-е, полный диф-л. Диф-ть фун.
Пусть имеем функцию z=f(х;у). Сообщив аргументу x приращение ∆x, а аргументу y приращение ∆y, получим для z новое приращение ∆z , кот наз. полным приращением. ∆z=f(x+∆x,y+∆y)-f(x,y).
Полный дифференциал: Если фун z=f(x;y) имеет непрерывные частные производные в данной точке, то она диф-ма в этой точке и имеет полный диф-л dz=(∂f/∂x)*∆x+(∂f/∂y)*∆y.
Дифференцируемость ф-и: Ф-я z=f(x,y) наз. дифференцируемой в т. (x>0>,y>0>), если её полное приращение ∆z можно представить в виде суммы 2 слагаемых ∆z=(A*∆x+B*∆y)+0(r), где r=Ö(∆x2+∆y2), т.е. lim>(>>D>>х>>®>>0,>>D>>у>>®>>0,>>r®>>0)>0(r)/r=0 бесконечная величина более высокого порядка малости, чем r. (A*∆x+B*∆y) линейное относительно ∆x ,∆y.
Полный диф-л в приближенных вычислениях: f(x+∆x>0>,y+∆y)»f(x,y)+[¶f(x,y)/¶x]*Dx+[¶f(x,y)/¶y]*Dy.
Необходимое усл диф-ти: Если z=f(x,y) диффер-ема в т.(x>0>,y>0>), то сущ. конечные частные производные (∂z/∂х;∂z/∂y) при x=x>0>, y=y>0>. A=∂z(х>0>;у>0>)/∂x; B=∂z(х>0>;у>0>)/∂y.
Достаточное усл диф-ти: Если функция z=f(x,y) в т.(x>0>,y>0>) и в нек. окресности непрерывна и имеет непрерывные частные производные (∂z/∂х;∂z/∂y), то ф-ия диф-ма.
Производные высших порядков.
∂z/∂x=φ(x,y); ∂z/∂y=φ(x,y); Вторая производная: ∂φ/∂x=∂2z/∂x2;z``>xx >здесь фун диф-я посл-но 2раза по х;
∂φ/∂y=∂z/∂x∂y;z``>xy>;∂φ/∂x=∂z/∂y∂x;z``>yx>; ∂φ/∂y=∂2z/∂y2;z``>yy>;
Третья производная: ∂3z/∂x3; ∂3z/∂x2∂y; ∂3z/∂x∂y¶х; ∂3z/∂y∂x2; ∂3z/∂y∂x∂y; ∂3z/∂y2∂x; ∂3z/∂y3.
Производная сложной ф-ии.
z=f(u,v)=F(x;y), u=j(х;у) и v=y(х;у). Если ф-ия f диф-ма по u и v, а u и v диф-ы по x и y, то выполняется след равенство ¶z/¶x=(∂z/∂u)(¶u/¶x)+(∂z/∂v)(¶v/¶x); ¶z/¶y=(∂z/∂u)(¶u/¶y)+(∂z/∂v)(¶v/¶y).
z=f(x;u;v)=F(x)
Полная производная по х:
dz/dx=¶z/¶x+(∂z/∂u)(du/dx)+(∂z/∂v)(dv/dx);
Полная производная по у:
dz/dу=¶z/¶у+(∂z/∂u)(du/dу)+(∂z/∂v)(dv/dу);
Экстремумы фун 2 переменных.
Ф-ия z=f(x,y) имеет максимум (минимум) в точке M>0>(x>0>,y>0>), если f(x>0>,y>0>)> f(x,y) {f(x>0>,y>0>)<f(x,y)} для всех точек (x,y) достаточно близких к точке (x>0>,y>0>) и отличных от неё.
Определение max и min при предположении, что х=х>0>+Dх и у=у>0>+Dу, тогда
f(x;y)-f(x>0>;y>0>)=f(х>0>+Dх;у>0>+Dу)-f(x>0>;y>0>)=Df. 1)Если Df<0 при всех достаточно малых приращениях независимых переменных, то фун f(x;y) достигает max в точке М>0>(х>0>;у>0>); 2)Если Df>0 при всех достаточно малых приращениях независимых переменных, то фун f(x;y) достигает min в точке М>0>(х>0>;у>0>);
Необходимое усл экстремум: Если функция z=f(x,y) достигает экстремума при x=x>0>, y=y>0>, то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не сущ.
Док-во: Действительно, дадим переменному y определённое значение, а именно y=y>0>. Тогда ф-ия f(x,y>0>) будет функцией одного переменного x. Т.к. при x=x>0> она имеет экстремум, то следовательно (∂z/∂x) при x=x>0>,y=y>0> или равно нулю или не сущ. Аналогично доказ, что (∂z/∂у) при x=x>0>, y=y>0> или равно нулю или не сущ.
Достаточное усл экстемум: Пусть в нек. Области, содержащей т.M(x>0>,y>0>), функция f(x,y) имеет непрерывные частные производные до третьего порядка включительно, пусть, кроме того т.M(x>0>,y>0>) является критической точкой функции f(x,y) т.е. ∂f(x>0>,y>0>)/∂x=0, ∂f(x>0>,y>0>)/∂y=0.
Тогда при x=x>0>, y=y>0>:
1)f(x,y) имеет максимум, если
∂2f(x>0>,y>0>)/¶x2*∂2f(x>0>,y>0>)/¶y2-(∂2f(x>0>,y>0>)/∂x∂y)2>0 и ∂2f(x>0>,y>0>)/¶x2<0
2)f(x,y) имеет максимум, если
∂2f(x>0>,y>0>)/¶x2*∂2f(x>0>,y>0>)/¶y2-(∂2f(x>0>,y>0>)/∂x∂y)2>0 и ∂2f(x>0>,y>0>)/¶x2>0
3)f(x,y) не имеет ни макс. ни мин.
∂2f(x>0>,y>0>)/¶x2*∂2 f(x>0>,y>0>)/¶y2-(∂2f(x>0>,y>0>)/∂x∂y)2<0
4)Если ∂2f(x>0>,y>0>)/¶x2*∂2f(x>0>,y>0>)/¶y2-(∂2f(x>0>,y>0>)/∂x∂y)2=0, то экстремум может быть, а может и не быть.
Неявнозаданная функция и нахождение ее производной.
Задана фун F(x,y,z)=0 наз заданная неявно, если существует z=(x,y) в некоторой области D что при подстановке получаем тождественно нуль. F(x,y,z)º0. Продифф. по x: F(x,y,z)º0, F¢>x>=0, ¶F/¶x+(¶F/¶z)*(¶z/¶x) ¶z/¶x=--[(¶F/¶x)/(¶F/¶z)];
Продифф. аналогично по у ¶z/¶y=--[(¶F/¶y)/(¶F/¶z)]
Двойной интеграл.
Рассмотрим в плоскости ОХУ замкнутую область D ограниченную линией L. Пусть в области D задана непрерывная функция z=f(x,y). Разобьем D на n частей(S>1>,S>2>,S>3>…S>n>). На каждой площадке возьмем по точке P>i> (P>1>,P>2>,P>3>…P>n>). f(P>i>) – значение функции в заданной точке. Возмем сумму произведений вида: f(P>i>)S>i>. V>n>=nå>i=1>f(P>i>)S>i> – это интегральная сумма для функции f(x,y) по обл D.

 Опр:
Предел lim>max>>
>>di>>®>>0>nå>i=1>f(P>i>)S>i>
интегральной
суммы nå>i=1>f(P>i>)S>i>,
если он сущ-ет
независимо от способа разбиения обл D
на DD>i>
и от выбора точек P>i>ÎD>i>
наз двойным
интегралом зад фун z=f(x;y)
по обл D.
Опр:
Предел lim>max>>
>>di>>®>>0>nå>i=1>f(P>i>)S>i>
интегральной
суммы nå>i=1>f(P>i>)S>i>,
если он сущ-ет
независимо от способа разбиения обл D
на DD>i>
и от выбора точек P>i>ÎD>i>
наз двойным
интегралом зад фун z=f(x;y)
по обл D.
Теорема: Если сущ-ет фун z=f(x;y) непрерывна в заданной обл `D, то сущ-ет предел lim>max>> >>di>>®>>0>nå>i=1>f(P>i>)S>i>
т.е. сущ-ет двойной интеграл для данной фун по данной области. lim>max>> >>di>>®>>0>nå>i=1>f(P>i>)S>i>=óó>D> f(x;y)dxdy=(или)= =óó>D> f(x;y)dS/¶
Св-ва:
1)>D>(f1(x,y)+f2(x,y))dxdy=ó>D>f1(x,y)dxdy+ó>D>f2(x,y)dxdy
2) >D>a f(x,y)dxdy=a >D> f(x,y)dxdy.
3) Если область D=D>1>ÈD>2>, то
>D>f(x,y)= >D>>1>f(x,y))+ >D>>2>f(x,y).
Док-во: Инегральную сумму по обл D можно представить в виде D>1> и D>2>.
>D>f(P>i>)S>i>= >D>>1>f(P>i>)S>i >+ >D>>2>f(P>i>)S>i> , где превая сумма содержит слагаемые, соот-е площади обл D>1>, вторая – соот-е площадкам обл D>2>. В самом деле, т.к. двойной интеграл не зависит от способа разбиения, то мы производим разбиение области D так, что общая граница областей D>1> и D>2> яв-ся границей площадок S>i>. Переходя в равенство
>D>f(P>i>)S>i>= >D>>1>f(P>i>)S>i >+ >D>>2>f(P>i>)S>i> к пределу при S>i>®0, получаем равенство
>D>f(x,y)= >D>>1>f(x,y))+ >D>>2>f(x,y).·
4) Если фун f(x,y)=1, то >D>1dxdy=S>D>
5) Если фун в данной области f(x,y)0, то интегр от этой фун отриц (полож) не может быть
>D> f(x,y)dxdy0
6) Если f1(x,y)f2(x,y), то
>D>f1(x,y)dxdy>D>f2(x,y)dxdy
7)Теорема о среднем: Двукратный интеграл I>D> от f(x,y) по области D с площадью S равен произведению площади S на значение функции в некоторой точке P области D.
в >а>> >( 2(x) >>>1(x)>f(x,y)dy)dx=f(P)*S.
Док-во: Из соот-я
mS£в>а>(2(x)>>>1(x)>f(x,y)dy)dx=f(P)*S£MS получаем mS£1/S*I>D>£MS. Число 1/S*I>D >заключено между наиболь и наимень знач f(x,y) в области D. В силу непрерывности фун f(x,y) принимает в некоторой точке P обл D принимает значение равное 1/S*I>D >.
Двукратный интеграл
Пусть дана область D такая, что любая прямая параллельная одной из осей пересекает эту область в двух точках. Пусть область D ограничена линиями y=f1(x), y=f2(x), y=a, y=b (a<b, f1(x)<f2(x)). Пусть f(x,y) непрерывна в области D.
Рассмотрим I>D>=в>а>f2(x)>f>>1(>>x>>)>f(x,y)dydx=вó>а>Ф(х)dx
-это двукратный интеграл.
Вычисление двойного интеграла есть вычисление двукратного интеграла.
Вычисление двойного интеграла в полярных координатах:
>D>f(x,y)dxdy=½x=pcos, y=psin , I=p½=
=>D>f(pcos;psin)pdpd=
=>>dp2()>p1(>>>>)>(pcos ;psin)pdp.
Геометрическое приложение двойного интеграла.
Площадь плоской поверхности.
>D> f(x,y)dxdy=S>D >
2) Объем цилиндроидов. z=f(x,y)>0. По определению область D разбивается на элементарные кусочки DDi; выбрать в этих кусочках точку принадлежащую DDi и найти значение функции в этой точке. DVi=f(xi,yi)*DSi. Сумма
DVi=nå>i>>=1>f(xi,yi)*DSi – это объем фигуры состоящей из элементарных параллелепипедов. Основания параллелепипедов заполняют область D.
lim>max>> >>di>>®>>0>nå>i>>=1>f(xi,yi)*DSi=V>Т> если этот предел сущ-ет, то это V тела (цилиндройда). f(x,y)dxdy=V>цил>> >
Площадь поверхности.
S>пов.>=[Ö1+(dz/dx)2+(dz/dy)2dxdy].
Диф-е ур-я (осн понятия).
Общий вид диф ур F(x;y;y’;у”…уn)=0. Наивысший порядок производ-й в ур-и F(x;y;y’;у”…уn)=0 наз порядковым ур-ем.
Решением ур F(x;y;y’;у”…уn)=0 наз любая фун вида у=j(х), которая будучи подставленная в F(x;y;y’;у”…уn)=0 вместе со своими произ-ми обращает в тождество. F(x;j(х);j(х)’;j(х)”… j(х)n)=0.
Фун вида у=j(х;С>1>;С>2>;…С>n>) наз общим решением ур F(x;y;y’;у”…уn)=0, если выполняется: 1) эта фун-я яв-ся решением при любых С>1>;С>2>;…С>n>; 2) для любых начальных усл х>0>, у>0>, у’>0>, уn>0 >можно найти конкретную совокупность С>1 0>;С>2 0>;С>3 0>;…С>n>> 0 >при которых фун у=j(х;С>1 0>;С>2 0>;С>3 0>;…С>n>> 0>), что эта фун будет удвл начальному условиям.
Соот-е вида j(х;С>1>;С>2>;С>3>;…С>n>)=0 полученная при решении ур F(x;y;y’;у”…уn)=0 наз общим интегралом ур F(x;y;y’;у”…уn)=0 (т.е. решение ур находиться в неявной форме).
Дифф. ур. 1-го порядка
Общий вид F(x;y;y’)=0 Решением данного ур. наз. любая фун.=j(x), кот. обращает ур. в тождество.
Опр-е: Фун. y=j(x;C) наз-ся общим решением, если она удов.:1)данная фун. яв-ся реш-м при любых C; 2)при любых x0;y0 можно найти такое C0, что фун. y= j(x,C0) удов. начальным усл-ям.
Рав-во вида Ф(x;y;C)=0, неявно задающее общее реш-е, наз-ся общим интегралом дифф. ур-я.
Опр: Частным реш-м наз-ся любая фун. y=j(x;C0), кот. получается из общего реш. y=j(x;C), если в последнем произ. постоянному С придать опред. значение С=С0. Соотн. Ф(x;y;C0)=0 наз-ся в этом случае частным интегралом ур.
Методы интегрирования диф-я уравнений 1 порядка:
1). Ур-е с разделенными переменными f1(x)y’=f2(y) f1(x)dy=f2(y)dx, dy/f2(y)=dx/f1(x), ∫dy/f2(y)=∫dx/f1(x) 2).Ур-е с разделяющимися переменными f(x;y)y’+j(x;y)=0, f1(x)f2(y)dy+j1(x)j2(y)dx=0 все разделим на j2(y)*f1(x)
{f2(y)/j2(y)}dy+{j1(x)/f1(x)}dx=0
∫{f2(y)/j2(y)}dy+∫{j1(x)/f1(x)}dx=C – общий интеграл 3).Линейные диффер. ур. y’+p(x;y)=Q(x) – общий вид, Если Q(x)º0, то линейное уравнение y’+p(x;y)=0.
Методы решений: 1) Метод вариации постоянной;
2)Решение этого ур будем искать как y=U(x)V(x) (диффер-ем) dy/dx=UdV/dx+VdU/dx (подставим) UdV/dx+VdU/dx+PUV=Q
U(dV/dx+PV)+VdU/dx=Q, dV/dx+PV=0, dV/V=-Pdx lnC1+lnV=-∫Pdx
V= C1e–∫Pdx и подставляем в UdV/dx+VdU/dx+PUV=Q
V(x)= e–∫Pdx, где ∫Pdx - какая-нибудь первообразная
V(x)dU/dx=Q(x), dU/dx=Q(x)/V(x), U=∫Q(x)/V(x)dx+C, y=V(x) ∫ Q(x)/V(x)dx+CV(x)
Уравнения приводящиеся к линейным(Бернулли)
y’+P(x)y=Q(x)yn, P(x) и Q(x) – непрерывные фун. от x (или пост.) n¹0,1. Это ур-е наз ур Бернулли, приводится к линейному следующим преобразованием.
Разделим на yn с наибольшим значением n, получим
(y–n)y’+P(y–n+1)=Q, Сделаем далее замену z=(y–n+1), тогда dz/dx=(-n+1)(y-n)y’. Подставляя эти значения в ур-е
(y–n)y’+P(y–n+1)=Q, будем иметь линейное ур-е
dz/dx=(1-n)Pz=(1-n)Q
Найдя его общий интеграл и подставив вместо z выражение (y–n+1), получим общий инт. ур.Бернулли
Однородные ур-я
Ур-е вида y’=f(x;y) наз-ся однор.ур-ем, если фун. f(x;y)
–однородная нулевого измерения или порядок однородности равен 0, т.е. f(tx;ty)=(t0)f(x;y).
Фун. f(x;y) наз-ся однор.ур-ем k-го порядка однородности, если вып. усл. f(tx;ty)=(tk)f(x;y); f(tx;ty)=(t0)f(x;y), где k=0; f(tx;ty)=f(x;y), где t=1/x; f[(1/x)*x;(1/y)*x)]=f(1;y/x), обозначим y/x=U(x) след-но y=U(x)x, y’=U’x+U подставим в исходное ур-е U’x+U=f(1;U), U’x+U=j(U) (dU/dx)*x=j(U)-U, dx/x=dU/(j(U)-U), ln|x|=[∫dU/(j(U)-U)] + C Þ вместо U подст. y/x и получим общий инт.
Замеч. Однор.ур. может выгл. так M(x;y)dx+N(x;y)dy=0 если обе фун. M(x;y) и N(x;y) однородные k-го порядка.
Дифф. ур. 2-го порядка
Общий вид дифф. ур.2-го порядка F(x;y;y’;y’’)=0. Решением урав. наз. любая фун.y=j(x), кот. обращает это ур. в тождество F(x;j(x);j’(x);j’’(x))=0
 Общим
решением
наз. ур. вида y=(x;C1;C2),
кот. яв-ся 1)реш. при любых знач. C1,C2,Cn;
2)для любых
x0,y0,y0’,y0’’
можно найти С10,С20, при кот. заданная фун.
y=j(x1;
С10;С20) будет удов. заданному нач. ур-ю,
т.е.
Общим
решением
наз. ур. вида y=(x;C1;C2),
кот. яв-ся 1)реш. при любых знач. C1,C2,Cn;
2)для любых
x0,y0,y0’,y0’’
можно найти С10,С20, при кот. заданная фун.
y=j(x1;
С10;С20) будет удов. заданному нач. ур-ю,
т.е.
j(x0;С10;С20)=y0 ,
j’(x0; С10;С20)=y0’
Линейные дифф. ур-я 2-го порядка
Общий вид линейн. диф. ур. 2-го порядка y’’+P(x)y’+q(x)y=f(x). (1)
Если f(x)=0 следовательно y’’+P(x)y’+q(x)y=0 (2)
– линейное однородное урав.
Структура реш. лин. одн.ур.2-го пор.
1)Если 2 реш. ур (2) y1(x) и y2 (x) – линейно-независ, т.е. нельзя одну вырозить через др, т.е.
y1(x)/y2(x)¹const, то общим решением ур (2) y=C1y1+C2y2
2) Если известно одно реш. y1, то др. найдем по форм. y2= y1∫[(e–∫P(x)dx)]/(y>1>2)dx. Общее реш. y=C1y1+C2y2
3) y1 находим подбором.
Структура общего реш. неоднородного ур.
1)Общее реш.y(x)=y(-)+y*, где y(-)=C1y1+C2y2 общее реш.(2), y*- нек. частное реш. самого ур.
2)Метод вариации произ. постоянной
y*= C1(x)y1+C2(x)y2
3)Для нахождения C1(x) и C2(x) созд.
сист. ур-ий. 0 y2
 C1’(x)y1+
C2’(x) y2=0 Þ
C1’(x)= f(x) y2’
C1’(x)y1+
C2’(x) y2=0 Þ
C1’(x)= f(x) y2’
C1’(x)y1’+ C2’(x) y2’=f(x) y1 y2
y1’ y2’
Þ C1(x)=∫(--)/(--)dx
y1 0
C2’(x)= y1’ f(x) Þ C2(x)=∫(--)/(--)dx
y1 y2
y1’ y2’
Лин. дифф. ур-ия со спец. правой частью.
Рассмотрим случай: y’’+py’+qy=f(x), p,q – числа. y=c>1>y>1>+c>2>y>2>+y*, где y>1>, y>2> – два лин-но незав. реш.
(1) y’’+ py’+qy=0 – лин. однород дифф. ур-ие 2ого порядка.
y=ekx k2+pk+q=0 – характерист. ур-ие ур-ия (1).
Рассмотрим 3 случия:
1. D>0, k>1,2>=(-p±Ö(p2-4q))/2, k>1>¹k>2> y>1>=ek>1>x, y>2>=ek>2>x.
Т.к. y>1>/y>2>¹const, то y=c>1> ek>1>x+c>2> ek>2>x.
2. D=0 k>1,2>=-p/2
y>1>=e-px/2, y>2>=y>1>∫(e--∫pdx)/y>1>2dx=e-px/2, y=e-px/2(c>1>+c>2>x).
3.Когда корни комплексные, т.е. D<0, k>1,2>=a±bi, y>1>=eaxCosbx, y>2>=eaxSinbx, y>1>/y>2>¹const, y=eax(c>1>Cosbx+c>2>Sinbx)
Неоднородные ур-ия со спец. правой частью.
1. f(x)=P>n>(x)eax 1) a - не явл-ся корнем хар. ур-ия
y*=(A>0>xn+A>1>xn-1 ++...+A>n>)=Q>n>(x)eax.
a - однократный корень y*=xQ>n>(x)eax.
3) a - двукрат. корень y*=x2Q>n>(x)eax.
2. f(x)=p(x)eaxCosbx+q(x)eaxSinbx
1) a+bi – не корень y*=U(x)eaxCosbx+V(x)eaxSinbx.
2) a+bi – корень y*=x[U(x)eaxCosbx+V(x)eaxSinbx].
3. f(x)=MCosbx+NSinbx
1)bi – не корень, y*=ACosbx+BSinbx.
2)bi – корень, y*=x(ACosbx+BSinbx).
РЯДЫ
Числовые ряды. Основные определения.
Пусть дана бесконечная послед-ть чисел U>1>, U>2>...U>n>,... Выражение U>1>+U>2>+...+U>n>+... наз-ся числовым рядом,
U>1>, U>2>...U>n> – члены ряда.
Сумма конечного числа n первых членов ряда наз-ся
n-ой частичной суммой ряда: S>n>= U>1>+U>2>+...+U>n>.
Если сущ-ет конечный предел lim>n>>®¥>S>n>=S, то этот предел наз суммой ряда.
Если предел lim>n>>®¥>S>n> равен ¥ или не сущ-ет, то говорят , что ряд расходится.
Если сущ-ет предел lim>n>>®¥>S>n>>, >то ряд сходится.
Некоторые очевидные свойства числовых рядов:
1)Теорема 1. На сходимость ряда не влияет отбрасывание конечного числа его членов.
Док-во: S>n> – сумма n первых членов ряда, C>k> – сумма k отброшенных членов, D>n>>->>k> – сумма членов ряда, входящих в сумму S>n> и не входящих в C>k>. Тогда имеем: S>n>=C>k>+D>n>>->>k>, где C>k> – постоянное число, не зависящее от n. Из последнего соотношения следует, что если сущ-ет limD>n>>->>k>, то сущ-ет и limS>n>; если сущ-ет lim S>n>, то сущ-ет limD>n>>->>k>, а это доказ-ет справедливость теоремы.
2)Теорема 2. Если ряд a>1>+a>2>+...(1) сходится, и его сумма равна S, то ряд ca>1>+ca>2>+...(2), где c=const, также сходится и его сумма равна сS.
Док-во: обозначим n-ю частичн сумму ряда (1) через S>n>, а ряда (2) – через D>n>. Тогда D>n>=ca>1>+...+ca>n>=c(a>1>+...+a>n>)=cS>n>. Отсюда ясно, что передел n-ой частичной суммы ряда (2) сущ-ет, т.к.
lim D>n>=lim(cS>n>)=climS>n>=cS. ч.т.д.
3)Теорема 3. Если ряды a>1>+a>2>+...(5) и b>1>+b>2>+...(6) сходятся, и их суммы, соответственно, равны S>1>и S>2>, то ряды (a>1>+b>1>)+(a>2>+b>2>)+...(7) и (a>1>–b>1>)+(a>2>–b>2>)+...(8) также сходятся, и их суммы, соответственно, равны S>1>+S>2> и
S>1>–S>2>.
Док-во: док-ем сходимость ряда (7). Обозначая его n-ую частичную сумму через D>n>, а n-е частичные суммы рядов (5) и (6) соответственно через S>1>>n> и S>2>>n>, получим: D>n>=(a>1>+b>1>)+...+(a>n>+b>n>)=(a>1>+...+a>n>)+(b>1>+...+b>n>)=S>1>>n>+S>2>>n>. Переходя к в этом равенстве к пределу при n®¥:, получим limD>n>=lim(S>1>>n>+S>2>>n>)= limS>1>>n>+limS>2>>n>=S>1>>n>+S>2>>n>.
Т.о., ряд (7) сходится и его сумма равна S>1>>n>+S>2>>n>.
4)Необходимый признак сходимости ряда. Если ряд сходится, то limU>n>=0 n®¥.
Док-во: пусть ряд U>1>+U>2>+...+U>n>+... сходится, т.е. limS>n>=S n®¥, тогда имеет место равенство limS>n>>-1>=S.
limS>n>–limS>n-1>=0, lim(S>n>–S>n-1>)=0. Но S>n>–S>n>>-1>=U>n> следов-но lim U>n>=0 ч.т.д.
Достат. призаки сходимости знакоположит. рядов.
1)Признак сравнения. Пусть дан ряд U>1>+U>2>+...+U>n>+...(1), S>1>>n>; V>1>+V>2>+...+V>n>+...(2) S>2>>n>; Известно,что V>n>³U>n> при n³N>0>.
если ряд (2) сходится, то ряд (1) также сходится;
если ряд (1) расходится, то ряд (2) расходится.
Док-во: Из сходимости ряда (2) следует, что $ lim S>2>>n>=S. S>1>>n>=U>1>+U>2>+...+U>N>>0>+U>N>>0+1>+...+U>n>=S>N>>0>+V>N>>0+1>+...+V>n>. limS>1>>n>=lim(S>N>>0>+D>n>>->>N>>0>)=S>N>>0>+D. S>1>>n> – возраст. послед-ть, ограниченная числом S>N>>0>+D => $ lim S>1>>n>=S>n>>1>.
2) Предельный признак сравнения. Если сущ-ет limU>n>/V>n>=L, но L¹0,¥ при n®¥, то ряды ведут себя одинаково.
3) Признак Даламбера. Если $ lim(U>n>>+1>/U>n>)=L(2) при n®¥, то: 1) ряд сходится, если L<1; 2) расходится, если L>1. Док-во: 1) пусть L<1. Рассмотрим число q, удовл. соотнош L<q<1. Из определения предела и соотношения (2) следует, что для всех n, n³ N, будет иметь место нер-во (U>n>>+1>/U>n>)<q (2’). Действительно, т.к. величина U>n>>+1>/U>n>> >стремится к пределу L, то разность м/у этой величиной и числом L м.б.сделана (начиная с некоторого номера N) по абсолютному значению меньше любого положит числа, в частности, меньше, чем q–L, т.е.
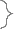 |
U>n>>+1>/U>n>
– L|<q–L.
из последнего нер-ва и следует нер-во
(2’). Записывая нер-во (2’)
для различных значений n,
начиная с номера N,
получим U>N>>+1><qU>N>>,>
|
U>n>>+1>/U>n>
– L|<q–L.
из последнего нер-ва и следует нер-во
(2’). Записывая нер-во (2’)
для различных значений n,
начиная с номера N,
получим U>N>>+1><qU>N>>,>
U>N>>+2><qU>N>>+1>< q2U>N>
Рассмотрим теперь два ряда:
U>1>+U>2>+...+U>N>+U>n+1>+... (1)
U>N>+qU>N>+q2U>N>+... (1’). Ряд (1’) есть геом прогрессия с положит знаменат q<1. Следоват-но, этот ряд сходится. Члены ряда (1), начиная с U>N>>+1>, меньше членов ряда (1’), следоват-но, ряд (1) сходится. Ч.т.д. 2) Пусть L>1. тогда из равенства lim(U>n>>+1>/U>n>)=L следует, что, начиная с некот. N, т.е. для n³N, будет иметь место нер-во (U>n>>+1>/U>n>)>1, или U>n>>+1>>U>n> для всех n³N. Но это озн-ет, что члены ряда возрастают, начиная с номера N+1, и поэтому общий член ряда не стремится к нулю. Значит, ряд расходится.
4)Признак Коши. Если для ряда с положит членами limnÖU>n>=L, то: 1) ряд сходится, если L<1; 2)расходится, если L>1.
Док-во: 1) пусть L<1. Рассмотр число q, L<q<1. Начиная с некот n=N, будет иметь место соотношение
| nÖU>n>–L|<q–L; осюда следует, что nÖU>n><q или U>n><qn для всех n³N. Рассмотрим теперь два ряда: U>1>+U>2>+...+U>N>+U>N>>+1>+... (1) и qN+qN+1+qN+2+... (1’). Ряд (1’) сходится, т.к. его члены обр-ют убыв. геом прогр. Члены ряда (1), начиная с U>N>, меньше членов ряда (1’). Значит, ряд (1) сходится. 2) Пусть L>1. Тогда, начиная с некот номера n=N, будем иметь: nÖU>n>>1 или U>n>>1. но если все члены рассматр ряда, начиная с U>N>, больше 1, то ряд расходится, т.к. его общий член не стремится к нулю.
5)Интегральный признак сходимости. Имеем ряд ¥å>n>>=1>U>n>, где члены ряда убывают U>n>>U>n>>+1>>0. Есть фун f(x)>0, хÎ[1;¥] непрерывная и убывающая и такая, что при целых значениях х=n значение фун-и f(n)=U>n>.
Если не собственный интеграл ¥ò>1>f(x)dx – сходиться, то ряд сходится. Если не собственный интеграл ¥ò>1>f(x)dx – расходиться, то ряд расходится.
Знакочередующиеся ряды.
Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны.
Т.Лейбница: Если члены знакочередующегося ряда убывают по абсолютной величине U>1>>U>2>>U>3>… и предел его общего члена при n®¥ равен 0
(Lim >n>>®¥> U>n>=0), то ряд сходится, а его сумма не превосходит первого члена: U>1>³S.
Д: Рассмотрим последовательность частичных сумм четного числа членов при n=2m:
S>2m>=(U>1>-U>2>)+(U>3>-U>4>)+…+(U>2m-1>-U>2m>). Эта последовательность возрастающая и ограниченная. На основании признака существования придела последовательность S>2>>m> имеет предел Lim>m>>®¥>S>2>>m>=S. Переходя к пределу в неравенстве S>2>>m><U>1> при m®¥, получим, что U>1>³S. Рассмотрим последовательность частичных сумм нечетного числа членов при n= 2m+1. Очевидно, что S>2>>m>>+1>=S>2>>m>+A>2>>m>>+1>; Поэтому учитывая необходимый признак сходимости ряда, Lim >m>>®¥> S>2>>m>>+1>=
=Lim>m>>®¥> S>2>>m>+ Lim >m>>®¥> А>2>>m>>+1>=S+0=S. Итак, при любом n (четном и нечетном) Lim >n>>®¥> Sn=S, т.е. ряд сходится.
Знакопеременные ряды.
Пусть U>1>+U>2>+U>3>….+U>n>+ знакопеременный ряд (*), в котором любой его член U>n> может быть как положительным, так и отрицательным.
Т.(Достаточный признак сходимости знакопеременного ряда): Если ряд, составленный из абсолютных величин членов данного ряда (*) и если ряд ¥å>n>>=1>½U>n>½; |U>1>|+|U>2>|+…+|U>n>|+…(1), сходится и наз абс. сходящимся. Обратное утверж не справедливо.
Д: Обозначим S>n>+ и S>n>- суммы абсолютных величин членов данного ряда (*), входящих со знаком плюс и минус. Тогда частичная сумма данного ряда S>n>>1>=S>n>+-S>n>- , а ряда составленного из абсолютных величин его членов S>n>>2>= S>n>++S>n>- . По условию ряд (1) сходится, значит сущ-т конечный предел Lim>n>>®¥>S>n>>2>=S. Последовательности S>n>+ и S>n>- являются возрастающими и ограниченными (S>n>+ ≤ S S>n>- ≤ S ), значит существуют пределы
Lim>n>>®¥>S>n>+ и Lim>n>>®¥>S>n>-, и соответственно предел частичной суммы данного ряда
Lim>n>>®¥>S>n1>=Lim> >>n>>®¥>S>n>+ -Lim> >>n>>®¥> S>n>- , т.е. ряд (*) сходится.·
Если ряд |U>1>|+|U>2>|+…+|U>n>|+…сходиться, то ряд U>1>+U>2>+U>3>….+U>n>+ наз абс. сходящимся.
Если ряд U>1>+U>2>+U>3>….+U>n>+ сходиться, а ряд |U>1>|+|U>2>|+…+|U>n>|+…расходиться, то ряд U>1>+U>2>+U>3>….+U>n>+ наз усл. сходящимся.
Св-ва абс сход рядов: Если ряд U>1>+U>2>+U>3>….+U>n>+ абс сходиться, то на сходимость не влияет перестановка членов ряда и группировка.
Степенные ряды.
C>0>+C>1>X+C>2>X2+…+C>n>Xn..-степенной ряд (*)
Св-ва: 1)Т. Абеля: 1)Если степенной ряд сходится при значении X=X>0>≠0, то он сходится и, притом абсолютно, при всех значениях Х таких что |Х|<|X>0>|, 2)Если степенной ряд расходится при Х=Х>1>, то он расходится при всех значениях Х таких что |Х|>|Х>1>|.
Д: 1)По условию ряд (*) сходится при Х=Х>0>≠0, следовательно, выполняется необходимый признак сходимости Lim>n>>®¥>U>n>=Lim>n>>®¥>C>n>X>0>n=0. Значит последовательность |C>n>X>0>n| Оганичена, т.е. сущ. Такое число М>0, что для всех n выполняется неравенство |C>n>X>0>n|<M. Рассмотрим ряд, составленный из абсолютных величинчленов ряда(*)
|С>0>|+ |C>1>X>0>||Х/X>0>|+…+ |C>n>X>0>n||X/X>0>|n+…(1). Члены ряда (1) меньше соответствующих членов ряда М+М|Х/X>0>|+…+М|X/X>0>|n+… представляющего геометрический ряд, к-й сходится, когда его знаменатель q=|X/X>0>|<1, т.е. при|X|<|X>0>|, на основании признака сравнения ряд (*) сходится. 2)Предположим противное, т.е. при|X|>|X>1>| ряд (*) сходится. Тогда по доказанному выше он должен сходится и в точке Х>1 >(т.к. |X|>|X>1>|), что противоречит условию.·
Из теоремы Абеля следует, что сущ. Такое число R≥0, что при │Х│<R ряд сходится, а при │Х│>R – расходится. Число R получило название радиуса сходимости, а интервал (-R;R)-интервала сходимости степенного ряда.
2) и 3) на любом отрезке [a,b], целиком принадлежащем интервалу сходимости(-R;R), ф-я F(x) является непрерывной, а следовательно степенной ряд можно почленно интегрировать и дифференцировать на этом отрезке.
4) Степенные ряды вида а>0>+а>1>х+а>2>х2+…+а>n>х2+…+а>n>>+1>хn+1+… и
а>0>+а>1>(х-х>0>)+а2(х-х>0>)2+…+аn(х-х>0>)2+… сходяться равномерно.
5) Степенные ряды сход к фун S(x), которая непрерывна в обл сходимости.
Функциональные ряды
Ряд U>1>+U>2>+..+Un+.. называется функциональным, если его члены являются функциями от Х. Рассмотрим функциональный ряд U>1>(Х)+U>2>(Х)+..+Un(Х)+...(1) Совокупность тех значений Х, при которых функциональный ряд сходится, называют областью сходимости этого ряда.
Обозначим через S>n>(Х) сумму первых n членов ряда (1). Если этот ряд сходится и сумма его равна S(x), то S(x)=S>n>(x)+r>n>(x), где r>n>(x) есть сумма ряда U>n>>+1>(x)+U>n>>+2>(x) +…, т.е. r>n>(x)= U>n+1>(x)+U>n+2>(x) +… В этом случае величина r>n>(x) называется остатком ряда (1). Для всех значений Х в области сходимости ряда имеет место соотношение Lim>n>>→∞> r>n>(x)= Lim>n>>→∞>[S(x)-S>n>(x)]=0, т.е. остаток r>n>(x) сходящегося ряда стремится к нулю при n→∞.
Функциональный ряд U>1>(Х)+U>2>(Х)+..+Un(Х)+.. (1) называется мажорируемым в нек-й области изменения Х, если существует такой сходящийся числовой ряд а>1>+а>2>+а>3>+…+а>n>..(2) с положительными членами, что для всех значений Х из данной области выполняются соотношения │U>1>(x)│≤a>1,>…,│U>n>(x)│≤a>n> ,… Иначе, ряд называется мажорируемым, если каждый его член по абсолютной величине не больше соответствующего члена нек-го сход. ряда с полож. членами.
Ряд Тейлор.
Для ф-и F(x) имеющей все производные до (n-1) порядка включительно, в окрестности точки х=а справедлива формула Тейлора: f(x)=f(a)+f¢(a)(x-a)+f¢¢(a)[(x-a)2/2!]+…
…+fn(a)[(x-a)n/n!]+R>n>(x), (1) где остаточный член R>n>(х)={[(x-a)n+1]/[(n+1)!]}f(n+1)[a+q(x-a)], где 0<q<1. Для того, чтобы ряд сходился к ф-и, необходимо и достаточно, чтобы при n®¥ остаток ряда стремился к 0, т.е. R>n>(x)®o. Переходя в формуле (1) к пределу при n®¥, получим справа бесконечный ряд, котороый наз рядом Тейлора:
f(x)=f(a)+f¢(a)(x-a)+…+fn(a)[(x-a)n/n!]+…
Если в ряде Тейлора предположим а=0, то получим ряд Маклорена: f(x)=f(0)+f¢(0)x+f¢¢(0)[x2/2!]+…
…+fn(0)[xn/n!]+….
Разложение нек-х ф-й в ряд Маклорена:
ex=1+x+x2/2!+…+xn/n!+… (-¥;¥)
sinX=x-x3/3!+x5/5!+…+(-1)n-1[X2n-1]/(2n-1)!+… (-¥;¥)
cosX=1-x2/2!+x4/4!-…+[(-1)nX2n]/(2n)!+… (-¥;¥)
(1+x)m=1+mx+[m(m-1)x2]/2!+[m(m-1)*
*(m-2)x3]/3!+[m(m-1)(m-n+1)xn]/n!+… (-1;1)
ln(1+x)=x-x2/2+x3/3-..+[(-1)nxn+1]/(n+1)+.. (-1;1]
1/(1-x)=1+x+x2+…+xn+..
1/(1+X2)=1-x2+x4-x6+…
arctgX=x-x3/3+x5/5-x7/7+…+[(-1)n+1x2n-1]/2n-1+…
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.shpori4all.narod.ru/