Лекции (1-18) по мат. анализу 1 семестр

Л

По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик

van_mo_mail@mtu-net.ru или на сотовый:

8-901-7271056 спросить Ваню

екция №1

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 5 сентября 2000 г.

Тема: Введение

Условные обозначения:

: - так, что def – по определению

 – включает ’’’ – [dⁿf(x)]/dxⁿ=(d/dx)([d^n-1f(x)]/dxⁿ)

 - следует, выполняется

 - тогда и только тогда

 - любой

 - существует

] – пусть

! – единственный

[x] – целая часть

~ - эквивалентно

о - малое

Все R представляют десятичной дробью.

Все Q представляют конечной дробью, либо периодичной дробью.

Все иррациональные числа представляют бесконечной десятичной дробью ( не периодичной).

Рассмотрим числовую ось. Числовая ось – направленная прямая с отмеченной точкой и отмеченным масштабом.

x

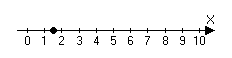
0 – отвечает за ноль.

Отрезок [0;1] отвечает за единицу

Единица за единицу.

Каждой точки х на числовой прямой отвечает некоторое действительное число. Если длинны отрезков [0;x] из заданного масштаба соизмеримы, тогда числу х отвечает рациональное число. Если не соизмеримы, то иррациональны.

Каждому R отвечает точка на числовой прямой и наоборот, каждой точке отвечает R.

Основные числовые множества.

x

Отрезок: [/////////] x

a b

Обозначается [a;b] ab

Частный случай отрезка точка

Или axb – в виде неравенства.

х

Интервал: (/////////) x – множество точек на числовой прямой.

a b

Обозначается (a;b) или в виде неравенства a<x<b

x

Полуинтервал: (/////////] x

a b

x

[/////////) x

a b

Обозначается: [a;b) axb

(a;b] a<xb

Всё это числовые промежутки.

Замечание: один из концов ( а или b) может быть символом .

x

///////////////] x (-;b] или -<xb

b

x

///////////////) x (-;b) или -<x<b

b

Вся числовая прямая – R=(-;+)

Окрестности.

Определение: ε –окрестностью числа а называется множество чисел х удовлетворяющие неравенству

a-ε<x<a+ε  x-a  (////////) x  О_>ε>(а)

ε>0 а-ε а а+ε

О_>ε>(а)={xR:x-a<ε}

Проколотая ε окрестность – О^_>ε>(а) это множество таких чисел включающих R, и отстаёт от точки на ε и не принадлежит а.

О^_>ε>(а)={xR:0<x-a<ε}

(////////) x

а-ε а а+ε

Правая ε поло окрестность точки а: О⁺_>ε>(а)={xR:ax<a+ε}

 ///////) x

a a+ε

Проколотая правая ε поло окрестность точки а: О^_>ε>(а)={xR:a<x<a+ε} Рисунок подобен предыдущему только с выколотой точкой а.

Левая ε поло окрестность точки а: O^-_>ε>(a)={xR:a-ε<xa}

(//////// x

a-ε a

Проколотая, левая ε поло окрестность точки а: О^-_>ε>(а)={xR:a-ε<x<a} Рисунок подобен предыдущему только с выколотой точкой а.

Модуль и основные неравенства.

x; x>0

х= 0; x=0

-x; x<0

|x|<h  -h<x<h |x|>h x>h

h>0 x<-h

 а,b  R: |ab|a|+|b|

 а,b  R: |a-b|||a|-|b||

Можно рассматривать окрестности бесконечности:

О_>ε>(+)={xR:x>ε} (////////// x

ε>0 ε

О_>ε>(-)={xR:x<-ε} ///////////)  x

ε>0 -ε 0

О_>ε>()={xR:x>ε} \\\\\\) _>> (////// x

x>ε;x<-ε -ε ε

Функция. Монотонность. Ограниченность.

х – называется независимой переменной.

у – зависимой.

Функцию можно задавать равенством (у=х²)

Таблицей

Х	Х>1>	Х>2>	Х>3>	Х>4>
У	У>1>	У>2>	У>3>	У>4>

Графиком, то есть множеством точек с координатами (x,f(x)) на плоскости:

Определение f(x) монотонности: Пусть Х принадлежит области определение D ( ]xD)

Пусть Х подмножество в области определения в f(x).

Функция у=f(x) называется:

Возрастающая на Х, если для любого х_>1>;х_>2> принадлежащие Х: х_>1><x_>2>f(x_>1>)<f(x_>2>)

Убывающий на Х, если для любого х_>1>;х_>2> принадлежащие Х: х_>1><x_>2>f(x_>1>)>f(x_>2>)

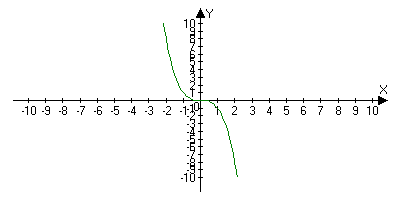
3) Не убывающий на Х, если для любого х_>1>;х_>2> принадлежащие Х: х_>1><x_>2>f(x_>1>)f(x_>2>)

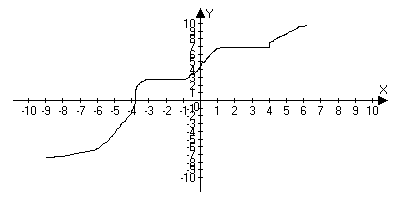
Не возрастающая на Х, если для любого х_>1>;х_>2> принадлежащие Х: х_>1><x_>2>f(x_>1>)f(x_>2>)

Определение:

Ограниченность. Пусть Х включает D y=f(x) называется:

Ограниченной сверху на Х если существует В, так что для любого х принадлежащего Х выполняется xR

Ограниченной снизу на Х если существует А, так что для любого х принадлежащего Х выполняется Ах

Ограниченной и сверху и снизу на Х если существует А,В, так что для любого х принадлежащего Х выполняется АхВ, или существует С, так что для любого х принадлежащего Х выполняется хС

Лекция №2

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 12 сентября 2000 г.

Тема: Функции

Определение (сложная функция):

Пусть задано D,E,G,C,R

На D: y=f(x) с областью значения E

На E: z=g(y) с областью значения G

Тогда на множестве D определена сложная функция z=g(f(x)) с областью значения G. Тогда говорят, что g(f(x)) есть суперпозиция функций g,f.

Пример: Пример

z=sin e^x w=arctgcos e^{xx-ln x}

y=e^x=f(x)

z=sin y=g(y)

D=R

E=R_>+>

G=[-1;1]

Определение (обратной функции):

Пусть существует D,E,C,R

На D: y=f(x) с областью значений Е. Если для каждого у из y=f(x) найдётся единственный х, то говорят, что на множестве Е задана функция обратная к функции f(x), с областью значений D. Иными словами две функции y=f(x) и x=g(y) являются взаимно обратными если выполняется тождества:

y=f(g(y)),  yE y=f(g(y)), для любого уЕ



x=g(f(x)),  xD x=g(f(x)), для любого хD

Примеры:

1)y=x³  x=³y

D=R

E=R

2)y=x²  x=y

D=R_>+> {0}=[0;+)

E=[0;+)

D=R_>-> {0}=(-;0]

E=[0;) x=-y

3)y=sinx

D=[-/2;/2]

E=[-1;1]

x=arcsiny

y[-1;1]; x[-/2;/2]

Пусть y=f(x)

D=[a;b]

E=[A;B]

Определение: y=f(x), nN

a_>1>=f(1)

a_>2>=f(2)

a_>n>=f(n)

{a_>n>} – множество значений силовой последовательности nN или а_>n>

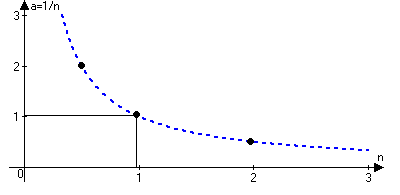{а_>n>}={1,1/2,1/3,…,1/n,…}

а_>n>=1/n

{а_>n>}={sin1;sin2;sinn}

а_>n>=sinn

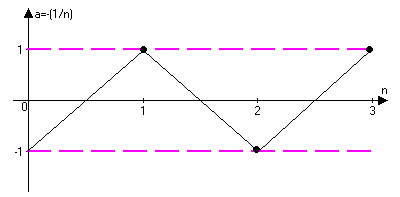
а_>n>=(-1)ⁿ/n

{(-1)ⁿ}={-1;1;-1;1;-1;1…}

Ограниченные последовательности.

Ограниченная сверху, то есть существует В так что а_>n>В, для любого nN

Ограниченная снизу, то есть существует А так что Аb_>n>, для любого nN

Ограниченная, то есть существует А,В так что Аа_>n>В, для любого nN  существует С>0 так что а_>n>С, для любого nN.

Монотонные последовательности

возрастающая a_>n><a_>n>_>+1>,  nN

убывающая a_>n>>a_>n+1>,  nN

не возрастающая a_>n>a_>n>_>+1>,  nN

не убывающая a_>n>a_>n>_>+1>,  nN

Пределы последовательности.

Определение: числа а , называется пределом числовой последовательности а_>n>, если для любого сколь угодно малого числа ε>0, найдётся натуральный номер N такой, что для всех чисел nN выполняется модуль разности a_>n>-a<ε   ε>0  N :  nN a_>n>-a<ε.

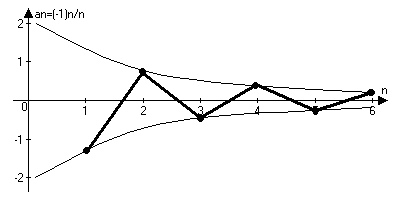Начиная с этого номера N все числа этой последовательности попадают в ε окрестность числа а. Другими словами начиная с номера N вне интервала а-ε;а+ε может находиться не более конечного числа членов последовательности.

Lim a_>n>=0

^n

Примеры: Доказать, что ln(-1)²/n=0

Зададим любое ε>0, хотим чтобы (-1)ⁿ-0<ε, начиная с некоторого номера N, 1/n<ε  n>1/ε

N=[1/ε]+1

ε=0.01

N=[1/0.01]+1=101

|a_>n>|<0.01, если n101

* * *

a_>n>=1-1/n²

lim(1-1/n²)=1

^n+

Для любого ε>0 (1-1/n²)-1<ε

-1/n²<ε  1/n²<ε  n²>1/ε  n>1/ε

N=[1/ε]+1

Лекция №3

Ведущая: Голубева Зоя Николаевна

Дата: среда, 13 сентября 2000 г.

Тема: Последовательности

Бесконечно малые последовательности

Последовательность а_>n> называется бесконечно малой , это означает, что предел этой последовательности после равен 0.

a_>n> – бесконечно малая  lim a_>n>=0 то есть для любого ε>0 существует N, такое что для любого n>N выполняется

^n+

a_>n><ε

Важные примеры бесконечно малой последовательности:

1)_>n>=1/n Докажем, что для любого ε>0 1/n<ε  1/n<ε n>1/ε N[1/ε]+1

Докажем, что lim1/n=0

^n+

2) _>n>= sin(1/n). Докажем, что для любого ε>0 sin(1/n)<ε, заметим, что 1/n принадлежит первой четверти, следовательно 1sin(1/n)>0, следовательно sin(1/n)<ε

Следовательно 1/n<arcsinε  n>1/arcsinε N=[1/arcsinε]+1. Докажем, что lim sin1/n=0

^n+

3) _>n>=ln(1+1/n)

n0; 1/n; 1+1/n1

lim ln(1+1/n)=0

^n+

Докажем ln(1+1/n)<ε ln(1+1/n)<ε  1+1/n<e^ε

1/n<e^ε-1

n>1/e^ε-1 N=[1/e^ε-1]+1

_>n>=1-cos(1/n)

lim(1-cos(1/n))=0

^n+

Докажем ε>0 1-cos(1/n)<ε

1/n первой четверти cos первой четверти положительный 0<cos(1/n)<1 1-cos(1/n)<ε

cos(1/n)>1-ε (считаем, что 0<ε<1)

1/n<arcos(1-ε) n>1/arcos(1-ε)

N=[1/arcos(1-ε)]+1

Свойства бесконечно малой последовательности.

Теорема. Сумма бесконечно малой есть бесконечно малое.

_>n>_>n>бесконечно малое  _>n>+_>n> – бесконечно малое.

Доказательство.

Дано:

_>n>- бесконечно малое  ε>0  N_>1>:_>n>>N_>1>  _>n><ε

_>n>- бесконечно малое  ε>0  N_>2>:_>n>>N_>2>  _>n><ε

Положим N=max{N_>1>,N_>2>}, тогда для любого n>N  одновременно выполняется оба неравенства:

_>n><ε _>n>+_>n>_>n>+_>n><ε+ε=2ε=ε_>1>n>N

_>n><ε

Зададим ε_>1>>0, положим ε=ε_>1>/2. Тогда для любого ε_>1>>0 N=maxN_>1>N_>2> :  n>N  _>n>+_>n><ε_>1>  lim(_>n>+_>n>)=0, то

^n

есть _>n>+_>n> – бесконечно малое.

Теорема Произведение бесконечно малого есть бесконечно малое.

_>n>,_>n> – бесконечно малое  _>n>_>n> – бесконечно малое.

Докозательство:

Зададим ε_>1>>0, положим ε=ε_>1>, так как _>n> и _>n> – бесконечно малое для этого ε>0, то найдётся N_>1>:  n>N  _>n><ε

N_>2>:  n>N_>2>  _>n><ε

Возьмем N=max {N_>1>;N_>2>}, тогда n>N = _>n><ε

_>n><ε

_>n>_>n>=_>n>_>n><ε²=ε_>1>

 ε_>1>>0 N:n>N _>n>_>n><ε²=ε_>1>

lim _>n>_>n>=0  _>n>_>n> – бесконечно малое, что и требовалось доказать.

^n

Теорема Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность

а_>n> – ограниченная последовательность

_>n> –бесконечно малая последовательность  a_>n>_>n> – бесконечно малая последовательность.

Доказательство: Так как а_>n> – ограниченная  С>0: nN  a_>n>C

Зададим ε_>1>>0; положим ε=ε_>1>/C; так как _>n> – бесконечно малая, то ε>0 N:n>N _>n><ε a_>n>_>n>=a_>n>_>n><Cε=Cε_>1>/C=ε_>1>

ε_>1>>0 N: n>N  a_>n>_>n>=Cε=ε_>1>  lim a_>n>_>n>=0 a_>n>_>n> – бесконечно малое

^n

Замечание: в качестве ограниченной последовательности можно рассматривать const  произведение постоянно.

Теорема о представление последовательности имеющий конечный предел.

lim a_>n>=a  a_>n>=a+_>n>

^n+

Последовательность a_>n> имеет конечный предел а тогда и только тогда, когда она представлена в виде a_>n>=a+_>n>

где _>n>_> >– бесконечно малая.

Доказательство:

lim a_>n>   ε>0 N:n>N  a_>n>-a<ε. Положим a_>n>-a=_>n>  _>n><ε, n>N, то есть _>n> - бесконечно малая

^n+

a_>n>=a+_>n> что и требовалось доказать

Доказательство (обратное): пусть a_>n>=a+_>n>, _>n> – бесконечно малая, то есть _>n>=a_>n>-a  ε>0 N: n>N 

_>n>=a_>n>-a<ε, то есть lim a_>n>-а

^n+

Теоремы о пределах числовых последовательностей.

Теорема о пределе суммы:

Пусть lim a_>n>=a lim b_>n>=b  lim a_>n>+_>n>=a+b

^{n+ n+ n+}

Докозательство: a_>n>=a+_>n> b_>n>=b+_>n> Сложим a_>n>+b_>n>=a+b+_>n>+_>n>=a+b+_>n> lim a_>n>+b_>n>=a+b

^n+

_> > 2) Теорема о произведение пределов:

Пусть lim a_>n>=a lim b_>n>=b  lim a_>n>b_>n>=ab

^{n+ n+ n+}

Доказательство: a_>n>=a+_>n> b_>n>=b+_>n>  a_>n>b_>n>=(a+_>n>)(b+_>n>) a_>n>b_>n>=ab+a_>n>+b_>n>+_>n>_>n>=ab+_>n >lim a_>n>b_>n>=ab что и

^n+

требовалось доказать.

Теорема о пределе частного

Пусть lim a_>n>=a lim b_>n>=b b0 lim a_>n/>b_>n>=a/b

^{n+ n+ n+}

Доказательство: a_>n>=a+_>n> b_>n>=b+_>n> так как b0, то N_>1>: n>N_>1>b_>n>0

_>bn>

_>0>^{ (////////}_>b>^{/////////)} x

a_>n>/b_>n>=a_>n>/b_>n>-a/b+a/b=a/b+(ba_>n>-ab_>n>)/bb_>n>=a/b+[b(a+_>n>)-a(b+_>n>)]/b(b+_>n>)=a/b+_>n>/b(1+b_>n>/b)

lim a_>n>/b_>n>=a/b

^n+

Лекция №4

Ведущая: Голубева Зоя Николаевна

Дата: понедельник, 19 сентября 2000 г.

Тема: Бесконечно большие последовательности .

а_>n>=(-1)ⁿ – не имеет предел.

{b_>n>}={1,1…}

{a_>n>}={-1;1;-1;1…} – предел не существует.

Бесконечно большие последовательности.

a_>n>=2ⁿ

N:n>N  a_>n>>ε

b_>n>=(-1)ⁿ2ⁿ

N:n>N  b_>n>>ε

c_>n>=-2ⁿ

N:n>N c_>n><-ε

Определение (бесконечно большие последовательности)

1) lim a_>n>=+, если ε>0N:n>N  a_>n>>ε где ε- сколь угодно малое.

^n

2)lim a_>n>=-, если ε>0 N:n>N  a_>n><-ε

^n+

3) lim a_>n>=  ε>0 N:n>N  a_>n>>ε

^n+

Последовательностью имеющий конечный предел называют сходящимися. В противном случае последовательность называют расходящимися. Среди них есть последовательности, которые расходятся в бесконечность. О них мы говорим, что они имеют бесконечный предел.

Доказательство:

a_>n>=2ⁿ

Берём ε>0; хотим 2ⁿ>ε

n>log_>2>ε

N=[log_>2>ε]+1

Правило формирования обратного утверждения: нужно поменять местами значки  и , а знак неравенства на дополнительный.

Пример:

Утверждение lim a_>n>=a< aR ε>0 NN:n>N  a_>n>-a<ε

^n

Обратное утверждение aR ε>0 NN: n>N  a_>n>-a<ε

Всякая бесконечно большая не ограниченная. Обратное утверждение неверно.

b_>n>{2;0;2ⁿ;0;2³;0….}

Теорема (об ограниченной сходящейся последовательности)

Пусть lim a_>n>=a<  a_>n> - ограниченная

^n+

Доказательство:

Дано:

ε>0N:n>N  a_>n>-a<ε

Раз ε>0 возьмем ε=1  N:n>N  a_>n>-a<1

a-1<a_>n><1+a, n>N

Этому неравенству может быть не удовлетворять только первые N члены последовательности.

N_>1>=max{a_>1>;a_>2>;…a_>n>;1+a;a-1}

a_>n>c, n>N

Теорема (о единстве предела сходящейся последовательности).

Если lim a_>n>=a <, то а- единственное.

^n+

Доказательство:(от противного)

Предположим, что  b: lim a_>n>=b и ba ε=b-a/2>0 для определенности пусть b>a N_>1>:n>N_>1> a_>n>-a<ε

^n+

N_>2>:n>N_>2>  a_>n>-b<ε N=max{N_>1>;N_>2>}, тогда оба неравенства выполняются одновременно 

 -(b-a)/2<a_>n>-a<(b-a)/2

-(b-a)/2<a_>n>-b<(b-a)/2

a_>n>-a<(b-a)/2

-

a_>n>-b>-(b-a)/2

b-a<b-a

0<0 – противоречие  предположение, что b>a неверно. Аналогично доказывается, что b<a, то же неверно ε=(a-b)/2

Связь между бесконечно большими и бесконечно малыми величинами.

Теорема:

1)a_>n>- бесконечно большая  1/a_>n> – бесконечно малая

2)_>т> – бесконечно малая, _>n>0 (n>N_>0>) 1/_>n> – бесконечно большая

Доказательство:

1)a_>n>- бесконечно большая  lim a_>n>=  для достаточно больших номеров n a_>n>0. Зададим любое сколько

^n+

угодно малое ε>0, положим ε=1/ε>0

Для ε N_>1>:n>N_>1> a_>n>>ε, то есть a_>n>>1/ε N=max{N_>1>;N_>0>}

Тогда n>N  1/a_>n><ε, то есть lim 1/a_>n>=0, то есть 1/a_>n> – бесконечно малое

^n+

2)_>n> – бесконечно малое lim _>n>=0

^n+

Дано: _>n>0, n>N_>0> зададим ε>0 положим ε=1/ε>0

N_>1>:n>N_>1> _>n><ε=1/ε

N=max{N_>0>;N_>1>}: n>N  1/_>n>=, то есть 1/_>n> – бесконечно большая.

Основные теоремы о существование предела последовательности.

Теорема Вейрштрасса:

Пусть a_>n>- ограниченная и моннатонна. Тогда  lim a_>n>=а<

^n+

Лемма. Среднее арифметическое чисел больше среднего геометрического. Равенство достигается только если все числа равны.

Л

По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик

van_mo_mail@mtu-net.ru или на сотовый:

8-901-7271056 спросить Ваню

екция №5

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 25 сентября 2000 г.

Тема: Бесконечно большие последовательности

Теорема:

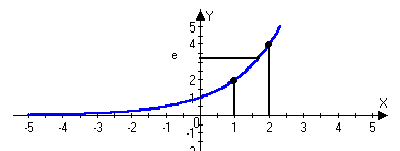
lim(1-1/n)ⁿ=1/e e=2,7183

^n+

0a_>n>=1-1/n1 nN, то есть a_>n>=(1-1/n)ⁿ- ограниченна.

ⁿ⁺¹a_>n>=ⁿ⁺¹(1-1/n)ⁿ1=ⁿ⁺¹(1-1/n)(1-1/n)…(1-1/n)1<[1+(1-1/n)+…+(1-1/n)]/n+1=(n+1-n1/n)/n+1=n/n+1=1-1/n+1

ⁿ⁺¹(1-1/n)ⁿ<1-1/n+1

(1-1/n)ⁿ<(1-1/n+1)ⁿ⁺¹

a_>n><a_>n>_>+1> nN  последовательность возрастает и ограниченная.

(1-1/n)ⁿ – имеет конечный предел

lim(1-1/n)ⁿ=1/e

^n+

Следствие

lim(1+1/n)ⁿ=e

^n+

lim1/(1+1/n)ⁿ=(n/n+1)ⁿ=[1-1/(n+1)]ⁿ⁺¹/ [1-1/(n+1)]=(1/e)/1=1/e

^n+

lim[1/(1+1/n)ⁿ]=1/e

^n+

lim(1+1/n)ⁿ=e

^n+

Определение под последовательности

Пусть дана a_>n> зададим произвольный набор натуральных чисел таких, что

n_>1><n_>2><n_>3><…<n_>k><….

a_>n1>,a_>n2>,…,a_>nk>,…

Полученная последовательность называется под последовательностью и сходной последовательности.

a_>n>=(-1)ⁿ

{a_>n>}={-1;1;-1;1….}

n_>1>=2;n_>2>=4,….,n_>k>=2k

{a_>nk>}={1,1,1,1…}

Теорема

Пусть последовательность a_>n> сходится, тогда последовательности

 lim a_>n>=a {a_>nk>} – гас и lim

^n+

lim a_>nk>=0

^n+

Доказательство так как a_>n> – сходиться, то ε>0 N: n>N  a_>n>-a<ε

a_>nk>; n_>k>>N_> >то есть a_>nk>-a<ε

Пример

a_>n>_>=>(-1)ⁿ – не имеет предела

{a_>2>_>n>}={1,…,1,…,}

{a_>2>_>n>_>-1>}={-1,….,-1,…}

имели бы тот же самый предел.

Предел функции.

Определение

Пусть y=f(x) определена в O(x_>0>). Мы говорим, что функция f(x) имеет предел в при хх_>0> если ε>0  >0

x:0<x-x_>0>< f(x)-b<ε

lim f(x)=b

^xx_>>

Через окрестности это определение записывается следующим образом

ε>0 >0 x0_>>(x_>0>)f(x)0_>ε>(b)

Если lim f(x)=0, то f(x) наз бесконечно малой при xx_>0>.

^xx_>>

Замечание. Необходимо указать в каком именно процессе f(x) бесконечно малое. Надо указать к какому числу  а.

f(x)=x-1

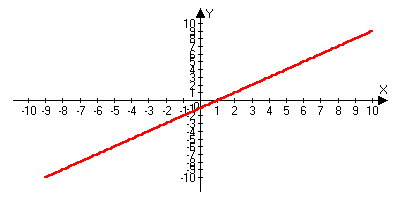
1.x1 lim(x-1)=0, то есть y=x-1 бесконечно малое при x1

^x1

2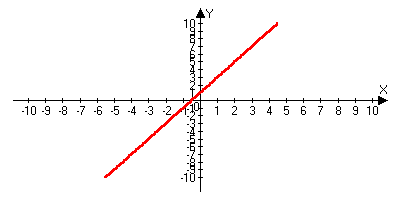.x2 lim(x-1)=1, то есть y=x-1 не является бесконечно малой при x2

^x1

Пример

f(x)=2x+1 x1

Докажем lim(2x+1)=3

^x1

ε>0 >0 x:0<x-1< (2x+1)-3<ε

(2x+1)-3<ε

|x-1<ε/2

x1

Положим =ε/2

Теорема о бесконечно малом

1)(x);(x) – бесконечно малое xx_>0>  (x)+(x) – бесконечно малое при xx_>0>

2)(x);(x) – бесконечно малое при xx_>0>

3)Если f(x) – ограниченна в O(x_>0>) и (x) – бесконечно малое при xx_>0>, то f(x);(x) – бесконечно малое при xx_>0>

Доказательство (3)

Так как f(x) – ограниченна в O(x_>0>), то  С>0: xO(x_>0>)|f(x)C;

Так как (x) – бесконечно малое при хх_>0>, то ε>0 >0 x: 0<x-x_>0><  (x)<ε ε_>1>>0

Положим ε=ε_>1>/c

>0 x: 0<x-x_>0>|< f(x)(x)=f(x)a(x)<Cε=ε_>1> lim f(x)(x)=0, то есть f(x)a(x) – бесконечно малое при xx_>0>

^xx_>>

Лекция №6

Ведущая: Голубева Зоя Николаевна

Дата: среда, 26 сентября 2000 г.

Тема: Замечательные пределы

Теорема

f(x)>g(x) в O(x_>0>) и  lim (f(x))=b и  lim (g(x))=c. Тогда bc

^xx_>>_> > ^xx_>>_> >

Доказательство:

Рассмотрим функцию (x)=f(x)-g(x)>0 в O(x_>0>)  lim ((x))= lim (f(x)) - lim (g(x))= b-c и в силу предыдущей

^xx_>>_> > ^xx_>>_> > ^xx_>>_> >

теоремы b-c0, то есть b0 что и требовалось доказать.

Теорема

f(x)(x)g(x)  xO(x_>0>) и  lim (f(x))=b и  lim (g (x))=b.  lim ( (x))=b

^xx_>>_> > ^xx_>>_> > ^xx_>>_> >

Доказательство:

f(x)=b+(x)

g(x)=b+(x)

где (x) и (x) – бесконечно малые при хх_>0>

b+(x)(x)b+(x)

Так как (х) и (х) – бесконечно малые то ε>0 _>1>>0:  xO_>>_>1>(x_>0>)  (x)<ε

_>2>>0:  xO_>>_>2>(x_>0>)  (x)<ε

Положим =min{_>1>;_>2>}

Тогда  xO_>>(x_>0>)  (x)<ε

(x)<ε

-ε<(x)<ε

-ε<(x)<ε

b-ε<b+(x)(x)b+(x)<b+ε

-ε<(x)-b<ε

(x)-b<ε  xO_>>(x_>0>)

 ε>0  =min{_>1>;_>2>}  (x)-b<ε xO_>>(x_>0>) то есть lim ( (x))=b

_> > ^xx_>>_> >

Первый замечательные пределы.

Терема lim (sin(x)/x)=1

^x0_> >

Д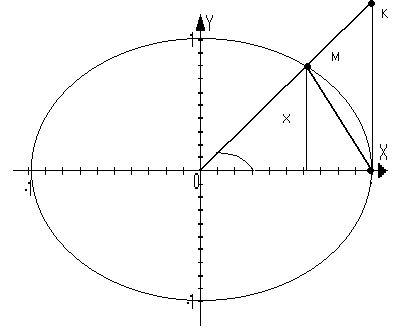оказательство:

S_>∆>_>OMN>=1/2 sin(x)

S_>сек>_>OMN>=1/2(x)

S_>∆>_>OKN>=1/2 tg(x)

S_>∆>_>OMN><S_>сек>_>OMN>< S_>∆>_>OKN>

1/2sin(x)<1/2(x)<tg(x)

sin(x)<x<tg(x)

1<x/sin(x)<1/cos(x)

lim (1-cos(1/n))=0

^n+_> >

lim (1-cos(x))=0  lim (cos(x))=1

^x0_> > ^x0_> >

lim (x/sin(x))=0

^x0_> >

x>0

lim (x/sin(x))=1

^x0

lim(1/(x/sin(x)))= lim(sin(x)/x)=1 что и требовалось доказать _> >

^x0_> > ^x0_> >

Определение бесконечного предела и пределов при х+.

lim (f (x))=+  ε>0 >0:  xO_>>(x_>0>)f(x)O_>ε>(+)

^xx_>>_> >

(x): 0<x-x_>0><

(////////// x

_> > ε

lim (f (x))=-  ε>0 >0:  xO_>>(x_>0>)f(x)O_>ε>(-)

^xx_>>_> >

(x): 0<x-x_>0><

lim (f (x))=  ε>0 >0:  xO_>>(x_>0>)f(x)O_>ε>()

^xx_>>_> >

f(x)>ε

lim (f (x))=b  ε>0 ∆>0:  xO_>∆>(+)f(x)O_>ε>(b)

^x+_> >

 x: x>∆ f(x)-b <ε

lim (f (x))=b  ε>0 ∆>0:  xO_>∆>(-)f(x)O_>ε>(b)

^x-_> >

 x: x<-∆ f(x)-b <ε

Односторонние пределы.

Определение

f(x) определена в O⁺(x_>0>)

lim (f (x))=b  ε>0 >0:  xO⁺_>>(x_>0>)f(x)O_>ε>(b) x_>0><x<x_>0>+

^xx_>>⁺⁰_> >

Определение

f(x) определена в O^-(x_>0>)

lim (f (x))=b  ε>0 >0:  xO^-_>>(x_>0>)f(x)O_>ε>(b) x_>0>-<x<x_>0>

^xx_>>^-0_> >

Теорема Пусть f(x) определена в O(x_>0>) Для того чтобы существо-

вал предел  lim(f(x))=b   lim(f(x))=lim(f(x))=b

^xx_>>_> >^xx_>>^{+0 xx}_>>^-0

Пусть  lim(f(x))=b, то есть ε>0 >0:  xO_>>(x_>0>)f(x)O_>ε>(b) f(x)O_>>(b) для  xO⁺_>>(x_>0>) и для  xO^-_>>

^xx_>>_> >

 xO^-_>>(x_>0>) lim(f(x));lim(f(x))=b что и требовалось доказать._> >

_> >^xx_>>^{+0 xx}_>>^-0

Второй замечательный предел.

Теорема lim(1+1/x)^x=e

^x+

Доказательство: Пусть n – целая часть х – n=[x] nx<n+1

[1+1/(n+1)]ⁿ(1+1/x)^x(1+1/n)ⁿ⁺¹

Если x+, то n+

[1+1/(n+1)]ⁿ⁺¹1/[1+1/(n+1)](1+1/x)^x(1+1/n)ⁿ(1+1/n)  lim(1+1/x)^x=e

^x+

Лекция №7

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 3 октября 2000 г.

Тема: Сравнение бесконечно больших и бесконечно малых.

Определение.

Пусть (x) и (x) – бесконечно малые при хх_>0> ()

(x) ~ (x) при хх_>0> () если lim (x)/(x)=1 ^{xx0 ()}

(x) и (x) одинакового порядка при хх_>0> () если lim (x)/(x)=с0 ^{xx0 ()}

(x) бесконечно малое более высокого порядка малости чем (x) при хх_>0> () если lim (x)/(x)=0 ^{xx0 ()}

Определение.

Пусть f(x) и g(x) – бесконечно большое при хх_>0> ()

1) f(x) ~ g(x) при хх_>0> () если lim f(x)/g(x)=1 ^{xx0 ()}

2)f (x) и g (x) бесконечно большие одинакового порядка роста, если при хх_>0> () если limf(x)/g(x)=с ^{xx0 ()} <

В частности, если с=1, то они эквивалентны

f (x) бесконечно большое более низкого порядка роста чем g (x) или иначе g(x) бесконечно большое более высокого порядка роста чем g(x) при хх_>0> () если lim f (x)/g (x)=0 ^{xx0 ()}

Примеры:

sin(x) – бесконечно малое

x при хх_>0> – бесконечно малое

Сравним их lim sin(x)/x=1  sin(x)~x

^x0

при х0

1n(1+x) – бесконечно малое

х при х0 – бесконечно малое

Сравним их lim ln(1+x)/x= lim ln(1+x)^1/x =1 

^{x0 x0}

ln(1+x) ~ x, при х0

x² – бесконечно большие

2х²+1, при х+ – бесконечно большие

Сравним lim x²/(2x²+1) = lim x²/x²(2+1/x²)=1/2

^{x+ x+}

то есть функция является бесконечно большой и

одинакового порядка. Замечание: если одну из

функций одинакового порядка роста домножить на

одинаковую const, то они станут эквивалентны.

Определение:

пусть (х)=о(х) – бесконечно малое при хх_>0>(). То мы говорим, что (х) и (х) при хх_>0> (), если (х)=(х)(х), бесконечно малое при хх_>0> (). Другими словами - (х) – бесконечно малое более высокого порядка, чем (х) така как (х)/(х)=(х) – бесконечно малое, то есть lim (x)/(x)=0 ^{x0 ()}

пусть f(х)=оg(х) – бесконечно большое при хх_>0>(). То мы говорим, что f(х) и g (х) при хх_>0> (), если f (х)=(х)g (х). Другими словами - f (х) – бесконечно большое более низкого порядка, чем g(х) так как f(х)/g (х)=(х) – бесконечно малое, то есть lim f (x)/g (x)=0 ^{x0 ()}

Шкала бесконечности.

Степенные бесконечности.

xⁿ=o(x^m), 0<n<m при х+. Из двух степенных бесконечностей сильнее та, у которой показатель степени больше.

Докажем:

xⁿ=x^m(xⁿ/x^m)=x^m(1/x^(m-n))=x^m(x) m-n>0 x^m(x)o(x^m)

Показательные бесконечности.

а^х=о(b^х), 1<a<b при x+. Из двух показательных бесконечностей сильнее та, у которой основание больше.

Докажам

a^x=a^x(b^x/b^x)=a^x(a/b)^x=b^x(xo(b^x) (0<a/b<1)

Логарифмическая бесконечность

ln(x)=o(x^), >0. Логарифмическая бесконечность слабее любой степенной бесконечности.

ln(x)<x x

lim ln(x)/x^=lim [(ln(x)/(x^/2x^/2))((/2)/(/2))]=

^{x0 x0}

lim [(ln(x)/x^/2)(2/(x^/2)]

^x0

Произведение бесконечно малых на ограниченную

равно бесконечно малой.

lim (ln(x)/x^)=0  (lim(x))/x^=(x)  ln=x^(x)ox^,

^x0

x+

Показательная и степенная.

X^k=o(a^x),  k>0,a>1 x+ lim(x^k)/(a^x)=0

^x+

Теорема: Пусть (x) ~ _>1>(x) при xx_>0> ()

(x) ~ _>1>(x) при xx_>0> ()

Тогда lim (x)/(x)=lim _>1>(x)/_>1>(x)

^{xx0 () xx0 ()}

Доказательство:

lim(x)/(x)=lim[(x)_>1>(x)_>1>(x)]/[_>1>(x)_>1>(x)(x)]=lim((x)/(x))lim(_>1>(x)/(x))lim(_>1>(x)/_>1>(x))=lim _>1>(x)/_>1>(x) что

^{x0 x0 x0 x0 x0 x0}

и требовалось доказать. Замечание: аналогичное утверждение справедливо для двух бесконечно больших.

Пример:

lim sin(x)/3x=limx/3x=1/3

^{x0 x0}

Определение: (главного слагаемого)

_>1>(x)+_>2>(x)+…+_>n>(x), при xx_>0> ()

Главным слагаемым в этой сумме называется то слагаемое по сравнению с которым остальные слагаемые являются бесконечно малыми более высокого порядка малости или бесконечно большие более низкого порядка роста.

_>1>(x) – главное слагаемое, если _>2>(х)=о(_>1>(х)),…,_>n>(x)=o(_>1>(x)) при xx_>0> ()

Конечная сумма бесконечно малых эквивалентна своему главному слагаемому:

_>1>(x)+_>2>(x)+…+_>n>(x) ~ _>1>(x) , при xx_>0> () если _>1>(х) – главное слагаемое.

Доказательство:

lim [_>1>(x)+_>2>(x)+…+_>n>(x)]/_>1>(x)=lim[_>1>(x)+_>1>(x)(x)+…+_>1>(x)(x)]/_>1>(x)=lim[_>1>(x)(1+_>1>(x)+…+_>n>(x))]/_>1>(x)=1 ^{xx0 () xx0 () xx0 ()}

Пример:

lim (e^x+3x¹⁰⁰+ln3x)/(2^x+1000x³+10000=lim e^x/2^x=lim e^x/(e^x(x))=+

^{x+ x+ x+}

2^x=o(e^x)e^x(x)

Основные эквивалентности.

e^x-1 – бесконечно малое при х0. lim (e^x-1)/x=1, то есть e^x-1 ~ x при x0

^x0

1-cosx – бесконечно малое при х0. lim (1-cos x)/(x²/2)=lim{2sin(2x/2)]/[x²/2]=lim [2(x/2)²]/[x²/2]=1,

то есть

1-cos(x) ~ x²/2 при х0 и (1+x)^p-1 ~ px при х0

Лекция №8

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 10 октября 2000 г.

Тема: «Асимптотические формулы»

Формулы содержащие символ о - называются асимптотические.

1) lim [sin(x)/x]=1  (по определению конечного предела sin(x)/x=1+(x), где (х) – бесконечно малое при х0

^x0

 sin(x)=x+(x)x, где (х) – бесконечно малое при х0  sin(x)=x+ox, при х0; sin(x)~x, при х0

2) lim [ln(1+x)/x]=1  (по определению конечного предела ln(1+x)/x=1+(x), где (х) – бесконечно малое при

^x0

х0  ln(1+x)=x+(x)x, где (х) – бесконечно малое при х0  ln(1+x)=x+ox, при х0; ln(1+x)~x, при х0

3) lim [(e^x-1)/x]=1  (по определению конечного предела (e^x-1)/x=1+(x), где (х) – бесконечно малое при х0

^x0

 (e^x-1)=x+(x)x, где (х) – бесконечно малое при х0  (e^x-1)=x+ox, при х0; (e^x-1)~x, при х0; e^x=1+x+o(x), при x0

4) lim [(1-cos(x)/(x²/2)]=1  (по определению конечного предела (1-cos(x)/(x²/2)=1+(x), где (х) – бесконечно

^x0

малое при х0  1-cos(x)=(x²/2)+(x)x²/2, где (х) – бесконечно малое при х0  1- cos(x)=(x²/2)+ox²; при х0; 1- cos(x)~x²/2, при х0; cos=1-x²/2+o(x²), при x0

1) lim [((1+x)^p-1)/px]=1  (по определению конечного предела ((1+x)^p-1)/px =1+(x), где (х) – бесконечно

^x0

малое при х0  (1+x)^p-1=px +(x)-p, где (х) – бесконечно малое при х0  (1+x)^p-1=px+ox, при х0; (1+x)^p-1~px, при х0;(1+x)^p=1+p(x)+o(x), при x0

Если f(x)~g(x), при хх_>0> (), то lim[f(x)/g(x)]=1  f(x)/g(x)=1+(x), где (х)–бесконечно малое при хх_>0 >()

^{хх0 ()}

 f(x)=g(x)+(x)g(x) f(x)=g(x)+og(x) при хх_>0> ()

Замечание: не всякие бесконечно малые, бесконечно большие можно сравнить.

Пример:

(x)=xsin(1/x), при х0

(х)=ф=х, при х0

(x)/(x)=sin(1/x)

lim[(x)/(x)]=lim[sin(1/x)] – который в свою очередь не существует.

^{x0 x0}

Эти бесконечно малые несравнимы.

Для удобства формул полагают по определению, что о(1)=(х), при хх_>0> ()

а⁰1 n!=123….n o!

Определение: Пусть y=f(x) определена в О(х_>0>) и  lim f(x)=f(x_>0>): y=f(x) при хх_>0> называется непрерывной в

^хх_>>

точке х_>0> (то есть  ε>0  >0:  xO_>>(x_>0>)  f(x)O_>ε>(f(x_>0>))

Непосредственно из определения предела следуют следуемые теоремы о непрерывных функциях.

Теорема: Пусть f(x), g(x) – непрерывны в точки х_>0>, тогда f(x)+g(x) – непрерывна в точки х_>0>

Доказательство:1) f(x), g(x) определена в О(х_>0>)  f(x)+g(x) определена в О(х_>0>)

2) lim (f(x)+g(x))=limf(x)+limg(x)=f(x)+g(x) что и требовалось доказать

^хх_>> ^хх_>>_> >^хх_>>

Теорема: Пусть f(x), g(x) – непрерывны в точки х_>0>, тогда f(x)g(x) – непрерывна в точки х_>0>

Доказательство:1) f(x), g(x) определена в О(х_>0>)  f(x)g(x) определена в О(х_>0>)

2) lim (f(x)g(x))=limf(x)limg(x)=f(x)g(x) что и требовалось доказать

^хх_>> ^хх_>>_> >^хх_>>

Теорема: Пусть f(x), g(x) – непрерывны в точки х_>0>, тогда f(x)/g(x) – непрерывна в точки х_>0>

Доказательство:1) f(x), g(x) определена в О(х_>0>)  f(x)/g(x) определена в О(х_>0>)

2) lim (f(x)/g(x))=limf(x)/limg(x)=f(x)/g(x) что и требовалось доказать

^хх_>> ^хх_>>_> >^хх_>>

Теорема(об ограниченности непрерывной функции в окрестности точки). Пусть y=f(x) непрерывна в точки х_>0>, тогда она ограниченна в некоторой окрестность этой точки.

Доказательство: limf(x)=f(x_>0>), то есть  ε>0  >0 x: x-x_>0><  f(x)-f(x_>0>)<ε . Предполагается, что  выбрано так, что f(x) определена в соответствующих точках. О_>>(х_>0>)О(х_>0>). Так как это справедливо для любого ε>0, то возьмем ε=1  >0 -1<f(x)-f(x_>0>)<1; xO_>>(x_>0>)O(x_>0>) f(x_>0>)-1<f(x)<1+f(x_>0>)x, то есть В<f(x)<A

xO_>>(x_>0>)O(x_>0>)

Теорема:(о непрерывности сложной функции) Пусть y=f(x) непрерывна в точки х_>0>, а z=g(y) непрерывна в точки y_>0>=f(x_>0>), тогда сложная функция имеет вид z=g(f(x_>0>)) – непрерывна в точки х_>0.>

Доказательство: Зададим  ε>0 в силу непрерывности z=g(y) в точки у_>0>  б>0x: y-y_>0>|<б g(y)-g(x_>0>)<ε

По найденному б>0 в силу непрерывности функции f(x) в точки х_>0>  >0 x: x-x_>0>< f(x)-f(x_>0>)<б

ε>0 >0 x:x-x_>0>< y-y_>0><б  g(y)-g(y_>0>)<ε g(f(x))-g(f(x_>0>)) то есть lim g(f(x))=g(f(x_>0>))

^xx_>>

Замечание: можно переходить к пределу под знаком непрерывной функции limf(x)=limg(y) limf(x)=f(x_>0>)=y_>0 > ^xx_>> ^xx_>> ^xx_>>

Непрерывность некоторых функций.

1) y=c (постоянная) непрерывна в х_>0> R lim c=c. Зададим ε>0 рассмотрим разность f(x)-f(x_>0>)=c-c=0<ε

^xx_>>

 x: x-x_>0>< (>0)!

2) y=x непрерывна в  x_>0>R, то есть lim x=x_>0. >Зададим ε>0 рассмотрим разность f(x)-f(x_>0>)=x-x_>0><ε

^xx_>>

 x: x-x_>0>< (>0)! =ε!

Следствие.

Многочлен p(x)=a_>n>xⁿ+ a_>n>_>-1>x^n-1+…+a_>1>x+a_>0>

(a_>n>,a_>n-1>…a_>1>,a_>0> – зададим число)

n=0,1,2,3…. непрерывен в любой точки х_>0> оси как сумма произведения непрерывной функции. Рациональная функция:

R(x)=p(x)/q(x). Частная двух многочленов непрерывна в любой точки х_>0> в которой q(x)0

Лекция №9

Ведущая: Голубева Зоя Николаевна

Дата: среда, 11 октября 2000 г.

Тема: «Точки разрыва»

1) Доказать, что lim [((1+x)^p-1)/px]=1

^x0

y=(1+x)^p-1

lim [((1+x)^p-1)/px]= x0  y0 =lim ([ln(1+x)]/x)([(1+x)^p-1]/[pln(1+x)]=lim ([ln(1+x)]/x)

^x0 (1+x)^p=y+1 ^{x0 x0}

p[ln(1+x)]=ln(y+1)

lim([(1+x)^p-1]/[pln(1+x)]=lim y/[ln(y+1)]=1 что и требовалось доказать  (1+x)^p-1~px при x0

^{x0 y0} (1+x)^p=1+px+o(x) при х0

2) Доказать, что lim (e^x-1)/x=1

^x0

y=e^x-1

lim (e^x-1)/x= x0  y0 =lim y/[ln(y+1)]=1 что и требовалось доказать 

^x0 e^x=y+1 ^y0

x=ln(y+1)

e^x-1~x при x0

e^x=1+x+o(x) при х0

Классификация точек разрыва функции.

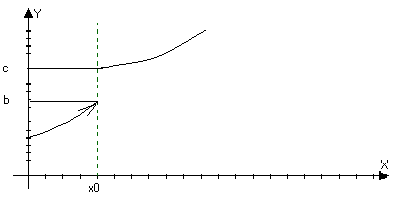
Определение: Пусть y=f(x) определена в О(х_>0>), а в самой точке х_>0> может быть как и определена, так и неопределенна.

1) Точка х_>0> называется точкой разрыва 1^ого рода функции, если

а) Существует lim f(x)’=lim f(x)’’ , но либо функция неопределенна в точки х_>0> либо f(x_>0>)b. Тогда точка х_>0>

^xx_>>^{+0 xx}_>>^-0

точка устранимого разрыва.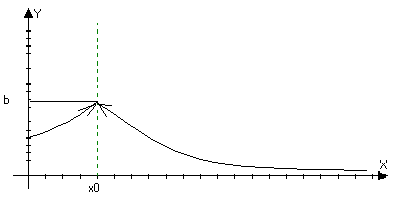

1,x=1

Y=(x-1)/(x-1)=

Не , x=1

б) f(x)=cb

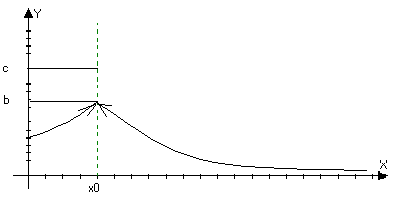
Можно доопределить или переопределить в точке х_>0>, так что она станет непрерывной.

 lim f(x)=b; lim f(x)=c, но bc

^xx_>>^{+0 xx}_>>^-0

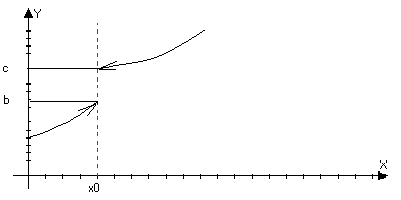
Может быть и определена f(x_>0>)=b

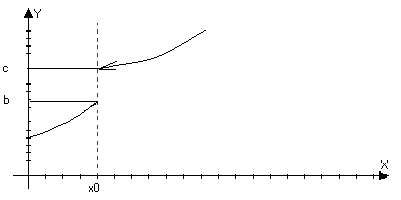
Или f(x_>0>)=d

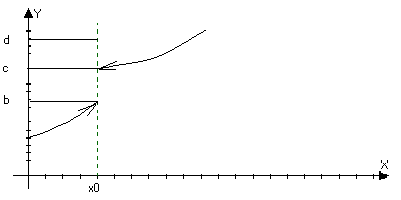
2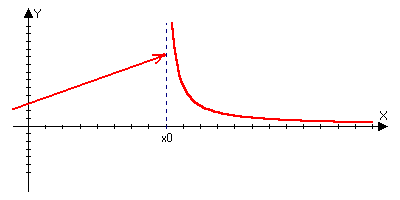)Точка х_>0> называется точкой разрыва 2^ого рода функции если она не является точкой разрыва 1^ого порядка, то есть если хотя бы один из односторонних пределов не существует или равен бесконечности.

y=sin(1/x)

Основные теоремы о непрерывных функциях.

Теорема: Все основные элементы функции непрерывны в любой точки своей области определения.

Определение: (функции непрерывной на отрезке)

y=f(x) – называется непрерывной на отрезке [a,b], если она непрерывна в любой точке х(a,b). В точке х=а функция непрерывна справа, то есть lim f(x)=f(a), а в точке х=b функция непрерывна слева lim f(x)=f(b).

^xx_>>^{+0 xx}_>>^-0

Функция непрерывна на множестве D если она непрерывна в этой точке.

Теорема: (о сохранение знака непрерывной функции)

Пусть y=f(x) непрерывна в точке х_>0> и f(x_>0>)>0 (f(x_>0>)<0), тогда f(x)>0 f(x)<0 непрерывна в некоторой точки О(х_>0>)

Доказательство:  lim f(x)=f(x_>0>) ε>0  >0 x: x-x_>0><  f(x)-f(x_>0>)|<ε.

^xx_>>

Пусть f(x_>0>)>0, выберем ε=f(x_>0>)  f(x)-f(x_>0>)<f(x_>0>) xO_>>(x_>0>) (>0!)

-f(x_>0>)<f(x)-f(x_>0>)<f(x_>0>); f(x)>0 xO_>>(x_>0>), если f(x_>0>)<0, то ε=-f(x_>0>)

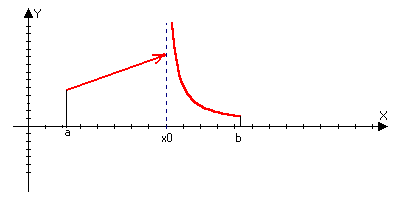
Теорема Коши: ( о нуле непрерывной функции)

Пусть f(x) непрерывна на [a,b] и на концах его принимает значение разных знаков f(a) f(b) <0, тогда  x_>0>(a,b): f(x_>0>)=0

Доказательство:

f(b)>0 f(a)<0

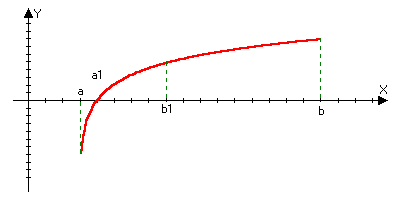
Разделим отрезок [a,b] пополам. Если в середине отрезка f(x)=0, то всё доказано, если нет, то выберем ту половину отрезка, на концах которой функция принимает значение разных знаков. Выбранной отрезок поделим пополам. Если в середине нового отрезка f(x)=0, то всё доказано, если нет, то выберем ту половину от той половины, на концах которой функция принимает значение разных знаков и т.д.

[a,b][a_>1>,b_>1>][a_>2>,b_>2>]

Последовательность левых концов удовлетворяет отношению a<a_>1><a_>2><…<a_>n><…<b

bb_>1>b_>2>…b_>n>…>a 

{a_>n>}-ограниченная не убывающая  lim a_>n>=b f(a)<0 f(a_>n>)<0 n

^x+ [a_>n>b_>n>]=(b-a)/2ⁿ 0 при n

{b_>n>}-ограниченная не возрастающая  lim b_>n>= f(b)>0 f(b_>n>)>0 n

^x+

В силу непрерывности функции lim f(a_>n>)=f (lim b_>n>)=f()0 lim (b_>n>-a_>n>)=-= lim (b-a)/2ⁿ=0=

^{x+ x+ x+ x+}

f()0

 f()=0 x_>0>=

f()=f()0

Условие непрерывности функции нельзя отбросить: f(b)>0; f(a)<0

Теоремы Вейштрасса.

1) Теорема: Пусть функция y=f(x) непрерывна на отрезке [a,b]. Тогда она ограниченна на нём.

Замечание: а) Условие непрерывности нельзя отбросить

Неограниченна сверху  неограниченна

б) Нельзя заменить отрезок на интервал или

полуинтервал.

Непрерывна на (0;1]

2) Теорема: Пусть функция y=f(x) непрерывна на отрезке [a,b]. Среди её значений есть наибольшее и наименьшее.

Замечание: а) Множество [0;1] наибольшее значение 1М

наименьшее значение 0  М

б) Множество (0;1]=М наибольшее значение 1М

нет наименьшего

в) Множество [0;1)=M нет наибольшего

наименьшее значение 0  М

г) Множество (0;1)=М нет ни того не другого.

Условие отрезка нельзя заменить на интервал или полуинтервал.

x(0;1] непрерывна на (0;1] нет наибольшего значения

Л

По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик

van_mo_mail@mtu-net.ru или на сотовый:

8-901-7271056 спросить Ваню

екция №10

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 17 октября 2000 г.

Тема: «Коши, производные»

Теорема: (Коши о промежуточных значениях)

Пусть функция y=f(x) непрерывна на отрезке [a,b] и на концах принимает значение разные значения.

f(a)=A f(b)=B AB. Тогда С лежащею между А и В,  х_>0>(a,b): f(x_>0>)=C. Другими словами нет точек которые не являются значением отрезка.

Доказательство: A<B, C(A,B) (x)=f(x)-C.

Эта функция непрерывна на отрезке [a,b]

(a)=f(a)-c=A-C<0 по теореме Коши №1¹  x_>0>(a,b):(x_>0>), то естьf(x_>0>)-C=0 f(x_>0>)=c

(b)=f(b)-c=B-C>0

Замечание: Условие непрерывности нельзя отбросить

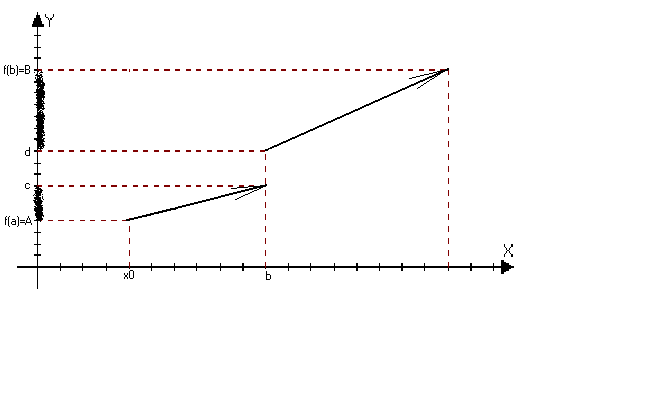
[c,d][A,B]

[c,d)E(f)

Теорема: (о существование и непрерывности обратной функции) «Без доказательства»

П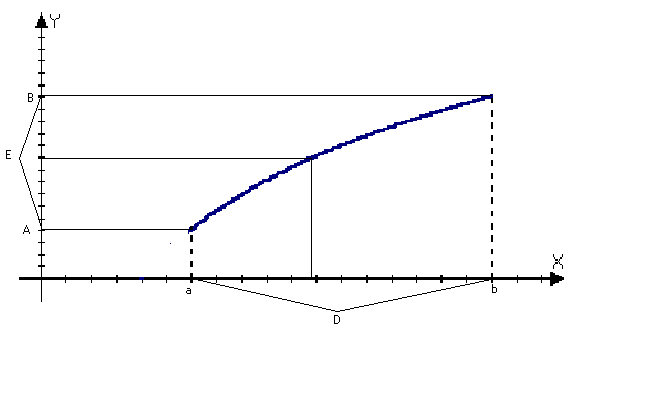усть на множестве D задана непрерывная возрастающая или убывающая функция y=f(x). Тогда на множестве её значений Е определена обратная ей функция x=g(y), которая непрерывна и возрастает или убывает на множестве Е.

Производная функции. ∆Х

Пусть y=f(x) определена в O(x_>0>)

∆x=x-x_>0> – называется приращением аргумента в т х_>0 > Х

^Х_>> ^Х

Разность значений функций.

∆y=∆f(x_>0>)=f(x)-f(x_>0>)=f(x_>0>+∆x)-f(x_>0>) – называется приращением функции в точки х_>0>. Через эти обозначения можно определить непрерывность функций:

f(x) – неопределенна в точки х_>0>, если она определена в O(x_>0>) и lim ∆y=0

^{∆ x0}

lim[f(x)-f(x_>0>)]=lim[f(x)-f(x_>0>)]0 lim[f(x)]=f(x_>0>)]

^x-x_>>^{0 xx}_>> ^xx_>>

Определение непрерывной функции в точки приращения:

f(x) – неопределенна в точки х_>0>, если она определена в O(x_>0>) и lim ∆y=0

^{∆ x0}

Определение: (производной функции)

Пусть y=f(x) определена в О(х_>0>) и  lim[∆y/∆x]<, тогда этот предел называется производной функции f(x) в

^∆х0

точке х_>0>.

Обозначения:

f’(x_>0>), y’(x_>0>), dy/dx, df(x_>0>)/dx=df(x)/d(x)

То есть f’(x_>0>) по определению = lim[f(x)-f(x_>0>)]/(x-x_>0>)lim∆y/∆xdy/dx

^{∆x0 ∆x0}

Физический смысл производной.

Рассмотрим прямолинейное движение материальной точки:

S

x

x_>0 > x

t_>0> t

s(t)x(t); ∆s=∆x(t)=x(t)-x(t_>0>)

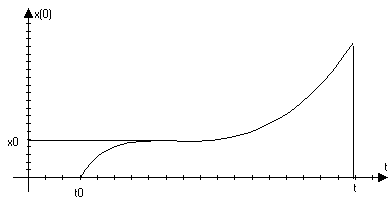∆s/∆t=[x(t)-x(t_>0>)]/[t-t_>0>]=v_>cp>. Если ∆t0

тогда v_>cp>v_>мнг>

lim ∆s/∆t=lim[x(t)-x(t_>0>)]/[t-t_>0>]=v_>мнг>

^{∆t0 tt}_>>

Геометрический смысл производной.

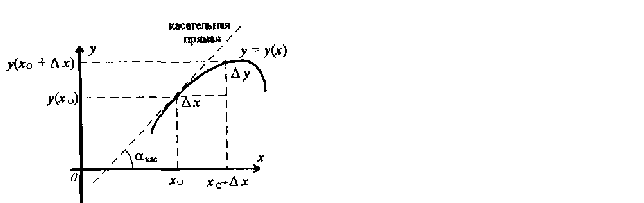y’(x_>0>)=lim∆y/∆x – производная функции у(х) и в точке х_>0>.

^∆х0

∆y=y(x_>0>+∆x)-y(x_>0>)

y’(x_>0>)=tg_>кас> где _>кас> – угол наклона в точке (х_>0>;y(x_>0>)) к оси

Основные теоремы о производной.

Теорема: Пусть  f’(x) и g’(x), тогда  [f(x)+g(x)]’= f’(x)+g’(x)

Доказательство: следует непосредственно из определения производной и свойств предела суммы.

Теорема: (связи между непрерывностью функции и существование производной)

Пусть  f’(x) функция f(x) – непрерывна.

Доказательство: Пусть f(x) определена в О(х_>0>) и lim[f(x)-f(x_>0>)]/(x-x_>0>)=f’(x_>0>)< [f(x)-f(x_>0>)]/(x-x_>0>)=f(x_>0>)+(x-x_>0>)²

^∆xx_>>

[f(x)-f(x_>0>)]=f’(x_>0>)(x-x_>0>)+(x-x_>0>)(x-x_>0>) при хх_>0>

lin[f(x)-f(x_>0>)]=limf’(x_>0>)(x-x_>0>)+lim(x-x_>0>)(x-x_>0>)=0+0=0linf(x)=f(x_>0>) то есть f(x) непрерывна в точки х_>0>

^xx_>>_> >^xx_>>_> >^xx_>>_> >^xx_>>

Замечание: обратное утверждение неверно, из-за непрерывности функции в точке х_>0> не следует существование функции в этой точки.

y=х

Непрерывна в точки х_>0>=0

limx, x0

^x+0

lim|x|= =0

lim(-x), x<0

^x-0

y(0)=0

limy(x)=limy(x)=y(0)=0   limy(x)=y(0)=0  функция непрерывна

^{x+0 x-0 x0}

lim∆y/∆x-не существует, действительно х+0y(x)=x

^x0

lim[y(x)-y(0)]/x=lim(x-0)/x=1

^{x+0 x+0}

x-0y(x)=-x

lim[y(0)-y(x)]/x=lim(0-x)/x=-1 то есть lim∆y/∆x – не существует

^{x-0 x-0 х0}

Теорема: Пусть  u’(x) и v’(x), тогда (uv)’=u’v+v’u

Доказательство: Зададим приращение ∆х в точки_> >х. Рассмотрим: lim[∆(uv)]/∆x=

^∆x0

lim[1/∆x][u(x+∆x)v(x+∆x)-u(x)v(x)]=lim[1/∆x][ u(x+∆x)v(x+∆x)-u(x)v(x+∆x)+u(x)v(x+∆x)-u(x)v(x)=

^{∆x0 ∆x0}

lim[(v(x+∆x))(u(x+∆x)-u(x))]/∆x+lim[(u(x))(v(x+∆x)-v(x))]/∆x=v(x)u’(x)+u(x)v’(x)

^{∆x0 ∆x0}

Теорема: (о произведение частного)

Пусть  u’(x) и v’(x), v’(x)0 в О(х), тогда (u/v)’=[u’v-v’u]/v²

Доказательство: (u/v)’=[u(1/v)]’=[u’(1/v)]+[(1/v)’u]. Функция u(x) и v(x) –непрерывны в точки х_>0>.

lim[∆(1/v)/∆x]=lim[1/∆x][1/(v(x+∆x))-1/v(x)]=lim[[v(x)-v(x-∆x)]/[∆xv(x)x(x+∆x)]]-[v’(x)/v²(x)]

^{∆x0 ∆x0 ∆x0}

(u/v)’=u’(1/v)-(uv)’/v²=[u’v-uv’]/v² что и требовалось доказать

Таблица производных

y=sinx

(sinx)’=lim[sin(x+∆x)-sinx]/∆x=lim[2sin(∆x/2)cos((2x+∆x)/2)]/∆x=lim[2(∆x/2)cos(x+(∆x/2))]/∆x=cosx

^{∆x0 ∆x0}

(sinx)’=cosx

где sin(x)

(sin(x))’=cos(x)

y=cos(x)

(cos(x))’=lim[cos(x+∆x)-cos(x)]/∆x=lim[-2sin(∆x/2)sin((2x+∆x)/2)]/∆x=lim[-2(∆x/2)sin(x+(∆x/2))]/∆x=-sinx

^{∆x0 ∆x0 ∆x0}

(cos(x))’=-sinx

где cosx

(cos(x))’=-sin(x)

y=tg(x)

(tg(x))’=(sin(x)/cos(x))’=[(sin(x))’cos(x)-(cos(x))’sin(x)]/cos²x=[cos²x+sin²x]/cos²x=1/cos²x

(tg(x))’=1/cos²x

где tg(x)

(tg(x))’=1/cos²x

Лекция №11

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 24 октября 2000 г.

Тема: «Производные, дифференциал»

y=xⁿ

y’(x)=lim[(x+∆x)ⁿ-xⁿ]/∆x=¹=lim[xⁿ(1+(∆x/x))-1]/∆x=/∆x/x0,∆x0\=lim[xⁿ(∆x/x)n]/∆x=nx^n-1

^{∆x0 ∆x0 ∆x0}

(xⁿ)’=nx^n-1

^{y=x^3}

_>y’=3x^2>

Рассмотрим когда х=0 y’(0)=lim(∆x)ⁿ/∆x=lim(∆x)^n-1=/n>1\=0 если n=1/0,n>1;1,n=1\

^{∆x0 ∆x0}

Дифференциал функции.

Определение: Пусть y=f(x) определена в некоторой О(х_>0>) – она называется дифференцируемой в точке х_>0>, если её приращение в этой точки представимо в виде:

∆y=∆f(x_>0>)=A∆x+(∆x)∆x)¹

(0)=0 A=const

Определение: линейная ∆х часть приращение дифференцируемой функции называется дифференциалом функции в точке х_>0>:

dy=df(x_>0>)A∆x

Теорема: Если функция дифференцируема в точке х_>0> то A=f’(x_>0>), то она имеет производную в этой точке, то A=f’(x_>0>); наоборот если функция имеет производную в этой точке, то она дифференцируема в этой точке – называется дифференциалом.

Доказательство: Пусть y=f(x) дифференцируема в точке х_>0>, то есть в некоторой О(х_>0>) справедливо равенство ∆f(x_>0>)=A∆x+(∆x)∆x¹; (0)=0. Поделим обе части этого равенства на ∆х и приведём к пределу при ∆х0:

lim(∆f(x_>0>))/∆x=lim(A+(x))=A. Этот предел существует, меньше , тогда по определению этот предел есть

^{∆x0 ∆x0}

производная.

Доказательство: (в обратную сторону) Пусть в точке х_>0>  f’(x_>0>)(<) – это означает, что f(x) определена в некоторой О(х_>0>) и  lim(∆f(x_>0>))/∆x=f’(x_>0>) по определению предела следует, что в некоторой О(х_>0>)

^∆x0

(∆f(x_>0>))/∆x=(∆х)+f’(x_>0>) при ∆х0  ∆f(x_>0>)=f’(x_>0>)+(∆x)∆x, так как lim(∆x)=0, то в точке х_>0> y (∆x) может

^∆х0

быть лишь устранимым разрывом . Устраним его, определим и доопределим:

(0)=0, тогда ∆f(x_>0>)=f’(x_>0>)∆x+(∆x)∆x  A=f’(x_>0>) из установленного соответствия получим выражения для дифференцируемой функции df(x_>0>)=f’(x_>0>)∆x

Следствие: по определению полагают дифференциал независимой переменной равной её приращению

dx=∆x (х - независимая переменная)

df(x)=f’(x)dx

f(x)=x – вычислим дифференциал f’(x)=1 df(x)=dx=f(x)∆x=1∆x

Замечание: дифференциал функции зависит от двух переменных – от самой точки х и от ей приращения

y=cosx x_>0>=/2 ∆x=/180

y’=-sinx y’(/2)=-sin(/2)=-1

dy(/2)=-1∆x=-1/180=-/180

Теорема: Пусть y=f(x) дифференцируема в точке х_>0>, а z=g(y) дифференцируема в точке у_>0>=f(x_>0>), тогда сложная функция z=g(f(x) - дифференцируема в точке х_>0 >и z’(x_>0>)=g’(f)f’(x)

Доказательство: (1) ∆z=g’(y_>0>)∆y+(∆y)∆y

(2) ∆y=f(x_>0>)∆x+(∆x)∆x (0)=0 (0)=0

Подставим в первое равенство второе:

∆z=g’(y_>0>)f(x_>0>)∆x+g’(y_>0>)(∆x)∆x+[f’(x_>0>)+(∆x)∆x][f’(x_>0>)∆x+(∆x0∆x]

lim∆z/∆x=limg’(x_>0>)f’(x_>0>)+limg’(x_>0>)(∆x)+lim (f’(x_>0>)+(∆x)∆x)[f’(x_>0>)+∆x]  z’(x_>0>)=g’(y_>0>)f’(x_>0>) что и требовалось

^{∆x0 ∆x0 ∆x0 ∆x0}

доказать.

Теорема: Пусть функция y=f(x) возрастает (убывает) в О(х_>0>) и дифференцируема в точке х_>0>. Тогда обратная у ней функция x=g(y) дифференцируема в точки y_>0>=f(x_>0>), причём g’(y_>0>)=1/f(x_>0>)

Доказательство: из дифференцируемой функции f(x) в точке х_>0> и из монотонности следует существование обратной функции в точке х_>0> и её непрерывность lim[∆y(y_>0>)]/∆y= ∆y0, то ∆у0  в силу строгой

^∆у0 монотонности функции и обратной =

к ней следует ∆х0

=lim∆x/∆y=lim1 /(∆y/∆x)= в силу непрерывности следует =1/[lim∆y/∆x]=1/[lim∆f(x_>0>)/∆x]=1/f(x_>0>) f(x_>0>)0

^{∆y0 ∆y0} ∆у0, то ∆х0 и наоборот ^{∆x0 ∆x0}

y=a^x

y’(x)=lim[a^x+∆x-a^x]/∆x=lim[a^x(a^∆x-1)]/∆x=lim[a^x(e^∆xlna-1)]/∆x=/∆x0, то ∆xlna0\=lim[a^x∆xlna]/∆x=a^xlna

^{∆x0 ∆x0 ∆x0 ∆x0}

y’=a^xlna, частный случай y=e^x  (e^x)’=e^x

^{y=x^2}

_{>y’=x^2 lnx}>

y=lnx

y’=lim[ln(x+∆x)-lnx]/∆x=lim[ln((x+∆x)/x)]/∆x=lim[ln(1+∆x/x)]/∆x=/∆x/x0 при ∆x0\=lim(∆x/x)/∆x=1/x

^{∆x0 ∆x0 ∆x0 ∆x0}

(lnx)’=1/x

^y=lnx

_>y’=1/x>

y=log_>a>x=lnx/lna (log_>a>x)’=1/xlna

^y=lgx

_{>y’=1/xln10}>

y=arcsinx обратная функция x=siny x[-1;1] y[-/2;/2]

(arcsinx)’_>x=x0>=1/(siny)’_>y0=y>=1/cosy_>y0=y>=

y[-/2;/2], cosy0 cosy>0, если y[-/2;/2] то есть x1

=1/(1-sin²y)_>y=y0>=1/(1-(sinarccosx)²)_>x=x0>=1/(1-x_>0>²)

(arcsinx)’=1/(1-x²)

^y=arcsinx

_>y’=1/>_>>_>(1-x^2)>

y=acrcosx, обратная x=cosy x[-1;1] y[0;]

(arcosx)’=1/(cosy)’_>y=y0>=1/-siny_>y=y0>=-1/(1-cos²y)_>y=y0>=-1/(1-(cosarccosy)²)_>x=x0>=-1/(1-x_>0>²)

(arcosx)’=-1/(1-x²)

^y=arccosx

_>y’=--1/>_>>_>(1-x^2)>

y=arctgx обратная функция x=tgy y(-/2;/2)

(arctgy)’=1/(tgy)’=cos²y= / 1+tg²y=1/cos²y \ =1/(1+x²)

(arctgy)’=1/(1+x²)

(arcctgy)’=-1/(1+x²)

^y=arctgsx

_{>y’=-1/ (1+x^2)}>

^y=arcctgx

_{>y’=--1/ (1+x^2)}>

Гиперболические функции.

chx=(e^x+e^-x)/2

shx=(e^x-e^-x)/2

chx²-shx²=1

chx²+shx²=cH3x

ch(-x)=chx

sh(-x)=-shx

chx shx

^cthx=chx/shx

^thx=shx/chx

(chx)’=sh(x)

(shx)’=ch(x)

(thx)=1

Лекция №12

Ведущая: Голубева Зоя Николаевна

Дата: среда, 25 октября 2000 г.

Тема: «Линеаризация»

Геометрический смысл дифференциала функции и уравнение касательной.

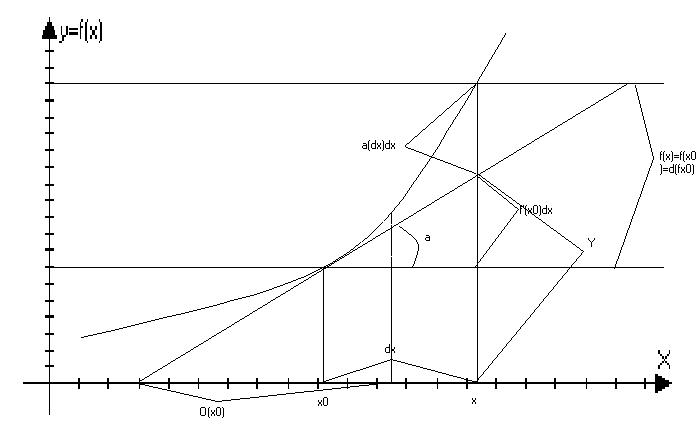
f’(x_>0>)=tg

уравнение прямой : Y=kx+b

y_>0>=f(x_>0>)=kx_>0>+b

k-угловой коэффициент прямой

k=tg=f’(x_>0>)

Y=f(x_>0>)+f(x_>0>)-f’(x_>0>)x_>0>

b=f(x_>0>)-kx_>0>

Y=f(x)+f’(x_>0>)(x-x_>0>)

∆f(x_>0>)=f’(x_>0>)∆x+(∆x)∆x при ∆х0  в некоторой

O(x_>0>) f(x_>0>)=f’(x_>0>)+f’(x_>0>)∆x+(∆x)∆x при ∆х0

Y¹=f(x_>0>)+f’(x_>0>)(x-x_>0>)^a=f’(x_>0>)+f’(x_>0>)∆x

df(x_>0>)=f’(x_>0>)∆x

Геометрический смысл дифференциала:

df(x_>0>) – это приращение ординаты при движение по касательной проведённой к графику функции в точки (х_>0>;f(x_>0>).

Замечание: Часто говорят о касательной проведённой в точке х_>0>.

Линеаризация функции.

Определение: Замена функции в окрестности данной точки линейной функции называется линеаризацией функции, точнее в О(х_>0>) заменяется отрезком касательной в точке х_>0>.

(*) f(x)-Y=(∆x)∆x-o(∆x)

Если в равенстве (*) отбросить правую часть, то мы

получим приближённое равенство:

f(x)f(x_>0>)+f’(x_>0>)(x-x_>0>), xx_>0>

Y=f(x_>0>)+f’(x_>0>)(x-x_>0>) – уравнение касательной в точке х_>0>

Формула получена из определения дифференциала в точке х_>0> функции

f(x)=f(x_>0>)+f(x_>0>)∆x+o∆x при ∆х0 – называется критерием дифференциальности функции в точке х_>0>.

Приближенные вычисления и оценка погрешности вычисления.

Можно приближенно вычислять значение функции в точках близких к заданной точки.

³8,001=1

х_>0>=8

х=8,000

f(x)=³x

f(x_>0>)=f(8)=2

Проведём линеаризацию выбранного корня.

f’(x)_>х=8>=(³x)’_>x>_>=8>=1/3x^-2/3_>x>_>=8>=1/12

³x2+1/12(x-8), x8

³x2+0,001/12

Y_>кас>=2+1/12(x-8)

³x=2+1/12(x-8)+o(x-8) при х8

Погрешности вычисления.

f(x)-f(x_>0>)=df(x_>0>)+o(x-x_>0>) при хх_>0>

∆f(x_>0>)df(x_>0>), xx_>0>

∆¹=∆f(x_>0>)df(x_>0>)

f(x)=10^x в точке х_>0>=4, если ∆х=0,001 х=40,001

10⁴∆=10⁴23

f’(x)=10^xln10; f’(4)=10⁴ln10=23000; ln102,2

∆230000,001=23

Изучение поведения функции при помощи первой производной.

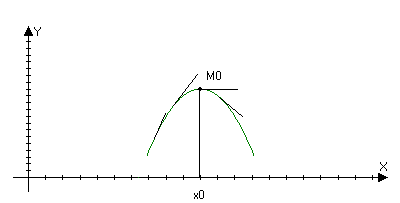
Слева от М_>0> tg >0; Справа от М_>0> tg <0

tg f’(x)>0 слева от М_>0>

tg f’(x)<0 справа от М_>0>

Теорема: Пусть y=f(x) дифференцируема  x(a,b) и f’(x)>0 (f’(x)<0), тогда f(x) возрастает (убывает) на (а,b)

_> > _>a>( |_>x1> |_>x2> )_>b>

x_>1>,x_>2>(a,b) x_>1><x_>2>

Надо доказать: f(x_>1>)<f(x_>2>)

Применим теорему Лангранджа на отрезке (х_>1>,x_>2>)^{Теорема}.

f(x_>2>)-f(x_>1>)=f’(c)(x_>2>-x_>1>) где c(x_>1>,x_>2>)

f(x_>2>)-f(x_>1>)>0  f(x_>2>)>f(x_>1>)

Экстремумы функции.

М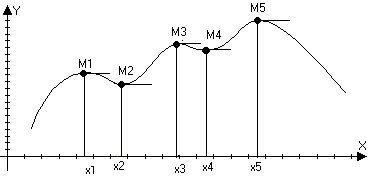ожно указать О(х_>1>) в которой все значения функции

f(x)<f(x_>1>) b и О_>>_>1>(х_>1>) анологично для точки х_>2>

f(x)>f(x_>1>) b и О_>>_>2>(х_>1>). Значенгие функции в точке М_>1>, М_>3> и М_>5 >–

max; M_>2> и М_>4> – min – такие точки назавыются точкками

экстремума или точками локального max и min.

Определение: (точки экстремума)

Пусть функия f(x) определена в некоторой О(х_>0>) и f(x)>f(x_>0>) в

О(х_>0>) или f(x)<f(x_>0>) в этом случае точка х_>0> – называется точкой локального max (min).

Замечание:

f(x)f(x_>1>) в О_>>_>1>(х_>1>)

f(x)f(x_>2>) в О_>>_>2>(х_>2>)

говорят, что точки х_>1> и х_>2 >точки не строгого локального

экстремума.

Теорема: (Ферма) (о необходимости условия экстремума дифференцируемой функции)

Пусть y=f(x) дифференцируема в точки х_>0> и точка х_>0> – точка экстремума, тогда f(x_>0>)=0

Доказательсто: Заметим, что х_>0> точка экстремума, то в её окрестности f(x) – f(x_>0>) сохраняет знак. Запишем условие ∆f(x_>0>)=f(x)-f(x_>0>)(x-x_>0>)+o(x-x_>0>)

f(x)-f(x_>0>)=(x-x_>0>)[f(x_>0>)+(x-x_>0>)] то при х – достаточно близких к х_>0> знак выражения стоящего в квадратных скобках совпадает со знаком f’(x_>0>)0 (x-x_>0>) – меняет знак при переходе черех точку х_>0>  f’(x_>0>)=0

Лекция №13

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 31 октября 2000 г.

Тема: «Экстремумы»

Замечание:

Обратное утверждение неверно. Из-за того, что произведение в данной точки равно нулю, не следует, что это экстремум.

y=(x-1)³

y’=3(x-1)²

y’(1)=0

x_>0>=1

xO^-_>>(1)f(x)<0

xO⁺_>>(1)f(x)<0

x=1 – не точка экстремума.

Теорема (Ролля):

Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b). Кроме того на концах интервала она принемает равные значения f(a)=f(b), тогда  с(a,b): f(c)=0

Доказательство: Така как функция непрерывна на отрезке [a,b], то по второй теореме Вейштрасса есть наибольшее и наименьшее значение (m,M), если m=M, то f(x)const (x[a,b]) (const)’=0.

Пусть m<M, тогда либо m, либо М отлична от значений на концах отрезка. Пусть например Mf(a): c(a,b):f(c)=M, то есть точка с точка экстремума максимума следовательно по теореме Ферма f’(c)=0

Замечание: условие дифференцируемсти нельзя отбросить.

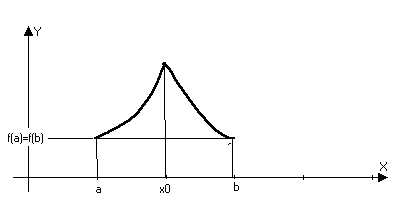
непрерывна на отрезке [a,b]

Геометрический смысл.

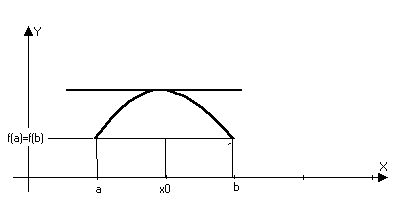
f’(x)=0, то касательная  оси х. Теорема не утверждает, что это единственная точка.

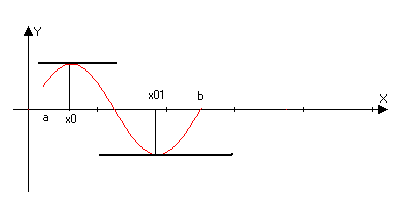
Теорема Лангранджа:

Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на отрезке (а,b), то  с(a,b): f(b)-f(a)=f(c)(b-a)

Доказательство:

F(x)=f(x)+x где  - пока неизвестное число.

F(x) – непрерывна на отрезке [a,b] как сумма непрерывной функции

f(x) – дифференцируема на отрезке [a,b] как сумма дифференцируемой функции.

Выберем число , так чтобы на отрезке [a,b] F(x) принимало равное значение.

F(a)=f(a)+a

F(b)=f(b)+b

F(a)=F(b)  f(a)-f(b)=(a-b)  =[f(b)-f(a)]/[b-a]

F(x) – удовлетворяет условию теоремы Роллера на отрезке [a,b]   c(a,b):F’(c)=0, то есть F’(x)=f’(x)+

0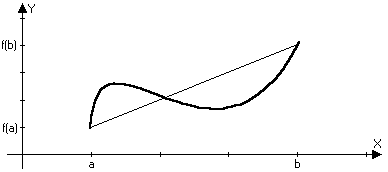=f’(c)+  f’(c)=-=[f(b)-f(a)]/[b-a]

То есть на кривой которая наклонена

к оси х под таким же углом как и секущая

[f(b)-f(a)]/[b-a]=tg=f(x)  c(a,b)

Замечание:

Часто точку с можно представить в

нужном виде:

с=х_>0>+∆х

0<(c-x_>0>)/(x-x_>0>)= <1

c-x_>0>=(x-x_>0>)

c=x_>0>+(x-x_>0>)¹

f(x)-f(x_>0>)=f’(x_>0>+∆x)(x-x_>0>)

0<<1

∆f(x_>0>)=f’(x_>0>+∆x)∆x

Теорема: (о необходимых и достаточных условиях экстремума по первой производной)

Пусть y=f(x) непрерывна на отрезке [a,b] и дифференцируема в О(х_>0>). Если f’(x) меняет знак при переходе через точку х_>0>, то точка х_>0> – точка экстремума. Если меняет знак:

с + на – то это точка максимума

с – на + то это точка минимума

Доказательство:  х_>1>  О^-(х_>0>) на [x_>1>,x_>0>];  c_>1>(x_>1>,x_>0>) f(x_>0>)-f(x_>1>)=f’(c_>1>)(x_>0>-x_>1>)  f(x_>0>)>f(x_>1>) x_>1>O^-(x_>0>)

 х_>2>  О⁺(х_>0>) на [x_>0>,x_>2>];  c_>2>(x_>0>,x_>2>) f(x_>2>)-f(x_>0>)=f’(c_>2>)(x_>2>-x_>0>)  f(x_>2>)<f(x_>0>) x_>2>O⁺(x_>0>)

f(x_>0>)>f(x) xO(x_>0>)  точка х точка максимума.

Если в точке х_>0> существует производная то она обязательно равна 0 в силе теоремы Ферма. Но могут быть точки в которых f(x) существует, а f’(x) не существует.

Принцип решения подобных задач:

Условие: найти наибольшее и наименьшее значение функции не отрезке [a,b].

Ход решения:

Находим точки в которых производная либо равна 0 либо не существует f’(x)=0 или f’(x)  x_>1>, x_>n>

Вычисляем знак функции на концах отрезка и в этих точках f(a), f(b), f(x_>1>)….f(x_>n>)

Выбираем наибольшее и наименьшее mf(x)<M

Определение: точки в которых функция определена, а производная либо равняется нулю, либо не существует называют критическими точками.

Производная функции высшего порядка.

Существует f’(x)  x(a,b), тогда эта производная сама является функцией х (х)=f’(x) и можно ставить о дифференцируемости этой функции.

Существует ’(x)  x(a,b), то мы называем её второй производной ’(x)f’’(x)

Лекция №14

Ведущая: Голубева Зоя Николаевна

Дата: среда, 8 ноября 2000 г.

Тема: Производная функции высшего порядка.

f⁽ⁿ⁾=^def=(f^(n-1)(x))’

’’’ – [dⁿf(x)]/dxⁿ=(d/dx)([d^n-1f(x)]/dxⁿ)

Теорема: (Коши – обобщение теоремы Лангранджа¹)

Пусть функция f(x) и g(x) непрерывны на отрезке [a,b], дифференцируема на интервале (a,b) и g’(x)0, x(a,b), тогда  с  (a,b) такая, что [f(b)-f(a)]/[g(b)-g(a)]=f’’(c)/g’(c)

Доказательство: Отметим прежде всего, что g(b)g(a), так как по теореме Лангранджа¹ для функции g(x)

g(b)-g(a)=g’(c_>1>)^II (b-a)^III0 (c_>1>(a,b)) Рассмотрим вспомогательную функцию

F(x)=f(x)-g(X) где  -неизвестное число

F(x) – непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b)

Потребуем F(a)=f(b)

F(b)=f(b)-g(b)

---

F(a)=f(a)-g(a)

___________________

0=f(b)-f(a)-(g(b)-g(a)) =[f(b)-f(a)]/[g(b)-g(a)]. Получим, что F(x) удовлетворяет условию теоремы Ролля⁴

с(a,b):F’(c)=0, то есть F’(c)=f’(c)-g’(c)  =f’(c)/g’(c)=[f(b)-f(a)]/[g(b)-g(a)], что и требовалось доказать.

Правила Лопиталя.

Это правило в случае дифференцируемости функции позволяет избавляться от неопределённостей типа 0/0 или / при вычисление пределов.

Теорема: Пусть функции f(x) и g(x) дифференцируемы в О(х_>0>), g’(x_>0>)0 в О(х_>0>), f(x_>0>)=g(x_>0>)=0 и 

lim f’(x)/g’(x)=k (конечный или бесконечный предел), тогда  lim f(x)/g(x)=lim f’(x)/g’(x)=k

^xx_>>_> >^xx_>>_> >^xx_>>

Доказательство: lim f(x)/g(x)=lim [f(x)-f(x_>0>)]/g(x)-g(x_>0>)=lim f’(c(x))/g’(c(x))= c=c(x) лежащая между х их_>0> если

^xx_>>_> > ^xx_>>_> > ^xx_>>

хх_>0> то сх_>0>=lim f’(x)/g’(x)=k

^xx_>>

Замечание(1): f(x_>0>)=g(x_>0>)=0 требование можно заменить требованием lim f(x)=0, lim g(x)=0, то есть в т х_>0> f(x) и

^xx_>>_> > ^xx_>>

g(x) могут иметь устранимый разрыв, действительно достаточно переопределить или доопределить f(x) и g(x) по непрерывности, так чтобы f(x_>0>)=g(x_>0>)=0

Замечание(2): Если  f’(x_>0>) и g’(x_>0>), g’(x_>0>)0, то утверждение теоремы будет:

lim f(x)/g(x)=lim f’(x)/g’(x)=lim [(x-x_>0>)(f’(x_>0>)+(x-x_>0>))]/ [(x-x_>0>)(g’(x_>0>)+ (x-x_>0>))]=f’(x_>0>)/g’(x_>0>)

^xx_>>_> > ^xx_>>_> > ^xx_>>

Теорема: (/) Пусть функции f(x) и g(x) непрерывны в О(х_>0>), g'(x)0 и О(х_>0>), дифференцируемы в О(х_>0>) и

lim f(x)=lim g(x)=;  lim f’(x)/g’(x)=k. Тогда lim f(x)/g(x)=lim f’(x)/g’(x)=k

^xx_>>_> >^xx_>>_> > ^xx_>>_> > ^xx_>>_> > ^xx_>>_> >

Без доказательства!

Замечание: Если функции f’(x) и g’(x) сами удовлетворяют условия теоремы то правило Лопиталя можно применить повторно:

f(x)=e^x g(x)=xⁿ x

lim e^x/xⁿ= lim e^x/1!= nN lim e^x/xⁿ= lim e^x/nx^n-1_>=> lim e^x/[n(n-1)x^n-2]=lim e^x/n!=+

^x+_> >^x+_> > ^x+_> > ^x+_> > ^x+_> > ^x+_> >

f(x)=lnx

x+

g(x)=xⁿ

lim lnx/xⁿ= lim (1/x)/nx^n-1= lim 1/nxⁿ=0

^x+_> > ^x+_> > ^x+_> >

Формулы Тейлора.

Определение: (многочлена Тейлора) Пусть функция y=f(x) – n – раз дифференцируема в точке х_>0> многочлен (полином) вида

T_>n>(х)=f(x_>0>)+[f’(x_>0>)(x-x_>0>)]/1!+ [f’’(x_>0>)(x-x_>0>)²]/2!+ [fⁿ(x_>0>)(x-x_>0>)]/n! называется многочлен Тейлора с центром в точке х_>0> или многочленом по степеням (х-х_>0>)

Свойства многочлена Тейлора.

Теорема: (основное свойство многочлена Тейлора) Пусть функция y=f(x) – n – раз дифференцируема в точке х_>0> f(x)=T_>n>(x_>0>); f’(x_>0>)=T_>n>’(x_>0>),…,f⁽ⁿ⁾(x_>0>)=T_>n>⁽ⁿ⁾(x_>0>)

Доказательство; (подстановкой) T_>n>(х)=f(x_>0>)+[f’(x_>0>)(x-x_>0>)]/1!+ [f’’(x_>0>)(x-x_>0>)²]/2!+ [fⁿ(x_>0>)(x-x_>0>)]/n! , подставим х_>0> получим T_>n>(x_>0>)=f(x_>0>). Продифференцируем многочлен Тейлора

T_>n>’(x)=f’(x_>0>)/1!+[f’’(x_>0>)2(x-x_>0>)]/2!+ [f’’’(x_>0>)3(x-x_>0>)²]/3!+ [fⁿ(x_>0>)n(x-x_>0>)^n-1]/n!, подставим вместо х х_>0>

T_>n>(x_>0>)=f(x_>0>)

T_>n>’’(x)=f’’(x_>0>)/1!+[f’’’(x_>0>)32(x-x_>0>)]/3!+…+ [f⁽ⁿ⁾(x_>0>)n(n-1)(x-x_>0>)^n-2]/n!

T_>n>’’(x)=f’’(x_>0>)

Формула Тейлора с остаточным членом пеано.

Теорема: Пусть функция y=f(x) – n – раз дифференцируема в точке х_>0>, тогда в О(х_>0>) f(x)=T_>n>(x)+o((x-x_>0>)ⁿ), xx_>0>

f(x)= f(x_>0>)+[f’(x_>0>)(x-x_>0>)]/1!+ [f’’(x_>0>)(x-x_>0>)²]/2!+ [fⁿ(x_>0>)(x-x_>0>)ⁿ]/n!+0((x-x_>0>)ⁿ)(x-x_>0>)¹

lim[f(x)-T_>n>(x)]/(x-x_>0>)ⁿ=(0/0)=lim [f’(x)-T_>n>’(x)]/n(x-x_>0>)^n-1=(0/0)=….=lim [f⁽ⁿ⁾(x)-T_>n>⁽ⁿ⁾(x)]/n!=0  функция

^xx_>>_> >^xx_>>_> > ^xx_>>

[f(x)-T_>n>(x)]/(x-x_>0>)ⁿ=(х-х_>0>)ⁱⁱ  f(x)-T_>n>(x)=(x-x_>0>)ⁿ(x-x_>0>)=0((x-x_>0>)ⁿ) при хх_>0> что и требовалось доказать.

Замечание: в случае если х_>0>=0 формула Тейлора называется Маклорена f(x)=f(0)+[f’(0)x]/1!+ [f’’(0)x²]/2!+ [fⁿ(0)xⁿ]/n!+0xⁿ при х0

1 На концах отрезка [a,b] и на концах принимает значение разных знаков

2 (x-x_>0>)-бесконечно малое при хх_>0>

1 x0

1 (∆x) – бесконечно малое при ∆х0, а (∆x)∆х – есть о∆х

1 Y – ордината касательной

a – x-x_>0> =∆x

1 ∆-погрешность вычисления.

Т^еорема –Если f(x) непрерывна на [a,b] дифференцируема на отрезке (а,b), то  с(a,b): f(b)-f(a)=f(c)(b-a)

1 (x-x_>0>)=∆x

1 Теорема – Если f(x) непрерывна на [a,b] дифференцируема на отрезке (а,b), то  с(a,b): f(b)-f(a)=f(c)(b-a)

I^I – g’(c_>1>)=0 по условия теоремы

I^II – (b-a)=0

4 - Теорема (Ролля): Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b). Кроме того на концах интервала она принемает равные значения f(a)=f(b), тогда  с(a,b): f(c)=0

1 0((x-x_>0>)ⁿ)(x-x_>0>) – остаточный член в форме пеано

iⁱ (х-х_>0>) – бесконечно малое при хх_>0>

Л

По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик

van_mo_mail@mtu-net.ru или на сотовый:

8-901-7271056 спросить Ваню

екция №15

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 14 ноября 2000 г.

Тема: Пять основных разложений

1)y=e^x, x_>0>=0

y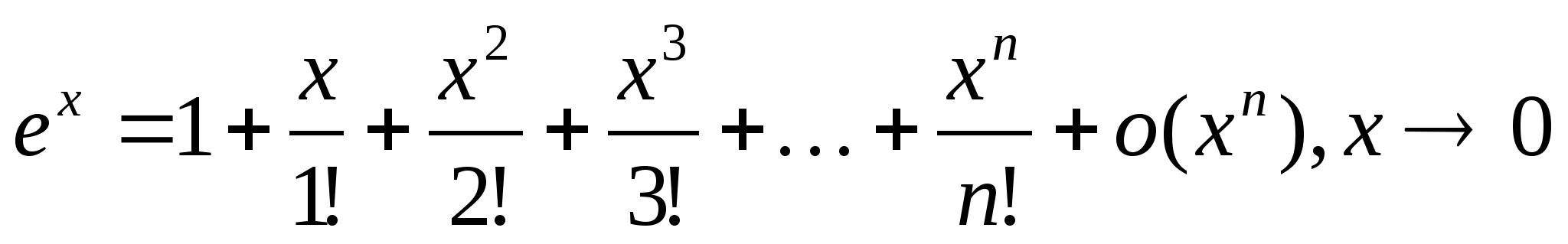(0)=1

y’(0)=e^x|_>x=0>=1

y’’(0)=e^x|_>x=0>=1

y⁽ⁿ⁾(0)=e^x|_>x=0>=1

n=1 e^x=1+x+o(x),xx_>0>

2) y=sinx, x_>0>=0

y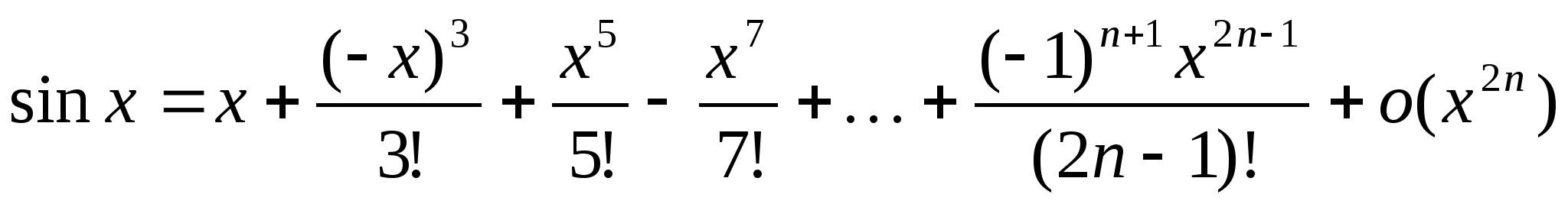(0)=0

y’(0)=cos|_>x=0>=1

y’’(0)=-sinx|_>x=0>=0

y’’’(0)=-cosx|_>x=0>=-1

y’’’’(0)=sinx|_>x=0>=0

если n – чётное, то y⁽ⁿ⁾(0)=0; n=2k+1 – нечётное y⁽ⁿ⁾(0)=(-1)^k

3) y=cosx, x_>0>=0

y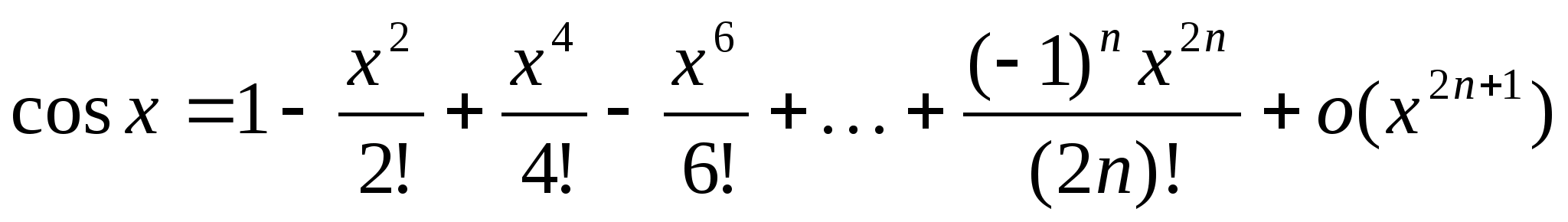(0)=1

y’(0)=-sinx|_>x=0>=0 ^*

y’’(0)=-cosx|_>x=0>=-1

y’’’(0)=sinx|_>x=0>=0

y’’’’(0)=cosx|_>x=0>=1

если n=2k – чётное, то y⁽ⁿ⁾(0)=(-1)^k; n=2k+1 – нечётное y⁽ⁿ⁾(0)=0

4) y=ln(1+x), x_>0>=0

y(0)=ln1=0

y’(0)=1/(1+x)|_>x=0>=1

y’’(0)=1(-1)/(x+1)²_>x=0>=-1

y’’’(0)=(-1)(-2)/(x+1)³_>x=0>=(-1)(-2)

y’’’’(0)= (-1)(-2)(-3)/(x+1)⁴_>x=0>=(-1)(-2)(-3)

y⁽ⁿ⁾=[(-1)(-2)(-3)…(-n+1)]/(1+x)ⁿ_>x=0>=(-1)^n-1123…(n-1)=(-1)^n-1(n-1)!

5) y=(1+x)^p, x_>0>=0

y(0)=1

y’(0)=p(1+x)^p-1|_>x=0>=p

y’’(0)= p(p-1)(1+x)^p-2_>x=0>=p(p-1)

y’’’(0)= p(p-1)(p-2)(1+x)^p-3_>x=0>=p(p-1)(p-2)

y⁽ⁿ⁾=p(p-1)(p-2)…(p-n+1)(1+x)^p-n_>x=0>=p(p-1)(p-2)…(p-n+1)

Если р – натуральное, то y⁽ⁿ⁾(0)=0 np+1

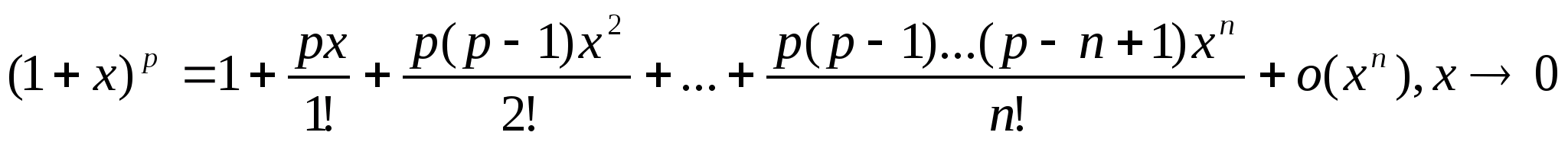
(либо n<p, если p-натуральное)

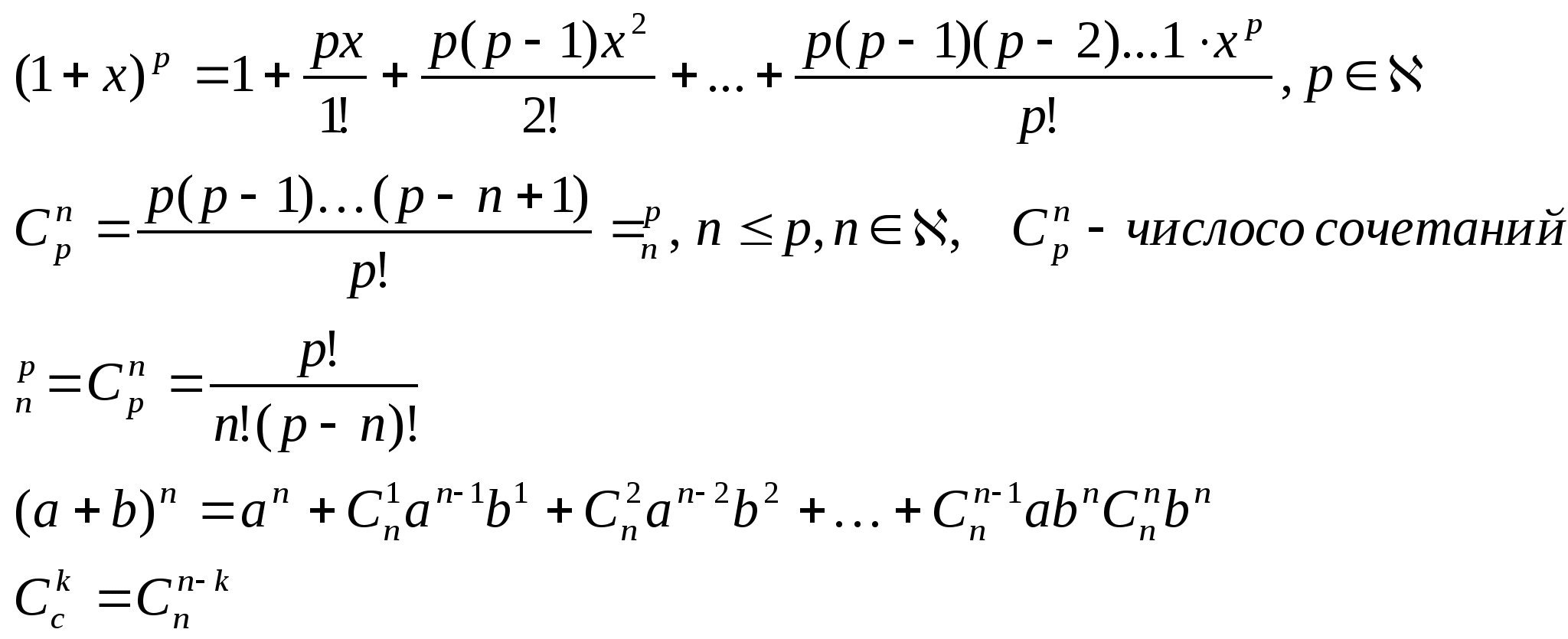
Формула Тейлора с остаточным членом в форме Лангранджа.

Теорема: Пусть функция y=f(x) – n+1 раз дифференцируема в О(х_>0>), тогда в некоторой О_>ε>(х_>0>)

^#

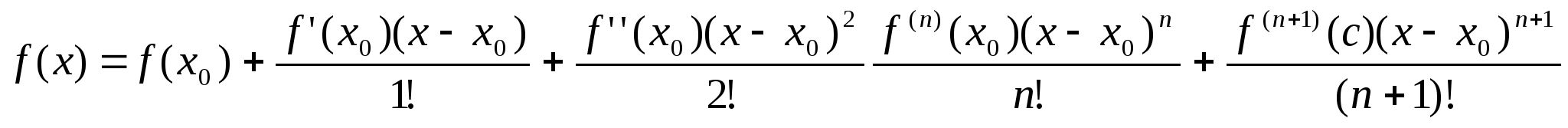где с лежит между х и x_>n>

Доказательство: Применим теорему Коши о двух функциях к следующим функциям

(x)=f(x)-T_>n>(x)^$

g(x)=(x-x_>0>)ⁿ⁺¹

(x_>0>)=0; ’(x_>0>)=0,…,⁽ⁿ⁾(x_>0>)=0; ⁽ⁿ⁺¹⁾(x)=f⁽ⁿ⁺¹⁾(x)

g’(x_>0>)=(n+1)(x-x_>0>)ⁿ_>x=0>=0; g⁽ⁿ⁺¹⁾(x)=(n+1)!

[a,b](x);(a,b)g(x);g’(x)0

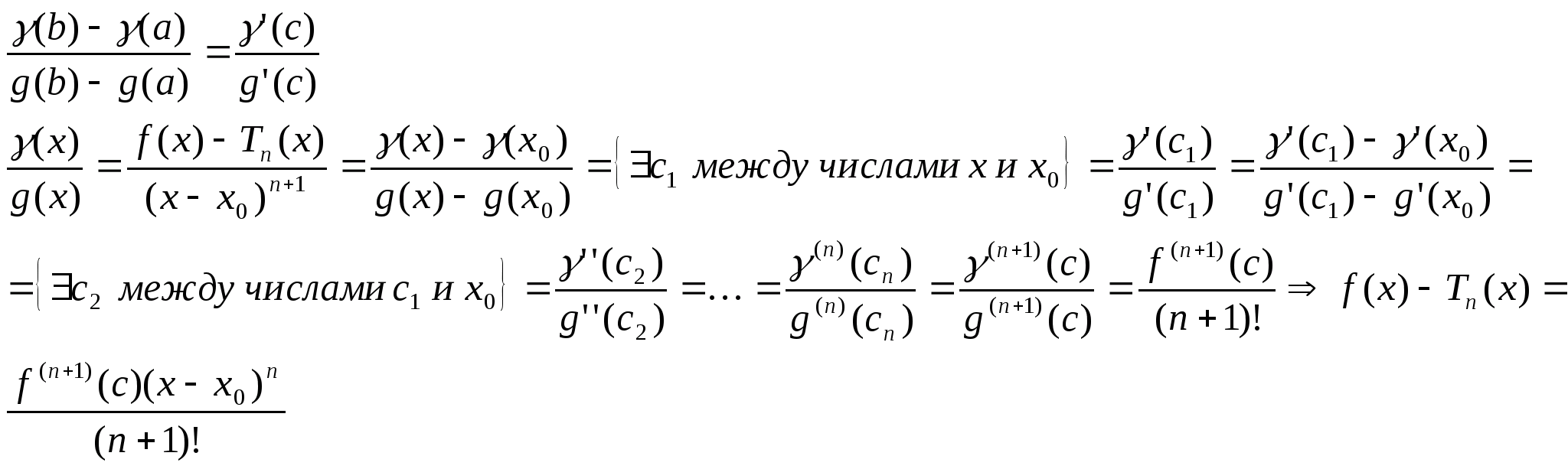
Лекция №16

Ведущая: Голубева Зоя Николаевна

Дата: вторник, 21 ноября 2000 г.

Тема: Применение формулы Тейлора с остаточным членом в форме Лангранджа, Выпуклость, Вогнутость.

Применение формулы Тейлора с остаточным членом в форме Лангранджа.

Пусть функция f(x) – два раза дифференцируема в О(х_>0>), тогда

f(x)=f(x_>0>)+f’(x_>0>)(x-x_>0>)+[f’’(c)(x-x_>0>)²]/2 где с лежит между х и х_>0>

уравнение касательной

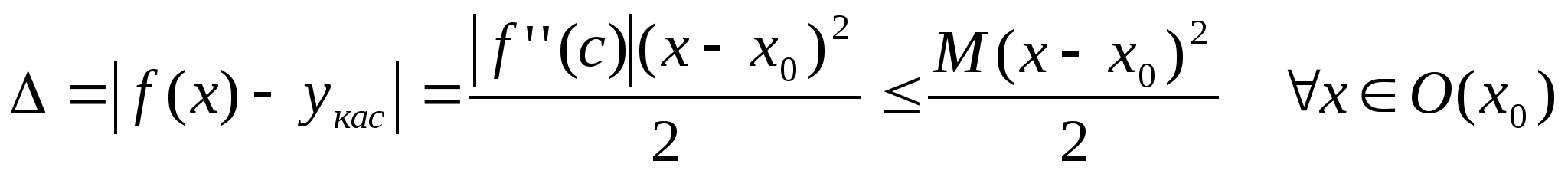
Если f’’(x)M xO(x_>0>)

f(x)-n+1 – дифференцируема в О(х_>0>)

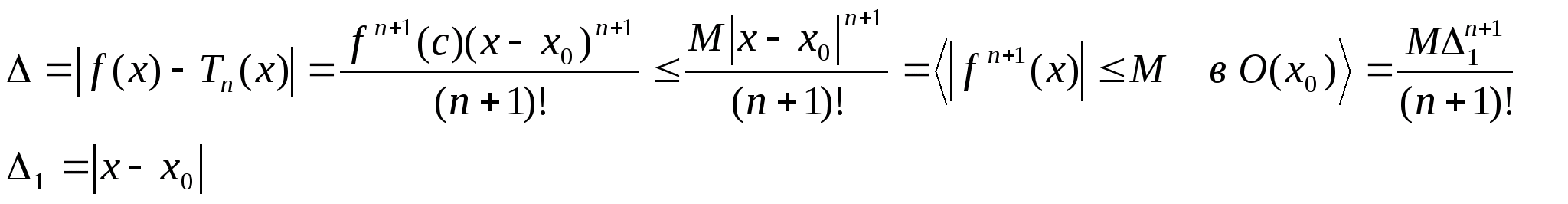
f(x)=T_>n>(x)+R_>n>(x)^ в О(х_>0>)

n=1

T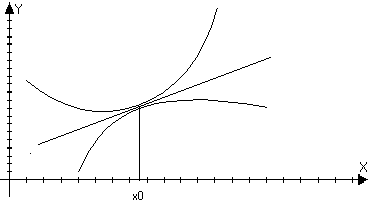_>1>(x) – линейная функция

n=2

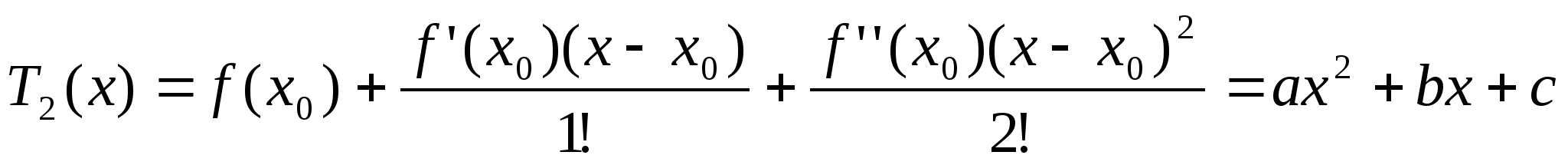
- график парабола

f(x)-T_>1>(x)=f’(x_>0>)x-x_>0>

f(x)-T_>2>(x)=[f’’(x_>0>)x-x_>0>²]/2

T_>3>(x)=ax³+bx²+cx+d – график кубическая парабола

Выпуклость и вогнутость.

Определение: Пусть функция f(x) – дифференцируема в

точке х_>0>, то она называется выпуклой (вогнутой) в верх

в точке х_>0>, если f(x)-y_>кас><0 в О(х_>0>)

Определение: Пусть функция f(x) – дифференцируема в

точке х_>0>, то она называется выпуклой (вогнутой) вниз в

точке х_>0>, если f(x)-y_>кас>>0 в О(х_>0>)

Определение: Пусть функция f(x) – дифференцируема в

точке х_>0>, то она называется выпуклой (вогнутой) в верх

(вниз) на интервале (a,b), если она выпукла в верх (вниз)

в каждой точке этого интервала.

Определение: (точки перегиба) Пусть функция f(x) диф-

ференцируема в О(х_>0>) и непрерывна в О(х_>0>). Точка х_>0> –

называется точкой перегиба графика f(x), если при пере-

ходе через точку меняется знак выпуклости.

Теорема: (о достаточном условии выпуклости функции).

Пусть функция f(x) дважды дифференцируема в точке х_>0> и f’’(x_>0>)<0 (f’’(x_>0>)>0), тогда f(x) – выпукла вверх (вниз) в тоске х_>0>.

Доказательство: Напишем формулу Тейлора с остаточным членом в форме пеано:

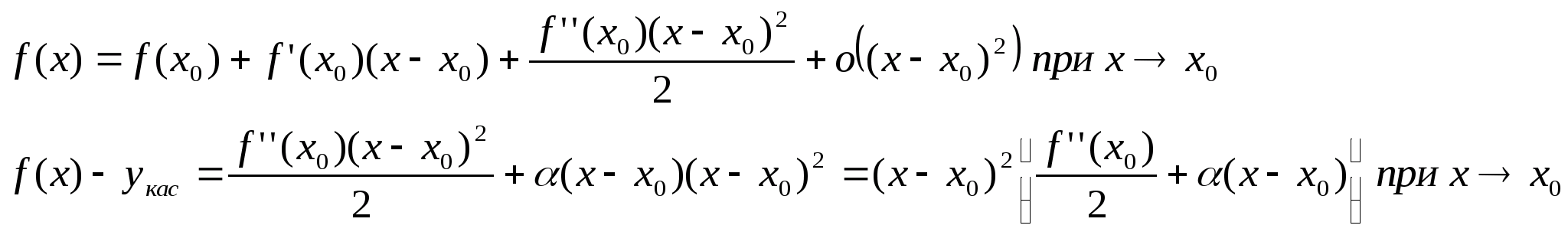
Если х близко к х_>0>, то знак квадрата скобки определяется знаком f(x_>0>). Если f’’(x_>0>)<0, то f(x)-y_>кас>>0 в О(х_>0>).

Если f’’(x_>0>)>0, то f(x)-y_>кас>>0 в О(х_>0>)

Теорема: Путь функция f(x) непрерывна в О(х_>0>) и дважды дифференцируема в О(х_>0>), причём f’(x) меняет знак при переходе через точку х_>0>, тогда точка х_>0> – точка перегиба.

Доказательство:

f’’(x) - +

^{(  ) x}

x_>0>

f’’(x)<0 в O^-(x_>0>) f(x) – выпукла вверх в О^-(х_>0>)

f’’(x)>0 в O⁺(x_>0>) f(x) – выпукла вниз в О⁺(х_>0>)

Следствие: Если f(x) дважды дифференцируемы в точке х_>0>. Если точке х_>0> точка перегиба, то f’’(x_>0>)=0

Путь точка х_>0> точка перегиба и существует f’’(x_>0>)>0, тогда

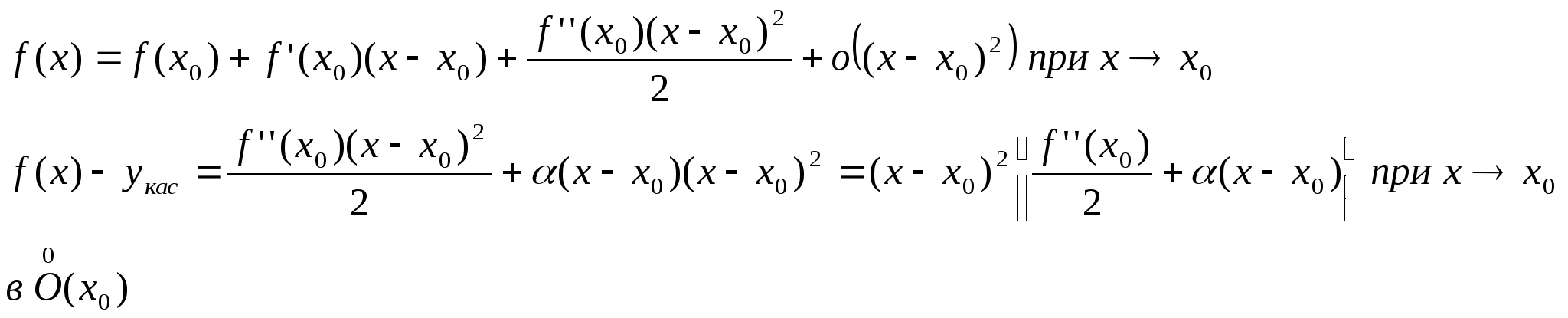
то есть при переходе через точку х_>0> левая часть равенства f(x)-y_>кас> не меняет знак. Аналогично получаем для f(x)>0 f’’(x_>0>)=0

Замечание: Условие равенства f’’(x_>0>)=0 необходимо, но недостаточно.

Теорема: (о достаточном условие экстремума по второй производной)

Пусть функция f(x) дважды дифференцируема в точке х_>0>, тогда точка х_>0> точка максимума если f’’<0, точка х_>0> точка минимума если f’’(x_>0>)>0.

Доказательство:

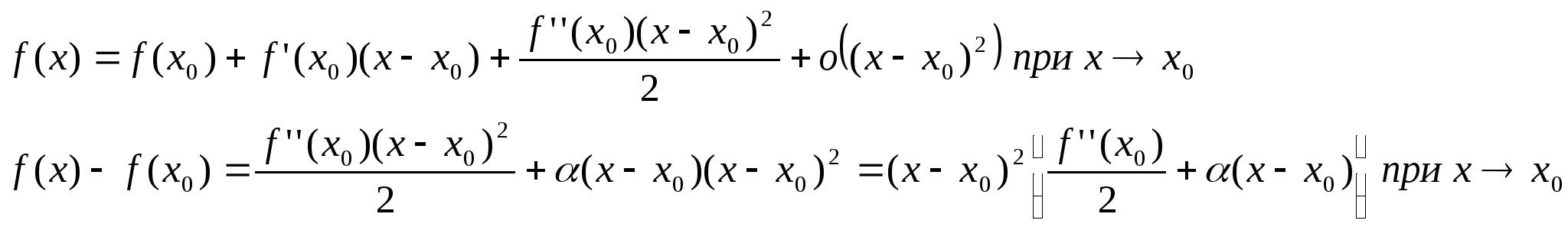
При х достаточно большим и х_>0> знак в квадратных скобках совпадает со знаком f’’(x_>0>) f(x)-f(x_>0>)>0 в О(х_>0>), если f’’(x_>0>)>0 то есть f(x)>f(x_>0>) в О(х_>0>) х_>0> точка минимума, если f(x)-f(x_>0>)<0 в О(х_>0>), и если f’’(x_>0>)<0 то есть f(x)<f(x_>0>) в О(х_>0>) х_>0> точка максимума.

Замечание: Если f’(x_>0>)=0 и f’’(x_>0>)=0, то нужны дополнительные исследования.

Лекция №17

Ведущая: Голубева Зоя Николаевна

Дата: среда, 22 ноября 2000 г.

Тема: Асимптоты. Полное исследование функции.

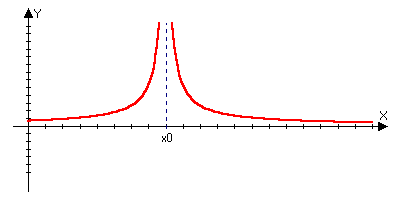
Асимптоты.

Вертикальные

Пусть функция f(x) определена в 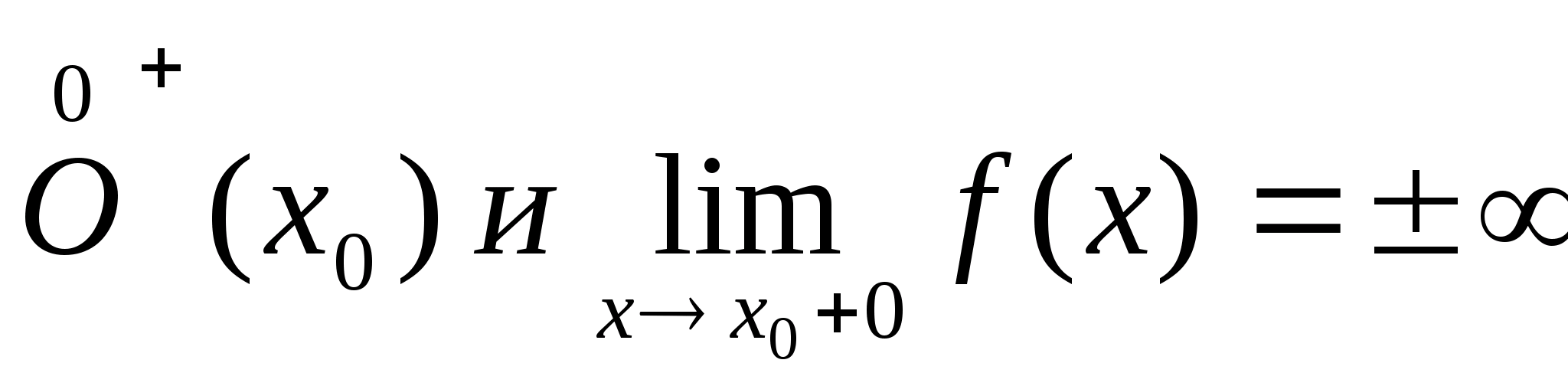, тогда прямая х=х_>0> называется правой вертикальной асимптотой для функции f(x)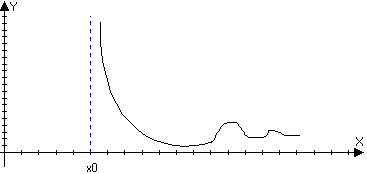

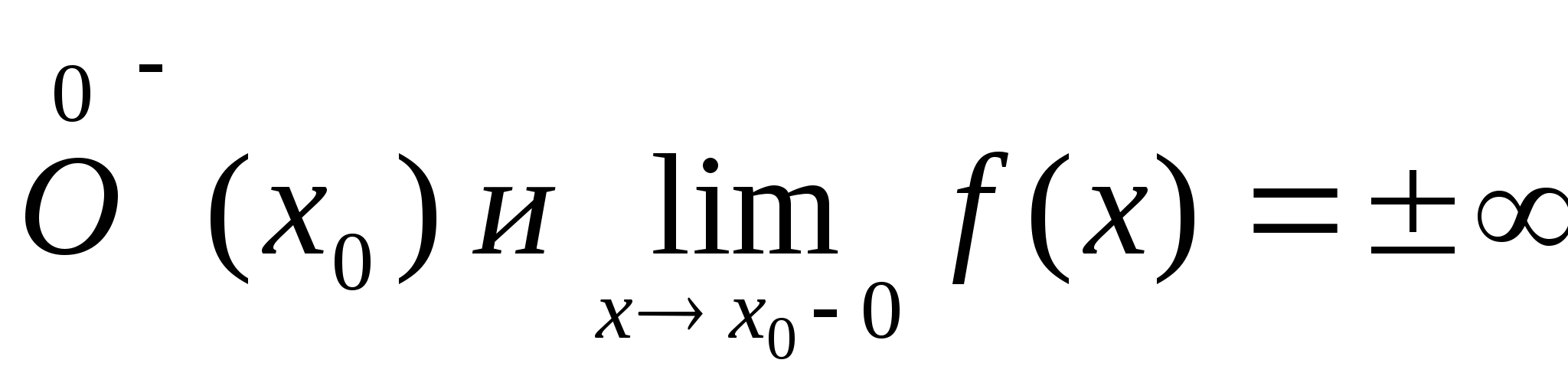Пусть функция f(x) определена в , тогда прямая х=х_>0> называется левой вертикальной асимптотой для функции f(x)

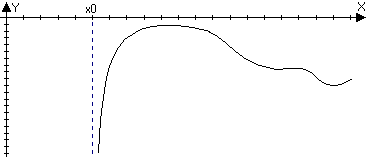
Наклонные асимптоты

2.1 Пусть функция f(x) определена в , тогда прямая y=kx+b называется правой наклонной асимптотой для функции f(x). (Если k=0, то говорят, что y=b – горизонтальная асимптота).

2.2 Пусть функция f(x) определена в 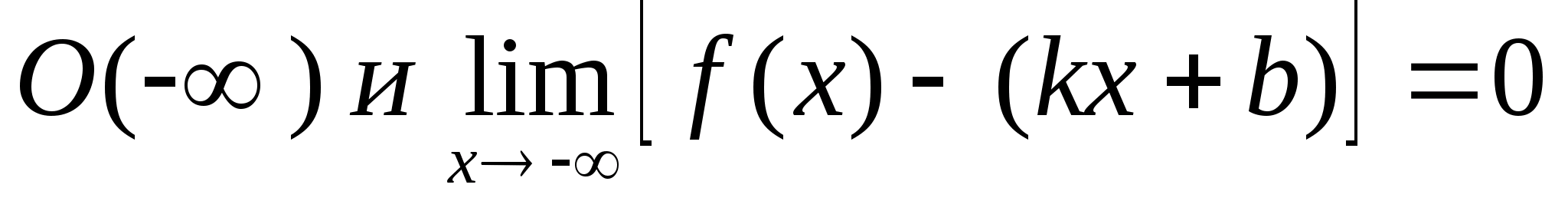, тогда прямая y=kx+b называется левой наклонной асимптотой для функции f(x).

Необходимые и достаточные условия существования наклонной асимптоты.

Пусть функция f(x) определена в О(+) и

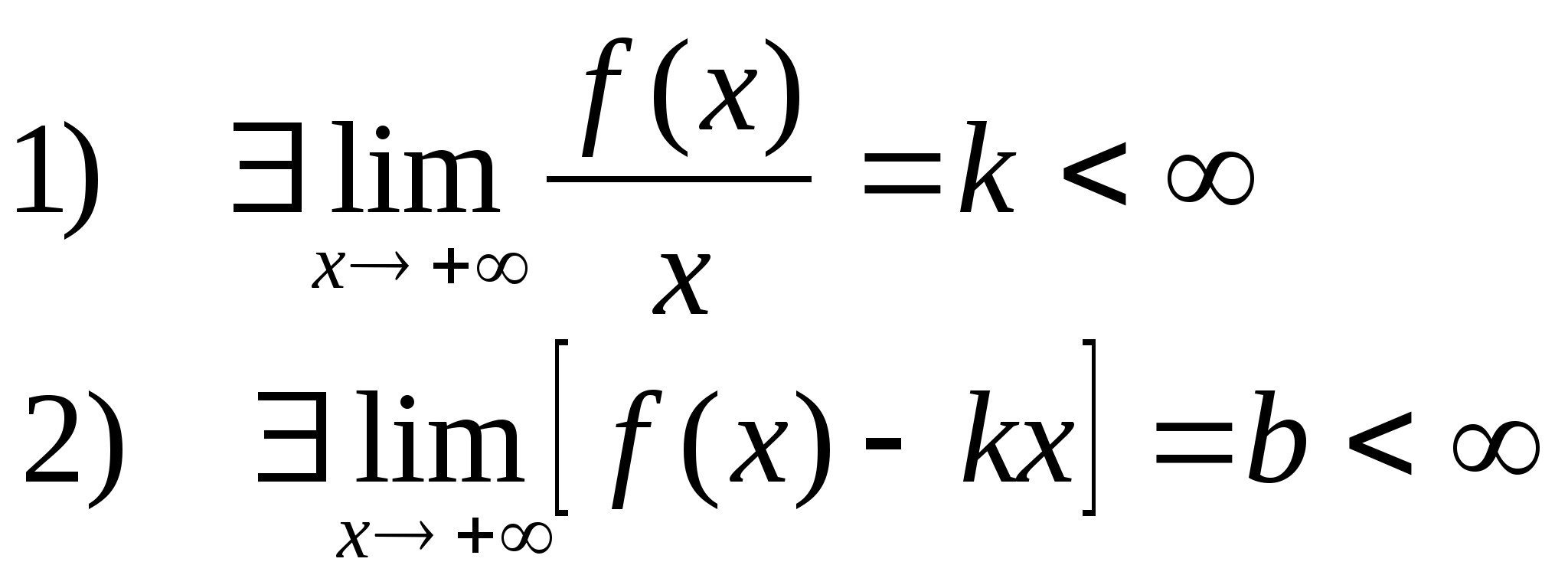
тогда прямая y=kx+b правая наклонная асимптота

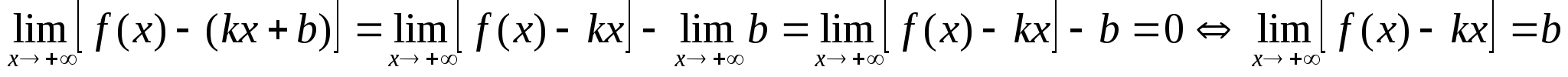
Замечание: если условие 1) не выполнено, то нужно посчитать предел lim(f(x)), чтобы выяснить поведение

^х+

функции на бесконечности.

Полное исследование функции.

1. Область определения

   Симметрия и периодичность

   Вертикальные асимптоты

   Наклонные асимптоты

   Критические точки, если есть, то находим точки экстремума и промежутки возрастания и убывания функции f'(x)=0 или f’(x) не существует, а f(x) существует

   Возможные точки перегиба f’’(x)=0, либо f’’(x) не существует, но f’(x) существует следовательно промежутки выпуклости и вогнутости

   Точки пересечения с осями координат и промежутки знака постоянства (если можно)

Пример:

_>>

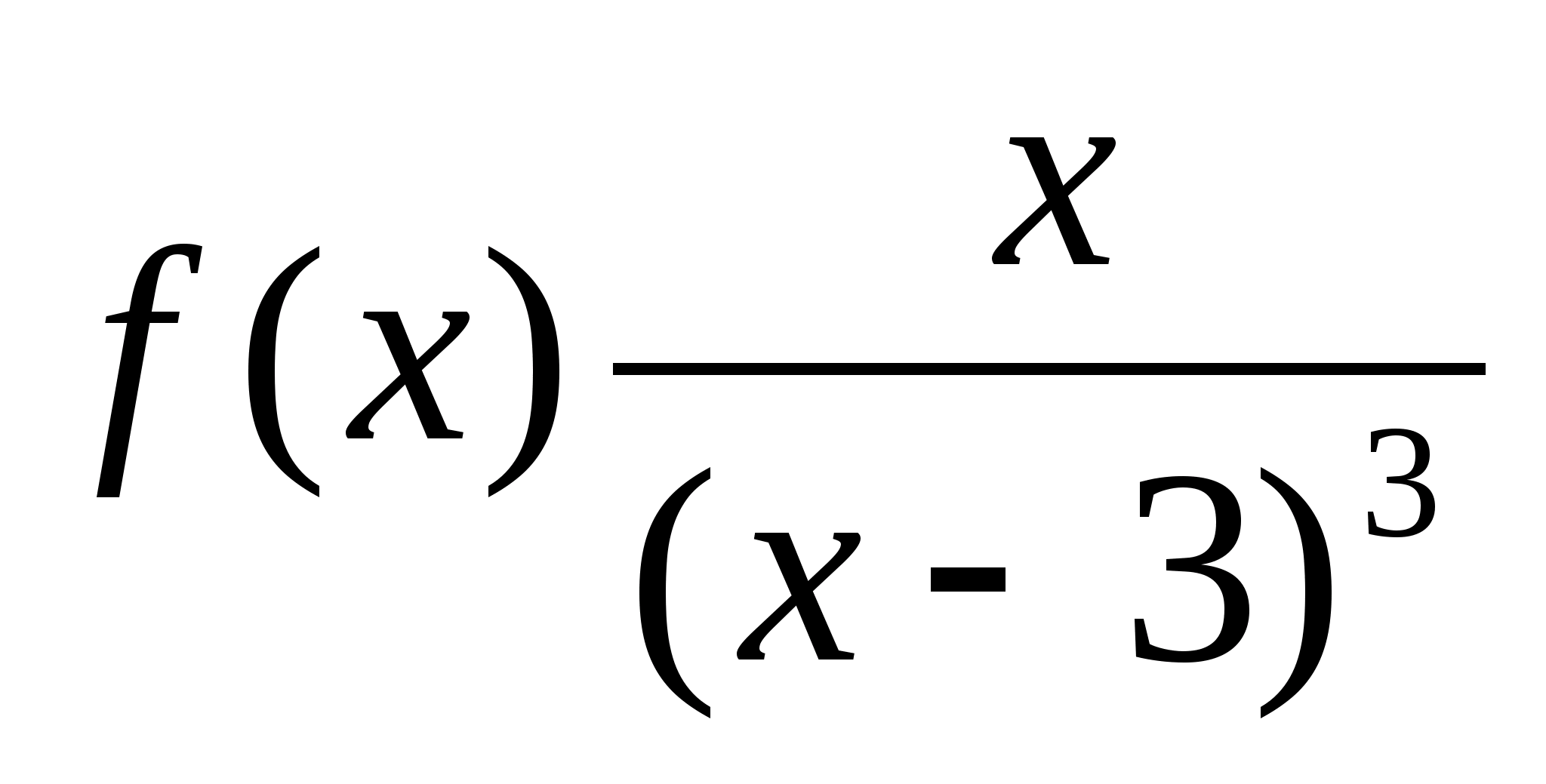1. Область определения D: x¹3

   Функция не симметрична и не периодична

   _>>

_> >

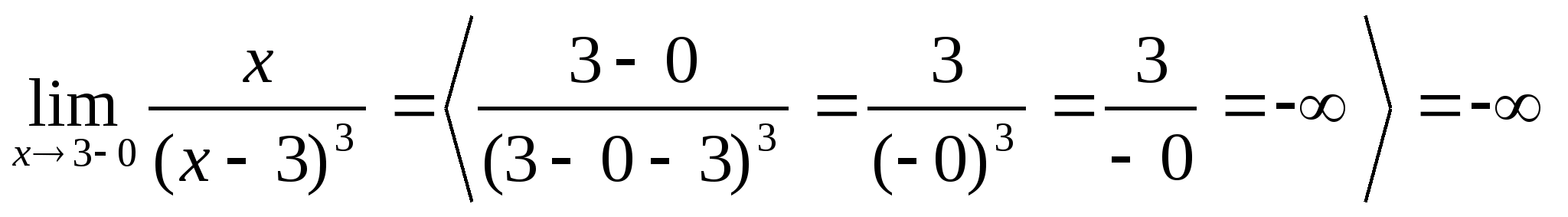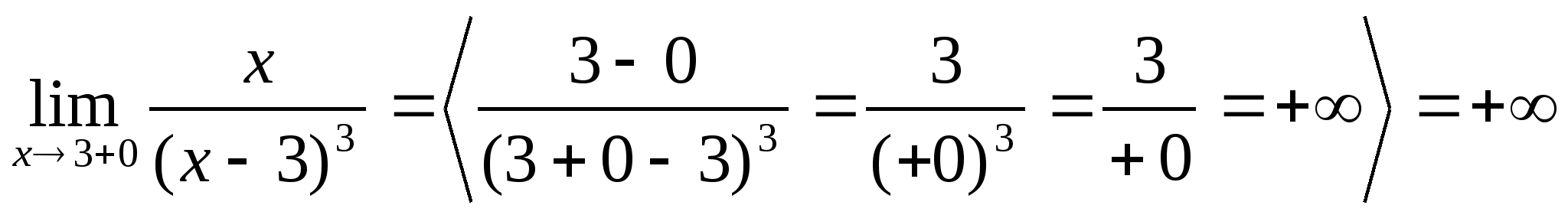Þ х=3 правая и левая вертикальная асимптота

4) _> >

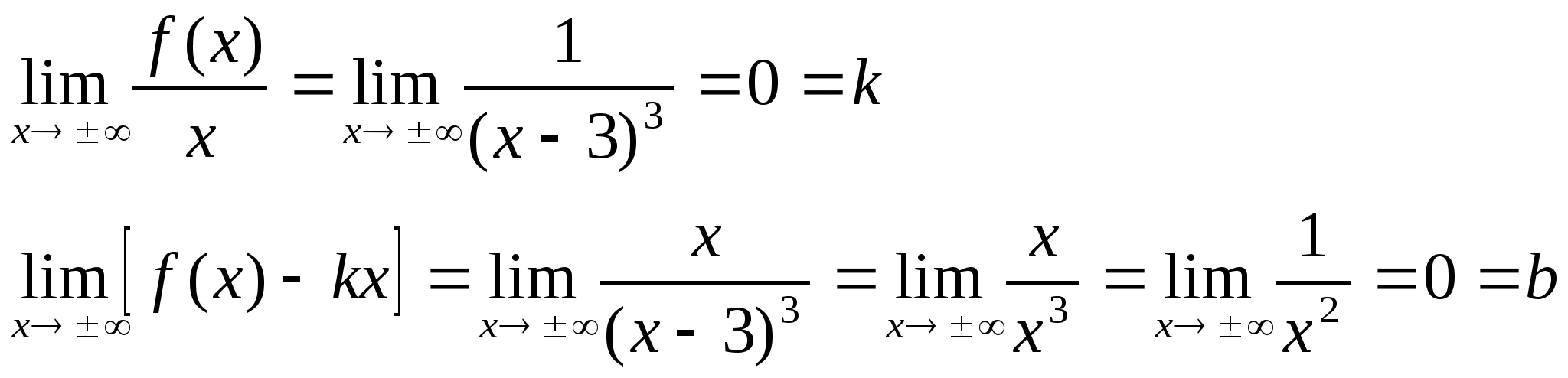Þ y=0 правая и левая горизонтальная асимптота

5)_>>

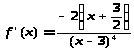критическая точка х_>1>=-3/2

f(-3/2)=4/243

6)_>>

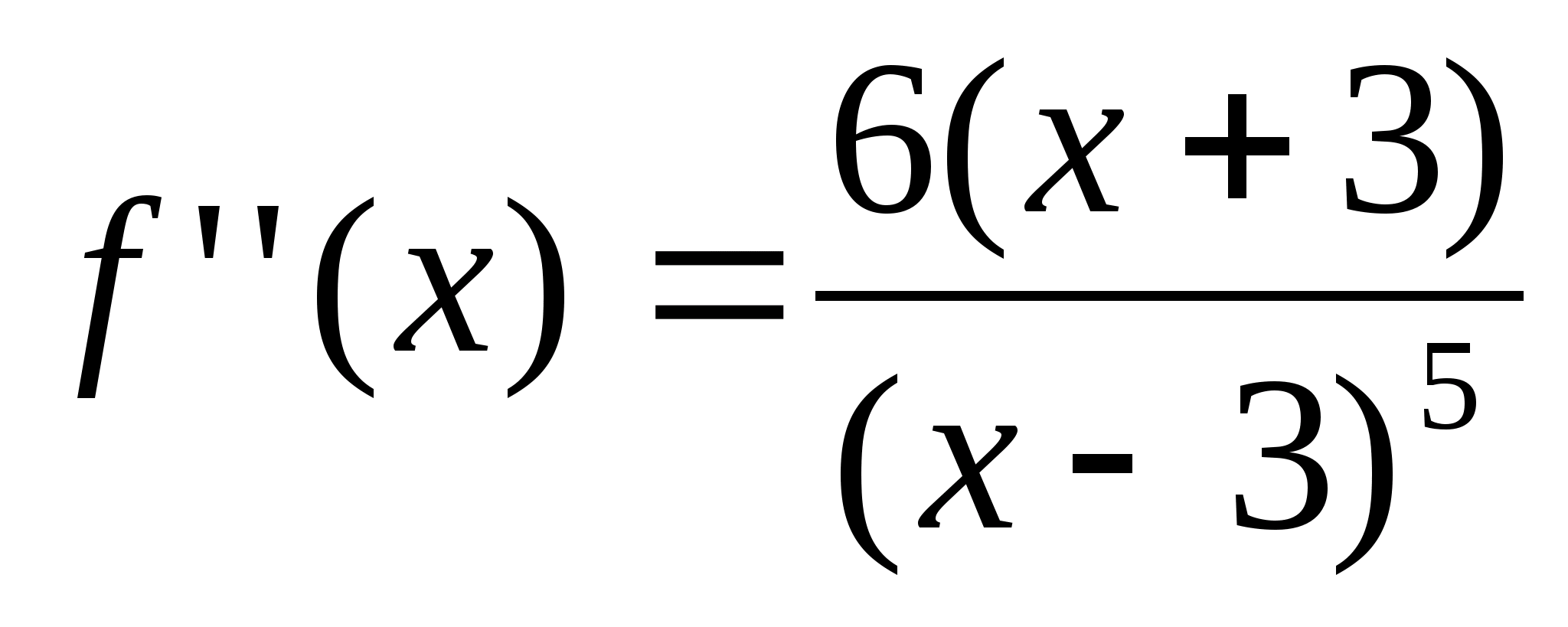критическая точка х_>2>=-3

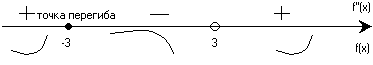
f(-3)=1/72

7)x=0 y=0

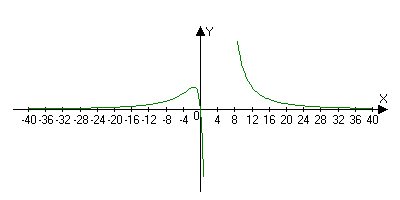
Приближенные методы решения уравнения f(x)=0

1) Метод хорд

а) f(x), f’(x), f’’(x) – непрерывны на отрезке [a,b]

б) f(a)f(b)<0

в) f’(x) и f’’(x) – сохраняют знаки на отрезке [a,b]

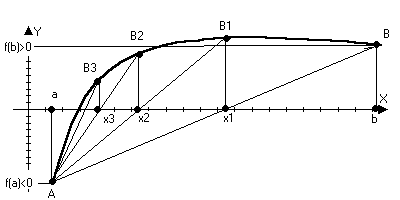
f()=0;A(a;(f(a)),B(b;f(b))

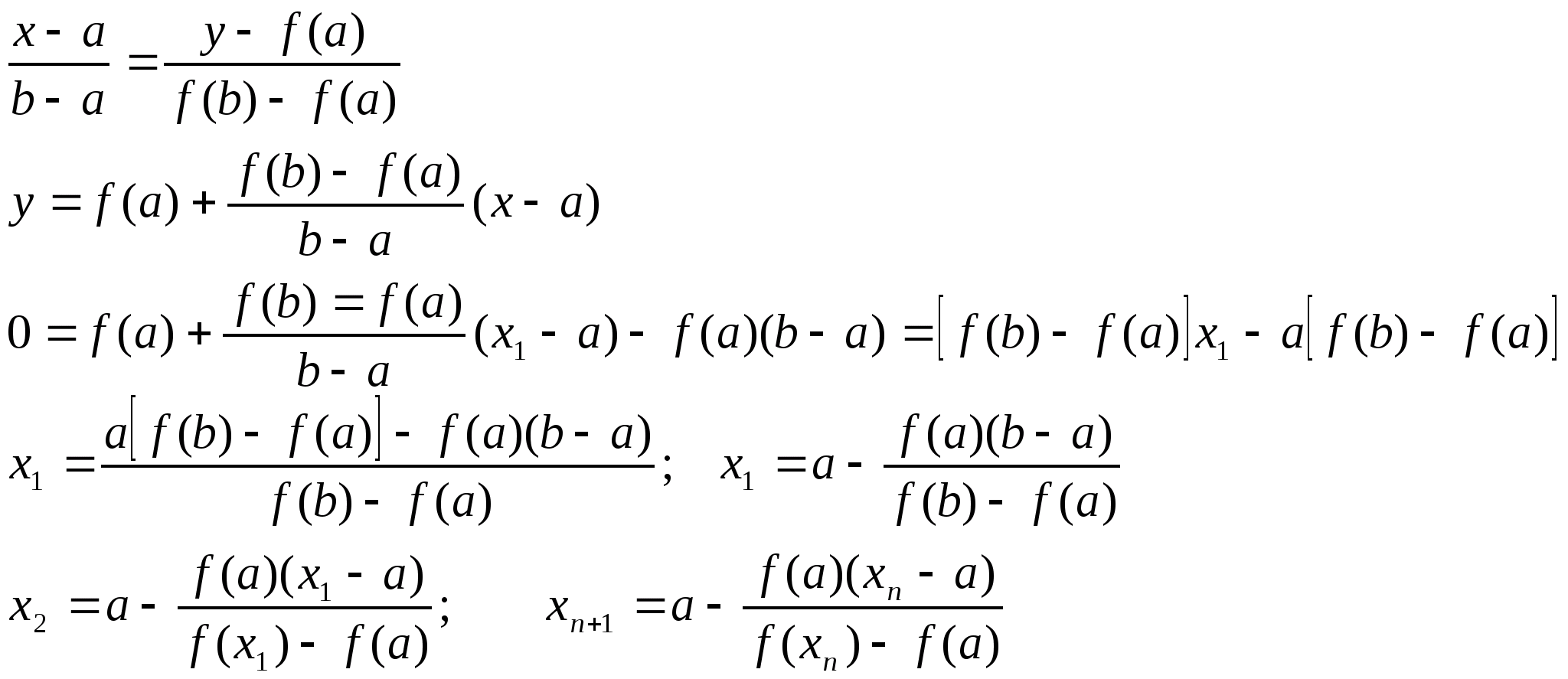
Лекция №18

Ведущая: Голубева Зоя Николаевна

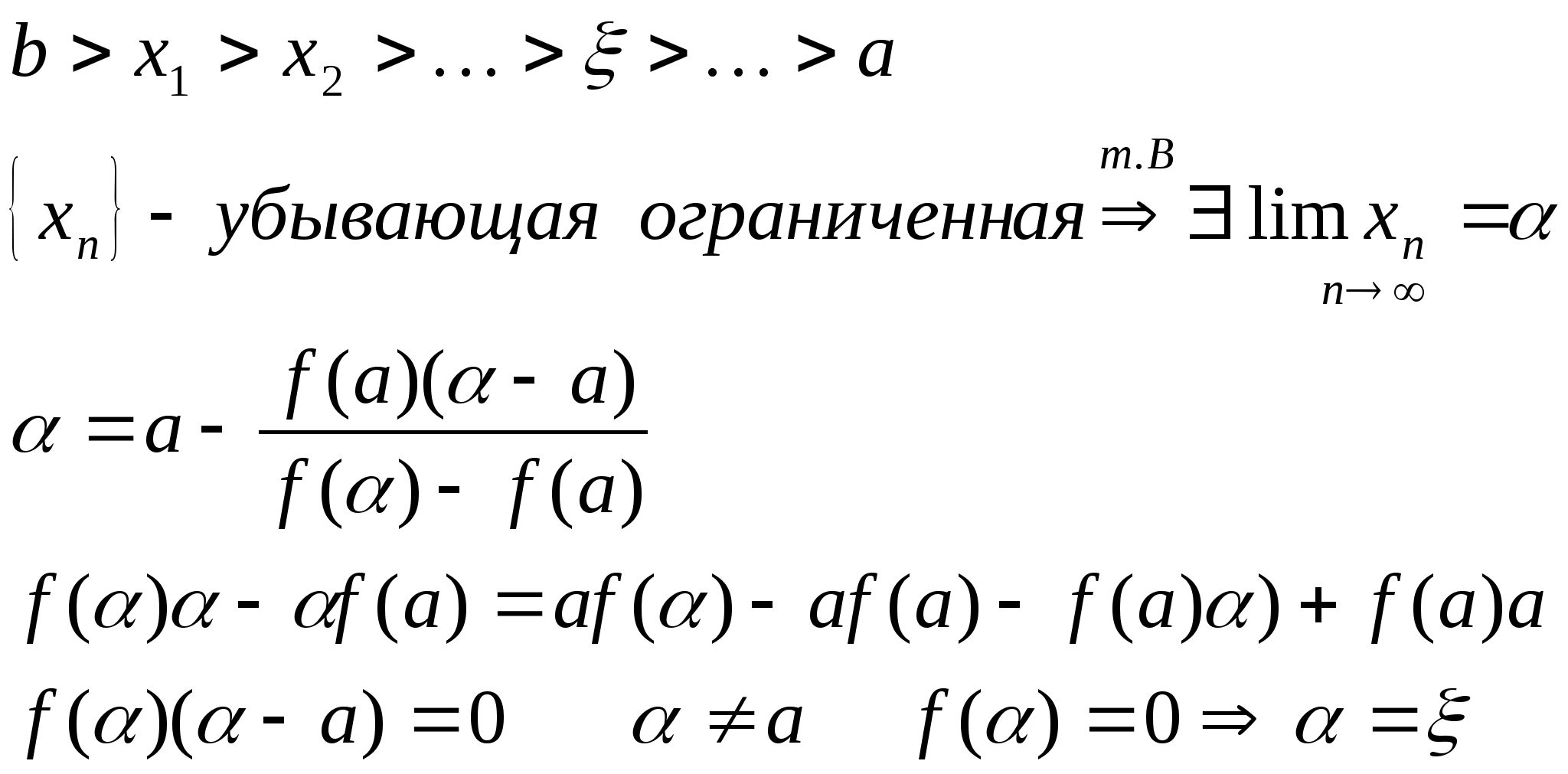
Оценка скорости сходимости.

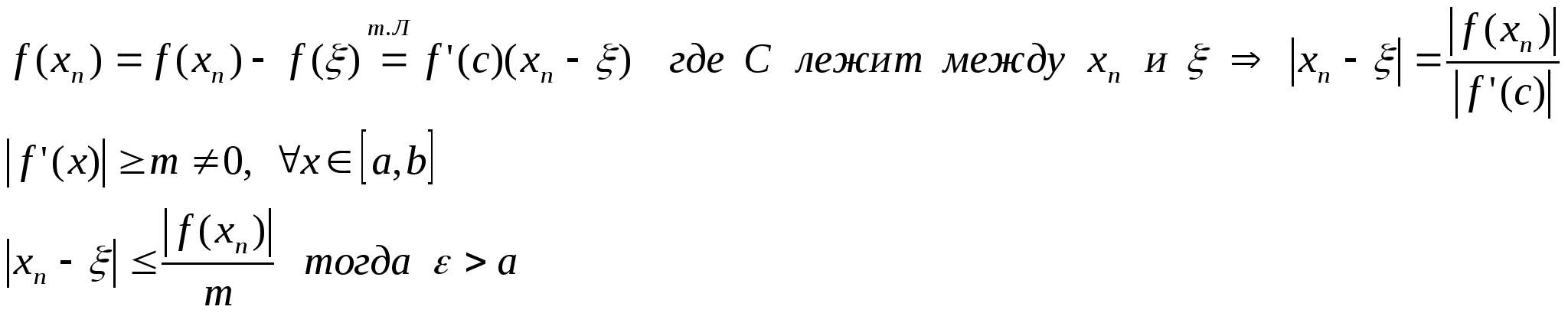2

2) Метод касательных (метод Ньютона)

f(x)=0

1)f(x),f’(x),f’’(x)-непрерывна на [a,b]

2)f(a), f(b) <0

3)f’(x),f’’(x) – сохраняет знак на [a,b]

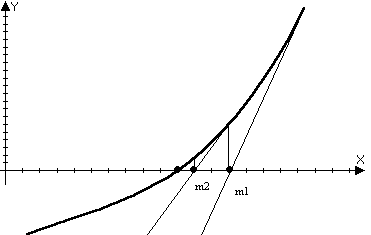
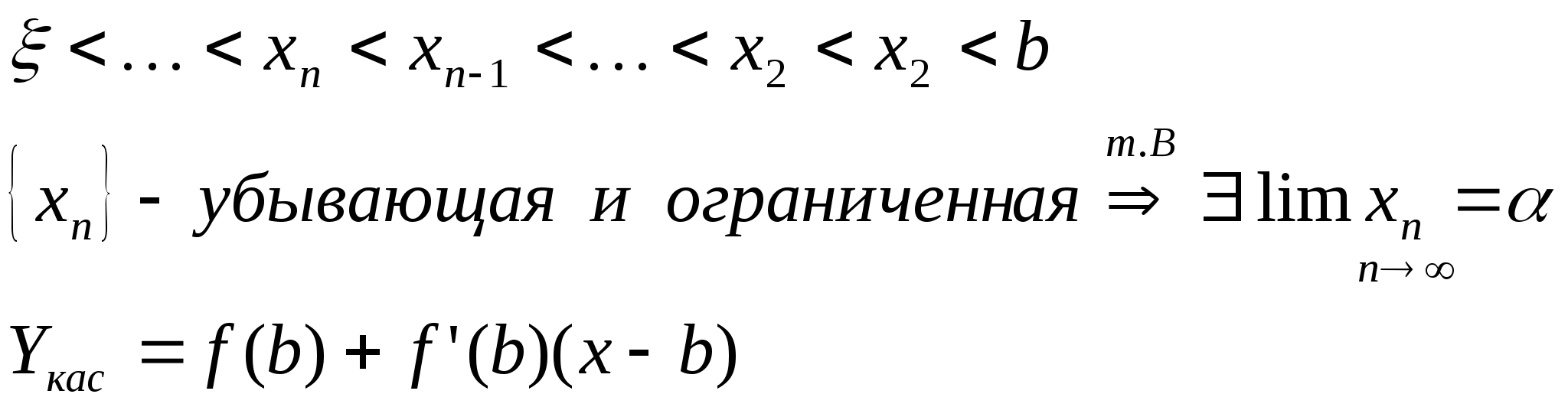
точка пересечения х_>1> – это точка пересечения касательной с осью Ох

Y_>кас>=0, x=x_>1>

0=f(b)+f’(b)(x_>1>-b)

f’(b)b-f(b)=f’(b)x_>1>

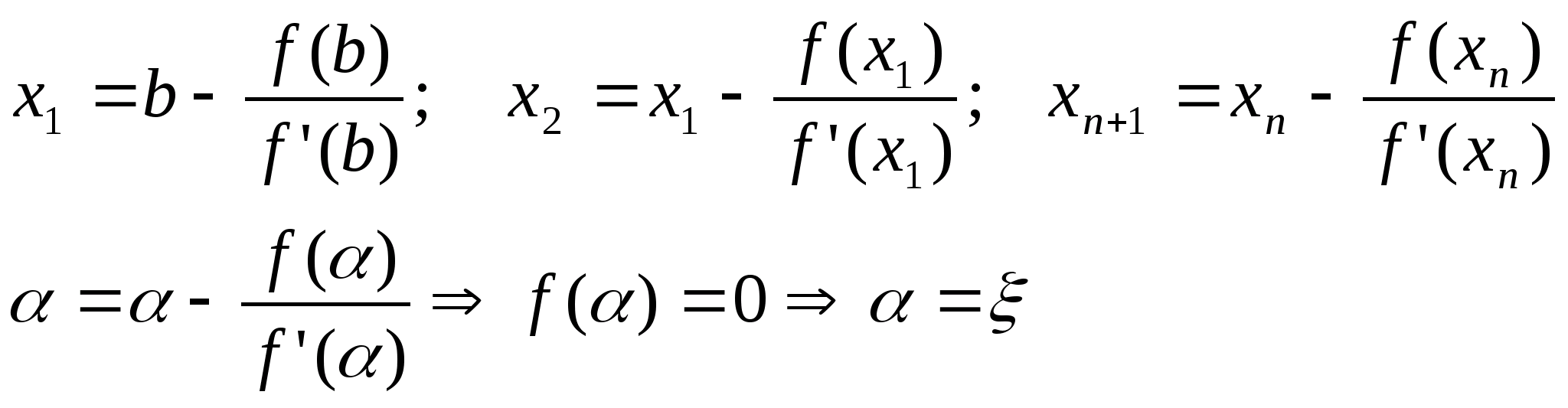
Формула Тейлора с остаточным членом в форме Лангранджа в точке x_>n>

_>>

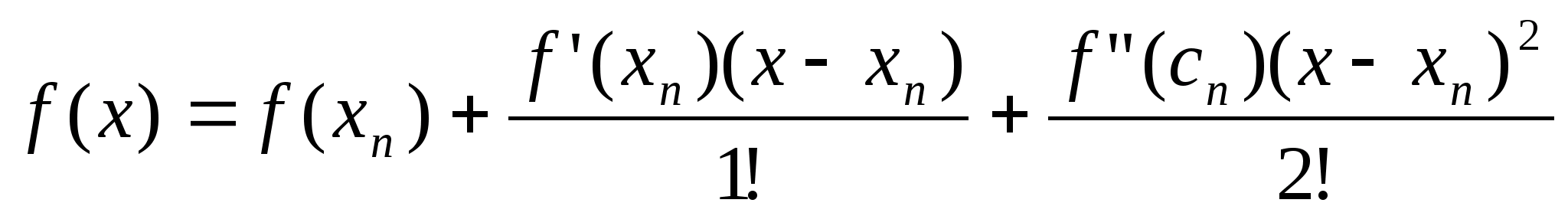c – лежит между х и х_>n>

Положим x=; f()=0

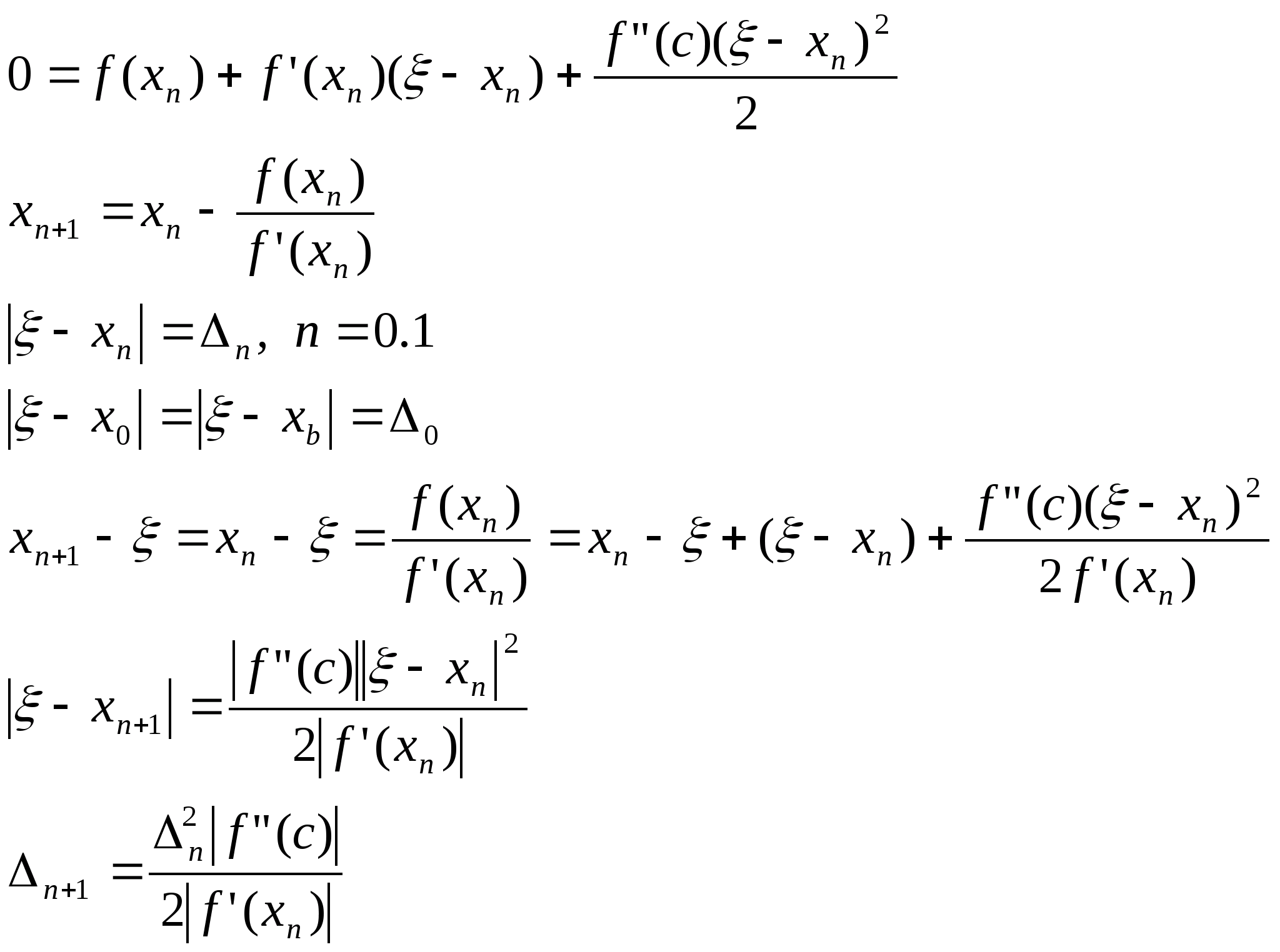
M>0:|f”(x)|M

x[a,b] m>0:|f’(x)|m;x[a,b]

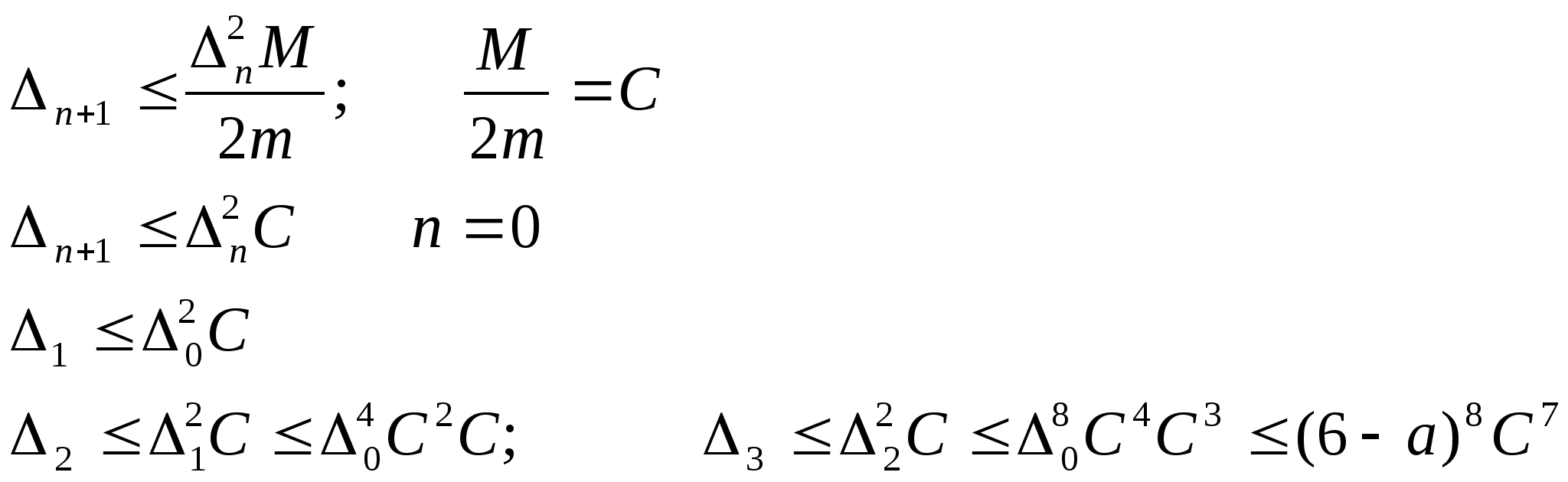
Надо выбирать отрезок так b-a<1

|f”(x)|M

Вектор функция. Параметрическая производная.

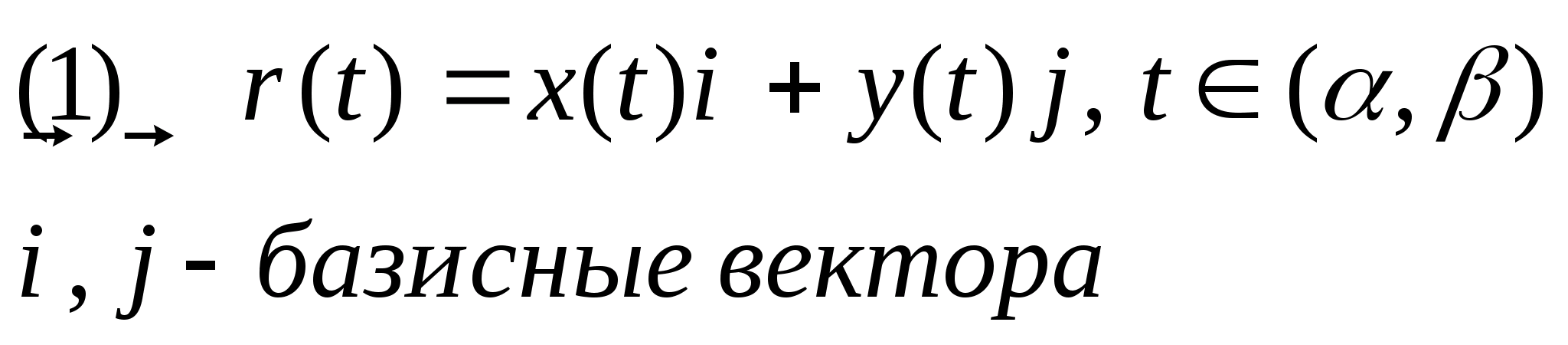
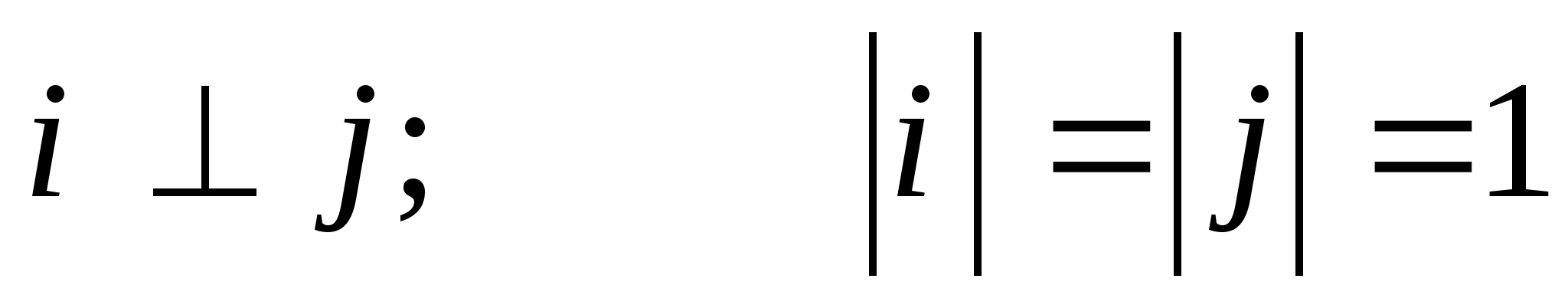
По закону (1) ставиться в соответствие вектор r(t). (x(t),y(t) – заданные числовые функции

r(t) – вектор функция. Кривая описываемая концом вектора – называется годографом.

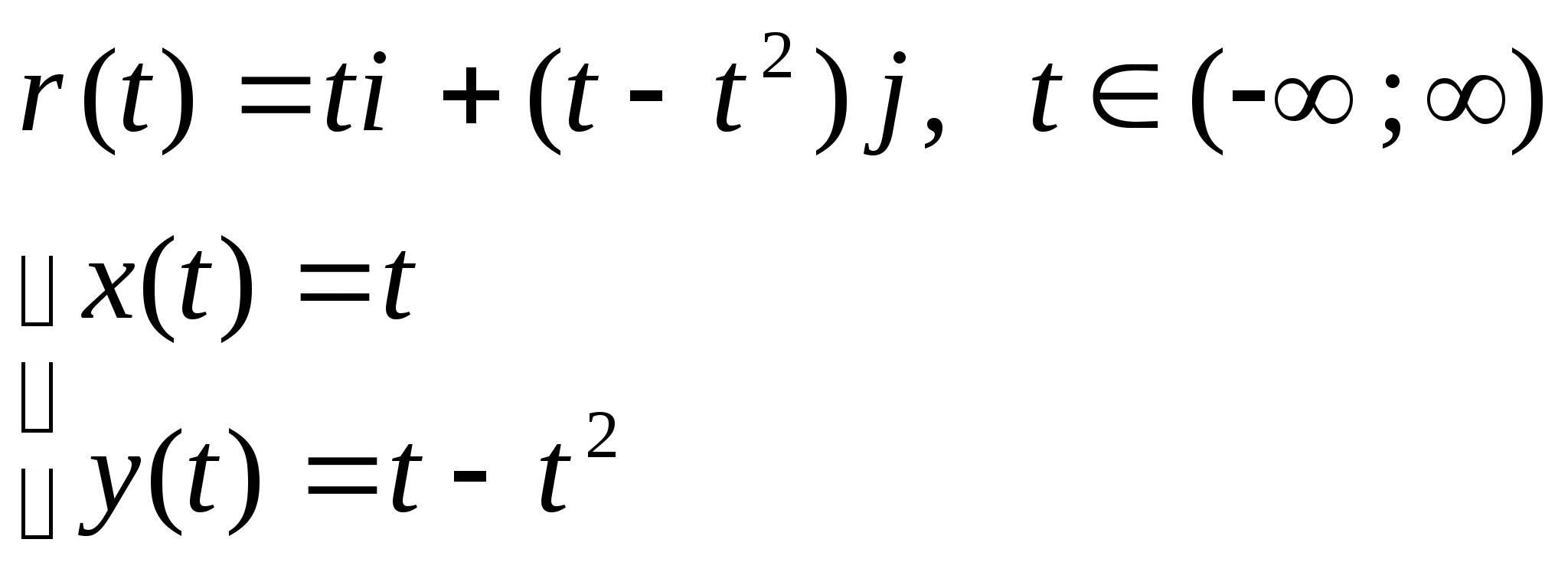
t	0	1	-1	2	3	½
x(t)	0	1	-1	2	3	½
y(t)	0	0	-2	-2	-6	1/4
r(t)	0	i	-i-2j	2i-2j	3j-6j	1/2i+1/4j

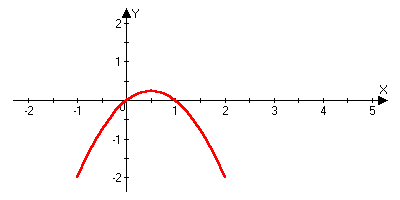
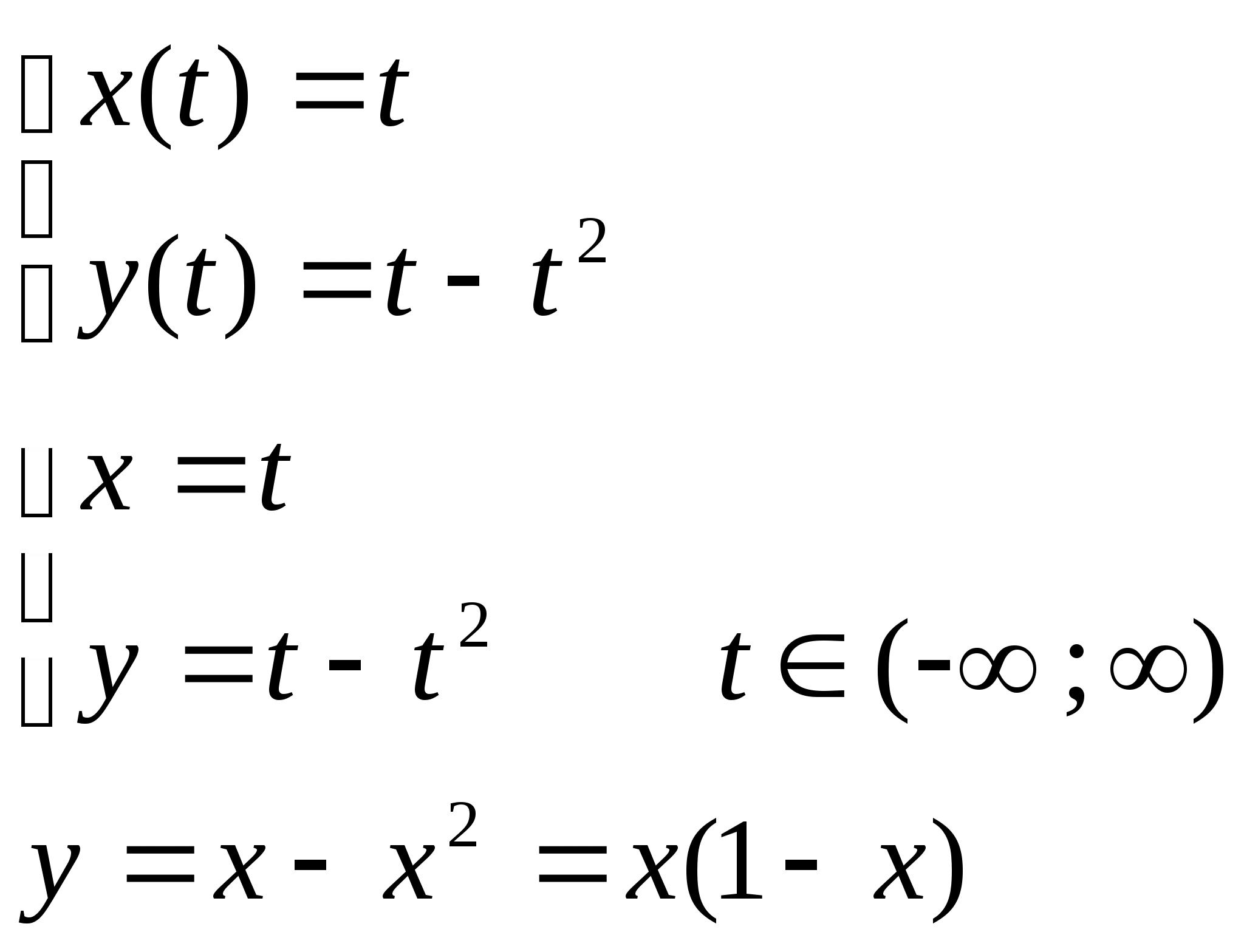
Видим, что кривые на плоскости можно задать в виде:

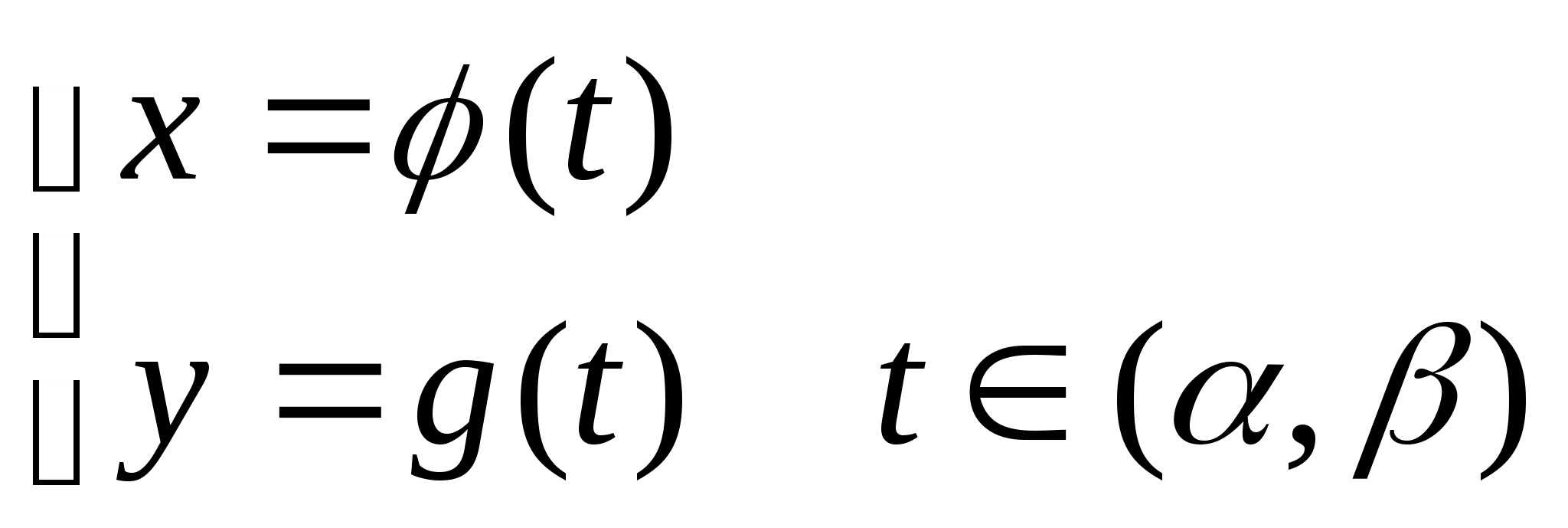
Называется параметрическое задание кривой, где t –параметр

x²+y²=r²

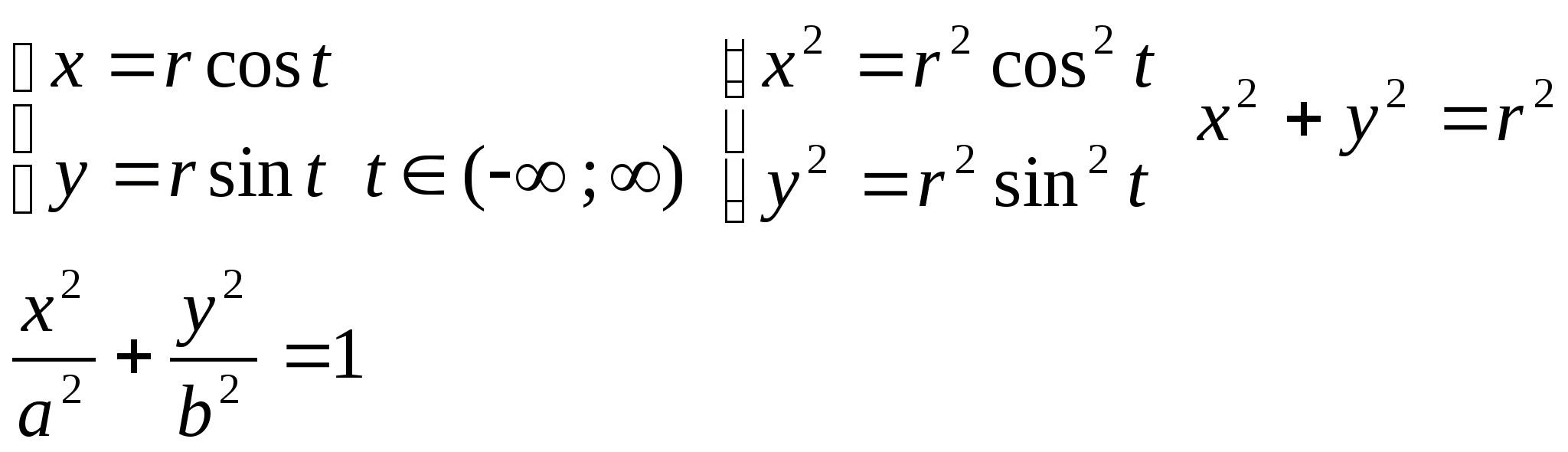
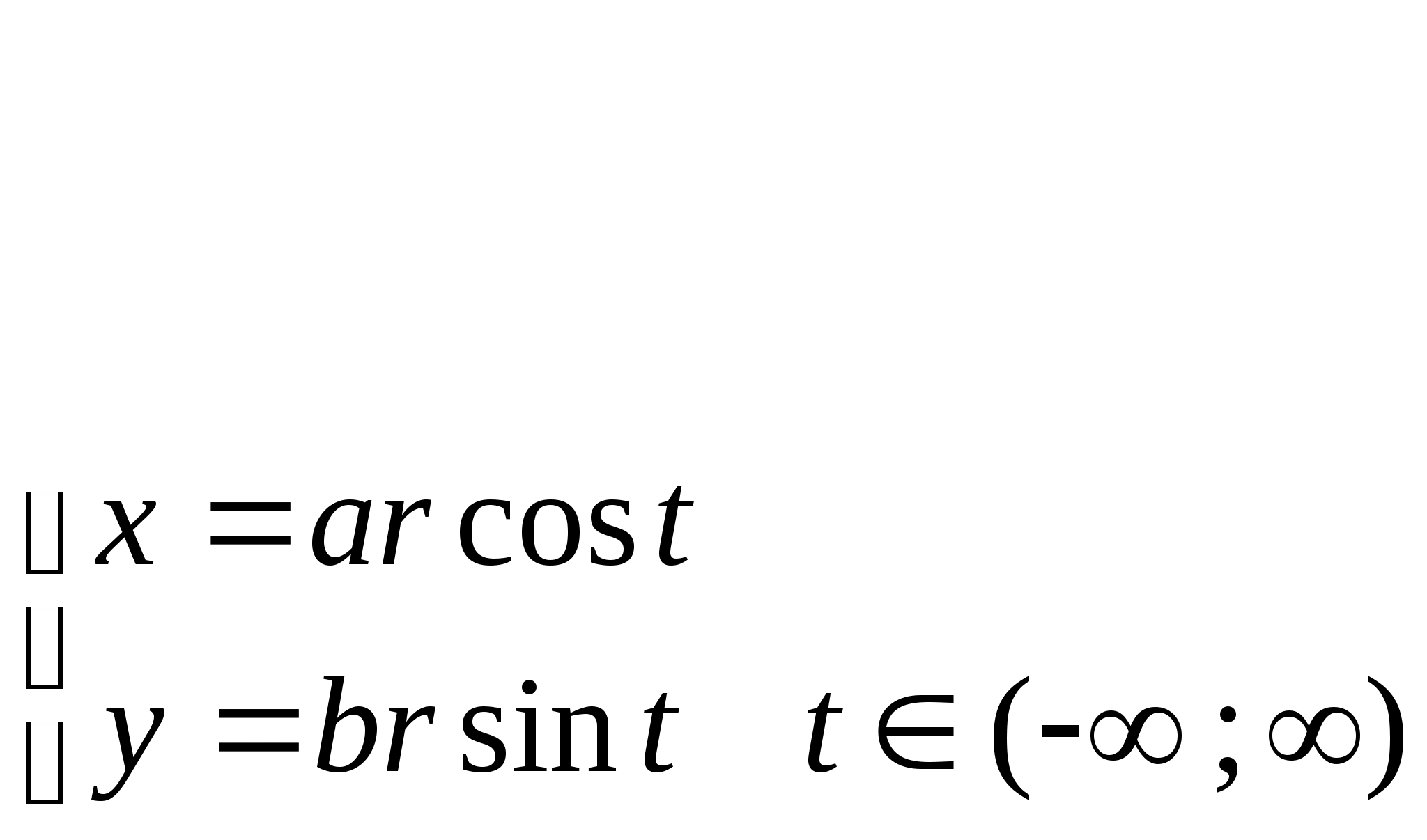
Остроида

x^2/3+y^2/3=a^2/3

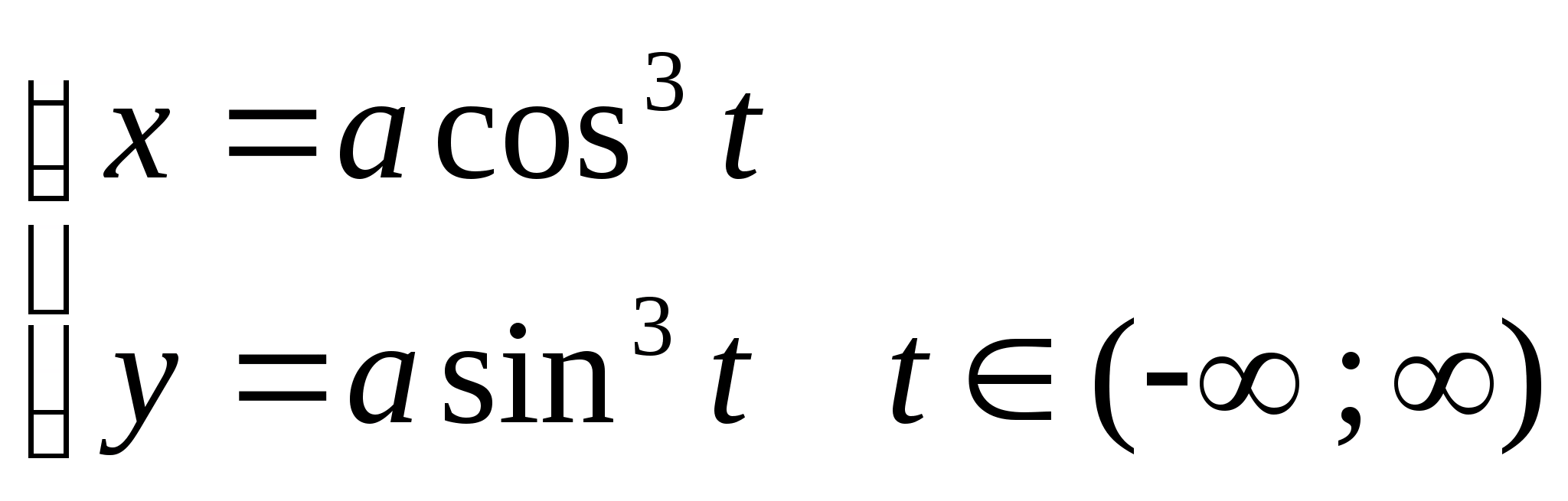
Циклоида

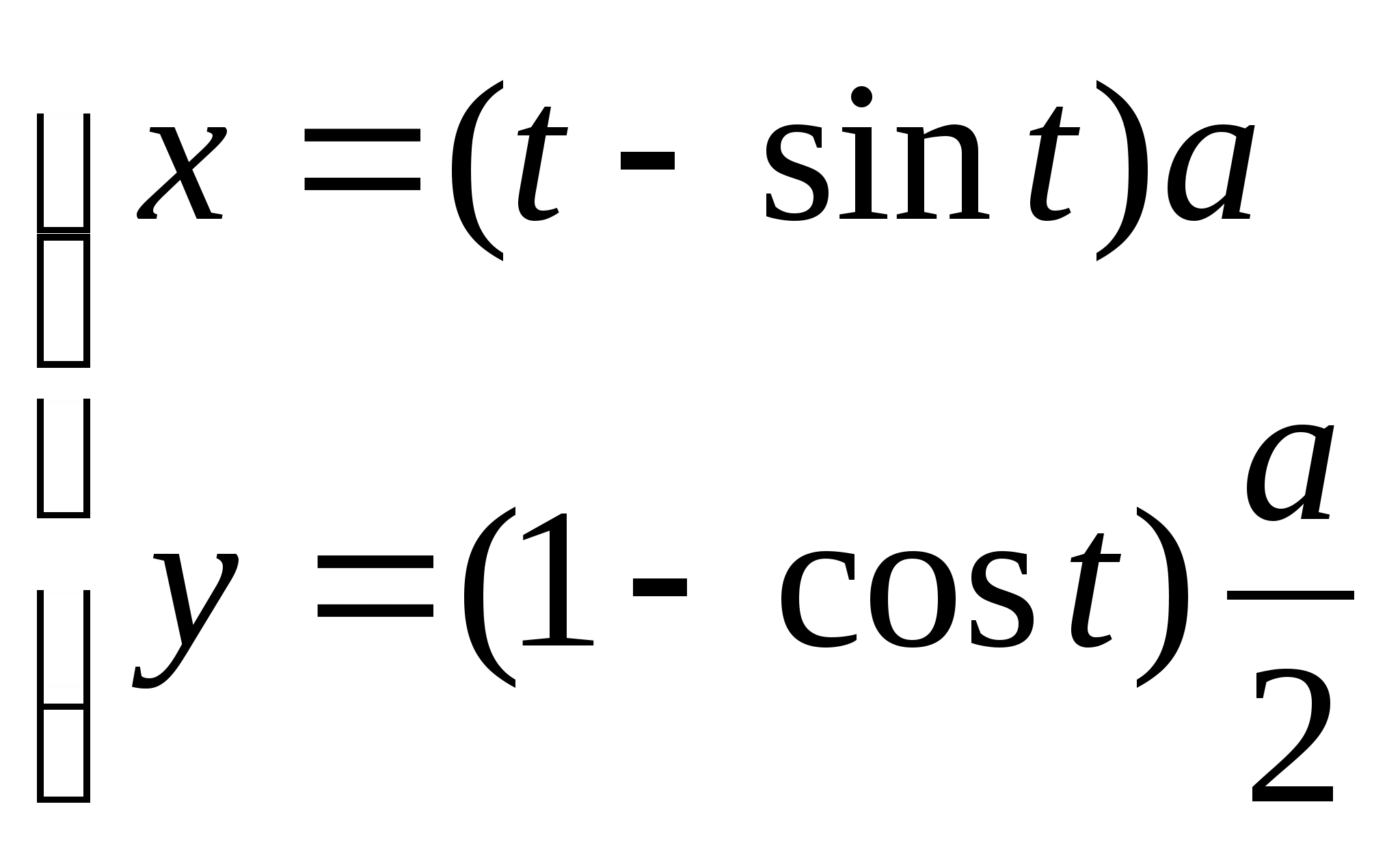
Лекция №19

Ведущая: Голубева Зоя Николаевна

Параметрическая производная.

* o’1 x²ⁿ⁺²=xx²ⁿ⁺¹=o(x²ⁿ⁺¹⁾

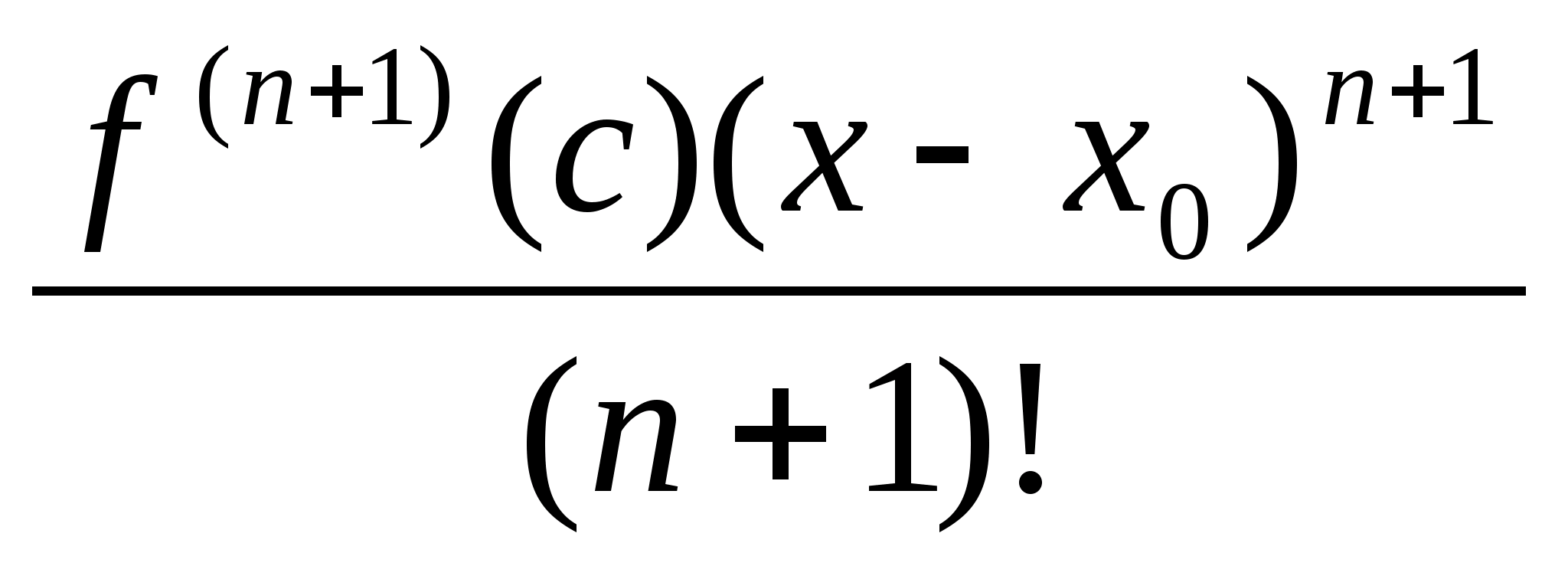# - остаточный член в форме Лангранджа

$ -T_>n>(x) – многочлен Тейлора

 R_>n>(x)-остаточный член в форме Лангранджа