Разбиения выпуклого многоугольника
Разбиения выпуклого многоугольника
П.1. Выпуклый многоугольник с n сторонами можно разбить на треугольники диагоналями, которые пересекаются лишь в его вершинах. Вывести формулу для числа таких разбиений.
Определение: назовем правильным разбиением выпуклого n-угольника на треугольники диагоналями, пересекающимися только в вершинах n-угольника.
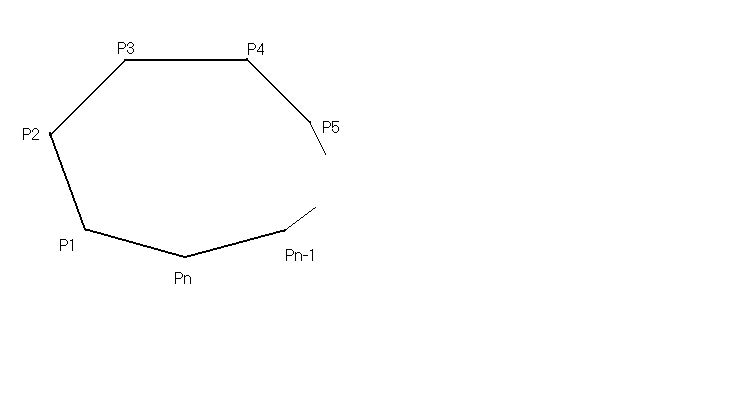
Пусть P>1>, P>2> , … ,P>n>–вершины выпуклого n-угольника, А>n>- число его правильных разбиений. Рассмотрим диагональ многоугольника P>i>P>n>.В каждом правильном разбиение P>1>P>n> принадлежит какому-то треугольнику P>1>P>i>P>n>, где1<i<n. Следовательно, полагая i=2,3, … , n-1, мы получаем (n-2) группы правильных разбиений, включающие все возможные случаи.
Пусть i=2 – одна группа правильных разбиений, которая всегда содержит диагональ P>2>P>n>> >.Число разбиений, входящих в эту группу совпадает с числом правильных разбиений (n-1) угольника P>2>P>3>…Pn, то есть равно А>n>>-1>.
Пусть i=3 – одна группа правильных разбиений, которая всегда содержит диагональ P>3>P>1 >и P>3>P>n>>.>Следовательно, число правильных разбиений, входящих в эту группу, совпадает с числом правильных разбиений (n-2)угольника P>3>P>4>…Pn, то есть равно А>n>>-2.>
При i=4 среди треугольников разбиение непременно содержит треугольник P>1>P>4>P>n>.К нему примыкают четырехугольник P>1>P>2>P>3>P>4> и (n-3)угольник P>4>P>5> …Pn.Число правильных разбиений четырехугольника равно A>4, >число правильных разбиений (n-3) угольника равно
А>n>>-3.>Следовательно, полное число правильных разбиений, содержащихся в этой группе, равно
А>n>>-3>A>4.>Группы с i=4,5,6,… содержат А>n>>-4>A>5,> А>n>>-5>A>6, >… правильных разбиений.
При i=n-2 число правильных разбиений в группе совпадает с числом правильных разбиений в группе с i=2,то есть равно А>n>>-1.>
Поскольку А>1>=А>2>=0, А>3>=1, A>4>=2 и т.к. n 3, то число правильных разбиений равно:
А>n=> А>n-1>+А>n-2>+А>n-3 >A>4>+А>n-4 >A>5>+ … + A >5>А>n-4>+ A>4>А>n-3>+ А>n-2>+ А>n-1.>
Например:
A >5>= A>4>+ А>3>+ A>4>=5
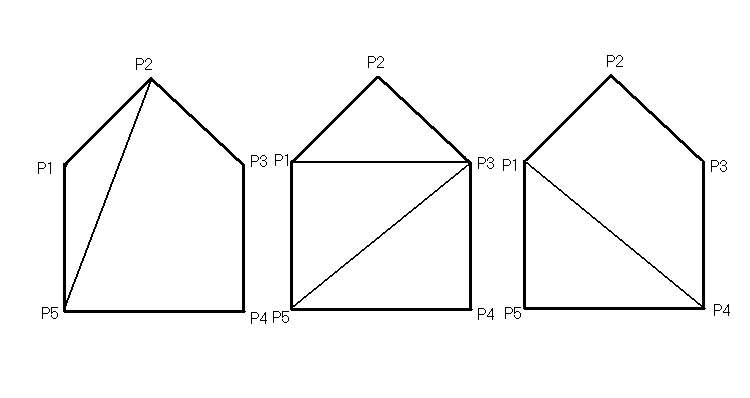
A>6>= A>5>+ А>4>+ А>4>+ A>5>=14
A>7>= A>6>+ А>5>+ А>4>> *>А>4>+А>5>+ A>6> =42
A>8>= A>7>+ А>6>+А>5>>*>А>4>+ А>4>>*>А>5>+А>6>+ A>7> =132
П.2.1. Найдем количество во всех диагоналей правильных разбиениях, которые пересекают внутри только одну диагональ.
Проверяя на частных случаях, пришли к предположению, что количество диагоналей в выпуклых n-угольниках равно произведению количества разбиений на (n-3)
Докажем предположение, что P1>n>= А>n>(n-3)
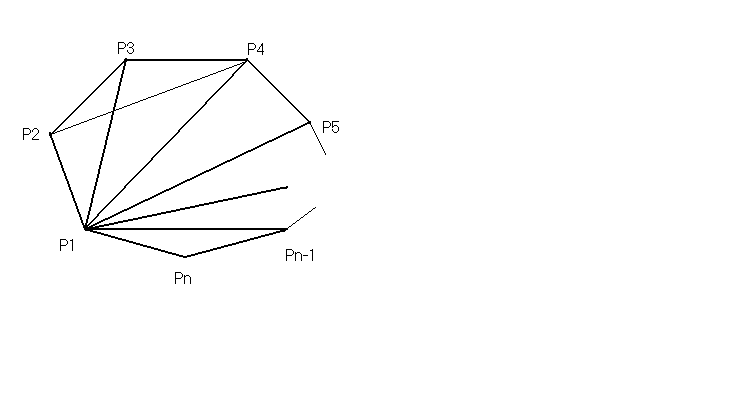
Каждый n-угольник можно разбить на (n-2) треугольника, из которых можно сложить (n-3) четырехугольника, причем каждый четырехугольник будет иметь диагональ. Но в четырехугольнике можно провести 2 диагонали, значит в (n-3) четырехугольниках можно провести (n-3) дополнительные диагонали. Значит, в каждом правильном разбиении можно провести (n-3) диагонали удовлетворяющих условию задачи.
П.2.2. Найдем количество во всех диагоналей правильных всех разбиениях, которые пересекают внутри только две диагонали.
Проверяя на частных случаях, пришли к предположению, что количество диагоналей в выпуклых n-угольниках равно произведению количества разбиений на (n-4), где n ≥ 5
Докажем предположение, что P2>n>=(n-4)А>n>> , >где> >n ≥ 5.
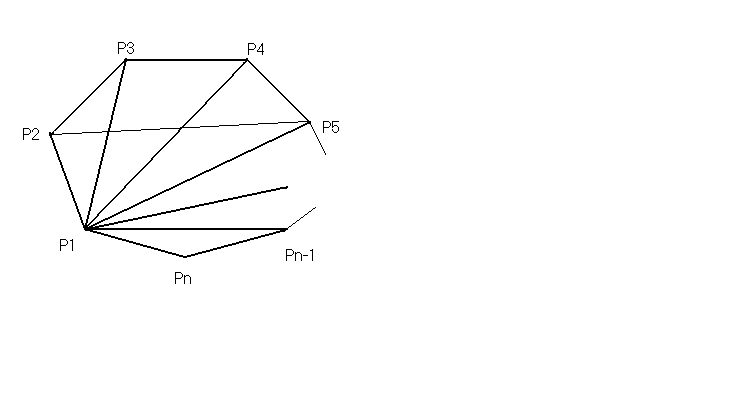
n-угольник можно разбить на (n-2) треугольников из которых можно сложить (n-4) пятиугольника, в котором будут содержаться две непересекающиеся диагонали. Значит, найдется третья диагональ, которая пересекает две другие. Так как имеется (n-4) пятиугольника, значит, существует (n-4) дополнительные диагонали удовлетворяющих условию задачи.
П.2.3. Разбиение n-угольника, в котором дополнительные диагонали пересекают главные k раз.
Определение 1:Главными диагоналями выпуклого n-угольника называются диагонали, которые разбивают его на треугольники, пересекаясь при этом только в вершинах n-угольника.
Замечание: их существует (n-3).
Определение 2:Дополнительными диагоналями выпуклого n-угольника называются диагонали, которые в данном разбиении пересекают главные диагонали.
Замечание: их существует менее (n-3).
I.Определение k:
Б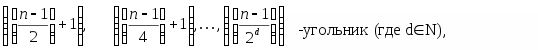
удем
выделять из выпуклого n-угольника
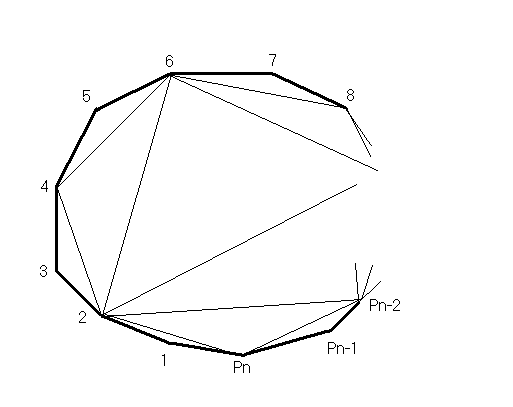
следующим образом: соединяем диагоналями через одну вершину данного n-угольника, причем выделением считается получение последующего a-угольника из предыдущего, используя не менее двух диагоналей. Выделение ведется до тех пор, пока не получится четырехугольник или треугольник (r = 4 или r = 3 (r – остаточный коэффициент)). Назовем каждое такое выделение циклом и введем величину, которая будет “считать” их (d). Для каждого d существует 2d+1 многоугольников, первый многоугольник для данного d ,будет (2d+1+1)-угольником. Для первой половины (для данного d) многоугольников r = 3, для второй - r = 4. Последним многоугольником, для которого r = 3 будет (32d )-угольником. Окончательно получаем: r = 3, если n[2d+1+1; 32d], в противном случае r = 4. За каждый цикл, если проводить дополнительные диагонали, будет добавляться по 2 пересечения и через d циклов число пересечений достигнет максимума в полученном данным способом разбиении. Обозначим это число буквой k.
Итак, за 1 цикл 2 пересечения, за 2 цикла – 4, за 3 – 6, очевидна арифметическая прогрессия с разностью 2, a1=2 и количество членов равным d; значит k=2+2(d-1)=2d – только в том случае, если конечной фигурой окажется треугольник. В противном случае k=2d+1, так как четырехугольник имеет собственную диагональ.
Рассчитаем d: т.к.: d=1,
n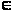
[22+1; 23]
d=2, n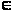
[23+1;
24]
d=3, n
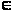[24+1;
25]
…
Зависимость d от n- логарифмическая по основанию 2; становится очевидным равенство: d=[log>2>(n-1)]-1. Выразим k через n:
k=2([log>2> (n-1)]-1), если n[2[log2(n-1)]+1; 32[log2(n-1)]-1]
или
k=2([log>2>(n-1)]-1)+1= 2[log>2 >(n-1)]-1, если n[2[log2(n-1)]+1; 32[log2(n-1)]-1]
Так как k – максимум пересечений, то уместны неравенства:
k≤2([log>2> (n-1)]-1), если n[2[log2(n-1)]+1; 32[log2(n-1)]-1]
или (*)
k≤2[log>2> (n-1)]-1, если n[2[log2(n-1)]+1; 32[log2(n-1)]-1]
II. Найдем число дополнительных диагоналей (m), которые пересекают главные не более k раз.
Выделим в данном выпуклом n-угольнике (k+3)-угольник (k+3)-угольник (если это возможно), зн.
уже ‘использовано’ (n+3)-2=k+1 всех
отбросили существующих треугольников
1 треугольник n-угольника (всего их (n-2)),потом добавили другой ‘отбросим’ крайний треугольник и реугольник и ‘добавим’ к получившейся фигуре еще опять получили один, имеющий общую с ней сторону, (k+3)-угольник ‘не использованный’ треугольник, тогда останется (k+2) не использованных треугольника, и так далее до тех пор, пока не ‘используем’ все (n-2)треугольника. Очевидна арифметическая прогрессия с разностью 1, a>m>=n-2 и c количеством членов равным m. Получим:n-2=k+1+(m-1)<=>n-2=k+m<=>m=n-k-2m=n-(k+2)Значит, в n-угольник можно вписать (k+3)угольник (n-(k+2))раз, то есть существуют такие (n-(k+2)) дополнительные диагонали, которые пересекут k главных диагоналей.
Окончательно получаем: Pk>n>=(n- (k+2))А>n>> , >где> >(*).
Список литературы
Скращук Дмитрий (г. Кобрин). Разбиения выпуклого многоугольника