Нахождение неопределенных интегралов
Нахождение неопределенных интегралов
Контрольная работа (вариант 8)
Найти неопределенные интегралы:
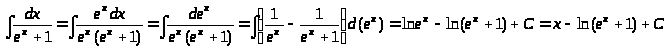
2. Интегрирование по частям
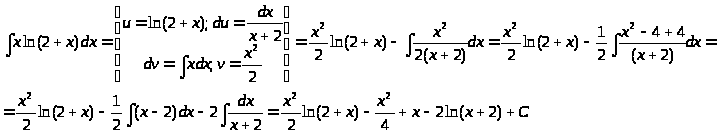
Вычислить определенные интегралы:
3.
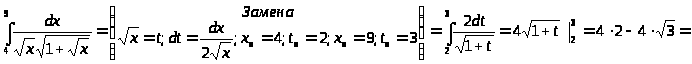
=8-6,92=1,08
Интегрирование по частям
4.
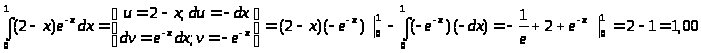
5. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями
.
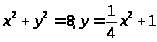Построить чертеж.
Решение.
В декартовой системе координат построим линии и найдем точки их пересечения.
Объем тела вращения
по формуле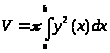
Точки пересечения линий
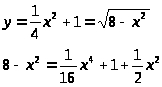
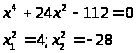
(второй вариант не подходит, т.к. отрицателен)
Отсюда
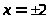
Границы фигуры:
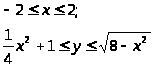
Фигура симметрична относительно оси ОУ, поэтому
Объем тела
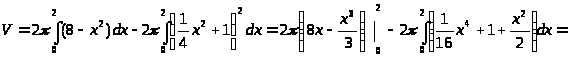
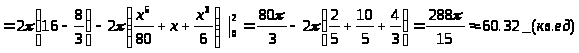
6. Методом наименьших квадратов найти эмпирическую формулу вида y=ax+b для функции, заданной следующей таблицей:
-
X
3.3
3.5
3.7
3.9
4.1
Y
13
13.5
11.4
11.2
9.7
Изобразить графически таблично заданную и соответствующую линейную функции. По эмпирической формуле вычислить значение переменной при х=4,0
Решение
Заполним таблицу
-
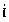
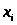
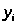
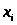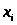
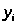
21
3,3
13
10,89
42,9
2
3,5
13,5
12,25
47,25
3
3,7
11,4
13,69
42,18
4
3,9
11,2
15,21
43,68
5
4,1
9,7
16,81
39,77
18,5
58,8
68,85
215,78
Составим для определения коэффициентов систему уравнений вида:
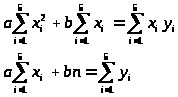
Получим
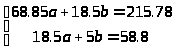
Решая систему методом исключения определяем:
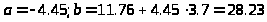
Искомая эмпирическая формула y=28.23-4.45x
Значение переменной при x=4.0
y=28.23-4.45*4=10.43
7. Исследовать сходимость ряда.
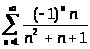
Исследуем ряд сначала на абсолютную сходимость. Общий член ряда
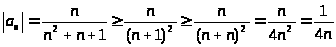
В свою очередь ряд
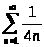расходится как гармонический. Значит
абсолютной сходимости у исходного ряда
нет. Исследуем на условную сходимость
по признаку Лейбница.
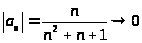при
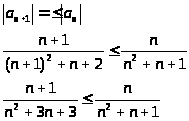
действительно для
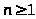
По признаку Лейбница, исходный ряд сходится условно.
Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа