Межотраслевой баланс (работа 1)
Межотраслевой баланс
Межотраслевой баланс (МОБ, метод «затраты-выпуск») — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Межотраслевой баланс составляется в денежной и натуральной формах.
Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостный состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли.
В межотраслевом балансе расположены три квадранта. В первом отражается промежуточное потребление и система производственных связей, во втором - структура конечного использования ВВП, в третьем - стоимостная структура ВВП.
Теоретические основы межотраслевого баланса были разработаны в СССР в 1923—1924 гг. В 30-е гг. для изучения американской экономики американский экономист Василий Леонтьев применил метод анализа межотраслевых связей с привлечением аппарата линейной алгебры. Метод стал известен под названием «затраты — выпуск».
Балансовый метод применяется для анализа, нормирования, прогноза, планирования производства и распределения продукции на различных уровнях - от отдельно предприятия до народного хозяйства в целом. Характерные черты и особенности этого метода описываются с помощью матричных моделей баланса. К этим моделям относят межотраслевые балансы районов республик и народного хозяйства в целом, межпродуктовые балансы в натуральном выражении, матричные модели трудоемкости и фондоемкости продукции, модели промфинплана предприятий. Все эти модели построены по единой матричной схеме, которую удобнее всего рассмотреть на примере межотраслевого баланса производства и распределения продукции в народном хозяйстве.
В модели межотраслевого баланса предполагается, что народное хозяйство состоит из множества отраслей, каждая из которых производит преимущественно один какой-либо продукт или оказывает определенные услуги. В процессе производства одна отрасль использует продукцию другой отрасли (сырье, материалы, оборудование, топливо, энергию, услуги) и между ними неизбежно возникают взаимные потоки товаров и услуг. Сложившаяся в соответствии с потребностями отраслей структура потоков товаров и услуг отражается в математической модели межотраслевого баланса системой уравнений следующего вида:
х>1> = х>11 >+ х>12 >+ … + х>1>>n>> >+ 0у>1;>
х>2> = х>21 >+ х>22 >+ … + х>2>>n>> >+ у>2;>
>………………………………………………>
х>n> = х>n>>1 >+ х>n>>2 >+ … + х>nn>> >+ у>n>>.(1)>
Различают два вида баланса: стоимостной – по отраслям производства и натуральный – по видам продукции в натуральном выражении.
В стоимостном балансе переменные х>1,> х>2, >… , х>n>> >означают объемы валовой продукции первой, второй, …, n-ой отрасли, x>ij>> >– объемы затрат i-й отрасли на производство продукции j-й отрасли, у>i>> >- конечный продукт, который не поступает в сферу текущего производственного потребления, а идет на конечное потребление (в личное и общественное, на накопление, экспорт, возмещение потерь и т.д.). Систему (1), которую учитывает структуру сложившихся взаимных затрат отраслей, можно назвать «экономической картой» народного хозяйства.
В натуральном балансе переменные х>1,> х>2, >… , х>n>> >означают объемы n видов производственных продуктов в натуральных единицах (автомобилей в штуках, угля в тоннах и т.д.). Величина x>ij> означает объем потребления продукта I при производстве продукта j (угля при производстве автомобилей, электроэнергии при добыче угля и т.д.), а величина у>i>> >– конечный продукт – ту часть продукции, которая не используется в производственном потреблении. Например, для производства сахара в необходимом объеме х>i>> >требуется предусмотреть объемы его расходов x>ij> в кондитерской и молочной, промышленности, расходы на производство безалкогольных напитков, винодельческое, плодоовощное и консервное производства, а также необходимо удовлетворить спрос населения на сахар как конечный продукт личного потребления.
В матричной форме системы уравнений (1) межотраслевой стоимостной и межпродуктовый натуральный балансы имеют одинаковое выражение. В том и другом случае общий объем продукции х>i>> >разделяется на объем производственного потребления – промежуточный продукт х>i>>1,> х>i>>2, >… , х>in>> >и объем> >непроизводственного потребления – конечный продукт у>i>>, >причем удельный вес их для разных отраслей стоимостного баланса и различных продуктов натурального баланса неодинаков.
Однако стоимостной баланс в отличие от натурального наряду с уравнениями
x>j>>
=
>в
форме распределения продукции допускается
построение уравнений в форме потребления
продукции
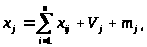(2)
где
- материальные затраты j-й
потребляющей отрасли; V>j>>
>+ m>j>>
>– ее чистая продукция;
V>j>>
>– сумма оплаты труда; m>j>>
>– чистый доход – прибыль.
Сделаем преобразование системы
уравнений (1) – каждое из слагаемых x>ij>
разделим и умножим на x>j>>
>и обозначим
………………………………………………………………………….
;
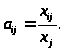
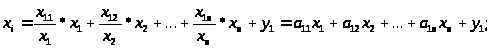
(3)
Это преобразование системы(1) приводит ее к обычной математической форме системы n линейных уравнений с n неизвестными х>1,> х>2, >… , х>n>> >(или у>1,> у>2, >… , у>n>>) >при заданных значениях коэффициентов а>ij>> >и величин у>1,> у>2, >… , у>n>> >(или х1, х2, … , хn).
Коэффициенты
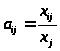называются коэффициентами прямых
затрат. Для всех отраслей их задают в
виде матрицы:
(4)
Коэффициенты прямых затрат в натуральном балансе означают технологические нормы расхода продукта i на производство единицы продукта j (например, расход сахара на банку плодово-ягодных консервов или на килограмм мороженного, киловатт-часов электроэнергии и тонн угля на один автомобиль и т.д.). в стоимостном балансе коэффициенты а>ij> означают затраты отрасли I на каждый рубль валовой продукции отрасли j.
В модели межотраслевого баланса коэффициенты прямых затрат а>ij> предполагаются постоянными. Это предположение позволяет с помощью уравнений (3) перейти от изучения и анализа сложившихся хозяйственных взаимосвязей к прогнозу пропорционального развития отраслей и планированию темпов их роста.
В системе уравнений (3) все неизвестные х>1,> х>2, >… , х>n>> >перенесем в левую часть уравнения ми получим новую фору записи системы уравнений межотраслевого баланса:
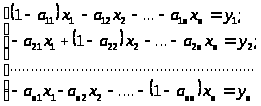(5)
Модель межотраслевого баланса (5) имеет простую матричную форму записи (Е – А) Х = У и позволяет решить следующие задачи:
1) определить конечный объем конечной продукции отраслей у>1,> у>2, >… , у>n>> >по заданным объемам валовой продукции у>1,> у>2, >… , у>n>> >(в матричной форме У = (Е – А) Х);
2) по заданной матрице коэффициентов прямых затрат А определить матрицу коэффициентов полных затрат Р, элементы которой служат важными показателями для планирования развития отраслей (в матричной форме Р = (Е – А)-1);
3) определить объемы валовой продукции отраслей х>1,> х>2, >… , х>n>> >по заданным объемам конечной продукции у>1,> у>2, >… , у>n>> >(в матричной форме Х = (Е – А)-1 У = Р У );
4) по заданным объемам конечной или валовой продукции отраслей х>1,> х>2, >… , х>n>> >определить оставшиеся n объемов.
В первой задаче планируется валовой выпуск продукции, а конечная продукция является производным показателем. Такой подход легче осуществить на практике, но он может привести к нерациональной структуре национального дохода и диспропорциям в развитии отдельных отраслей третья задача предлагает более прогрессивный принцип планирования – от национального дохода. Однако рассчитанные уровни валовой продукции для одних отраслей могут оказаться завышенными и ресурсно-необеспеченными, а для других – заниженными, не загружающими даже действующие производственные мощности. Четвертая задача в определенной степени отражает существую практику планирования.
Для того чтобы матрица коэффициентов прямых материальных затрат А была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
матрица (Е - А) неотрицательно
обратима, т.е. существует обратная
матрица (Е – А)-1
0;
матричный ряд Е + А + А2
+ А3 +….=
сходится, причем его сумма равна обратной
матрице (Е – А)-1;
наибольшее по модулю собственное
значение
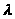матрицы А, т.е. решение характеристического
уравнения
,
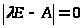строго меньше единицы;
все главные миноры матрицы (Е – А), т.е. определители матриц, образованные элементами первых строк столбцов этой матрицы, порядка от 1 до n, положительны.
Более простым способом проверки продуктивности матрицы А является ограничение на величину ее нормы. Если норма матрицы А строго меньше единицы, то эта матрица продуктивна. Данное условие являеться достаточным, но не необходимым условием продуктивной.
Список использованной литературы
1. И.В.Орлова Экономико-математическое моделирование: М. ВЗФЭИ 2007.
2. В.Д.Коновалов Экономико-математические модели и методы: Волгоград 1998.