Роль умственного приема классификации в формировании математических понятий у младших школьников

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

КРЫМСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ ИНСТИТУТ

ЕВПАТОРИЙСКИЙ ПЕДАГОГИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА МЕТОДИКИ НАЧАЛЬНОГО И ДОШКОЛЬНОГО ОБРАЗОВАНИЯ

ДИПЛОМНАЯ РАБОТА

РОЛЬ УМСТВЕННОГО ПРИЕМА КЛАССИФИКАЦИИ В ФОРМИРОВАНИИ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ У МЛАДШИХ ШКОЛЬНИКОВ

Студентки 5 курса

Свирской Натальи Витальевны

Евпаторийского

педагогического факультета

(специальность: «Начальное

обучение»)

Научный руководитель:

Глузман Неля Анатольевна.

Евпатория – 2004

СОДЕРЖАНИЕ

ВВЕДЕНИЕ……………………………………………………………………..3

РАЗДЕЛ 1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ

1.1. «Понятие» в психолого-педагогической, философской, учебно-методической литературе………………………………………………………..8

1.2. Виды и определения математических понятий в начальной математике……………………………………………………………………….16

1.3. Роль, функции классификации при формировании математических понятий ………………………………………………………………………….24

РАЗДЕЛ 2. МЕТОДИКА ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ В КУРСЕ НАЧАЛЬНОЙ МАТЕМАТИКИ

Общеметодические требования к усвоению и формированию математических понятий……………………………………………………..…32
Методическая система формирования математических понятий…………………………………………………………………………...40

2.3. Планирование, организация и анализ результатов процесса исследования……………………………………………………………………..72

ЗАКЛЮЧЕНИЯ И ВЫВОДЫ………………………………………………..90

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ………………………….92

ПРИЛОЖЕНИЯ

ВВЕДЕНИЕ

Проводимые в нашей стране преобразования ставят перед школой задачу не только вооружить школьников знаниями, но и научить их применять на практике, проявлять познавательный интерес и пытливость ума. Характерным признаком развития дидактики конца ХХ столетия является направленность на развитие личности. Умственное развитие личности, которое в государственной национальной программе «Освіта. Україна ХХІ століття» определено как приоритетное направление реформирования образования, требует не только определенного количества знаний, но и сформированности математических понятий, умственных действий и приемов. В Государственном стандарте общего среднего образования указано, что: «Ознакомление школьников с математикой должно рассматриваться, как особый метод миропонимания, познания ими диалектической связи математики с действительностью и математического моделирования сопутствующего развитию их научного мировоззрения».

Решающее значение для системы школьного математического образования имеет формирующий аспект предмета математики, широкие возможности для умственного развития личности.

В последние годы одним из основных образовательных заданий начальной школы является усвоение учениками математических понятий и формирование у них общих и специфических умственных действий.

С точки зрения современной психологии и дидактики ошибочным является утверждение о том, что овладение самим содержанием курса математики автоматически формирует мышление школьников. Необходимо специально учить умению мыслить, давать учащимся знания о содержании и последовательности умственных действий, обеспечивающих усвоение курса математики. Однако конкретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, пока нет. В результате работа над развитием логического мышления школьников идет без знания системы необходимых приемов, без знания их содержания последовательности формирования. Это приводит к тому, что большинство учащихся не овладевают основными приемами мышления даже в старших классах школы, а эти приемы необходимы уже младшим школьникам: без них не происходит полноценного усвоения материала.

Образование и становление понятий, переход к ним от чувственных форм отражения – сложный процесс, в котором применяются такие приемы умственной деятельности, как анализ, синтез, сравнение, классификация, обобщение, абстрагирование. Понятие – «это мысль, в которой отражаются общие, и притом существенные свойства предметов. Вместе с тем понятие не только отражают общее, но и расчленяют вещи, группируют их, классифицируют в соответствии с их различиями» [40 с.27] Таким образом, умственные действия (анализ, синтез, сравнение, классификация, обобщение, аналогия) составляют внутреннюю структуру понятия, его механизм.

Следовательно, не овладев основными приемами мышления, учащиеся испытывают трудности в усвоении системы понятий, в том числе и математических, которые в свою очередь служат опорным моментом в познании действительности и являются своеобразным итогом познания. Поэтому понятия являются одной из главных составляющих в содержании любого учебного предмета начальной школы, в том числе - и математики. Понятийное мышление формируется в начальных классах и раскрывается, совершенствуется в течение всей жизни.

Изложенное выше обусловило выбор темы исследования «Роль умственного приема классификации в формировании математических понятий у младших школьников».

К числу фактов, определивших выбор темы нашего исследования, относится также недостаточная научная разработанность данной проблемы. Анализируя подходы и концепции, сложившиеся в теории и практике умственного развития, следует отметить исследования, посвященные формированию математических понятий у детей (Л. С. Выготский, Ж. Пиаже, Д.Б.Эльконин, В.В. Давыдов, П.Я.Гальперин, Л.И. Айдарова), развитию компонентов мышления, методикам формирования приемов умственной деятельности у школьников (Н.Ф. Талызиной, Н.Б. Истоминой, Е.Н. Кабановой-Меллер, В.Н. Осинской, В. Ф. Паламарчук, Н.А. Менчинской, З.И. Слепкань, К.А. Степановой, Н.Г. Салминой, В.П. Сохиной, В.И. Зыковой, М.Б. Волович), формированию алгоритмов, способов и приемов мышления учащихся средней школы (В.М. Косатая, Л.Н. Ланда, И.С. Якиманская), но развитие и формирование отдельных умственных приемов, их значение в формировании математических понятий в условиях обучения младших школьников еще не нашла своего места в содержании математики начальных классов.

Объектом исследования является процесс формирования математических понятий у учащихся начальных классов.

Предмет исследования – организация учебной деятельности по формированию математических понятий с использованием умственного приема классификации у младших школьников.

Гипотеза исследования базируется на предположении о том, что систематическое и целенаправленное формирование и использование приема умственной деятельности классификации будет способствовать более глубокому и сознательному усвоению математических понятий младшими школьниками.

Цель исследования – заключается в обосновании и реализации методики формирования системы математических понятий у младших школьников с использованием приема классификации.

Цель работы и выдвинутая гипотеза позволили определить следующие основные задачи исследования:

- исследовать состояние проблемы в психолого-педагогической теории и практике школьного обучения;

- установить место и роль математических понятий в процессе обучения математики;

- определить методические требования к формированию математических понятий;

- обобщить опыт работы учителей, личный опыт по работе над математическими понятиями при обучении математике;

- проверить сформированность математических понятий у учащихся процессе опытно-экспериментальной работы.

Методы исследования:

- анализ отобранного программного материала, на котором можно реализовать проблему формирования математических понятий у младших школьников;

анализ методов, средств, форм организации по формированию математических понятий у младших школьников;

- изучение психолого-педагогической, методической, философской литературы по проблеме формирования математических понятий в начальной школе.

– изучение результатов деятельности младших школьников (проверка контрольных, самостоятельных работ и устного опроса) с целью определения уровня знаний и умений младших школьников при изучении отдельных тем.

Теоретическая значимость состоит в теоретическом обосновании идеи формирования математических понятий с использованием приема умственной деятельности классификации у учеников начальных классов. Разработке теоретической модели системы работы над математическими понятиями, что обеспечивает высокий уровень осмысления хода решения математического задания, а также способствуют развитию элементов творческого мышления у младших школьников.

Практическая значимость полученных результатов исследования состоит в апробации тестов и разработке комплекса тестовых заданий для определения сформированности понятий учеников в процессе изучения курса математики, в подготовке методических разработок, а также программ для статистической обработки результатов экспериментальной работы.

Дипломная работа состоит из введения, 2 глав, заключения, выводов, списка использованной литературы, приложений. Общий объем работы - 96.

Базой проведения экспериментального исследования был учебно-воспитательный комплекс «средняя общеобразовательная физико-математическая школа I – III ступеней № 6 – дошкольное учебное учреждение № 31.

РАЗДЕЛ 1

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ

Понятие в психолого-педагогической, философской, учебно-методической литературе

В педагогической, психологической, методической литературе указано, что мышление лежит в основе познания. Одна из характерных особенностей детского мышления – его наглядность, чувственно-практическая направленность.

В процессе отражения окружающей действительности различают познание чувственное и логическое. У младших школьников познание окружающей действительности осуществляется через формирование у них ощущений на основе деятельности органов чувств. В головном мозге идет отражение отдельных, изолированных свойств, внешних сторон предметов, явлений, которые непосредственно действуют на органы чувств. Но отдельных, изолированных свойств от предметов, явлений материального мира не существует. Поэтому отражение отдельных свойств предметов неизбежно приводит к отражению в сознании предмета в целом, таким образом, из ощущений возникает восприятие, в котором ученик отражает уже совокупность свойств, характерных для данного объекта, «строит» чувственно-наглядный образ, отражая уже объект в целом, во взаимосвязи его особенностей.

Чувственно-наглядный образ предметов и явлений действительности, сохраненный в сознании и без непосредственного воздействия самих предметов и явлений действительности на органы чувств называется представлением. Они возникают не мгновенно и не в законченном виде, а формируются, постепенно совершенствуются, изменяются под влиянием новых, целенаправленных актов восприятия. Представления возникают в сознании детей в виде наглядных образов, носят конкретный характер, тем не менее, эти образы могут отражать несущественные признаки, так как часть ощущений упускается.

Возникнув на основе ощущений и восприятия, являясь формой более обобщенного, но вместе с тем наглядно-чувственного отражения окружающей действительности, представления служат переходной ступенью к высшей форме познания – логическому, которое опирается на систему взаимосвязанных понятий. Формирование понятий невозможно без мыслительной деятельности школьников.

В педагогике понятие – это «форма научного знания, отражающая объективно существенное в вещах и явлениях и закрепляемая специальными терминами или обозначениями. В отличие от чувственных образов понятие – это нечто непосредственное, взятое во всем многообразии его качественных его особенностей. Из всего этого многообразия понятие отвлекает существенное и тем самым получает знание всеобщности, в чем и состоит его главная отличительная черта» [52, с.156].

Понятие – «одна из форм мышления, высший уровень обобщения, характерный для мышления словесно-логического» [38, С.123].

Понятием называют также «мысль, представляющую собой обобщение (и мысленное выделение) предметов некоторого класса по их специфическим (в совокупности отличительным) признакам» [63, с. 134].

В системе знаний об объектах и предметах окружающей действительности понятия служат опорным моментов в познании ее и являются своеобразным итогом познания. Поэтому понятия являются одной из главных составляющих в содержании любого учебного предмета, в том числе - и предметов начальной школы.

Проблема формирования понятий давно привлекает внимание психологов и педагогов (Л. С. Выготский, Д. Б. Эльконин, В. В. Давыдов, Н. А. Менчинская, Ж. Пиаже, П. Я.Гальперин, Л. И. Айдарова, Н. Г. Салмина, К. А. Степанова, В. И. Зыкова). В исследованиях, касающихся формирования понятий авторы часто обращаются к математике.

Л. С. Выготский впервые ввел в психологию деление понятий на научные и ненаучные - «житейские», при этом он имел в виду не содержание усваиваемых понятий, а путь их усвоения. Ребенок застает сложившуюся в обществе систему понятий. Усвоение этой системы всегда происходит с помощью взрослых. До систематического обучения в школе взрослые не ведут специальной работы по формированию понятий у детей. Они обычно ограничиваются лишь указанием на то, верно или неверно ребенок отнес предмет к соответствующему понятию. Вследствие этого ребенок усваивает понятия путем «проб и ошибок». При этом в одних случаях ориентировка фактически происходит по несущественным признакам, но в силу сочетания их в предметах с существенными в определенных пределах оказывается верной. В других - ориентировка происходит на существенные признаки, но они остаются неосознанными. Именно в этой неосознанности существенных признаков Л.С. Выготский и видел специфику так называемых житейских понятий. Такое усвоение понятий не отражает всех сторон специфически человеческого способа приобретения новых знаний.

Совсем другое дело, считал Л. С. Выготский, когда ребенок попадает в школу. Процесс обучения предполагает переход от стихийного хода деятельности ребенка к деятельности целенаправленной, организованной. Понятия, которые формируются у ребенка в школе, характеризуются тем, что их усвоение начинается с осознания существенных признаков понятия, что достигается введением определения.

Именно в этой осознанности существенных признаков Л. С. Выготский и видел специфику научных понятий. Этот путь, по его мнению, дает возможность ребенку в дальнейшем произвольно и сознательно действовать с понятием.

Исследования, проведенные впоследствии Н. А. Менчинской, показали, что предположение Л. С. Выготского не подтверждается.

Большинство учащихся безошибочно воспроизводят определение понятия, то есть обнаруживают знание его существенных признаков, но при встрече с реальными объектами опираются на случайные признаки, установленные в непосредственном опыте. И только постепенно, через ряд переходных этапов, в результате своей собственной практики учащиеся научаются ориентироваться на существенные признаки предметов.

Таким образом, словесное знание определения понятия не меняет, по существу, хода процесса усвоения этого понятия, что убедительно доказывает невозможность передачи понятия в готовом виде. Ребенок может получить его лишь в результате своей собственной деятельности, направленной не на слова, а на те предметы, понятие о которых мы хотим у него сформировать.

Н. Ф. Талызина говорит о том, что знание существенных признаков понятия может изменить ход и характер познавательной деятельности только в том случае, когда эти признаки войдут в нее в качестве ориентиров, то есть будут реально участвовать в процессе решения задач, поставленных перед ребенком. Поскольку при обычной организации учебного процесса это не обеспечивается, то со стороны познавательной деятельности учащихся усвоение житейских и научных понятий у значительной части обучаемых идет весьма сходным путем.

Н. Ф. Талызина, М. Б. Волович указывают, что для усвоения понятий обязательны такие действия:

подведение под понятие;
выбор необходимых и достаточных признаков для распознавания объекта;
выведение следствий о принадлежности и не принадлежности объекта к понятию.

Эти действия необходимы при усвоении любых понятий.

В.Н. Осинская считает, что для овладения понятиями необходимы следующие существенные компоненты:

усвоение определенной системы знаний о понятии;
овладение специальной операционной системой действий (подведение под понятие, выбор необходимых и достаточных признаков для распознавания объекта, выведение следствий);
установление системы понятий и их родовидовых отношений внутри системы, взаимосвязи их признаков;
раскрытие генезиса понятий.

Понятия должны формироваться не изолированно друг от друга, а выступать как элементы системы, находящиеся друг с другом в определенных отношениях.

Исследования К. А. Степановой показывают, что среднеуспевающие учащиеся шестого класса при решении задач на подведение под начальные геометрические понятия дали 72,5% правильных ответов. Однако обоснование правильности ответа имело место только в 27,5% случаев. В исследовании В. И. Зыковой отмечается, что такой уровень усвоения понятий наблюдается вплоть до восьмого-девятого классов. К. А. Степанова и В. И. Зыкова отмечают, что знание существенных признаков не обеспечивает сознательного использования их при ориентировке в соответствующей действительности.

Ж. Пиаже считал, что дети до подросткового возраста не способны к понятийному мышлению. До этого возраста ребенок использует различные интеллектуальные образования, функционально заменяющие понятия.

В.В. Давыдов и Д.Б. Эльконин указывали на возможность более раннего формирования понятийных структур у ребенка в условиях специального обучения по сравнению с их стихийным формированием.

В.В. Давыдов считает, что «овладеть понятием – это значит не только знать признаки предметов и явлений, охватываемых данным понятием, но и уметь применять понятие на практике, уметь оперировать им» [50, с. 81].

П.Я. Гальперин выдвинул теорию о поэтапном формировании математических понятий. В соответствии с этой теорией формирования математических понятий осуществляется через шесть этапов:

Первый этап – создание мотивации;
Второй этап - формирование схемы ориентировочной основы деятельности. Выделяют три типа построения структуры обучения, которые зависят от полноты ориентирования учеников:

- Ученикам дается образец действия и его результат. В полном объеме им не дают сведений о способе выполнения задача, поэтому ученики действуют путем попыток и ошибок. При таком типе обучения учителю приходится больше заниматься устранением ошибок, переучиванием, чем правильным обучением.

- При втором типе ориентирования ученикам дается алгоритм выполнения задача. При строгом выполнении указаний алгоритма обучение идет без ошибок и более скорое, чем при первом типе. Новая задача ученик сначала сравнивает с задачей, которую он уже решил, и если они одного типа, данный учителем алгоритм переносится на новую задачу. Недостатками такого обучения есть то, что ученику дается полный перечень операций для выполнения задачи, при этом слабо развивается эвристическая деятельность. Если ученику всегда давать готовые алгоритмы, схемы, он мало продвинется в умственном развитии, не смотрясь на то, что предметными привычками и умениями он будет владеть успешно.

- Третий тип: ученики не столько учатся способа выполнения действия при решении конкретной задачи, сколько учатся анализировать задачи и самостоятельно составлять схему действия. Ориентировочная основа действия может даваться учителем только в обобщенном виде, а ученики самостоятельно дополняют ее при выполнении конкретной задачи. Такой способ обучения оказывает содействие созданию у учеников фундамента знаний, умений и привычек, благодаря чему ученик быстро ориентируется в новых обстоятельствах и может овладевать новыми знаниями, привычками самостоятельно. Работа по третьему типу ориентирования отвечает закономерностям формирования содержательных обобщений, оказывает содействие развитию творческого теоретического мышления.

3. Третий этап обучения сводится к выполнению действия в материальной или материализованной форме.

4. На четвертом этапе происходит формирование действия с помощью устной речи без опоры на материальные или материализованные средства (все операции алгоритма, предписания проговариваются вслух по мере их выполнения). Такая система обучения разрешает ученику следить за ходом выполнения действия, обеспечивает единство предметной (внешней) и умственной (внутренней) деятельности. Со временем громкое произношение начинает снижать производительность обучения, поэтому она должна постепенно переходить в произношение «про себя».

5. Пятый этап – формирование действия с помощью внутренней речи (операции проговариваются про себя, действие начинает сокращаться и автоматизироваться).

6. Шестой этап - этап интериоризации действия, то есть формирование действия во внутренней речи. Действие становится внутренним процессом, максимально автоматизируется, становится актом мышления.

Обучение, проведенное на основе этой теории, показало, что дети способны усваивать абстрактные понятия, обобщенные знания уже в первом классе начальной школы, причем в условиях массового обучения (Д. Б. Эльконин, В. В. Давыдов, Л. И. Айдарова, Н. Г. Салмина, В. П. Сохина).

Образования понятий, переход к ним от чувственных форм отражения – сложный процесс, в котором применяются такие приемы умственной деятельности, как анализ, синтез, сравнение, классификация, обобщение, абстрагирование. Понятие – «это мысль, в которой отражаются общие, и притом существенные свойства предметов. Вместе с тем понятие не только отражают общее, но и расчленяют вещи, группируют их, классифицируют в соответствии с их различиями» [41, с.27].

С. Л. Рубинштейн дал такое определение классификации: «Выявляя тождество одних и различие других вещей, сравнение приводит к классификации. Тождество и различие, основные категории рассудочного познания выступает сначала как внешнее отношение. Более глубокое познание требует раскрытия внутренних связей, закономерностей и существенных свойств. Это осуществляется всеми видами мыслительных операций – анализа, синтеза, обобщения, абстракции»[54, с 87].

С. Д. Максименко обосновал свое видение классификации не через сравнение, а через обобщение. Он пишет: «Обобщение выделенных черт предметов и явлений дает возможность группировать объекты по видовым, родовым и другим признакам» [44, с. 98].

Чтобы осуществить классификацию, необходимо четко определить ее цель, признаки объектов, которые подлежат классификации, сравнивать их по существенным признакам, определить общие основания классификации, сгруппировать объекты по определенному признаку.

Р. С. Немов говорит о том, что «Сравнение вскрывает тождество и различие вещей. Результатом сравнения может являться классификация. Она выступает как первичная форма теоретического и практического познания».[42, с. 125]

Ю. Л. Трофимова определяла классификацию как: «Мысленное объединение предметов и явлений по их общим и существенным признакам».

К определению приема умственной деятельности классификации через сравнение подходила Д. М. Дубравская. «Сравнивая предметы и явления, мы выделяем наиболее общие их признаки и на этой основе осуществляем классификацию».

Как видно из определений классификация связана в учебном познании со всеми основными приемами умственной деятельности (анализ, синтез, сравнение, обобщение).Учитель должен обратить особое внимание на формирование специальных умений и навыков, овладение приемами мышления, понятий, познавательного интереса, которые формируются и развиваются в начальных классах. Недостаточное внимание учителя начальных классов к этим вопросам приводит к большим трудностям при последующем изучении не только математики, но и других учебных предметов.

1.2. Виды и определения математических понятий в начальной математике

При усвоении научных знаний учащиеся начальной школы сталкиваются с разными видами понятий. Неумение ученика дифференцировать понятия приводит к неадекватному их усвоению.

Логика в понятиях различает объем и содержание. Под объемом понимается тот класс объектов, которые относятся к этому понятию, объединяются им. Так, в объем понятия треугольник входит все множество треугольников независимо от их конкретных характеристик (видов углов, размера сторон и др.).

Под содержанием понятий понимается та система существенных свойств, по которой происходит объединение данных объектов в единый класс.

Чтобы раскрыть содержание понятие, следует путем сравнения установить, какие признаки необходимы и достаточны для выделения его отношения к другим предметам. До тех пор, пока не установлены содержание и признаки, не ясна сущность предмета, отражаемого этим понятием, невозможно точно и четко отграничить этот предмет от смежных с ним, происходит путаница мышления.

Например, понятии треугольник к таким свойствам относятся следующие: замкнутая фигура, состоит из трех отрезков прямой. Совокупность свойств, по которым объединяются объекты в единый класс, называются необходимыми и достаточными признаками. В одних понятиях эти признаки дополняют друг друга, образуя вместе то содержание, по которому и объединяются объекты в единый класс. Примером таких понятий могут служить треугольник, угол, биссектриса и многие другие.

Совокупность данных объектов, на которые распространяется данное понятие, составляет логический класс объектов.

Логический класс объектов – это совокупность объектов, имеющие общие признаки, вследствие чего они выражаются общим понятием. Логический класс объектов и объем соответствующего понятия совпадают.

Понятия делятся на виды по содержанию и объему в зависимости от характера и количества объектов, на которые они распространяются.

По объему математические понятия делятся на единичные и общие. Если в объем понятия входит только один предмет, оно называется единичным.

Примеры единичных понятий: «наименьшее двузначное число», «цифра 5», «квадрат, длина стороны которого 10 см», «круг радиусом 5 см».

Общие понятие отображает признаки определенного множества предметов. Объем таких понятий всегда будет больше объема одного элемента.

Примеры общих понятий: «множество двузначных чисел», «треугольники», «уравнения», «неравенства», «числа кратные 5», «учебники математики для начальной школы».

По содержанию различают понятия конъюнктивные и дизъюнктивные, абсолютные и конкретные, безотносительные и относительные.

Понятия называются конъюнктивными, если их признаки взаимосвязаны и по отдельности ни один из них не позволяет опознать объекты этого класса, признаки связаны союзом «и». Например, объекты, относящиеся к понятию треугольник, обязательно должны состоять из трех отрезков прямой и быть замкнутыми.

В других понятиях отношение между необходимыми и достаточными признаками другие: они не дополняют друг друга, а заменяют. Это означает, что один признак является эквивалентом другого. Примером такого вида отношений между признаками могут служить признаки равенства отрезков, углов. Известно, что к классу равных отрезков относятся такие отрезки, которые: а) или совпадают при наложении; б) или порознь равны третьему; в) или состоят из равновеликих частей и т.д.

В данном случае перечисленные признаки не требуются все одновременно, как это имеет место при конъюнктивном типе понятий; здесь достаточно какого-то одного признака из всех перечисленных: каждый из них эквивалентен любому из остальных. В силу этого признаки связаны союзом «или». Такая связь признаков называется дизъюнкцией, а понятия соответственно называются дизъюнктивными.

Важно также учитывать деление понятий на абсолютные и относительные.

Абсолютные понятия объединяют предметы в классы по определенным признакам, характеризующим суть этих предметов как таковых. Так, в понятии угол отражены свойства, характеризующие сущность любого угла как такового. Аналогично положение со многими другими геометрическими понятиями: окружность, луч, ромб и т.д.

Относительные понятия объединяют объекты в классы по свойствам, характеризующим их отношение к другим объектам. Так, в понятии перпендикулярные прямые фиксируется то, что характеризует отношение двух прямых друг к другу: пересечение, образование при этом прямого угла. Аналогично в понятии число отражено отношение измеряемой величины и принятого эталона.

Относительные понятия вызывают у учащихся более серьезные трудности, чем понятия абсолютные. Суть трудностей состоит именно в том, что школьники не учитывают относительность понятий и оперируют с ними как с понятиями абсолютными. Так, когда учитель просит учеников изобразить перпендикуляр, то некоторые из них изображают вертикаль. Особое внимание следует уделить понятию число.

Число - это отношение того, что подвергается количественной оценке (длина, вес, объем и др.) к эталону, который используется для этой оценки. Очевидно, что число зависит как от измеряемой величины, так и от эталона. Чем больше измеряемая величина, тем больше будет число при одном и том же эталоне. Наоборот, чем больше будет эталон (мера), тем меньше будет число при оценке одной и той же величины. Следовательно, учащиеся с самого начала должны понять, что сравнение чисел по величине можно производить только тогда, когда за ними стоит один и тот же эталон. В самом деле, если, например, пять получено при измерении длины сантиметрами, а три - при измерении метрами, то три обозначают большую величину, чем пять. Если учащиеся не усвоят относительной природы числа, то они будут испытывать серьезные трудности и при изучении системы счисления.

Трудности в усвоении относительных понятий сохраняются у учащихся и в средних, и даже в старших классах школы.

Между содержанием и объемом понятия существует зависимость: чем меньший объем понятия, тем больше его содержание.

Например, понятие «квадрат» имеет меньший объем, чем объем понятия «прямоугольник» так как любой квадрат - это прямоугольник, но не всякий прямоугольник есть квадрат. Поэтому понятие «квадрат» имеет большее содержание, чем понятие «прямоугольник»: квадрат имеет все свойства прямоугольника и некоторые другие (у квадрата все стороны равны, диагонали взаимно перпендикулярны).

В процессе мышления каждое понятие не существует в отдельности, а вступает в определенные связи и отношения с другими понятиями. В математике важной формой связи есть родовидовая зависимость.

Например, рассмотрим понятия «квадрат» и «прямоугольник». Объем понятия «квадрат» есть частью объема понятия «прямоугольник». Поэтому первое называют видовым, а второе - родовым. В родо-видовых отношениях следует различать понятие ближайшего рода и следующие родовые ступени.

Например, для вида «квадрат» ближайшим родом будет род «прямоугольник», для прямоугольника ближайшим родом будет род «параллелограмм», для «параллелограмма» - «четырехугольник», для «четырехугольника» - «многоугольник», а для «многоугольника»- «плоская фигура».

В начальных классах впервые каждое понятие вводится наглядно, путем наблюдения конкретных предметов или практического оперирования (например, при счете их). Учитель опирается на знание и опыт детей, которые они приобрели еще в дошкольном возрасте. Ознакомления с математическими понятиями фиксируется с помощью термина или термина и символа.

Такая методика работы над математическими понятиями в начальной школе не означает, что в этом курсе не используются различные виды определений.

Определить понятие - это перечислить все существенные признаки объектов, которые входят в данное понятие. Словесное определение понятия называется термином.

Например, «число», «треугольник», «круг», «уравнение» - термины.

Определение решает две задачи: выделяет и отмежевывает какое-то определенное понятие от всех других и указывает те главные признаки, без которых не может существовать понятие и от которых зависят все остальные признаки.

Определение может быть более или менее глубоким. Это зависит от уровня знаний о понятии, которое означается. Чем лучшее мы его знаем, тем большая вероятность, что мы сможем дать для него лучшее определение.

В практике обучения младших школьников применяются явные и неявные определения.

Явные определения имеют форму равенства или совпадения двух понятий.

Например: «Пропедевтика есть вступление в любую науку». Здесь приравнивают один к одному два понятия – «пропедевтика» и «вступление в любую науку».

В определении «Квадрат - это прямоугольник, у которого все стороны равны» имеем совпадение понятий.

В обучении младших школьников особый интерес среди неявных определений составляют контекстуальные и остенсивные определения.

Любой отрывок из текста, будь какой контекст, в котором случается понятие, которое нас интересует есть, в некотором понимании, неявным его определением. Контекст ставит понятие в связь с другими понятиями и тем самим раскрывает ее содержание.

Например, употребляя в работе с детьми такие выражения, как «найти значения выражения», «сравнить значение выражений 5 + а и (а - 3)  2, если а = 7», «прочитать выражения, которые являются суммами», «прочитать выражения, и потом прочитать уравнения», мы раскрываем понятие «математическое выражение» как запись, которая складывается из чисел или переменных и знаков действий.

Почти все определения, с которыми мы встречаемся в повседневной жизни - это контекстуальные определения. Услышав, неизвестное слово, мы стараемся сами установить его значение на основании всего сказанного.

Подобное имеет место и в обучении младших школьников. Много математических понятий в начальной школе определяются через контекст. Это, например, такие понятия, как «большой — маленький», «какой-нибудь», «любой», «один», «много», «число», «арифметическое действие», «уравнение», «задача» и т.д.

Контекстуальные определения остаются большей частью неполными и незавершенными. Они применяются в связи с неподготовленностью младшего школьника к усвоению полного и тем более научного определения.

Остенсивные определния - это определения путем демонстрации. Они напоминают обычные контекстуальные определения, но контекстом здесь есть не отрывок какого-либо текста, а ситуация, в которой оказывается объект, обозначенный понятием.

Например, учитель показывает квадрат (рисунок или бумажную модель) и говорит «Смотрите - это квадрат». Это типичное остенсивное определение.

В начальных классах остенсивные определения применяются при рассмотрении таких понятий как «красный (белый, черный и т.д.) цвет», «левый - правый», «слева направо», «цифра», «предшествующее и следующее число», «знаки арифметических действий», «знаки сравнения», «треугольник», «четырехугольник», «куб» и т.д.

На основе усвоения остенсивным путем значений слов есть возможность вводить в словарь ребенка уже вербальное значение новых слов и словосочетаний. Остенсивные определения - и только они - связывают слово с вещами. Без них язык - лишь словесное кружево, которое не имеет объективного, предметного содержания.

Заметим, что в начальных классах допустимые определения наподобие «Словом «пятиугольник» мы будем называть многоугольник с пятью сторонами». Это так называемое «номинальное определение».

В математике используются разные явные определения. Наиболее распространенное из них - определение через ближайший род и видовой признак. Родовидовое определение еще называют классическим.

Примеры определений через род и видовой признак: «Параллелограмм - это четырехугольник, у которого противоположные стороны параллельные», «Ромбом называется параллелограмм, стороны которого равны», «Прямоугольником называется параллелограмм, у которого углы прямые», «Квадратом называется прямоугольник, в которым стороны равны», « Квадратом называется ромб, у которого прямые углы».

Рассмотрим определения квадрата. В первом определении ближайшим родом будет «прямоугольник», а видовым признаком – «все стороны равны». В втором определении ближайший род «ромб», а видовой признак – «прямые углы».

Если же взять не ближайший род («параллелограмм»), то видовых признаков квадрата будет два «Квадратом называется параллелограмм, у которого все стороны равны и все углы прямые».

В родовидовом отношении находятся понятия «сложение (вычитание, умножение, деление)» и «арифметическое действие», понятие «острый (прямой, тупой) угол» и «угол».

Примеров явных родовидовых отношений среди множества математических понятий, которые рассматриваются в начальных классах, не так уже и много. Но с учетом важности определения через род и видовой признак в дальнейшем обучении желательно добиваться понимания учениками сущности определения этого вида уже в начальных классах.

Отдельные определения могут рассматривать понятие и по способу его образования или возникновения. Определение такого типа называют генетическими.

Примеры генетических определений: «Угол - это лучи, которые выходят с одной точки», «Диагональ прямоугольника - отрезок, который соединяет противоположные вершины прямоугольника». В начальных классах генетические определения применяют для таких понятий, как «отрезок», «ломаная», «прямой угол», «круг».

К генетическим понятиям можно отнести и определение через перечень.

Например, «Натуральный ряд чисел — это числа 1, 2, 3, 4 и т.д.».

Некоторые понятия в начальных классах вводят только через термин.

Например, единицы времени год, месяц, час, минута.

Есть в начальных классах понятия, которые подаются символическим языком в виде равенства, например, а 1= а, а 0=0

В начальных классах много математических понятий сначала усваиваются поверхностно, расплывчато. При первом ознакомлении школьники узнают только о некоторых свойствах понятий, очень узко представляют их объем. И это закономерно. Не все понятия легко усвоить. Но бесспорно, что понимание и своевременное использование учителем тех или других видов определений математических понятий - одна из условий формирования у учеников твердых знаний об этих понятиях.

1.3. Роль, функции классификации при формировании понятий

В организации учебной деятельности младших школьников в процессе формирования математических понятий особую роль играет прием классификации. Для того чтобы решать вопрос о принадлежности предмета к данному понятию учащиеся должны уметь дифференцировать признаки на существенные и несущественные, необходимые и достаточные, выделять различные свойства – то есть владеть целой системой логических приемов (анализ, синтез, сравнение, классификация, обобщение).

Классификация - это прием умственной деятельности, представляющий собой систематическое распределение элементов данного множества по классам, согласно наиболее существенным признакам.

В теории множеств классификация - это действие распределения объектов по классам на основании сходств объектов внутри класса и их отличия от объектов других классов.

Этот прием умственной деятельности является средством упорядочения изучаемых объектов, установления закономерных связей между ними. Именно в этом случае классификация выявляет существенные сходства и различия между предметами и имеет большое познавательное значение. Классификация основывается на способности видеть общее в каждом конкретном единичном случае и преследует цель уточнить, обобщить знание о связях и отношениях между изучаемыми объектами.

Признак, который является классификационным основанием, должен быть наиболее пригодным и удобным для определения предметов в классификационной системе.

Структуру классификации, как приема умственной деятельности образуют следующие действия:

определение цели классификации объектов (понятий, отношений);
выбор основания (существенное свойство, признак) для классификации;
деление по этому основанию всего множества объектов (понятий, отношений) на непересекающиеся подмножества, входящих в объем данного понятия;
построение иерархической классификационной системы.

Разновидность объектов для классификации достаточно обширна даже в рамках одного учебного предмета, не говоря уже о всей совокупности предметов, которые изучают в школе. В теории множеств это могут быть свойства функций, понятия, виды отношений и соответствий, законы, теоремы и т.д.

В процессе овладения умением классифицировать необходимо сформировать у учеников на практических примерах представления о таких понятиях, как вид, род, класс, объем понятия, деление объема понятия.

Класс - это совокупность (разряд или группа) предметов, выделенных по некоторому общему признаку, мыслимая как единое целое.

Вид - подразделение в систематике, входящее в состав высшего разряда - род. Вид представляет собой специфическое, особенное в пределах общего.

Род - группа, которая объединяет несколько видов, обладающих общими признаками. Род представляет собой нечто общее в предметах, составляющих его виды. Видовое понятие обязательно обладает всеми свойствами родового, которое выступает по отношению к видовому как следующая ступень обобщения.

Из определений видно, что деление на виды, роды, классы весьма относительно. Одно и то же понятие в разных классификационных системах может выступать и как видовое и как родовое. Установление родовидовых отношений, выделение в понятиях рода и видового различия - один из основных этапов классификации.

При выполнении классификации должно выполнятся следующие требования:

Классификация должна проводится по одному и тому же основанию.
Образованные подмножества (классы) непересекающиеся, т.е. никакая пара их не имеет общих элементов. Символическая запись этого условия: Кi  Kj =  для i, j, где i j.
Классификация должна быть соразмерной, т.е. объединение всех подмножеств (классов) образует все множество. Классификация должна быть непрерывной, т.е. классами должны быть ближайшие видовые понятия по отношению к понятию, подлежащему классификации.

В качестве оснований для классификации выделяют свойства данных объектов. В связи с этим можно выделить следующие уровни классификации:

Классификация (типология) - деление всего объема понятия на непересекающиеся подмножества, группы (классы) согласно наиболее общего существенного свойства.
Ошибочная классификация - деление объектов (понятий, отношений) на группы (классы) согласно наиболее общего свойства, выделенного непосредственным восприятием объектов (понятий, отношений). Обычно такие ошибочные классификации осуществляются на эмпирическом уровне усвоения знаний.

Существуют различные способы проведения классификации:

Классификация по видоизмененному признаку. Элементы понятия, подлежащего классификации, обладают несколькими признаками. В качестве основания классификации могут использоваться различные признаки классифицируемого понятия.

Пример: ученики третьего класса легко могут разбить множество Х треугольников на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются (среди остроугольных нет прямоугольных и тупоугольных, среди прямоугольных – тупоугольных) и их объединение совпадает с множеством Х. Однако то, что не всякая система подмножеств данного множества представляет собой разбиение этого множества им понять сложно. Например, если из множества Х треугольников выделить подмножества равнобедренных, равносторонних и разносторонний, то разбиения множества Х на классы мы не получим, поскольку множества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными).

Из таблицы видно, что образовалось девять классов, из которых некоторые пусты (см. табл.1.1 ).

В случае алгебраических уравнений при одновременном использовании двух оснований классификаций получаем, например, класс уравнений первой степени с двумя переменными или класс уравнений второй степени с одной переменной и т. д. При одновременной классификации натуральных чисел по признаку делимости их на 2 и на 3 получаем класс натуральных чисел, делящихся на 6, и др.

Выбор признака классификации зависит от целей классификации, от практических задач. Важнейшим требованием к признаку (основанию) классификации является его объективность. Нельзя делить книги на интересные и неинтересные, задачи на легкие и трудные, так как такие признаки носят субъективный характер. В самом деле, одни и те же теоремы могут быть легкими для одних учеников и трудными для других.

2) Дихотомическая (от греческих слов dicha и tome «сечение на две части») классификация представляет собой деление объема классифицируемого понятия на два видовых понятия, один из которых обладает данным признаком, а другой не обладает им.

Сравнивая дихотомическую классификацию с классификацией по видоизмененному основанию, можно выделить ряд преимуществ. Эта классификация всегда удовлетворяет требованию соразмерности, так как объединение образованных классов полностью исчерпывает объем понятия, подлежащего классификации. Кроме того, образованные классы всегда исключают друг друга.

Однако дихотомическая классификация не лишена недостатков. Так, разделив объем понятий на два противоречащих друг другу видовых понятия, мы оставляем весьма неопределенным то видовое понятие, которое содержит частицу «не». Например, разделив класс тригонометрических уравнений на простейшие уравнения и не простейшие, оставляем достаточно неясным объем класса не простейших тригонометрических уравнений.

Пример. Применяя дихотомию можно провести классификацию треугольников и четырехугольников так:

Дихотомия часто используется при разбиении данного множества одновременно по нескольким основаниям.

3) Дихотомия по разным основаниям – разбиение объема классифицируемого понятия по независимым основаниям на 2п класса.

Имеет место следующая теорема: при разбиении множества М по n независимым основаниям образуется 2 n класса (n ).

Эта теорема о разбиении множества по n независимым основаниям может быть использована для решения задач определенного типа.

Для решения таких задач целесообразно использовать наглядную интерпретацию разбиения множества на классы с помощью диаграмм Эйлера - Венна. В диаграмме заполняется числом элементов каждая ее часть (класс) в соответствии с условиями задачи, что и ведет к решению задачи.

Пример. Рассмотрим два свойства натуральных чисел: «быть кратным 3» и «быть кратным 5».При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А - подмножество чисел, кратных 3, и В – подмножество чисел, кратных 5. Эти подмножества пересекаются, но ни одно из них не является подмножеством другого.

П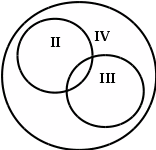роанализируем получившуюся картину. Круг, изображающий множество N натуральных чисел, разбился на 4 непересекающиеся области – они пронумерованы римскими цифрами. Каждая область изображает некоторое подмножество множества N . Определим, какие числа оказались в каждом из этих непересекающихся подмножеств. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II – из чисел, кратных 3 и не кратным 5; подмножество III – из чисел, кратных 5 и не кратных 3; подмножество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.

Для формирования умений по классификации и систематизации целесообразно на практических занятиях (или в качестве самостоятельной работы) предлагать упражнения на составление классификационных схем. Порядок составления таких схем предполагает схематическое изображение изученных в данной теме понятий на основе их родо - видовых отношений.

Классификационные схемы целесообразно составлять в конце изучения темы или раздела.

При изложении математики в школе часто приходится прибегать к классификации. В процессе классификации образуется система изучаемых понятий. Полезны классификации при повторении, так как при этом систематизируется изучаемый материал, ученики получают более полное представление о взаимосвязях между понятиями и о системе математических понятий. В процессе этой работы важно широко использовать таблицы, схемы, диаграммы, иллюстрирующие вопросы классификации и их применение при решении задач.

Применение приема классификация на уроках позволяет существенно расширить имеющиеся в практике приемы работы, способствуют формированию положительных мотивов в учебной деятельности, так как подобная работа содержит и элементы игры и элементы поисковой деятельности, что в свою очередь повышает активность учащихся и обеспечивает самостоятельное выполнение работ.

РАЗДЕЛ 2.

МЕТОДИКА ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ В КУРСЕ НАЧАЛЬНОЙ МАТЕМАТИКИ

2.1. Общеметодический подход к формированию математических понятий в школьной практике

В школьной практике многие учителя добиваются от учеников заучивания определений понятий и требуют знания их основных доказываемых свойств. Однако результаты такого обучения обычно незначительны. Это происходит потому, что большинство учащихся, применяя понятия, усвоенные в школе, опираются на малосущественные признаки, существенные же признаки понятий ученики осознают и воспроизводят только при ответе на вопросы, требующие определения понятия. Часто учащиеся безошибочно воспроизводят понятия, то есть обнаруживают знание его существенных признаков, но применить эти знания на практике не могут, опираются на те случайные признаки, выделенные благодаря непосредственному опыту. Процессом усвоения понятий можно управлять, формировать их с заданными качествами

Достигается это через выполнение следующей системы условий.

Первое условие. Наличие адекватного действия: оно должно быть направлено на существенные свойства. Выбор действия определяется, прежде всего, целью усвоения понятия. Допустим, понятие усваивается для того, чтобы распознавать объекты, относящиеся к данному классу. В этом случае необходимо использовать действие распознавания, действие подведения под понятие. Если учащиеся не знакомы с этими действиями, то необходимо раскрыть их содержание, показать, как следует их выполнять.

Второе условие. Знание состава используемого действия. Так, действие распознавания включает: а) актуализацию системы необходимых и достаточных свойств понятия; б) проверку каждого из них в предлагаемых объектах; в) оценку полученных результатов с помощью одного из логических правил распознавания (для понятий с конъюнктивной и понятий с дизъюнктивной системой признаков). При раскрытии содержания действия особое внимание уделяется его ориентировочной основе, которая должна быть не только адекватной, но и полной.

Действие распознавания может быть использовано при формировании понятий с конъюнктивной структурой признаков; дизъюнктивные понятия требуют некоторого изменения в процессе распознавания объектов.

Для понятий с дизъюнктивной структурой признаков правило распознавания, как было показано, имеет такой вид:

- объект относится к данному понятию, если он обладает, хотя бы одним признаком из числа альтернативных;

- если объект не обладает ни одним из этих признаков, то он не относится к данному понятию;

- если ни про один из признаков неизвестно, есть он или его нет, то неизвестно, относится или не относится этот объект к данному понятию

Кроме действия распознавания можно использовать и другие, которые мы рассмотрели ранее: выведение следствий, сравнение, классификация, действия, связанные с установлением иерархически» отношений внутри системы понятий. Порядок формирования логических действий определяется как содержанием каждого из них, так и отношениями друг с другом.

Третье условие. Все элементы действия представлены во внешней, материальной (или материализованной) форме. Применительно к действию подведения под понятие это выглядит следующим образом. Система необходимых и достаточных признаков понятия выписывается на карточку, эти признаки материализуются. (При усвоении, например, понятия перпендикулярные прямые даются модели прямой линии, прямого угла.)

Учащимся разъясняют, что плюс означает наличие соответствующего признака, минус - отсутствие, знак вопроса - «неизвестно» (невозможность дать определенный ответ). Плюс после вертикальной черты означает, что определяемый предмет подходит под данное понятие, знак минус - не подходит, знак вопроса - неизвестно, подходит или нет. Кроме того, указывается, что во втором и третьем случаях ответ не изменится, если минус и знак вопроса будут относиться не ко второму, а к первому признаку. Алгоритм распознавания выписывается также на карточку.

Четвертое условие - поэтапное формирование введенного действия. В случае использования действия подведения под понятие проведение его через основные этапы осуществляется следующим образом. На этапе предварительного знакомства с действием учащемуся, после создания проблемной ситуации, раскрывают назначение действия подведения под понятие, важность проверки всей системы необходимых и достаточных признаков, возможность получения разных результатов, все это поясняя на конкретных случаях в материализованной форме. После этого учащемуся предлагается самому выполнить действие (это уже материализованный этап).

Учащиеся, используя ориентиры (признаки, правила) в материальной или материализованной форме, устанавливают наличие необходимой системы признаков у предметов, задаваемых непосредственно или в виде моделей и чертежей. Результаты выполнения каждой операции фиксируются с помощью тех же условных знаков («+», «-», «?») на заранее заготовленных схемах.

Система может, конечно, состоять из большего или меньшего числа необходимых и достаточных признаков.

Пятое условие - наличие пооперационного контроля при усвоении новых форм действия. Как было уже указано, контроль лишь по конечному продукту действия не позволяет следить за содержанием и формой выполняемой учащимися деятельности. Пооперационный контроль обеспечивает знание и того, и другого. При формировании понятий с помощью действия подведения под понятие в качестве операций выступает проверка каждого признака, сравнение с логическим правилом и так далее.

Естественно, что перед формированием действия подведения под понятие необходимо установить исходный уровень познавательной деятельности учащихся и произвести формирование необходимых предварительных знаний и действий.

Более подробно остановимся на поэтапном формировании понятий.

После выполнения пяти-восьми заданий с реальными предметами или моделями учащиеся без всякого заучивания запоминают и признаки понятия, и правило действия. Затем действие переводится во внешнеречевую форму, когда задания даются в письменном виде, а признаки понятий, правило, и предписание называются или записываются учащимися по памяти. На этом этапе учащиеся могут работать парами, поочередно выступая то в роли исполнителя, то в роли контролера.

В том случае, когда действие легко и верно выполняется во внешнеречевой форме, его можно перевести во внутреннюю форму. Задание дается в письменном виде, а воспроизведение признаков, их проверку, сравнение полученных результатов с правилом учащийся совершает про себя. Учащийся все еще получает указания типа «Назови про себя первый признак», «Проверь, есть ли он» и т.д. Вначале контролируется правильность каждой операции и конечного ответа. Постепенно контроль осуществляется лишь по конечному результату и производится по мере необходимости.

Если действие выполняется правильно, то его переводят на умственный этап: учащийся сам и выполняет, и контролирует действие. В программе обучения на этом этапе предусматривается контроль со стороны обучающего только за конечным продуктом действия; обучаемый получает обратную связь при наличии затруднений или неуверенности в правильности результата. Процесс выполнения теперь скрыт, действие стало полностью умственным, идеальным, но содержание его известно обучающему, так как он сам его строил и сам преобразовал из действия внешнего, материального.

Так постепенно происходит преобразование действия по форме. Преобразование действия по обобщенности обеспечивается специальным подбором заданий. При этом учитывается как специфическая, так и общелогическая часть ориентировочной основы действия.

Для обобщения специфической части, связанной с применением системы необходимых и достаточных признаков, даются для распознавания все типичные виды объектов, относящихся к данному понятию. Так, при формировании понятия угол важно, чтобы учащиеся поработали с углами, отличающимися по величине (от 0° до 360° и больше), по положению в пространстве и т.п. Кроме того, важно взять и такие объекты, которые имеют лишь некоторые признаки данного понятия, но к нему не относятся.

Для обобщения логической части действия распознавания даются для анализа все основные случаи, предусмотренные логическим правилом подведения под понятие, т.е. задания с положительным, отрицательным и неопределенным ответами. Можно включать также задания с избыточными условиями. Характерно, что в практике обучения, как правило, дается лишь один тип задач: с достаточным составом условий и положительным ответом. В результате учащиеся усваивают действие распознавания в недостаточно обобщенном виде, что, естественно, ограничивает пределы его применения. Задачи с избыточными, неопределенными условиями дают возможность научить учащихся не только обнаруживать те или иные признаки в предметах, но и устанавливать достаточность их для решения стоящей задачи. Последние в жизненной практике часто выступают как самостоятельная проблема.

Преобразование действия по двум другим свойствам достигается повторяемостью однотипных заданий. Делать это целесообразно, как было указано, лишь на последних этапах - шестом или пятом. На всех других этапах дается лишь такое число заданий, которое обеспечивает усвоение действия в данной форме. Задерживать действие на переходных формах нельзя, так как это приведет к автоматизации его в данной форме, что препятствует переводу действия в новую, более позднюю форму.

Во всех случаях, когда реализовались указанные условия, то есть процесс усвоения шел не стихийно, а контролировался учителем, понятия формировались с заданным содержанием и со следующими характеристиками:

Шестое условие - разумность действий испытуемых. Главное, что постоянно подтверждалось, - это ориентировка учащихся с самого начала на всю систему существенных признаков, т.е. имела место разумность действий.

Для установления разумности действий используются три вида задач:

а) задачи, в которых имеется полный состав условий, но чертеж не соответствует условиям задачи;

б) задачи с неполным составом условий и без чертежа;

в) задачи с неполным составом условий и не адекватным условию задачи чертежом. (Например, в условии сказано, что даны два равных угла с общей вершиной. Спрашивается, будут ли они вертикальными. На чертеже изображены вертикальные углы. Правильный ответ: «Неизвестно», так как нет данных о том, составляют ли стороны одного угла прямые линии со сторонами другого.) Этот вид задач объединяет в себе особенности первых двух. Проверку разумности целесообразно начинать с предъявления именно таких задач. Если испытуемый справляется с ними, то это достаточный показатель разумности его действий. В самом деле, подобные задачи могут быть правильно решены только при ориентировке на обобщенную систему существенных признаков и на логическое правило распознавания. В том случае, когда ученик ориентируется на чертеж, он обязательно ошибается. Если он учитывает лишь отдельные существенные признаки, то задача также будет решена неверно. Наконец, решение этих задач требует знания всех возможных случаев, которые могут быть при решении задач на распознавание. В частности, умения дифференцировать случай, когда ответ неопределенный, и случай, когда ответ отрицательный, то есть когда условия полные, но известно, что предмет не обладает какими-то необходимыми признаками.

Седьмое условие - осознанность усвоения. Все учащиеся при работе с понятиями должны правильно аргументировать свои действия, указывая при этом основания, на которые они опирались при ответе.

Восьмое условие - уверенность учащихся в знаниях и действиях. Учащиеся обнаруживают не только разумность и осознанность, но и большую уверенность в своих действиях.

Если действия выступают как предмет специального усвоения, где имеет место управление ходом их формирования, - действия и знания формируются как разумные, сознательные, произвольные, и это приводит к тому, что дети действуют адекватно и уверенно.

Девятое условие - отсутствие связанности чувственными свойствами предметов. При школьном обучении учащиеся лишены адекватной ориентировочной основы, поэтому они учатся дифференцировать предметы, опираясь на те их свойства, которые лежат на поверхности. Таким образом, ученики идут на поводу внешних, чувственных свойств не в силу особенностей своего мышления, а потому, что не имеют в своем распоряжении ничего более надежного. Но как только мы даем им средства опоры на существенные свойства, которые далеко не всегда являются наглядными, они успешно используют их, не попадают во власть случайных свойств, если даже последние являются яркими и постоянными в предметах.

Десятое условие - обобщенность понятий и действий. Обобщенность формируемых понятий и действий проверяется двумя путями. Во-первых, устанавливается возможность испытуемых применить сформированные понятия и действия в новых условиях, в той или иной степени отличающихся от условий обучения (например, сохраняя в процессе обучения устойчивость материала, цвета и формы объектов, в контрольных заданиях предъявляются объекты данного класса, имеющие другой цвет, другую форму, сделанные из другого материала). Во-вторых, устанавливается влияние сформированных понятий на процесс усвоения новых - как из той же области знаний, так и существенно иной.

Одиннадцатое условие - прочность сформированных понятий и действий. Сформированные знания и действия не только приводят к правильным ответам, но и сохраняют все рассмотренные качества: разумность, сознательность.

Используя данную систему условий можно добиться от учеников сознательного и систематического усвоения математических понятий, применения на практике.

2.2. Методическая система по формирования математических понятий: множества, величины, числа, алгебраических и геометрических понятий.

В начальных классах формируются следующие математические понятия:

Множество, частные случаи операций над множествами.
Величина.
Геометрический материал.
Число, количественный и порядковый (аксиоматический) подходы к множеству натуральных чисел.
Операции над натуральными числами (количественный и аксиоматический подходы), их свойства.
Числовые выражения. Числовые равенства и неравенства, их свойства.
Выражения с переменными, их область определения. Тождество.
Уравнения и неравенство; их область определения и множество решений. Свойства уравнений и неравенств.
Функции: понятие, область определения, область значений, способы задания.

Множество, частные случаи операций над множествами.

Множество – это основное неопределяемое понятие.

При формировании понятия «множество» нужно научить детей задавать множество указанием характеристических свойств, перечислением элементов, с помощью кругов Эйлера-Венна; уметь определять принадлежит ли данный элемент множеству или нет; находить мощность конечного множества (количество элементов множества).

Так, показав картину, учитель спрашивает: «Что на ней изображено?» Дети отвечают, например, «Яблоки» (то есть задается множество указанием характеристического свойства). Затем учитель показывает изображение груши и спрашивает: «Входит ли она в заданное множество?» Дети отвечают: «Нет».

Формирование смысла арифметических действий над натуральными числами и их свойств базируется на основе соответствующих операций над множествами и их законов. Здесь важно использовать множества, а не их мощности, то есть при формировании смысла арифметических действий нужно избегать возможности нахождения результата операции с помощью пересчета элементов получившегося множества.

Над множествами можно выполнять 5операций.

Рассмотрим их.

Объединение множеств.

Объединением двух множеств называется такое множество, элементы которого принадлежат хотя бы одному из этих множеств.

Это определение легко можно проиллюстрировать на кругах Эйлера-Венна, где заштрихованная часть является результатом объединения двух множеств (рис. 2.1):

а) б) в) г)

Рис. 2.1

Основные свойства этой операции:

а) коммуникативный закон: А В = В А

б) ассоциативный закон: {А В} C = A {B C}.

Случай а) является теоретической основой формирования смысла операции сложения натуральных чисел, а коммуникативный и ассоциативный законы выступают в начальных классах как переместительное и сочетательное свойства суммы натуральных чисел.

Операцию сложения натуральных чисел можно сформировать с помощью такой практической работы. Слева на парте лежат треугольники, а справа квадраты. Учитель просит собрать вместе и назвать получившееся множество. Дети отвечают: «Мы получили геометрические фигуры». Учитель обобщает: «Мы выполнили сложение, которое обозначается знаком «+» и называется суммой (рис.2.2).

сумма

Рис. 2.2

Таким образом, сложение натуральных чисел рассматривается как частный случай объединения двух чисел.

Так как объединение множеств коммунитативно и ассоциативно, то переместительное и сочетательное свойства сложения можно сформировать сразу же после введения слова «сумма». Так учитель может задать вопрос: «Изменится ли сумма, если сначала в центр парты положить квадраты, а потом треугольники?

Показать прикладную сторону использования коммунитативности сложения можно на такой практической работе.

На партах учеников выложены треугольники и квадраты. Количество квадратов в 3 – 4 раза превышает количество треугольников. Кто быстрее по одной геометрической фигуре соберет их в одну группу. После практической работы ученики должны сделать вывод, как быстрее можно выполнить работу и почему.

Пересечение множеств.

Пересечением двух множеств называется такое множество, элементы которого принадлежат первому и второму множеству (рис. 2.3).

а) б) в) г)

Рис. 2.3

Основные свойства этой операции:

а) коммуникативный закон: А В = В А

б) ассоциативный закон: {А В} C = A {B C}.

Пересечение двух множеств можно формировать в начальных классах при рассмотрении, например, общей части геометрических фигур: прямоугольника АВСД и квадрата КСМЕ (рис. 2.4).

В С

А К

Рис. 2.4

Разность множеств.

Разностью множеств А и В называется такое множество, элементы которого принадлежат множеству А и не принадлежит множеству В (рис.2.5).

Случаи г) и д) являются теоретической основой формирования смысла операции вычитания натуральных чисел.

а) б) в) г) д)

Рис. 2.5

Операцию вычитания натуральных чисел можно сформировать с помощью такой практической работы.

В пенале лежат письменные принадлежности (ручки и карандаши), выложили на парту все ручки, а карандаши с пеналом положили в портфель. Надо узнать, сколько было карандашей. Чтобы ответить на вопрос задачи, надо знать, сколько было письменных принадлежностей всего, сколько было ручек. Разность между ними и есть карандаши. Таким образом операция вычитания натуральных чисел рассматривается как случай разности двух множеств.

Декартово произведение двух и более множеств.

До сих пор порядок записи элементов множества роли не играли. Однако в практике, зачастую, порядок записи элементов имеет большое значение. Например, порядок букв в слове, или порядок записи однозначных чисел в многозначном числе (23 = 32).

Кортежем длины n называется упорядоченная n – ка (а , а , …а ), где а А ,а А ,…, а А .

Декартовым произведением множеств А х А х…х А называется множество всевозможных кортежей ( а , а ,…а ), где а А , а А,… а А .

Декартово произведение обладает следующими основными свойствами:

А х В = В х А;
M (A x B) = m (B x A) – количество элементов декартова произведения В х А.

В начальных классах операция умножения натуральных чисел рассматривается как мощность декартова произведения.

Операцию умножения натуральных чисел можно сформировать с помощью такой практической работы.

На парте лежат короткие, средние, длинные палочки красного, синего, желтого и белого цветов. Надо разложить их по цвету и по размеру.

По цвету По размеру

Красные- Короткие – красная, синяя, желтая, белая

Синие - Средние – красная, синяя, желтая, белая

Желтые - Длинные - красная, синяя, желтая, белая

Белые –

В первом случае палочек 3 + 3 + 3 + 3 = 3 х 4, во втором – 4 + 4 + 4 = 4х3.

Так как в обоих случаях были разложены все палочки, то 3 х 4 = 4 х 3. Таким образом, эта практическая работа позволяет сформировать не только смысл операции умножения как мощности декартового произведения, но и переместительное свойство умножения.

Разбиение.

Операция разбиения на попарно непересекающееся подмножества характеризуются следующими свойствами:

ни одно из подмножеств не пусто;
любые два подмножества не имеют общих элементов;
объединение всех подмножеств дает данное множество.

Операция деление натуральных чисел опирается на разбиение конечного множества на попарно непересекающиеся равномощные подмножества. Она раскрывается путем рассмотрения задач на деление по содержанию и равные части. Это можно осуществить на примере таких работ.

Пример № 1. Несколько карандашей надо раздать трем ученикам. Сколько карандашей получит каждый ученик и сколько их было?

Сначала раздадим по одному карандашу, потом еще по одному и так далее. Пусть каждый ученик получил по 4 карандаша, тогда всего карандашей было: 4 кар. х 3 =12 кар.

Пример № 2. Несколько карандашей надо раздать детям по 4 карандаша. Сколько учеников получит карандаши и сколько их было всего?

Сначала 4 карандаша дали одному ученику, потом 4 карандаша дали второму и так далее. Пусть 3 ученика получили по 4 карандаша, тогда всего карандашей было : 4 кар. х 3 = 12 кар.

Затем учитель должен обобщить полученные результаты: «В первой задаче мы искали первый сомножитель, а во второй задаче мы искали второй сомножитель. Так как умножение обладает переместительным свойством, то мы выполнили в обеих задачах одну и ту же операцию, которая называется делением». После этого учитель записывает:

4 х 3 = 12; 12 3 = 4;

4 х 3 = 12, 12 4 = 3.

2. Величина

Понятие величины является фундаментальным в школьном курсе математики и, в особенности, в начальном обучении. Ведь исторически работа с величинами и привела к появлению математики как таковой. Рассматривая величину как свойство однородных предметов или явлений «быть сравнимым», учитель может с помощью конкретных предметных действий сформировать у учащихся такие важнейшие понятия, как положительное действительное число, операции над числами и их законы, измерение величин и именованные числа, тесно связать геометрический и арифметический материал.

Величины бывают трех видов: скалярные, аддитивно-скалярные, векторные.

Примером скалярных величин является свойство химических элементов быть сравнимыми по активности. Так, натрий более активен, чем железо. Однако, сказать, на сколько он более активен нельзя, то есть нельзя выполнить операцию сложения: к активности железа нельзя, например, добавить активность свинца и получить активность натрия поэтому скалярные величины не являются той основой, на которой возникла математика.

Аддиктивно-скалярные величины (аддитивность – это наличие операции сложения; аддитивная операция – операция сложения) можно не только сравнивать, но и определять, на сколько один элемент множества, обладающего величиной, больше (меньше) другого элемента этого же множества.

Таким образом, аддитивно-скалярные величины можно складывать и поэтому именно на их основе возникла в результате абстрагирования математика. Примером аддитивно-скалярных величин является множество отрезкой, площадей.

Векторные величины можно сравнивать не только с позиции «столько», «больше». «меньше», но и по направлению. Примерами векторных величин является скорость, ускорение.

В начальных классах специальным предметом изучения являются следующие аддитивно-скалярные величины: количество, длина, площадь, масса, емкость, время.

В дальнейшем, для упрощения, вместо того, чтобы говорить «аддитивно-скалярная величина», или «множество, обладающее величиной», будем говорить просто «величина».

Рассмотрим основные свойства величин.

1. Свойство быть сравнимым.

Это свойство должно формироваться в начальных классах в три этапа на основе предметных действий детей.

а) Визуальное сравнение.

Приведем примеры практических работ.

Пример 1. (рис. 2.6). Приложив полоски, выяснить, какие из них длиннее (рис. 2.6).

Пример 2. Наложив друг на друга два листа бумаги, выяснить, какой из них больше (рис. 2.7).

Рис. 2.7

Пример 3. Взяв в одну руку деревянный шар, а другую металлический шар, определить, какой из них тяжелее (шары одинаковые по размеру).

Пример 4. Сравнить два ведра одинаковой формы и ответить, в какое из них больше поместиться воды (рис. 2.8).

Рис. 2.8

б) Опосредованное сравнение.

Пример 1. Ученикам предлагается сравнить длины двух отрезков, изображенных на доске; определить по рисунку в книге, кто из детей живет ближе к школе.

Чтобы ответить на поставленный вопрос, используются две веревочки. Ими измеряют длины, а затем наложением сравнивают.

Пример 2. Ученикам предлагается сравнить массы двух тел, с этой целью используются рычажные весы.

2). Сравнение с помощью посредников.

Пример 1. Учащимся предлагается сравнить расстояние Евпатория – Симферополь, Евпатория – Киев.

Пример 2. Ученикам предлагается сравнить две площади разной конфигурации (рис. 2.9).

Рис. 2.9

Пример 3. Ученикам предлагается сравнить возраст своих родителей.

В каждом случае ученики придут к выводу, что ни визуально, ни опосредовано провести сравнение невозможно. Они сделают вывод о том, что величины необходимо сначала измерить, а потом сравнить числа, полученные в результате измерения. Тем самым ученики подводятся к пониманию причины возникновения числа.

Наличие операции сложения.

Величины можно складывать, то есть имеет место операция сложения. Эта операция имеет такие важные свойства:

единственность суммы;
коммутативность сложения (переместительное свойство);
ассоциативность сложения (сочетательное свойство).

Операцию сложения и ее свойство нужно формировать у учащихся не только на примере такой величины, как количество, но и на примерах других величин.

Пример 1. Ученикам предлагается перевязать большой пакет имеющимися маленькими веревочками.

Ученики связывают обрывки веревок и перевязывают пакет. При этом подчеркивают, что порядок, в котором связываются обрывки веревок, роли не играет (переместительное и сочетательное свойство сложения).

Пример 2. Ученику предлагается угостить соком своих друзей, если у него имеется разное количество сливового сока и грушевого.

Ученик сливает сок в одну посуду и получает грушево – сливовый сок, которым угощает друзей. Подчеркивается, что количество сока не измениться от того, в каком порядке он сливается.

Так как сложение величин является теоретической основой формирования смысла операции сложения, а не нахождения результата сложения, поэтому при рассмотрении данных примеров учитель должен избегать возможности измерения величин, в том числе и пересчета.

Умножение величины на натуральное число.

Пол умножением величины а на натуральное число n понимается сумма в одинаковых величин: а + а +…+ а = а n.

Это свойство является теоретической основой операции умножения в начальных классах. Поэтому, при ее формировании необходимо подчеркивать, что одна и та же величина повторяется несколько раз, то есть именованное число нужно ставить при умножении на первое место.

Пример 1. Учащимся предлагается составить полоску из четырех одинаковых полосок и измерить ее. Дети получают в результате измерения 40 см.

Учитель предлагает найти длину полоски не измеряя ее, если известно, что она состоит из четырех одинаковых полосок по 10 см каждая.

Дети записывают: 10 см + 10 см + 10 см + 10см = 40 см.

Учитель обращает внимание на громоздкость записи и знакомит их с другой записью и новой операцией – умножением: 10 см 4 = 40 см.

Учащиеся под руководством учителя делают вывод о том, что в данном случае умножение представляют сумму одинаковых величин, то есть, что умножение есть частный случай сложения.

Пример 2. Задача. Сколько минут отводится ученику на выполнение контрольной работы, если надо решить 5 примеров и на каждый пример отводится 4 минуты?

4 мин x 5 = 15 мин (4 минуты повторятся 5 раз).

Примечание. Подход к операции умножения как к сумме одинаковых величин позволяет объяснить смысл умножения натуральных чисел, начиная с двух. Умножение на 1, на 0, умножение дробных чисел нельзя рассматривать с позиции суммы одинаковых слагаемых.

Свойство неограниченной делимости.

Любую величину а при произвольном натуральном числе m можно представить в виде суммы одинаковых величин b: а = b + b + …+ b или а = b m. Это означает, что b является той m –той частью а, то есть величина b есть 1/m доля величины а.

Доля является одним из случаев обыкновенной дроби, что и надо подчеркнуть при изучении доли в начальных классах. Это можно сделать, например, в ходе решения следующих задач.

Задача 1. 12 яблок разделить поровну между четырьмя детьми. Сколько яблок получит каждый ребенок?

Каждый ребенок получит четвертую часть от 12 яблок, то есть по 3 яблока.

Задача 2. Одно яблоко надо разделить поровну между четырьмя детьми. Сколько яблок получит каждый?

Каждый получит четвертую часть, то есть 1/4 яблока.

Задача 3. Пять яблок надо разделить поровну между четырьмя детьми. Сколько яблок получит каждый?

Каждый получит четвертую часть, то есть 1 яблоко и еще 1/4 яблока, что составляет 1и 1/4 яблока или 5/4 яблока.

Аксиома Архимеда.

Если а и b две однородные величины и а > b, то найдется такое натуральное число n, что а < b n.

Эта аксиома позволяет выполнять измерения величин, что широко применяется в начальных классах.

В ходе измерения ученики получают конкретное натуральное число (в данном случае это число 4).

Пример 2. Измерить емкость банки с помощью стакана. Сколько стаканов помещается в банке?

Пример 3. Измерить площадь многоугольника данной меркой (рис. 2.11).

Рис. 2.11

Наличие общей мерки.

Общей меркой однородных величин a и b называется такая величина c, которая помещается в a и b целое число раз: a = c x n и b = c x m.

Свойство двух однородных величин иметь общую мерку лежит в основе формирования понятия обыкновенной дроби.

В начальных классах представление об обыкновенной дроби можно сформировать с помощью следующей практической работы.

Детям предлагается измерить отрезок AB с помощью отрезка CD (рис. 2.12).

Дети убеждаются, что отрезок CD не помещается в AB целое число раз. Тогда им предлагается в качестве мерки отрезок МК, с помощью которого они измеряют отрезки AB и CD. Пусть в отрезке AB отрезок МК помещается 4 раза, а в отрезке CD – 3 раза. Значит, отрезок МК является 1/3 частью отрезка CD и поэтому в отрезке AB отрезок CD помещается 5/3 раза. Таким образом, в результате измерения отрезка AB отрезком CD получилась дробь 5/3.

Примечание. Еще в глубокой древности ученые пришли к выводу, что существуют и величины, которые не имеют общей мерки. Таким образом, в результате измерения могут получиться натуральные числа, дробные числа (положительные рациональные числа) и иррациональные числа, то есть любое положительное действительное число есть результат измерения величин. Поэтому измерению различных величин в начальных классах должно быть уделено серьезное внимание.

Требования к измерению величин.

1. Равным однородным величинам должно быть поставлено в соответствие единственное число.

Формирование в начальных классах этого требования к измерению величин осуществляется в следующей последовательности:

а) визуальное сравнение;

б) опосредованное сравнение;

в) создание проблемной ситуации: как быть, если ни визуально, ни опосредованно сравнить нельзя. Ученики подводится к выводу, что нужно сравнить числа, которые получаются в результате измерения.

Примеры практических работ на визуальное сравнение, опосредованное сравнение, необходимость измерения величин были приведены выше.

Из множества однородных величин выбирается одна, которой ставится в соответствие число один.

Здесь важно показать, что за единицу измерения может быть взят любой элемент. Однако, если одинаковые по величине элементы будут измеряться разными единицами измерения, то полученные числа не помогут сделать верный вывод по сравнению этих элементов. Этот момент можно сформировать у учащихся с помощью следующей практической работы.

Пример 1. Учитель показывает три одинаковые полоски красного, белого и черного цветов и просит, не накладывая их назвать, какая из них короче, а какая – длиннее. Дети называют черную полоску самой короткой, а белой – самой длинной. Тогда, раздав одному ряду красные полоски, другому – белые, третьему черные, учитель просит измерить их мерками (полосками), которые заранее розданы на парты. В результате измерения красных полосок дети получают число 3, черных – 4, белых – 2. После этого учитель наложением полосок убеждает детей, что они одинаковой длины, и задает вопрос: «Почему в результате измерения получились разные числа?» Учащиеся приходят к выводу, что нужно договориться и измерять одинаковыми мерками (единицами измерения). После этого можно провести беседу о разных единицах измерения длин.

Пример 2. Аналогичную работу можно провести по измерению площадей, взяв одинаковые листы бумаги белого, черного и красного цветов, а за единицу измерения белого листа бумаги взять 1/2 листа, красного листа бумаги –1/4 листа, черного листа бумаги – 1/8.

Если величина «а» есть сумма величин «b» и «c», то ее мера равна сумме их мер.

Сформировать это требование можно при помощи следующих практических работ.

Пример 1. Надо перевязать пакет с помощью нескольких коротких веревочек. Ученики связывают нужное количество обрывков и перевязывают пакет. Дается задание: какой длины веревку нужно взять оператору почты, чтобы перевязать пакет такого же размера, если веревку связали из трех кусков длиной 10 см, 15 см и 30 см. Дети находят: 10см +25см +30 см =55 см.

Пример 2. Нужно сравнить две геометрических фигуры разной формы (рис. 2.12). В ходе измерения дети приходят к выводу, что фигуры равновелики, так как они равносоставлены.

Рис. 2.12

Пример 3. Учитель дает задание составить из одинакового набора геометрических фигур дом и собаку (рис. 2.13).

Рис.2.13

III. Геометрический материал.

Обычно геометрический материал рассматривается в начальных классах как некоторое вкрапление, не связанное с основным программным материалом. Однако, если обучение математике в начальных классах строить на понятии величины, то геометрический материал выступает не как изолированный, а как базовый, позволяющий формировать многие математические понятия (см. раздел "Величины").

Изучение геометрического материала должно начинаться с формирования представления о точке, линии, прямой линии, отрезке, луче, угле. Это можно осуществить с помощью, например, таких практических работ.

Пример 1. Учитель просит детей два раза ткнуть карандашом в лист бумаги и сообщает, что они получили две точки. Затем он просит, как угодно соединить их и говорит, что они получили линии, каждый свою (рис.2.14). Затем учитель просит отметить на линии красным карандашом несколько точек, синим карандашом - несколько точек над линией, зеленым карандашом - несколько точек под линией.

Рис. 2.14

Тем самым у учеников формируется представление о линии как множестве точек, о положении точек относительно линии (на, над, под).

Пример 2. Учитель предлагает детям бросить на парту веревочки, которые были им розданы. Ученики получают разные линии. Учитель предлагает взять веревочку за концы я натянуть, У детей получается отрезок прямой линии. Затем дети в тетрадях отмечают две точки и с помощью линейки проводят через них прямую линию.

Пример 3. Ученики отмечают в тетрадях три точки одна под одной и проводят через одну точку прямую линию, луч до второй точки и луч от третьей точки (рис. 2.15). Учитель вводит понятие луча и дети подводятся к выводу, что прямая, в данном случае, состоит из двух лучей.

Рис. 2.15

Пример 4. Детям предлагается соединить два луча так, чтобы получилась прямая линия, и не получилась прямая линия. Вводится понятие угла, вершины утла, сторон угла (рис. 2.16).

Рис. 2.16

Пример 5. Детям дается задание соединить три отрезка, которые заранее розданы на парты, концами так, чтобы получилась замкнутая ломанная линия. Учитель просит сосчитать углы у получившейся геометрической фигуры и говорит, что, так как у нее три угла, эту фигуру называют треугольником. Затем учитель просит составить треугольник из трех отрезков, сумма двух из которых меньше третьего отрезка (рис. 2.17).

Делается вывод, что в треугольнике обязательно две любые стороны вместе больше третьей стороны.

Аналогично учащиеся знакомятся и с другими геометрическими фигурами и их свойствами.

Вопрос об измерении геометрических фигур, о единицах измерения и взаимосвязях между ними достаточно подробно рассмотрен в разделе "Величины".

IV. Натуральные числа

Натуральное число имеет двоякую природу, так как отвечает на вопросы "сколько" и "какой по счету". Например, если стоит очередь, то

прежде, чем стать в нее, человек интересуется сколько в ней всего людей. А, когда он уже стоит в очереди, то его интересует, какой он по счету, т.е. сколько людей стоит пред ним.

Таким образом, существует два подхода к понятию натурального числа:

- теоретико-множественный (количественная теория) и аксиоматический (порядковая теория), которые тесно переплетаются в методике преподавания. Поэтому, чтобы избежать ошибок, учитель должен знать, какой из подходов лежит в основе изучения конкретного вопроса.

Теоретико-множественный подход к понятию натурального числа базируется на понятиях конечного множества и взаимно-однозначного соответствия. Приведем схему введения натуральных чисел.

1. Определение. Два конечных множества называются равночисленными, если между ними можно установить взаимно-однозначное соответствие.

2. Отношение "быть равночисленным" разбивает все конечные множества на классы эквивалентности.

3. Каждый класс эквивалентности характеризуется мощностью, поэтому каждому множеству данного класса приписывают как характеристику одно и то же натуральное число.

4. Мощность пустого множества принимается за натуральное число ноль.

Понятие "быть равночисленным" и умение разбивать конечные множества на классы эквивалентности формируется у детей в дочисловой период при изучении темы "Столько, больше, меньше". Покажем, как на основе практической деятельности учащихся можно сформировать понятия о натуральных числах от 0 до 10.

Пример 1. Тема урока "Число и цифра 3".

На одной полке наборного полотна два кружочка, на второй - три, третья полочка пустая (рис. 2.17). Учитель, показывая разные конечные множества, просит разложить их по полкам, т.е. предлагает выполнить классификацию.

Рис. 2.17

После этого задаются вопросы:

1. Одинаковые ли группы предметов на второй полке? - Нет.

2. Почему же вы их поставили на одну полку? - Количество предметов у них одинаковое.

Учитель делает вывод о том, что это свойство (количество элементов каждого множества данного класса) и есть число 3.

Затем учитель показывает написание цифры 3, т.е. значка, с помощью которого изображается число три.

Следующий этап урока - закрепление. Учитель предлагает найти в классной комнате множество, содержащее по три элемента; выполнить с помощью заданной мерки измерение длины отрезка или площади геометрической фигуры, В этом случае число выступает в новом качестве: оно выражает отношение одной величины к другой. Так, выполняя задание по измерению емкости банки с помощью кружки, ученики получают натуральное число как результат отношения одной емкости к другой. Такой подход приводит к расширению понятия о положительном числе, так как результатом измерения может быть натуральное число, дробное число (положительное рациональное), иррациональное число. Таким образом, рассматривая с первого класса натуральное число как результат измерения величин, ученики постигают причины возникновения любого положительного действительного числа, что очень важно для последующего обучения в школе.

Пример 2. Тема урока "Число нуль".

Учитель задает вопросы типа: "Сколько холодильников в классе?", "Сколько грузовых автомобилей в классе?", Дети отвечают, что этого ничего нет. Тогда учитель говорит, что это соответствует числу нуль и можно записать с помощью цифры 0.

Аксиоматический подход к понятию "натуральное число" базируется на следующих основных (неопределяемых) понятиях: "натуральное число" с выделенным числом "О" (или "I") и "непосредственно следовать за..,".

В целом ряде книг за выделенное число принимается число 1. На наш взгляд целесообразнее выделять число 0, так как методика его введения аналогична методике выделения любого однозначного натурального числа (см. примеры 1 и 2). Кроме того, легче вводить тогда использование линейки.

Свойства этих основных понятий, соотношение между ними раскрываются в аксиомах Пеано (итальянский математик). Приведем некоторые из них.

Аксиома 1. Нуль непосредственно не следует ни за каким натуральным числом.

Эта аксиома формируется у учащихся при пользовании линейкой для измерения длины отрезка: учитель подчеркивает, что линейку надо прикладывать так, чтобы начало отрезка совпадало с делением 0.

Аксиома 2. Для любого натурального числа существует только одно натуральное число, которое непосредственно следует за ним.

Эта аксиома формируется у учащихся с помощью вопросов: "Какое число идет за числом V ? "Может ли за числом 2 идти число 5 ?"

Аксиома 3. Любое натуральное число непосредственно следует не более чем за одним натуральным числом.

Эта аксиома формируется у детей с помощью вопросов: "За каким числом идет число 5 ?", "Может ли число 5 идти за числом 3 ?", "За каким числом идет число О?"

Таким образом, аксиоматический подход к понятию натурального числа позволяет охарактеризовать следующие свойства натурального ряда чисел (порядковую структуру множества натуральных чисел).

1. Множество натуральных чисел бесконечно, с начальным элементом О и без конечного элемента.

2. Множество натуральных чисел упорядочено (любые два натуральных числа можно сравнить). "

3. Множество натуральных чисел дискретно (между двумя любыми натуральными числами можно поместить конечное множество натуральных чисел).

V. Операции над натуральными числами

Ранее уже неоднократно подчеркивалось, что в методике обучения операциям над натуральными числами следует отличать саму операцию от результата операции.

Смысл операций над натуральными числами и их законы формируются на теоретико-множественной основе. Нахождение результата операций раскрывается в аксиоматической теории. Так, операции сложения и умножения натуральных чисел базируется на следующих аксиомах

Операция сложения Операция умножения.

1. а + 0 = а; 3. а • 0 = 0;

2. а + b' я (а + b)' 4. а • b' = а ' b + а . Следствие: а + 1 = а' . Следствие: а • 1 =5 а .

Аксиомы 1 и 3 и следствия из этих аксиом ученики должны твердо знать Нахождение результата сложения (до таблиц сложения) определяется путем присчитывания по одному (т.е. используется первое следствие).

Нахождение результата умножения в начальных классах нельзя рассматривать с позиции аксиом 3 и 4. Поэтому в традиционной методике умножение рассматривается как частный случай сложения, что позволяет умножать натуральные числа только начиная с двух. Естественно, такой подход к операции умножения нельзя считать удачным, так как не позволяет найти результат умножения в таких случаях, как а • 1; а - 0;

(а/b) • (с/а).

В разделах I и III достаточно подробно рассмотрена операция умножения как мощность декартова произведения и как сумма одинаковых величин. Существует и другой подход к операции умножения, с позиции которого можно обосновать не только умножение натуральных чисел, начиная с двух, но и умножение на 1 и на 0, умножение обыкновенных дробей. Этот подход заключается в том, что умножение рассматривается как переход от одной единицы измерения к другой Сформировать у учащихся смысл операции умножения с этой позиции можно на таких практических работах.

Пример 1. Нужно измерить емкость банки сначала кружками, а потом стаканами (рис. 2.18). В ходе измерения получили 5 кружек или 15 стаканов. Учитель обращает внимание на то, что стаканами измерять долго, и задает

Рис. 2.18

вопрос: "Нельзя ли узнать, не измеряя, сколько стаканов в банке?" Дети предлагают для этого измерять стаканами кружку. Так как в банке 5 кружек (старая мерка) и в одной кружке 3 стакана (новая мерка), то в банке 5 • 3 = 15 (стаканов).

Пример 2. Учитель предлагает быстро пересчитать тетради. Ученики считают по две тетради (старая мерка) и получают 15 пар, поэтому в пачке 15 - 2 = 30 (тетрадей).

Пример 3. Ученикам предлагается быстро измерить полоску и даются две мерки: в 1 дм и в 1 см Дети меряют сначала большой меркой и получают число 4. Так как 1 дм содержит 10 см (новая мерка 1 см), то вся полоска содержит 4 • 10 = 40 (см).

Пример 4. Задача. Сколько нужно плиток кафеля, чтобы обложить такую же стенку, которая изображена на рис. 31? Дети считают сначала рядами (1 ряд -старая мерка), а потом -сколько в ряду плиток (1 плитка - новая мерка). Всего плиток 4 • 9 = 36. •

Умножение на 1 можно объяснить так: пусть в примере 1 в кружке помещается ровно один стакан, тогда в банке будет 5 • 1 = 5 (стаканов).

Умножение на 0 можно объяснить на примерах, в которых новая мерка значительно больше старой мерки и измеряемой величины.

Нахождение результата вычитания основывается на следующем определении.

Определение. Разностью из натурального числа " а " натурального числа " b " называется такое натуральное число " с ", что а = b + с.

Таким образом, вычитание рассматривается как действие обратное сложению. Это позволяет находить результат вычитания не только путем отсчитывания по одному, но и используя зависимость между компонентами операции сложения: 5 - 2 = (5 - 1) -1 и 2 + П =5.

Нахождение результата деления основывается на следующем определении.

Определение. Частным от деления натурального числа " а" на натуральное неравное нулю число " b " называется такое натуральное число " с ", что а • b == с.

Так как деление есть операция обратная умножению, то для нахождения результата деления используется зависимость между компонентами операции умножения: 3 •П=6. На этом же основывается и составление таблиц вычитания и деления:

а) 2+3=5; 5 - 2=3; . б) 2 • 3 = 6; 6:2=3.

Деление с остатком в начальных классах основывается на следующем определении.

Определение. Делением натурального числа " а " на натуральное число «b» с остатком называется отыскание такого частного q и остатка г , что а = b • q + г, где г < b.

Согласно этому определению, наряду с записью, например, 23 : 5 = 4 (остаток 3), ученикам должна даваться и такая запись: 23 = 5 • 4 + 3. Это

позволяет разнообразить примеры на деление с остатком: П =5*4+3 (проверка деления с остатком); 23 = П • 4 + П; 23 == 5 • О + О. Ученик + О. Учеников должны знать не только порядковую структуру множества натуральных чисел, которая была приведена выше, но и алгебраическую структуру натуральных чисел. Приведем ее.

1. В множестве натуральных чисел всегда выполнима операция сложения.

2. В множестве натуральных чисел всегда выполнима операция умножения.

3. а + b = b + а (переместительное свойство сложения).

4. а • b = b • а (переместительное свойство умножения).

5. (а + b) +с = а + (b +с) (сочетательное свойство сложения).

6. (а • b) • с =а • (b • с) (сочетательное свойство умножения).

7. (а+b) • с =а *с+b *с (распределительное свойство умножения относительно сложения).

8. а + 0 = а.

9. а • 0 = 0.

10.а + 1 = а'.

11. а • 1= а.

Операции над многозначными числами основываются на позиционной системе счисления.

Определение. Счислением (нумерацией) называется совокупность способов устного наименования и письменного обозначения чисел.

Существуют непозиционные и позиционные системы счисления.

В непозипионной системе счисления каждый знак (цифра) служит для обозначения одного и того же числа. Примером непозиционной системы счисления является римская нумерация, которой широко пользуются в настоящее время. Например, XII - это 10 + 1 + 1 =12.

Позиционная система счисления базируется на поместном значении цифр, заключающееся в том, что один и тот же знак (цифра) означает одно и то же число единиц разных разрядов независимо от того, на каком месте в записи числа стоит этот знак. Например, в числе 737 цифра 7 означает числа семь и семьсот.

Изучение темы "Нумерация чисел" учитель должен начинать с формирования представления о позиционной системе счисления, в которой дети не только знакомятся с существованием систем счисления с разными основаниями, но и понимают необходимость существования позиционной системы счисления. Это можно осуществить в ходе такой практической работы.

Пример 1. Дается задание измерить достаточно большой отрезок маленькой меркой (рис. 2.19). Дети уже знают, что лучше взять для измерения большую мерку, им предлагается тогда мерка, которая содержит 41маленьких мерки (большая мерка может содержать какое угодно число маленьких мерок, но обязательно целое их число). Ученики получили, например, что большая мерка поместилось 3 раза, а в остатке поместилось 2 маленькие мерки. В результате у них получилось число 32 с основанием системы счисления 4.

Рис. 2.19

В зависимости от длины измеряемого отрезка можно брать для измерения большие мерки, которые содержат по 2, 3, 4, 5, ... маленьких мерок. Тем самым, ученики приходят к выводу, что существуют позиционные системы счисления с различными основаниями. Далее можно провести беседу о существовании в практической деятельности человека систем счисления с основанием 7 (число дней в неделе), 12 (число месяцев в году), 100 (число лет в веке), 60 (число минут в часе) и т. д.

В традиционном обучении при изучении нумерации чисел у учащихся отрабатываются понятия "десятки", "сотни", что приводит к смешению устной нумерации и письменной. Этого нельзя делать, потому, что это может привести к ошибкам. Например, дети часто говорят, что в числе 325 два десятка (вместо - 32 десятка), В дальнейшем это приводит к затруднениям в выполнении операций над многозначными числами, которые базируются на операциях над однозначными числами. Поэтому при изучении многозначных чисел нужно обращать внимание детей на разряды и на число единиц в разрядах. Например, в числе 6325 шесть единиц четвертого разряда, три единицы третьего разряда, две единицы второго разряда и пять единиц первого разряда. Такая работа позволит ученикам легче и быстрее усвоить операции над многозначными числами, которые производятся над разрядами. Законы операций над многозначными числами должны использоваться учителем для формирования вычислительных навыков.

VI. Числовые выражения. Числовые равенства и неравенства, их свойства

Любое число уже является числовым выражением. Если А и В -числовые выражения, то А + В, А - В, А • В, А : В также являются числовыми выражениями. Выполнив операции; которые имеют место в числовом выражении, получают значение числового выражения. Существуют выражения, которые не имеют значения. Например, выражение 28 ; 8 - 44 не имеет числового значения.

С первых дней пребывания в школе дети сталкиваются с различными числовыми выражениями и учатся находить их числовое значение. Значительно меньше в школе уделяется внимание числовым равенствам и неравенствам, их свойствам, что сказывается при их обучении в старших классах. Поэтому учитель должен предлагать учащимся достаточное количество упражнений следующих видов.

1. Являются ли данные равенства верными:

10-3*2=2*2; 5+2*3=6+4?

2. Являются ли данные неравенства верными:

8-3 • 2<3 +4; 14: (5 + 2) >2 + 3 ?

3. Зная, что 2 + 3 = 10 : 2 и 4 +7 > & + 2, поставьте вместо звездочки знак " - ", " > ", " < ", не вычисляя значения числовых выражений, стоящих в правой и левой частях числовых равенств и неравенств:

(2 + 3) + 4 * 10 : 2 + 4 ; (2 + 3) - 4 *10 : 2 - 4 ;

(2 + 3) • 3 * (10 : 2) • 3 ; 4+7-3*8+2-3;

(4 + 7) • 2 • (8 + 2) • 2 .

VII. Выражение с переменными, его область определения

Если числовое выражение содержит и буквы, то мы имеем выражение с переменными. Например, 2а - 3 ; За + 2b с + 8 .

Выражение с переменными обычно обозначают так: f(х); А(b;с); В(х;у) Если в выражение с переменными подставить вместо букв их значения, то получится числовое выражение.Те значения переменной, при которых выражение с переменной имеет числовое значение, называется областью определения выражения с переменной. Например, областью определения выражения с переменной 2а - 3 на множестве действительных чисел является все множество действительных чисел, а на множестве натуральных чисел - натуральные числа, начиная с двух (если а = 1 , то 2 • 1 - 3 не является натуральным числом).

В начальных классах учитель обязан сформировать понятие о выражении с переменной и его области определения. Покажем на примерах, как это можно сделать.

Пример 1. Цель; сформировать у детей понимание необходимости введения в числовое выражение букв и представление об области определения выражения с переменной.

Учитель записывает на доске несколько числовых выражений: 1 + 2; 2+2; 3+2; 4+2. Затем он обращает внимание на то, что первое слагаемое меняется, а второе - нет. Поэтому, чтобы не продолжать ряд,

можно все эти выражения заменить одним П+ 2, где в окошечко можно подставить любое натуральное число. Учитель предлагает в окошечко подставить числа 1 ; 2 ; 3 ; 4 ; 5 и найти значение получившихся числовых выражений. Здесь область определения задана учителем.

Пример 2. Цель: научить учащихся самим находить область определения выражения с переменной.

Учитель спрашивает, какие числа можно подставить в следующие выражения: 8 - П; 3-2; П : 2; 5 – П : 3; П : 5 - 7. Дети подбором находят область определения каждого выражения с переменной.

Пример 3. Цель: научить учащихся находить область определения выражения с переменной в задачах.

Учитель предлагает следующую задачу. Сколько килограммов сахара, расфасованного в пакеты, принесли Коля и Оля, если в каждом пакете по два килограмма сахара?

Ученики записывают задачу в виде выражения 2а + 2b (или 2 • (а + b)), где а - количество пакетов, которые принес Коля, и b - количество пакетов, которые принесла Оля. Затем в ходе анализа задачи дети делают вывод, что Коля может нести не более 8 кг (от одного до четырех пакетов), а Оля - не более 6 кг (от одного до трех пакетов). Таким образом, ае{1;2;3;4} и

b е { 1; 2; 3}.

Задача имеет 12 решений, если перебрать все варианты наборов а и b .

VIII. Уравнения и неравенства, область определения, множество решений. Свойства уравнений и неравенств

Равенство (неравенство), содержащее неизвестное, называется уравнением (неравенством). Множество, элементы которого можно подставить в уравнение (неравенство) вместо неизвестного, называется областью определения уравнения (неравенства).

Те значения неизвестного из области определения, при которых уравнение (неравенство) обращается в верное числовое равенство (неравенство), называется корнями уравнения (множеством решения неравенств).

Если область определения уравнения (неравенства) не задана, то она совпадает с областью определения выражений, входящих в данное уравнение (неравенство). Например, областью определения уравнения (3 х2): х • 2 = 4 является множество (- °о; 0) U(0;оо).

Два уравнения (неравенства) называются равносильными, если у них совпадают области определения и множества решений.

Например, уравнения (3 х2 ) : х - 2 = 4 (1) и 3 х - 2=4 (2) не равносильны, так как их области определения не совпадают. Уравнения Корень (2х - 1) 2 = х (3) и 2 х - 1 = х2 (4) не равносильны, хотя их области определения и совпадают, так как уравнение (3) имеет один корень (х = 1), а уравнение (4) - два корня (х = 1 ; х = 1).

При решении любого уравнения (неравенства) его заменяют более простым равносильным уравнением (неравенством). В начальных классах формируется следующие два основных свойства равносильных преобразований.

1. Если к обеим частям уравнения (неравенства) прибавить (вычесть) выражение, имеющее ту же область определения, что и данное уравнение (неравенство), то получим уравнение (неравенство) равносильное данному.

Например, уравнения Зх=2х+4 и 3х- 2х=4 равносильны.

2 а. Если обе части уравнения умножить на выражение, имеющее ту же область определения, и которое не обращается в нуль на этой области определения, то получим уравнение, равносильное данному.

Например уравнения (3 х - 1) • (х2 + 1) = 5 (х2 + 1) и 3х - 1=5 равносильны, а (3 х 1)* (х + 1) = 5 (х + 1) и 3 х - 1=5 не равносильны.

2 б. Если обе части неравенства умножить на выражение, имеющее ту же область определения и большее нуля на этой области определения, то получим неравенство, равносильное данному.

Например, неравенства (3 х - 1) • (х2 I) > (5 х2 1) и (3 х - 1) > 5 равносильны.

В начальных классах формируется понятие об уравнении и неравенстве, их области определения, множестве решений, равносильных преобразованиях. Покажем на примерах, как можно построить обучение по их формированию.

Пример 1. Ученикам предлагается записать с помощью уравнения решение такой задачи. Сколько детей взяло яблоки, если в вазе лежало 10 яблок и каждый из детей взял по 2 яблока и осталось в вазе два яблока?

Ученики записывают 10 - 2 х == 2 и определяют, что вместо "х" можно подставить числа 1, 2, 3, 4, 5 (находят область определения). Подбором они убеждаются, что х == 4 является корнем уравнения.

Пример 1. Для отработки умений находить область определения и множество решений неравенства учащимся можно предложить ответить на вопрос: "Какие числа можно подставить в неравенство 8 - х < 3 вместо "х" и при каких из них неравенство превращается в верное числовое неравенство?" (Вместо "х" можно взять любое число, которое меньше 9; при х = б ; 7 ; 8 получается верное числовое неравенство).

Пример 3. Для формирования понятий о равносильных уравнениях (неравенствах) и их свойствах ученикам можно предложить следующее задание.

Найдите область определения и множество решений неравенства 8 - х < 3 (1), Пользуясь неравенством (1), не решая неравенства 8-х+ 4 < 3 + 4 (2) и (8 - х) • 2 < 3 • 2 (3), найдите их области определения и множество решений.

IX. Функция: область определения, область значений, способы заданий.

Определение. Функцией называется такая зависимость переменной у от переменной X , при которой каждому значению х соответствует единственное значение у . Значения, которые может принимать х называются областью определения функции. Значения, которые принимает у называются областью значений функции.

Если функциональное соответствие задается на числовом множестве, то мы имеем числовую функцию.

Числовую функцию, как и любую другую, можно задать аналитически, парами, таблицей, графом, графиком на координатной плоскости. Например, функция у =2х-1 задана аналитически.

В начальных классах функция чаще всего задается словесно (в виде текста задачи) таблицей, выражением, парами.

В начальных классах учитель должен формировать у учащихся понятие об области определения функции, области значений функции, однозначности соответствия, способах задания функции.

Пример. Детям предлагается записать в виде выражения решение следующей задачи.

Сколько килограммов крупы, расфасованной в пакеты по 2 кг осталось перенести детям, если было 20 пакетов, и каждый ребенок берет один пакет?

Дети, записывая 20 - 2 X, учатся задавать функцию аналитически.

Для отработки умений находить область определения учитель предлагает найти наибольшее количество детей, которое необходимо для переноса крупы.

Для отработки умений находить область значений функции учитель предлагает ответить на вопрос задачи, если х = 1; 2; 3; ... ; 10. При этом ученики учатся задавать функцию парами и таблицей:

х	1	2	3		10
20-2х	18'	16	14		0

Для формирования понятия об однозначности функционального соответствия учитель задает вопрос: "Может ли остаться 10 кг крупы, если ее переносили трое ребят, шестеро ребят? "Аналогичная работа должна проводиться не только при решении различных задач, в том числе и задач на прямую и обратную пропорциональность, но и при изучении выражений с переменными.

2.3. Реализация основных положений опытно-экспериментальной методики.

Экспериментальная проверка основных положений данного исследования проводилась на базе учебно-воспитательного комплекса «Евпаторийская средняя общеобразовательная физико-математическая школа I – III ступеней № 6 – дошкольное учебное учреждение № 31 1-В (26 человек) и 1-Г(26 человек) классы. Во время экспериментального исследования анализировались полученные результаты, вносились необходимые коррективы.

Объект исследования - процесс формирования математических понятий у учащихся начальных классов.

Экспериментальное исследование состояло из констатирующего, аналитико-поискового, формирующего и заключительного этапов.

Цель констатирующего этапа эксперимента состояла в выяснении уровня сформированности математических понятий у младших школьников.

Для реализации методики были подготовлены соответствующие дидактические материалы и методические указания.

На констатирующем этапе исследования в экспериментальном 1-В и контрольном 1 – Г классах с целью определения уровня сформированности понятий у младших школьников было проведено тестирование, по переработанной методике Л. С. Выготского.

По методике Л. С. Выготского

Тест № 1

Задание состоит в следующем: школьнику показывали одну фигуру (№5) красного цвета, определенной формы (экспериментальное понятие гацун), и просили ее запомнить. После этого фигура – образец убиралась, и перед ребенком выкладывался набор из 16 фигур (см. Приложение А рис.1) отличающихся по форме (2 вида), по цвету (красный и зеленый), по величине (2 варианта), и ребенку предлагалось выбрать ту фигуру, которую ему показывали. Время проведения – 5 минут.

В правильности ответа ученик мог убедиться, перевернув фигуру (отмечена +), при неправильном ответе он должен объяснить, почему это не та фигура.

Тест № 2

«Найди прямоугольник»

Задание состоит в следующем: на столе выкладываются четырехугольники (см. Приложение А, рис. 3), ученик должен выбрать из них все прямоугольники (подвести под понятие прямоугольник), которые для сложности были разных вариантов: в форме полоски, положены на высоту, а так же в том виде, к которому школьники уже привыкли. Время - проведения 5 минут.

Эти экспериментальные задания помогали изучить такие особенности учащихся, как умение отвлекаться от несущественных признаков единичных предметов, одновременный анализ предметов по нескольким признакам (основаниям), умение соблюсти координацию объема и содержания классифицируемых классов объектов, удерживать в сознании определение понятия (как совокупность существенных признаков).

По результатам методики были определены три уровня сформированности у детей математических понятий: низкий, средний и высокий.

Первый (самый низкий) уровень выполнения подведения под понятие опирается на односторонний элементарный анализ, на классификацию, или носящую глобально-недифференцированный характер, или опирающуюся только на один признак, не могут определить даже два признака для экспериментального понятия, и поэтому делают множество ошибочных выборов, попеременно ориентируясь то на цвет, то на форму. Эти дети не удерживают положительное и отрицательное подкрепление, в результате чего не могут осуществить классификацию по заданным признакам, подвести под понятие.

Для второго уровня характерно то, что подведение под понятие проходит с опорой на классификацию, которая уже дифференцирована, но осуществляется не сразу, а в результате упражнений. Ученики на этом уровне не способны увидеть связь между подкрепленными признаками, анализ ведется то по одному (форма), то по другому (цвет) признаку, они возвращаются к неподкрепленным признакам и не могут удержать все подкрепленные. Между подкрепленными признаками не могут установить связь. Эти дети способны осуществить классификацию, подвести под понятие, но лишь допустив несколько ошибочных выборов.

Третий уровень основывается на всестороннем анализе и синтезе, классификация проходит по всем заданным основаниям, ученики устанавливают как положительные, так и отрицательные связи, прочно удерживают подкрепленные признаки и отбрасывают неподкрепленные, не возвращаясь к ним, таким образом, подводят под понятие. Характерно то, что при выборе фигурок ученики с этим уровнем владения приемом классификация пытаются формулировать в словах те признаки (основания), на которые надо опираться при подведении под понятие. За выполнение задания на третьем уровне начислялось 2 балла, на втором – 1 балл, на первом – баллов не начислялось.

Результаты эксперимента приведены в таблице (табл. 2.1 и 2.2), они дают основание считать, что для каждого ученика характерен определенный уровень сформированности математических понятий и приема классификации, а также необходимости работы по их формированию.

Таблица 2.1

Результаты констатирующего эксперимента (1 – Г).

№	Фамилия, имя учащихся	Уровень сформированности понятий
1	Андронова Анастасия	II
2	Андросюк Дмитрий	II
3	Атемов Разим	I
4	Бабешко Татьяна	I
5	Боймистрюк Роман	I
6	Болик Георг	III
7	Васильева Людмила	II
8	Вашкевич Наталья	II
9	Воропаев Вова	II
10	Данилов Никита	II
11	Дашкова Валентина	I
12	Дорогин Иван	II
13	Андронова Анастасия	II
14	Андросюк Дмитрий	II
15	Атемов Разим	I
16	Бабешко Татьяна	I
17	Боймистрюк Роман	I
18	Болик Георг	III
19	Васильева Людмила	II
20	Вашкевич Наталья	II
21	Воропаев Вова	II
22	Данилов Никита	II
23	Дашкова Валентина	I
24	Дорогин Иван	II
25	Дубровина Оксана	I
26	Яблоненко Саша	I

Из 26 учащихся в контрольном классе низкий уровень сформированности понятий показало 10 учеников (39 %), средний – 12 (46 %), высокий – 4 (15 %) .

Таблица 2.2

Результаты констатирующего эксперимента (1 – В).

№	Фамилия, имя учащихся	Уровень сформированности понятий
1	Абляметова Эльнара	II
2	Аджи-Аметов Эскандер	II
3	Алексеева Валерия	II
4	Боков Ахмед	III
5	Боков Тимур	I
6	Бутенко Сергей	II
7	Васильев Михаил	III
8	Галкина Татьяна	II
9	Голуб Дарья	I
10	Загоруй Алексей	I
11	Иванщик Ирина	II
12	Кириченко Александр	II
13	Кенджаев Элемдар	III
14	Корягин Всеволод	II
15	Котеленец Вячеслав	I
16 17	Никитин Никита Незамаев Иван	I I
18	Мартыненко Тамила	I
20	Маслюк Дарья	II
20	Салмина Ксения	II
21	Соловьев Юрий	II
22	Сейдаметова Кериме	III
23	Таранщук Илья	III
24	Толосиенко Тимофей	I
25	Яблонева Виктория	I
26	Яценко Станислав	II

Из 26 учащихся в экспериментальном классе низкий уровень сформированности понятий показало 9 учеников (35 %), средний – 12 (46 %), высокий – 5 (19 %).

Своеобразие выполнения задания на первом уровне можно раскрыть на примере Тамила М.

После показа образца Тамила берет первую зеленую фигуру, по форме соответствующую образцу, выделив, таким образом, первый существенный признак – форму. Увидев после перевертывания фигурки, что знака «+» на ней нет (т. е. получив отрицательное подкрепление), девочка выбирает фигурку другой формы зеленого цвета. После этого она случайно взяла нужную фигурку (гацун), но при следующем выборе опять-таки приняла во внимание только один признак (цвет) – выбрала красную фигурку, которая по форме была похожа на образец.

И в дальнейшем Тамила не могла объединить два признака, характерные фигуре-образцу, и в силу этого делала множество ошибочных выборов, попеременно ориентируясь то на цвет, то на форму. Результаты выполнения задания Тамила выглядели в виде выбора следующих фигурок: № 6, 8, 5, 11, 9, 14,2, 10, 15, 1, 12, 13, 3. Процесс выбора у Тамилы затянулся потому, что она не реагировала на положительное и отрицательное подкрепление, не удерживала их памяти в процессе решения задачи. В результате Тамила не смогла подвести под понятие гацун.

При выполнении задания теста «Найди прямоугольник» Таня правильно определила, что такое прямоугольник, однако не руководствовалась этим определением, а фактически опиралась на общее впечатление от формы фигур.

В результате вместо 12 прямоугольников эта ученица выбрала только 7, она не выбирала прямоугольники, которые по соотношению сторон резко отличались от прямоугольных фигур, обычно демонстрируемых в классе ( она не взяла прямоугольные фигурки, узкие, длинные и короткие). В то же время Таня ошибочно отнесла к группе прямоугольников 4 квадрата и ромб, опять руководствуясь общим впечатлением от внешнего вида.

Таковы особенности выполнения заданий, на основании которых был установлен первый уровень сформированности понятий.

Типичным представителем группы учащихся, обнаруживших при прохождении теста второй уровень сформированности понятий, является Сережа Б.

Сначала Сереже выбрал фигурку зеленого цвета, имеющую форму образца, затем красную, но другой формы. Не получив подкрепления, Сережа продолжил поиски, и следующую фигурку он выбрал фигуру-образец (гацун), однако не увидел связи между подкрепленными признаками, а поэтому анализ продолжал вести то по одному (форма), то по другому (цвет) основанию, возвращаюсь к неподкрепленным признакам и удерживая не все подкрепленные.

На пятой пробе он выбрал зеленую фигурку формы-образца и снова, получив отрицательное подкрепление, стал анализировать выбранные фигурки: «Последняя не та фигура, потому что она зеленая, четвертая не та фигура, потому что она без крыши, а третья та. А, я знаю – это должна быть фигурка красного цвета и с крышей». Выполнил Сережа задание так: №10, 7, 5, 11, 12,9 (см. рис. 2).

Можно сказать, что этот ученик сумел подвести под понятие, однако допустил несколько ошибочных выборов, так как не сразу установил основания классификации.

Задание теста «Найди прямоугольник» Сереже выполнил более успешно, чем Тамила. Он руководствовался не только общим впечатлением от формы фигур, но и существенными признаками (наличие 4 прямых углов, и правильное соотношение сторон). Однако Сережа не увидел существенные признаки в узких и длинных прямоугольниках: «Эти фигурки как полоски, они не прямоугольники», - заявил Сережа. Из 12 прямоугольников он выбрал 10, не взяв при этом ни одной сходной фигуры (квадрат, ромб).

Своеобразие выполнения задания на третьем уровне можно раскрыть на примере Кериме С.

Приступив к выполнению задания, Кериме прежде всего отметила, что есть фигурки разные по форме, по цвету и величине. Первую фигуру она взяла гацун, но приняла во внимание, по-видимому, не все основания по которым должно проходить подведение под понятие, так как вторую фигурку точно такой же формы и величины, но зеленого цвета.

Получив отрицательное подкрепление (не гацун), Кериме задумалась и стала сравнивать выбранные фигурки по трем признакам (форме, величине и цвету): «Формой они одинаковые, как домики, величиной тоже, только цветом разные, знак «+» поставлен на красной фигурке, значит, надо выбирать красные. Ой, я теперь знаю, это фигуры красные с крышечкой, разные по величине». После этого она уверенно выбрала все нужные фигурки. Результат решения у Кериме выглядел так: №5, 12, 4, 8, 10.

Таким образом, Кериме самостоятельно сформулировала экспериментальное понятие «галун», подчиняя процесс мышления поставленной задаче.

При выполнении задания теста «Найди прямоугольник» Кериме успешно применила определение понятия «прямоугольник», это было обусловлено, умением Кериме удерживать комплекс существенных признаков прямоугольника (данных в определении) и при выборе конкретной фигур она ими руководствовалась. Она отвлекалась от несущественных признаков (величины, соотношения длины и стороны сторон). Дав определение, она быстро и правильно отобрала все прямоугольники, при чем неодинаковый внешний вид не мешал процессу подведения под понятие.

По результатам данной диагностики можно сделать вывод о необходимости и значимости формирования у младших школьников математических понятий с использованием умственного приема классификации, разработки системы заданий, как средства организации учебно-познавательной деятельности школьников, направленных на формирование математических понятий.

На аналитико-поисковом этапе эксперимента была изучена педагогическая, методическая литература по проблеме формирования математических понятий у младших школьников, обобщен опыт, внесены коррективы.

На следующем этапе исследования проводился формирующий эксперимент, цель которого - установить влияние умственного приема классификации на формирование математических понятий у младших школьников.

При этом мы исходим из общей рабочей гипотезы исследования, которая заключается в том, что систематическое и целенаправленное формирование и использование приема умственной деятельности классификации будет способствовать более глубокому и сознательному усвоению математических понятий младшими школьниками. Основными задачами работы по формированию математических понятий у младших школьников является выявить влияние обучения школьников умственному приему классификации на формирование математических понятий; определить условия эффективного формирования математических понятий в процессе решения заданий с применением умственного приема классификации.

Формирующий эксперимент осуществлялся на базе учебно-воспитательного комплекса «Евпаторийская средняя общеобразовательная физико-математическая школа I – III ступеней № 6 – дошкольное учебное учреждение № 31 в период прохождения преддипломной практики с14 января по 5 марта 2004 года.

При формировании у младших школьников математических понятий с опорой на умственный прием классификации были выявлены трудности, которые необходимо учитывать. Они состояли в следующем:

- овладение умственным приемом классификации требует выработки определенных действий (определение цели классификации, выбор основания, деление по этому основанию множества понятий на непересекающиеся подмножества);

овладение математическими понятиями требует не только воспроизведения определения, но применения его на практике. Для успешного усвоения математических понятий ученик должен пройти все необходимые этапы усвоения:

мотивационный (постановка проблемы);
составления схемы (показ процесса решения);
наглядная фиксация (составление схем, опор);

- работа по схемам (работа с моделями, предметами);

работа с описаниями.

Ученики далеко не всегда смогут сразу запомнить все звенья введенных знаний и все условия для подведение объекта под понятие. Вот почему их работа должна сопровождаться внешней, наглядной фиксацией знаний и формируемой деятельности.

1. Признаки прямоугольника:

1) четырех угольник;

2) параллельные стороны равны;

3) прямой угол.

2. Логическое правило работы с признаками:

Если все признаки «+», ответ «+».

2) Если хотя бы один признак «-», ответ «-».

а) 1. + б) 1. ?

2. + ? 2. - -

3. - 3. +

3) Если хотя бы один признак «?» и нет признаков «-», ответ будет «?».

? ?

3. Предписание по выполнению задания:

Прочтите задание.
Выделите условие и вопрос задания.
Прочтите первый признак понятия.
Проверьте, есть ли он у данного объекта.
Отметьте результат с помощью знаков «+», «-», «?».
Проделайте то же самое с последующими признаками.
Сравните полученные результаты с логическим правилом.

8) Запишите ответ с помощью «+», «-», «?».

При этом важно, чтобы все используемые характеристики были зафиксированы, четко выделены и в дальнейшем находились в распоряжении учащихся. Для этого используется доска, различные таблицы, памятки. Например:

Таблица 2.3

Существенные признаки фигур	Понятия
Бат	Дек	Роц	Муп
Площадь основания
Высота

Логическая схема распознавания

Таблица 2.4

Площадь основания	+	+	-	-	+	?	-	?	?
Высота	+	-	+	-	?	+	?	-	?
Ответ	+	-	-	-	?	*	-	-	?

В результате работы над этими заданиями учащиеся не только запомнят без специального заучивания признаки понятия и логическое правило подведения под понятие, но и научатся правильно применять то и другое, т.е. освоят один из логических приемов работы с понятиями. Дети сразу усваивают целую систему понятий, в данном случае - искусственных (бат, дек, роц, муп), которые были рассмотрены нами при анализе обобщенности действия. Каждое понятие характеризуется двумя существенными признаками: величина площади основания и высоты. Дети имеют мерки, по которым определяют, большая или маленькая площадь (высота). Меркой для площади служит монетка. Если фигурка умещается на монетку, значит, «донышко» (основание) маленькое, если не умещается - «донышко» большое. Эталоном высоты служит спичка: если «рост» меньше или равен спичке -фигурка низкая, у нее «маленький рост»; если высота превосходит спичку - высокая, у нее «большой рост».

Во второй таблице представлено логическое правило распознавания в развернутом виде, где предусмотрены все сочетания признаков, с которыми встретится ребенок в процессе работы.

Слишком долго задерживать учащихся на этапе внешних практических действий не следует. Как только они научились их выполнять правильно, надо действия переводить в теоретическую форму: учить обучаемых оперировать признаками понятия и логическим правилом без опоры на внешние предметы. Теперь ученики называют признаки по памяти. Для анализа им теперь уже даются не предметы и модели, а их описания. Так, если мы продолжим работу с понятием прямоугольник, то на этапе внешнеречевых действий учащимся можно предложить задания такого типа: «Дан четырехугольник с равными параллельными сторонами. Будет ли эта фигура прямоугольником?» К задаче не дается ни чертежа, ни модели. Учащиеся учатся теперь анализировать словесные условия. Они читают (или слушают) и выделяют то, что касается первого признака. Если задание дано в письменном виде, то учащиеся должны подчеркнуть слово «четырехугольник» и поставить знак того, что первый признак имеется: «1. +». Таким же образом идет работа со вторым признаком. После этого учащиеся определяют, что же у них получилось: первый признак есть, второй признак так же известен, «2. +». Третий признак не известен. «3. ?»

Результаты работы с признаками фиксируются обычно на бумаге, но могут и просто называться. Для оценки полученных результатов учащиеся теперь уже вспоминают логическое правило подведения, доказывают верность своего ответа. При этом они все время опираются именно на те свойства предметов, которые существенны для понятия. При таком обучении у всех учащихся формируется умение выделять в предметах существенные свойства и на их основе решать, подходят предметы под данное понятие или не подходят.

Для эффективного формирования математических понятий необходима специально организованная работа над умственным приемом классификации, которая составляет внутреннюю структуру понятия, его механизм, это позволит обеспечить успешность овладения ими.

Цель итогового эксперимента: исследовать влияние предложенной системы работы на уровень сформированности математических понятий с использованием умственного приема классификации в экспериментальном (1-В) и контрольном (1–Г) классе.

С целью выявления уровня сформированности математических понятий учащимся 1-В (экспериментального) и 1-Г (контрольного) классов была предложена методика Л. С. Выготского с измененными заданиями.

Тест № 1

Задание состоит в следующем: школьнику показывали одну фигуру (№6) зеленого цвета, определенной формы (экспериментальное понятие нат), и просили ее запомнить. После этого фигура – образец убиралась, и перед ребенком выкладывался набор из 16 фигур (см. Приложение А рис.1) отличающихся по форме (2 вида), по цвету (красный и зеленый), по величине (2 варианта), и ребенку предлагалось выбрать ту фигуру, которую ему показывали. Время проведения – 5 минут.

Тест № 2

«Найди прямоугольник»

Задание состоит в следующем: на столе выкладываются четырехугольники (см. Приложение А рис. 2), ученик должен выбрать из них все квадраты(подвести под понятие квадрат), которые для сложности были разных вариантов: разного цвета, размера. Время - проведения 5 минут.

Результаты эксперимента приведены в таблицах 2.5 и 2.6.

Таблица 2.5

Результаты итогового эксперимента (1 – Г).

№	Фамилия, имя учащихся	Уровень сформированности понятий
1	Андронова Анастасия	II
2	Андросюк Дмитрий	II
3	Атемов Разим	I
4	Бабешко Татьяна	II
5	Боймистрюк Роман	I
6	Болик Георг	III
7	Васильева Людмила	II
8	Вашкевич Наталья	II
9	Воропаев Владимир	II
10	Данилов Никита	II
11	Дашкова Валентина	I
12	Дорогин Иван	II
13	Дубровина Оксана	I
14	Злобин Сергей	III
15	Калинина Дарья	II
16	Красик Алла	II
17	Колмыкова Алена	III
18	Лысак Юрий	I
19	Ляшок Дарья	II
20	Менаджиева Венера	I
21	Сосько Рита	II
22	Сейдаметова Ленара	II
23	Филлипова Софья	II
24	Эмиросанов Эльдар	I
25	Эмирометова Фарида	I
26	Яблоненко Александр	I

Таблица 2.6

Результаты итогового эксперимента (1 – В).

№	Фамилия, имя учащихся	Уровень сформированности понятий
1	Абляметова Эльнара	II
2	Аджи-Аметов Эскандер	II
3	Алексеева Валерия	II
4	Боков Ахмед	III
5	Боков Тимур	I
6	Бутенко Сергей	III
7	Васильев Михаил	II
8	Галкина татьяна	II
9	Голуб Дарья	I
10	Загоруй Алексей	II
11	Иванщик Ирина	II
12	Кириченко Александр	II
13	Кенджаев Элемдар	III
14	Корягин Всеволод	III
15	Котеленец Вячеслав	I
16	Никитин Никита	II
17	Незамаев Иван	II
18	Мартыненко Тамила	II
19	Маслюк Дарья	II
20	Салмина Ксения	II
21	Соловьев Юрий	III
22	Сейдаметова Кериме	III
23	Таранщук Илья	I
24	Толосиенко Тимофей	I
25	Яблонева Виктория	II
26	Яценко Станислав	II

В результате было установлено, что уровень сформированности математических понятий в 1-В (экспериментальный) классе следующий: низкий уровень показало 6 учеников (23 %), средний – 14 (54%), высокий – 6 (23 %); в 1 - Г (контрольный) классе: низкий уровень сформированности понятий показало 9 учеников (35 %), средний – 13 (50 %), высокий – 4 (15 %).Таким образом, проанализировав полученные результаты в контрольном и экспериментальном классах, мы можем убедиться в эффективности предложенной системы. Полученные данные наглядно представлены и в графиках 2.1. – 2.3., они позволяют судить о динамике формирования математических понятий с использованием умственного приема классификации.

ЗАКЛЮЧЕНИЯ И ВЫВОДЫ

1. Во время работы над дипломным проектом было изучено состояние данной проблемы и выявлено следующее: в психолого-педагогической теории большое внимание уделяется математическим понятиям и приемам умственной деятельности, однако конкретной программы работы над умственными приемами, которые должны быть сформированы при изучении данного предмета нет, поэтому работа над развитием логического мышления школьников идет без знания системы необходимых приемов. Образование и становление понятий – сложный процесс, в котором применяются такие приемы умственной деятельности, как анализ, синтез, сравнение, классификация, обобщение, абстрагирование. Таким образом, эти приемы составляют внутреннюю структуру понятия, его механизм и не овладев ими учащиеся испытывают трудности в усвоении системы математических понятий.

2. В начальных классах впервые каждое понятие вводится наглядно, путем наблюдения конкретных предметов или практического оперирования. Учитель опирается на знание и опыт детей, которые они приобрели еще в дошкольном возрасте. Ознакомления с математическими понятиями фиксируется с помощью термина или термина и символа. Математические понятия служат опорным моментом в познании действительности и являются своеобразным итогом познания. Поэтому понятия являются одной из главных составляющих в содержании любого учебного предмета начальной школы, в том числе - и математики. Понятийное мышление формируется в начальных классах и раскрывается, совершенствуется в течение всей жизни.

3. При формировании математических понятий у младших школьников необходимо соблюдать следующие методические требования:

работа должна вестись целенаправленно и осознанно, в основе которой должны лежать принципы системности и последовательности;
необходим учет характера изучаемого материала и сравниваемых объектов;
учет возрастных, индивидуальных особенностей учеников, уровня их развития.

4. Понимание и своевременное использование учителем тех или других видов определений математических понятий - одна из условий формирования у учеников твердых знаний об этих понятиях. В организации учебной деятельности младших школьников в процессе формирования математических понятий особую роль играет прием классификации. Этот прием умственной деятельности является средством упорядочения изучаемых объектов, установления закономерных связей между ними. Именно в этом случае классификация выявляет существенные сходства и различия между предметами. Классификация основывается на способности видеть общее в каждом конкретном единичном случае и преследует цель уточнить, обобщить знание о связях и отношениях между изучаемыми объектами. Применение приема классификация на уроках позволяет существенно расширить имеющиеся в практике приемы работы.

5. Было выявлено три уровня владения младшими школьниками математическими понятиями: низкий, средний и высокий. В процессе опытно-экспериментальной части было установлено, что систематическое и целенаправленное формирование и использование приема умственной деятельности классификации способствует глубокому и сознательному усвоению математических понятий младшими школьниками.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

Державна національна доктрина. Затв. Указом Президента України від 17 квітня 2002 р. № 347 // Освіта, - 2002. - № 26.
Державна національна програма «Освіта. Україна XXI століття”. Затв. постановою Кабінету Міністрів України від 3 грудня 1993, № 896 // Освіта, - 1993. - № 44-46.
Державний стандарт початкової загальної освіти. Затв. постановою Кабінету Міністрів України від 16.11.2000р. №1717// Поч. школа. - 2001. - № 1. – С. 28.
Слєпкань З.І., Шкіль М.І., Дороговцев А.Я. та ін. Концепція базової математичної освіти в Україні.- К.: Мін. осв. України, Інститут системних досліджень, 1993. – 31 с.
Аверьянов А.Н. Системное познание мира: Методологические проблемы. - М.: Политиздат, 1985. – 263 с.
Актуальные проблемы начального обучения математики в начальных классах / Моро М.И., Пышкало А.М. и др. - М.: Педагогика, 1977.- 247 с.
Бабанский Ю.К. Оптимизация учебно-воспитательного процесса. – М.: Просвещение, 1982. – 192 с.
Бертон В.А. Принципы обучения и его организация. – М.:Учпедгиз, 1934с.
Белоколонна Н. В. Iнтелактуальний розвиток школярiв на уроках мови. // Початкова школа – 1998. - № 1 .
Богданович М. Определение математических понятий //«Початкова школа» 2001 № 4.
Богоявленский Д.Б., Менчинская Н.А. Психология усвоения знаний в школе. - М.: Изд-во АПН РСФСР, 1959. - 347 с.
Бирюкова Л.А. Прием классификации при обучении математике. //Начальная школа 1998 № 5.
Богданович М.В. Методика розв’язування задач у початковій школі: Навч. посібник.–К.: Вища школа, 1990. – 183 с.
Богданович М.В., Кочина Л.П. Математика: Підручник для 1 кл. чотирирічної школи. – К.: Освіта, 1997.- 216 с.
Богданович М.В., Козак М.В., Король Я.А. Методика викладання математики в початкових класах: Навч. посібник. - К.: А.С.К., 1998.- 352 с.
Богданович М.В. Математика: Підручник для 3 кл. трирічної і 4 кл. чотирирічної початкової школи. – К.: Освіта, 1998.- 240 с.
Богданович М.В. Математика: Підручник для 1 кл. трирічної і 2 кл. чотирирічної початкової школи. – К.: Освіта, 1999.- 208 с.
Богданович М.В. Математика: Підручник для 2 кл. трирічної і 3 кл. чотирирічної початкової школи. – К.: Освіта, 1999.- 224 с.
Богданович М.В. Определение математических понятий //Начальная школа 2001. - № 4 .
Васильева М.И. Математика и конструирование // Начальная школа. – 2000. - № 7.
Выготский Л.С. Умственное развитие детей в процессе обучения: Сборник статей. – М.-Л.: Гос. учеб.-пед. изд., 1935. – 133 с.
Глузман Н. А. Формирование обобщенных приемов умственной деятельности у младших школьников. – Ялта: КГГИ, 2001. – 34 с.
Гальперин П.Я. Методы обучения и умственное развитие ребенка. – М.: Изд-во МГУ, 1985. – 45 с.
Гальперин П.Я. Психология мышления и учение о поэтапном формировании умственных действий. – М. Педагогика 1986 – 240 с.
Возрастная и педагогическая психология: Учебник для студентов педагогических институтов // Под ред. Петровского А.В. - 2-е изд., испр. и доп. - М.: Просвещение, 1979. – 288 с.
Давыдов В.В. Виды обобщения в обучении: Логико-психологические проблемы построения учебных предметов. - М.: Педагогика, 1972. – 423 с.
Дрозд В.Л. Урбан М.А. От маленьких проблем – к большим открытиям. //Начальная школа. – 2000. - № 5.
Дубровська Д. М. Основи психологii. – Львiв: Спалах. – 2001.-324 с.
Жабо Т. О. Iнтелектуальний розвиток молодших школярiв в процессi навчання математики. // Початкова школа – 1998. - № 7 .
Закон України «Про внесення змін і доповнень до Закону Української РСР «Про освіту». - К.: Генеза. - 1996.
Иванова Л.Г. Овладение обобщенными образами и использование их учащимися в решении учебных задач // Вопросы психологии. - 1980.-№ 2.-С.118-121.
Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах: Пособие для учителей. М. – Просвещение 1985 – 65с.
Истомина Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и высш. пед. учеб. заведений. - 2-е изд., испр. - М.: Академия, 1998. - 288 с.
Кабанова-Меллер Е.Н. Формирование приемов умственной деятельности и умственное развитие учащихся. - М.: Просвещение, 1968. - 288 с.
Концепція загальної середньої освіти як базової в єдиній системі неперервної освіти. - К.: МО України, 1992. – 177 с.
Кочина Л.П. Математика в 1 кл. 4-х лет. нач. шк.: Методич. пособие. – К.: Рад. школа, 1986. – 144 с.
Кочина Л.П. Математика во 2 кл. 4-х лет. нач. шк.: Методич. пособие. – К.: Рад. школа, 1986. – 173 с.
Кочина Л. П. Математика: Підручник для 1кл. трьорічної почат.школи.– К.: Спалах ЛТД, 1996. – 192 с.
Краткий психологический словарь// Сост Карпенко Л. А.; Под общ. ред Петровского А. В., Ярошевского М. Г. – М.: Политиздат, 1985. – 431 с.
Крутецкий В.А. Психология математических способностей школьников. - М.: Просвещение, 1968. – 431 с.
Логачевська С. В., Каганець Т. Р. Iндивiдуалiзацiя заданiй на етапi закрiплення знань по математицi //Початкова школа – 1998. - № 4. – с.17.
Логика: Курс лекций //Ерышев А. А., Лукашевич Н. П., Сластенко Е. Ф. – 3-е изд., перераб. и доп. – К.: МАУП, 2000. – 184 с.]
Немов Р. С. Психология: Учеб. для студ. пед. вузов: В 3 кн. – 3-е изд. – М.: Гуманит. изд. Центр ВЛАДОС,1999. – Кн. 1.
Немов Р. С. Психология: Учеб. для студ. пед. вузов: В 3 кн. – 3-е изд. – М.: Гуманит. изд. Центр ВЛАДОС,1999. – Кн. 3.
Максименко С. Д. Общая психология. – К. : Вакляр 2001. – 235с.
Махмутов М.И. Организация проблемного обучения в школе. Кн. для учителей. – М.: Просвещение, 1977. – 240 с.
Менчинская Н.А. Проблемы учения и умственного развития школьника: Избранные психологические труды - М.: Педагогика, 1989. – 224 с.
Митник О. К. Математична логiка як навчальний предмет // Початкова школа. – 1998. - № 2 .
Моро М.И., Пышкало А.М. Методика обучения математике в 1-3 классах: Пособие для учителя. - 2-е изд. - М.: Просвещение, 1978. – 336 с.
Моро М.И. и др. Математика: Учебник для 1 кл. трехлет. нач. шк./Моро М.И., Бантова М.А., Бетлюкова Г.В. –М.: Просвещение, 1990. – 176 с.
Осинская В.Н. Формирование умственной культуры учащихся в процессе обучения математике: Кн. для учителя. - К.: Рад. школа, 1989. – 192 с. Паламарчук В.Ф. Школа учит мыслить. - 2-е изд., доп. и перераб.- М.: Просвещение, 1987. – 20.
Подгорецкая Н.А. Изучение приемов логического мышления у взрослых. - М.: Изд-во МГУ, 1980. - 147 с.
Практическая логика: Учебное пособие / Ивин А. А. – М.: ФАИР – ПРЕСС, 2002. – 288с
Рубинштейн С.А. О мышлении и путях его исследования. - М.: Изд - во АН СССР, 1958. – 148 с.
Рубиншнейн С.Л. Проблемы общей психологии. - М.: Педагогика, 1973. – 369 с.
Рубиншнейн С.Л. Основы общей психологии. – Санкт-Петербург –2000. – 348с.
Слепкань З.И. Психолого-педагогические основы обучения математике. - К.: Радянська школа, 1983. - 193 с.
Столяр А.А. Методика начального обучения математики.- Минск: Высшая школа, 1986. – 253 с.
Талызина Н.Ф. Педагогическая психология: Учеб. для студентов сред. пед. учеб. заведения. - 2-е изд., стереотип. - М.: Академия, 1998. – 288 с.
Трофимова Ю. Л. Психология. –К.: Либидь, 2001. - 325с.
Философский словарь //Под ред. И. Т. Фролов. – 5-е изд. – М.: Политиздат, 1987. –590 с.
Фокина С.Л. Формирование обобщенных познавательных умений и их влияние на развитие познавательных интересов учащихся: Автореф. дис... канд. пед. наук / ЛГУ. - Л., 1977. – 20 с.
Якиманская И.С. Знания и мышление школьника. - М.: Знание, 1985. - 80 с.

ПРИЛОЖЕНИЕ

СОДЕРЖАНИЕ

ПРИЛОЖЕНИЕ А. Раздаточный материал к методике.

ПРИЛОЖЕНИЕ Б. Тесты на сформированность математических понятий.

ПРИЛОЖЕНИЕ В. Игры на формирование у учащихся начальных классов математических понятий и умственного приема классификация.

ПРИЛОЖЕНИЕ Г. Комплекс заданий на формирование математических понятий и умственного приема классификации.

ПРИЛОЖЕНИЕ Д. Статья по проблеме исследования

ПРИЛОЖЕНИЕ Е. Самостоятельная работа

Приложение А

Раздаточный материал к методике

К тесту № 1

1 2 3 4

5 6 7 8

8 9 10 11

12 13 14 15

Рис. 1

К тесту № 2

Рис. 2

Приложение Б

Методика «Классификация понятий»

Выявляются такие особенности мышления, как способность выделять существенные признаки (для объединения карточек в группы) и уровень обобщения доступный школьнику.

Ход выполнения задания.

Задание проходит в три этапа с тремя последовательными инструкциями. Испытуемому дается набор карточек с напечатанными на них словами.

Первый этап процедуры начинается при так называемой «глухой» инструкции: «Разложи карточки так, чтобы слова, которые подходят друг другу, оказались в одной группе». Количество возможных групп не оговаривается. В случае, если испытуемый задает вопросы, прежде чем приступить к выполнению задания, ему говорят: «Начинай, дальше увидишь сам».

После того, как испытуемый самостоятельно сформировал несколько мелких групп карточек, у него спрашивают, почему, те или иные, карточки помещаются вместе и какое название им дается. Затем происходит период переход ко второму этапу.

Инструкция на втором этапе звучит так: «Ты верно объединил карточки в группы. Дай теперь этим группам короткие названия. Продолжай работать таким же образом».

После того, как все карточки оказались помещенными в группы и всем группам даны короткие названия, экспериментатор переходит к третьему этапу методики. Дается следующая инструкция: «Точно так же, как ты объединял карточку с карточкой, объедини теперь группу с группой, не перекладывая отдельных карточек. Они также должны иметь короткие названия». Если испытуемый на этом этапе формирует больше, чем три группы, ему предлагается сформировать из оставшихся две – три основные. В протоколе фиксируются этапы выполнения работы, названия групп и карточки в них, а также ответы и вопросы испытуемого.

При анализе результатов большое значение имеет то, на каком этапе допущены те или иные ошибки; отстаивал ли он свои принципы объединения карточек в группы, использовал ли помощь экспериментатора, какие еще особенности мышления проявлял в классификации. Так, если испытуемый на втором этапе сформировал отдельные группы диких, домашних, водоплавающих, летающих животных и отказался объединить эти группы в одну, то это свидетельствует о степени использования конкретных, детализированных признаков в направленности его мышления. Если подобные объединения проходили легко, самостоятельно, без указания экспериментатора на необходимость укрупнения групп, то это можно квалифицировать как достигнутый уровень обобщения мышления, способности испытуемого ориентироваться не только на существенные признаки, но учитывать их иерархии, то есть использовать существенные связи между понятиями. Показателем этого является степень затруднений или легкости в поиске обобщающих понятий, которые фиксируют основания классификации карточек в группы.

Если на третьем этапе выполнения методики испытуемый легко объединял группы и адекватно называл обобщающие признаки, то есть основание считать, что мышление его характеризуется использованием обобщенных ориентиров и протекает на категориальном уровне.

Кроме того, анализ поведения школьника в ходе исследования позволяет говорить о наличии или отсутствии у него внушаемости, эмоциональной устойчивости. Эти предположения проверяются с помощью навязывания испытуемому неадекватных оснований для объединения групп, дискретизации экспериментатором тактики работы испытуемого или похвалы при ошибках.

Материал к методике.

Телевизор, рубль, яблоня, светлячок, прожектор, свеча, керосиновая лампа, электролампа, фонарь, сантиметр, весы, часы, грузовик, самолет, термометр, радиоприемник, лев, тигр, слон, скворец, карп, голубь, гусь, ласточка, муравей, муха пианино, скрипка, кит, клоп, огурец, капуста, свекла, лук, лимон, груша, яблоко, примус, велосипед, платье, кукла, тюльпан, компас, ботинки, тетрадь, пароход, телега, барабан, мяч, портфель, глобус, электродуховка, колесо, сазан (рыба), книга, кровать, овощехранилище, щипцы, топор, ножницы, молоток, пила, моряк, уборщица, доктор, ребенок, футболист, солнце, медведь, луна, электроплита, град, подушка, шкаф, одеяло, буфет, дождь, роза, матрац, стакан, сосна, шапка, снег, юла, ложка, вилка, тарелка.

Образец протокола.

Испытуемый Дата

Инструкция экспериментатора	Действия испытуемого	Высказывания испытуемого
I этап
II этап
III этап

Методика «Формирование понятий»

Методика представляет набор плоскостных фигур – квадратов, треугольников, кругов – трех разных цветов (красный, синий, желтый) и трех различных размеров (рис.3). Признаки этих фигур: форма, цвет и величина - вместе образуют трехбуквенные искусственные понятия, не имеющие смысла на родном языке. В данном эксперименте использованы следующие искусственные понятия:

Понятия с одним признаком:

Биг – круглый, каб – большой, сур – красный, цен – треугольный, бос – квадратный, див – средний, лаг – зеленый, гур – маленький.

Понятия с двумя признаками: Дис – красный и большой, буд – зеленый и большой, вар – желтый и маленький, роз желтый и большой, веч – зеленый и маленький, кир – красный и средний по размеру, зум – желтый и средний по размеру, куд – зеленый и средний по размеру, сим – красный и маленький.

Понятия с тремя признаками:

Мук – красный, треугольный маленький, чар – красный, круглый, средний, бек – красный, квадратный, большой, вич – зеленый треугольный, маленький, сев – зеленый, круглый, средний, бал – зеленый, квадратный, большой, нур – желтый, треугольный, маленький, гон – желтый, круглый, средний, сов – желтый, средний, круглый.

Как видно из приведенных выше списков, в предложенные искусственные понятия входят от одного до трех различных признаков. Фигуры соответствующего размера, формы и цвета (всего 27 фигур с разными признаками) вырезаются из цветной бумаги и наклеиваются на квадратные картонные карточки размером 8 х 8 см.

Перед ребенком в произвольном порядке рядом друг с другом раскладываются карточки с цветными фигурами на них таким образом, чтобы все эти карточки ребенок мог одновременно видеть и изучать. Карточки можно разложить в три ряда по семь карточек в каждом, поместив шесть из них в неполный ряд.

Рис 3.

По команде экспериментатора испытуемый в соответствии с полученным от экспериментатора заданием начинает искать задуманное им понятие. Делая первый шаг на этом пути, ан отбирает одну из карточек и кладет ее отдельно от других. Экспериментатор подтверждает или отрицает наличие искомого Признака (признаков) понятия на отобранный испытуемым карточке, и тот продолжает поиск дальше, до тех пор и пока не будут отобраны карточки, содержащие в себе все признаки искомого понятия. После того как экспериментатор подтвердит испытуемому данный факт, испытуемый должен дать определения соответствующему понятию, т.е. сказать, какие конкретные признаки в него входят.

Экспериментатор в начале исследования задумывает понятие, содержащее только один признак, затем - понятие, включающее два признака, и, наконец, понятие, содержащее в себе сразу три признака. Задумав понятие, экспериментатор сообщается испытуемому трехбуквенное название данного понятия и количества признаков, которое оно содержит. Испытуемому предлагается самостоятельно, найти эти признаки, отобрав из предложенного набора карточек с фигурами те, которые содержат эти признаки, и назвать само понятие, определив его через найденные признаки.

Понятие, содержащее в себе только один из признаков - цвет, форму или величину, отбирается экспериментаторам произвольно из верхнего списка; понятие, включающее два признака, - из среднего списка; понятие, включающее три признака, - из нижнего списка.

На решение испытуемым каждой из трех задач (поиск трех понятий, включающих в себя от одного до трех признаков) отводится по 3 минуты. Если за это время испытуемый не справится самостоятельно с задачей, то экспериментатор дает ему подсказку: сам отбирает одну из карточек, которая содержит искомый признак, и говорит: «На этой карточке есть нужный признак» (ребенок должен обнаружить этот признак и назвать его без дальнейшей подсказки). Еще через минуту, если ребенок по-прежнему не справляется с заданием, экспериментатор предлагает ему вторую подсказку: показывает еще одну карточку, содержащую искомый признак (или признаки). Наконец, если спустя 5 минут после начала выполнения очередного задания ребенок так и не нашел все признаки и не дал словесное определение искомому понятию, то ему предлагается следующая задача того же самого типа. Если и с ней не справится, то эксперимент прекращается.

В том случае, если ребенок справится с первым заданием (поиск и определение понятия с единственным признаком) самостоятельно или после подсказок экспериментатора, ему предлагается следующее, более сложное задание, связанное с поиском и определением понятия, содержащего два признака, и так далее. Более сложное задание, касающееся формирования понятий с большим числом признаков, дается ребенку только в том случае, если до этого он справился с выполнением менее сложного задания.

Оценка результатов.

10 баллов ребенок получает в том случае, если он полностью самостоятельно, без подсказок со стороны экспериментатора, сумел за отведенное время с первой попытки решить все три задачи, то есть нашел все признаки и дал определение трем понятиям, содержащем в себе от одного до трех разных признаков.

8 –9 баллов ребенок получает тогда, когда за отведенное время он решил все три задачи, но ему для этого понадобилось более трех попыток, больше 9 минут и одна – две подсказки.

6 – 7 баллов за выполнение данного задания ребенок получает в том случае, если ему понадобилось больше трех попыток и получить как минимум две – три подсказки при решении первой и второй задач, а с третьей он не справился даже после двух попыток и получения всех подсказок.

4 - 5 баллов соответствует тому случаю, когда ребенок с трудом, больше чем за две попытки решил первые две6 задачи (поиск и определение понятий с одним и двумя признаками), а третью задачу не решил.

2 – 3 балла ребенок получает тогда, когда после двух попыток и подсказок он справится только с первой задачей, а вторую и третью не решил.

0 – 1 балл – тот случай, когда после всех попыток и подсказок ребенок не смог решить ни одной задачи.

Выводы об уровне развития

10 баллов – очень высокий

8 – 9 баллов – высокий

4 – 7 баллов – средний

2 – 3 балла – низкий

0 – 1 балл – очень низкий.

Тест

Испытуемым предлагался бланк с 20-ю рядами слов. В каждом из них набор из 5-ти слов, два из которых более всего с ними связаны. Задача испытуемого – найти в каждом ряду по два слова, наиболее соответствующих понятию, и подчеркнуть их.

Сад (растения, садовник, собака, забор, земля).
Река (берег, рыба, рыболов, тина, вода).
Город (автомобиль, здание, толпа, улица, велосипед).
Сарай (сеновал, лошадь, крыша, скот, стены).
Куб (углы, чертеж, сторона, камень, дерево).
Деление (класс, делимое, карандаш, делитель, бумага).
Кольцо (диаметр, алмаз, проба, округлость, печать).
Чтение (глава, книга, печать, картина, слово).
Газета (правда, приложение, телеграммы, бумага, редактор).
Игра (карты, игроки, штрафы, наказания, правила).
Война (самолеты, пушки, сражения, ружья, солдаты).
Книга (рисунки, война, бумаги, любовь, текст).
Пение (звон, искусство, голос, аплодисменты, мелодия).
Землетрясение (смерть, пожар, колебания почвы, шум, наводнение).
Библиотека (голод, книги, лекция, музыка, читатели).
Лес (лист, яблоня, дерево, охотник, волк).
Спорт (медаль, оркестр, состязание, победа, стадион).
Больница (помещение, сад, враг, радио, больные).
Любовь (розы, чувства, человек, город, природа).
Патриотизм (город, друзья, родина, семья, человек).

Правильные ответы подчеркнуты.

Тест

(Гуревич К. М., Акимова М. К., Борисова Е. М.)

Инструкция

Этот тест предназначен для диагностики умения детьми осуществлять классификацию. Инструкция испытуемым дается в устной форме: «Сейчас, вам будут предложены задания, которые предназначены для выявления вашего умения рассуждать, находить общее и различное. Эти задания отличаются от того, что вам приходится выполнять на уроках. Для выполнения заданий вам понадобятся ручки и бланки, которые я вам раздам».

На выполнение этого задания отводится 7 минут. Начинать и заканчивать работу по команде.

В бланке должны содержаться сведения о фамилии учащегося, дате проведения эксперимента, классе и школе, где учится испытуемый. Экспериментатор должен проконтролировать заполнение этих граф.

На бланке даны 5 слов, 4 из них объедены общим признаком. Пятое слово к ним не подходит. Его надо найти и подчеркнуть. Лишним может быть только одно слово.

Например:

а) тарелка, б) чашка, в) стол, г) кастрюля, д) чайник. а, б, г,. д – обозначают посуду, а в – мебель, поэтому оно подчеркнуто.

Форма А.

1. а) приставка, б) предлог, в) суффикс, г) окончание, д) корень.

2. а) прямая, б) ромб, в) прямоугольник, г) квадрат, д) треугольник.

3. а) барометр, б) флюгер, в) термометр, г) компас, д) азимут.

4. а) рабовладелец, б) раб, в) крестьянин, г) рабочий, д) ремесленник.

5. а) пословица, б) стихотворение, в) поэма, г) рабочий, д) повесть.

6. а) цитоплазма, б) питание, в) рост, г) раздражимость, д) размножение.

7. а) дождь, б) снег, в) иней, г) град, д) туман.

8. а) треугольник, б) отрезок, в) длина, г) круг, д) квадрат.

9. а) пейзаж, б) мозаика, в) икона, г) фреска, д) кисть.

10. а) очерк, б) роман, в) рассказ, г) сюжет, д) повесть.

11. а) параллель, б) карта, в) меридиан, г) экватор, д) полюс.

12. а) литература, б) наука, в) живопись, г) зодчество, д) художественное искусство.

13. а) длина, б) метр, в) масса, г) объем, д) скорость.

14 а) углекислый газ, б) свет, в) вода, г) крахмал, д) хлорофилл.

15. а) пролог, б) кульминация, в) информация, г) развязка, д) эпилог.

16. а) скорость, б) колебание, в) сила, г ) вес, д) плотность.

17. а) Куба, б) Япония, в) Вьетнам, г) Великобритания, д) Исландия.

18. а) товар, б) деньги, в) город, г) ярмарка, д) натуральное хозяйство.

19. а) описание, б) сравнение, в) характеристика, г) сказки, д) иносказание.

20. а) аорта, б) вена, в) сердце, г) артерия, д) капилляр.

Форма Б.

1. а) запятая, б) точка, в) двоеточие, г) тире, д) союз.

2. а) глобус, б) меридиан, в) полюс, г) параллель, д) экватор.

3. а) морфология, б) синтаксис, в) пунктуация, г) орфография, д) терминология.

4. а) движение, б) инерция, в) вес, г) колебание, д) деформация.

5. а) круг, б) треугольник, в) трапеция, г) квадрат, д) прямоугольник.

6. а) картина, б) мозаика, в) икона, г) скульптура, д) фреска.

7. а) рабочий, б) крестьянин, в) раб, г) феодал, д) ремесленник.

8. а) легенда, б) драма, в) комедия, г) трагедия, д) пьеса.

9. а)аорта, б) пищевод, в) вена, г) сердце, д) артерия.

10. а) Канада, б) Бразилия, в) Вьетнам, г) Испания, д) Норвегия.

11. а) тело, б) площадь, в) объем, г) вес, д) скорость.

12. а) направление, б) курс, в) маршрут, г) азимут, д) компас.

13. а) корень, б) стебель, в) лист, г) тычинка, д) цветок.

14. а) землетрясение, б) цунами, в) стихия, г) ураган, д) смерч.

15. а) метафора, б) монолог, в) эпитет, г) аллегория, д) преувеличение.

16. а) товар, б) город, в) ярмарка, г) натуральное хозяйство, д) деньги.

17. а) цилиндр, б) куб, в) многоугольник, г) шар, д) деньги.

18. а) пословица, б) басня, в) поговорка, г) сказка, д) былина.

19. а) история, б) астрология, в) раздражимость, г) рост, д) сознание.

20. а) питание, б) дыхание, в) раздражимость, г) рост, д) сознание.

Оценка выставляется по 9-балльной шкале.

Оценка в баллах	9	8	7	6	5	4	3	2	1
Количество правильных ответов	18	17	16	14 - 15	12 - 13	10 - 11	8 – 9	6 – 7	5

Каждая из методик дает надежные результаты при использовании ее в комплексе с другими методиками, направленными на выявление доступного испытуемому уровня обобщений, целенаправленности мыслительной деятельности, ригидности, характера понятийных связей.

Приложение В

Игры на формирование у учащихся начальных классов математических понятий, умственного приема классификация

«Ромбы»

Эта игра на закрепление представлений о пересекающихся понятиях. Для игры необходим комплект из 18 букв – это латинские буквы А, В, С, различной величины (большие и маленькие) и разной окраски (белые, черные и серые). Каждая такая буква имеет свое название, например, «А большая черная», «а маленькая белая», «С большая полосатая» и т. д. Игра имеет три варианта.

Вариант 1.

Перед началом этого варианта игры ребенку показывают, что есть две части игрового поля – внутри ромба и вне его. Затем делят случайным образом комплект букв поровну – половину себе, половину ребенку. Правила игры следующие: нужно расположить буквы так, чтобы все белые буквы (и только они) были внутри ромба. Ходы делаются по очереди, каждый использует буквы своего комплекта. За каждый ошибочный ход – штрафное очко. После того как все буквы разложены, у ребенка спрашивают: «Какие буквы оказались вне ромба?» Важно, чтобы он ответил, что вне ромба находятся все небелые буквы.

Правильным также является ответ – все черные и серые буквы. Если ребенок начинает перечислять, какие именно буквы там находятся, например, буквы А большие и малые, буквы В и т.п., то необходимо обратить его внимание на то, что и внутри круга есть такие буквы, что размер и наименование этих букв в этой игре не имеет значения. Главное, что внутри ромба находятся все белые буквы, а снаружи – небелые.

Цель этого варианта игры – научится выражать свойства букв, оказавшихся вне ромба, через свойство тех, которые лежат внутри него. Эту игру можно повторять несколько раз, меняя свойство букв, которые должны оказаться внутри ромба (например, внутри должны быть только все буквы В, или только маленькие буквы и т.д.). Ребенок должен научиться называть все буквы, находящиеся вне ромба, одним словом или словосочетанием.

Вариант 2.

Здесь для игры понадобятся уже два ромба. Они должны быть разного цвета или иметь какие-нибудь другие отличия. Перед началом игры необходимо показать ученику, что есть четыре области, определяемые двумя ромбами: 1) внутри белого, но не внутри черного ромба, 2) внутри черного, но не внутри белого, 3) внутри обоих ромбов, 4) вне обоих ромбов. Суть игры та же, что и в первом варианте только задание несколько сложнее. Нужно расположить буквы, так, чтобы внутри белого оказались все полосатые буквы, а внутри черного – все буквы С. Если ребенок не догадается, что внутри обоих ромбов должны оказаться полосатые буквы, подскажите ему и объясните, почему эти буквы должны одновременно относиться к обеим областям.

В данной игре задание может варьироваться следующим образом:

Буквы

Внутри белого ромба

Внутри черного ромба

Все А

Все В

Все большие

Все маленькие

Все черные

Все С

Все полосатые

Все черные

Все С

Все белые

Все полосатые

Все А

Все большие

После игры спросить у ребенка, как можно назвать буквы, находящиеся внутри обоих ромбом, внутри белого, но вне черного, внутри черного, но не внутри белого, вне обоих ромбов. Обратить внимание на то, чтобы он называл буквы, используя их наименование и размер.

Вариант 3.

Этот вариант значительно сложнее, так как здесь используется уже три ромба – белый. Черный и полосатый. Начать необходимо со знакомства с областями, образующими пересечение трех ромбов: первая область - внутри трех ромбов, вторая внутри – черного и белого, но вне полосатого ромба, третья – внутри белого и полосатого, но вне черного, … восьмая – вне всех ромбов.

Играть можно так же, как и во втором варианте, - поочередно раскладывая буквы в соответствии с заранее установленным правилом (например, внутри белого ромба должны быть все полосатые буквы, внутри черного – все буквы А, а внутри черного – все маленькие буквы). Но возможна и другая постановка задачи. Педагог сам раскладывает все буквы по определенному правилу, а ребенок должен проанализировать расположение букв и определить, по какому правилу они были разложены.

Этот вариант игры важно повторить несколько раз. Можно придумать такие задания, в которых одна или несколько областей оказались бы пустыми. Пусть ребенок попробует объяснить, почему так получилось.

«Дай определение».

С помощью данной игры ребенок научиться четко выражать свои мысли, давать лаконичные определения знакомых ему понятий, ориентируясь на существенные признаки и отвлекаясь от второстепенных.

Необходимо назвать знакомый ребенку предмет, например, «карандаш», и попросить его дать этому предмету наиболее точное определение. Это определение должно включать родовое понятие и видовое отличие. Можно дать, например, такое определение понятию «карандаш» - пишущий предмет (родовое понятие), имеющий графитовый стержень, оправленный в дерево или пластмассу (видовое отличие)».

Вот несколько понятий, которые можно предложить ребенку для определения (в скобках указан правильный ответ):

1. Стакан – это … (посуда для питья, изготовленная из стекла).

2. Яблоня – это… (дерево, на котором растут яблоки).

3. Утюг – это … (бытовой прибор, предназначенный для глажения).

4. Лампа – это … (электроприбор, предназначенный для освещения).

5.Штангист – это … (спортсмен, который занимается тяжелой атлетикой).

6. Учитель – это … (человек, который учит других людей).

«Белый и желтый».

Дидактическая игра для обучения умения отображать с помощью кругов Эйлера пересекающиеся понятия. Берут сначала два понятия «желтый» и «цветы» и предлагают отобразить ученику с помощью кругов. Скорее всего у него это не получится. Он либо изобразит один круг в другом, мотивируя, например, тем, что «Цветы бывают желтыми», либо нарисует их независимо друг от друга. Такие ошибки естественны, поскольку ребенок еще не знаком с понятием пересечения классов.

Предлагают ребенку подумать. Цветы бывают желтыми. Но ведь они могут иметь и другой цвет, например, красный, белый, синий. Значит понятие «цветы» не может полностью войти в понятие «желтый», там ему будет тесно.

«Желтый» «Цветы»

«Желтые цветы»

Рис. 4

Теперь рассматриваем понятие «желтый». Среди желтых объектов могут быть и цветы. Но не только цветы. Ведь есть много других предметов, которые нельзя отнести к цветам, например, скатерть, солнечный свет, обложка тетради. Следовательно, и

Понятие «желтый» не может полностью войти в понятие «цветы». Как же это можно показать графически?

Если ребенок понял, как можно отображать пересекающиеся понятия, ему предлагают выполнить несколько заданий самостоятельно.

«Поезд».

Эта игра – для обучения приему классификация. Для ее проведения необходимо подготовить комплект из 18 геометрических фигур разной формы (круг, треугольник, квадрат), величины (большие и маленькие) и окраски (черные, белые, полосатые). Таким образом, каждая фигура имеет три свойства – форму, величину, цвет, и соответствующие им названия: белый большой треугольник, полосатый маленький круг, черный большой квадрат и т. д.

Суть игры следующая. На разветвлении железнодорожных путей, по которым из начальной станции (находящейся внизу) фигурки паровозики должны попасть на конечные (расположенные вверху). При этом двигаться они должны в соответствии со знаками, указывающими, кто по данному отрезку пути может ехать. Например: полосатый маленький треугольник должен «попасть», следуя указателю цвета, должен двигаться по левой «ветке». Доходит до разветвления. Как двигаться дальше? По правой «ветке», так как она отмечена треугольником. Подъехали к следующему разветвлению. Здесь показывают, что по левой «ветке» должна двигаться большая фигура, а по правой – маленькая. Таким образом мы нашли конечную станцию для полосатого маленького треугольника. Эту станцию можно отметить , после чего следует провести остальные паровозики.

В эту игру можно играть и вдвоем. Тогда комплект фигур нужно разделить пополам. Ходы делаются по очереди. Кто меньше сделает ошибок, тот и выиграет.

«Универсальный магазин».

Игра на классификацию, умение осуществлять обобщение, абстракцию. Для игры нужны карточки с изображением предметов четырех групп: фрукты, овощи, музыкальные инструменты, школьные принадлежности (по 3 – 4 карточки каждой группы). Сюжет игры следующий. В универмаг привезли много разного товара, но сложили его в беспорядке. Ребенку, который играет роль продавца, предстоит трудная работа разложить товары по отделам. В один отдел должны попасть товары, которые подходят друг другу так, что их можно назвать одним словом. Можно подсказать ребенку, что должно получиться четыре отдела. После этого надо предложить ребенку сократить количество отделов в два раза, но так, чтобы в каждом из двух оставшихся отделов товары также подходили друг другу, были чем то похожи, чтобы их тоже можно было назвать одним словом. Второе задание является более сложным. Оно требует осуществления обобщения на более высоком уровне. В конце игры важно, чтобы ребенок объяснил свои действия и ответы.

«Форма – цвет».

Цель: тренировка детей в распознавании формы и цвета фигур.

Описание игры. Играют двое. Оба имеют одинаковое количество фигур (один – малые фигуры, другой – большие). Первый игрок кладет в какую-нибудь клетку соответствующую фигуру. Второй игрок должен ответным ходом положить соответствующую фигуру той же формы или того же цвета в одну из соседних клеток. Далее первый игрок ответным ходом кладет соответствующую фигуру в одну из соседних клеток относительно любой из размещенных фигур и т. д. Неправильный ход, т. е. Несоответствие фигуры по форме или цвету клетке таблицы, наказывается изъятием у игрока этой фигуры. Проигрывает тот у кого меньше останется фигур.

«Логическое домино».

Цель: тренировать детей различать свойства фигур (форму, цвет, величину).

Описание игры. Играют двое. Оба игрока имеют наборы фигур. Один кладет на стол фигуру. Ответный ход второго игрока состоит в том, что он прикладывает к этой фигуре другую, отличающуюся от нее только одним каким-нибудь свойством. Например, если первый положил на стол большой красный треугольник, то второй может ответить, приложив к нему малый красный треугольник, или большой желтый треугольник, или большой красный круг и т. п. Но если второй ответит, приложив к первой фигуре вторую, не отличающуюся от первой или отличающуюся от нее более, чем одним признаком, то ответный ход не правильный и у игрока изымается эта фигура.

При такой организации игры проигрывает тот, кто останется без фигур.

Возможна и другая организация игры, при которой неправильные ходы не допускаются, т. е. Игрок наказывается потерей хода.

При такой организации игры выигрывает тот, кто первый останется без фигур.

Приложение Г.

1. Поместите в верхний ряд картинки (рис. 1), на которых вишен меньше, чем 4, а в нижний ряд картинки, на которых вишен больше, чем 4.

Рис.1

Выпишите числа, в которые меньше, чем 8. Выпишите числа, которые больше, чем 8: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

3. Разбейте данные числа на группы. В первую запишите четные числа, а во вторую — нечетные числа:

1, 2, 3, 4, 6, 7, 8, 9, 10

Какие числа вы записали в первую группу? Какие числа вы записали во вторую группу? Все ли числа вы разбили на группы?

4. Назови наибольшее (наименьшее) число в ряду:

2, 9, 4, 5, 3, 7, 8, 1.

Посчитай в порядке возрастания (убывания):

5, 1, 4, 8, 10, 3, 7, 2.

6. Решите примеры и разбейте их на группы:

3+2 4+5 4+1 10-1 6+4

6-3 9-2 7-2 6+1 3+4

В данном случае имеется возможность различного разбиения, за основу которого можно взять или арифметическое действие, или полученный результат.

Посчитай и скажи, сколько домиков изображено на рисунке (рис. 2) (в ряду, в столбике)?

Сколько всего домиков в рядках и сколько в столбиках? На сколько домиков во втором рядке больше, чем в первом? На сколько домиков больше в третьем ряду, чем в первом? На сколько домиков во втором столбике меньше, чем в первом? На сколько домиков в третьем ряде меньше, чем во втором? Сколько домиков вместе в первом столбике и в третьем ряде? Сколько домиков вместе во втором столбике и втором ряде?

8. Назови цифры в середине фигуры? Сколько их? Назови цифры над фигурой, сколько их? Назови цифры под фигурой, сколько их? Назови цифры слева от фигуры, сколько их? Назови цифры справа от фигуры, сколько их? Назови цифры вне фигуры, сколько их?

8 3

6 1

5 0

1 4

9. Какие фигуры изображены на рисунке (рис. 3)? Назови цифры, которые записаны в середине квадрата. Назови цифры, которые записаны не в квадрате. Назови цифры, которые записаны не в круге. Назови цифры, которые записаны не в середине квадрата. Назови цифры, которые записаны не в середине круга. Назови цифры. Которые записаны в середине квадрата и не в круге. Назови цифры, записанные в середине круга и не в квадрате. Как расположена цифра 2 относительно круга, квадрата? Как расположена цифра 3 относительно круга, квадрата? Как расположена цифра 1 относительно круга, квадрата?

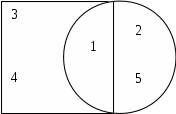
Рис.3

10. Убери лишнюю фигуру (рис.4). Разложи данные фигуры так, чтобы в каждой группе были похожие между собой фигуры. Сколько групп получилось? Сколько фигур в каждой группе? Можно ли дополнить вторую группу треугольником (кругом, квадратом)? Почему?

Рис.4

11. Назови фигуры в середине круга (рис.5). Назови фигуры не в круге. Назови фигуры, которые расположены справа от круга. Назови фигуры, которые расположены слева от круга. Назови фигуры над кругом. Назови фигуры под кругом. Сколько всего четырехугольников на рисунке? Сколько всего треугольников на рисунке? Сколько всего отрезков на рисунке? Сколько всего кругов на рисунке? Чего больше треугольников или кругов.? На сколько?

Рис. 5

12. Закрась больший квадрат на рисунке (рис. 6) синим цветом. Закрась меньший квадрат желтым цветом. Зарисуй общую часть зеленым цветом (или она уже закрашена)? Покажи часть меньшего квадрата, которая лежит под большим квадратом. Покажи часть большего квадрата, которая лежит над меньшим квадратом. Покажи часть меньшего квадрата, которая лежит за большим квадратом. Покажи часть большего квадрата, которая лежит за меньшим квадратом. Покажи часть большего квадрата, которая является частью меньшего квадрата. Покажи часть меньшего квадрата, которая лежит в середине большего квадрата.

Рис.6

13. Приложив полоски, выясни, какая из них длиннее (рис 7). На сколько?

Рис. 7

14. Покажи круг, который полностью лежит в середине другого круга. Найди точку А на рисунке (рис. 8), в середине какого круга она находится большего или меньшего)? Найди точку В, в середине какого круга она находится большего или меньшего)? Покажи общую часть двух кругов. Поставь точку, которая не принадлежит большому кругу. Поставь точку, которая не принадлежит меньшему кругу. Поставь точку, которая принадлежит меньшему и большему кругу. Поставь точку, которая не принадлежит меньшему и большему кругу.

Рис. 8

15. Сколько больших кружков? Сколько маленьких? Сколько красных? Сколько синих? Сколько больших красных? Сколько маленьких красных? Сколько больших синих? Сколько маленьких синих?

Рис. 9

16. Сравни площади четырехугольников (рис. 10). Назови фигуры. Какая фигура больше? Какая фигура меньше?

Рис. 2.9

Рис.10

17. Измерь полоску АB данной меркой CD (рис.11).

А В

С D

Рис. 11

18. На парте лежат короткие, средние, длинные палочки красного, синего, желтого и белого цветов. Надо разложить их по цвету и по размеру.

По цвету По размеру

Красные- Короткие – красная, синяя, желтая, белая

Синие - Средние – красная, синяя, желтая, белая

Желтые - Длинные - красная, синяя, желтая, белая

Белые –

Приложение Д.

Статья по проблеме исследования

РОЛЬ КЛАССИФИКАЦИИ В ФОРМИРОВАНИИ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ У МЛАДШИХ ШКОЛЬНИКОВ

Свирская Наталья 51-ЕН

Научный руководитель: Глузман Н. А.

В системе знаний об объектах и предметах окружающей действительности понятия служат опорным моментом в ее познании и являются своеобразным итогом познания. Поэтому понятия являются одной из главных составляющих в содержании любого учебного предмета, в том числе - и предметов начальной школы.

Проблема формирования понятий давно привлекает внимание психологов и педагогов (Л. С. Выготский, Д. Б. Эльконин, В. В. Давыдов, Н. А. Менчинская, Ж. Пиаже, П. Я.Гальперин, Н. Ф. Талызина, В. Н. Осинская Л. И. Айдарова, Н. Г. Салмина, К. А. Степанова, В. И. Зыкова, М. Б. Волович). В исследованиях, касающихся формирования понятий авторы часто обращаются к математике.

Классификация является частным случаем деления – логической операции над понятиями. Деление – это распределение на группы тех предметов, которые мыслятся в исходном понятии. Классификация представляет собой многоступенчатое, разветвленное деление. В процессе классификации образуется система изучаемых понятий. Полезны классификации при повторении, так как при этом систематизируется изучаемый материал, ученики получают более полное представление о взаимосвязях между понятиями и о системе математических понятий.

Достигается это через выполнение следующей системы условий.

Первое условие. Наличие адекватного действия: оно должно быть направлено на существенные свойства. Выбор действия определяется, прежде всего, целью усвоения понятия.

Третье условие. Все элементы действия представлены во внешней, материальной (или материализованной) форме. Применительно к действию подведения под понятие это выглядит следующим образом. Система необходимых и достаточных признаков понятия выписывается не карточку, эти признаки материализуются.

Пятое условие - наличие пооперационного контроля при усвоении новых форм действия. Контроль лишь по конечному продукту действия не позволяет следить за содержанием и формой выполняемой учащимися деятельности. Пооперационный контроль обеспечивает знание и того, и другого. При формировании понятий с помощью действия подведения под понятие в качестве операций выступает проверка каждого признака, сравнение с логическим правилом и так далее.

Восьмое условие - уверенность учащихся в знаниях и действиях.

Десятое условие - обобщенность понятий и действий

Понятия являются одной из главной составляющих в содержании любого учебного предмета начальной школы, поэтому задача учителя обеспечить полноценное усвоение понятий.

Литература:

1. Логика: Курс лекций //Ерышев А. А., Лукашевич Н. П., Сластенко Е. Ф. – 3-е изд., перераб. и доп. – К.: МАУП, 2000. – 184 с.

2. Практическая логика: Учебное пособие / Ивин А. А. – М.: ФАИР – ПРЕСС, 2002 г. – 288с.

3. Талызина Н. Ф. Педагогическая психология: Учебник для студ. – 2-е изд., стереотип. – М.: Издательский центр «Академия», 1998. – 288с.

Роль умственного приема классификации в формировании математических понятий у младших школьников

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

КРЫМСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ ИНСТИТУТ

ДИПЛОМНАЯ РАБОТА

Студентки 5 курса

Свирской Натальи Витальевны

Евпаторийского

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ

Рис. 2.12

По методике Л. С. Выготского

Фамилия, имя учащихся

Фамилия, имя учащихся

Абляметова Эльнара

Фамилия, имя учащихся

Фамилия, имя учащихся

Абляметова Эльнара

Тест

(Гуревич К. М., Акимова М. К., Борисова Е. М.)

Инструкция

Рис. 4

Статья по проблеме исследования