23. Логические уравнения – продолжение
23. Логические уравнения – продолжение – Сколько различных решений имеет система уравнений
(X1 ∨ X2) ∧ (¬X3 ∨ ¬X4) = 0
(X3 ∨ X4) ∧ (¬X5 ∨ ¬X6) = 0
(X5 ∨ X6) ∧ (¬X7 ∨ ¬X8) = 0
(X7 ∨ X8) ∧ (¬X9 ∨ ¬X10) = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение:
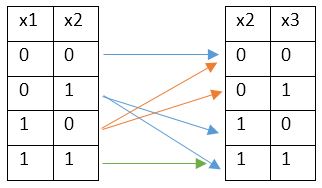
| x1 | x2 | x3 | x4 |
| 0 | 0 | 0 | 0 |
| 1 | |||
| 1 | 0 | ||
| 1 | |||
| 1 | 1 | 1 | |
| 1 | 0 | 1 | 1 |
| 1 |
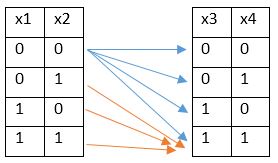
| x1x2 | x3x4 | 5x6 | x7x8 | x9x10 | |
| 00 | 1 | 1 | 1 | 1 | 1 |
| 01 | 1 | 1 | 1 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 1 |
| 11 | 1 | 4 | 7 | 10 | 13 |
| 16 |
Ответ: 16
Сколько различных решений имеет система уравнений
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
…
(X5 ≡ X6) → (X6 ≡ X7) = 1
где x1, x2, …, x7 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение:
| x1 | x2 | x3 |
| 0 | 0 | 0 |
| 1 | 0 | |
| 1 | ||
| 1 | 0 | 0 |
| 1 | ||
| 1 | 1 |
| x1x2 | x2x3 | x3x4 | x4x5 | x5x6 | x6x7 | |
| 00 | 1 | 2 | 3 | 4 | 5 | 6 |
| 01 | 1 | 1 | 1 | 1 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 1 | 1 |
| 11 | 1 | 2 | 3 | 4 | 5 | 6 |
| 14 |
Ответ: 14
Сколько различных решений имеет система логических уравнений
(x1 ∧ x2 → x3) ∧ (x1 ∨ y1) = 1
(x2 ∧ x3 → x4) ∧ (x2 ∨ y2) = 1
(x3 ∧ x4 → x5) ∧ (x3 ∨ y3) = 1
(x4 ∧ x5 → x6) ∧ (x4 ∨ y4) = 1
(x5 ∧ x6 → x7) ∧ (x5 ∨ y5) = 1
x6 ∨ y6 = 1
где x1, …, x6, y1, …, y6, – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение:
| x1x2 | x2x3 | x3x4 | x4x5 | x5x6 | x6x7 | ||
| 00 | 1 | 3 | 5 | 11 | 21 | 43 | |
| 01 | 1 | 3 | 5 | 11 | 21 | 43 | |
| 10 | 1 | 1 | 3 | 5 | 11 | 21 | 42 |
| 11 | 1 | 3 | 9 | 23 | 57 | 135 | 270 |
43+43+42+270=398
Ответ: 398
Сколько различных решений имеет система логических уравнений
(x1 → y1) ∧ ((x2 ∨ y2) → (x1 ≡ y1)) = 1
(x2 → y2) ∧ ((x3 ∨ y3) → (x2 ≡ y2)) = 1
…
(x6 → y6) ∧ ((x7 ∨ y7) → (x6 ≡ y6)) = 1
x7 ≡ y7 = 1
где x1,x2,…,x7, у1,у2,…,у7 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполняются данные равенства. В качестве ответа нужно указать количество таких наборов.
Решение:
| x1 | y1 | x2 | y2 |
| 0 | 0 | 0 | 0 |
| 1 | |||
| 1 | 0 | ||
| 1 | |||
| 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 |
| 1 | |||
| 1 | 0 | ||
| 1 |
| x1y1 | x2y2 | x3y3 | x4y4 | x5y5 | x6y6 | x7y7 | |
| 00 | 1 | 3 | 7 | 17 | 41 | 99 | 239 |
| 01 | 1 | 2 | 5 | 12 | 29 | 70 | 169 |
| 10 | 0 | 2 | 5 | 12 | 29 | 70 | 169 |
| 11 | 1 | 2 | 5 | 12 | 29 | 70 | 169 |
| 408 |
Ответ: 408
Сколько существует различных наборов значений логических переменных x1, x2, … x8, y1, y2, … y8, которые удовлетворяют всем перечисленным ниже условиям?
(x1→x2) /\ (x1→y1) = 1
(x2→x3) /\ (x2→y2) = 1
…
(x7→x8) /\ (x7→y7) = 1
(x8→y8) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x8, y1, y2, … y8, при которых выполнена данная система равенств.
В качестве ответа Вам нужно указать количество таких наборов.
Ответ:
Источник: СтатГрад 2017−2018
Решение:
(x1→x2) = 1
(x2→x3) = 1
…
(x7→x8) = 1
(x8→y8) = 1
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | (x1→y1) для каждого 0’а, y может 0 или 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28=256 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 27=128 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 26=64 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 25=32 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 24=16 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 23=8 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 22=4 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 22=2 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 20=1 | |
| 256+128+64+32+16+8+4+2+1=511 |
Ответ: 511