Единый государственный экзамен ЕГЭ по математике. Юг. Основная волна 06.06.2016. Вариант 437

Единый государственный экзамен ЕГЭ по математике. Юг. Основная волна 06.06.2016 Вариант 437

1. В летнем лагере 164 ребёнка и 23 воспитателя. Автобус рассчитан не более чем на 45 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?

Решение:

164+23=187/4=4,1

Ответ: 5

2. На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по приведённой диаграмме, сколько месяцев среднемесячная температура превышала 20 градусов Цельсия.

Решение:

Ответ:

3. На клетчатой бумаге с размером клетки 1х1 изображен параллелограмм. Найдите его площадь.

Решение:

15-2,5-2,5=10

Ответ: 10

4. Научная конференция проводится в 4 дня. Всего запланировано 30 докладов: в первые два дня по 9 докладов, остальные распределены поровну между третьим и четвёртыми днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?

Решение:

1д.	2д.	3д.	4д.
9	9	6	6

Ответ: 0,2

5. Найдите корень уравнения 

Решение:

Ответ: 0,8

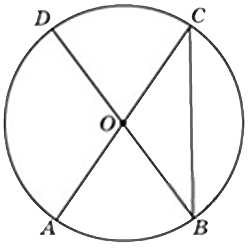
6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:

 

Так как угол ∠ACB и ∠DBC опираются на одну и ту же хорду, то ∠ACB=∠DBC, следовательно ΔOCB – равнобедренный треугольник. Т.к. ∠AOB=66° и ∠AOB=∠BOC, то ∠BOC=66°. Т.к. сумма углов треугольника равна 180°. а ∠ACB=∠DBC и ∠BOC=66°, то можем найти ∠ACB.

180 = 66° + x + x

2x=114

x=57

Ответ: 57

7. На рисунке изображён график  – производной функции f(x), определённой на отрезке (−11; 2). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.

Решение:

Т.к. угловой коэффицент равен нулю, то и производная в этой точке равна нуля, т.е. точка пересечения оси обцисс и графика x=-7.

Ответ: -7

8. Объём треугольной пирамиды равен 94. Через вершину пирамиды и среднюю линию её основания проведена плоскость. Найдите объём отсечённой треугольной пирамиды.

Решение:

Обьём пирамиды 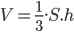 (S_осн). т.к. вершина у пирамид общая, то h не изменяется. Т.к. площадь отсечённой части основания в 4 раза меньше площади основания, то V_{отсеченной пирамиды} = 

Ответ: -28

9. Найдите значение выражения 

Решение:

cos2x=cos²x-sin²x

Ответ: -28

10. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t)=T₀+bt+at² где t — время (в мин.), T₀ = 680 К, а = −16 К/мин², b = 224 К/мин. Известно, что при температуре нагревательного элемента свыше 1400 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Решение:

 

Ответ: 5

11. Имеется два сплава. Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение:

Ответ: 4

12. Найдите точку минимума функции

Решение:

y=1,5x^2-27x+42lnx-10

Исследуем функцию:

Ответ: 7

13. а) Решите уравнение 

б) Укажите корни этого уравнения, принадлежащего отрезку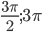 

Решение:

а) 

Ответ: 

б)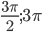 

Ответ: 

14. В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 16, а высота пирамиды равна 4. На рёбрах AB, CD и AS отмечены точки M, N и K соответственно, причём AM = DN = 4 и AK = 3.

а) Докажите, что плоскости MNK и SBC параллельны.

б) Найдите расстояние от точки M до плоскости SBC.

Решение:

а) M(8;-4;0), N(-8;-4;0), A(8;-8;0), S(0;0;4)

AS(-8;8;4), AK(-2;2;1)

K(6;-6;1), B(8;8;0), C(-8;8;0)

16+128=144=12²

Угол между плоскостями равен углу между их перпендикулярами.

Найдем , который ⊥ пл-ти MNK, с помощью уравнения пл-ти:

=(x+8.0-(y+4)(16-0)+z.(-32.0) = 0.x-16y-64-32z = 0.x+y+2z+4=0 ⇒ (0;1;2)

Найдем , который ⊥ пл-ти SBC, с помощью уравнения пл-ти:

=x(-32+32)-y(-32-32)+(z-4)(64+64) = 0.x+64y+128z-512 = 0.x+y+2x-8 = 0 ⇒ (0;1;2)

cosα, где α угол между  и .

Ответ: 90

б) Расстояние от (.) M_o до пл-ти Ax+By+Cz+D=0:

Нам нужно найти ρ от (.) M до пл-ти SBC/

M(8;-4;0)

Уравнения пл-ти SBC:

0.x+64y+128z-512 = 0

Тогда ρ:

Ответ:

15. Решите неравенство 

Решение:

ОДЗ 4x-5.2x+4≠0 ⇒ x≠2;x≠0 2x-4≠0 ⇒ x≠2 2x-6≠0 ⇒ x≠log26

t ∈ (-∞;4) ∪ (6;8]

x ∈ (-∞;2) ∪ (log₂6;3]

Включая ОДЗ получаем:

Ответ: x ∈ (-∞;0) ∪ (0;2) ∪ (log₂6;3]

16. В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.

а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.

б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.

17. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019	Июль 2020
Долг (в млн рублей)	S	0,8S	0,5S	0,1S	0

Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.

Решение:

1-ая выплата: 0,15S+0,2S=0,35S

2-ая выплата: 0,8.0,15S+0,3S=0,12S+0,3S=0,42S

3-ая выплата: 0,5.0,15S+0,4S=0,075S+0,4S=0,475S

4-ая выплата: 0,1.0,15S+0,1S=0,015S+0,1S=0,115S

Сумма выплат: 0,35S+0,42S+0,475S+0,115S=1,36S

Нам нужно наидольшее S, при котором сумма выплат < 50 млн.

1,36S < 50

S < 50/1,36

S=36

Наибольшее целое решение = 36

Ответ: 36

18. Найдите все значение a, при каждом из которых уравнение имеет ровно один корень.

19. На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8).

а) Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел.
б) Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7?
в) На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?