Досрочный вариант Единый государственный экзамен ЕГЭ 14 апреля 2017 по математике профильный уровень
Досрочный вариант Единый государственный экзамен ЕГЭ 14 апреля 2017 по математике профильный уровень
13. a) Решите уравнение -sin(x+-frac{3-pi}{2})=0.png)
б) Укажите корни этого уравнения, принадлежащие отрезку 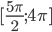
Ответ:
a) 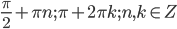
=-cosx.png)
=-cosx.png)

=0.png)

б) 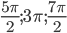
Корни из пункта а на единичной окружности лежат так
Приведем их к виду, входящему в заданный отрезок



Запишем все корни в ответ: 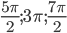
14. Длина диагонали куба ABCDA1B1C1D1 равна 3. На луче A1C отмечена точка P так, что A1P=4
А) Докажите, что грань PBDC1 ‐ правильный тетраэдр
Б) Найдите длину отрезка AP
A1C=3, A1P=4,CP=1
H – точка пересечения A1C и плоскости DBC1
ΔDBC1 – равностор.


О – точка пересечения диагоналей основания куба
C1O и A1C пересекаются в точке Н.




H – … опис.окр. и DC1BP – правильное пирамида

 ⇒ DC_1BP – правильный тетраэдр
⇒ DC_1BP – правильный тетраэдр
Б) Ответ: 

 по теореме косинусов
по теореме косинусов



15. Решите неравенство: ^2-62(9^x-2.3^x)-63-geq 0.png)
Ответ: 0;[2;∞]
9x-2.3x=t
t2-62t-63 ≥ 0
(t+1)(t-63) ≥ 0
| 9x-2.3x ≤ -1
32x-2.3x+1 ≤ 0 (3x-1)2 ≤ 0 3x=1 x=0 |
9x-2.3x ≥ 63
(3x)2 – 2.3x – 63 ≥ 0 Δ=4+4.63 = 64.4 3x=(2-16)/2 = -7 3x=(2+16)/2 = 9
3x > 0 3x ≥ 9 x ≥ 2 |
Ответ: 0;[2;∞]
16. Точка М – середина гипотенузы АВ треугольника АВС. Серединныйперпендикуляр к гипотенузе пересекает катет ВС в точке N.
а) Докажите, что ∠CAN=∠CMN
б) Найдите отношение радиусов окружностей, описанных около треугольников ANB и CBM, если 
Ответ: 
∠CAN = ∠CMN
α = ∠CBM = ∠NAB (т.к. NAM=NBM)
2α + β = 90°
CM = AM = MB (медиана из ⊥ угла)
тогда ∠MCB = ∠MBC = α
∠CMN = 180-90-2α = β
∠CAN = β
б) 
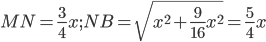


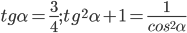





17. В июле 2026 года планируется взять кредит в банке на три года в размере S млнрублей, где S – целое число. Условия его возврата таковы:
‐ каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года
‐ с февраля по июнь каждого года необходимо выплатить одним платежом часть долга
‐ в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
| Месяц и год | Июль 2026 | Июль 2027 | Июль 2028 | Июль 2029 |
| Долг (в млн рублей) |
S | 0,8S | 0,4S | 0 |
Найдите наибольшее значение S, при котором каждая из выплат будет меньше 5 млн рублей.
Очевидно, что выплат 2028 и 2029 больше, чем первая. Поэтому будет достаточно сравнить их и найти наибольшую.
2027-2028)
1,2.08S-x1 = 0,4S
x1=0,56S
2028-2029)
1,2.0,4S=x2=0,48
Берем 2027-28 год.
x1=0,56S<5
S<
S≤8
Ответ: 8
18. Найдите все значения параметра a , при каждом из которых система неравенств

имеет хотя бы одно решение на отрезке [- 1;0]
Ответ: 

(x+12)-lt a.png)
Это паробола
Приравняем ее и нижнюю границу ромба = -x-4
(x+12) = -x-4.png)




эта точка лежит правее вершины параболы, она нам и нужна
Чтобы узнать значение а подставим 
 (это нижняя удовлетворяющая условиям граница)
(это нижняя удовлетворяющая условиям граница)
Верхняя будет в точке a=4 так как выше уже решений не будет.
Ответ: 
19. На доске написано несколько (более одного) различных натуральных чисел, причем любые два из них отличаются не более чем в три раза
а) Может ли на доске быть 5 чисел, сумма которых равна 47?
б) Может ли на доске быть 10 чисел, сумма которых равна 94?
в)Сколько может быть чисел на доске, если их произведение равно 8000?
Ответ: а) да; б) нет; в) 2 или 3
а) да
a<b<c<d<e
e ≤ 3a
Пусть a=5, e=15
b+c+d=27
7+9+11=27
да, может.
б) Мы не можем взять 4, как наименьшее число так как 4.3=12, а между 4 и 12 не 10ти чисел. Посмотрим 5:1 0 чисел от 5 до 14
 , нельзя.
, нельзя.
в) 8000=26.53
Можно разложить на 26 и 53
или 52 и 5.22 и 24
Попробуем разллжить на большее количество чисел. Если наименьшее число 5, то наибольшее ≤ 15, но между ними можно разместить 5, 8 и 10. Если наименьшее 23, то наибольшее ≤ 24 между ними нельзя использовать 5 три раза (только 10 и 20). Получается, что число 24 наименьшее в разложении и разложить больше, чем на три множителя, невозможно.
Публикуется ПОСЛЕ окончания экзамена в ознакомительных целях








