Ответы и решение – досрочный вариант Единый государственный экзамен ЕГЭ 2017 по математике профильный

Ответы и решение – досрочный вариант Единый государственный экзамен ЕГЭ 2017 по математике профильный
Часть 1
1. (131 – 121) ∙ 13,5 = 10 ∙ 13,5 = 135 руб
Ответь: 135 руб
2. По рисунку наименьшую цену меди за данный период = 8085
3. 
Ответь: 4
4. В трёх матчах возможно 23 = 8 различных исходов: 000, 001, 010, 100, 101, 110, 011, 111. Их них подходят только 000, 001, 010, 100 (не более одного раза).

5. log7 (1− x) = log75
1-x=5
x=-4
Ответь: -4
6. CA2=AB2-BC2=25-16=9 ⇒ CA=3

Ответь: 0,6
7. Значение производной функции в точке равно тангенсу угла наклона касательной к графику функции в этой точке.

Ответь: 1,5
8. 

Ответь: 60
9. 

Ответь: 11
10. 1380+165-15t2 ≤ 1800
15t2-165t+420 ≤ 0
t2-11t+28 ≤ 0
t ≤ 4 , t ≥ 7
Ответь: 4
11. 
Ответь: 55
12. 


т.к. sinx∈[-1;1], то данное ур-ие не будет выполняться.
Следовательно, нужно проверить границы:
1) -24-6=-5-30=-35.png)
2) -6=10.1-6=4.png)
Наименьшее: -35
Ответь: -35
Часть 2
13. а)

^3-9.2.2^x+-frac{2^5}{2^x}=0.png)
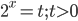





|
 
|
б) [log52;log520]



Ответ: а) 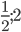
б) 
14.
15. -7log_2(25-x^2)+12 -geq 0.png)
=t.png)
|
ОДЗ: 
|

|

|
Обьединяя с ОДЗ получаем:

16. Составим функцию прибыли за 25 лет:
25 лет
t лет 25-t
t2 (1+r)25-t
f(t)=t2(1+r)25-t
По условию задачи сказано, что down- наибольшей прибыли ценные бумаги нужно продать строго в конце 21 года, т.е. t=21. Следовательно, нам нужно обеспечить, чтобы f(21)>f(20) иf(21)>f(22):
-f(20) --
f(21)-f(22).png) ⇒
⇒ ⇒
 --
21^2(1+r)-22^2.png)
 ⇒
⇒  ⇒
⇒ .png)
17.
| t | 1 | 2 | 3 | 4 | 5 | 6 |
| t2 | 1 | 4 | 9 | 16 | 25 | 36 |
^2}.png) |
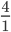 |
 |
 |
 |
 |
^2 - 1+r.png)
^2 - 1+r.png)
^2 - 1+r - (-frac{21}{20})^2.png)

18.
1) 

.png)
2) 
=-sqrt{4-1}=-sqrt{3}.png)
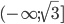
3) 



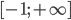
Ответ: .png)
19.
а) да; 6,7,8,9,10
б) нет
в) 35; 7,8,9,11








=4.png)


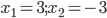
=3.png)