Досрочный вариант Единый государственный экзамен ЕГЭ 2017 по математике профильный уровень
Досрочный вариант Единый государственный экзамен ЕГЭ 2017 по математике профильный уровень 31 марта 2017
1. В квартире установлен счетчик холодной воды. Показания 1 марта – 270 куб. м., а 1 апреля – 320 куб. м. Сколько нужно заплатить за холодную воду за март, если стоимость 1 куб. м. воды равна 14 руб. 50 коп.?
2. На рисунке жирными точками показана цена палладия на момент закрытия торгов. По горизонтали указываются числа месяца, по вертикали – цена палладия в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку максимальную стоимость металла во второй половине месяца.
3. На клетчатой бумаге с размером клетки 1 х 1 изображен четырехугольник. Найдите радиус окружности, которую можно вписать в данный четырехугольник.
4. Перед началом футбольного матча капитаны команд подбрасывают монету. Какова вероятность того, что команда «Статор» будет начинать все три матча?
5. Найдите корень уравнения log7(5x−3)=2log73
6. Найдите cosA, если известно, что AB = 10, CB = √19
7. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y=f(x) в точке x0.
8. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Известно, что AA1 = 5, BC = 4 и D1C1 = 3. Найдите объем многогранника ADA1B1C1D1.
9. Найдите значение выражения 
10. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t)=T0+bt+at2, где t – время в минутах, T0=1400 К, a=−10 К/мин2, b=200 K/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
11. Первый час автомобиль ехал со скоростью 60 км/ч, затем 2 часа со скоростью 110 км/ч, а следующие 2 часа со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на всем пути. Ответ выразите в км/ч
12. Найдите наименьшее значение функции 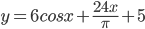 на промежутке [−2π/3;0]
на промежутке [−2π/3;0]
13. а) Решите уравнение 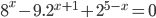
б) Укажите корни этого уравнения, принадлежащие отрезку [log52;log520]
14. Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α, содержащей прямую BD1 и параллельной прямой АС, является ромб.
а) Докажите, что грань ABCD – квадрат.
б) Найдите угол между плоскостями α и BCC1, если AA1 = 6 и AB = 4.
15. Решите неравенство -7log_2(25-x^2)+12-geq 0.png)
16. В треугольнике ABC точки A1, B1 и C1 – середины сторон BC, AC и AB соответственно, AH – высота, угол BAC равен 60o, угол BCA равен 45o.
а) Докажите, что точки A1, B1, C1 и H лежат на одной окружности.
б) Найдите A1H, если BC равно 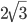
17. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t=1;2;,…). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счет в банке, при этом в конце каждого следующего года сумма на счете будет увеличиваться в r+1 раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счете была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?
18. Найдите все значения параметра a, при каждом из которых система неравенств

имеет хотя бы одно решение на отрезке [3;4]
19. На доске написано несколько различных натуральных чисел, произведение любых двух из которых больше 40 и меньше 100.
а) Может ли на доске быть 5 чисел?
б) Может ли на доске быть 6 чисел?
в) Какое наибольшее значение может принимать сумма чисел на доске, если их четыре?
1. 725
2. 315
3. 3
4. 0,125
5. 2,4
6. 0,9
7. -0,5
8. 30
9. 6
10. 2
11. 104
12. -14
13. а) 2; 1/2 б) 1/2
14. arctg(5/3)
15. (−5;−√17]∪[−3;3]∪[√17;5)
16. 1
17. (43/441;41/400)
18. [0,5;√3)
19. а) да; б) нет; в) 35




