11. Арифметические и геометрические прогрессии

Основнóй госудáрственный экзáмен ОГЭ Математика задание №11 Демонстрационный вариант 2018-2017 В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.

Демонстрационный вариант Основнóй госудáрственный экзáмен ОГЭ 2016 г. – задание №6 Модуль «Алгебра»

Последовательность задана условиями $b_{1}=4$ , $b_{n+1}=-\frac{1}{b_{n}}$ . Найдите $b_{4}$ .

Демонстрационный вариант Основнóй госудáрственный экзáмен ОГЭ 2015 г. – задание №6

Выписаны первые несколько членов арифметической прогрессии: $- 7$ ; $- 5$ ; $- 3$ ; … Найдите сумму первых пятидесяти её членов.

Решение:

Находим а50

а50=-7+2*(50-1)

а50=91

Находим сумму

S50=(-7+91)/2*50

S50=2100

Ответ: 2100

Выписано несколько последовательных членов геометрической прогрессии:

…; -6; х; -24; -48 ; …

Найдите х.

Решение:

Знаменатель геометрической прогрессии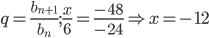

Ответ: -12

Найдите количество отрицательных членов числовой последовательности, заданной формулой

$a_{n} = 1 - \frac{104}{6 n - 5}$

Решение:

$\begin{matrix} = 1 - \end{matrix}$

$\begin{matrix} 104 > 6 n - 5 \end{matrix}$

$\begin{matrix} 6 n < 109 \end{matrix}$

$\begin{matrix} n < 18 \end{matrix}$

Ответ: 18

Выписано несколько последовательных членов арифметической прогрессии:

…, -10; х; -14; -16; …

Найдите х.

Решение:

Разность геометрической прогрессии x-(-10)=-16-(-14)

x+10=-16+14=>x=-12

Ответ: -12

Найдите количество отрицательных членов числовой последовательности, заданной формулой

$a_{n} = 1 - \frac{95}{4 n + 3}$

Решение:

=1−<0

4n+3<95

4n<92

n<23 ⇒ n=22

Ответ: 22

Выписано несколько последовательных членов арифметической прогрессии: …; 8; x; 16; 20; … Найдите х.

Решение:

Из приведенных чисел видно, что , и тогда

Ответ: 12.

Источник: И.В. Ященко. Типовые экзаменационные варианты

Последовательность задано условиями:

Найдите

Решение:

Из формулы зависимости последовательно вычислим все члены до 6, получим:

из первых полученных значений видно, что далее все чередуется, то есть .

Ответ: -2.

Источник: И.В. Ященко. Типовые экзаменационные варианты

Выписаны первые несколько членов геометрической прогрессии: -250; 150; -90; … Найдите её пятый член.

Решение:

Первый член прогрессии равен , тогда пятый ее член можно найти по формуле

и равен

Ответ: -32,4.

Источник: И.В. Ященко. Типовые экзаменационные варианты

Последовательность (bn) задана условиями: b1=-6, Найдите b5.

Решение:

Найдем значение вычисляя по порядку значения членов последовательности, получим:

видим, что последующие члены чередуются в этом порядке, то есть их можно найти не вычисляя:

Ответ: -6.

Источник: И.В. Ященко. Типовые экзаменационные варианты

Дана арифметическая прогрессия ( an ), разность которой равна -5, a1 = 9,2. Найдите a11.

Решение:

Арифметическая прогрессия – это последовательность вида где – d разность прогрессии. Так как то по формуле арифметической прогрессии , величина

Ответ: -40,8.

Источник: И.В. Ященко. Типовые экзаменационные варианты

Последовательность (an), n>1, задана формулой . Сколько членов этой последовательности больше 6?

Решение:

Упростим выражение, получим неравенство:

Так как число n должно быть целым, то наибольшее целое будет равно n=10,

Ответ: 10

Источник: И.В. Ященко. Типовые экзаменационные варианты

Последовательность (cn) задана условиями: c1 = 5 Найдите c6.

Решение:

Приведенный закон изменения членов последовательности соответствует арифметической прогрессии с разностью . В задаче дан первый член этой прогрессии , тогда 6-й член можно найти по формуле n-го члена арифметической прогрессии при n=6: