Контрольные работы по алгебре 8 класс
Контрольные работы по алгебре 8 класс
Итоговая контрольная работа по алгебре 8 класс
1. Упростите выражение:
a) .png)
b)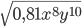 
, если y<0
2. Решите уравнение:
a) 
b)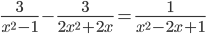 
3. Решите систему неравенств:
(3x+4)-3x^2 - 2x+1 --
5x-2 -leq 7x+10.png)
4. Представьте выражение 
в виде степени с основанием 10 (n – целое число).
5. Водонапорный бак наполняется двумя трубами за 3,6 ч. Одна перавя труба может наполнить его на 3 ч быстрее, чем одна вторая труба. За сколько часов первая труба, действуя отдельно, может наполнить бак?
6. Постройте график функции y=x2+6x−2.
а) найдите промежутки возрастания функции;
б) найдите промежутки убывания функции;
в) найдите наименьшее значение функции;
7. Постройте график функции 
.
а) найдите значение функции при x = 4; -2; −2/3.
б) найдите значение аргумента, если функция равна 4; -2; -0,25 .
в) найдите максимальное и минимальное значение функции на отрезке [-8; -1].
8. Постройте график функции 
.
а) найдите область значений функции.
б) найдите промежутки монотонности.
в) найдите наименьшее значение функции.
1. a) 1
^2 = (2--sqrt{3})^2.png)
^2}.(-sqrt{3}+2).png)
.(2+-sqrt{3})=2^2-(-sqrt3)^2=4-3=1.png)
b) -0,9x4y5
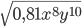
^2.(x^4)^2.(y^5)^2}=0,9.x^4.-y^5=-0,9x^4y^5.png)
2. a) x=2
и 
Δ=112-4.5.2=121-40=81
--sqrt{81}}{2.5}=-frac{11-9}{10}=-frac{1}{5}.png)
=> деление на ноль, не подходит
+-sqrt{81}}{2.5}=-frac{11+9}{10}=2.png)
b) x=3
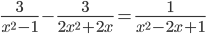
(x+1)} - -frac{3}{2x(x+1)} = -frac{1}{(x-1)^2}.png)
.3}{2x.(x-1)(x-1)(x+1)} - -frac{(x-1)^2.3}{(x-1)^2.2x(x+1)} = -frac{2x.(x+1).1}{2x.(x+1).(x-1)^2}.png)
=2x^2+2x.png)
-2x^2-2x=0.png)
(x+1)=0.png)
x=-1 => деление на ноль, не подходит
x=3
3. [-6;-2,25)
(3x+4)-3x^2 - 2x+1 -- 5x-2 -leq 7x+10.png)
a) (3x+4)-3x^2 - 2x+1.png)
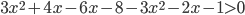
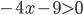
b) 
[-6;-2,25)
4. 103n
0,001.1000n+1 = 10-3.103.(n+1) = 10-3.103n+3 = 103n+3-3 = 103n
5. За 6 ч.
Водонапорный бак наполняется двумя трубами за 3,6 ч. Одна перавя труба может наполнить его на 3 ч быстрее, чем одна вторая труба. За сколько часов первая труба, действуя отдельно, может наполнить бак?
Пусть за х часов наполняет бак первая труба одна
тогда (х+3) часа наполняет бак одна вторая труба
1/х часть бассейна наполняет в час первая труба
1/(х+3) часть бассейна наполняет в час вторая труба
1/3,6 = 10/36 часть бассейна наполняют обе трубы за час
уравнение
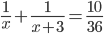
.1}{(x+3).x} + -frac{x.1}{x.(x+3)} = -frac{10}{36}.png)
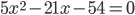
=1521=39^2.png)
-39}{10}=-frac{21-39}{10}=-1,8.png)
(Отрицательный не может быть)
+39}{10}=-frac{21+39}{10}=6.png)
6. y=x2+6x−2
^2+6.(-3)-2=9-20=-11.png)
а) найдите промежутки возрастания функции: [-3; +∞)
б) найдите промежутки убывания функции: (-∞; -3)
в) найдите наименьшее значение функции: -11
7.
а) y = -1; 2; 6;
x=4 ⇒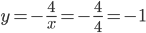 
x=-2 ⇒ 
x=−2/3 ⇒ 
б) x = -1; 2; 16;
y=4 ⇒ 
y=-2 ⇒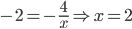 
y=-0,25 ⇒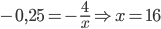 
в) максимальное значение = 4; минимальное значение = 0,5
на отрезке [-8; -1]
максимальное значение = 
минимальное значение = 
8. График функции получается из графика функции y=√x смещение на 4 единицы влево и 2 единицы вниз.
а) область значений функции = [-2; +∞);
б) функция возрастает на отрезке [-4; +∞), промежутков убывания нет.
в) наименьшее значение функции – -2.