14. Графики и диаграммы
Демонстрационный вариант Единый государственный экзамен ЕГЭ 2018 – 2017 г. – задание №14 На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия. Пользуясь графиком, поставьте в соответствие каждому интервалу времени характер.
В таблице под каждой буквой укажите соответствующий номер.
Решение:
На графике отчетливо видно сразу, где падает температура: Г) – 2). Приложим линейку горизонтально к ординате 30 и заключаем, что А) – 4). Выбирая теперь только из двух оставшихся временных промежутков Б) и В), нетрудно заметить, что на Б) температура растет медленнее, чем на участке В). Значит Б) – 1), В) – 3) соответственно.
Ответ:4132
ИЛИ
На рисунке изображен график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. В правом столбце указаны значения производной в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
Решение:
Значение производной функции в данной точке равно тангенсу угла наклона касательной к графику функции, проведенной в этой самой точке. А тангенс угла наклона касательной есть угловой коэффициент при аргументе в уравнении касательной. Касательная (прямая) в точке A растет быстрее других, положительный коэффициент в уравнении этой прямой будет самым большим из представленных, A – 2). Еще одна касательная растёт только в точке D, коэффициент в уравнении этой прямой положителен. Методом исключения, D – 3). Проведя аналогичные рассуждения, только для убывающих прямых, получаем ответ.
Ответ:2143
Демонстрационный вариант Единый государственный экзамен ЕГЭ 2016 г. (досрочный) – задание №14
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами 
и 
.
В правом столбце указаны значения производной функции в точках и . Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
Решение:
Если график функции возрастает, то производная положительная.
Если график функции убывает, то производная отрицательная.
В точках 
и функция возрастает, следовательно функция должна быть положительна.
На графике видно, что 
(расстояние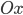 
), поэтому 
, а 
.
В точках 
и функция возрастает, следовательно функция должна быть положительна.
На графике видно, что 
(расстояние 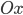), поэтому 
, а 
Ответ: 4132
Демонстрационный вариант Единый государственный экзамен ЕГЭ 2016 г. – задание №14
На рисунке изображен график функции = (), к которому проведены касательные в четырех точках. Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
В таблице под каждой буквой укажите соответствующий номер.
Решение:
Значение производной функции в данной точке равно тангенсу угла наклона касательной к графику функции, проведенной в этой самой точке. А тангенс угла наклона касательной есть угловой коэффициент при аргументе в уравнении касательной.
Касательная (прямая) в точке 
растет быстрее других, коэффициент в уравнении этой прямой будет самым большим из представленных, – 2). Еще одна касательная растёт только в точке 
, коэффициент в уравнении этой прямой положителен. Методом исключения, – 3). Проведя аналогичные рассуждения, только для убывающих прямых, получаем ответ.
Ответ: 2413