20. Задачи на смекалку
Демонстрационный вариант Единый государственный экзамен ЕГЭ 2018 – 2017 г. – задание №20 В обменном пункте можно совершить одну из двух операций:
 за 2 золотых монеты получить 3 серебряных и одну медную;
за 2 золотых монеты получить 3 серебряных и одну медную;
 за 5 серебряных монет получить 3 золотых и одну медную.
за 5 серебряных монет получить 3 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
Решение:
Отсутствие золотых монет говорит о том, что Николай все золотые монеты, полученные с помощью второй операции, обменял с помощью первой. Значит, вторых операций было четное число. Пусть вторых операций было ровно  . Тогда при применении второй операции:
. Тогда при применении второй операции:
.png) серебряных <=>
серебряных <=> .png) золотых +
золотых +  медных.
медных.
Теперь нужно обменять все .png) золотых монет с помощью первой операции. Всего таких операций будет
золотых монет с помощью первой операции. Всего таких операций будет -2=3n.png) .
.
золотых <=>
серебряных +
 медных.
медных.
Получается, что затратив  серебряных монет, Николай при реализации всех золотых получает
серебряных монет, Николай при реализации всех золотых получает  серебряных. Значит всего он потратил n серебряных. При этом Николай по итогу применения всех операций получил
серебряных. Значит всего он потратил n серебряных. При этом Николай по итогу применения всех операций получил  медных. Возвращаясь к условию задачи:
медных. Возвращаясь к условию задачи:
 ,
, 
Ответ: 10
ИЛИ
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными отрезками. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны
 и
и  . Найдите периметр четвёртого прямоугольника.
. Найдите периметр четвёртого прямоугольника.

Решение:
Составим уравнения с помощью формулы периметра прямоугольника:

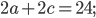
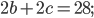
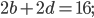

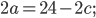
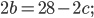
;.png)
=12.png) .
.
Ответ: 12