23. Функции и их свойства. Графики функций
Демонстрационный вариант 2018-2017 Основнóй госудáрственный экзáмен ОГЭ Математика задание №23 Постройте график функции (x+2)}.png)
и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку.
Решение:
Разложим числитель дроби на множители:
x4 −13x2 + 36 = (x2 − 4)(x2 − 9) = (x − 2)(x + 2)(x − 3)(x + 3)
При x ≠ −2 и x ≠ 3 функция принимает вид:
y = (x − 2)(x + 3) = x2 + x − 6 ,
её график — парабола, из которой выколоты точки (−2; −4) и (3; 6).
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая.
Вершина параболы имеет координаты (−0,5; −6,25).
Поэтому c = −6,25, c = −4 или c = 6.
Демонстрационный вариант Основнóй госудáрственный экзáмен ОГЭ 2015 г. – задание №23
Модуль «Алгебра»
Постройте график функции 
и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку.
Решение:
Преобразуем выражение: 
при условии, что x ≠−5. Построим график. Прямая y = m не имеет с графиком ни одной общей точки при m=3 и 
.
Ответ: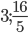 
Демонстрационный вариант Основнóй госудáрственный экзáмен ОГЭ 2015г. – задание №23
Модуль «Алгебра»
При каких значениях m вершины парабол 
и 
расположены по одну сторону от оси x?
Решение:
оордината x вершины параболы определяется по формуле 
. Координата yB вершины находится подстановкой xB в уравнение параболы. Вершины парабол будут находится по одну сторону от оси x, если координаты их вершин имеют одинаковые знаки. Вспомнив, что два сомножителя имеют одинаковый знак тогда и только тогда, когда их произведение положительно, составим и решим неравенство:
(4m2 – 8m2 + m)(-16m2 + 32m2 + 4) > 0
(-4m2 + m)(16m2 + 4) > 0
Заметим, что второй множитель всегда больше нуля, поэтому на него можно разделить.
 - 0.png)
 - 0.png)
Произведение двух сомножителей будет меньше нуля, если сомножители имеют разный знак (см. рисунок). Таким образом, получаем ответ: 
Ответ: .png)