Основнóй госудáрственный экзáмен ОГЭ ГИА по математике 28.05.2013. Основная волна.

Задание №1

На координатной прямой отмечены числа a и b:

Какое из следую­щих утверждений неверно?

 

1)

2)

3)

4) 

Задание №2

В каком случае числа расположены в порядке возрастания?

В ответе укажите номер правильного варианта.

1)   

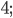
2)  ; 

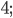
3) ;   

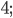
4)     

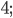
Задание №3

Решение какого из данных неравенств изображено на рисунке?

1)  

2) 

3) 

4) 

Задание №3

Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

Номер поезда Отправление из Москвы Прибытие в Санкт-Петербург
026A 23:00 06:30
002A 23:55 07:55
038A 00:44 08:48
016A 01:00 08:38

Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.

В ответе укажите номер правильного варианта.

1) 026А

2) 002А

3) 038А

4) 016А

Задание №5

На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.

Какое из следую­щих утверждений неверно?

 

1) Пользователей из России больше, чем пользователей с Украины.

2) Пользователей из Белоруссии больше, чем пользователей из Швеции.

3) Больше трети пользователей сети — из Украины.

4) Пользователей из России больше 4 миллионов.

В ответ запишите номер этого утверждения.

Задание №6

Найдите значение выражения

Задание №7

Найдите корни уравнения .

Задание №8

Установите соответствие между графиками функций и формулами, которые их задают.

1)

2)  

3)

4)

Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке

А Б В

Задание №9

Арифметическая прогрессия   задана условиями:  , . Найдите


Решение:

Определим разность арифметической прогрессии:

 
 

Член арифметической прогрессии с номером может быть найден по формуле

 

Необходимо найти , имеем:

Ответ: 

39

Задание №10

 Упростите выражение , найдите его значение при  . В ответ запишите полученное число.


Решение:

Упростим выражение:

 

Найдём значение выражения при  :

Ответ: 

8

Задание №11

Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.


Решение:

 Поскольку в треугольнике сумма всех углов равна 180°, угол ADС равен 180° − 30° − 80° = 70°. В равнобедренной трапеции углы BCD и CDA — односторонние, значит, угол ABC равен 110°.

Ответ: 

110

Задание №12

Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.


Решение:

 Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу. Углы при основании равнобедренного треугольника равны. Пусть BAO равен x, тогда x + x + 60° = 180°, где x = 60°. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, AB = 5.

Ответ: 

5

Задание №13

Найдите площадь параллелограмма, изображённого на рисунке.


Решение:

Площадь параллелограмма равна произведению длины основания на высоту:

 

Ответ: 

40

Задание №14

Найдите тангенс угла А треугольника ABC, изображённого на рисунке.


Решение:

Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

 

 

Ответ: 

0,4

Задание №15

Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

Если утверждений несколько, запишите их номера в порядке возрастания.


Решение:

Проверим каждое из утверждений.

1) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно по признаку подобия треугольников.

2) «Вертикальные углы равны» — верно, это теорема планиметрии.

3) «Любая биссектриса равнобедренного треугольника является его медианой» — неверно, это утверждение справедливо только для равностороннего треугольника.

Ответ: 

12

Задание №16

На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.


Решение:

Цена деления шкалы давления: мм рт. ст. Наименьшее значение давления во вторник равно мм рт. ст. плюс половина цены деления шкалы давления:

 

Ответ: 

751

Задание №17

Чашка, которая стои­ла 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?


Решение:

Стоимость одной чашки равна 90 − 0,1 · 90 = 81 руб. Стои­мость 10 чашек равна 810 руб. Значит, сдача с 1000 рублей составит 190 рублей.

 

Ответ: 

190

Задание №18

От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстоя­ние от дома до столба 8 м. Вычислите длину провода.


Решение:

Проведём отрезок, параллельный горизонтальной прямой, как показано на рисунке. Таким образом, задача сводится к нахождению гипотенузы прямоугольного треугольника; обозначим её за По теореме Пифагора:

 

Ответ: 

10

Задание №19

В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.


Решение:

Вероятность благоприятного случая() — отношение количества благоприятных случаев к количеству всех случаев. В данной задаче благоприятным случаем является старт спортсмена не из России под номером 1. Всего благоприятных случаев 2 + 5 = 7, а количество всех случаев 13 + 2 + 5 = 20. Отношение соответственно равно

Ответ: 

0,35

Задание №20

В фирме «Эх, прокачу!» стои­мость поездки на такси (в рублях) рассчитывается по формуле , где — длительность поездки, выраженная в минутах . Пользуясь этой формулой, рассчитайте стои­мость 15-минутной поездки.


Решение:

Подставим в формулу значение переменной :

 рублей

Ответ: 

260