Методические аспекты построения и анализа электродинамических уравнений Максвелла
Методические аспекты построения и анализа электродинамических уравнений Максвелла
В.В. Сидоренков, МГТУ им. Н.Э. Баумана
На основе первичных фундаментальных соотношений электромагнетизма - закона Кулона взаимодействия неподвижных электрических точечных зарядов и закона сохранения электрического заряда цепочкой последовательных физико-математических рассуждений построена система дифференциальных уравнений Максвелла классической электродинамики.
В курсе общей физики при изложении природы электричества [1] концепция электромагнитного поля является центральной, поскольку посредством такого поля реализуется один из видов фундаментального взаимодействия разнесенных в пространстве материальных тел. Физические свойства указанного поля математически представляются системой функционально связанных между собой уравнений в частных производных первого порядка, первоначальная версия которых была получена во второй половине XIX века Дж.К. Максвеллом [2] обобщением эмпирических фактов. В структуре этих уравнений, описывающих поведение электромагнитного поля в неподвижной среде, заложена основная аксиома классической электродинамики - неразрывное единство переменных во времени электрического и магнитного полей. В современной форме такая система дифференциальных уравнений имеет следующий вид:
(a)
 ,
(b)
,
(b)
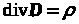 ,
,
(c)
 ,
(d)
,
(d)
 .
(1)
.
(1)
Здесь векторные поля: электрической
 и магнитной
и магнитной
 напряженности, соответственно,
электрической
напряженности, соответственно,
электрической
 и магнитной
и магнитной
 индукции, а также плотности электрического
тока
индукции, а также плотности электрического
тока
 ;
;
 и
и
 - абсолютные электрическая и магнитная
проницаемости,
- абсолютные электрическая и магнитная
проницаемости,
 - удельная электрическая проводимость
материальной среды,
- удельная электрическая проводимость
материальной среды,
 -
объемная плотность стороннего
электрического заряда.
-
объемная плотность стороннего
электрического заряда.
Покажем, как на основе первичных фундаментальных соотношений электромагнетизма - закона Кулона взаимодействия электрических точечных неподвижных зарядов
 (2)
(2)
и закона сохранения электрического заряда [1]
 (3)
(3)
цепочкой последовательных физико-математических рассуждений можно построить систему электродинамических уравнений Максвелла (1). Представляется, что логика таких рассуждений позволит обучаемым яснее и глубже понять сущность корпускулярно-полевого дуализма природы электричества.
Фундаментальность закона Кулона
(2) состоит в том, что его посредством
описывается силовое взаимодействие
разнесенных в пространстве неподвижных
электрически заряженных материальных
тел, где для изучения следствий такого
взаимодействия вводят понятие
электрического поля в виде напряженности
– силы Кулона на единицу заряда:
 ,
где
,
где
 - пробный точечный заряд. Топология
структуры электрического поля точечного
заряда
- пробный точечный заряд. Топология
структуры электрического поля точечного
заряда
 такова, что интеграл от этой функции по
сфере любого радиуса константен:
такова, что интеграл от этой функции по
сфере любого радиуса константен:
 ,
а при использовании понятия телесного
угла несложно убедиться: поток вектора
поля электрической индукции (смещения)
,
а при использовании понятия телесного
угла несложно убедиться: поток вектора
поля электрической индукции (смещения)
 через произвольную замкнутую поверхность
S тождественно равен суммарному стороннему
электрическому заряду
через произвольную замкнутую поверхность
S тождественно равен суммарному стороннему
электрическому заряду
 в объеме
в объеме
 внутри этой поверхности, причем на самой
указанной поверхности посредством
интегрирования поля электрической
индукции
внутри этой поверхности, причем на самой
указанной поверхности посредством
интегрирования поля электрической
индукции
 определяется индуцируемый поляризационный
электрический заряд
определяется индуцируемый поляризационный
электрический заряд
 ,
так что
,
так что
 :
:
 .
.
Такие рассуждения называют
электростатической теоремой Гаусса.
Она описывает результат электрической
поляризации. Правда, обычно в физические
подробности процесса поляризации не
вникают, а потому в данной теореме о
заряде
 в теореме просто не говорят. Здесь надо
иметь в виду, что равенство нулю суммарных
величин указанных зарядов, соответственно,
электрического потока:
в теореме просто не говорят. Здесь надо
иметь в виду, что равенство нулю суммарных
величин указанных зарядов, соответственно,
электрического потока:
 ,
вовсе не означает отсутствие электрического
поля в этой области пространства,
поскольку электрические заряды бывают
положительными и отрицательными, и
указанное поле может создаваться
электронейтральными источниками,
например, электрическими диполями. Это
свойство электростатического поля
качественно отличает его от ньютоновского
поля тяготения, где источники такого
поля – гравитирующие массы имеют один
знак. В системе электродинамических
дифференциальных уравнений (1) теорема
Гаусса представлена (см. теорему
Гаусса-Остроградского) соотношением
(1b), описывающим результат электрической
поляризации среды, где в случае
электронейтральности (
,
вовсе не означает отсутствие электрического
поля в этой области пространства,
поскольку электрические заряды бывают
положительными и отрицательными, и
указанное поле может создаваться
электронейтральными источниками,
например, электрическими диполями. Это
свойство электростатического поля
качественно отличает его от ньютоновского
поля тяготения, где источники такого
поля – гравитирующие массы имеют один
знак. В системе электродинамических
дифференциальных уравнений (1) теорема
Гаусса представлена (см. теорему
Гаусса-Остроградского) соотношением
(1b), описывающим результат электрической
поляризации среды, где в случае
электронейтральности ( )
среды оно имеет вид
)
среды оно имеет вид
 .
.
Воспользуемся теперь другим
первичным фундаментальным законом
электромагнетизма - законом сохранения
электрического заряда (3), структурно
представляющим собой уравнение
непрерывности. Закон гласит: изменение
заряда в данной точке пространства
 единственно возможно лишь за счет
транспорта зарядов извне
единственно возможно лишь за счет
транспорта зарядов извне
 ,
ведь по определению (теорема
Гаусса-Остроградского) дивергенция -
это объемная плотность потока векторного
поля в данной точке. Тогда подстановка
в (3) уравнения (1b) дает формулу
,
ведь по определению (теорема
Гаусса-Остроградского) дивергенция -
это объемная плотность потока векторного
поля в данной точке. Тогда подстановка
в (3) уравнения (1b) дает формулу
 .
И с учетом того, что для любого векторного
поля
.
И с учетом того, что для любого векторного
поля
 ,
получаем еще одно уравнение обсуждаемой
здесь системы:
,
получаем еще одно уравнение обсуждаемой
здесь системы:
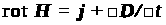 (1с). Это уравнение обычно называют
законом полного тока: электрические
токи проводимости и смещения порождают
вихревое магнитное поле, силовые линии
векторов напряженности
(1с). Это уравнение обычно называют
законом полного тока: электрические
токи проводимости и смещения порождают
вихревое магнитное поле, силовые линии
векторов напряженности
 которого охватывают линии этих токов.
которого охватывают линии этих токов.
Итак, в области существования
движущихся зарядов и переменных во
времени электрических полей
 ,
то есть в уравнении (1с) функция
,
то есть в уравнении (1с) функция
 является чисто вихревой, а потому для
математического уточнения данной
топологии магнитного поля введем
соотношение
является чисто вихревой, а потому для
математического уточнения данной
топологии магнитного поля введем
соотношение
 .
Тем самым получим следующее уравнение
системы (1) – уравнение (1d). Поскольку
дивергенция - объемная плотность потока
векторного поля в данной точке, то
уравнение
.
Тем самым получим следующее уравнение
системы (1) – уравнение (1d). Поскольку
дивергенция - объемная плотность потока
векторного поля в данной точке, то
уравнение
 способно описать не только вихревые
свойства функции
способно описать не только вихревые
свойства функции
 ,
но и ее потенциальную версию, случай
когда
,
но и ее потенциальную версию, случай
когда
 .
В этой ситуации соотношение (1d)
математически представляет физический
результат магнитной поляризации
материальной среды. Комментируя
физическое содержание такого уравнения,
обычно говорят, что оно наглядно
иллюстрирует отсутствие в Природе
сторонних магнитных зарядов, подобных
зарядам электрическим, при этом, входя
в противоречие, безосновательно называют
.
В этой ситуации соотношение (1d)
математически представляет физический
результат магнитной поляризации
материальной среды. Комментируя
физическое содержание такого уравнения,
обычно говорят, что оно наглядно
иллюстрирует отсутствие в Природе
сторонних магнитных зарядов, подобных
зарядам электрическим, при этом, входя
в противоречие, безосновательно называют
 теоремой Гаусса магнитного поля, хотя
в рамках логики уравнений Максвелла
базы для этой теоремы - магнитного закона
Кулона принципиально не существует.
теоремой Гаусса магнитного поля, хотя
в рамках логики уравнений Максвелла
базы для этой теоремы - магнитного закона
Кулона принципиально не существует.
Наконец, частным дифференцированием
по времени
 уравнения (1d) получаем на основе
уравнения (1d) получаем на основе
 адекватное с учетом знака закону
электромагнитной индукции Фарадея
уравнение (1а), последнее в системе (1).
Итак, изменяющееся во времени поле
магнитной индукции порождает в данной
точке пространства вихревое электрическое
поле. Ввиду того, что в уравнении (1a)
адекватное с учетом знака закону
электромагнитной индукции Фарадея
уравнение (1а), последнее в системе (1).
Итак, изменяющееся во времени поле
магнитной индукции порождает в данной
точке пространства вихревое электрическое
поле. Ввиду того, что в уравнении (1a)
 ,
то функция поля
,
то функция поля
 является вихревой, и эту топологию
способно уточнить, согласно вышесказанному
о дивергенции, уже полученное нами ранее
уравнение (1b) в виде
является вихревой, и эту топологию
способно уточнить, согласно вышесказанному
о дивергенции, уже полученное нами ранее
уравнение (1b) в виде
 .
Как видим, дивергентные уравнения (1b) и
(1d) как математически, так и физически
весьма содержательны.
.
Как видим, дивергентные уравнения (1b) и
(1d) как математически, так и физически
весьма содержательны.
И это только то, что лежит на
поверхности. А если взглянуть глубже,
то уравнения
 и
и
 содержат сведения о полях электрического
содержат сведения о полях электрического
 и магнитного
и магнитного
 векторных потенциалов, связанных с
электрической -
векторных потенциалов, связанных с
электрической -
 и магнитной -
и магнитной -
 поляризациями. На сегодня установлено
[3, 4], что векторные потенциалы –
полноправные физически значимые поля,
и учет этого обстоятельства позволяет
углубить и кардинально модернизировать
концептуальные основы классической
электродинамики, где обсуждаемая здесь
система уравнений Максвелла будет лишь
рядовым частным следствием.
поляризациями. На сегодня установлено
[3, 4], что векторные потенциалы –
полноправные физически значимые поля,
и учет этого обстоятельства позволяет
углубить и кардинально модернизировать
концептуальные основы классической
электродинамики, где обсуждаемая здесь
система уравнений Максвелла будет лишь
рядовым частным следствием.
Однако вернемся к уравнениям системы (1). Убедимся, что данная система замкнута и может быть представлена в виде математической задачи Коши - решение уравнений с заданными начальными условиями. Для этого, прежде всего, надо показать, что уравнение (1d) является следствием уравнения (1а), а уравнение (1b) есть следствие уравнения (1c). Вообще говоря, все это уже установлено в наших рассуждениях при построении уравнений системы (1), и все же проделаем обратное в явном виде. Итак, возьмем дивергенцию от (1а):




 .
.
Поскольку уравнение (1d)
 удовлетворяется при любых
удовлетворяется при любых
 ,
то оно верно и для
,
то оно верно и для
 .
Таким образом, уравнение (1d) действительно
является начальным условием для уравнения
(1а). Аналогичная процедура с уравнением
(1c) и сравнение этого результата с
уравнением непрерывности (3) дает цепочку:
.
Таким образом, уравнение (1d) действительно
является начальным условием для уравнения
(1а). Аналогичная процедура с уравнением
(1c) и сравнение этого результата с
уравнением непрерывности (3) дает цепочку:




 .
.
А так как уравнение (1b)
 справедливо при любых
справедливо при любых
 ,
то оно верно и для
,
то оно верно и для
 .
Следовательно, уравнение (1b) - это
начальное условие для уравнения (1c).
.
Следовательно, уравнение (1b) - это
начальное условие для уравнения (1c).
В итоге с учетом уравнения
непрерывности (3) система (1) действительно
замкнута – 16 скалярных уравнений: (1a),
(1c), (3) - 7 и материальные соотношения - 9
для нахождения 16 скалярных функций:
компонент векторов
 ,
,
 ,
,
 ,
,
 ,
,
 и плотности заряда
и плотности заряда
 .
.
Важнейшим фундаментальным
следствием уравнений Максвелла является
тот факт, что
 и
и
 компоненты электромагнитного поля
распространяются в пространстве в виде
волн. Например, из (1а) и (1c) сравнительно
просто получить волновое уравнение для
поля электрической напряженности
компоненты электромагнитного поля
распространяются в пространстве в виде
волн. Например, из (1а) и (1c) сравнительно
просто получить волновое уравнение для
поля электрической напряженности
 :
:
 .
(4)
.
(4)
Аналогично получается и уравнение
волн поля магнитной напряженности
 ,
структурно полностью тождественное
уравнению (4). Видно, что скорость
распространения этих волн определяется
только лишь электрическими и магнитными
параметрами пространства материальной
среды:
,
структурно полностью тождественное
уравнению (4). Видно, что скорость
распространения этих волн определяется
только лишь электрическими и магнитными
параметрами пространства материальной
среды:
 ,
,
 и
и
 ,
в частности, в отсутствие поглощения
(
,
в частности, в отсутствие поглощения
( )
скорость волн
)
скорость волн
 .
.
С целью ответа на вопрос, что переносят эти волны, воспользуемся уравнениями Максвелла (1), являющиеся, в сущности, первичными уравнениями электромагнитной волны, откуда на основе уравнений (1а) и (1с) получаем закон сохранения энергии в форме, так называемой теоремы Пойнтинга:
 .
(5)
.
(5)
Видно, что поступающий извне в
данную точку среды поток электромагнитной
энергии, определяемый вектором Пойнтинга
 ,
идет на компенсацию джоулевых (тепловых)
потерь в процессе электропроводности
и изменение электрической и магнитной
энергий, либо наоборот - эти физические
процессы вызывают излучение наружу
потока электромагнитной энергии.
Например, уравнение энергетического
баланса (5) показывает, что излучение
вовне потока энергии
,
идет на компенсацию джоулевых (тепловых)
потерь в процессе электропроводности
и изменение электрической и магнитной
энергий, либо наоборот - эти физические
процессы вызывают излучение наружу
потока электромагнитной энергии.
Например, уравнение энергетического
баланса (5) показывает, что излучение
вовне потока энергии
 возникает при джоулевых потерях
возникает при джоулевых потерях
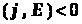 за счет работы источника ЭДС, в котором
за счет работы источника ЭДС, в котором
 и
и
 - антипараллельны. Соответственно, при
- антипараллельны. Соответственно, при
 производные от слагаемых других энергий
меньше нуля.
производные от слагаемых других энергий
меньше нуля.
Существенно, что вектор плотности
потока электромагнитной энергии
 ,
отличен от нуля только там, где одновременно
присутствуют электрическая и магнитная
компоненты поля, векторы
,
отличен от нуля только там, где одновременно
присутствуют электрическая и магнитная
компоненты поля, векторы
 и
и
 которых неколлинеарны. Соответственно,
как видно из уравнений (1а) и (1с), переносящая
энергию электромагнитная волна
принципиально состоит из двух векторных
взаимно ортогональных
которых неколлинеарны. Соответственно,
как видно из уравнений (1а) и (1с), переносящая
энергию электромагнитная волна
принципиально состоит из двух векторных
взаимно ортогональных
 и
и
 компонент. При этом несложно убедиться
[1], что уравнения Максвелла (1) описывают
электромагнитную волну, колебания
компонент. При этом несложно убедиться
[1], что уравнения Максвелла (1) описывают
электромагнитную волну, колебания
 и
и
 компонент которой синфазны между собой.
Но такие колебания этих двух компонент
в принципе не отвечают механизму переноса
энергии посредством волн произвольной
физической природы, когда в данной точке
пространства происходит взаимное
преобразование во времени потенциальной
(в нашем случае электрической) энергии
в кинетическую (магнитную) энергию, и
наоборот.
компонент которой синфазны между собой.
Но такие колебания этих двух компонент
в принципе не отвечают механизму переноса
энергии посредством волн произвольной
физической природы, когда в данной точке
пространства происходит взаимное
преобразование во времени потенциальной
(в нашем случае электрической) энергии
в кинетическую (магнитную) энергию, и
наоборот.
Упрощенно, ради наглядности этот
процесс можно пояснить на примере
колебаний физического маятника, когда
такой вид движения реализуется при
сдвиге фазы колебаний смещения и скорости
маятника на
 ,
то есть благодаря обмену кинетической
и потенциальной энергиями, где полная
энергия незатухающих колебаний неизменна
во времени. Следовательно, и в случае
волны перенос энергии возможен только
при сдвиге фазы колебаний между ее
компонентами на
,
то есть благодаря обмену кинетической
и потенциальной энергиями, где полная
энергия незатухающих колебаний неизменна
во времени. Следовательно, и в случае
волны перенос энергии возможен только
при сдвиге фазы колебаний между ее
компонентами на
 ,
причем в среде без потерь поток энергии
не зависит от времени и точек пространства.
Однако, согласно уравнениям Максвелла,
электромагнитных волн с такими
характеристиками в Природе не существуют.
,
причем в среде без потерь поток энергии
не зависит от времени и точек пространства.
Однако, согласно уравнениям Максвелла,
электромагнитных волн с такими
характеристиками в Природе не существуют.
Правда, традиционная логика
обсуждения переноса электромагнитной
энергии такова, что проблемы здесь как
бы и нет - всем все понятно. Действительно,
из решения уравнений (1) для волновых
амплитуд
 формально, но абсолютно строго следует
формально, но абсолютно строго следует
 - закон сохранения энергии. В итоге
однозначно доказано, что электрическая
энергия в точности равна энергии
магнитной, переносимых волнами
соответствующих компонент электромагнитного
поля. Именно так этот вопрос излагается
учащимся, причем правомерность такой
методики аргументируется тем, что
перенос энергии электромагнитными
волнами реален, и это физическое явление
широко и всесторонне используется во
многих областях жизни современного
общества. Однако это не ответ на вопрос:
как же все-таки эти энергии переносятся?
- закон сохранения энергии. В итоге
однозначно доказано, что электрическая
энергия в точности равна энергии
магнитной, переносимых волнами
соответствующих компонент электромагнитного
поля. Именно так этот вопрос излагается
учащимся, причем правомерность такой
методики аргументируется тем, что
перенос энергии электромагнитными
волнами реален, и это физическое явление
широко и всесторонне используется во
многих областях жизни современного
общества. Однако это не ответ на вопрос:
как же все-таки эти энергии переносятся?
В качестве конструктивного
замечания отметим, что хотя
 и
и
 компоненты электромагнитных волн
распространяются только совместно и
их энергии равны, но при этом связи этих
энергий между собой нет (синфазность
колебаний). Более того, в случае электро-
и магнитостатики эти энергии независимы
в принципе. Следовательно, необходимо
приходим к выводу об объективности
раздельного существования электрической
и магнитной энергий, при отсутствии
каких-либо физических оснований считать,
что электромагнитная волна распространяется
так же, как и все другие волны, посредством
взаимной перекачки энергии одного вида
в другой. Но тогда становится совершенно
неясным, казалось бы, очевидное для
каждого понятие электромагнитной
энергии, а также каков реальный механизм
волнового переноса этого вида энергии?
компоненты электромагнитных волн
распространяются только совместно и
их энергии равны, но при этом связи этих
энергий между собой нет (синфазность
колебаний). Более того, в случае электро-
и магнитостатики эти энергии независимы
в принципе. Следовательно, необходимо
приходим к выводу об объективности
раздельного существования электрической
и магнитной энергий, при отсутствии
каких-либо физических оснований считать,
что электромагнитная волна распространяется
так же, как и все другие волны, посредством
взаимной перекачки энергии одного вида
в другой. Но тогда становится совершенно
неясным, казалось бы, очевидное для
каждого понятие электромагнитной
энергии, а также каков реальный механизм
волнового переноса этого вида энергии?
Таким образом, проблема с выяснением физического механизма переноса энергии волнами электромагнитного поля объективно существует, она актуальна и для ее разрешения требуется далеко нестандартный подход. Информация: в настоящее время данная проблема активно, а главное успешно исследуется и находится в заключительной стадии разрешения (например, [3]).
Резюме. Показано, как на основе первичных соотношений электромагнетизма - закона Кулона взаимодействия неподвижных электрических точечных зарядов и закона сохранения электрического заряда цепочкой последовательных физико-математических рассуждений можно построить систему дифференциальных уравнений Максвелла классической электродинамики.
Материал этого сообщения может быть полезен студентам при самообразовании, а преподавателям для занятий по курсам общей физики, классической электродинамики и сопутствующим им техническим дисциплинам.
Список литературы
1. Сивухин Д.В. Общий курс физики. Электричество. М.: Наука, 1977.
2. Максвелл Дж.К. Трактат об электричестве и магнетизме. Т. I и II. М.: Наука, 1989.
3. Сидоренков В.В. // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37; // Вестник Воронежского государственного технического университета. 2007. Т. 3. № 11. С. 75-82; // Материалы X Международной конференции «Физика в системе современного образования». - Санкт-Петербург: РГПУ, 2009. Том 1. Секция 1. “Профессиональное физическое образование”. С. 114-117; // Материалы VI Международного семинара «Физико-математическое моделирование систем» - Воронеж: ВГТУ, 2009. Часть 1. С. 172-177; // Необратимые процессы в природе и технике: Сборник научных трудов. Вып. 3. М.: МГТУ им. Н.Э. Баумана, 2010. С. 56-83;
// http://scipeople.ru/publication/67585.
Для подготовки данной применялись материалы сети Интернет из общего доступа