Кольца. Примеры колец. Гомоморфизмы и изоморфизмы колец. Подкольца. Кольцо целых чисел
Кольца. Примеры колец. Гомоморфизмы и изоморфизмы колец. Подкольца. Кольцо целых чисел
Для изучения предлагаются понятия кольца, коммутативного кольца и области целосности, гомоморфизма и изоморфизма колец, подкольца, а так же свойства кольца целых чисел.
п.1. Понятие кольца.
Определение. Алгебра
 ,
где
,
где
 -
бинарные операции,
-
бинарные операции,
 -
унарная операция,
-
унарная операция,
 называется кольцом, если выполнены
аксиомы.
называется кольцом, если выполнены
аксиомы.
I.
 -
абелева группа.
-
абелева группа.
1)


2)


3)


4)


II. 1)

 -
ассоциативность умножения.
-
ассоциативность умножения.
2) законы дистрибутивности:

 -
левый дистрибутивный закон,
-
левый дистрибутивный закон,

 -
правый дистрибутивный закон.
-
правый дистрибутивный закон.
 -
называется аддитивной группой кольца.
-
называется аддитивной группой кольца.
Определение. Кольцо
 называется кольцом с единицей
называется кольцом с единицей
 ,
если существует
,
если существует



Определение. Кольцо
 называется коммутативным, если
называется коммутативным, если


Определение. Элементы
 называются делителями
называются делителями
 ,
если
,
если

Определение. Кольцо
 называется областью целостности, если
оно обладает свойствами:
называется областью целостности, если
оно обладает свойствами:
Кольцо
 -
коммутативно.
-
коммутативно.
Кольцо
 с единицей
с единицей
 ,
где
,
где
 .
.
Кольцо не имеет делителей нуля.
п.2. Примеры колец.
Рассмотрим
 .
Операции
.
Операции
 -
бинарная операция на множестве
-
бинарная операция на множестве
 ,
операция
,
операция
 -
унарная операция на множестве
-
унарная операция на множестве
 ,
,
 ,
значит
,
значит
 -
алгебра. Аксиомы кольца на множестве
-
алгебра. Аксиомы кольца на множестве
 выполнены, это следует из свойств целых
чисел, значит
выполнены, это следует из свойств целых
чисел, значит
 -
кольцо. Это кольцо с единицей 1, так как
-
кольцо. Это кольцо с единицей 1, так как
 и
и

 .
Это коммутативное кольцо, так как
.
Это коммутативное кольцо, так как

 .
Это кольцо без делителей нуля. Кольцо
целых чисел является областью целостности.
.
Это кольцо без делителей нуля. Кольцо
целых чисел является областью целостности.
Пусть
 -
множество целых чётных чисел,
-
множество целых чётных чисел,
 -
алгебра, кольцо без единицы, коммутативное,
без делителей нуля, не является областью
целостности.
-
алгебра, кольцо без единицы, коммутативное,
без делителей нуля, не является областью
целостности.
 -
проверим, будет ли на множестве
-
проверим, будет ли на множестве
 -
кольцо.
-
кольцо.



 -
бинарная операция на множестве
-
бинарная операция на множестве
 .
.


 -
бинарная операция на множестве
-
бинарная операция на множестве
 .
.


 -
унарная операция на множестве
-
унарная операция на множестве
 .
.

Значит
 -
алгебра.
-
алгебра.
Аксиомы кольца для данной алгебры
выполнены, так как
 ,
а на
,
а на
 аксиомы выполнены (из свойств действительных
чисел), значит
аксиомы выполнены (из свойств действительных
чисел), значит
 -
это кольцо.
-
это кольцо.
 .
.

 .
Кольцо с единицей
.
Кольцо с единицей
 -
это коммутативное кольцо без делителей
нуля, является областью целостности.
-
это коммутативное кольцо без делителей
нуля, является областью целостности.
Пусть
 .
Определим операции
.
Определим операции

 ,
,
 ;
;
 ,
,
 .
.


 -
бинарные операции на множестве
-
бинарные операции на множестве


 значит
значит


 -
унарная операция на множестве
-
унарная операция на множестве
 .
.

 ,
,
 ,
значит
,
значит
 -
алгебра. Проверим, является ли эта
алгебра кольцом. Для этого проверим
аксиомы кольца. Равенство
-
алгебра. Проверим, является ли эта
алгебра кольцом. Для этого проверим
аксиомы кольца. Равенство
 -
равенство функции:
-
равенство функции:
 из определения операций. Рассмотрим
произведение
из определения операций. Рассмотрим
произведение
 ,
вычислим значения левой и правой частей
от
,
вычислим значения левой и правой частей
от
 а)
а) б)
б)


 .
Аналогично проверяется, что все аксиомы
кольца выполнены, значит
.
Аналогично проверяется, что все аксиомы
кольца выполнены, значит
 является кольцом. Это кольцо с единицей
является кольцом. Это кольцо с единицей

 .
Действительно,
.
Действительно,

 (свойство единицы). Это коммутативное
кольцо, так как
(свойство единицы). Это коммутативное
кольцо, так как

 .
Покажем, что это кольцо с делителями
нуля. Пусть
.
Покажем, что это кольцо с делителями
нуля. Пусть
 ,
,
 ,
,
 ,
,
 (нулевая функция). Вычислим
(нулевая функция). Вычислим
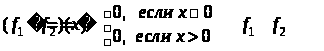 (равно нулевой функции). Значит
(равно нулевой функции). Значит
 ,
,
 -
делители нуля, значит кольцо
-
делители нуля, значит кольцо
 -
не является областью целостности.
-
не является областью целостности.
п.3. Простейшие свойства кольца.
Пусть
 -
кольцо. Выпишем и проверим аксиомы
кольца:
-
кольцо. Выпишем и проверим аксиомы
кольца:

 .
.
Доказательство.
 -
абелева группа, имеем
-
абелева группа, имеем



 .
.
Доказательство.
 -
абелева группа, имеем
-
абелева группа, имеем

 .
.
 ,
если
,
если
 ,
если
,
если
 .
.
Доказательство. По закону
сокращения в группе, определенной на
множестве
 .
.
 ,
если
,
если
 ,
если
,
если
 .
.
Доказательство. Следует из свойства 4 групп.
 если
если
 ,
если
,
если
 .
.
Доказательство. Следует из 5 свойства групп.

 .
.
Доказательство. Следует из 6 свойства групп.

 .
.
Доказательство. Докажем, что
 .
.


 .
.
Доказательство. Докажем, что

 рассмотрим сумму
рассмотрим сумму
 .
Аналогично доказывается, что
.
Аналогично доказывается, что
 .
.

 .
Обозначение:
.
Обозначение:

 .
.

 (правый дистрибутивный закон),
(правый дистрибутивный закон),
 (левый дистрибутивный закон).
(левый дистрибутивный закон).
Доказательство. Правый
дистрибутивный закон: левая часть равна

 равна правой части. Аналогично доказывается
левый дистрибутивный закон.
равна правой части. Аналогично доказывается
левый дистрибутивный закон.

 .
.
Доказательство. Вычислим сумму

 .
.
п.4. Гомоморфизмы и изоморфизмы колец.
Дано два кольца
 и
и
 .
.
Определение. Гомоморфизмом
кольца
 в кольце
в кольце
 называется функция
называется функция
 и обладающая свойствами:
и обладающая свойствами:







Другими словами, гомоморфизм
колец – это отображения, сохраняющие
все операции кольца. Если
 -
гомоморфизм кольца
-
гомоморфизм кольца
 в
в
 ,
то
,
то
 -
гомоморфизм абелевых групп
-
гомоморфизм абелевых групп
 в группу
в группу
 .
.
Теорема. Пусть
 и
и
 -
кольца и
-
кольца и
 ,
обладающих свойствами:
,
обладающих свойствами:



Тогда
 -
гомоморфизм колец.
-
гомоморфизм колец.
Доказательство. Из свойства


 является гомоморфизмом групп
является гомоморфизмом групп
 и
и
 ,
поэтому
,
поэтому
 обладает свойствами:
обладает свойствами:
 ,
,
 ,
значит по определению
,
значит по определению
 -
гомоморфизм колец.
-
гомоморфизм колец.
Определение. Отображение
 называется изоморфизмом кольца
называется изоморфизмом кольца
 на
на
 ,
если
,
если
 обладает свойствами:
обладает свойствами:
 -
гомоморфизм колец.
-
гомоморфизм колец.
 -
биекция.
-
биекция.
Другими словами: изоморфизм – это гомоморфизм, являющийся биекцией.
п.5. Подкольца.
Пусть
 -
кольцо,
-
кольцо,
 ,
,
 .
.
Определение. Множество
 -
замкнуто относительно операции
-
замкнуто относительно операции
 ,
если
,
если

 .
.
Множество
 -
замкнуто относительно операции
-
замкнуто относительно операции
 ,
если
,
если

 .
Множество
.
Множество
 -
замкнуто относительно операции
-
замкнуто относительно операции
 ,
если
,
если

 .
.
Теорема. Пусть
 -
кольцо,
-
кольцо,
 ,
,
 ,
если
,
если
 -
замкнуто относительно операции
-
замкнуто относительно операции
 ,
то
,
то
 -
кольцо, которое называется подкольцом,
кольца
-
кольцо, которое называется подкольцом,
кольца
 .
.
Доказательство.
 -
бинарные операции,
-
бинарные операции,
 -
унарная операция, так как
-
унарная операция, так как
 -
замкнутое множество. Так как
-
замкнутое множество. Так как
 ,
то существует
,
то существует
 ,
так как
,
так как
 -
замкнуто относительно операции
-
замкнуто относительно операции
 ,
то
,
то


 ,
значит
,
значит
 -
алгебра, так как аксиомы выполнены на
-
алгебра, так как аксиомы выполнены на
 ,
то они выполнены и на
,
то они выполнены и на
 ,
потому алгебра
,
потому алгебра
 -
кольцо.
-
кольцо.
Теорема. Пусть
 -
числовое кольцо с единицей 1, тогда оно
содержит подкольцо целых чисел.
-
числовое кольцо с единицей 1, тогда оно
содержит подкольцо целых чисел.
п.6. Аксиоматическое определение кольца целых чисел.
Алгебраическая система
 ,
где
,
где
 бинарные операции,
бинарные операции,
 -
унарная операция,
-
унарная операция,
 ,
,
 ,
,
 называется системой целых чисел, если
выполнены три группы аксиом:
называется системой целых чисел, если
выполнены три группы аксиом:
I.
 -
кольцо.
-
кольцо.
Абелева группа









Аддитивная группа






II. Множество
 -
замкнуто относительно операций
-
замкнуто относительно операций
 и алгебраическая система
и алгебраическая система
 является системой натуральных чисел
(системой Пеано).
является системой натуральных чисел
(системой Пеано).
Для
 ,
,

Для
 ,
,

Для
 ,
,

Для
 ,
,

Для
 ,
,

Для
 ,
,

Аксиома индукции: пусть
 .
Если множество
.
Если множество
 удовлетворяет условиям:
удовлетворяет условиям:
а)

б)
 ,
,
 ,
то
,
то

III. Аксиома минимальности.
Если
 и обладает свойствами:
и обладает свойствами:
а)

б)

 ,
то
,
то
 .
.
Свойства целых чисел.
Теорема 1. О делении с остатком.


 |
|
 ,
где
,
где
 .
Число
.
Число
 называется делимым,
называется делимым,
 -
делителем,
-
делителем,
 -
частным,
-
частным,
 -
остатком при делении
-
остатком при делении
 на
на
 .
.
Доказательство. Докажем
существование хотя бы одной пары чисел
 ,
,
 .
Для этого рассмотрим множество
.
Для этого рассмотрим множество
 .
Множество
.
Множество
 содержит как отрицательные, так и
неотрицательные числа, пусть
содержит как отрицательные, так и
неотрицательные числа, пусть
 -
наименьшее неотрицательное число в
-
наименьшее неотрицательное число в
 ,
тогда
,
тогда
 .
Докажем, что
.
Докажем, что
 ,
предположим противное
,
предположим противное
 .
Рассмотрим число
.
Рассмотрим число
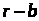 .
.

 противоречие с выбором
противоречие с выбором
 .
Доказано, что
.
Доказано, что
 ,
,
 .
Докажем единственность чисел
.
Докажем единственность чисел
 и
и
 ,
пусть
,
пусть

 .
.
 ,
,
 .
Докажем, что
.
Докажем, что
 ,
предположим противное
,
предположим противное
 .
Пусть
.
Пусть
 .
Имеем
.
Имеем

 противоречие, так как между числами
противоречие, так как между числами
 нет чисел, делящихся на
нет чисел, делящихся на
 .
Доказано, что
.
Доказано, что
 ,
если
,
если
 ,
то
,
то
 ,
а отсюда следует, что
,
а отсюда следует, что
 .
Доказана единственность чисел
.
Доказана единственность чисел
 и
и
 .
.
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
Для подготовки данной применялись материалы сети Интернет из общего доступа