Інваріантні підпростори. Власні вектори і власні значення лінійного оператора

Інваріантні підпростори. Власні вектори і власні значення лінійного оператора

Як ми вже знаємо один і той же лінійний оператор в різних базисах задається різними матрицями. Виникає питання: чи не можна знайти такий базис векторного простору, в якому матриця лінійного оператора має найпростіший вигляд. Таким виглядом буде діагональний вигляд. До вияснення цього питання ми і приступаємо.

1. Інваріантні підпростори.

Нехай U підпростір векторного простору V_>n>, а φ – лінійний оператор, заданий на просторі V_>n>.

Означення. Підпростір U векторного простору V_>n> називається інваріантним відносно лінійного оператора φ, якщо образ φ кожного вектора із U належить цьому підпростору U, тобто

.

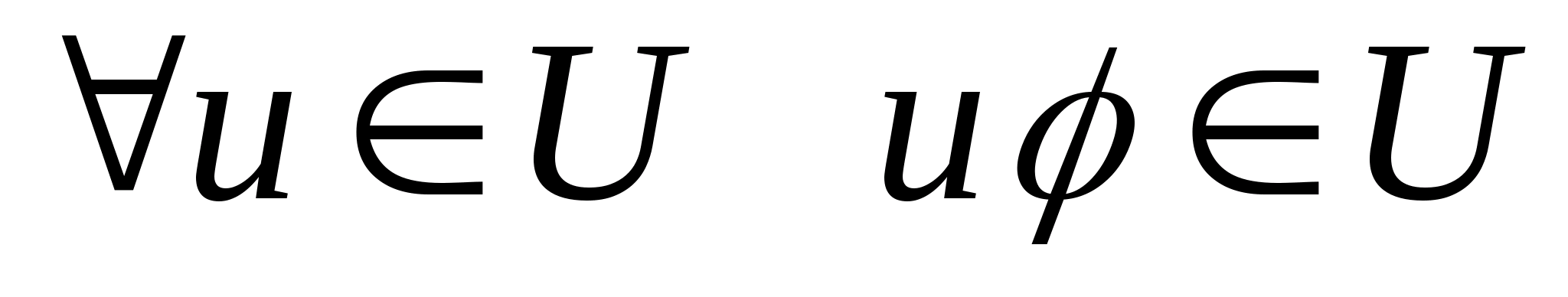Приклади.

1. Розглянемо звичайний тривимірний простір V_>3> і нехай φ – поворот навколо осі OZ. Інваріантними підпросторами будуть, наприклад, площина XOY і сама вісь OZ.

2. Розглянемо знову векторний простір V_>3> і лінійний оператор φ, який полягає в ортогональному проектуванні векторного простору V_>3> на площину XOY. Інваріантними підпросторами будуть: площина XOY, сама вісь OZ, всі площини, які проходять через вісь OZ і всі прямі площини XOY, які проходять через початок координат.

3. В будь-якому векторному просторі кожен підпростір інваріантний відносно тотожного і нульового оператора.

4. В будь-якому векторному просторі сам простір і його підпростір, який складається тільки з нульового вектора, інваріантні відносно будь-якого лінійного оператора.

Доведемо, що перетин і сума підпросторів, інваріантних відносно лінійного оператора φ, інваріантні відносно цього оператора φ.

Нехай підпростори U_>1> і U_>2> – інваріантні відносно лінійного оператора , і нехай . Тоді і , а значить і , тобто . Отже, - інваріантний підпростір відносно оператора .

Нехай , де і . Тоді і , .Отже, – інваріантний підпростір відносно оператора .

Особливу роль відіграють одновимірні інваріантні підпростори.

2. Власні вектори і власні значення.

Означення. Власним вектором лінійного оператора φ називається ненульовий вектор , для якого виконується рівність , де – деяке число, яке називається власним значенням лінійного оператора, якому відповідає власний вектор .

Властивості власних векторів.

Якщо – власний вектор лінійного оператора з власним значенням , то вектор при будь-якому також є власним вектором з тим самим власним значенням .

Якщо , ,…, – власні вектори лінійного оператора , які належать до того самого власного значення , то будь-яка їхлінійна комбінація також буде власним вектором цього оператора з тим самим власним значенням .

Теорема. Власні вектори, які відповідають різним власним значенням, лінійно незалежні.

Доведення. Нехай , ,…, – власні вектори лінійного оператора , які відповідають різним власним значенням , відповідно, тобто . Доводимо теорему методом математичної індукції за кількістю векторів.

Для теорема справедлива, бо за означенням, і тоді і тільки тоді, коли .

Нехай теорема справедлива при , тобто 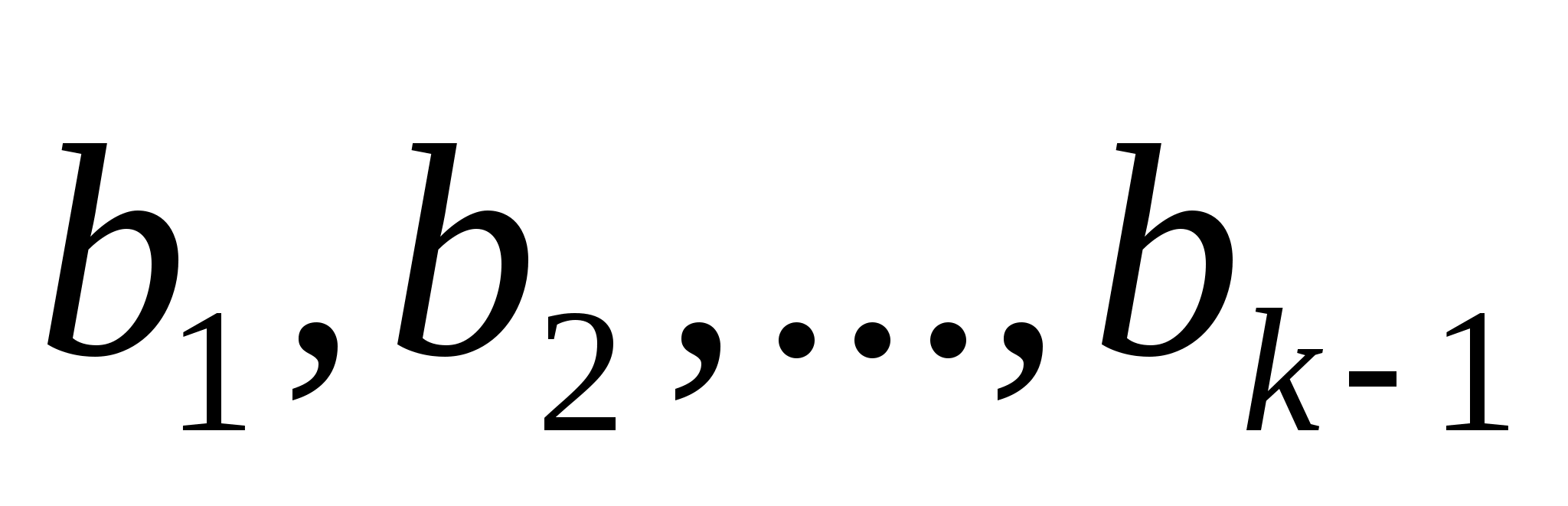- лінійно незалежні. Припустимо, що

(1)

і доведемо, що рівність (1) виконується тоді і тільки тоді, коли всі .

Подіємо на рівність (1) лінійним оператором :

використавши лінійність оператора , одержимо

звідси

. (2)

Віднімемо від рівності (2) рівність (1), помножену на . Одержимо

. (3)

За припущенням індукції вектори лінійно незалежні, тому рівність (3) виконується тоді і тільки тоді, коли всі коефіцієнти при дорівнюють нулю. Але за умовою (), а тому .

Підставивши ці значення у рівність (1), одержимо , звідси , бо . Отже, рівність (1) виконується тоді і тільки тоді, коли всі () одночасно. Тому – лінійно незалежні.

Теорему доведено. Повернемось до питання, як знайти власні значення і власні вектори лінійного оператора. Для цього нам потрібно розглянути деякі додаткові поняття.

Характеристична матриця

Нехай дана квадратна матриця

.

Матриця

називається характеристичною матрицею. Детермінант цієї матриці

називається характеристичним многочленом.

Корені цього многочлена називаються характеристичними числами.

Теорема. Характеристичні многочлени подібних матриць однакові.

Доведення. Нехай . Тоді

Теорема доведена.

Нехай лінійний оператор в базисі векторного простору задано матрицею

і – власний вектор оператора , який відповідає власному значенню , тобто .

Позначимо координати вектора в базисі через .

Тоді з одного боку , а з другого боку .

Тоді

або в розгорнутому вигляді

(4)

Звідси одержимо систему лінійних однорідних рівнянь

Власний вектор є ненульовим розв’язком системи (4´). Як відомо, однорідна система n лінійних рівнянь з n невідомими має ненульові розв’язки тоді і тільки тоді, коли її детермінант дорівнює нулю, тобто, коли виконується умова

Так як детермінант при транспонуванні не змінюється, то одержимо рівняння відносно невідомого

(5)

Отже, ми довели теорему: кожне власне значення лінійного оператора , заданого матрицею А, є коренем характеристичного многочлена.

Провівши міркування знизу вверх, одержимо твердження: кожний корінь характеристичного многочлена лінійного оператора буде його власним значенням.

В ході доведення теореми ми одержали схему знаходження власних значень і власних векторів лінійного оператора.

Приклад. Знайти власні значення і власні вектори лінійного оператора заданого матрицею

Схема розв’язування:

Складаємо характеристичну матрицю

.

Шукаємо характеристичний многочлен

=

Розв’язуємо характеристичне рівняння

(2-

Отже, власними значеннями лінійного оператора є числа 1, 2, -1.

Для знаходження власних векторів розв’язуємо систему рівнянь

тобто (5)

а) Шукаємо власні вектори, які відповідають власному значенню підставивши у (5) замість одиницю:

або в розгорнутому вигляді

Ранг цієї системи дорівнює 2, тому фундаментальна система її розв’язків складається з одного розв’язку. Знаходимо його. Зліва залишаємо змінні , а перенесемо в праву частину і вважаємо її відомою: звідси Покладемо 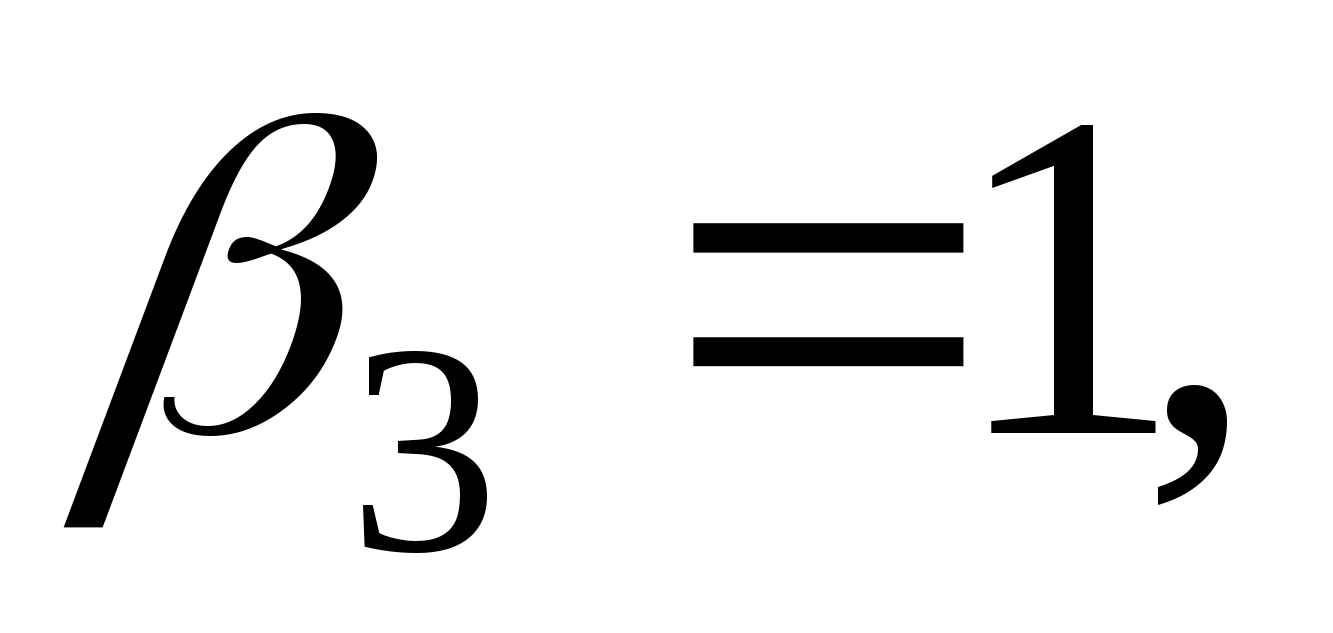тоді . Отже, одним із власних векторів, які відповідають власному значенню є вектор Всі власні вектори, які відповідають цьому значенню мають вигляд , де 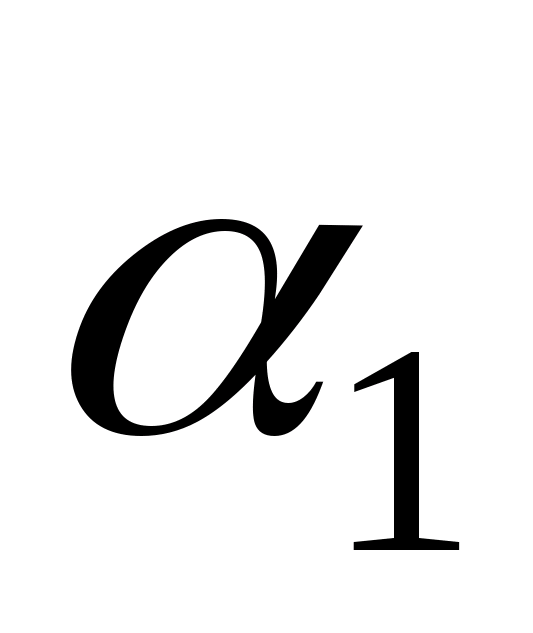-будь-яке дійсне число, відмінне від нуля.

Самостійно знайти власні вектори, які відповідають власним значенням 2 і .

Весь набір характеристичних коренів оператора (причому кожний корінь береться з тією кратністю, яку він має в характеристичному рівнянні) називається спектром лінійного оператора.

Сукупність власних векторів оператора , яким відповідає одне і те саме власне значення , збігається з сукупністю всіх ненульових розв’язків систем лінійних однорідних рівнянь.

Лінійні оператори з простим спектром

Кажуть, що лінійний оператор у n – вимірному просторі над полем Р має простий спектр, якщо всі його n характеристичні корені різні.

Повернемося до питання: чи існує базис простору , в якому лінійний оператор задається діагональною матрицею.

Нехай в просторі існує базис, який складається з власних векторів , які відповідають власним значенням , відповідно. Знайдемо матрицю цього оператора в цьому базисі:

тобто оператор заданий діагональною матрицею, причому по діагоналі стоять власні значення лінійного оператора, які відповідають власним векторам базису.

Навпаки. Нехай лінійний оператор в деякому базисі задається довільною матрицею .

За означенням матриці лінійного оператора в даному базисі

звідси тобто вектори базису є власними векторами оператора з власними значеннями . Таким чином ми довели теорему:

Якщо вектори базису є власними векторами лінійного оператора , то в цьому базисі оператор задається діагональною матрицею. Навпаки, якщо в деякому базисі матриця оператора є діагональною, то всі вектори цього базису є власними векторами оператора .

Як бачимо, матриця оператора в базисі, що складається з власних векторів цього оператора, має досить простий вигляд. Саме це і обумовлює важливість ролі власних векторів, а, отже, і одновимірних інваріантних підпросторів при вивченні лінійних операторів.

Виникає питання: як встановити, знаючи матрицю оператора в деякому базисі, чи має цей оператор власні вектори, які утворюють базис простору тобто, чи можна оператор задати в деякому базисі діагональною матрицею?

Теорема. Якщо лінійний оператор має простий спектр, то існує базис простору , в якому цей оператор задається діагональною матрицею.

Доведення. Дано: – різні власні значення оператора , яким відповідають власні вектори , відповідно, тобто , і=1, 2,…, n.

Оскільки , і , то – лінійно незалежні, а значить утворюють базис векторного простору . В цьому базисі оператор задається діагональною матрицею

вектор ортогональний інваріантний матриця

.

Теорему доведено.

Зведення матриці до діагонального вигляду

Нехай квадратна матриця порядку з елементами з поля P.

Вважають, що матриця A зводиться до діагонального вигляду, якщо існує діагональна матриця, подібна матриці A.

Часто трапляється, що треба знати, чи зводиться квадратна матриця до діагонального вигляду. На основі попередніх результатів можна довести теорему, яка встановлює достатні умови звідності матриці до діагонального вигляду.

Теорема. Кожна квадратна матриця n-го порядку над полем Р, яка має в полі Р n різних характеристичних коренів, зводиться до діагонального вигляду, тобто подібна до діагональної матриці.

Доведення. Дано A – квадратна матриця n – го порядку над полем P. Нехай - різні характеристичні корені матриці і (i=1,2,… n).

Розглянемо векторний простір над полем P. Матриця A в деякому базисі задає деякий лінійний оператор . Характеристичні корені є власними значеннями оператора , яким відповідають власні вектори цього оператора , . За властивістю власних векторів, які відповідають різним власним значенням вектори – лінійно незалежні, тому вони утворюють базис простору . В цьому базисі матриця лінійного оператора має вигляд .

i A подібні, бо вони задають один і той самий оператор в різних базисах. Діагональними елементами матриці є характеристично корені матриці A.

Знаходження діагональної матриці, подібної матриці A, називається зведенням матриці A до діагонального вигляду.

Приклад. Звести квадратну матрицю A до діагонального вигляду, якщо

.

Розв’язуємо характеристичне рівняння:

, . (Розв’язати самостійно)

Отже, .