Комплексные числа (работа 7)

Содержание

§ 1.Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа

Комплексные равенства

Геометрическое изображение комплексных чисел

Модуль и аргумент комплексного числа

Алгебраическая и тригонометрическая формы комплексного числа

Арифметические действия над комплексными числами

Показательная форма комплексного числа

Формулы Эйлера

§ 2.Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел

Определение алгебраического уравнения -й степени

Основные свойства многочленов

Примеры решения алгебраических уравнений на множестве комплексных чисел

Вопросы для самопроверки

Глоссарий

1. Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа (Сформулируйте определение комплексного числа)

Комплексным числом z называется выражение следующего вида:

Комплексное число в алгебраической форме,(1)

Где x, y ;

i — это мнимая единица, определяемая равенством i2 = –1.

Основные термины:

x = Re z — действительная часть комплексного числа z;

y = Im z — мнимая часть комплексного числа z;

— комплексно сопряженное число числу z;

— противоположное число числу z;

— комплексный ноль;

– так обозначается множество комплексных чисел.

Примеры

1)z = 1 + i  Re z = 1, Im z = 1,  = 1 – i,  = –1 – i;

2)z = –1 + i  Re z = –1, Im z = ,  = –1 – i,  = –1 –i;

3)z = 5 + 0i = 5  Re z = 5, Im z = 0,  = 5 – 0i = 5,  = –5 – 0i = –5

 если Im z = 0, то z = x — действительное число;

4)z = 0 + 3i = 3i  Re z = 0, Im z = 3,  = 0 – 3i = –3i,  = –0 – 3i = – 3i

 если Re z = 0, то z = iy — чисто мнимое число.

Комплексные равенства (Сформулируйте смысл комплексного равенства)

1) ;

2) .

Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства разделением действительных и мнимых частей.

Примеры

1) ;

2) .

Геометрическое изображение комплексных чисел (В чём состоит геометрическое изображение комплексных чисел?)

Комплексное число z изображается точкой (x, y) на комплексной плоскости или радиус-вектором этой точки.

Знак z во второй четверти означает, что система декартовых координат будет использоваться как комплексная плоскость.

Модуль и аргумент комплексного числа (Что такое модуль и аргумент комплексного числа?)

Модулем комплексного числа называется неотрицательное действительное число

.(2)

Геометрически модуль комплексного числа — это длина вектора, изображающего число z, или полярный радиус точки (x, y).

Аргумент комплексного числа z — это угол между положительным направлением действительной оси и вектором z (геометрически – это полярный угол точки (x, y)).

Обозначение , причем , или .

Для вычисления аргумента комплексного числа используется формула

Аргумент комплексного числа ,(3)

причем, при определении угла по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z:

Алгебраическая и тригонометрическая формы комплексного числа (Что такое алгебраическая и тригонометрическая формы комплексного числа?)

Так как геометрически очевидно, что и , то

Тригонометрическая форма комплексного числа .(4)

Запись z = x + iy называется алгебраической формой комплексного числа z; запись z = r(cos + i sin) называется тригонометрической формой комплексного числа z.

Примеры

Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.

1)z = 1 + i 

,



;

2) 

,



;

3) 

,





;

4),

;

5),

;

6),

то есть для z = 0 будет

,  не определен.

Арифметические действия над комплексными числами (Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.)

Сложение (вычитание) комплексных чисел

z1  z2 = (x1 + iy1)  (x2 + iy2) = (x1  x2) + i(y1  y2),(5)

то есть при сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и мнимые части.

Примеры

1)(1 + i) + (2 – 3i) = 1 + i + 2 –3i = 3 – 2i;

2)(1 + 2i) – (2 – 5i) = 1 + 2i – 2 + 5i = –1 + 7i.

Основные свойства сложения

1)z1 + z2 = z2 + z1;

2)z1 + z2 + z3 = (z1 + z2) + z3 = z1 + (z2 + z3);

3)z1 – z2 = z1 + (– z2);

4)z + (–z) = 0;

5).

Умножение комплексных чисел в алгебраической форме

z1∙z2 = (x1 + iy1)∙(x2 + iy2) = x1x2 + x1iy2 + iy1x2 + i2y1y2 = (6)

 = (x1x2 – y1y2) + i(x1y2 + y1x2),

то есть умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой и приведением подобных по действительным и мнимым слагаемым.

Примеры

1)(1 + i)∙(2 – 3i) = 2 – 3i + 2i – 3i2 = 2 – 3i + 2i + 3 = 5 – i;

2)(1 + 4i)∙(1 – 4i) = 1 – 42 i2 = 1 + 16 = 17;

3)(2 + i)2 = 22 + 4i + i2 = 3 + 4i.

Умножение комплексных чисел тригонометрической форме

z1∙z2 = r1(cos1 + isin1)r2(cos2 + isin2) = 

= r1r2(cos1cos2 + icos1sin2 + isin1cos2 + i2 sin1sin2) = 

= r1r2((cos1cos2 – sin1sin2) + i(cos1sin2 + sin1cos2))



Произведение комплексных чисел в тригонометрической форме , то есть при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.

Пример

Основные свойства умножения

1)z1z2 = z2z1 — коммутативность;

2)z1z2z3 = (z1z2)z3 = z1(z2z3) — ассоциативность;

3)z1(z2 + z3) = z1z2 + z1z3 — дистрибутивность относительно сложения;

4)z0 = 0; z1 = z;

5).

Деление комплексных чисел

Деление — это обратная умножению операция, поэтому

если zz2 = z1 и z2  0, то .

При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю:

Деление комплексных чисел в алгебраической форме .(7)

При выполнении деления в тригонометрической форме модули делятся, а аргументы вычитаются:

Деление комплексных чисел в тригонометрической форме .(8)

Примеры

1);

2).

Возведение комплексного числа в натуральную степень

Возведение в натуральную степень удобнее выполнять в тригонометрической форме:

В результате получается формула Муавра:

Формула Муавра,(9)

то есть при возведении комплексного числа в натуральную степень его модуль возводится в эту степень, а аргумент умножается на показатель степени.

Пример

Вычислить (1 + i)10.

Решение:

Замечания

При выполнении операций умножения и возведения в натуральную степень в тригонометрической форме могут получаться значения углов за пределами одного полного оборота. Но их всегда можно свести к углам или сбрасыванием целого числа полных оборотов по свойствам периодичности функций и .

Значение называют главным значением аргумента комплексного числа ;

при этом значения всех возможных углов обозначают ;

очевидно, что , .

Извлечение корня натуральной степени из комплексного числа

Корнем степени n из комплексного числа z, где , называется комплексное число , такое что n = z

.

Примеры

, так как ;

, так как ;

или , так как и .

Из определения очевидно следует, что операция извлечения корня из комплексного числа является многозначной.

Если использовать формулу Муавра, то нетрудно доказать следующее утверждение:

существует при z и если z  0, то имеет n различных значений, вычисляемых по формуле

Извлечение корня натуральной степени из комплексного числа ,(10)

где,

— арифметический корень на .

Все значения расположены регулярным образом на окружности радиусом с начальным углом и углом регулярности .

Примеры

1)

, k = 0, 1, 2 

,

,

.

Ответ:

2) ,

.

Показательная форма комплексного числа

Показательной формой комплексного числа называется форма

Показательная форма комплексного числа,(11)

где.

Примеры

1);

2);

3) .

Действия над комплексными числами в показательной форме выполняются по правилам действий со степенями:

,(12)

,(13)

,(14)

, .(15)

Примеры

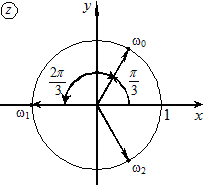
Пусть ,

.

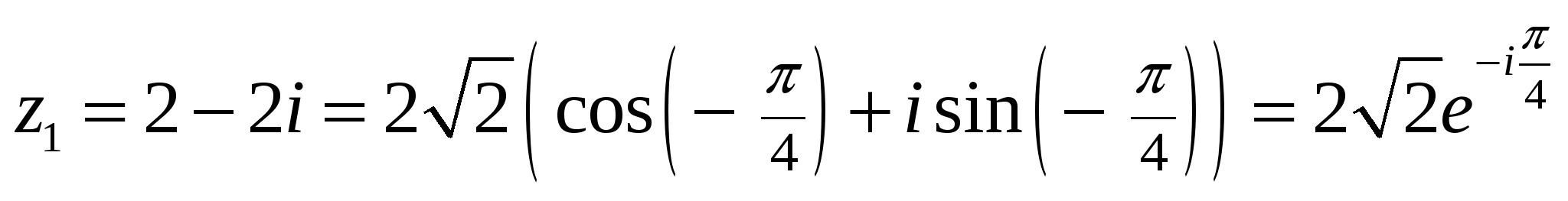Тогда ;

;

;

,

Числа являются вершинами правильного пятиугольника, вписанного в окружность радиуса .

Формулы Эйлера

Используем определение  ,

так как , .

Из этих равенств следуют формулы Эйлера

Формулы Эйлера(16)

по которым тригонометрические функции и действительной переменной выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.

2. Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел

Целой функцией или алгебраическим многочленом (полиномом) аргумента x называется функция вида

.(1)

Здесь n – степень многочлена (натуральное число или 0),

x – переменная (действительная или комплексная),

a0, a1, …, an – коэффициенты многочлена (действительные или комплексные числа), причем, a0  0

Примеры

;

;

, – квадратный трехчлен;

, ;

.

Определение алгебраического уравнения -й степени

Уравнение называется алгебраическим уравнением n-й степени относительно неизвестной x, если его левая часть является многочленом степени n относительно переменной x:

Pn(x) = 0, (2)

Число х0 такое, что Pn(x0)  0, называется нулем функции Pn(x) или корнем уравнения .

Примеры

– алгебраическое уравнение первой степени,

его корень ;

– алгебраическое уравнение седьмой степени,

его корни , , .

числа и являются нулями функции 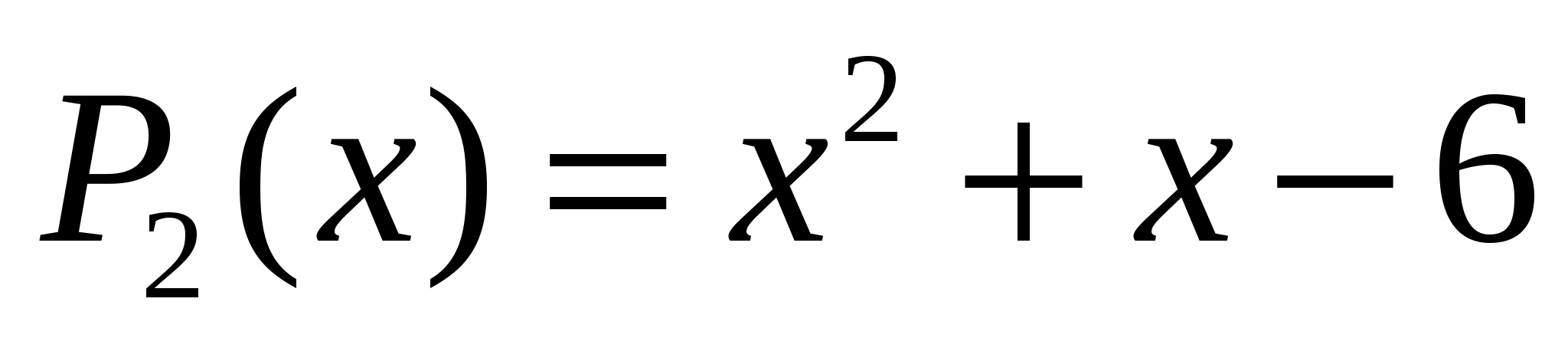, так как и .

Замечание

В литературе часто нули функции называются ее корнями. Например, числа и называются корнями квадратичной функции .

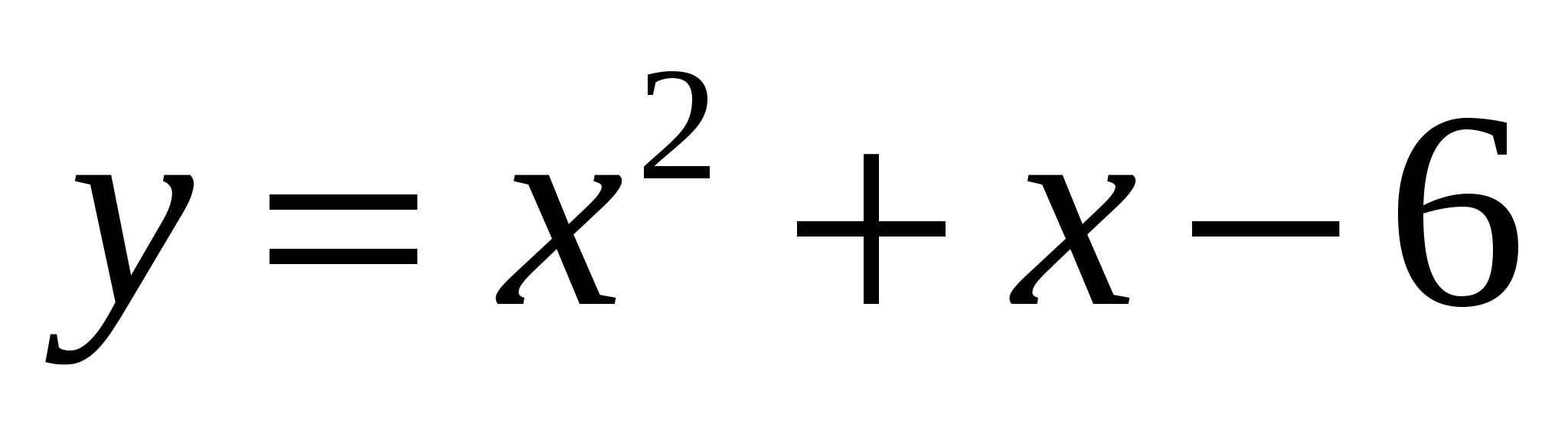Основные свойства многочленов (Перечислите основные свойства многочленов)

Свойство 1 (о тождественном равенстве многочленов)

Два многочлена одной степени n тождественно равны друг другу тогда и только тогда, когда совпадают их коэффициенты при одинаковых степенях переменной x, то есть

(3)

.

Доказательство

 Тождество (3) справедливо при x  (или x  )

 оно справедливо при ; подставляя , получим аn = bn.

Взаимно уничтожим в (3) слагаемые аn и bn и поделим обе части на x:

.(3’)

Это тождество тоже верно при x, в том числе при x = 0

 полагая x = 0, получим аn – 1 = bn – 1.

Взаимно уничтожим в (3') слагаемые аn – 1 и an – 1 и поделим обе части на x, в результате получим

.

Аналогично продолжая рассуждение, получим, что аn – 2 = bn –2, …, а0 = b0.

Таким образом, доказано, что из тождественного равенства 2-x многочленов следует совпадение их коэффициентов при одинаковых степенях x.

Обратное утверждение справедливо очевидно, т.е. если два многочлена имеют одинаковыми все коэффициенты, то они есть одинаковые функции, следовательно, их значения совпадают при всех значениях аргумента, что и означает их тождественное равенство. Свойство 1 доказано полностью. 

Пример

при .

Свойство 2 (о делении многочлена на разность (x – х0))

Теорема Безу

При делении многочлена Pn(x) на разность (x – х0) получается остаток, равный Pn(x0), то есть

Теорема Безу,(4)

гдеQn – 1(x) — целая часть от деления, является многочленом степени (n – 1).

Доказательство

 Запишем формулу деления с остатком:

Pn(x) = (x – х0)∙Qn – 1(x) + A,

гдеQn – 1(x) — многочлен степени (n – 1),

A — остаток, который является числом вследствие известного алгоритма деления многочлена на двучлен «в столбик».

Это равенство верно при x, в том числе при x = х0 

Pn(x0) = (x0 – x0)Qn – 1(x0) + A 

A = Pn(х0), ч.т.д. 

Следствие из теоремы Безу. О делении многочлена на двучлен без остатка

Если число х0 является нулем многочлена, то этот многочлен делится на разность (x – х0) без остатка, то есть

  .(5)

Примеры

1) , так как P3(1)  0

 .

2) , так как P4(–2)  0

 .

3) , так как P2(–1/2)  0

 .

Деление многочленов на двучлены «в столбик»:

_

_

_

_

_

Свойство 3 (о существовании нуля многочлена)

Теорема алгебры основная

Всякий многочлен степени n  1 имеет, по крайней мере, один нуль, действительный или комплексный

Доказательство этой теоремы выходит за рамки нашего курса. Поэтому примем теорему без доказательства.

Поработаем по этой теореме и по теореме Безу с многочленом Pn(x).

После n-кратного применения этих теорем получим, что

,

гдеa0 — это коэффициент при xn в Pn(x).

Следствие из основной теоремы алгебры. О разложении многочлена на линейные множители

Любой многочлен степени на множестве комплексных чисел разлагается на n линейных сомножителей, то есть

Разложение многочлена на линейные множители ,(6)

гдех1, х2, … хn — это нули многочлена.

При этом если k чисел из набора х1, х2, … хn совпадают между собой и с числом , то в произведении (6) получается множитель (x – )k. Тогда число x =  называется k-кратным нулем многочлена Pn(x). Если k = 1, то нуль называется простым нулем многочлена Pn(x).

Примеры

1)P4(x) = (x – 2)(x – 4)3  x1 = 2 — простой нуль, x2 = 4 — трехкратный нуль;

2)P4(x) = (x – i)4  x = i — нуль кратности 4.

Свойство 4 (о количестве корней алгебраического уравнения)

Любое алгебраическое уравнение Pn(x) = 0 степени n имеет на множестве комплексных чисел ровно n корней, если считать каждый корень столько раз, какова его кратность.

Примеры

1)x2 – 4x + 5 = 0 — алгебраическое уравнение второй степени

 x1,2 = 2   = 2  i — два корня;

2)x3 + 1 = 0 — алгебраическое уравнение третьей степени

 x1,2,3 =  — три корня;

3)P3(x) = x3 + x2 – x – 1 = 0  x1 = 1, т.к. P3(1) = 0.

Разделим многочлен P3(x) на (x – 1):

x3	+	x2	–	x	–	1	x – 1
x3	–	x2					x2 + 2x +1
		2x2	–	x
		2x2	–	2x
				x	–	1
				x	–	1
						0

Исходное уравнение

P3(x) = x3 + x2 – x – 1 = 0  (x – 1)(x2 + 2x + 1) = 0  (x – 1)(x + 1)2 = 0

 x1 = 1 — простой корень, x2 = –1 — двукратный корень.

Свойство 5 (о комплексных корнях алгебраического уравнения с действительными коэффициентами)

Если алгебраическое уравнение с действительными коэффициентами имеет комплексные корни, то эти нули всегда парные комплексно сопряженные, то есть если x0 = a + bi является корнем уравнения Pn(x) = 0, то число также является корнем этого уравнения.

Доказательство

 нужно использовать определение и следующие легко проверяемые свойства операции комплексного сопряжения:

если , то ;

; ; , ;

если – действительное число, то .

Так как является корнем уравнения , то

, где , – действительные числа.

Возьмем сопряжение от обеих частей последнего равенства и используем перечисленные свойства операции сопряжения:

, то есть число также удовлетворяет уравнению , следовательно, является его корнем, ч.т.д. 

Примеры

– парные комплексно сопряженные корни;

.

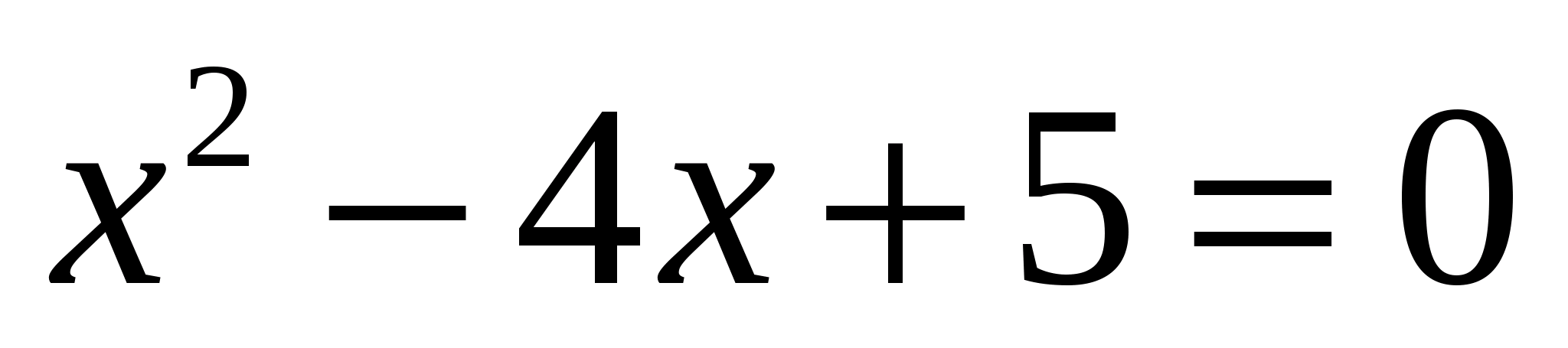
Свойство 6 (о разложении многочлена с действительными коэффициентами на линейные и квадратичные множители)

Любой многочлен с действительными коэффициентами разлагается на произведение линейных и квадратичных функций с действительными коэффициентами.

Доказательство

 Пусть x0 = a + bi — нуль многочлена Pn(x). Если все коэффициенты этого многочлена являются действительными числами, то тоже является его нулем (по свойству 5).

Вычислим произведение двучленов :

комплексный число многочлен уравнение

Получили (x – a)2 + b2 — квадратный трехчлен с действительными коэффициентами.

Таким образом, любая пара двучленов с комплексно сопряженными корнями в формуле (6) приводит к квадратному трехчлену с действительными коэффициентами. 

Примеры

1)P3(x) = x3 + 1 = (x + 1)(x2 – x + 1);

2)P4(x) = x4 – x3 + 4x2 – 4x = x(x –1)(x2 + 4).

Примеры решения алгебраических уравнений на множестве комплексных чисел (Приведите примеры решения алгебраических уравнений на множестве комплексных чисел)

Алгебраические уравнения первой степени:

, – единственный простой корень.

Пример

.

Ответ: .

Квадратные уравнения:

, – всегда имеет два корня (различных или равных).

Примеры

.

Ответ: .

.

Ответ: .

,.

Ответ: , .

Двучленные уравнения степени :

, – всегда имеет различных корней.

Пример

,

;

;

.

Ответ: , .

Решить кубическое уравнение .

Решение.

Уравнение третьей степени имеет три корня (действительные или комплексные), при этом нужно считать каждый корень столько раз, какова его кратность. Так как все коэффициенты данного уравнения являются действительными числами, то комплексные корни уравнения, если они есть, будут парными комплексно сопряженными.

Подбором находим первый корень уравнения , так как .

По следствию из теоремы Безу . Вычисляем это деление «в столбик»:

_
	_
		_

Представляя теперь многочлен в виде произведения линейно и квадратного множителя, получим:

.

Другие корни находим как корни квадратного уравнения:

.

Ответ: , .

Составить алгебраическое уравнение наименьшей степени с действительными коэффициентами, если известно, что числа x1 = 3 и x2 = 1 + i являются его корнями, причем x1 является двукратным корнем, а x2 — простым.

Решение.

Число тоже является корнем уравнения, т.к. коэффициенты уравнения должны быть действительными.

Всего искомое уравнение имеет 4 корня: x1, x1, x2, . Поэтому его степень равна 4. Составляем многочлен 4-й степени с нулями x1, x1, x2, по формуле (6):



.

Искомое уравнение имеет вид P4(x) = 0.

Ответ: .

Вопросы для самопроверки

Сформулируйте определение комплексного числа

Что называется комплексным числом?

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что такое мнимая единица?

Что такое действительная часть комплексного числа z?

Что такое мнимая часть комплексного числа z?

Что такое комплексно сопряженное число?

Что такое противоположное число?

Что такое комплексный ноль?

Что такое чисто мнимое число?

Сформулируйте смысл комплексного равенства.

В чём состоит геометрическое изображение комплексных чисел?

Что такое модуль и аргумент комплексного числа?

Что называется модулем комплексного числа?

Что такое аргумент комплексного числа?

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что такое алгебраическая и тригонометрическая формы комплексного числа?

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что называется алгебраической формой комплексного числа?

Что называется тригонометрической формой комплексного числа?

Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂.

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что такое формула Муавра?

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что называется корнем степени n из комплексного числа?

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что называется показательной формой комплексного числа?

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что такое формулы Эйлера?

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что называется целой функцией?

Что называется алгебраическим многочленом?

Что называется полиномом?

Что такое степень многочлена?

Что такое коэффициенты многочлена?

Что называется алгебраическим уравнением n-й степени?

Что называется нулем функции?

Что называется корнем уравнения?

Перечислите основные свойства многочленов.

Сформулируйте свойство о тождественном равенстве многочленов.

Сформулируйте свойство о делении многочлена на разность (x – х0).

Сформулируйте теорему теорема Безу.

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Сформулируйте свойство о существовании нуля многочлена.

Сформулируйте теорему теорема алгебры основная.

Какое название или смысл имеет формула?

Поясните смысл обозначений в этой формуле:

⌂ .

Что называется k-кратным нулем многочлена?

Что называется простым нулем многочлена?

Сформулируйте свойство о количестве корней алгебраического уравнения.

Сформулируйте свойство о комплексных корнях алгебраического уравнения

с действительными коэффициентами.

Сформулируйте свойство о разложении многочлена с действительными коэффициентами на линейные и квадратичные множители.

Приведите примеры решения алгебраических уравнений на множестве комплексных чисел

Глоссарий

k-кратным нулем многочлена называется... (стр. 18)

алгебраическим многочленом называется... (стр. 14)

алгебраическим уравнением n-й степени называется... (стр. 14)

алгебраической формой комплексного числа называется... (стр. 5)

аргумент комплексного числа это... (стр. 4)

действительная часть комплексного числа z это... (стр. 2)

комплексно сопряженное число это... (стр. 2)

комплексный ноль это... (стр. 2)

комплексным числом называется... (стр. 2)

корнем степени n из комплексного числа называется... (стр. 10)

корнем уравнения называется... (стр. 14)

коэффициенты многочлена это... (стр. 14)

мнимая единица это... (стр. 2)

мнимая часть комплексного числа z это... (стр. 2)

модулем комплексного числа называется... (стр. 4)

нулем функции называется... (стр. 14)

показательной формой комплексного числа называется... (стр. 11)

полиномом называется... (стр. 14)

простым нулем многочлена называется... (стр. 18)

противоположное число это... (стр. 2)

степень многочлена это... (стр. 14)

тригонометрической формой комплексного числа называется... (стр. 5)

формула Муавра это... (стр. 9)

формулы Эйлера это... (стр. 13)

целой функцией называется... (стр. 14)

чисто мнимое число это... (стр. 2)