Численные характеристики дискретных случайных величин

Введение

Как и всякие явления, случайные явления вызываются вполне определенными причинами. Все явления окружающего нас мира взаимно связаны и влияют одно на другое (закон всеобщей связи явлений). Поэтому каждое наблюдаемое явление связано причинной зависимостью с бесчисленным множеством других явлений и течение его зависит от бесчисленного множества факторов. Проследить все это бесконечное множество связей и определить действие каждой из них принципиально невозможно. Поэтому, изучая то или иное явление, человек ограничивается лишь основными факторами, определяющими его течение, и пренебрегает огромным количеством второстепенных явлений. Это дает возможность глубже проникнуть в сущность явления, установить его закономерность. Вместе с тем, поступая так, человек обедняет явление, схематизирует его. Иными словами, он заменяет изучаемое явление подходящей упрощенной его моделью. Вследствие этого любой закон науки отражает сущность изучаемого явления, но он всегда значительно беднее, уже самого явления. Никакой закон не может характеризовать явление всесторонне, во всей полноте и многообразии. Наблюдаемые в реальном явлении отклонения от закономерности, вызываемые совместным действием бесчисленного множества неучтенных факторов, и представляют собой случайные явления.

При экспериментальном изучении какого-либо явления с целью установления его закономерностей приходится наблюдать его многократно в одинаковых условиях. При этом под одинаковыми условиями мы понимаем одинаковые значения всех количественных характеристик контролируемых факторов. Все неконтролируемые факторы будут при этом различными. Вследствие этого действие контролируемых факторов будет практически одинаковым при разных наблюдениях одного и того же явления. В этом как раз и проявляются законы данного явления. Случайные же отклонения от закономерности, вызванные действием неконтролируемых факторов, будут различными при разных наблюдениях, причем предвидеть заранее, какими они будут при данном конкретном наблюдении, принципиально невозможно. Роль случайностей в разных явлениях различна. В некоторых явлениях случайные отклонения от закономерностей настолько малы, что их можно не учитывать. Однако есть и такие явления, в которых невозможно подметить никаких закономерностей, и случайность играет основную роль. Примером такого явления может служить движение малой частицы твердого вещества, взвешенной в жидкости, так называемое броуновское движение. Под действием толчков огромного количества движущихся молекул жидкости частица движется совершенно беспорядочно, без всякой видимой закономерности. В подобных явлениях сама случайность является закономерностью. При многократном наблюдении случайных явлений в них самих можно заметить определенные закономерности. Изучив эти закономерности, человек получает возможность в известной степени управлять случайными явлениями, ограничивать их влияние, предсказывать результаты их действия и даже целенаправленно использовать их в своей практической деятельности. Так, например, можно проектировать измерительные системы, обладающие максимальной доступной точностью, радиоприемные устройства с максимальной помехозащищенностью, обладающие минимальным уровнем шумов, системы управления движением летательных аппаратов, обеспечивающие наибольшую возможную точность навигации или наименьшее действие «болтанки» на летательный аппарат. Можно также проектировать технические системы, обладающие заданной надежностью. Изучением закономерностей массовых случайных явлений занимается особая математическая наука — теория вероятностей. Методы теории вероятностей, называемые вероятностными или статистическими, дают возможность производить расчеты, позволяющие делать определенные практические выводы относительно случайных явлений. Как и всякая прикладная наука, теория вероятностей нуждается в исходных экспериментальных данных для расчетов. Раздел теории вероятностей, изучающий методы обработки результатов опытов и получения из них необходимых данных, называется математической статистикой.

дискретный дисперсия ковариация корреляция

Математическое ожидание дискретной случайной величины

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина может принимать только значения вероятности которых соответственно равны Тогда математическое ожидание случайной величины определяется равенством

Если дискретная случайная величина принимает счетное множество возможных значений, то

Причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.

Определение математического ожидания в общем случае

Определим математическое ожидание случайной величины , распределение которой не обязательно дискретно. Начнем со случая неотрицательных случайных величин. Идея будет заключаться в том, чтобы аппроксимировать такие случайные величины с помощью дискретных, для которых математическое ожидание уже определено, а математическое ожидание положить равным пределу математических ожиданий приближающих ее дискретных случайных величин. Кстати, это очень полезная общая идея, состоящая в том, что некоторая характеристика сначала определяется для простых объектов, а затем для более сложных объектов она определяется с помощью аппроксимации их более простыми.

Лемма 1. Пусть есть произвольная неотрицательная случайная величина. Тогда существует последовательность дискретных случайных величин, таких, что

Доказательство. Разобьем полуось на равные отрезки длины и определим

если

Тогда свойства 1 и 2 легко следуют из определения случайной величины , и

Лемма 2. Пусть –неотрицательная случайная величина и и две последовательности дискретных случайных величин, обладающих свойствами 1-3 из леммы 1. Тогда

Доказательство. Отметим, что для неотрицательных случайных величин мы допускаем

В силу свойства 3 легко видеть, что существует последовательность положительных чисел, такая что

Отсюда следует, что

. Используя свойства математических ожиданий для дискретных случайных величин, получаем

Переходя к пределу при получаем утверждение леммы 2.

Определение 1. Пусть – неотрицательная случайная величина, –последовательность дискретных случайных величин, обладающих свойствами 1-3 из леммы 1. Математическим ожиданием случайной величины называется число

Лемма 2 гарантирует, что 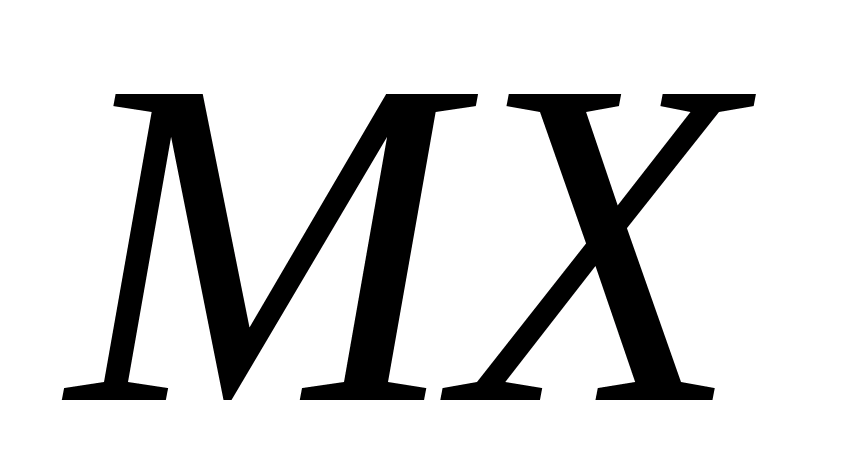не зависит от выбора аппроксимирующей последовательности .

Пусть теперь – произвольная случайная величина. Определим

Из определения и легко следует, что

Определение 2. Математическим ожиданием произвольной случайной величины называется число

Если хотя бы одно из чисел в правой части этого равенства конечно.

Свойства математического ожидания

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:

Доказательство. Будем рассматривать постоянную как дискретную случайную величину, которая имеет одно возможное значение и принимает его с вероятностью следовательно,

Замечание 1. Определим произведение постоянной величины на дискретную случайную величину как дискретную случайную возможные значения которой равны произведениям постоянной на возможные значения ; вероятности возможных значений равны вероятностям соответствующих возможных значений Например, если вероятность возможного значения равна то вероятность того, что величина примет значение также равна

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

Доказательство. Пусть случайная величина задана законом распределения вероятностей:

Учитывая замечание 1, напишем закон распределения случайной величины

Итак,

Замечание 2. Прежде, чем перейти к следующему свойству, укажем, что две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины зависимы. Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа их них не зависят от того, какие возможные значения приняли остальные величины.

Замечание 3. Определим произведение независимых случайных величин и как случайную величину возможные значения которой равны произведениям каждого возможного значения на каждое возможное значение вероятности возможных значений произведения равны произведениям вероятностей возможных значений сомножителей. Например, если вероятность возможного значения равна , вероятность возможного значения равна то вероятность возможного значения равна

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

Доказательство. Пусть независимые случайные величины и заданы своими законами распределения вероятностей:

Составим все значения, которые может принимать случайная величина Для этого перемножим все возможные значения на каждое возможное значение ; в итоге получим и учитывая замечание 3, напишем закон распределения предполагая для простоты, что все возможные значения произведения различны (если это не так, то доказательство проводится аналогично):

Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:

или

Итак,

Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

Доказательство. Пусть случайные величины и заданы следующими законами распределения:

Составим все возможные значения величины Для этого к каждому возможному значению прибавим каждое возможное значение ; получим Предположим для простоты, что эти возможные значения различны (если это не так, то доказательство проводится аналогично), и обозначим их вероятности соответственно через и

Математическое ожидание величины равно сумме произведений возможных значений на их вероятности:

или

(*)

Докажем, что Событие, состоящее в том, что примет значение (вероятность этого события равна ), влечет за собой событие, которое состоит в том, что примет значение или (вероятность этого события по теореме сложения равна 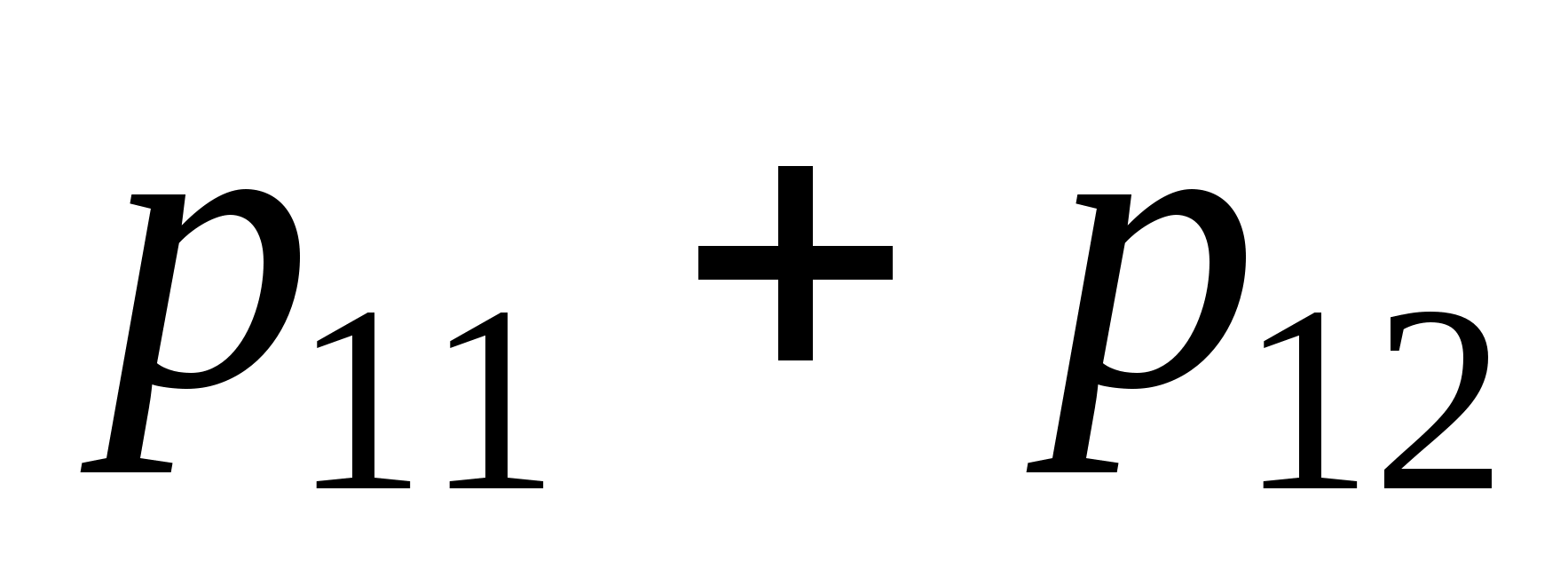), и обратно. Отсюда и следует, что Аналогично доказываются равенства

и

Подставляя правые части этих равенств в соотношение (*), получим

или окончательно

Дисперсия и среднее квадратическое отклонение

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.

На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т.е. для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, т.е. вычисляют среднее значение квадрата отклонения, которое и называется дисперсией.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Пусть случайная величина задана законом распределения

Тогда квадрат отклонения имеет следующий закон распределения:

…

По определению дисперсии,

Таким образом, для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.

Формула для вычисления дисперсии

Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

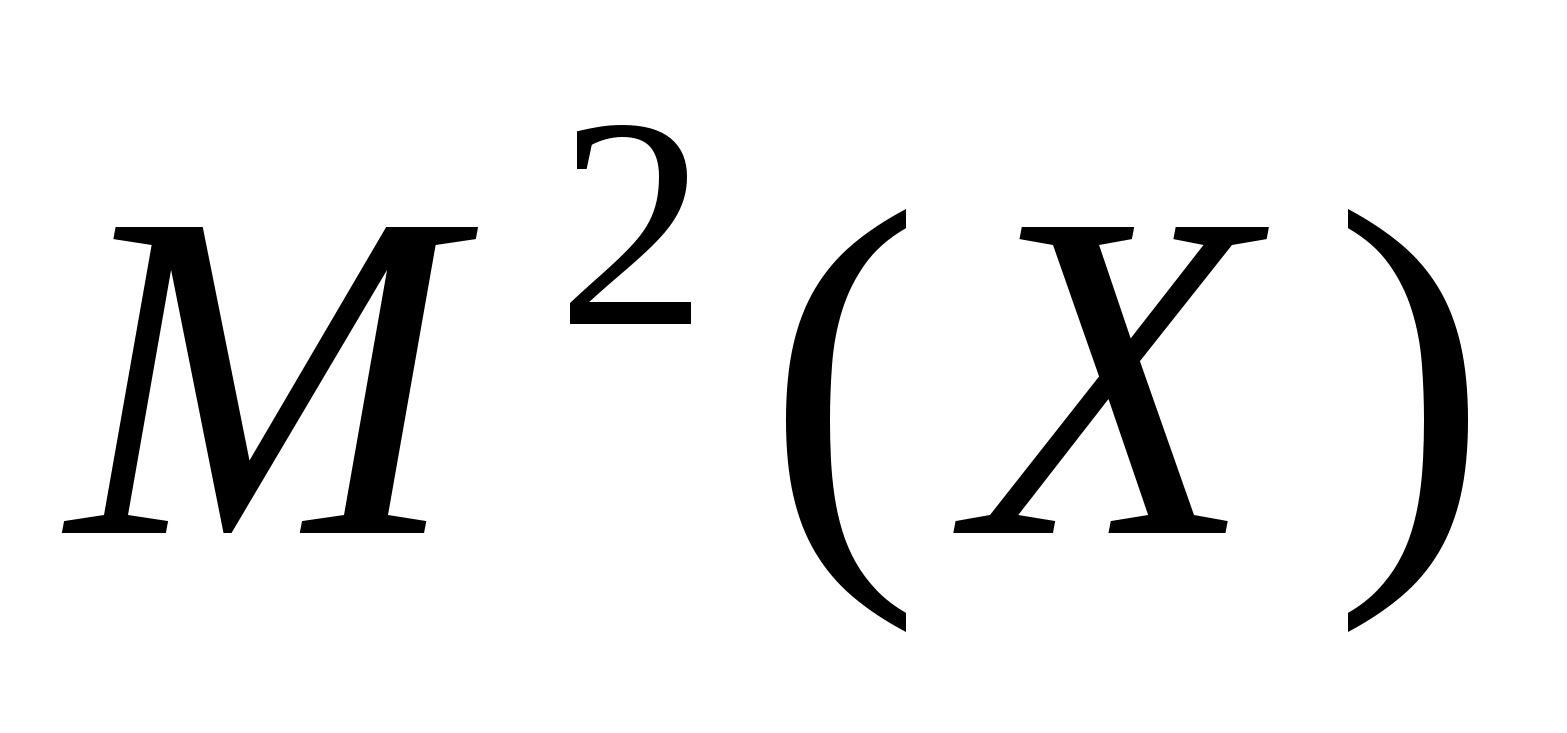Доказательство. Математическое ожидание есть постоянная величина, следовательно, и есть также постоянные величины. Приняв это во внимание и пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии:

Итак,

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины равна нулю:

Доказательство. По определению дисперсии,

Пользуясь первым свойством математического ожидания, получим

.

Итак,

Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

Доказательство. По определению дисперсии имеем

Пользуясь вторым свойством математического ожидания (постоянный множитель можно выносить за знак математического ожидания), получим

Итак,

Свойство становится ясным, если принять во внимание, что при величина имеет возможные значения (по абсолютной величине), большие, чем величина Отсюда следует, что эти значения рассеяны вокруг математического ожидания больше, чем возможные значения вокруг т.е. Напротив, если то

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

Доказательство. По формуле для вычисления дисперсии имеем

Раскрыв скобки и пользуясь свойствами математического ожидания суммы нескольких величин и произведения двух независимых случайных величин, получим

Итак,

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

Свойство 4. дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

Доказательство. В силу третьего свойства

По второму свойству,

или

Среднее квадратическое отклонение

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность совпадает с размерностью . Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если выражается в линейных метрах, то будет выражаться также в линейных метрах, а в квадратных метрах.

Среднее квадратическое отклонение суммы взаимно независимых случайных величин

Пусть известны средние квадратические отклонения нескольких взаимно независимых случайных величин. Чтобы найти среднее квадратическое отклонение суммы этих величин, воспользуемся следующей теоремой.

Теорема: Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

Доказательство. Обозначим через сумму рассматриваемых взаимно независимых величин:

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий слагаемых, поэтому

Отсюда

Или окончательно

Ковариация и коэффициент корреляции

Ковариацией скалярных случайных величин и называется математическое ожидание произведения центрированной первой случайной величины и сопряженной центрированной второй случайной величины:

Чтобы получить формулу для вычисления ковариации действительных случайных величин и , достаточно рассматривать как функцию случайных величин и :

где совместная плотность величин и .

Чтобы получить формулу для вычисления ковариации комплексных случайных величин и достаточно рассматривать произведение как функцию четырехмерного случайного вектора с координатами Тогда получим

где совместная плотность случайных величин

За характеристику зависимости между двумя случайными величинами и принимается отношение их ковариации к произведению их средних квадратических отклонений. Эта безразмерная величина называется коэффициентом корреляции величин и :

Таким образом, чтобы получить числовые характеристики двумерного случайного вектора, следует добавить к математическим ожиданиям и дисперсиям его координат еще и ковариацию или коэффициент корреляции.

Очевидно, что ковариация случайной величины с сама с собой равно ее дисперсии, а ее коэффициент корреляции с самой собой равен единице, и в более общем случае, когда

Коррелированные и некоррелированные случайные величины

Зависимость между случайными величинами, характеризуемая коэффициентом корреляции, называется, корреляцией. Случайные величины называются коррелированными, если их коэффициент корреляции равен нулю. Из формулы следует, что случайные величины не коррелированны тогда и только тогда, когда их ковариация равна нулю.

Легко видеть, что для некоррелированности случайных величин достаточно, чтобы их совместное распределение было симметрично относительно какой-нибудь прямой, параллельной одной из осей координат.

Моменты первого и второго порядков случайной величины

Математическое ожидание, дисперсия и ковариация представляют собой частные виды моментов случайных причин.

Моментом первого порядка (первым моментом) случайной величины называется ее математическое ожидание.

Моментом второго порядка (вторым моментом) скалярной (в общем случае комплексной) случайной величины называется математическое ожидание квадрата ее модуля:

Центральным моментом второго порядка величины называется момент второго порядка центрированной величины т.е. ее дисперсия.

Моментом второго порядка величины относительно точки называется момент второго порядка разности

(*)

Очевидно, что

Смешанным моментом второго порядка скалярных случайных величин и называется математическое ожидание произведения первой величины и сопряженной второй:

Центральным смешанным моментом второго порядка величин и называется смешанный второй момент центрированных случайных величин и , т.е. ковариация величин и .

Смешанным моментом второго порядка величин и относительно точек и называется смешанный второй момент разностей и

(**)

Ясно, что

Подставив в и и пользуясь свойствами математических ожиданий, получим выражения моментов второго порядка через математические ожидания и центральные моменты второго порядка:

Аналогично из (*) и (**) получаем

Таким образом, все моменты второго порядка выражаются через математические ожидания случайных величин и их центральные моменты второго порядка.

Формула показывает, что дисперсия случайной величины представляет собой наименьший из всех ее моментов второго порядка.

Момент второго порядка случайных векторов, ковариационная матрица, корреляционная матрица

Моментом второго порядка (вторым моментом) случайного вектора называется матрица вторых моментов всех его координат:

Момент второго порядка центрированного случайного вектора называется ковариационной матрицей случайного вектора

Представив вектор в форме матрицы-столбца, можем переписать определения второго момента и ковариационной матрицы случайного вектора в виде

где звездочка означает операцию транспонирования матрицы с заменой всех ее комплексных элементов соответствующими сопряженными числами.

Матрица, элементами которой служат коэффициенты корреляции координат случайного вектора называется его корреляционной матрицей:

Подставив в 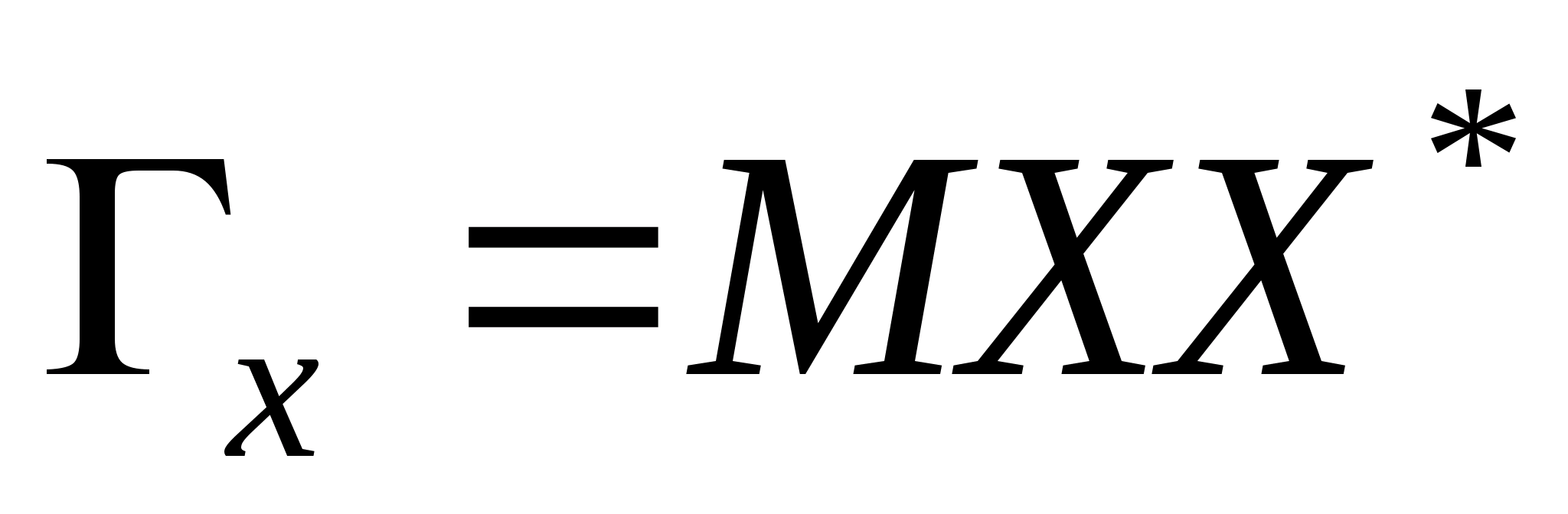формулу и пользуясь свойствами математических ожиданий, получаем соотношение между моментом второго порядка, ковариационной матрицей и математическим ожиданием случайного вектора:

Взаимный момент второго порядка и взаимная ковариационная матрица

Взаимным моментом второго порядка (вторым моментом) двух случайных векторов и назовем матрицу (в общем случае прямоугольную)

Взаимной ковариационной матрицей или ковариацией случайных векторов и назовем взаимный момент второго порядка соответствующих центрированных случайных векторов и

Взаимный момент второго порядка, ковариационная матрица и математические ожидания векторов и связаны соотношением:

Случайные векторы и называются коррелированными, если , и некоррелированными, если Из этого определения следует, что векторы и не коррелированы тогда и только тогда, когда каждая координата одного из них не коррелирована со всеми координатами другого.

Заключение

Теория вероятностей является мощным инструментом исследования, и поэтому она находит большое число самых разнообразных применений в различных областях науки и инженерной практики. Области ее применения непрерывно расширяются. В прошлом веке теория вероятностей получила применение в теории измерений, в теории стрельбы и в физике. В нашем веке она постепенно проникла в аэродинамику и гидродинамику, радиотехнику, теорию управления, динамику полета, теорию связи, строительную механику, теорию механизмов и машин, теорию волнения моря и качки кораблей, метеорологию и во многие другие области знания. Сейчас трудно назвать отрасль науки, которая не пользовалась бы вероятностными методами. В современной теории процессов управления, в теоретической радиотехнике теория вероятностей стала основным инструментом исследований. Вся теория современных сложных систем и процессов управления основана на применении статистических методов. Теория вероятностей служит фундаментом для теории надежности технических систем и для многих других прикладных научных теорий. Этот процесс непрерывного расширения областей применения теории вероятностей вполне естествен и легко объясняется. Дело в том, что в начале развития каждой отрасли науки человек стремится открыть основные законы этой науки и ему достаточно довольно грубого совпадения результатов расчета с данными опытов. Кроме того, техника эксперимента на начальной стадии несовершенна и не может обеспечить высокую точность измерений. По мере развития науки требования к точности расчетов повышаются, техника эксперимента совершенствуется, и случайные явления, которыми можно было пренебрегать в начале развития данной отрасли науки, начинают играть все более и более значительную роль. В результате старая теория начинает во многом расходиться с экспериментальными данными и возникает необходимость обратиться к теории вероятностей. Теория вероятностей во всех таких случаях неизменно дает новую теорию, более точно описывающую изучаемые явления и обеспечивающую совпадение результатов теоретических расчетов с экспериментальными данными. Так случилось в начале тридцатых годов с теорией турбулентности в аэродинамике и в сороковых годах с теорией автоматического управления и радиотехникой, а потом и с другими прикладными научными теориями.Особенность вероятностных методов состоит в том, что они рассматривают исследуемое явление в целом, изучают результаты совокупного действия всех причинных связей, которые невозможно проследить по отдельности.

Список используемой литературы

Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. – М.: Высшая школа, 2001.

Пугачев В.С. Теория вероятностей и математическая статистика.-М.: Физматлит, 2002.

Хохлов Ю.С. Теория вероятностей и математическая статистика: Ч./М-во общ. И проф. Образован. РФ; ТГУ. Тверь:[ТГУ], 1997.

Вентцель Е.С. Теория вероятностей. М., «Наука», 1969.

Вентцель Е.С., Овчаров Л.А. Теория вероятностей. М., «Наука», 1969.

Ермаков В.А. Теория вероятностей и математическая статистика:–М.: Инфа – М, 2008.

Кибзун А.И., Горяинова Е.Р., Наумов А.В., Сиротин А.И. Теория вероятностей и математическая статистика. – М. Физматлит, 2002.

Гнеденко Б.В. Курс теории вероятности – М.: Наука, 1986.

Розанов Ю.А. Лекции по теории вероятностей – М.: Наука, Гл. ред. Физю-мат. Лит., 1986.

Захаров В.К., Севастьянов Б.А., Чистяков В.П. Теория вероятностей – М.: Наука, 1983.

Солодовников А.С. Теория вероятностей:/ – М. Просвещение, 1983.