–§—Г–љ–Ї—Ж–Є—П –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П
–Ч–∞–і–∞–љ–Є–µ
-
–љ–Њ–Љ–µ—А –Є–љ—В–µ—А–≤–∞–ї–∞
–≥—А–∞–љ–Є—Ж—Л –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ t
—З–∞—Б—В–Њ—В–∞ m
—Б–≤—Л—И–µ
–і–Њ(–≤–Ї–ї—О—З–Є—В–µ–ї—М–љ–Њ)
1
57,997
57,999
2
2
57,999
58,001
2
3
58,001
58,003
8
4
58,003
58,005
25
5
58,005
58,007
33
6
58,007
58,009
50
7
58,009
58,011
65
8
58,011
58,013
71
9
58,013
58,015
32
10
58,015
58,017
37
11
58,017
58,019
26
12
58,019
58,021
6
13
58,021
58,023
3
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П. –У—А–∞—Д–Є—З–µ—Б–Ї–Њ–µ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Њ–≥–Њ –Є —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–є
–њ–ї–Њ—В–љ–Њ—Б—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –і–Њ–≤–µ—А–Є—В–µ–ї—М–љ—Л–є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є –Њ–ґ–Є–і–∞–љ–Є–µ
–Я—А–Є –њ–Њ—Б—В—А–Њ–µ–љ–Є–Є –≥–Є—Б—В–Њ–≥—А–∞–Љ–Љ –Є –њ–Њ–ї–Є–≥–Њ–љ–Њ–≤ –њ–Њ –Њ—Б–Є –∞–±—Б—Ж–Є—Б—Б –Њ—В–Ї–ї–∞–і—Л–≤–∞—О—В –Ј–љ–∞—З–µ–љ–Є—П —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ –Є–Ј–Љ–µ—А–µ–љ–Є–є (—Б–µ—А–µ–і–Є–љ—Л –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ x>i>), –њ–Њ –Њ—Б–Є –Њ—А–і–Є–љ–∞—В вАУ —З–∞—Б—В–љ–Њ—Б—В–Є –њ–Њ—П–≤–ї–µ–љ–Є—П —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤ –Ї–∞–ґ–і–Њ–Љ i-–Љ –Є–љ—В–µ—А–≤–∞–ї–µ.
–Ш–Ј-–Ј–∞ –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ—Б—В–Є —З–Є—Б–ї–∞ —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤
–Є–Ј–Љ–µ—А–µ–љ–Є–є –њ—А–Є –Њ–±—А–∞–±–Њ—В–Ї–µ –≤–Љ–µ—Б—В–Њ
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–ґ–Є–і–∞–љ–Є—П –Є –і–Є—Б–њ–µ—А—Б–Є–Є
–њ–Њ–ї—Г—З–∞—О—В –Є—Е –њ—А–Є–±–ї–Є–ґ–µ–љ–љ—Л–µ –Њ—Ж–µ–љ–Ї–ЄвАУ
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Њ–µ —Б—А–µ–і–љ–µ–µ
 –Є —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї—Г—О –і–Є—Б–њ–µ—А—Б–Є—О S2,
—Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–Є–µ —Б—А–µ–і–љ–Є–є —А–µ–Ј—Г–ї—М—В–∞—В
–Є–Ј–Љ–µ—А–µ–љ–Є–є –Є —Б—В–µ–њ–µ–љ—М —А–∞–Ј–±—А–Њ—Б–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–є.
–Є —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї—Г—О –і–Є—Б–њ–µ—А—Б–Є—О S2,
—Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–Є–µ —Б—А–µ–і–љ–Є–є —А–µ–Ј—Г–ї—М—В–∞—В
–Є–Ј–Љ–µ—А–µ–љ–Є–є –Є —Б—В–µ–њ–µ–љ—М —А–∞–Ј–±—А–Њ—Б–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–є.
 –Є S2 –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П
–Є–Ј –≤—Л—А–∞–ґ–µ–љ–Є–є:
–Є S2 –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П
–Є–Ј –≤—Л—А–∞–ґ–µ–љ–Є–є:

–Ч–љ–∞—З–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –њ–Њ–њ–∞–і–∞–љ–Є—П —А–µ–Ј—Г–ї—М—В–∞—В–∞ –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤ –Ї–Њ–љ–Ї—А–µ—В–љ—Л–є –Є–љ—В–µ—А–≤–∞–ї –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М, –Є—Б–њ–Њ–ї—М–Ј—Г—П –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є:
 ,
,
–≥–і–µ
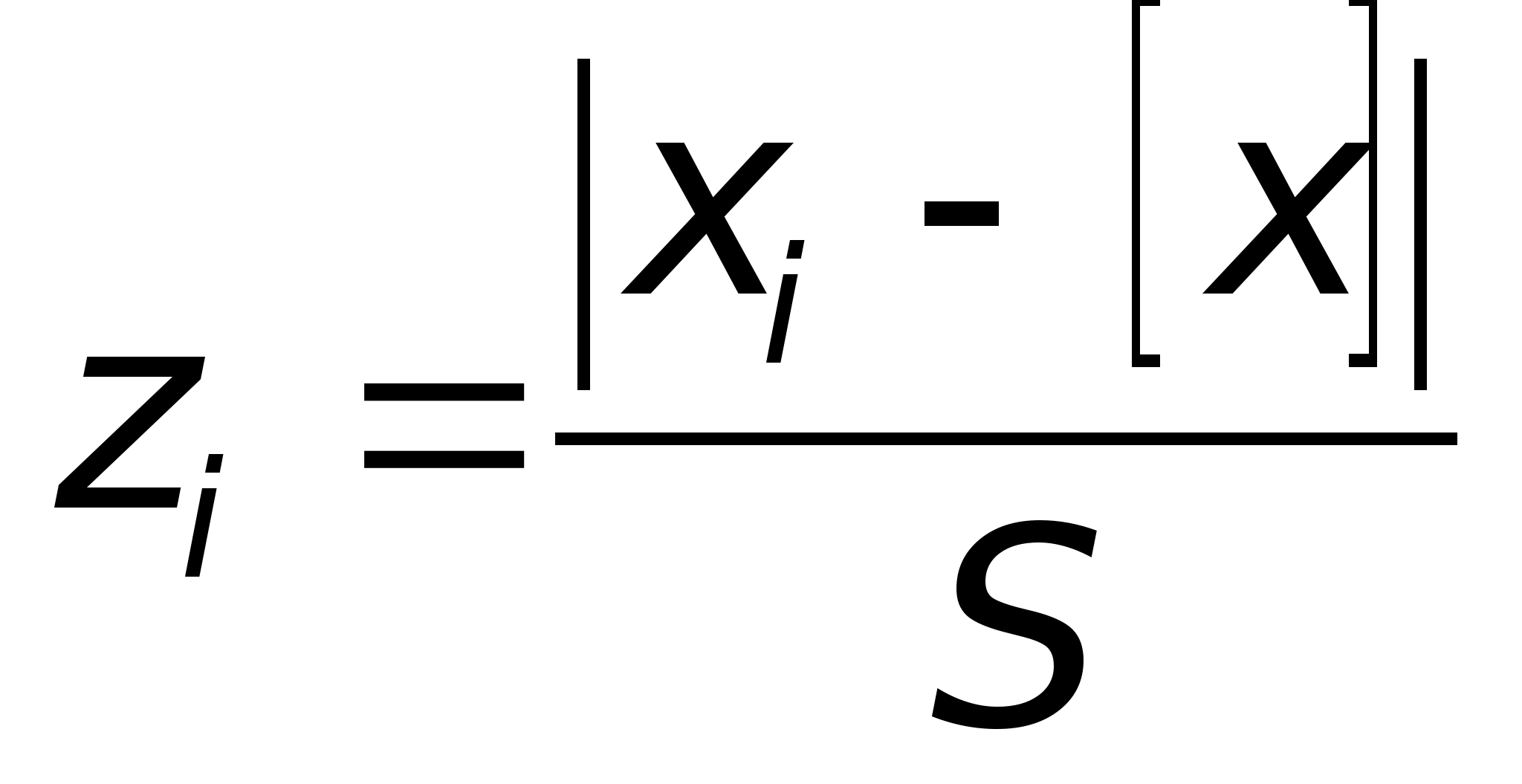 .
.
–Ґ–Њ–≥–і–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ–Њ–њ–∞–і–∞–љ–Є—П —А–µ–Ј—Г–ї—М—В–∞—В–∞ –≤ i-–є –Є–љ—В–µ—А–≤–∞–ї –≤–µ–ї–Є—З–Є–љ–Њ–є h
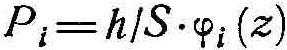 .
.
–Т–љ–µ—Б–µ–Љ –≤—Б–µ –≤—Л—З–Є—Б–ї–µ–љ–Є—П –≤ —В–∞–±–ї–Є—Ж—Г –Є –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –њ–Њ–ї—Г—З–µ–љ–љ—Л—Е —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ –њ–Њ—Б—В—А–Њ–Є–Љ –Ї—А–Є–≤—Г—О —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П, –∞ —В–∞–Ї –ґ–µ –≥–Є—Б—В–Њ–≥—А–∞–Љ–Љ—Г –Є –њ–Њ–ї–Є–≥–Њ–љ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П:
|
–°–µ—А–µ–і–Є–љ–∞ –Є–љ—В–µ—А–≤–∞–ї–∞ x>i> |
–≠–Љ–њ–Є—А–Є—З. —З–∞—Б—В–Њ—Б—В–Є PвАЩ>i> |
m>i>x>i> |
x>i>- |
z>i> |
m>i>x>i>2 |
ѕЖ>i>(z) |
P>i> |
|
|
57,998 |
0,006 |
115,996 |
-0,01285 |
2,874965 |
6727,536 |
0,006399 |
0,002863 |
|
|
58 |
0,006 |
116 |
-0,01085 |
2,4275 |
6728 |
0,020956 |
0,009377 |
|
|
58,002 |
0,022 |
464,016 |
-0,00885 |
1,980034 |
26913,86 |
0,056179 |
0,025138 |
|
|
58,004 |
0,069 |
1450,1 |
-0,00685 |
1,532569 |
84111,6 |
0,123277 |
0,055162 |
|
|
58,006 |
0,092 |
1914,198 |
-0,00485 |
1,085103 |
111035 |
0,221427 |
0,099081 |
|
|
58,008 |
0,139 |
2900,4 |
-0,00285 |
0,637638 |
168246,4 |
0,325553 |
0,145674 |
|
|
58,01 |
0,181 |
3770,65 |
-0,00085 |
0,190173 |
218735,4 |
0,391793 |
0,175314 |
|
|
58,012 |
0,197 |
4118,852 |
0,00115 |
0,257293 |
238942,8 |
0,385954 |
0,172701 |
|
|
58,014 |
0,089 |
1856,448 |
0,00315 |
0,704758 |
107700 |
0,311212 |
0,139257 |
|
|
58,016 |
0,103 |
2146,592 |
0,00515 |
1,152223 |
124536,7 |
0,20541 |
0,091914 |
|
|
58,018 |
0,072 |
1508,468 |
0,00715 |
1,599689 |
87518,3 |
0,110976 |
0,049658 |
|
|
58,02 |
0,017 |
348,12 |
0,00915 |
2,047154 |
20197,92 |
0,049077 |
0,02196 |
|
|
58,022 |
0,008 |
174,066 |
0,01115 |
2,494619 |
10099,66 |
0,017765 |
0,007949 |
|
|
–°—Г–Љ–Љ–∞ |
20883,91 |
1211493 |
-
 =
=58,01085
S2=
1,99775E-05
S=
0,00446962

–Ъ—А–Є—В–µ—А–Є–є —Б–Њ–≥–ї–∞—Б–Є—П —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Њ–≥–Њ –Є —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–є
–°—З–Є—В–∞—О—В, —З—В–Њ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Њ–µ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Е–Њ—А–Њ—И–Њ —Б–Њ–≥–ї–∞—Б—Г–µ—В—Б—П —Б —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є–Љ, –µ—Б–ї–Є (1 - пБІ) –±–Њ–ї—М—И–µ 0,1. –°–Њ–≥–ї–∞—Б–љ–Њ –Ї—А–Є—В–µ—А–Є—О –Ъ–Њ–ї–Љ–Њ–≥–Њ—А–Њ–≤–∞, —Б—А–∞–≤–љ–Є–≤–∞—О—В —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є–µ –Є —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є–µ –Ј–љ–∞—З–µ–љ–Є—П, –љ–Њ —Г–ґ–µ –љ–µ –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П, –∞ –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є. –Ч–љ–∞—З–µ–љ–Є–µ –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–є (–њ–Њ –∞–±—Б–Њ–ї—О—В–љ–Њ–є –≤–µ–ї–Є—З–Є–љ–µ) —А–∞–Ј–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г –љ–Є–Љ–Є D>N> –њ–Њ–і—Б—В–∞–≤–ї—П—О—В –≤ –≤—Л—А–∞–ґ–µ–љ–Є–µ:
 ,
,
–≥–і–µ N вАУ –Њ–±—К–µ–Љ –≤—Л–±–Њ—А–Ї–Є.
–Т—Л—З–Є—Б–ї–µ–љ–Є–µ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є—Е FвАЩ>i> –Є —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є—Е F>i> –Ј–љ–∞—З–µ–љ–Є–є –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Њ–Є–Ј–≤–Њ–і–Є–Љ –њ—Г—В–µ–Љ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ–≥–Њ —Б—Г–Љ–Љ–Є—А–Њ–≤–∞–љ–Є—П —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Ј–љ–∞—З–µ–љ–Є–є PвАЩ>i> –Є P>i>. –†–µ–Ј—Г–ї—М—В–∞—В—Л –≤—Л—З–Є—Б–ї–µ–љ–Є–є —Б–≤–µ–і–µ–љ—Л –≤ —В–∞–±–ї–Є—Ж—Г:
-
–Э–Њ–Љ–µ—А –Є–љ—В–µ—А–≤–∞–ї–∞
P>i>
PвАЩ>i>
F>i>
FвАЩ>i>
Fi-Fi'
1
0,002863
0,005556
0,002863
0,005556
0,002692
2
0,009377
0,005556
0,01224
0,011111
-0,00113
3
0,025138
0,022222
0,037379
0,033333
-0,00405
4
0,055162
0,069444
0,092541
0,102778
0,010237
5
0,099081
0,091667
0,191622
0,194444
0,002823
6
0,145674
0,138889
0,337295
0,333333
-0,00396
7
0,175314
0,180556
0,512609
0,513889
0,00128
8
0,172701
0,197222
0,68531
0,711111
0,025801
9
0,139257
0,088889
0,824566
0,8
-0,02457
10
0,091914
0,102778
0,91648
0,902778
-0,0137
11
0,049658
0,072222
0,966138
0,975
0,008862
12
0,02196
0,016667
0,988098
0,991667
0,003568
13
0,007949
0,008333
0,996048
1
0,003952
D>N>= F'>8 >вАУ F >8>= 0,025801,
N=пГ•m>i>=360,
–Ґ–Њ–≥–і–∞ –њ–Њ–ї—Г—З–∞–µ–Љ:
ќї= 0,48953
–Ф–ї—П пБђ>N>=0,52 пБІ пВї 0,05 пГЮ (1 вАУ 0,05)=0,95 >0,1.
–Ю—В—Б—О–і–∞ –Љ–Њ–ґ–љ–Њ —Б–і–µ–ї–∞—В—М –≤—Л–≤–Њ–і: —Б–Њ–≥–ї–∞—Б–Є–µ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П —Б –љ–Њ—А–Љ–∞–ї—М–љ—Л–Љ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є–Љ –Љ–Њ–ґ–љ–Њ —Б—З–Є—В–∞—В—М —Е–Њ—А–Њ—И–Є–Љ.
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –і–Њ–≤–µ—А–Є—В–µ–ї—М–љ—Л—Е –Є–љ—В–µ—А–≤–∞–ї–Њ–≤
–Т —А—П–і–µ –Ј–∞–і–∞—З, –Њ—Б–Њ–±–µ–љ–љ–Њ –њ—А–Є –Љ–∞–ї–Њ–Љ —З–Є—Б–ї–µ –Є–Ј–Љ–µ—А–µ–љ–Є–є, —В—А–µ–±—Г–µ—В—Б—П –љ–µ —В–Њ–ї—М–Ї–Њ –љ–∞–є—В–Є —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї—Г—О –Њ—Ж–µ–љ–Ї—Г –і–ї—П —В–Њ–≥–Њ –Є–ї–Є –Є–љ–Њ–≥–Њ –њ–∞—А–∞–Љ–µ—В—А–∞, –љ–Њ –Є –Њ–њ—А–µ–і–µ–ї–Є—В—М –і–Њ–≤–µ—А–Є—В–µ–ї—М–љ—Л–є –Є–љ—В–µ—А–≤–∞–ї, –≤ –Ї–Њ—В–Њ—А–Њ–Љ —Б –і–Њ–≤–µ—А–Є—В–µ–ї—М–љ–Њ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О –±—Г–і–µ—В –љ–∞—Е–Њ–і–Є—В—М—Б—П —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –њ–∞—А–∞–Љ–µ—В—А–∞.
–Ф–Њ–≤–µ—А–Є—В–µ–ї—М–љ—Л–є –Є–љ—В–µ—А–≤–∞–ї –і–ї—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–ґ–Є–і–∞–љ–Є—П –Њ–њ—А–µ–і–µ–ї—П–µ–Љ –Є–Ј –≤—Л—А–∞–ґ–µ–љ–Є—П:
–Є–љ—В–µ–≥—А–∞–ї—М–љ—Л–є –і–Њ–≤–µ—А–Є—В–µ–ї—М–љ—Л–є –Є–љ—В–µ—А–≤–∞–ї –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є –Њ–ґ–Є–і–∞–љ–Є–µ

–Ч–љ–∞—З–µ–љ–Є—П t>ќ≥> —В–∞–±—Г–ї–Є—А–Њ–≤–∞–љ—Л –Є —А–∞–≤–љ—П–µ—В—Б—П t>ќ≥> = 2,18 –і–ї—П N=13 –Є ќ≥*=0,95.
58,00814756 <M< 58,01355244
–Ф–Њ–≤–µ—А–Є—В–µ–ї—М–љ—Л–є –Є–љ—В–µ—А–≤–∞–ї –і–ї—П —Б—А–µ–і–љ–µ–≥–Њ –Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П –Њ–њ—А–µ–і–µ–ї—П–µ–Љ –Є–Ј –≤—Л—А–∞–ґ–µ–љ–Є—П:

–Ч–љ–∞—З–µ–љ–Є—П ѕЗ>1>2, ѕЗ>2>2 —В–∞–±—Г–ї–Є—А–Њ–≤–∞–љ—Л –Є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В —З–Є—Б–ї–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–є N –Є –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є—Е –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є ќ≥>1>, ќ≥>2>:

–Ч–љ–∞—З–µ–љ–Є–µ ѕЗ>1>2 –Њ–њ—А–µ–і–µ–ї—П–µ–Љ –њ—А–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є (1- ќ≥>1>), ѕЗ>2>2 вАУ –њ—А–Є ќ≥>2>.
ѕЗ>1>2=24,1 ѕЗ>2>2=4,18
–Ш —В–Њ–≥–і–∞
-
0,003024897
<ѕГ<
0,008194587
4. –Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –і–Є–∞–њ–∞–Ј–Њ–љ–∞ —А–∞—Б—Б–µ–Є–≤–∞–љ–Є—П –Ј–љ–∞—З–µ–љ–Є–є
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –≥—А–∞–љ–Є—Ж –і–Є–∞–њ–∞–Ј–Њ–љ–∞ —А–∞—Б—Б–µ–Є–≤–∞–љ–Є—П –Ј–љ–∞—З–µ–љ–Є–є –њ–Њ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –Є–Ј–Љ–µ—А–µ–љ–Є–є, –њ—А–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є —А–Є—Б–Ї–∞ 0,0027 .
–Ь пВї
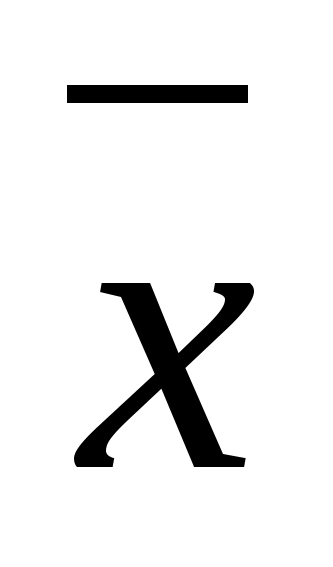 =58,01085
=58,01085
 пВї
S> >=0,00446962
пВї
S> >=0,00446962
–Ь-3 пВї
57.997442
пВї
57.997442
–Ь+3 пВї
58.024258
пВї
58.024258
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –≥—А–∞–љ–Є—Ж –і–Є–∞–њ–∞–Ј–Њ–љ–∞ —А–∞—Б—Б–µ–Є–≤–∞–љ–Є—П –Ј–љ–∞—З–µ–љ–Є–є –њ–Њ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –Є–Ј–Љ–µ—А–µ–љ–Є–є, –њ—А–Є –і–Њ–њ—Г—Б–Ї–∞–µ–Љ–Њ–Љ –Ј–љ–∞—З–µ–љ–Є–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є —А–Є—Б–Ї–∞ 2ќ≤=0,001
–Ь¬± ѕГ
ѕГ


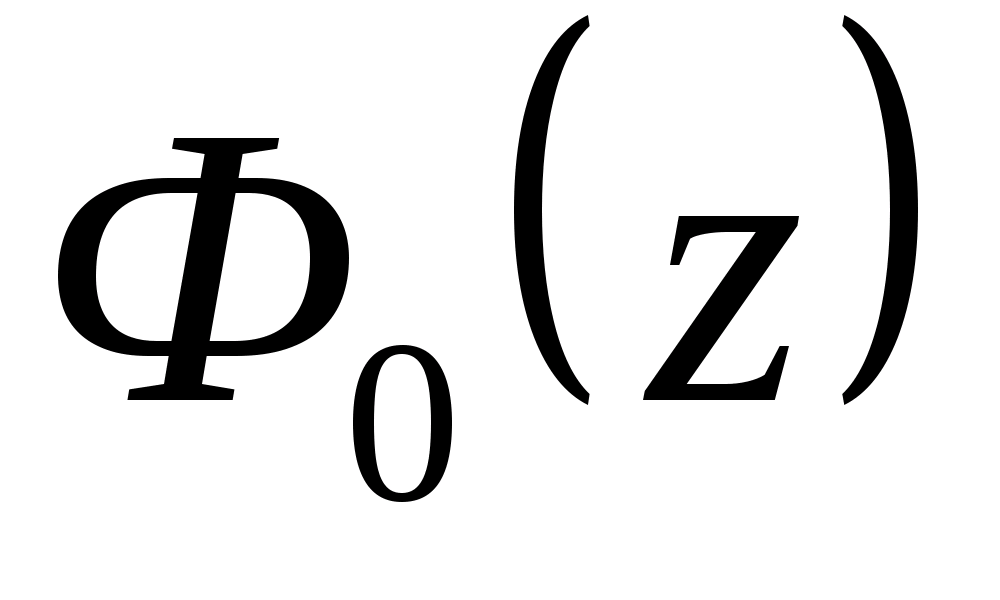 =0,4995
–њ—А–Є —Н—В–Њ–Љ
=0,4995
–њ—А–Є —Н—В–Њ–Љ
 =3,29
(–њ–Њ —Б–њ—А–∞–≤–Њ—З–љ–Є–Ї—Г)
=3,29
(–њ–Њ —Б–њ—А–∞–≤–Њ—З–љ–Є–Ї—Г)
–Ь-3,29 =57,996146
=57,996146
–Ь+3,29 =58,025554
=58,025554
–°–њ–Є—Б–Њ–Ї –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–љ–Њ–є –ї–Є—В–µ—А–∞—В—Г—А—Л
–Ч—П–±—А–µ–≤–∞ –Э.–Э. –Є –і—А. –Я–Њ—Б–Њ–±–Є–µ –Ї —А–µ—И–µ–љ–Є—О –Ј–∞–і–∞—З –њ–Њ –Ї—Г—А—Б—Г "–Т–Ј–∞–Є–Љ–Њ–Ј–∞–Љ–µ–љ—П–µ–Љ–Њ—Б—В—М, —Б—В–∞–љ–і–∞—А—В–Є–Ј–∞—Ж–Є—П –Є —В–µ—Е–љ–Є—З–µ—Б–Ї–Є–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П". –£—З–µ–±. –Я–Њ—Б–Њ–±–Є–µ –і–ї—П –≤—Г–Ј–Њ–≤. –Ь., "–Т—Л—Б—И. —И–Ї–Њ–ї–∞", 1977.