Уравнения смешанного типа
Содержание
Введение
1. Нелокальная граничная задача Ι рода
2. Нелокальная граничная задача II рода
Литература
уравнение спектральный нелокальный дифференциальный
Введение
В современной теории дифференциальных уравнений с частными производными важное место занимают исследования вырождающихся гиперболических и эллиптических уравнений, а также уравнений смешанного типа. Уравнения смешанного типа стали изучаться систематически с конца 40-х годов, после того, как Ф.И. Франкль указал их приложения в околозвуковой и сверхзвуковой газовой динамике. Позже И.Н. Векуа были найдены приложения этих уравнений и в других разделах физики и механики, в частности, в теории бесконечно малых изгибаний поверхностей и безмоментной теории оболочек. Также повышенный интерес к этим классам уравнений объясняется как теоретической значимостью полученных результатов, так и их многочисленными приложениями в гидродинамике, в различных разделах механики сплошных сред, акустике, в теории электронного рассеяния и многих других областях знаний. Исследования последних лет также показали, что такие уравнения являются основой при моделировании биологических процессов.
Начало исследований краевых задач для уравнений смешанного типа было положено в работах Ф. Трикоми и С. Геллерстедта. В дальнейшем основы теории уравнений смешанного типа были заложены в работах Ф.И. Франкля, А.В. Бицадзе, К.И. Бабенко, С. Агмона, Л. Ниренберга, М. Проттера, К. Моравец и многих других авторов. Результаты, полученные ими и их последователями приведены в монографиях А.В. Бицадзе [4], Л. Берса [2], К.Г. Гудейлея [6], Т.Д. Джураева [7], М.М. Смирнова [14], Е.И. Моисеева [9], К.Б. Сабитова [12], М.С. Салахитдинова [13].
Среди краевых задач особое место занимают нелокальные задачи. Нелокальные задачи для дифференциальных уравнений рассматривались в работах Ф.И. Франкля [15], А.В. Бицадзе и А.А. Самарского [3], В.А. Ильина, Е.И. Моисеева, Н.И. Ионкина, В.И. Жегалова [8], А.И. Кожанова, А.М. Нахушева, Л.С. Пулькиной [10], О.А. Репина [11], А.Л. Скубачевского, А.П. Солдатова и других.
Особо выделим работу А.В. Бицадзе и А.А. Самарского [3], которая повлекла за собой систематическое изучение нелокальных краевых задач для эллиптических и других типов уравнений.
Первые фундаментальные исследования вырождающихся гиперболических уравнений были выполнены Ф. Трикоми в начале прошлого столетия. Для уравнения
(0.1)
он поставил
следующую задачу: пусть
область, ограниченная при
гладкой кривой
с концами в точках
и
оси
а при
характеристиками
уравнения (0.1). Требуется найти функцию
(
отрезок
оси
),
удовлетворяющую уравнению (0.1) в
и принимающую заданные значения на
Ф. Трикоми доказал существование и
единственность решения этой задачи при
определённых дополнительных требованиях
относительно поведения
в
гладкости граничных данных и характера
дуги
.
Эта краевая задача и уравнение (0.1)
называются сейчас задачей и уравнением
Трикоми.
М.А. Лаврентьев с целью упрощения исследований краевых задач для уравнений смешанного типа предложил новое модельное уравнение
(0.2)
Подробное исследование задачи Трикоми и её различных обобщений для уравнения (0.2) провёл А.В. Бицадзе. Уравнение (0.2) называют сейчас уравнением Лаврентьева-Бицадзе.
Нахушев А.М. установил критерий единственности решения задачи Дирихле для уравнений смешанного типа в цилиндрической области .
В работах Сабитова К.Б. исследована задача Дирихле для вырождающегося уравнения смешанного типа
в прямоугольной области. Методами спектрального анализа установлен критерий единственности и доказана теорема существования решения задачи Дирихле.
Изложенный в работах Е.И. Моисеева, К.Б. Сабитова спектральный метод применён при обосновании корректности постановки нелокальных начально-граничных и граничных задач для различных типов вырождающихся дифференциальных уравнений.
Целью данной работы является доказательство единственности и существования решения следующих задач:
Рассмотрим вырождающееся уравнение
(0.3)
где
в прямоугольной области
заданные
положительные числа, и для него исследуем
следующую нелокальную задачу.
Задача 1.
Найти в области
функцию
,
удовлетворяющую условиям:
;
(0.4)
; (0.5)
(0.6)
(0.7)
где
и
заданные достаточно гладкие функции,
причём
Для того же уравнения исследована и следующая задача:
Задача 2.
Найти в области
функцию
,
удовлетворяющую условиям:
(0.8)
; (0.9)
(0.10)
(0.11)
где
и
–
заданные достаточно гладкие функции,
причём
,
,
Для указанных задач установлены критерии их однозначной разрешимости. Решения получены явно в виде соответствующих рядов.
1. Нелокальная граничная задача Ι рода
Рассмотрим вырождающееся уравнение смешанного типа
(1)
где
в прямоугольной области
заданные
положительные числа, и для него исследуем
следующую нелокальную задачу.
Задача 1.
Найти в области
функцию
,
удовлетворяющую условиям:
;
(2)
; (3)
(4)
(5)
где
и
заданные достаточно гладкие функции,
причём
Пусть
решение
задачи (2)
Рассмотрим
функции
(6)
(7)
(8)
Дифференцируя дважды равенство (8), учитывая уравнение (1) и условия (4), получим дифференциальное уравнение
(9)
с граничными условиями
,
(10)
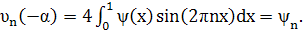(11)
Общее решение уравнения (9) имеет вид
где
и
функции Бесселя первого и второго рода
соответственно,
модифицированные
функции Бесселя,
и
произвольные постоянные,
Подберём
постоянные
и
так, чтобы выполнялись равенства
(13)
Опираясь на асимптотические формулы функций Бесселя
и модифицированных функций Бесселя
в окрестности
нуля, первое из равенств (13) выполнено
при
и любых
и
,
а второе равенство выполнено при
Подставим
полученные выражения для постоянных
и
в (12), тогда функции
примут
вид
Отметим, что для функций (14) выполнено равенство
Отсюда и из
равенств (13) вытекает, что
является
продолжением решения
на промежуток
и,наоборот,
является продолжением решения
на промежуток
.
Следовательно, функции (14) принадлежат
классу
и удовлетворяет уравнению (9) всюду на
.
Теперь на основании (10) и (11) получим
систему для нахождения
и
:
(15)
Если определитель системы (15):
(16)
то данная система имеет единственное решение
(17)
. (18)
С учётом (17) и (18) из (14) найдём окончательный вид функций
(19)
Где
(20)
(21)
(22)
(23)
Дифференцируя
дважды равенство (7) с учётом уравнения
(1) и условий (4) для функции
,
получим однородное дифференциальное
уравнение
(24)
с граничными условиями
(25)
Решение задачи (24) и (25) будет иметь вид
(26)
Аналогично
для функции
получаем неоднородное уравнение
(27)
с граничными условиями
(28)
(29)
Общее решение уравнения (27) имеет вид
Равенства
будут выполняться при следующих значениях
постоянных
,
при любых
и
Подставим выражения для постоянных
и
в (30), тогда функции
примут
вид
(31)
Для нахождения
и
на основании (28) и (29) получим систем
(32)
Если выполнено
условие (16), то
и
определяются по формулам:
(33)
,
(34)
Найденные
значения
и
по формулам (33) и (34) подставим в (31), тогда
функции
будут однозначно построены в явном
виде:
(35)
Из формул
(19), (26), (35) следует единственность решения
задачи (2)
так
как если
на
,
то
,
для
на
Тогда из (6)
имеем:
Отсюда в силу полноты системы
в пространстве
следует, что функция
почти всюду на
при любом
.
Таким образом, нами доказана следующая
Теорема 1.
Если существует решение
задачи (2)то
оно единственно только тогда, когда
при всех
Действительно,
если выполнено условие (16) и решение
задачи (2)
существует, то оно единственно. Пусть
при некоторых
и
нарушено условие (16), т. е.
Тогда однородная задача (2)
(где
имеет нетривиальное решение
Выражение
для
на основании следующих формул
приводим к виду
Поскольку
при любом
и
где
и
положительные
постоянные, то функция
где
в силу теоремы Хилби
имеет счётное множество положительных
нулей.
Следовательно,
при
некоторых
может иметь счётное множество нулей
независимо от
.
Поскольку
любое положительное число ,то оно может
принимать значения, близкие к нулям
Поэтому при больших n
выражение
может стать достаточно малым, т.е.
возникает проблема
Чтобы такой ситуации не было, надо
показать существование
и
таких, что при любом
и больших
справедлива оценка
Представим (16) в следующем виде
(36)
где
Как известно
функция
строго убывает, функция
строго возрастающая по
,
поэтому величина
есть бесконечно
малая более высокого порядка, чем
при больших
.
Поэтому рассмотрим только выражение
Используя
асимптотическую формулу функции
при
Получаем
Где
Отсюда видно,
что если, например,
где
то при
Тем самым справедлива следующая
Лемма 1.
Существует
и постоянная
такие, что при всех
и больших
справедлива оценка
(37)
Рассмотрим следующие отношения:
,
Лемма 2. При
любом
для достаточно больших n
справедливы оценки:
;
;
где
,
здесь и в дальнейшем, положительные
постоянные.
Доказательство.
С учётом (36) функция
примет вид
Оценим функцию
при
и больших
:
.
На основании
поведений функций
в
окрестности бесконечно-удалённой точки
и леммы 1, получим
(38)
где
здесь
и далее произвольные постоянные.
При 0
и n>>1
в силу асимптотических формул имеем
(39)
Сравнивая
(38) и (39) при любом
получим
Далее вычислим производную
Оценим эту
функцию при
и больших
:
(41)
При
и больших фиксированных
имеем
(42)
Из оценок
(41) и (42) следует, что при всех
Вторую
производную функции
вычислим следующим образом:
Используя формулы ([1], стр. 90)
Получаем
Зная оценку
(40) для
из последнего равенства при всех
имеем
Функция
с учётом (36) примет вид:
.
Оценим её,
используя лемму 1 при 0
и больших n:
(43)
При
и больших фиксированных
:
(44)
Из оценок (43) и (44) имеем:
(45)
Вычислим
производную
:
.
Оценим функцию
при
и
:
(46)
При
и
имеем:
(47)
Сравнивая
(46) и (47) при всех
,
получим
Теперь вычислим вторую производную функции
Используя формулы
Получим
Отсюда на основании оценки (45) будем иметь
(48)
Аналогично
получаем оценку для функции
и
:
Лемма 3. При
любом
для достаточно больших
справедливы оценки:
Доказательство.
Используя
и
функцию
,
определяемую формулой (19), представим
в следующем виде:
(49)
Из (49) в силу
леммы 2 получим оценки для функций
и
Аналогичные оценки справедливы и для
функций
и
Лемма доказана.
Лемма 4. Пусть
то справедливы оценки:
(50)
При получении
оценок (50) дополнительно применяется
теорема о скорости убывания коэффициентов
ряда Фурье функции, удовлетворяющей на
условию
Гёльдера с показателем
Теорема 2.
Пусть
и выполнены условия (16) и (37). Тогда задача
(2)-(5) однозначно разрешима и это решение
определяется рядом
(51)
где функции
,
определены соответственно по формулам
(26), (35), (19).
Доказательство. Поскольку системы функций
образуют
базис Рисса, то если
,
тогда функцию
можно представить в виде биортогонального
ряда (51), который сходится в
при любом
.
В силу лемм 3 и 4 ряд (51) при любом
из
мажорируется сходящимся рядом
поэтому ряд
(51) в силу признака Вейерштрасса сходится
абсолютно и равномерно в замкнутой
области
.
Следовательно, функция
непрерывна на
как сумма равномерно сходящегося ряда
(51). Ряды из производных второго порядка
в
мажорируются также сходящимся числовым
рядом
Поэтому сумма
ряда (51) принадлежит пространству
и удовлетворяет уравнению (1) в
.
Следствие 1. Построенное решение
задачи (2)-(5) принадлежит классу
и функция
всюду в
является решением уравнения (1).
Следовательно, линия изменения типа
уравнения (1) как особая линия устраняется.
2. Нелокальная граничная задача II рода
Рассмотрим
уравнение (1) в прямоугольной области
и исследуем сопряжённую относительно
задачи 1 задачу.
Задача 2.
Найти в области
функцию
,
удовлетворяющую условиям:
(52)
; (53)
(54)
(55)
где
и
–
заданные достаточно гладкие функции,
причём
,
,
Пусть
решение
задачи (52)- (55). Вновь воспользуемся
системами
Рассмотрим функции
, (56)
(57)
(58)
Дифференцируя дважды равенство (56) и учитывая уравнение (1), получим дифференциальное уравнение
(59)
с граничными условиями
(60)
(61)
Следуя §1 решение задачи (59)-(61) построим в виде
(62)
C
учётом уравнения (1) продифференцируем
дважды равенство (57). Получим для функции
однородное дифференциальное уравнение
(63)
с граничными условиями
(64)
Решение задачи (63) и (64) имеет вид
(65)
Дифференцируя
дважды равенство (58) и учитывая уравнение
(1) и условия (54), получаем неоднородное
уравнение для функции
(66)
с граничными условиями
,
(67)
.
(68)
Решение этой задачи определяется по формуле
(69)
Из формул
(62), (65), (69) следует единственность решения
задачи (52)-(55), так как если
на
то
,
,
для
на
Тогда
из (56)-(58) имеем:
,
,
Отсюда в силу полноты системы
в пространстве
следует, что функция
почти всюду на
при любом
.
Теорема 3.
Если существует решение
задачи (52)-(55), то оно единственно тогда
и только тогда, когда при всех n
выполняется условие (16).
Действительно,
если выполнено условие (16) и решение
задачи (52)-(55) существует, то оно единственно.
Пусть при некоторых
и
нарушено условие (16), т. е.
.
Тогда однородная задача (52)-(55) (где
) имеет нетривиальное решение
Теорема 4.
Если
,
и выполнены условия (16) и (37), то существует
единственное решение задачи (52)-(55) и оно
представимо в виде суммы ряда
где функции
,
определены соответственно по формулам
(65), (62), (69).
Доказательство теоремы 4 аналогично доказательству теоремы 2.
Следствие
2. Построенное решение
задачи (52)-(55) принадлежит классу
и функция
всюду в
является решением уравнения (1).
Следовательно, линия изменения типа
уравнения (1) как особая линия устраняется.
Литература
Бейтмен, Г.
Высшие трансцендентные функции / Г.
Бейтмен, А. Эрдейн.
М.:
Наука, 1966. Т.
Берс, Л.
Математические вопросы дозвуковой и
околозвуковой газовой динамики / Л.
Берс.
М.:
ИЛ,
Бицадзе, А.В. О некоторых простейших обобщениях эллиптических задач/ А.В. Бицадзе, А.А. Самарский // Докл. АН СССР. – 1969. – Т. 185. – № 4. – С. 739 – 740.
Бицадзе, А.В. Некоторые классы уравнений в частных производных /
А.В. Бицадзе. – М.: Наука, 1981.– 448 с.
Ватсон, Г.Н. Теория бесселевых функций.I./ Г.Н. Ватсон.–М.: ИЛ, 1940.– 421 с.
Гудерлей, К.Г. Теория околозвуковых течений / К.Г. Гудерлей. – М.: ИЛ, 1960. – 421 с.
Джураев, Т.Д. Краевые задачи для уравнений смешанного и смешанно-составного типов /Т.Д. Джураев – М.: ИЛ, 1961. – 208 с.
Жегалов, В.И. Нелокальная задача Дирихле для уравнения смешанного типа / В.И. Жегалов // Неклассич. уравнения матем. физики. – Новосибирск: ИМ СО АН СССР. 1985. – С.172 с.
Моисеев, Е.И. Уравнения смешанного типа со спектральным параметром / Е.И. Моисеев. – М.: МГУ, 1988. – 150 с.
Пулькина, Л.С. Нелокальная задача с нелокальным условием для гиперболического уравнения / Л.С. Пулькина // Неклассич. уравнения матем. физики. Новосибирск: ИМ СО РАН, 2002. – С. 176 – 184 с.
Репин, О.А. Задача Трикоми для уравнения смешанного типа в области, эллиптическая часть которой – полуполоса / О.А. Репин // Дифференциальные уравнения. – 1996. – Т. 32, №4. – С. 565 – 567 с.
Сабитов, К.Б. К теории уравнений смешанного типа с двумя линиями изменения типа / К.Б. Сабитов, Г.Г. Биккулова, А.А. Гималтдинова – Уфа.: Гилем, 2006. – 150 с.
Салахитдинов, М.С. Уравнения смешанно-составного типа – М.С. Салахитдинов. – Ташкент: Фан, 1974. – 156 с.
Смирнов, М.М. Уравнения смешанного типа / М.М Смирнов. – М.: Высшая школа, 1985. – 304 с.
Франкль, Ф.И. Обтекание профилей потоком дозвуковой скорости со сверхзвуковой зоной, оканчивающейся прямым скачком уплотнения / Ф.И. Франкль // ПММ. – 1956. – Т. 20. – №2. – с. 196 –202 с.