Похідні та диференціали функції багатьох змінних

ПОХІДНІ ТА ДИФЕРЕНЦІАЛИ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ

1 Частинні похідні

Нехай функція визначена в деякому околі точки .
Надамо змінній x приросту, залишаючи змінну незмінною, так, щоб точка належала заданому околу.

Величина

називається частинним приростом функції за змінною x.

Аналогічно вводиться частинний приріст функції за змінною:

.

Якщо існує границя

,

то вона називається частинною похідною функції в точці за змінною x і позначається одним із таких символів:

.

Аналогічно частинна похідна функції за визначається як границя

і позначається одним із символів:

.

Згідно з означенням при знаходженні частинної похідної обчислюють звичайну похідну функції однієї змінної x, вважаючи змінну сталою, а при знаходженні похідної сталою вважається змінна x. Тому частинні похідні знаходять за формулами і правилами обчислення похідних функцій однієї змінної.

Частинна похідна (або) характеризує швидкість зміни функції в напрямі осі (або).

З’ясуємо геометричний зміст частинних похідних функції двох змінних. Графіком функції є деяка поверхня (рис 1). Графіком функції є лінія перетину цієї поверхні з площиною. Виходячи з геометричного змісту похідної для функції однієї змінної, отримаємо, що, де– кут між віссю і дотичною, проведеною до кривої в точці. Аналогічно.

Рисунок 1 – Геометричний зміст частинних похідних

Для функції n змінних можна знайти n частинних похідних:

,

де

,

.

Щоб знайти частинну похідну, необхідно взяти звичайну похідну функції за змінною, вважаючи решту змінних сталими.

Якщо функція задана в області і має частинні похідні в усіх точках, то ці похідні можна розглядати як нові функції, задані в області.

Якщо існує частинна похідна за x від функції, то її називають частинною похідною другого порядку від функції за змінною x і позначають або .

Таким чином, за означенням

або.

Якщо існує частинна похідна від функції за змінною, то цю похідну називають мішаною частинною похідною другого порядку від функції і позначають, або.

Отже, за означенням

або .

Для функції двох змінних можна розглядати чотири похідні другого порядку:

.

Якщо існують частинні похідні від частинних похідних другого порядку, то їх називають частинними похідними третього порядку функції, їх вісім:

.

Виникає запитання: чи залежить результат диференціювання від порядку диференціювання? Інакше кажучи, чи будуть рівними між собою мішані похідні, якщо вони взяті за одними і тими самими змінними, одне й те саме число разів, але в різному порядку? Наприклад, чи дорівнюють одна одній похідні

і або і?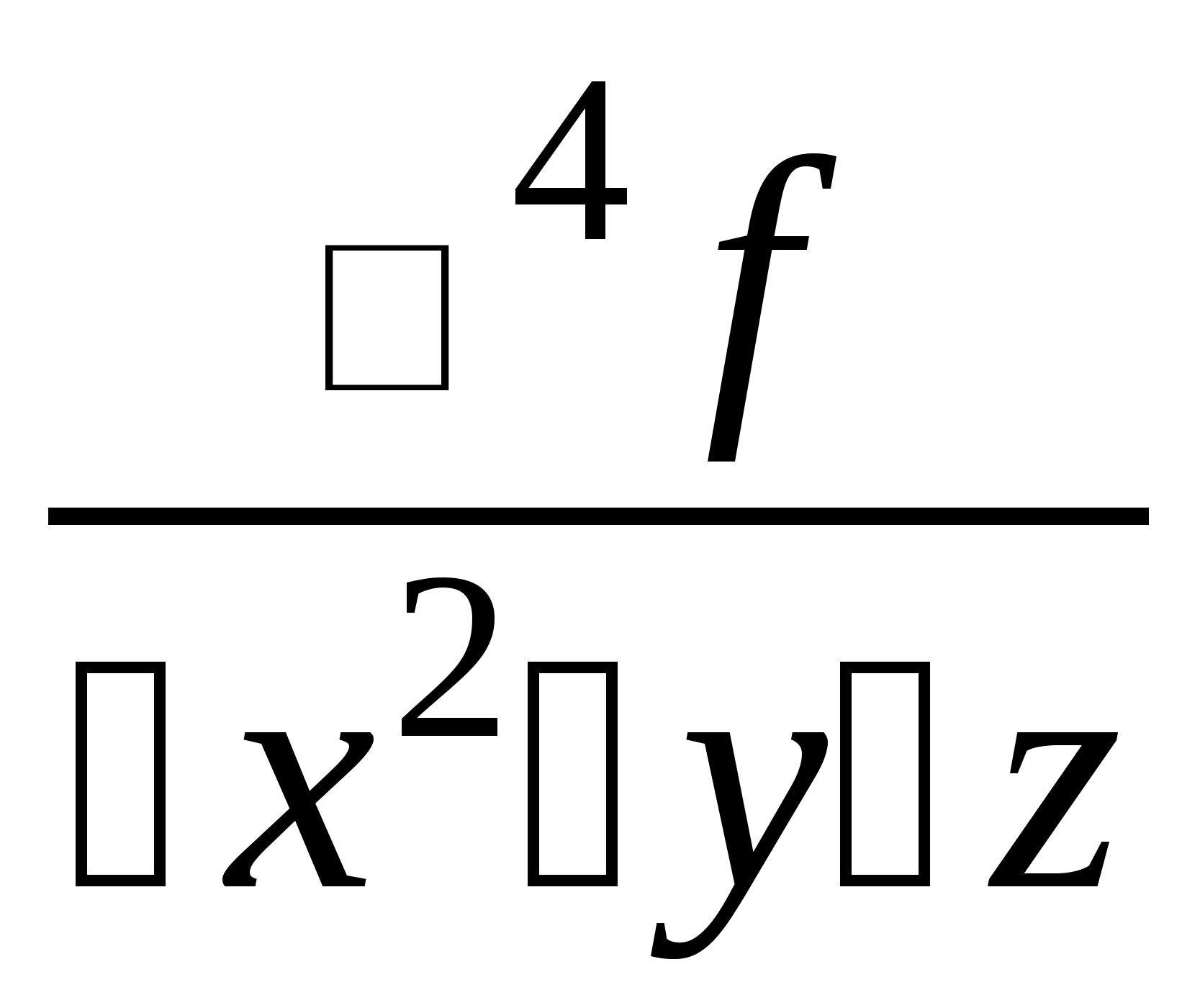

У загальному випадку відповідь на це запитання негативна.

Проте справедлива теорема, яку вперше довів К.Г.Шварц.

Теорема (про мішані похідні). Якщо функція визначена разом із своїми похідними в деякому околі точки , причому похідні та неперервні в точці, то в цій точці

.

Аналогічна теорема справедлива для будь-яких неперервних мішаних похідних, які відрізняються між собою лише порядком диференціювання.

2 Диференційованість функції

похідна диференціал функція змінна

Нехай функція визначена в деякому околі точки. Виберемо прирости і так, щоб точка належала розглядуваному околу і знайдемо повний приріст функції в точці:

.

Функція називається диференційовною в точці М, якщо її повний приріст в цій точці можна подати у вигляді

, (1)

де та – дійсні числа, які не залежать від та , – нескінченно малі при і функції.

Відомо, що коли функція однієї змінної диференційовна в деякій точці, то вона в цій точці неперервна і має похідну. Перенесемо ці властивості на функції двох змінних.

Теорема 1 (неперервність диференційовної функції).

Якщо функція 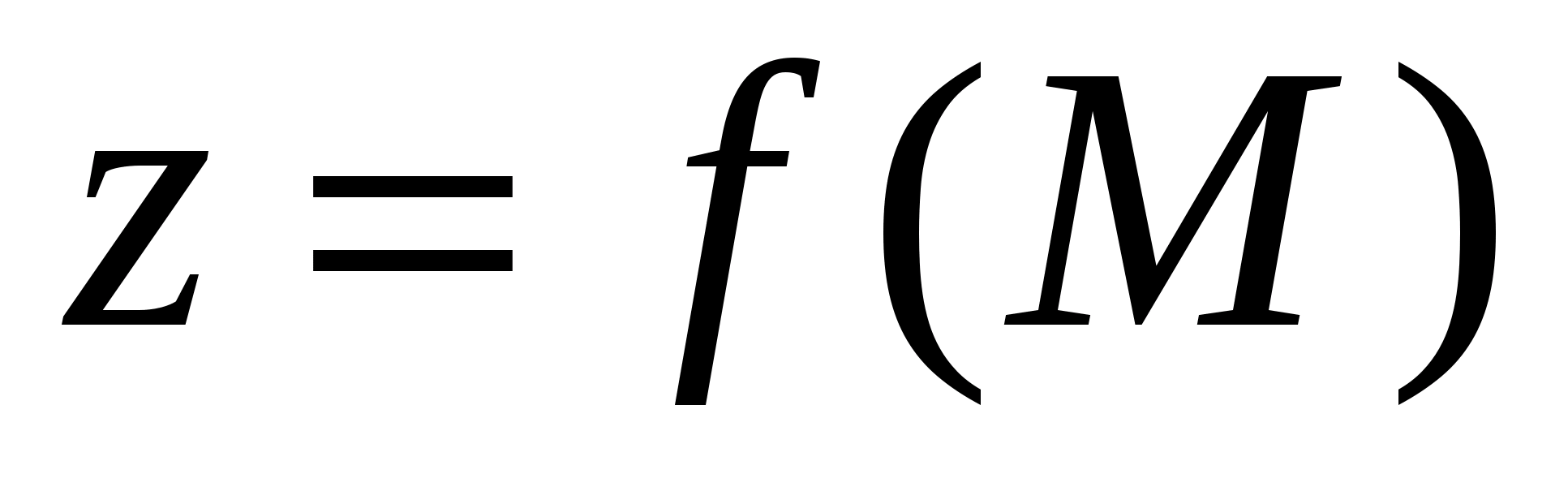диференційовна в точці М, то вона неперервна в цій точці.

Доведення

Якщо функція диференційовна в точці М, то з рівності (1) випливає, що. Це означає, що функція неперервна в точці М.

Теорема 2 (існування частинних похідних диференційовної функції). Якщо функція 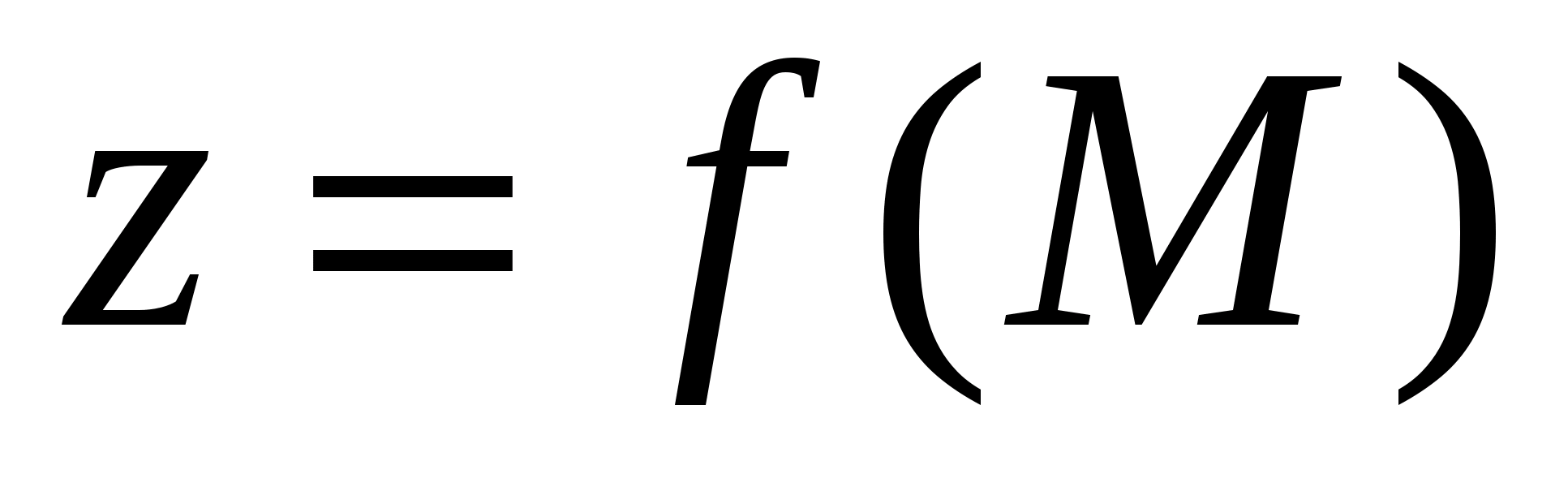диференційовна в точці , то вона має в цій точці похідні та і.

Доведення

Оскільки диференційовна в точці, то справджується рівність (1). Поклавши в ній, отримаємо,

.

Поділимо обидві частини цієї рівності на і перейдемо до границі при:

.

Отже, в точці існує частинна похідна. Аналогічно доводиться, що в точці існує частинна похідна.

Твердження, обернені до теорем 1 і 2, взагалі кажучи, неправильні, тобто із неперервності функції або існування її частинних похідних ще не випливає диференційовність. Наприклад, функція неперервна в точці, але не диференційовна в цій точці. Справді, границі

не існує, тому не існує й похідної. Аналогічно впевнюємося, що не існує також похідної. Оскільки задана функція в точці не має частинних похідних, то вона в цій точці не диференційовна.

Більш того, відомо приклади функцій, які є неперервними в деяких точках і мають в них частинні похідні, але не є в цих точках диференційовними.

Теорема 3 (достатні умови диференційовності ).

Якщо функція має частинні похідні в деякому околі точки і ці похідні неперервні в точці М, то функція диференційовна в точці М.

Доведення

Надамо змінним x і приростів , таких, щоб точка належала даному околу точки . Повний приріст функції запишемо у вигляді

. (2)

Вираз у перших квадратних дужках рівності (2) можна розглядати як приріст функції однієї змінної x, а в других – як приріст функції змінної . Оскільки дана функція має частинні похідні, то за теоремою Лагранжа отримаємо:

.

Похідні та неперервні в точці М, тому

,

.

Звідси випливає, що

,

,

де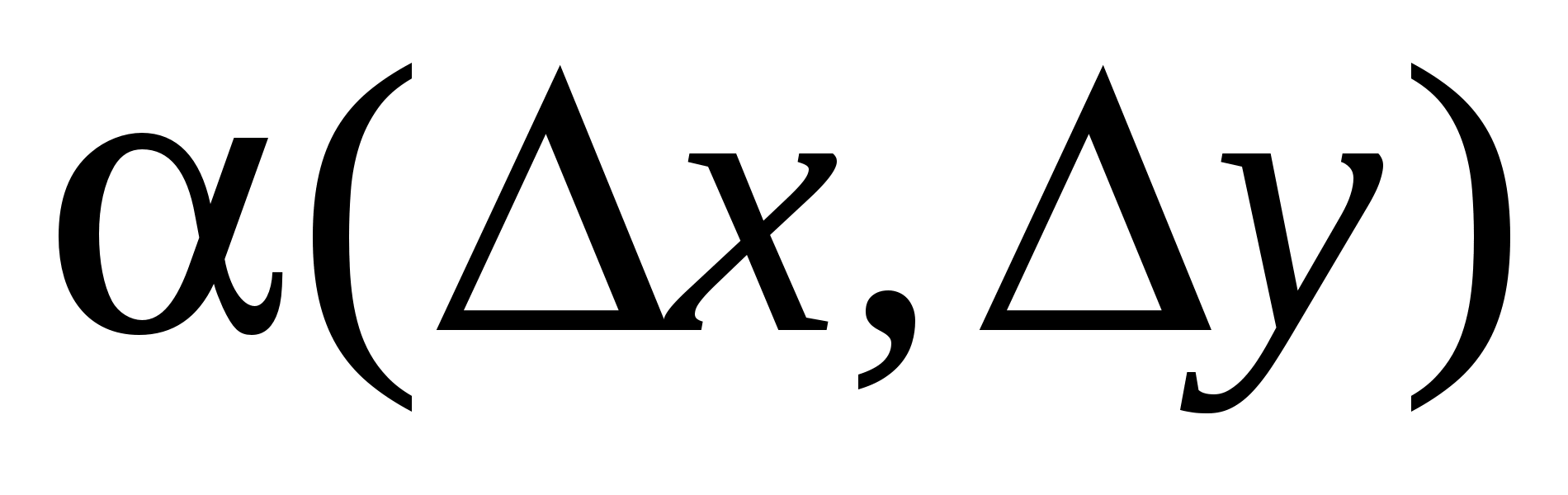, – нескінченно малі функції при і.

Підставляючи ці вирази у рівність (2), знаходимо

, а це й означає, що функція диференційовна в точці.

З теорем 2 і 3 випливає такий наслідок: щоб функція була диференційовною в точці, необхідно, щоб вона мала в цій точці частинні похідні, і достатньо, щоб вона мала в цій точці неперервні частинні похідні.

Зазначимо, що для функції однієї змінної існування похідної в точці є необхідною і достатньою умовою її диференційовності в цій точці.

3 Повний диференціал функції та його застосування до обчислення функцій і похибок. Диференціали вищих порядків

Нагадаємо, що коли функція 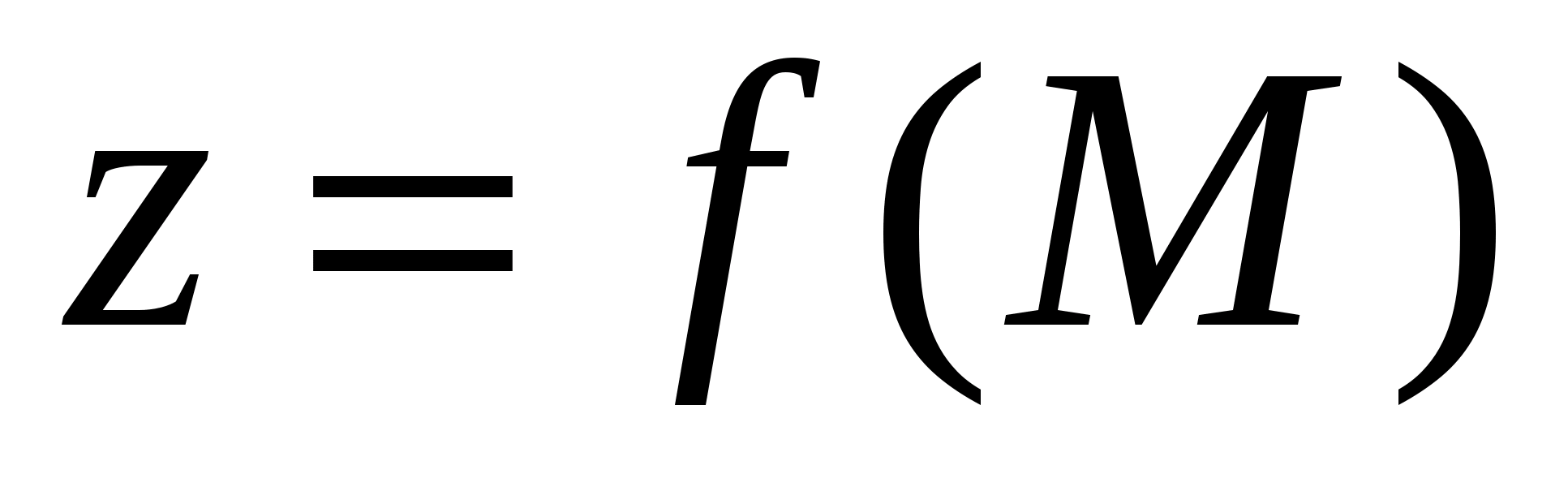диференційовна в точці, то її повний приріст у цій точці можна подати у вигляді

,

де і при.

Повним диференціалом диференційовної в точці функції 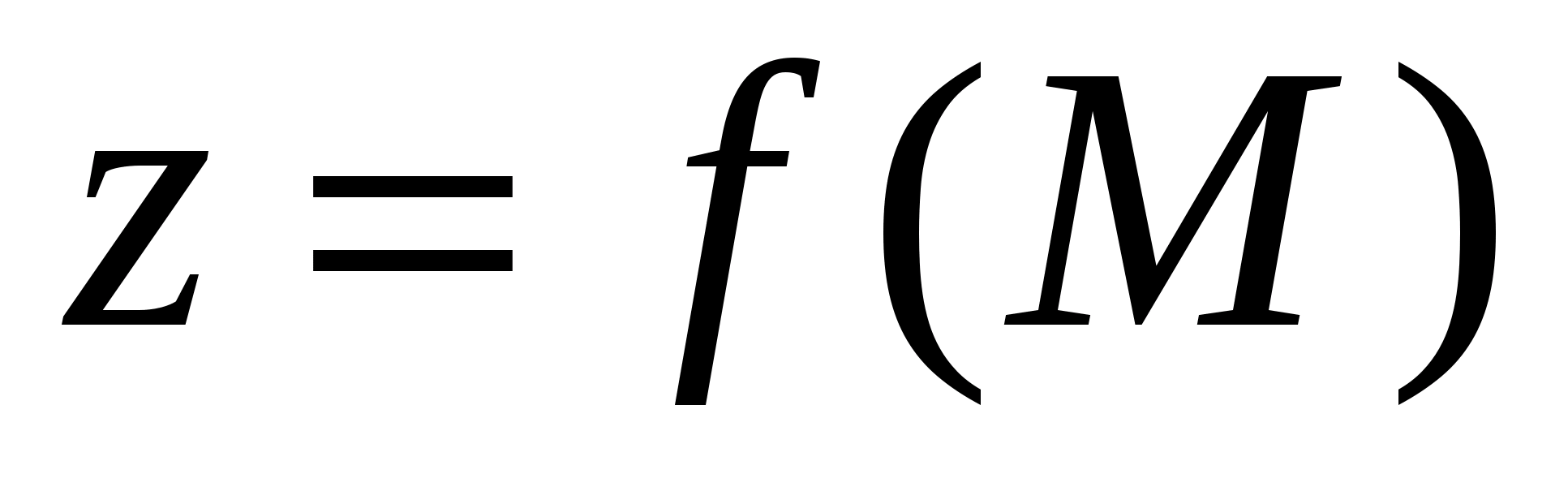називається лінійна відносно та частина повного приросту цієї функції в точці M, тобто

. (3)

Диференціалами незалежних змінних x та назвемо прирости цих змінних. Тоді з урахуванням теореми 2 рівність (3) можна записати так:

. (4)

Аналогічна формула має місце для диференційовної функції трьох змінних:

. (5)

З формул (4) і (5) може здатися, що повний диференціал існуватиме у кожній точці, в якій існують частинні похідні. Але це не так. Згідно з означенням, повний диференціал можна розглядати лише стосовно диференційовної функції.

Теореми та формули для диференціалів функції однієї змінної повністю зберігаються і для диференціалів функцій двох, трьох і т.д. змінних . Так, незалежно від того, від яких аргументів залежать функції u і , завжди справедливі рівності

Покажемо, що різниця між повним приростом і диференціалом при і є нескінченно мала величина вищого порядку, ніж величина.

Дійсно, з формул (1) і (3) маємо

,

оскільки функції – нескінченно малі при, , а та – обмежені функції:

.

Отже, різниця – нескінченно мала величина вищого порядку, ніж. Тому повний диференціал називають також головною частиною повного приросту диференційовної функції. При цьому виконується наближена рівність або

. (6)

Ця рівність тим точніша, чим менша величина. Рівність (6) широко використовується у наближених обчисленнях, оскільки диференціал функції обчислюється простіше, ніж повний приріст.

Покажемо, як за допомогою диференціала можна оцінити похибку в обчисленнях.

Нехай задана диференційовна функція, незалежні змінні якої виміряні з точністю. Потрібно знайти похибку, з якою обчислюється u.

Природно вважати, що ця похибка дорівнює величині

.

Для малих значень маємо

,

звідки

.

Якщо через позначити максимальну абсолютну похибку змінної , то можна отримати значення максимальної абсолютної похибки функції :

. (7)

Щоб оцінити максимальну відносну похибку функції u, поділимо обидві частини рівності (7) на:

.

Оскільки, то

,

або

,

тобто максимальна відносна похибка функції дорівнює максимальній абсолютній похибці її логарифма.

Введемо поняття диференціала вищого порядку.

Нехай функція незалежних змінних ,. Повний диференціал цієї функції, знайдений за формулою (3), називають ще диференціалом
першого порядку. Диференціал другого порядку визначають за формулою

.

Тоді, якщо функція має неперервні частинні похідні, то

,

звідки

. (8)

Символічно це записують так:

.

Аналогічно можна отримати формулу для диференціала третього порядку:

.

Застосовуючи метод математичної індукції, можна отримати формулу для диференціала n-го порядку:

. (9)

Зазначимо, що формула (9) справедлива лише для випадку, коли змінні x і функції є незалежними змінними.

4 Похідна складеної функції. Повна похідна. Інваріантність форми повного диференціала

Нехай – функція двох змінних та , кожна з яких, у свою чергу, є функцією незалежної змінної :

тоді функція є складеною функцією змінної .

Теорема. Якщо функції диференційовні в точці , а функція диференційовна в точці , то складена функція також диференційовна в точці . Похідну цієї функції знаходять за формулою

. (10)

Доведення

За умовою теореми ,

де та при,.

Поділимо на і перейдемо до границі при:

Аналогічно знаходять похідну, якщо число проміжних змінних більше двох. Наприклад, якщо , де , то

. (11)

Зокрема, якщо, а, то

,

а оскільки , то

. (12)

Цю формулу називають формулою для обчислення повної похідної
(на відміну від частинної похідної).

Розглянемо загальніший випадок. Нехай – функція двох змінних та, які, в свою чергу, залежать від змінних :, , тоді функція є складеною функцією незалежних змінних та, а змінні та – проміжні.

Аналогічно попередній теоремі доводиться таке твердження.

Якщо функції та диференційовні в точці , а функція диференційовна в точці , то складена функція диференційовна в точці і її частинні похідні знаходяться за формулами:

; . (13)

Формули (13) можна узагальнити на випадок більшого числа змінних. Якщо, де, то

Знайдемо диференціал складеної функції. Скориставшись формулами (13), отримаємо

Отже, диференціал функції, де , , визначається формулою

, (14)

де

.

Порівнявши формули (14) і (4) дійдемо висновку, що повний диференціал функції має інваріантну (незмінну) форму незалежно від того, чи є x та незалежними змінними, чи диференційовними функціями змінних u та v. Проте формули (4) і (14) однакові лише за формою, а по суті різні, бо у формулі (4) і– диференціали незалежних змінних, а у формулі (14) і– повні диференціали функцій та .

Диференціали вищих порядків властивості інваріантності не мають. Наприклад, якщо, де , , то

(15)

Формула (15) відрізняється від формули (8), оскільки для складеної функції диференціали та можуть і не дорівнювати нулю. Отже, для складеної функції, де , , формула (8) неправильна.

5 Диференціювання неявної функції

Нехай задано рівняння

, (16)

де – функція двох змінних.

Нагадаємо, що коли кожному значенню x з деякої множини відповідає єдине значення, яке разом з x задовольняє рівняння (16), то кажуть, що це рівняння задає на множині неявну функцію.

Таким чином, для неявної функції, заданої рівнянням (16), має місце тотожність

.

Які ж умови має задовольняти функція щоб рівняння (16) визначало неявну функцію і при тому єдину? Відповідь на це запитання дає така теорема існування неявної функції [8].

Теорема. Нехай функція і її похідні та визначені та неперервні у будь-якому околі точки і , а; тоді існує окіл точки , в якому рівняння визначає єдину неявну функцію, неперервну та диференційовну в околі точки і таку, що .

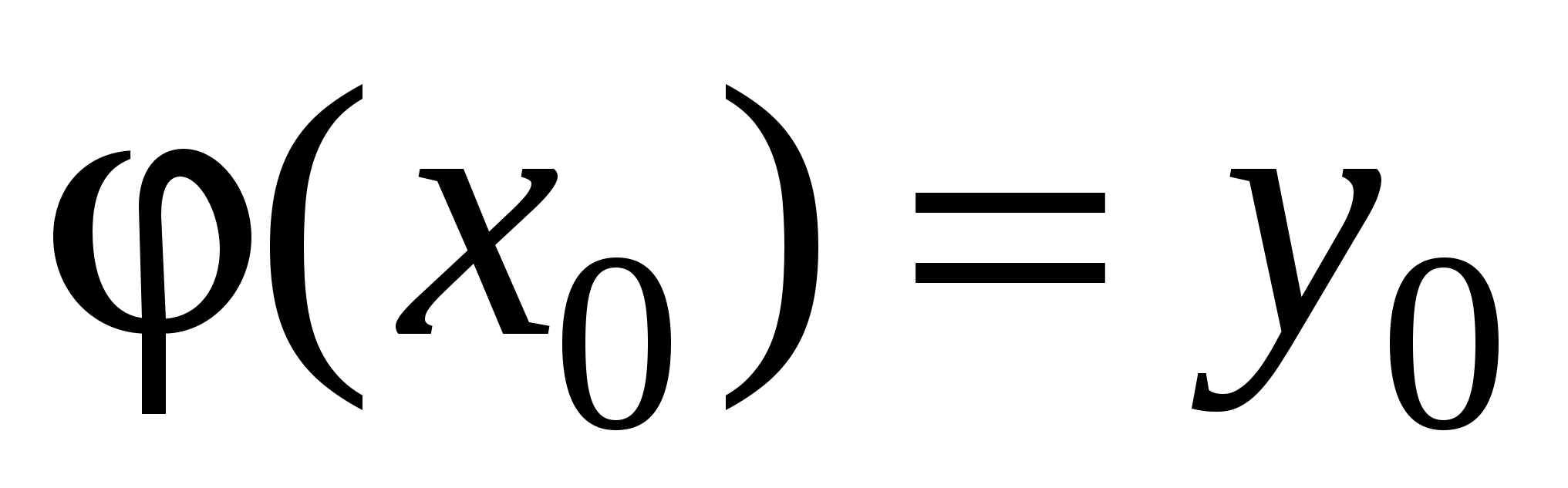Знайдемо похідну неявної функції. Нехай ліва частина рівняння (16) задовольняє зазначені в теоремі умови, тоді це рівняння задає неявну функцію, для якої на деякій множині точок x має місце тотожність. Оскільки похідна функції, що тотожно дорівнює нулю, також дорівнює нулю, то повна похідна. Але за формулою (12) маємо , тому , звідки

. (17)

За цією формулою знаходять похідну неявної функції однієї змінної.