Методи розв’язування одновимірних та багатовимірних нелінійних оптимізаційних задач та задач лінійного цілочислового програмування
Міністерство освіти і науки України
Полтавський національний технічний університет імені Юрія Кондратюка
Факультет інформаційно-телекомунікаційних технологій та систем
Кафедра прикладної математики, інформатики і математичного моделювання
КУРСОВА РОБОТА
з дисципліни «Методи оптимізації і дослідження операцій»
на тему: «Методи розв’язування одновимірних та багатовимірних нелінійних оптимізаційних задач та задач лінійного цілочислового програмування»
301-ЕІ. 20 06165 КР
Керівник роботи
кандидат фіз.-мат. Наук Радченко Г.О.
Розробила
студентка гр. 301-ЕІ Клюєва А.Ю.
Полтава 2009
Зміст
1. Методи розв’язування одновимірних оптимізаційних задач
2. Визначення найменшого значення функції на заданому відрізку за допомогою методів одновимірної оптимізації
3. Розв’язання задачі мінімізації за допомогою методу Ньютона і методу найшвидшого спуску
4. Розв’язання задачі умовної оптимізації за допомогою методу Франка-Вулфа і методу штрафних функції
5. Розв’язання задачі цілочислового програмування
6. Вихідний код програм
Список використаної літератури
1. Методи розв’язування одновимірних оптимізаційних задач
Розглянемо детально методи розв’язування одновимірних задач, а саме: метод дихотомії, метод золотого перерізу і метод Фібоніччі.
Одновимірна
оптимізація полягає в знаходженні точки
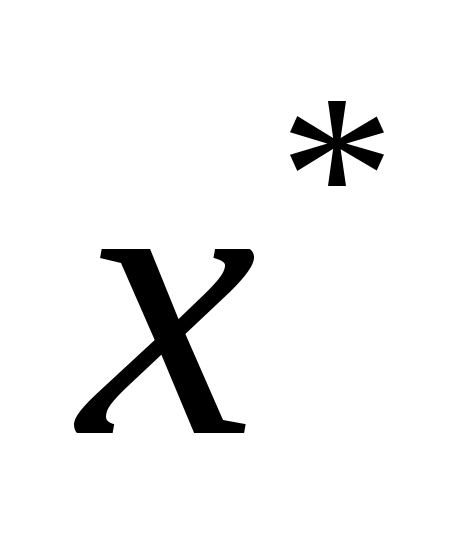 ,
в якій цільова функція
,
в якій цільова функція
 приймає
максимальне або мінімальне значення.
Часто в постановках задач може бути
заданий відрізок
приймає
максимальне або мінімальне значення.
Часто в постановках задач може бути
заданий відрізок
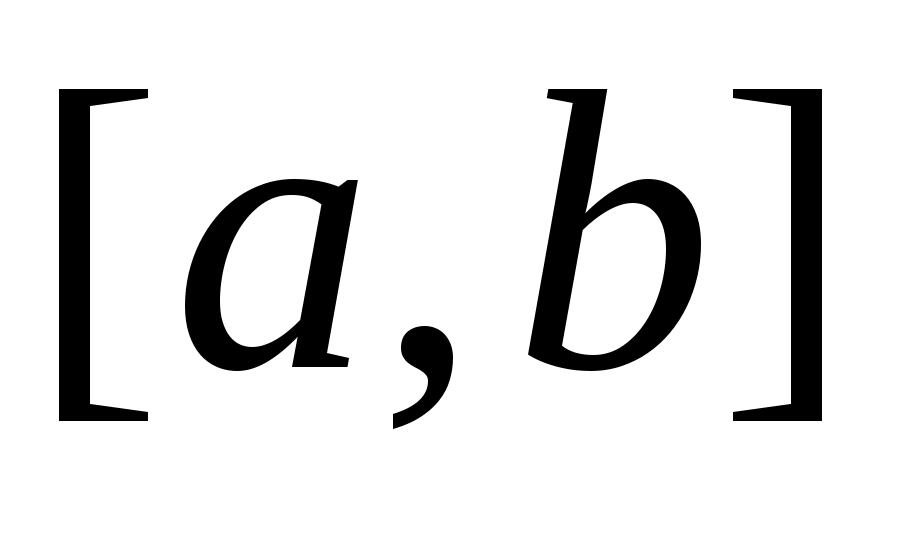 ,
в якому знаходиться оптимальне рішення.
,
в якому знаходиться оптимальне рішення.
Функція
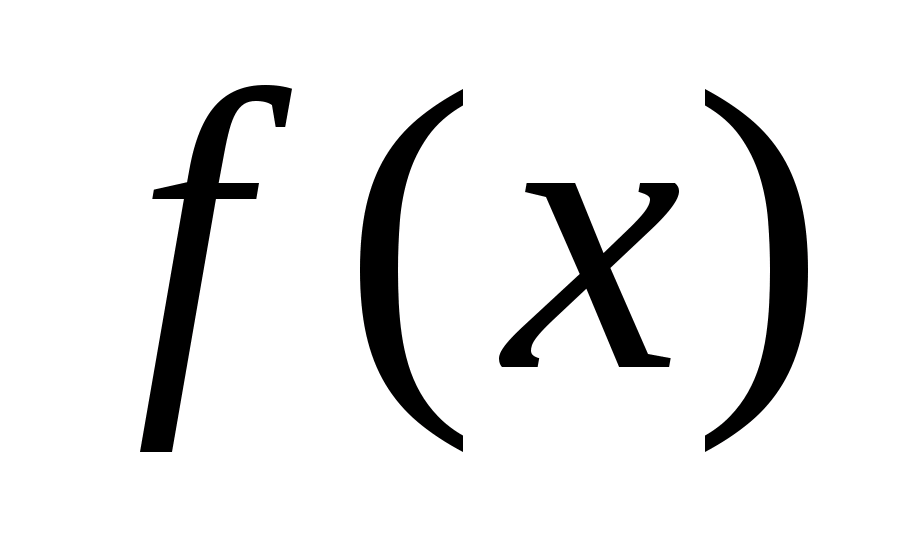 має
локальний мінімум в точці
має
локальний мінімум в точці
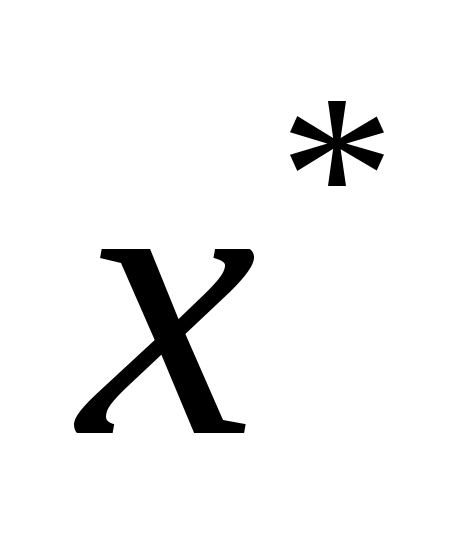 ,
якщо при довільному
,
якщо при довільному
 існує окіл
існує окіл
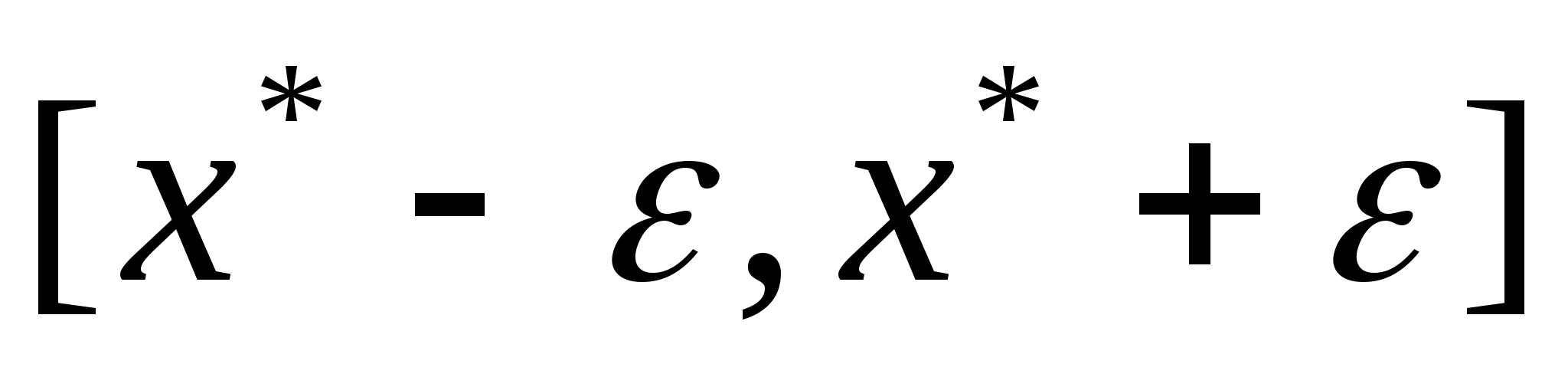 такий, що для всіх значень
такий, що для всіх значень
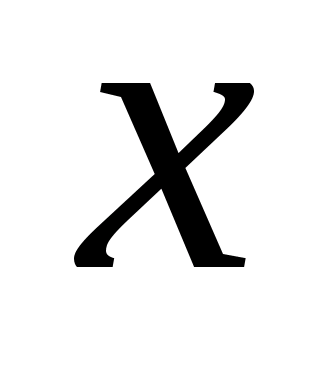 в цьому околі
в цьому околі
 .
Функція
.
Функція
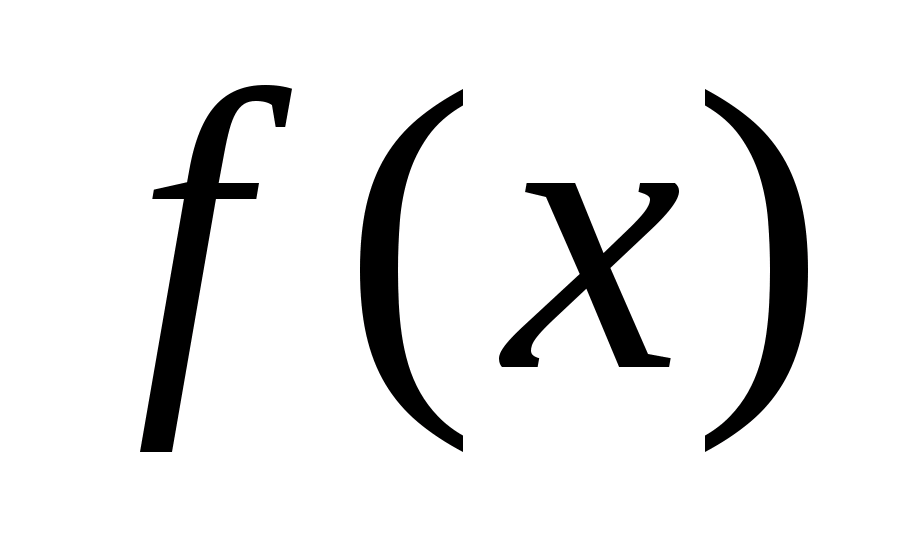 має глобальний мінімум в точці
має глобальний мінімум в точці
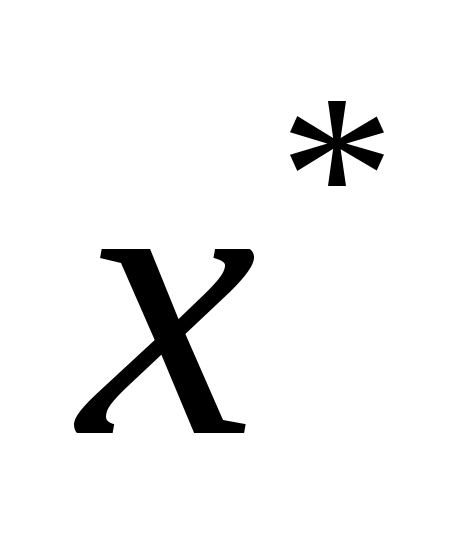 ,
якщо для всіх х
справедлива рівність
,
якщо для всіх х
справедлива рівність
 .
.
Відповідно
функція
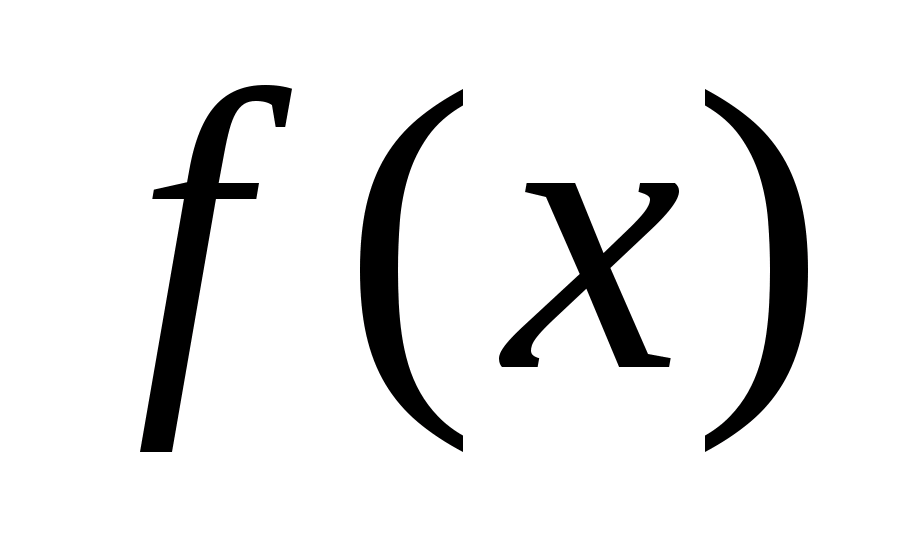 має
локальний максимум в точці
має
локальний максимум в точці
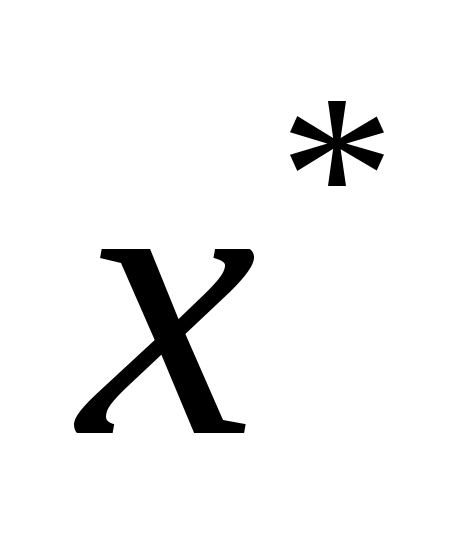 ,
якщо при довільному
,
якщо при довільному
 існує окіл
існує окіл
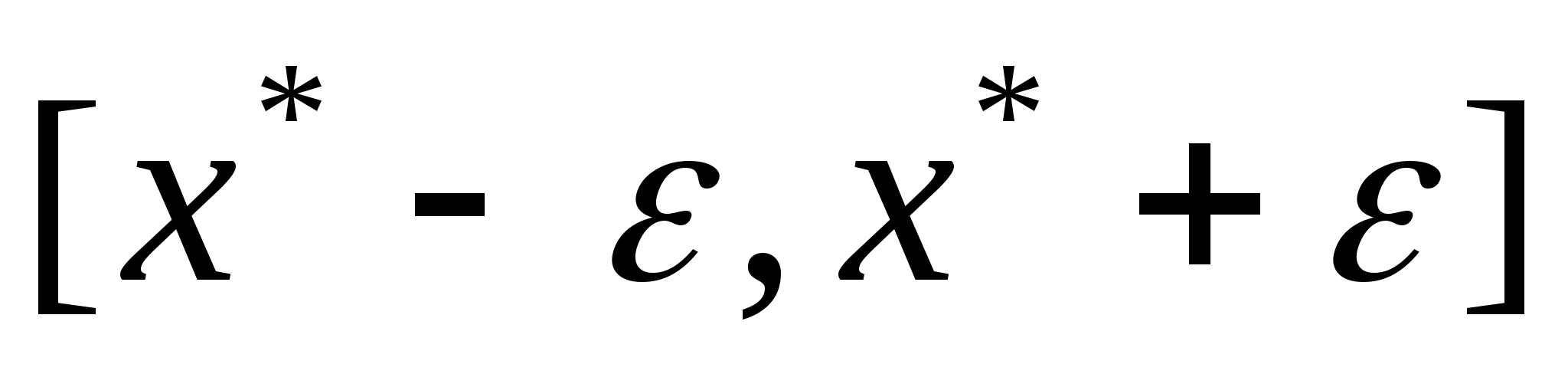 такий, що для всіх значень
такий, що для всіх значень
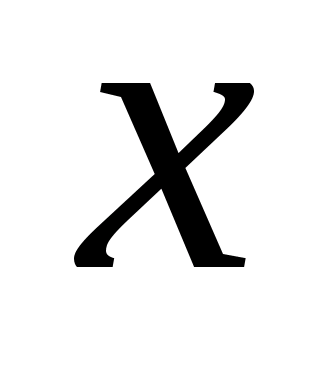 в цьому околі
в цьому околі
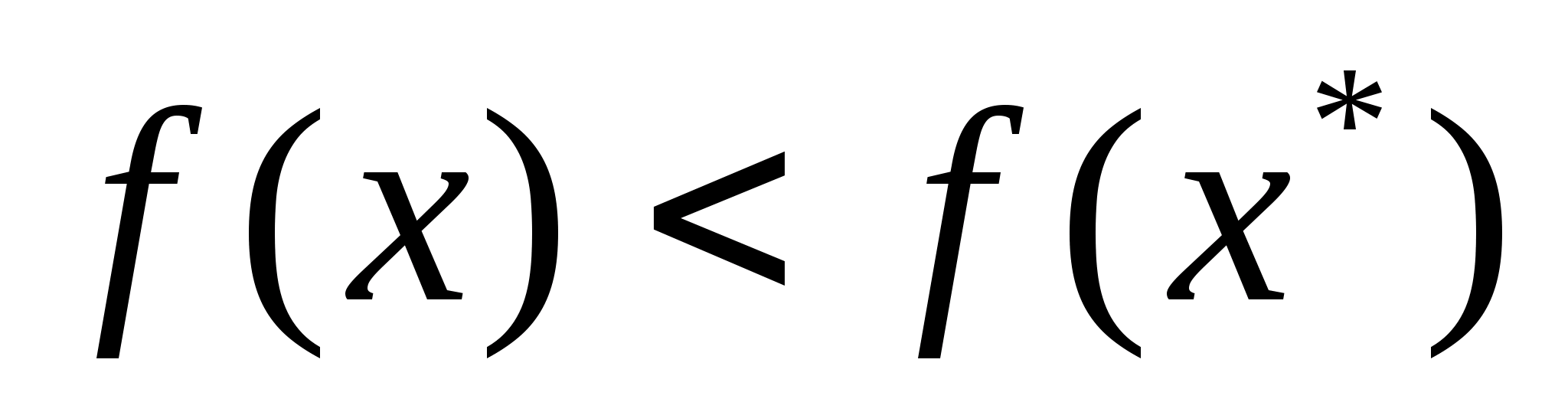 .
Функція
.
Функція
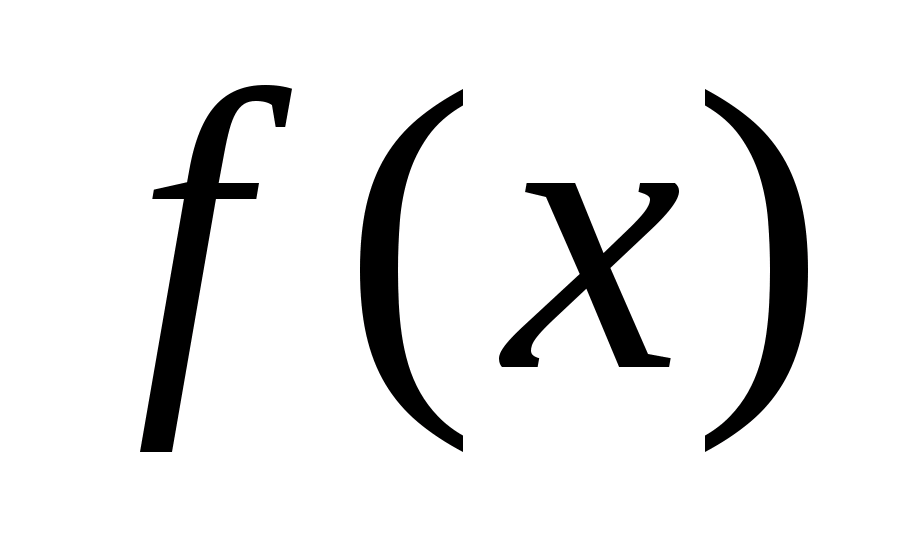 має глобальний мінімум в точці
має глобальний мінімум в точці
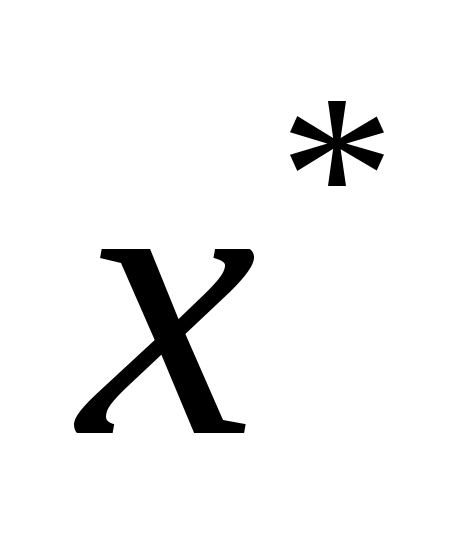 ,
якщо для всіх х
справедлива рівність
,
якщо для всіх х
справедлива рівність
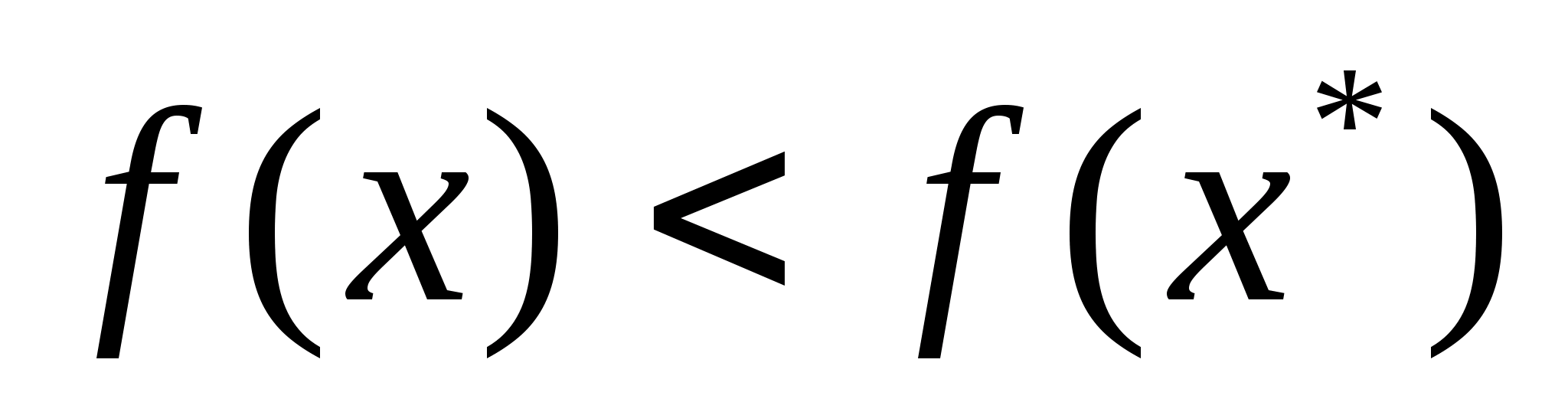 .
.
Класичний
підхід до задачі знаходження екстремумів
функції полягає в пошуку умов, яким вони
повинні задовольняти. Необхідною
умовою
екстремуму в точці
 являється рівність нулю першої похідної
(теорема Ферма), тобто вимагається
розв’язати рівняння:
являється рівність нулю першої похідної
(теорема Ферма), тобто вимагається
розв’язати рівняння:
 .
Даному рівнянню задовольняють як
локальні та глобальні екстремуми, так
і точки перегину функції, тому приведена
умова є лише необхідною умовою, але не
достатньою.
.
Даному рівнянню задовольняють як
локальні та глобальні екстремуми, так
і точки перегину функції, тому приведена
умова є лише необхідною умовою, але не
достатньою.
З
метою отримання достатніх
умов
вимагається обчислення значень других
похідних в точках, що задовольняють
рівняння
 .
При цьому доведено, що мінімуму функції
відповідає додатне значення другої
похідної, тобто
.
При цьому доведено, що мінімуму функції
відповідає додатне значення другої
похідної, тобто
 ,
а максимуму – від’ємне, тобто
,
а максимуму – від’ємне, тобто
 .
Однак, якщо друга похідна дорівнює 0,
ситуація залишається невизначеною і
необхідно досліджувати вищі похідні.
При цьому якщо перша вища похідна не
рівна нулю має парний порядок, то
екстремум існує, в іншому випадку – ні.
.
Однак, якщо друга похідна дорівнює 0,
ситуація залишається невизначеною і
необхідно досліджувати вищі похідні.
При цьому якщо перша вища похідна не
рівна нулю має парний порядок, то
екстремум існує, в іншому випадку – ні.
Дамо визначення унімодальної функції при пошуку мінімуму.
Неперервна
функція
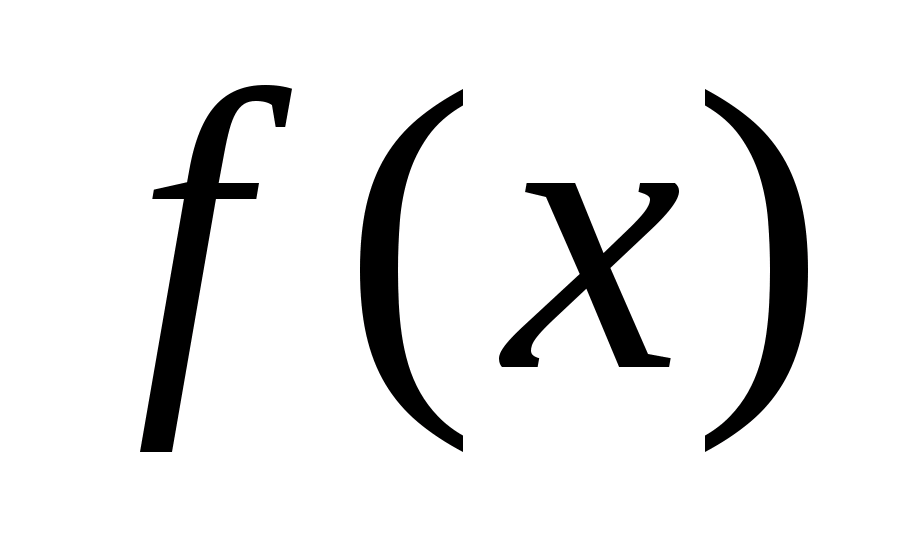 називається унімодальною на відрізку
називається унімодальною на відрізку
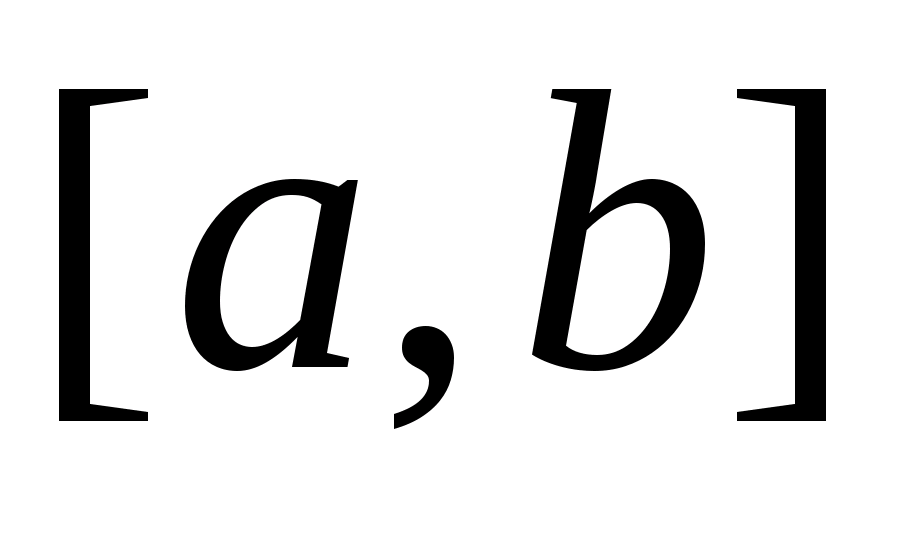 якщо:
якщо:
точка
 локального мінімуму функції належить
відрізку
локального мінімуму функції належить
відрізку
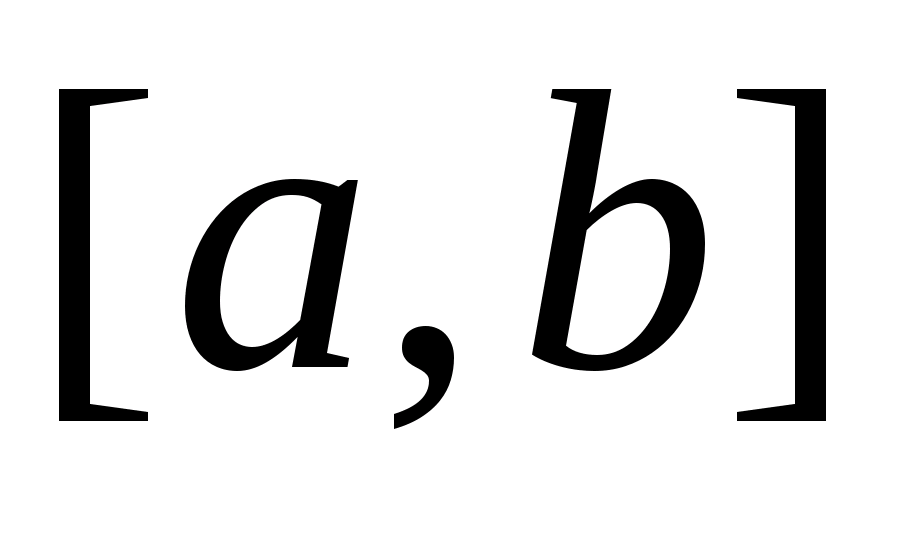 ;
;
для
довільних двох точок відрізка х1
і х2,
взятих по одну сторону від точки
мінімуму, точці х1
більш близькій до точки мінімуму
відповідає менше значення функції,
тобто при
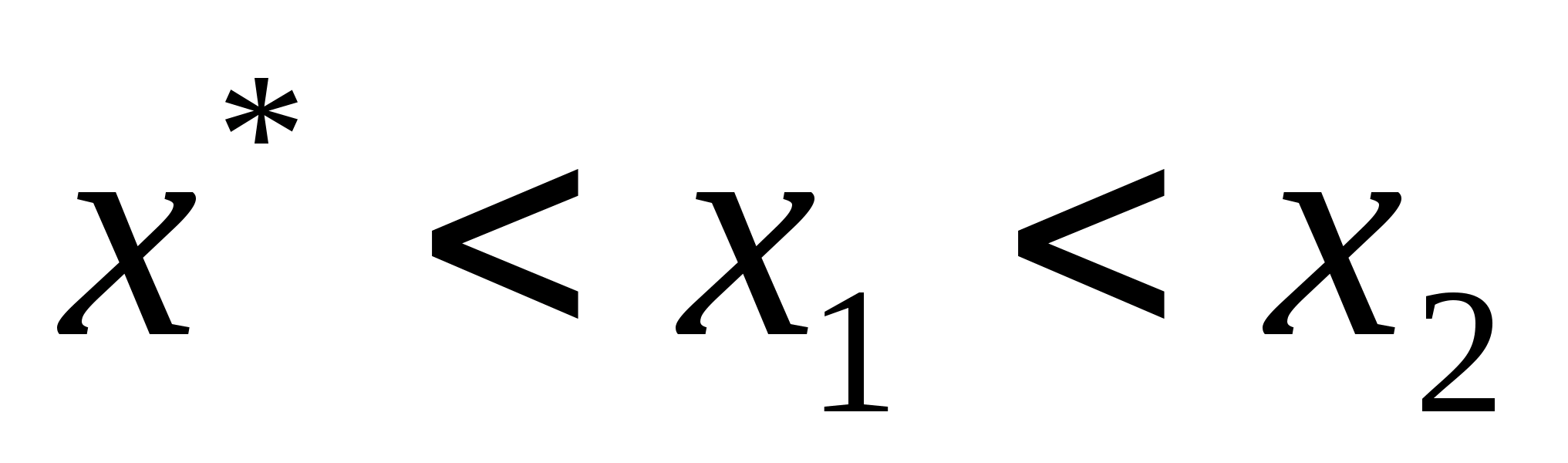 або при
або при
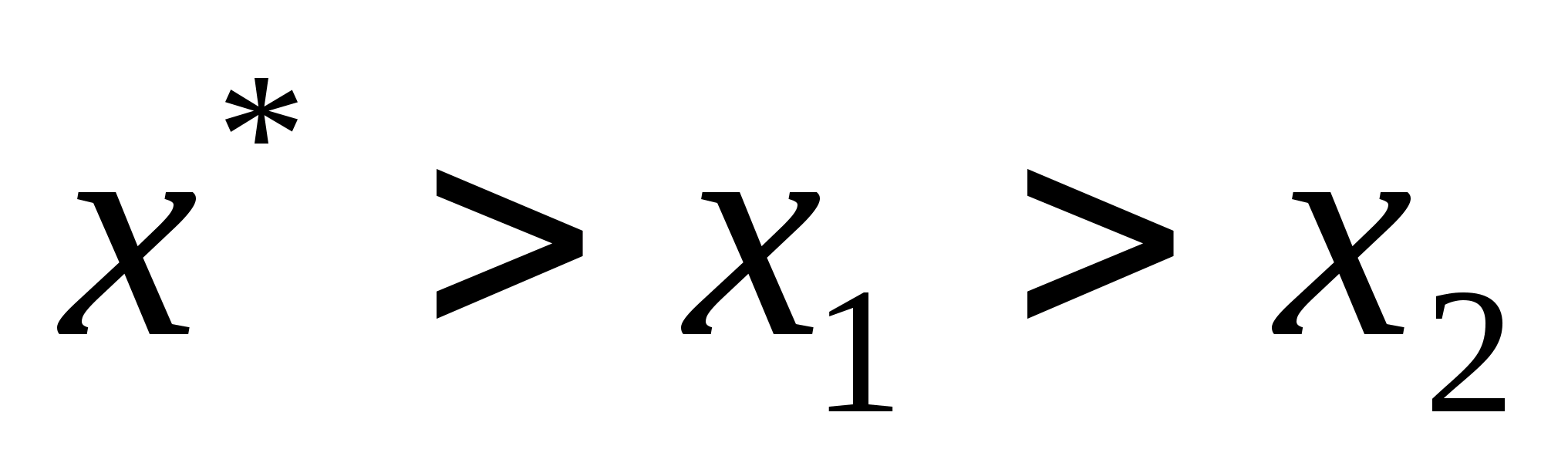 справедлива нерівність
справедлива нерівність
 .
.
Достатня
умова унімодальності функції
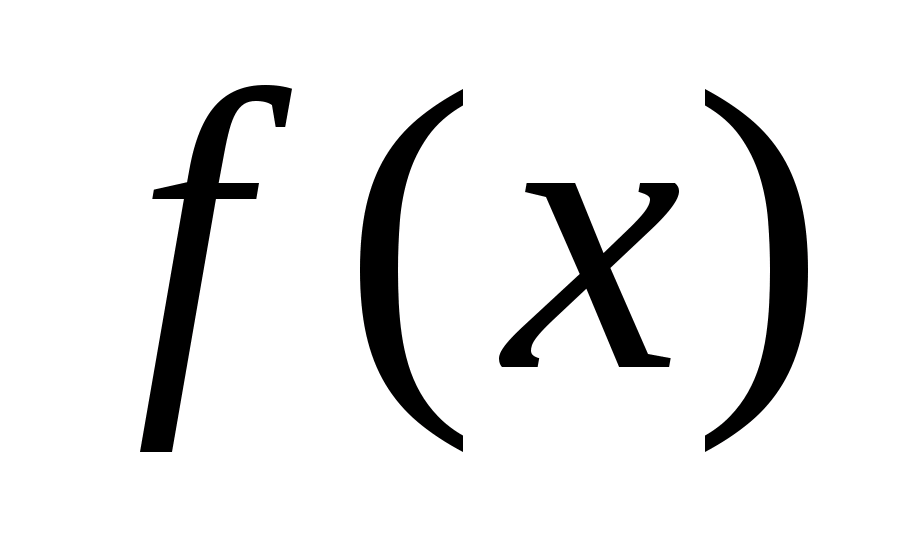 на відрізку
на відрізку
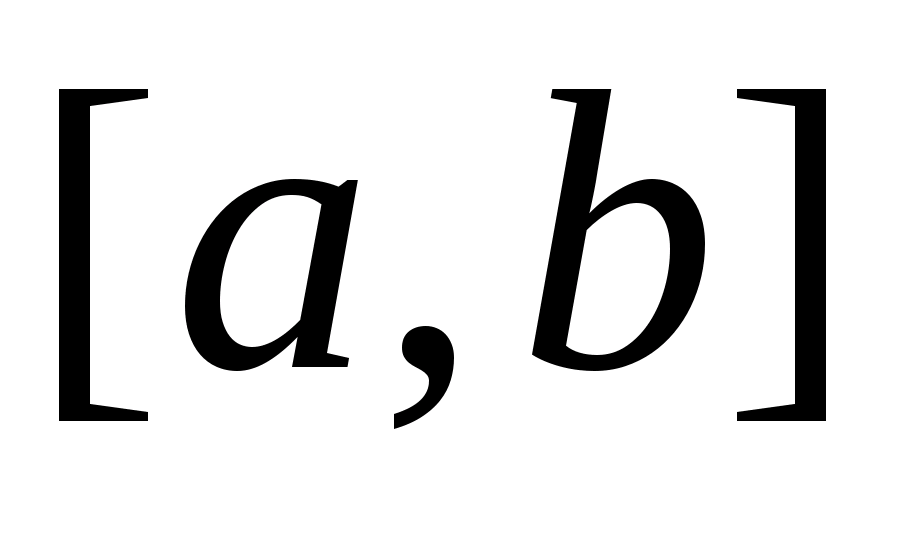 ґрунтується на наступній теоремі:
ґрунтується на наступній теоремі:
Якщо
функція
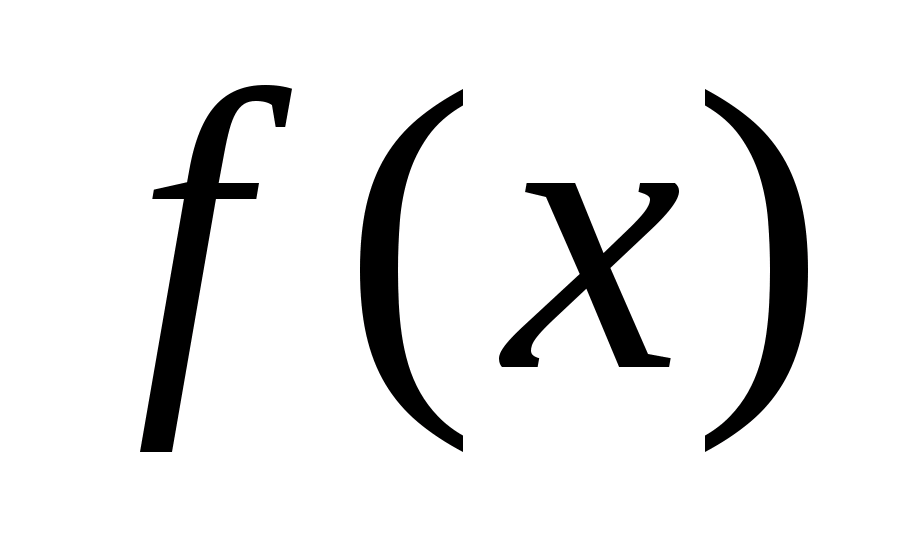 двічі диференційована на відрізку
двічі диференційована на відрізку
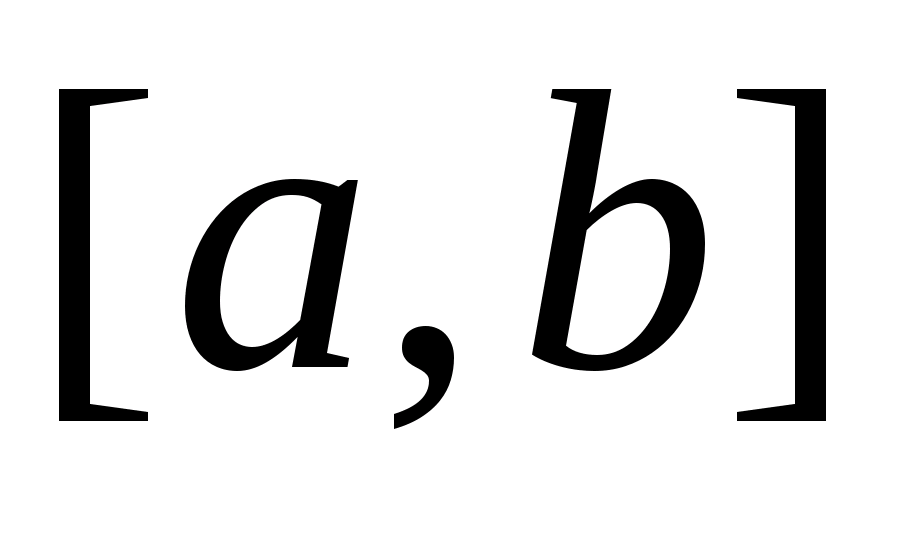 і
і
 в будь-якій точці цього відрізка, то
в будь-якій точці цього відрізка, то
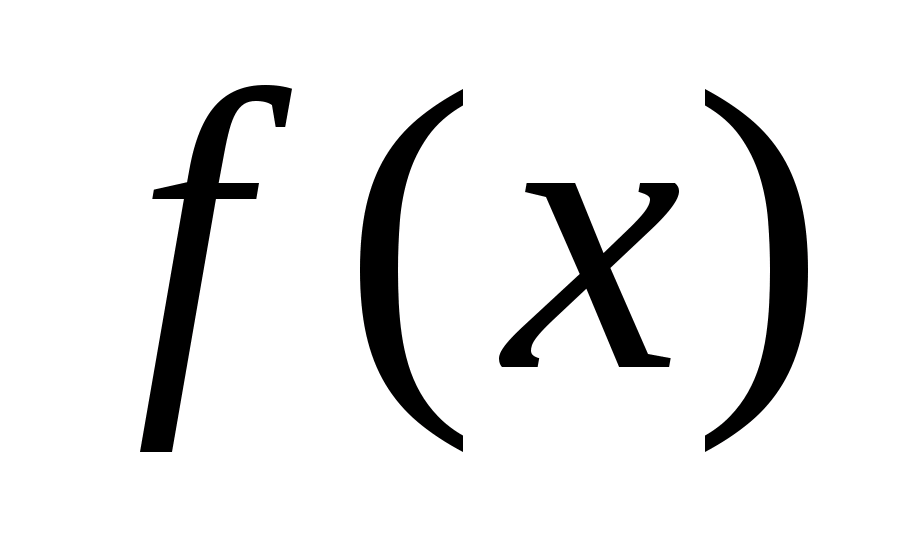 -
унімодальна функція на відрізку
-
унімодальна функція на відрізку
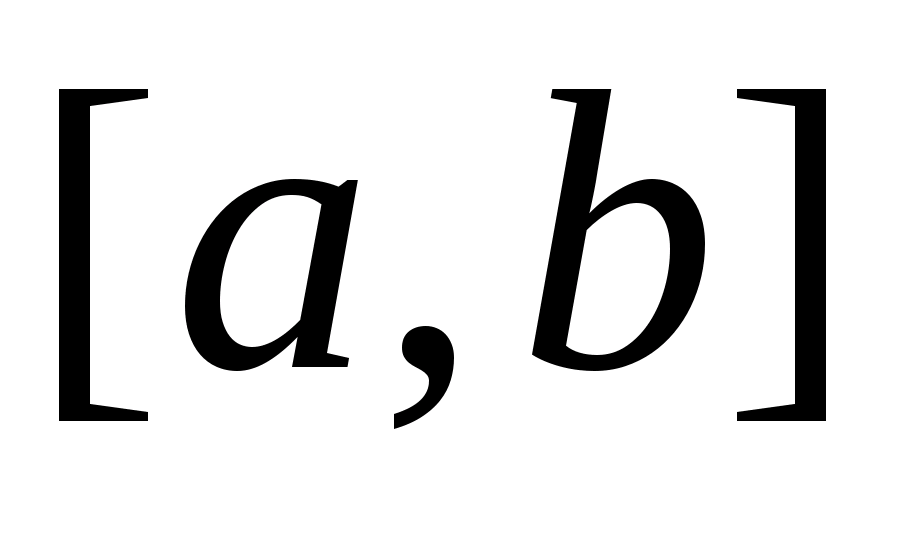 .
.
Відмітимо,
що умова
 визначає множину точок, на якій функція
являється опуклою вниз. Умова ж
визначає множину точок, на якій функція
являється опуклою вниз. Умова ж
 визначає опуклу вгору функцію, яка на
відрізку
визначає опуклу вгору функцію, яка на
відрізку
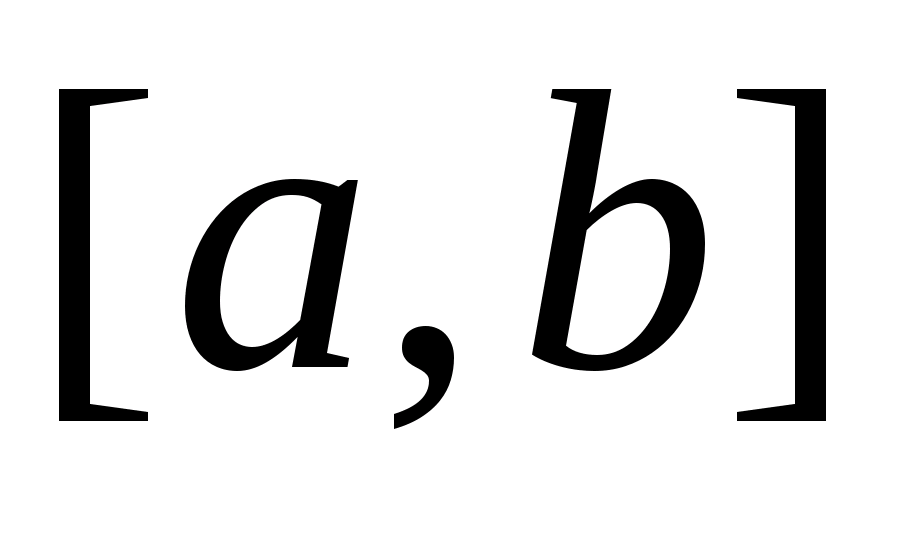 має максимум і також являється
унімодальною.
має максимум і також являється
унімодальною.
Метод
половинного ділення,
який також називається методом
дихотомії,
являється процедурою послідовного
пошуку мінімуму фунуції. Нехай визначено
відрізок
 ,
якому належить точка локального мінімуму
х,
і функція
,
якому належить точка локального мінімуму
х,
і функція
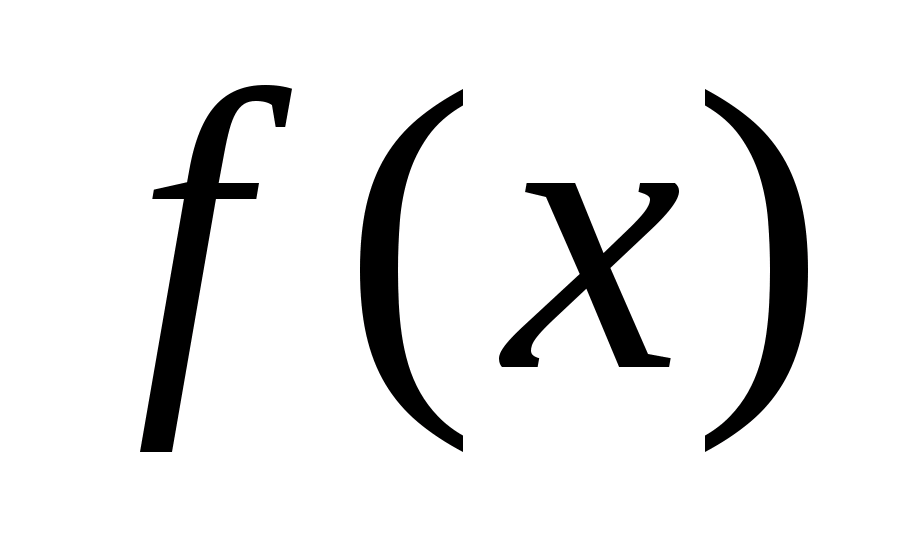 являється унімодальною на цьому відрізку.
Далі для звуження проміжку унімодальності
використовуються дві точки
являється унімодальною на цьому відрізку.
Далі для звуження проміжку унімодальності
використовуються дві точки
 і
і
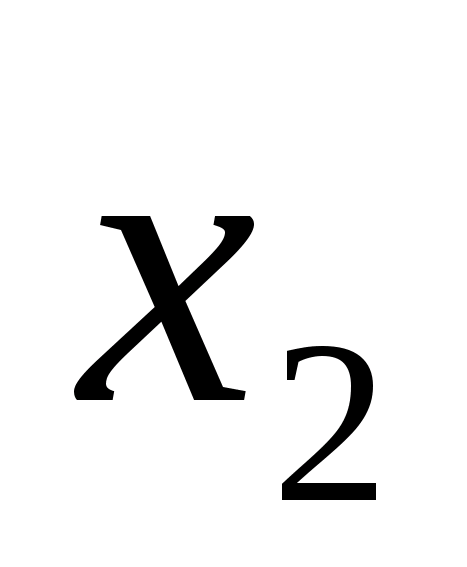 ,
розташовані симетрично на відстані
,
розташовані симетрично на відстані
 від середини відрізка:
від середини відрізка:
 ;
;
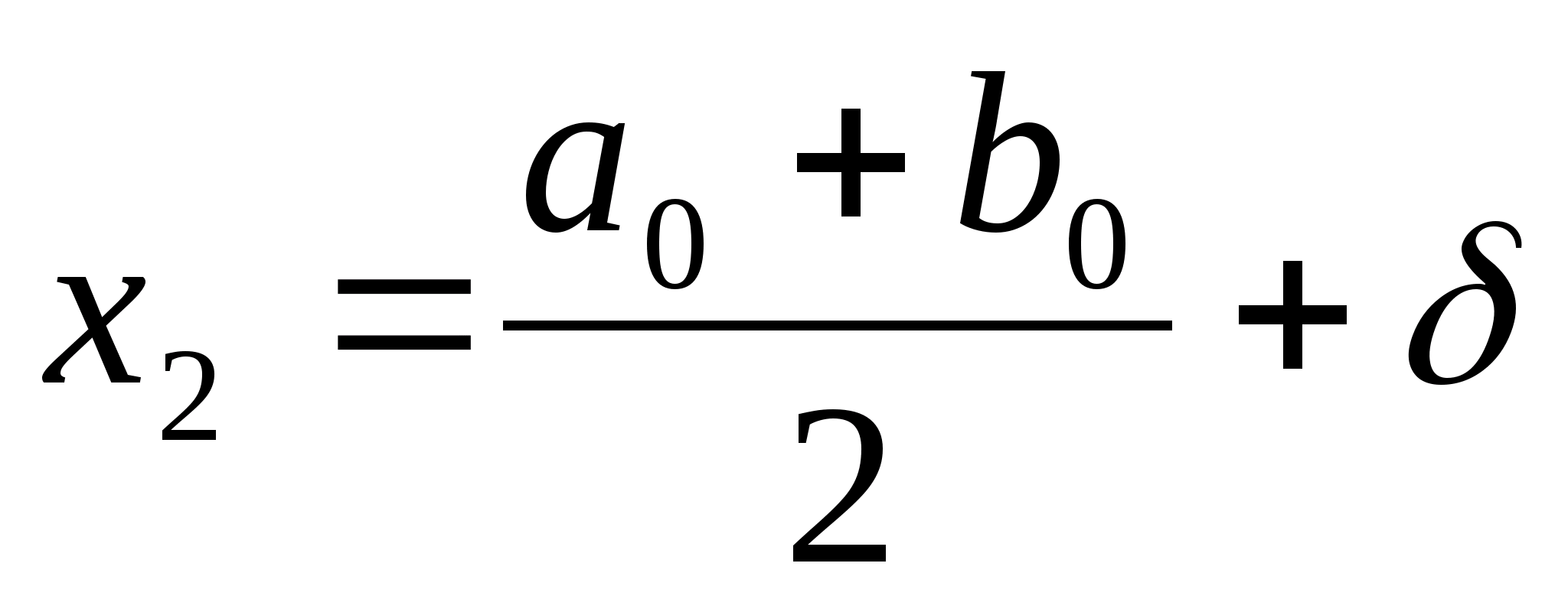 .
.
Константа
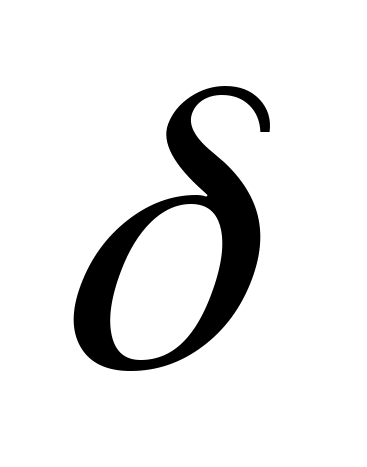 повинна бути меншою допустимої кінцевої
довжини відрізка, Δk=
bk-
ak
>
0.
повинна бути меншою допустимої кінцевої
довжини відрізка, Δk=
bk-
ak
>
0.
Потім обчислюють значення функції в цих точках y1=f(x1) і y2=f(x2) і в залежності від їх співвідношення нові межі відрізка унімодальності [a1, b1] будуть наступні:
• y1 < y2, a1=a0 і b1=x2 ;
• y1 > y2, a1=x1 і b1=b0 ;
• y1 = y2, a1=x1 і b1= x2 .
В цьому
звуженому проміжку
[a1,
b1]
знову
розраховуються дві точки х1(1)
і
х2(1),
симетричні відносно його середини і
значення функції в цих точках. Процедура
буде продовжуватись до тих пір, поки не
буде виконуватись умова Δk
= bk-ak
≤ ε,
де
ε
– точність пошуку, і тоді в якості точки
локального мінімуму можна наближено
прийняти середину відрізку
 .
.
Назва методу половинного ділення мотивована тим, що якщо величина ε достатньо мала, то довжина відрізка унімодальності (b – a) зменшується майже вдвічі.
Наступним методом знаходження екстремуму для задач одновимірної оптимізації є метод золотого перерізу.
Термін
“золотий
переріз”
ввів Леорандо да Вінчі. Точка х1
являється золотим перерізом відрізка
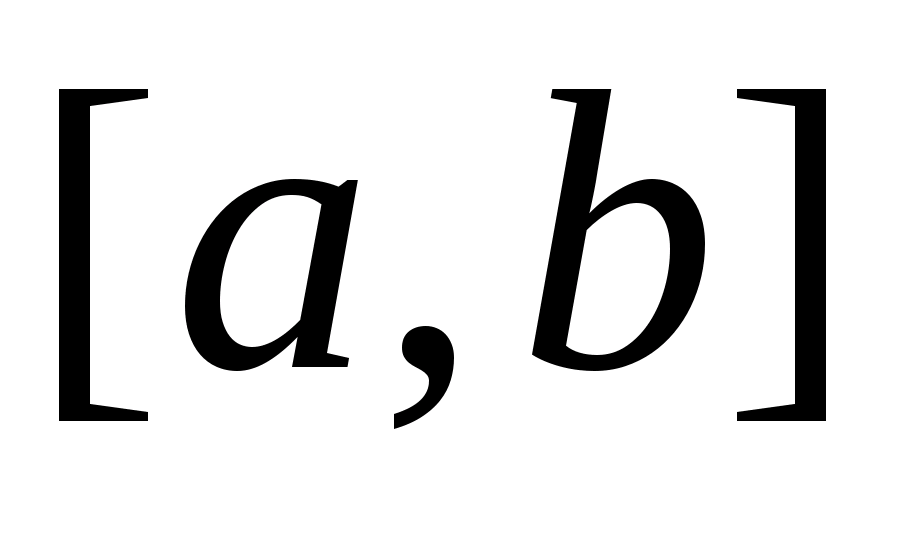 ,
якщо відношення довжини b-a
всього відрізка до довжини b-х1
більшої
частини дорівнює відношенню довжини
більшої до довжини х1-а
меншої
частини, тобто х1
– золотий
переріз, якщо справедлива рівність:
,
якщо відношення довжини b-a
всього відрізка до довжини b-х1
більшої
частини дорівнює відношенню довжини
більшої до довжини х1-а
меншої
частини, тобто х1
– золотий
переріз, якщо справедлива рівність:
 .
Аналогічно, точка х2
симетрична
точці х1
відносно
середини відрізка
.
Аналогічно, точка х2
симетрична
точці х1
відносно
середини відрізка
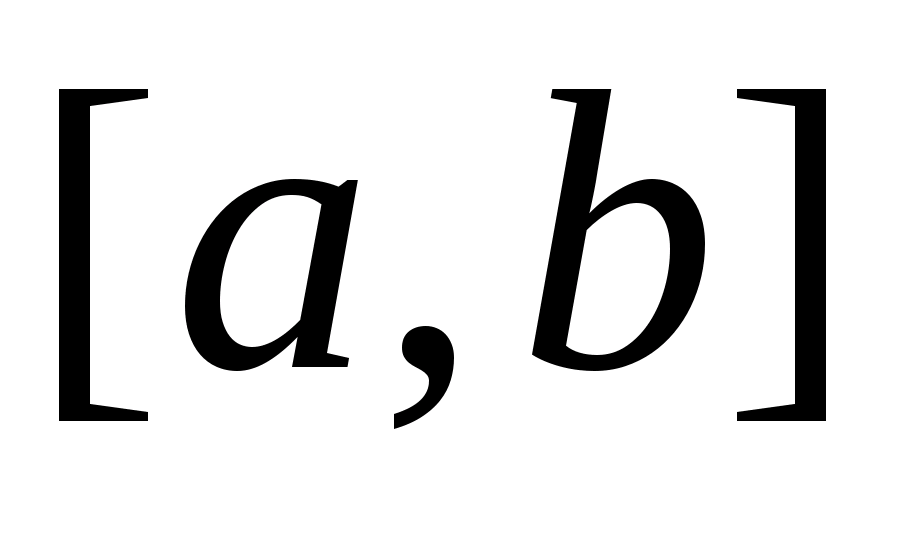 ,
являється другим золотим перерізом
цього відрізка.
,
являється другим золотим перерізом
цього відрізка.
Відмітимо
властивість золотого перерізу: точка
х1
одночасно
являється золотим перерізом відрізка
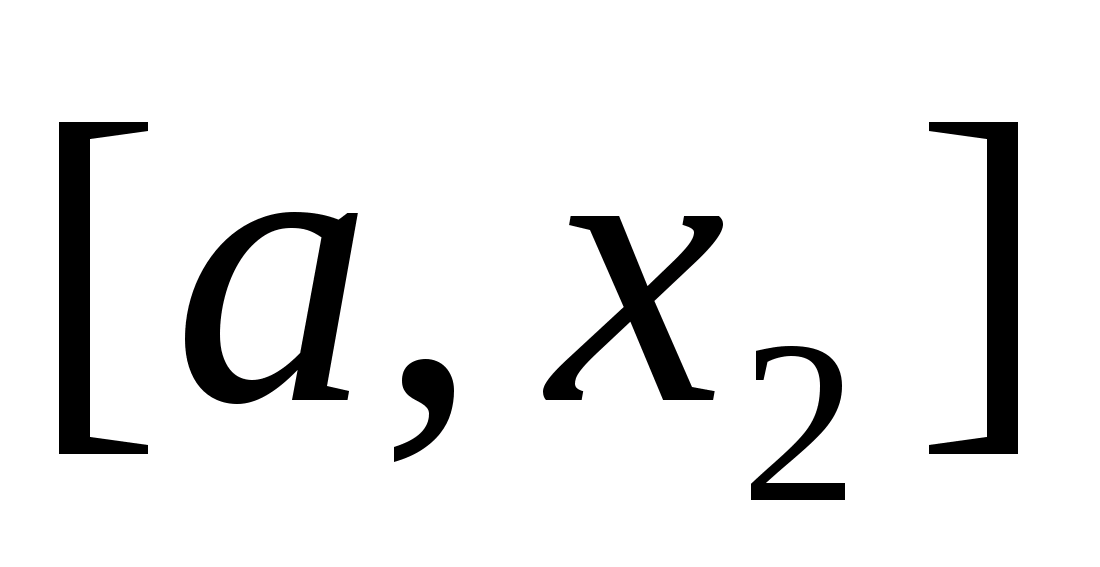 ,
а друга точка х2
–
золотим перерізом відрізка
,
а друга точка х2
–
золотим перерізом відрізка
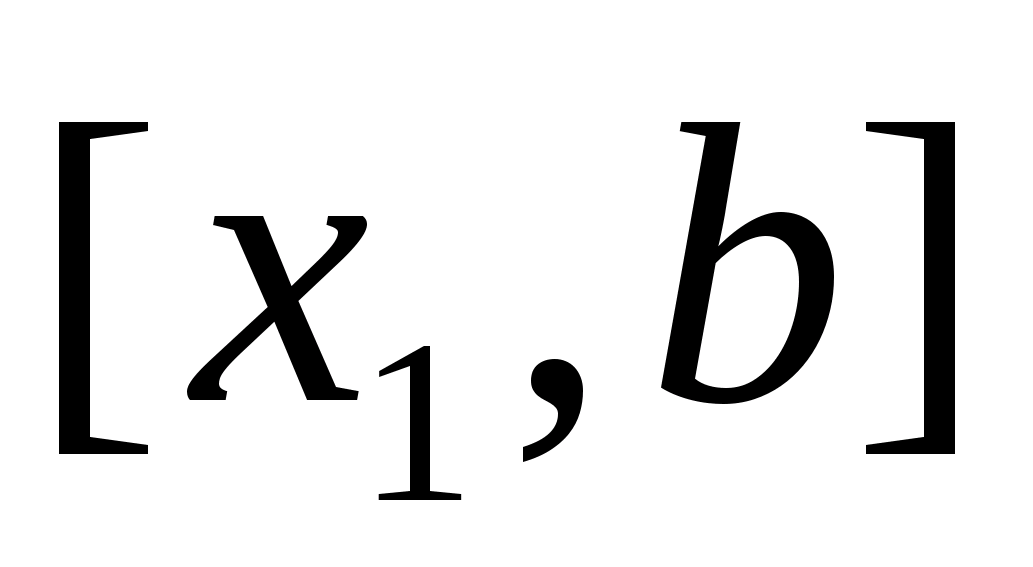 .
.

Суть
методу золотого перерізу заклечається
в наступному. Спочатку на вихідному
відрізку
 знаходяться точки х1
і х2
по наступним формулам:
знаходяться точки х1
і х2
по наступним формулам:
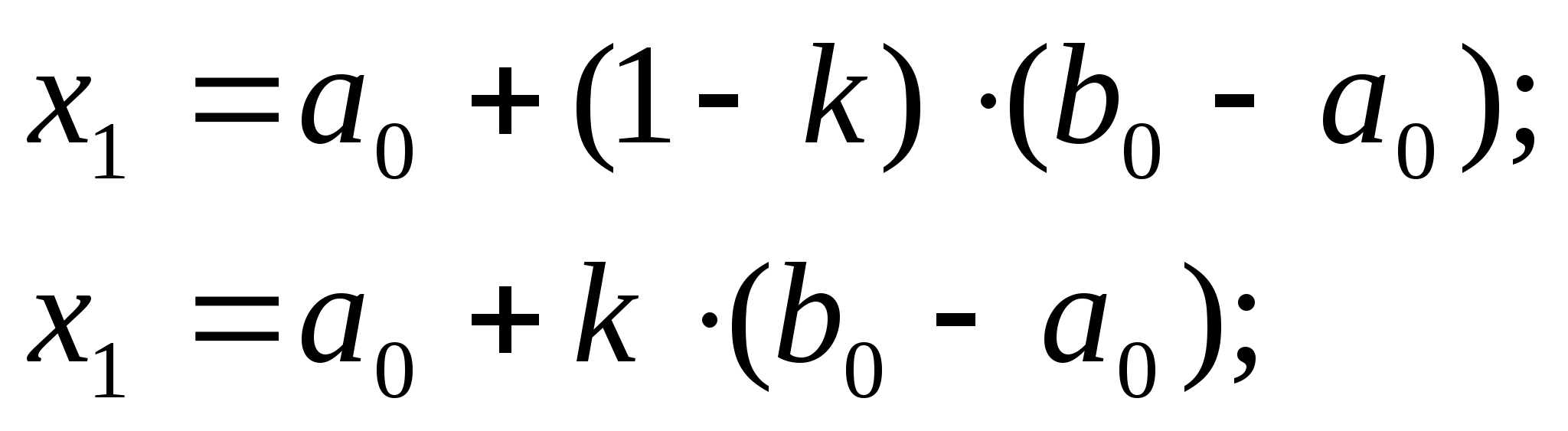
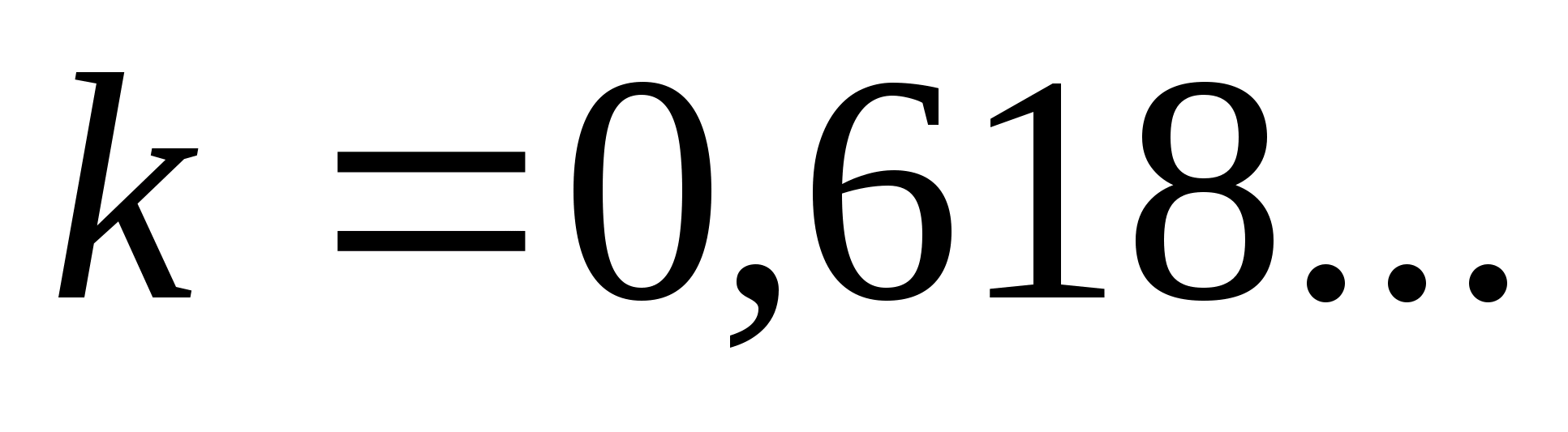 - коефіцієнт
зжимання.
- коефіцієнт
зжимання.
Потім
обчислюють значення функції в точках
х1
і х2,
тобто
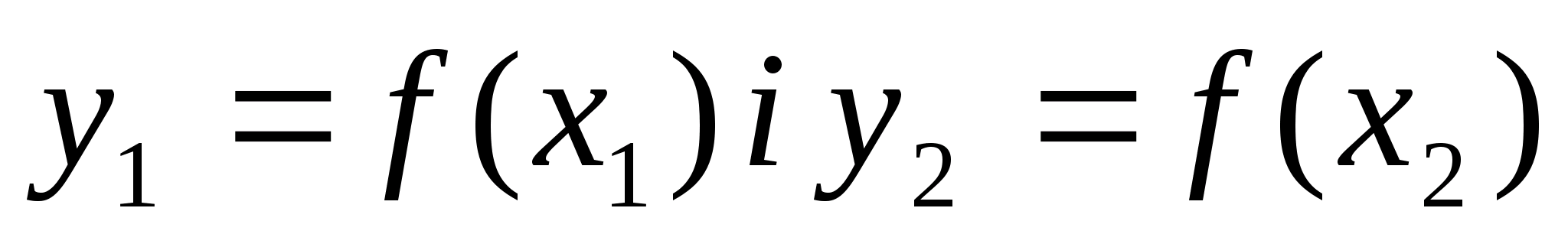 .
При цьому можливі два випадки:
.
При цьому можливі два випадки:
 ,
в цьому випадку новий відрізок буде
рівним
,
в цьому випадку новий відрізок буде
рівним
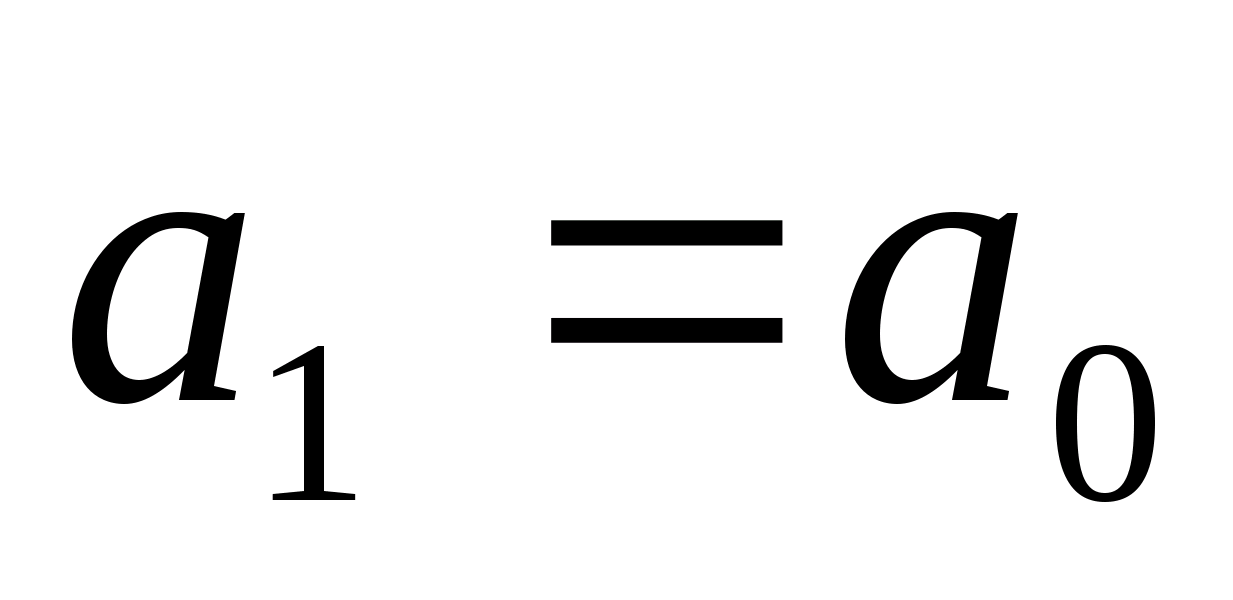 і
і
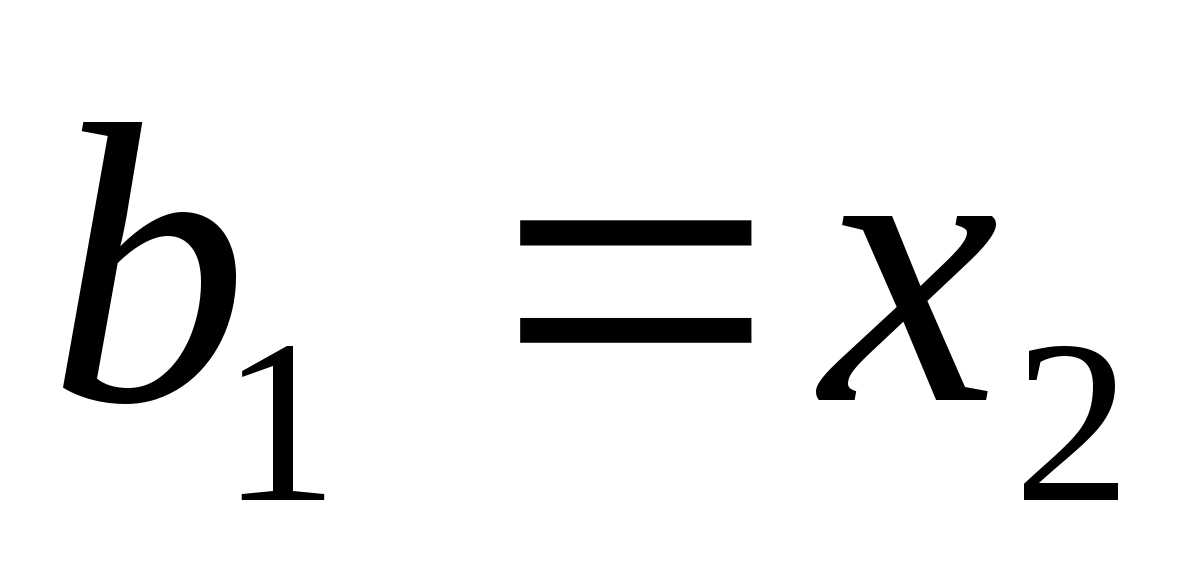 .
На цьому відрізку знову обираються дві
точки
.
На цьому відрізку знову обираються дві
точки
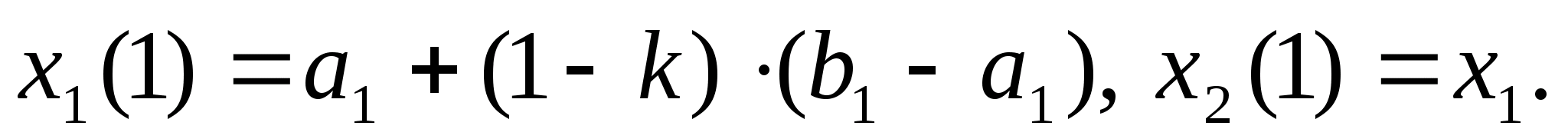
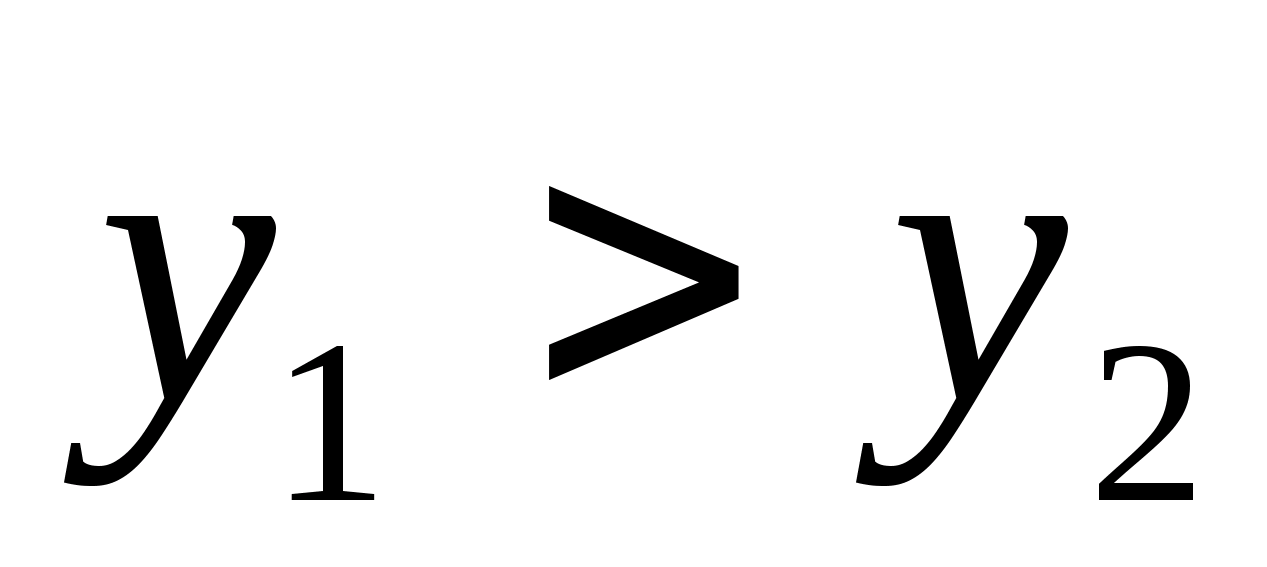 ,
тоді новий відрізок будуть становити:
,
тоді новий відрізок будуть становити:
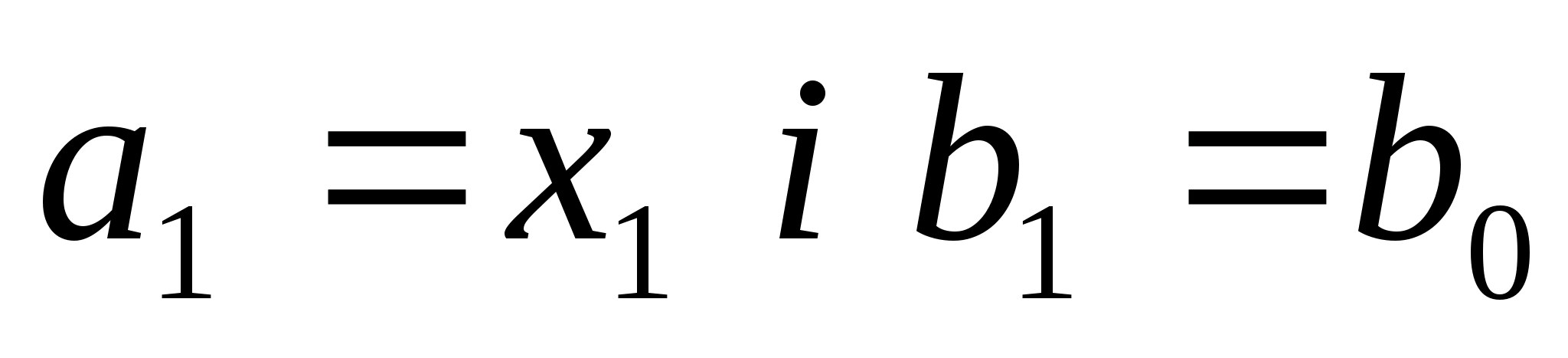 .
На новому відрізку також обираються
дві точки
.
На новому відрізку також обираються
дві точки

І
в першому і в другому випадках
розраховується лише одна нова точка
(друга відома). В новій точці обчислюється
значення функції і знову відбувається
порівняння в двох точках, і в залежності
від цього обирається новий відрізок.
Процедура виконується до тих пір, доки
не буде виконуватись умова
 ,
де
,
де
 - точність пошуку.
- точність пошуку.
Розглянемо також метод Фібоначчі для розв’язування одновимірних задач . Цей метод названий так зважаючи на появу при пошуку проміжків унімрдальності чисел Фібоначчі і використовується, якщо кількість ітерації обмежена . Суть методу в тому, що на кожному кроці точка наступного обчислення обирається симетрично відносно середини відрізка локалізації до точки, що лежить всередині цього відрізку, уже проведеного обчислення. Тобто в процесі пошуку інтервалу (x1; x3) з точкою х2, вже лежачою в цьому інтервалі, наступна точка х4 завжди вибирається так, що х3–х4 = х2–х1 або х4-х1 = х3-x2, тобто x4=х1-х2+х3.
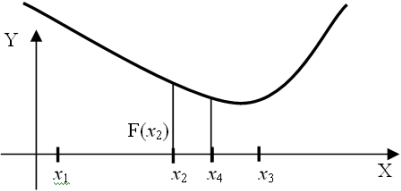
Алгоритм методу Фібоначчі поляга в наступному:
задаються
початкові границі відрізку
 і
і
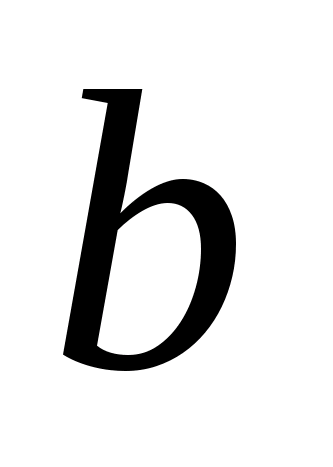 ,
точність обчислень
,
точність обчислень
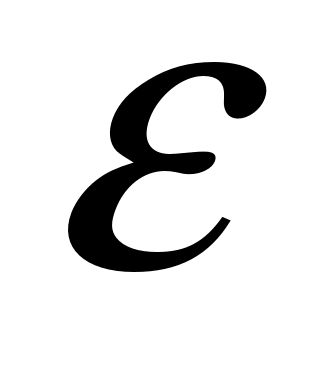 .
.
розраховуються початкові точки ділення:
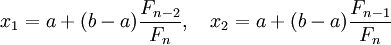
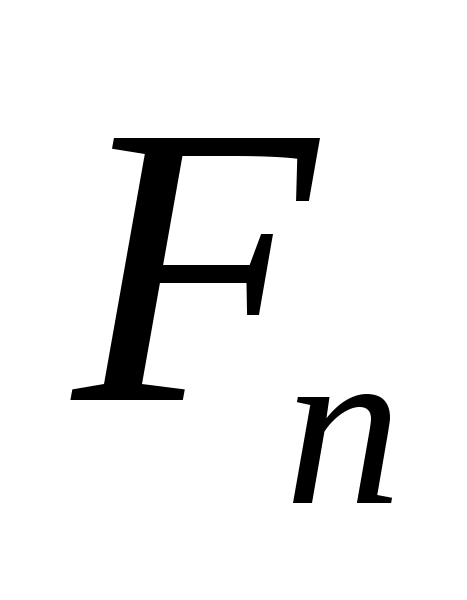 - це число із
послідовності Фібоначчі, яке знаходиться
з умови
- це число із
послідовності Фібоначчі, яке знаходиться
з умови
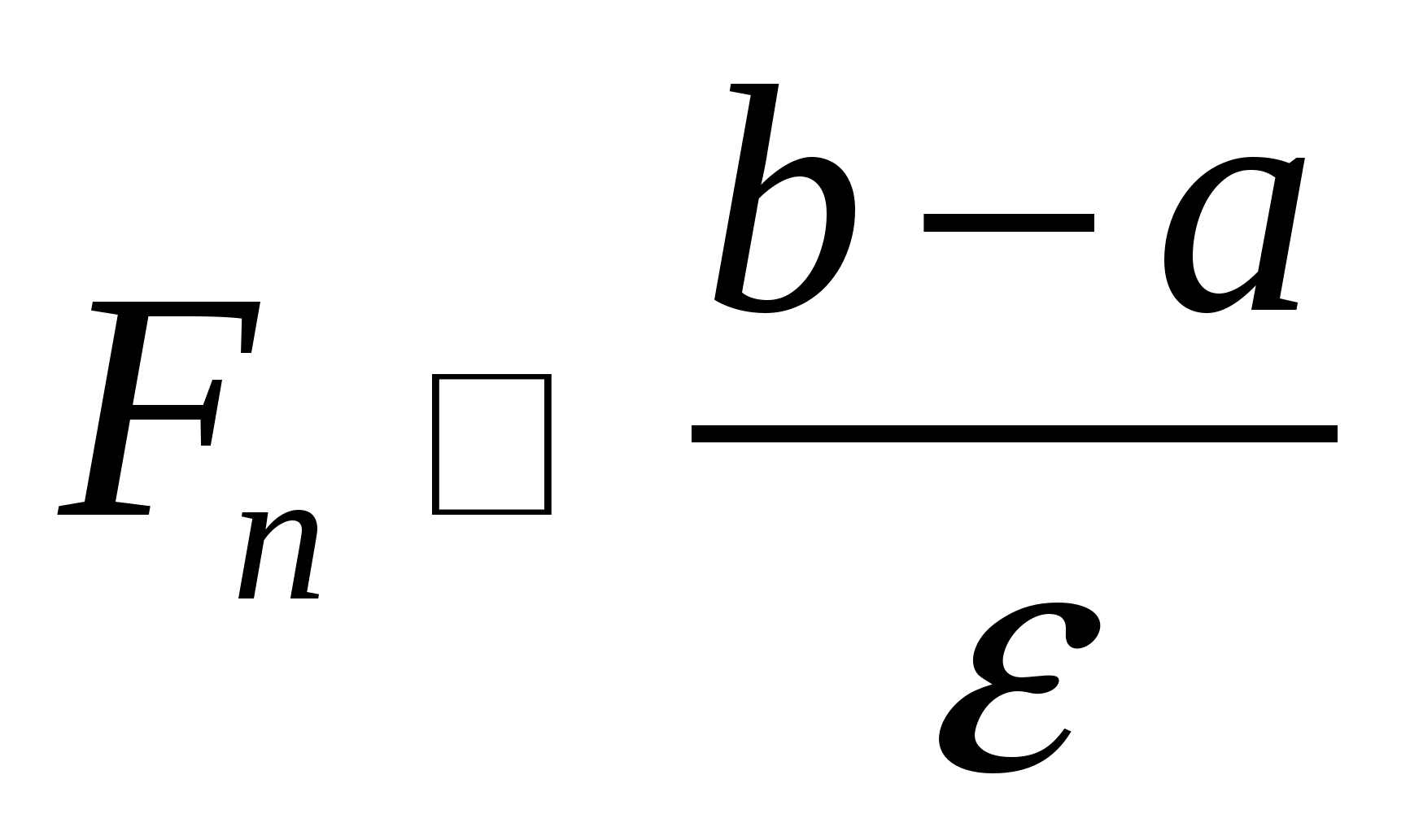 ,
Таким чином визначається також число
ітерацій n.
В точках
,
Таким чином визначається також число
ітерацій n.
В точках
 знаходять значення цільової функції:
знаходять значення цільової функції:
 .
.
покладають
 .
Тоді
.
Тоді
якщо
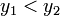 ,
то
,
то
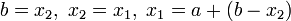 ,
,
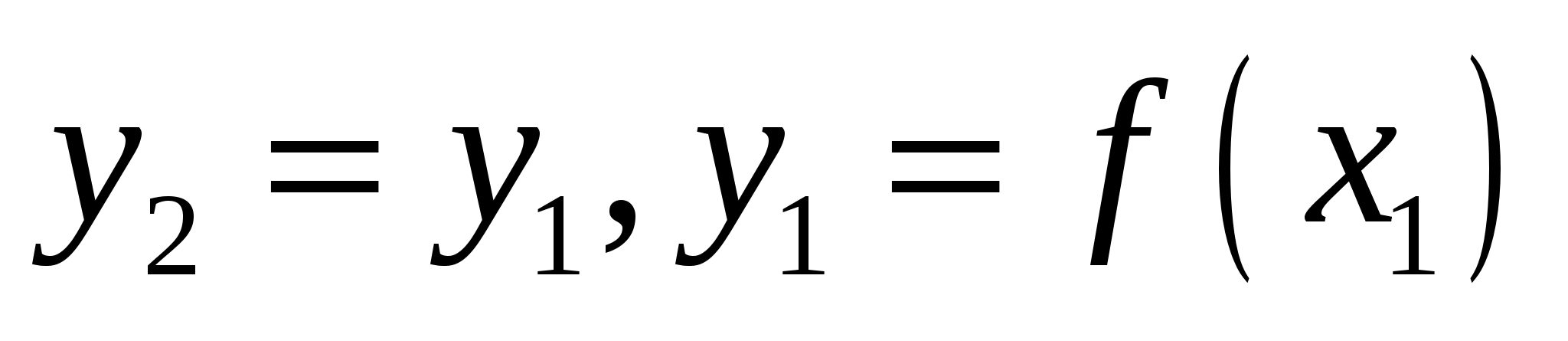 .
.
інакше
 ,
,
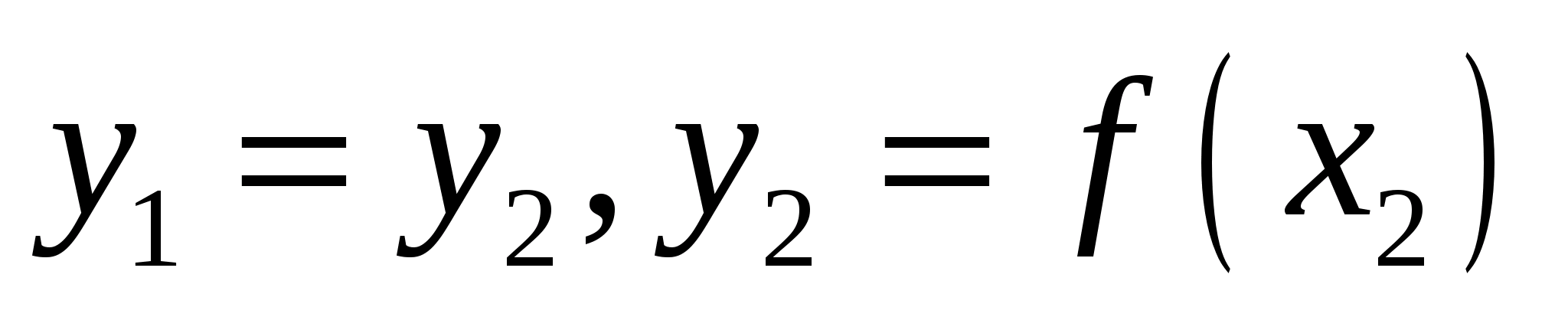 .
.
якщо
n=1,
то
 і зупиняються. Значення цільової функції
в цій точці і буде мінімумом функції.
Інакше повертаються до 3-го кроку.
і зупиняються. Значення цільової функції
в цій точці і буде мінімумом функції.
Інакше повертаються до 3-го кроку.
Відмітимо, що на кожному кроці методу Фібоначчі точка, що лежить середині відрізку локалізації, ділить його у відношенні двох послідовних чисел Фібоначчі.
2. Визначення найменшого значення функції на заданому відрізку за допомогою методів одновимірної оптимізації
Визначимо
найменше значення функції
 на відрізку
на відрізку
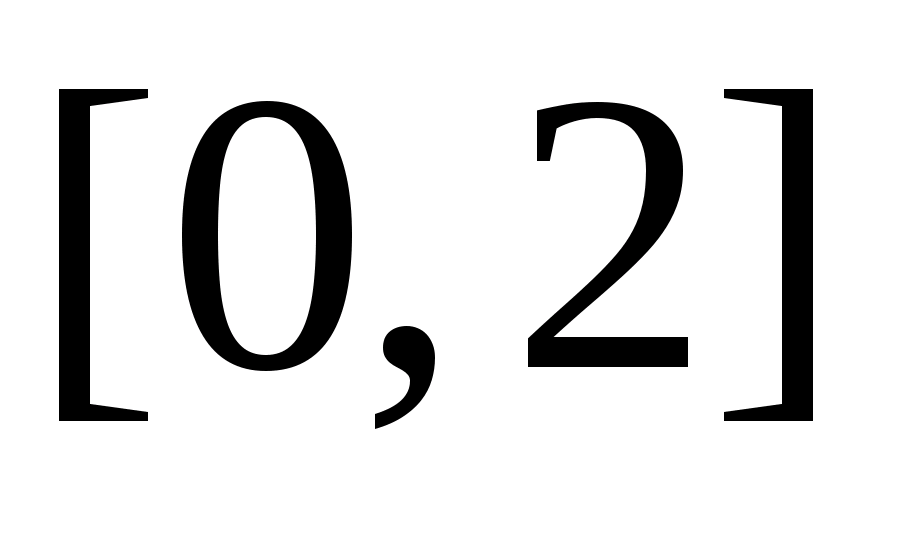 з точністю
з точністю
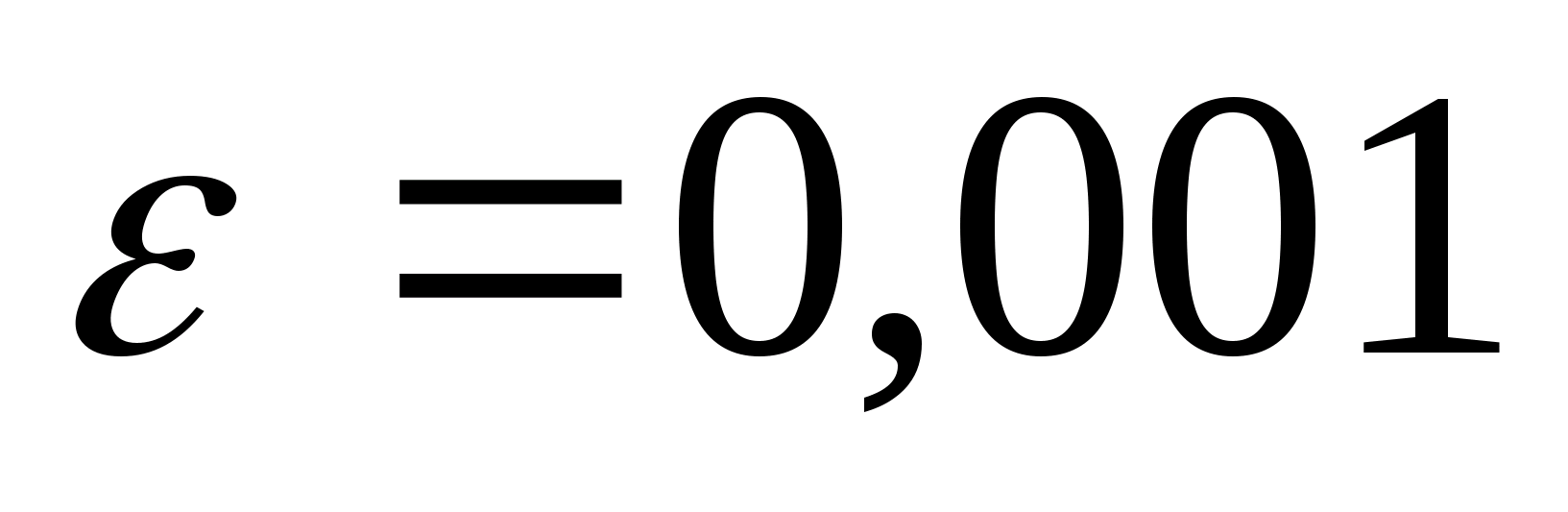 ,
використовуючи
,
використовуючи
метод дихотомії:
Розіб’ємо
відрізок
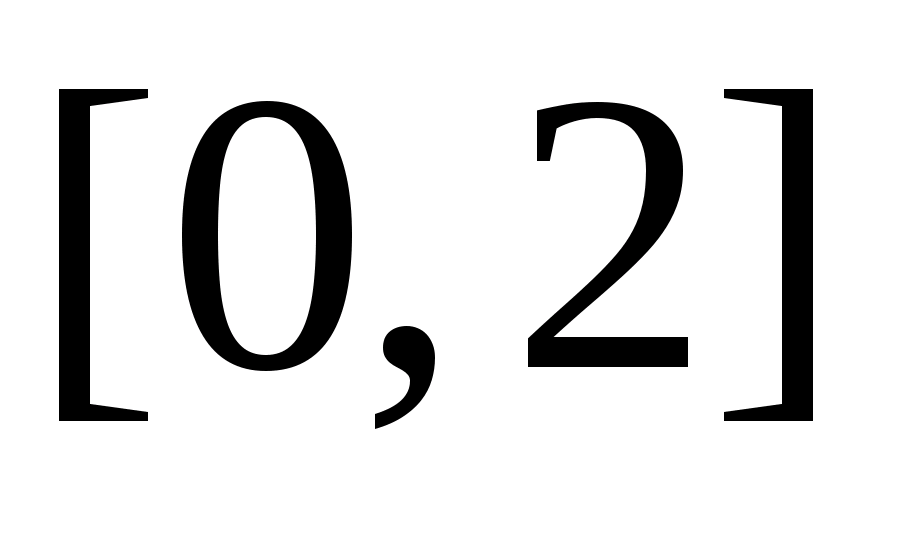 навпіл і візьмемо дві симетричні відносно
центру точки
навпіл і візьмемо дві симетричні відносно
центру точки
 такі, що
такі, що
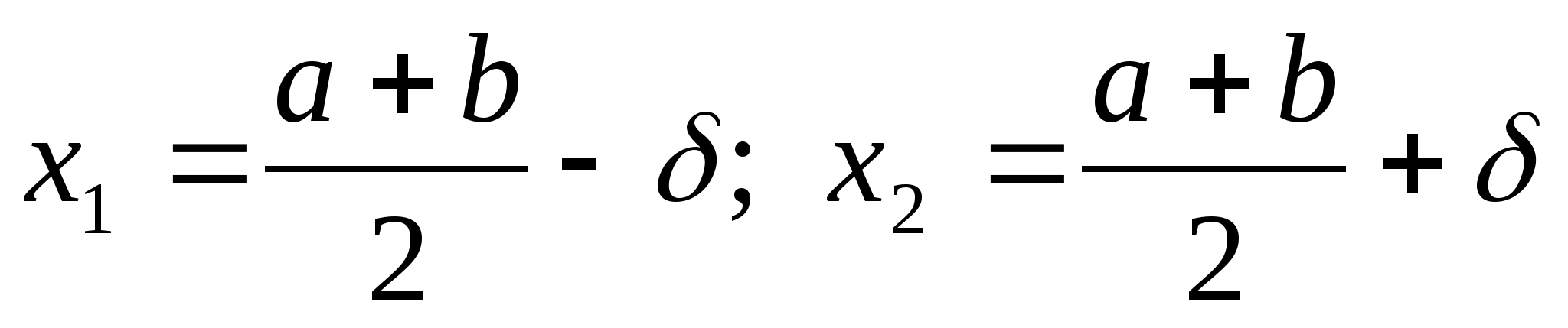 ,
де
,
де
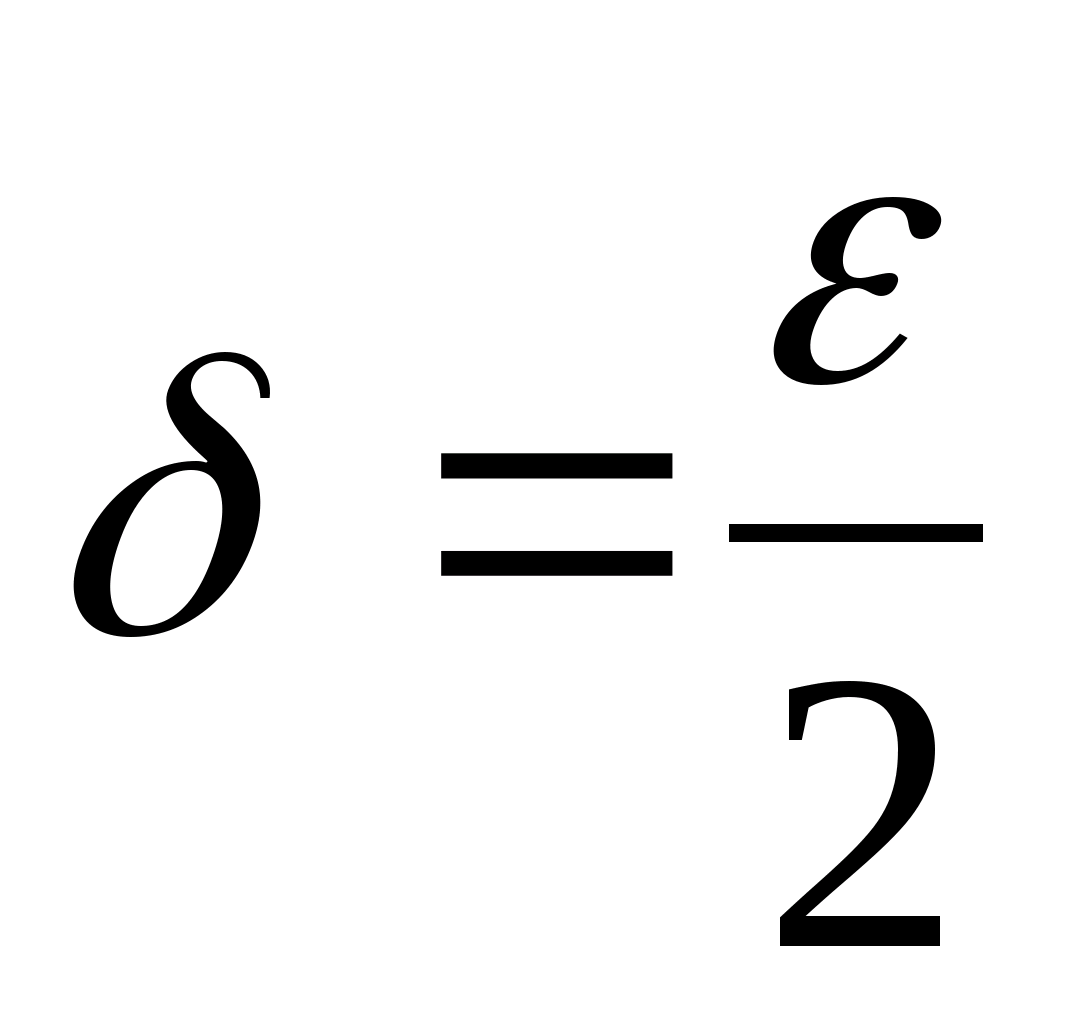 і відкинемо ту з точок, до якої ближче
виявилась одна з двох знову поставлених
точок з максимальним значенням.
і відкинемо ту з точок, до якої ближче
виявилась одна з двох знову поставлених
точок з максимальним значенням.

Обчислюємо
значення функції
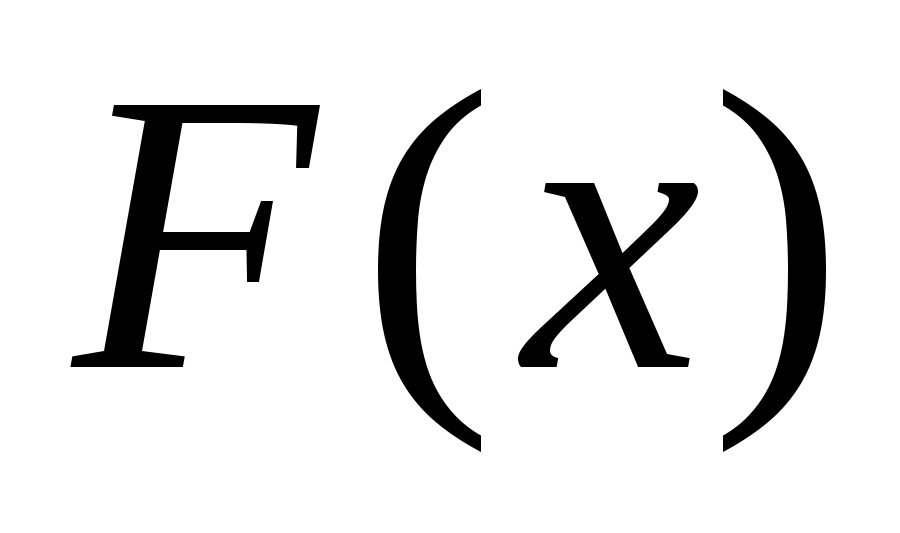 в цих точках:
в цих точках:
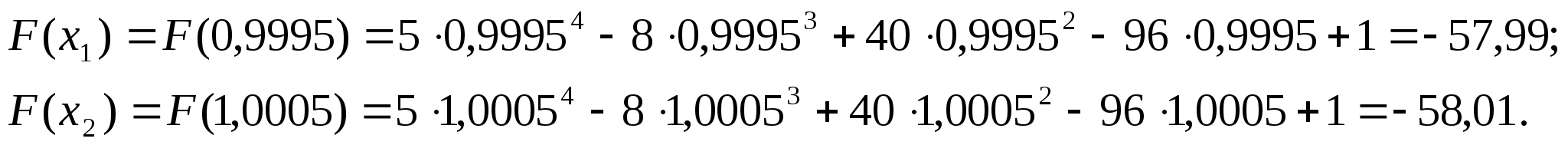
Оскільки
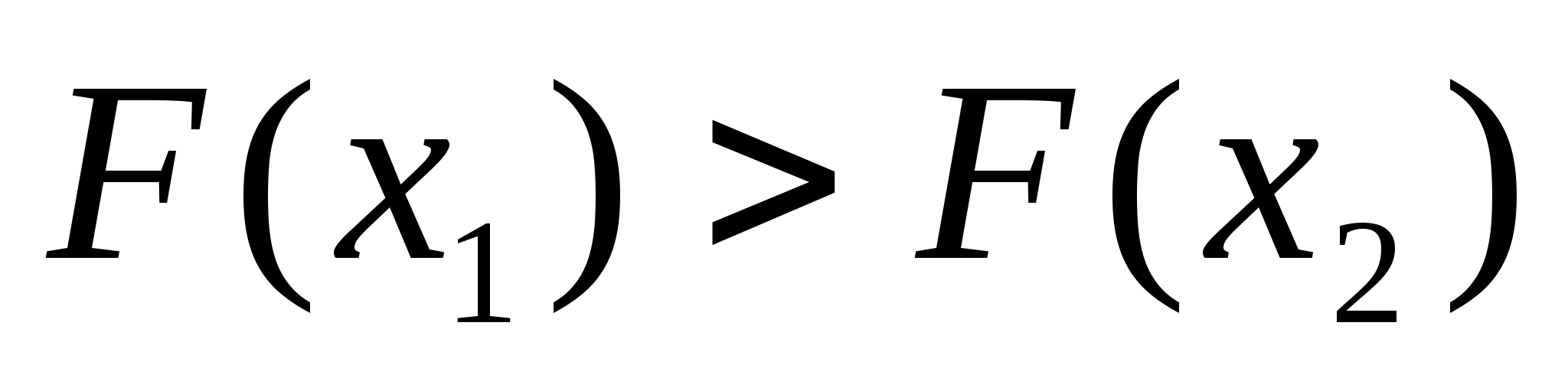 ,
то нові межі відрізка
,
то нові межі відрізка
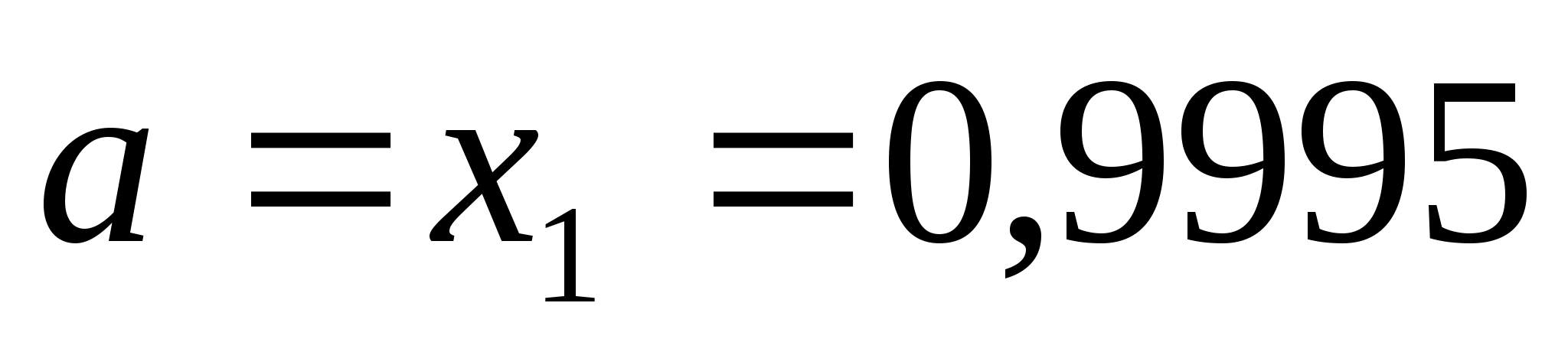 і
і
 .
В цьому
звуженому проміжку
знову
розраховуємо дві точки,
симетричні відносно його середини і
значення функції в цих точках. Процедура
буде продовжуватись до тих пір, поки не
буде виконуватись умова
.
В цьому
звуженому проміжку
знову
розраховуємо дві точки,
симетричні відносно його середини і
значення функції в цих точках. Процедура
буде продовжуватись до тих пір, поки не
буде виконуватись умова
 .
.
В
нашому випадку
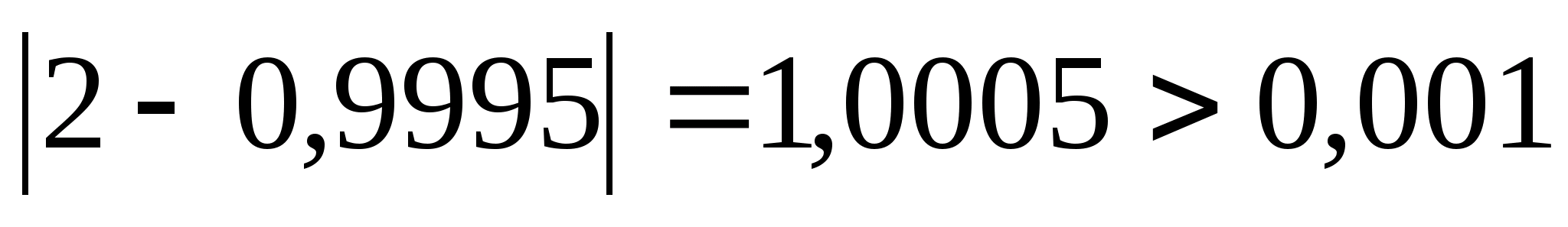 .
Тому знову розраховуємо дві точки:
.
Тому знову розраховуємо дві точки:
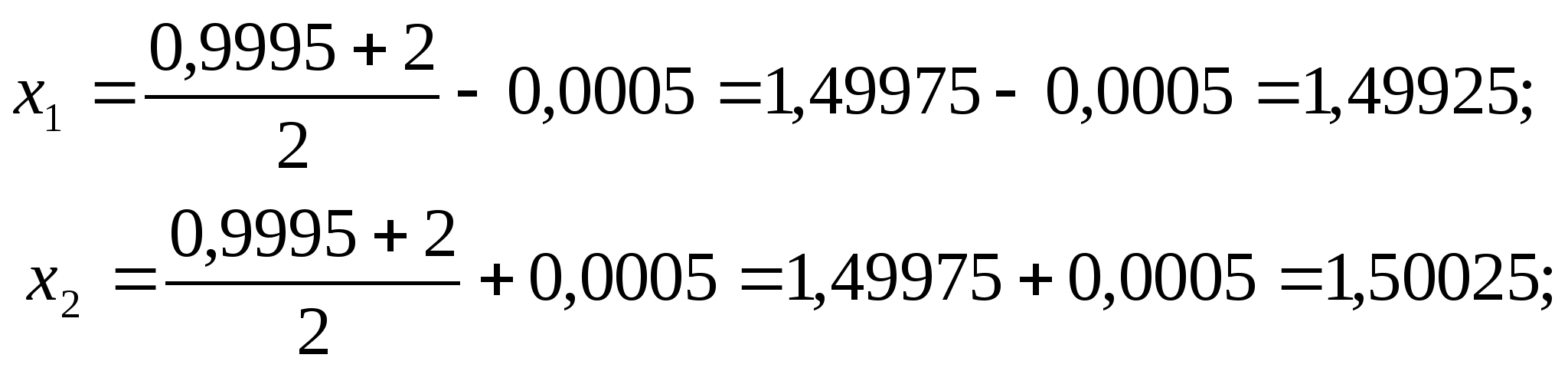
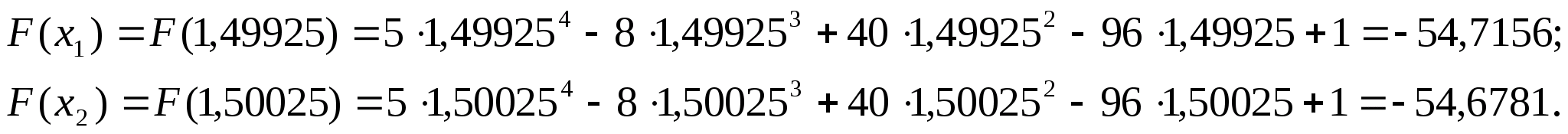
Оскільки
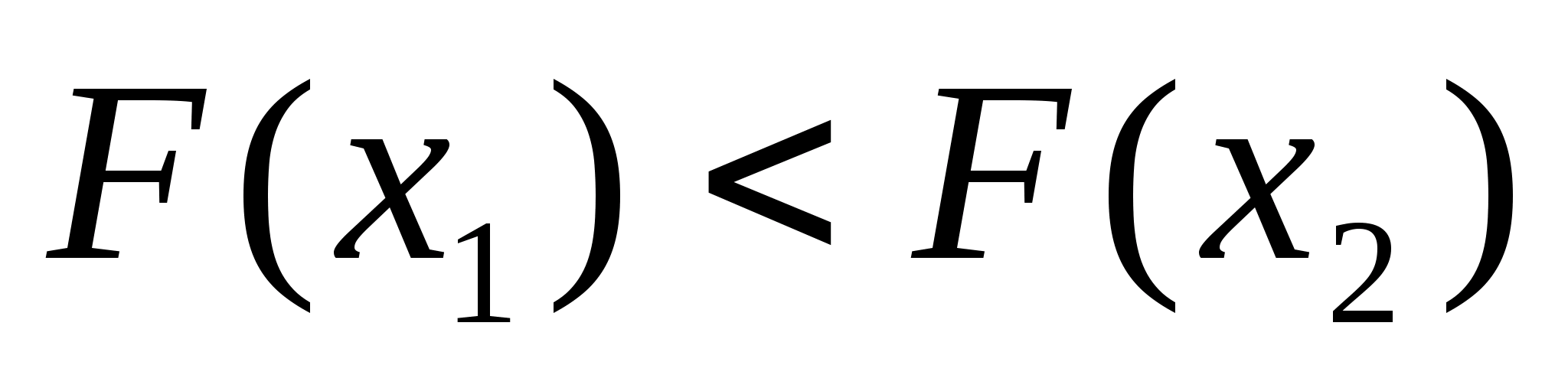 то нові межі відрізка
то нові межі відрізка
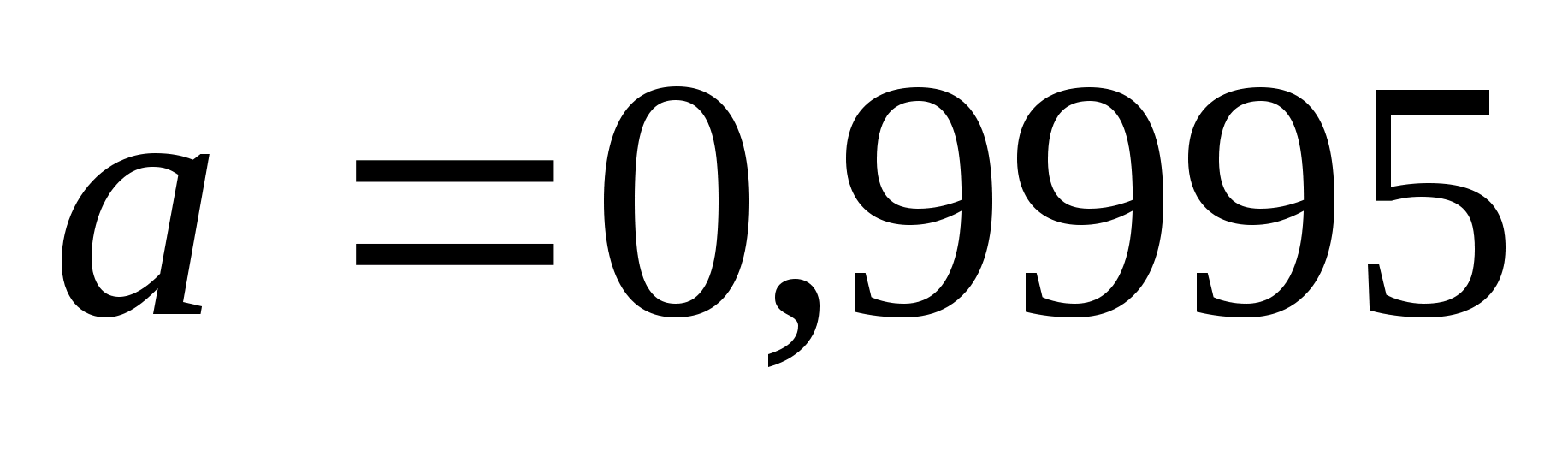 і
і
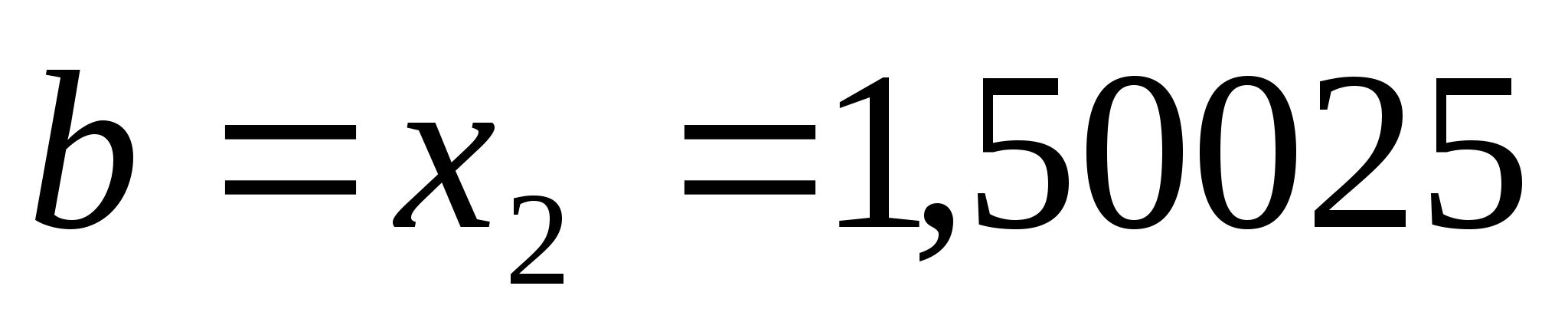 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
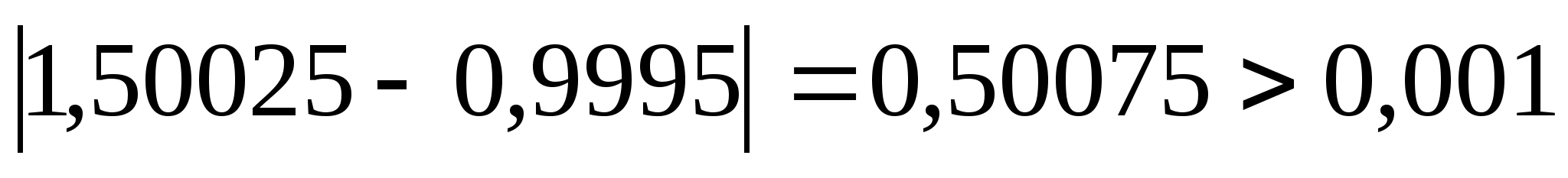 .
Отже продовжуємо процедуру.
.
Отже продовжуємо процедуру.

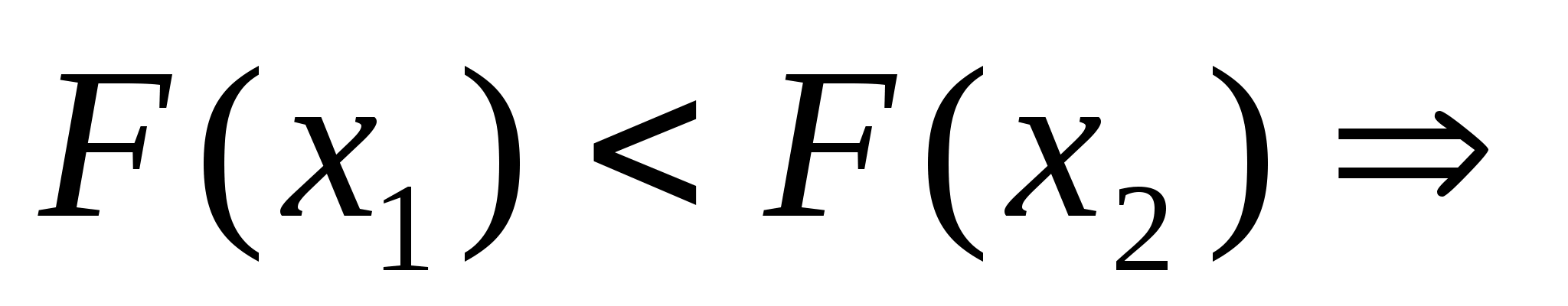 нові межі
відрізка
нові межі
відрізка
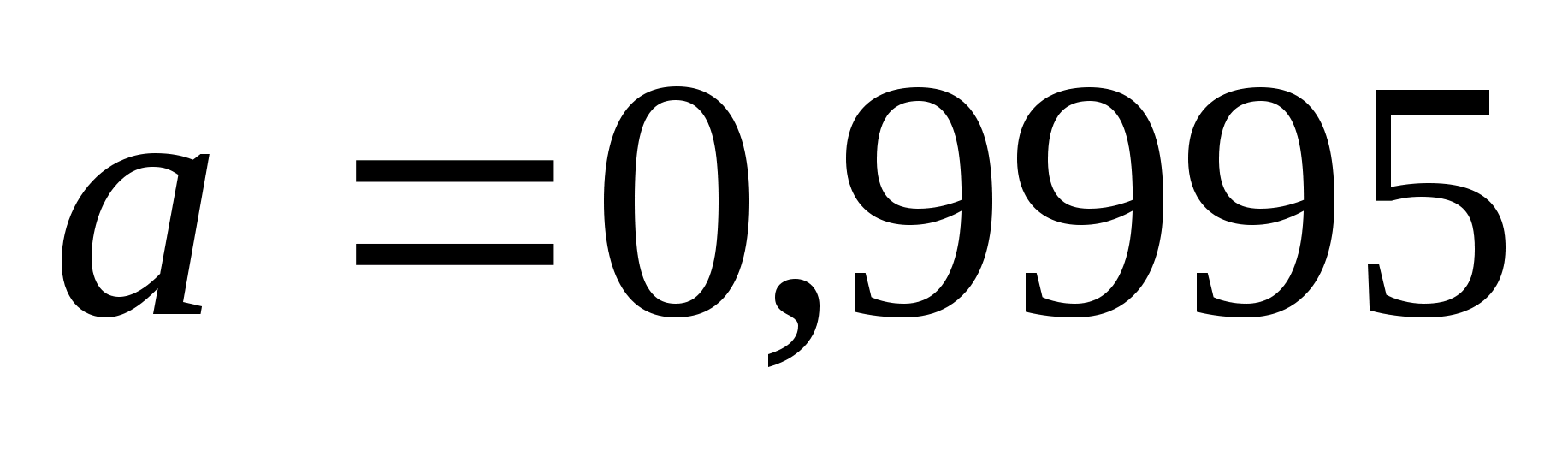 ,
,
 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
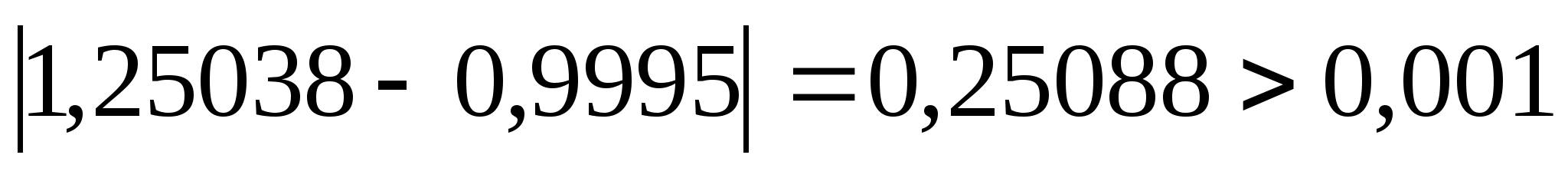 .
Отже продовжуємо процедуру.
.
Отже продовжуємо процедуру.

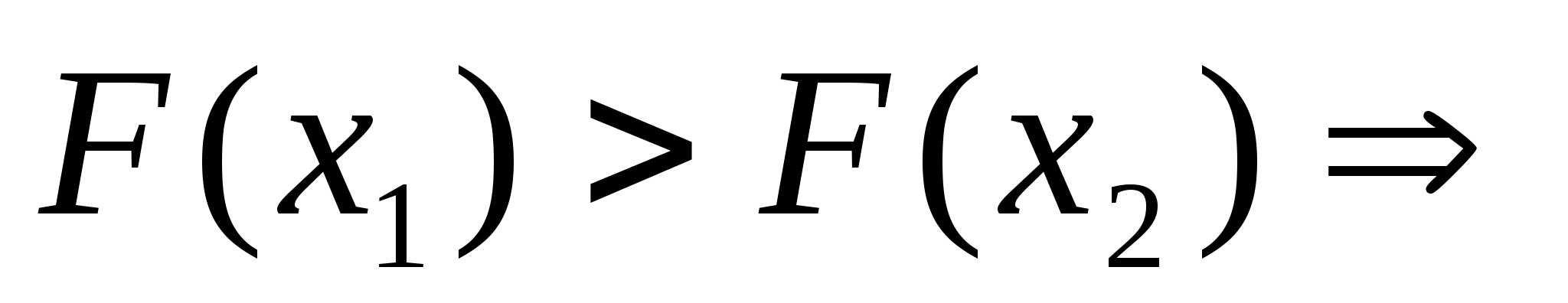 нові межі
відрізка
нові межі
відрізка
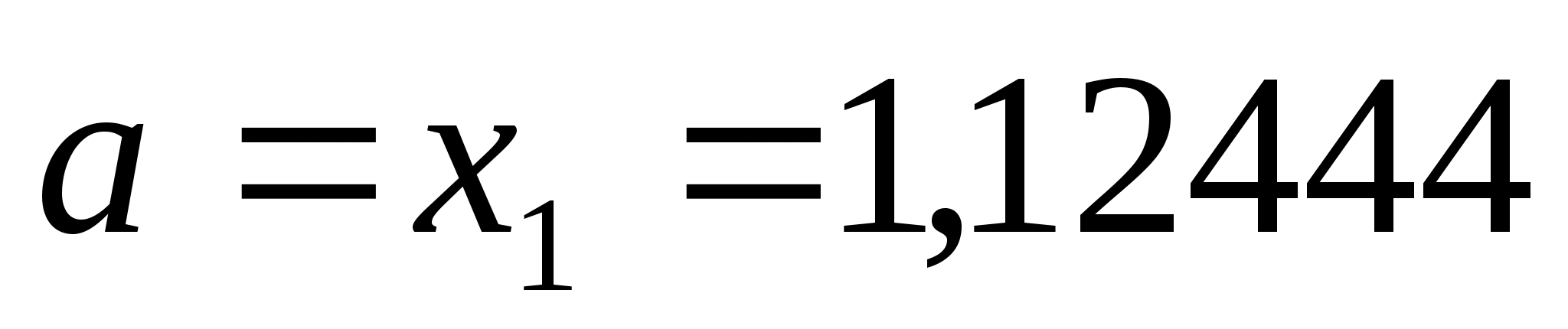 ,
,
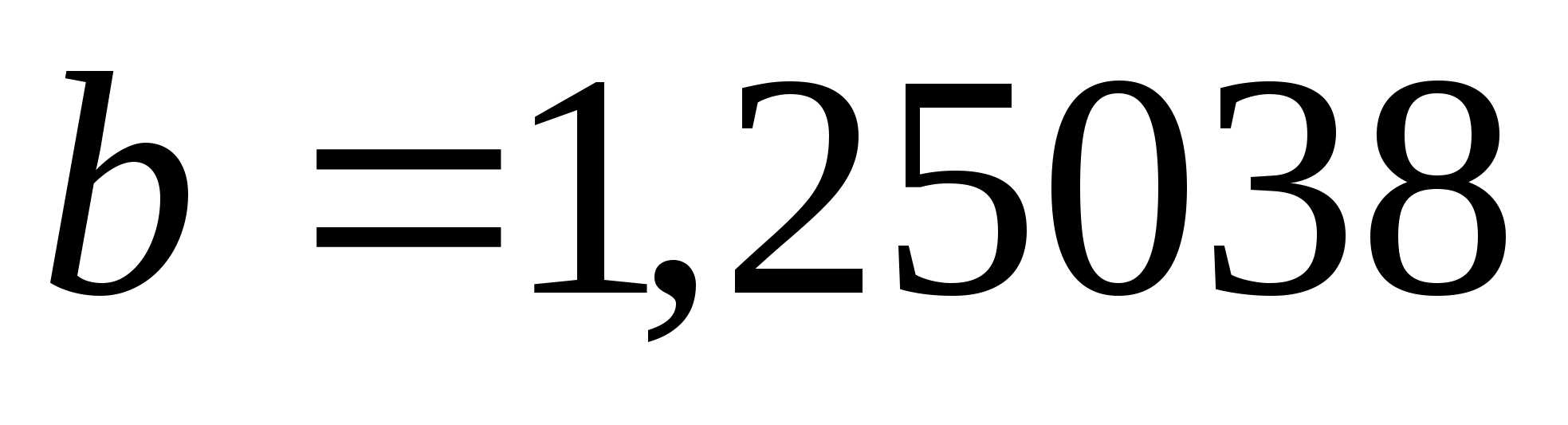 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
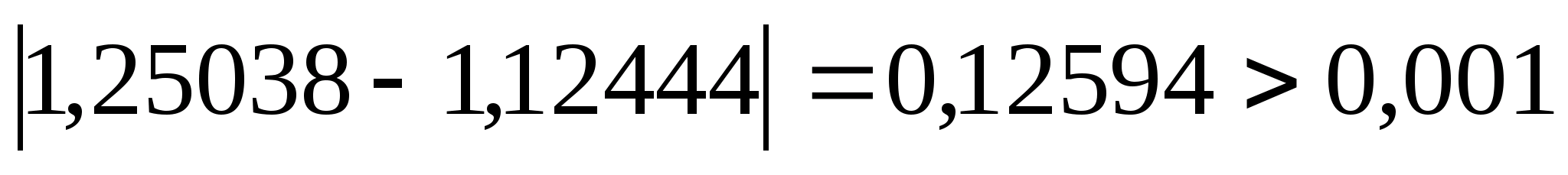 .
Продовжуємо процедуру.
.
Продовжуємо процедуру.
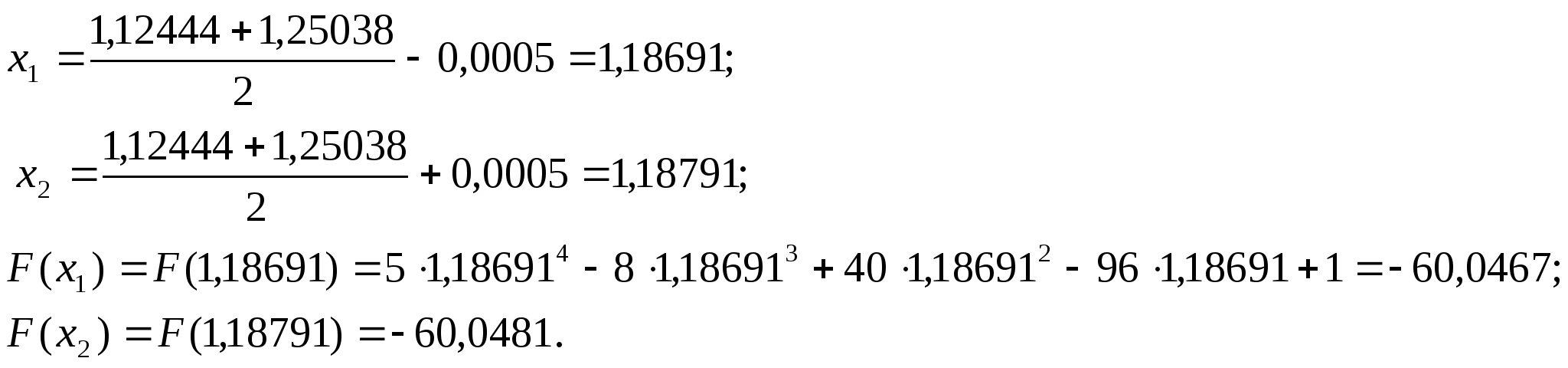
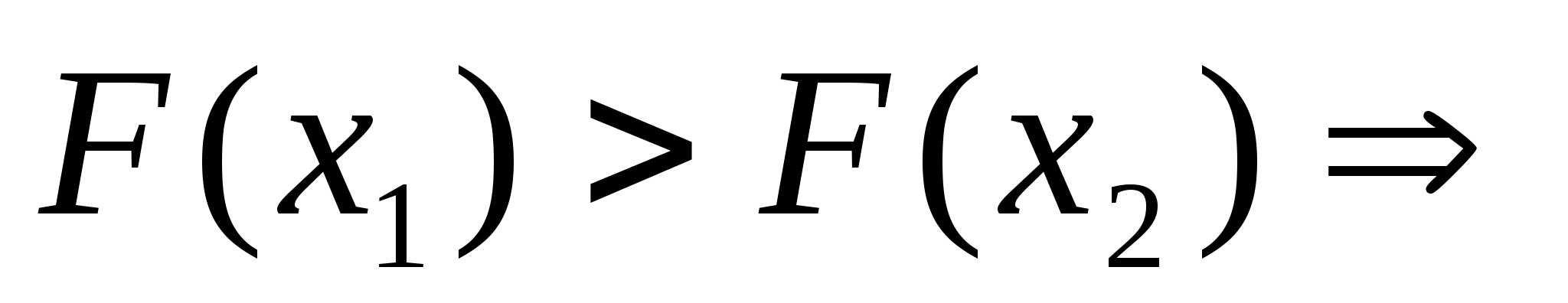 нові межі
відрізка
нові межі
відрізка
 ,
,
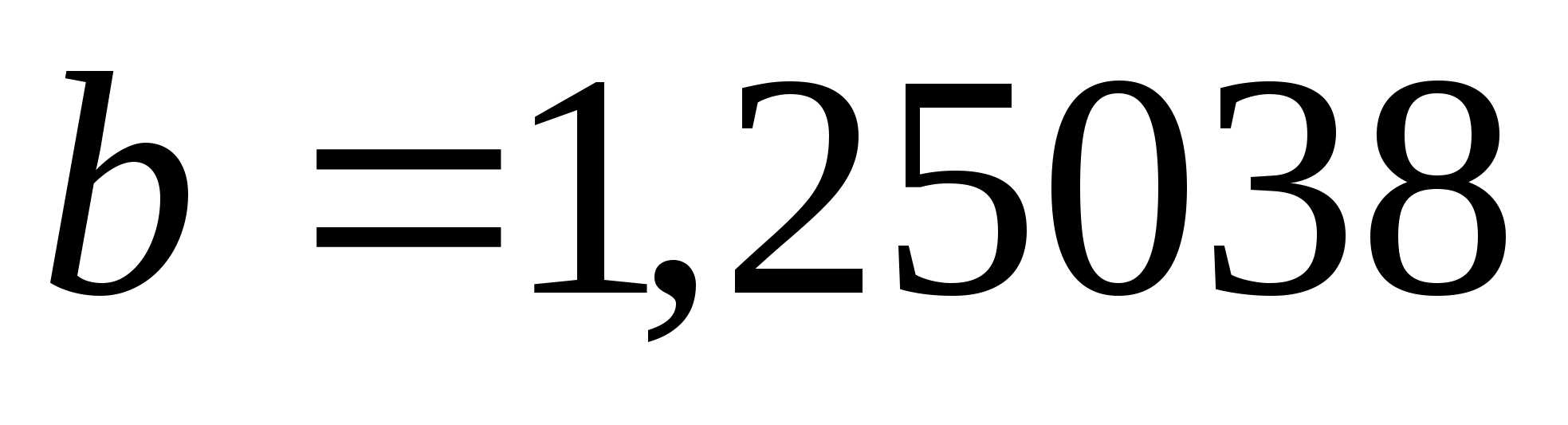 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
 .
Отже продовжуємо процедуру.
.
Отже продовжуємо процедуру.
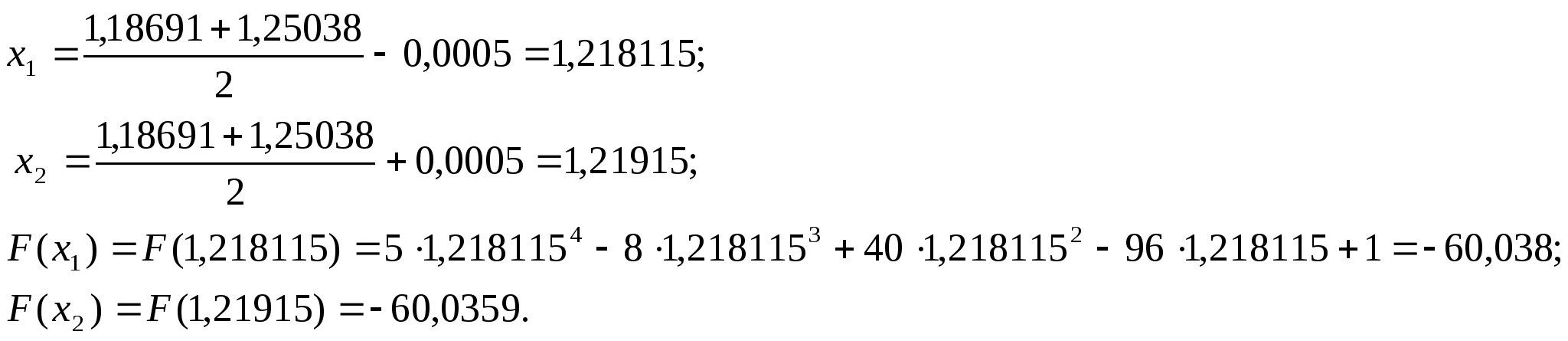
 нові межі
відрізка
нові межі
відрізка
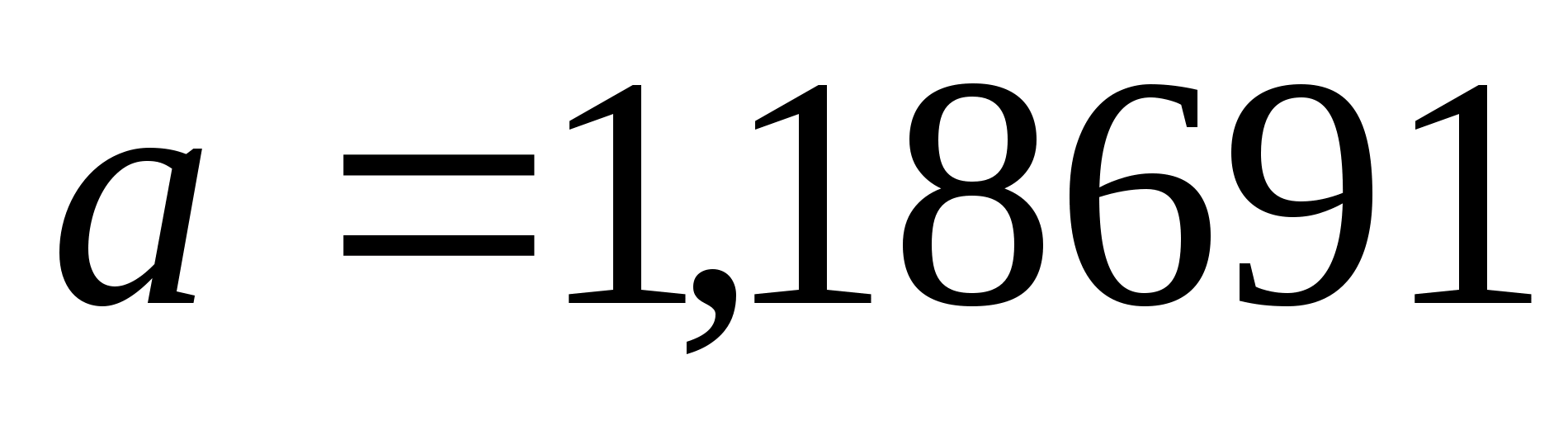 ,
,
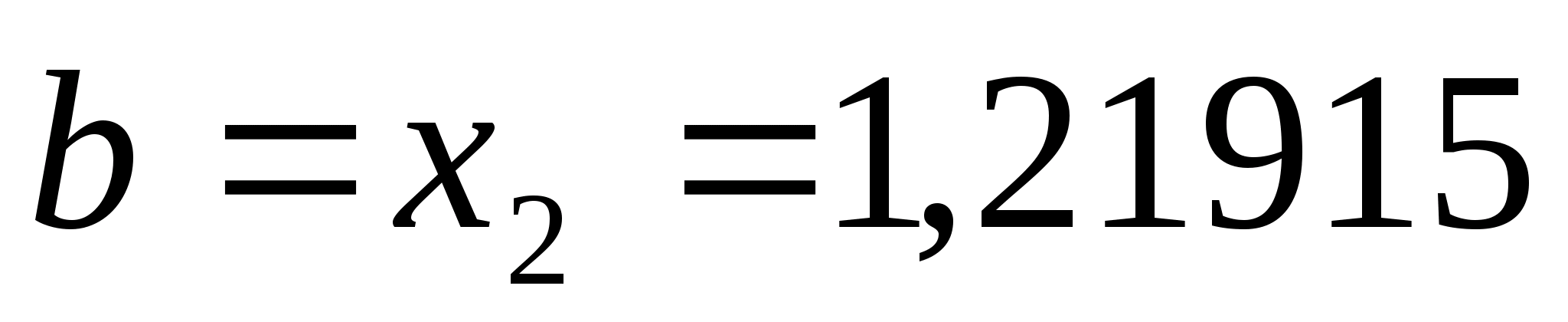 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
 .
Отже продовжуємо процедуру.
.
Отже продовжуємо процедуру.
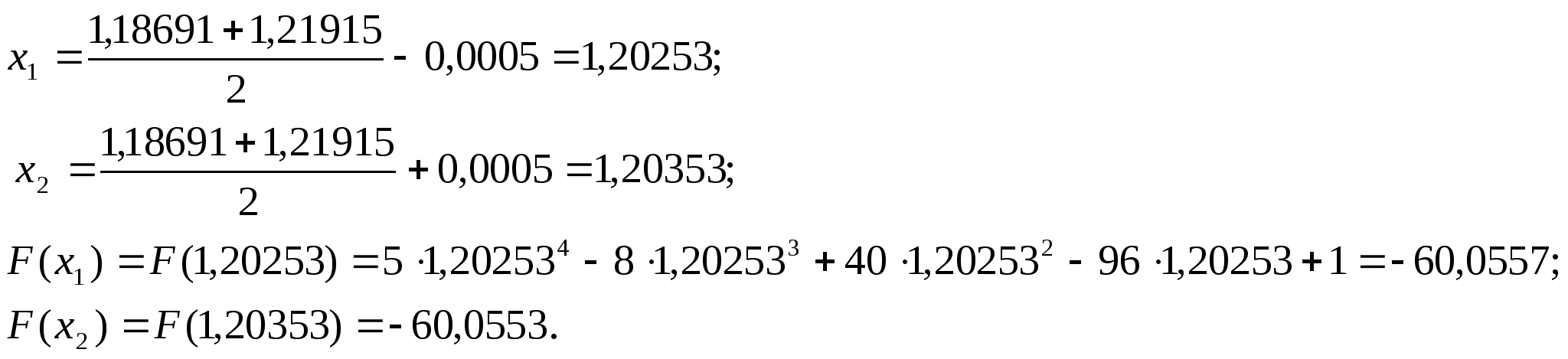
 нові межі
відрізка
нові межі
відрізка
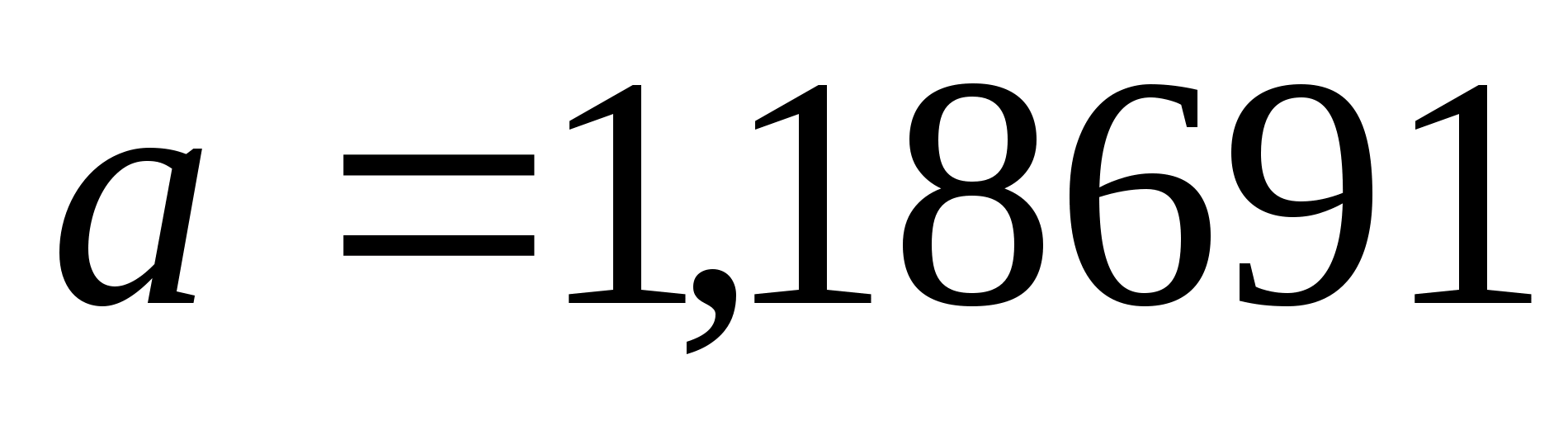 ,
,
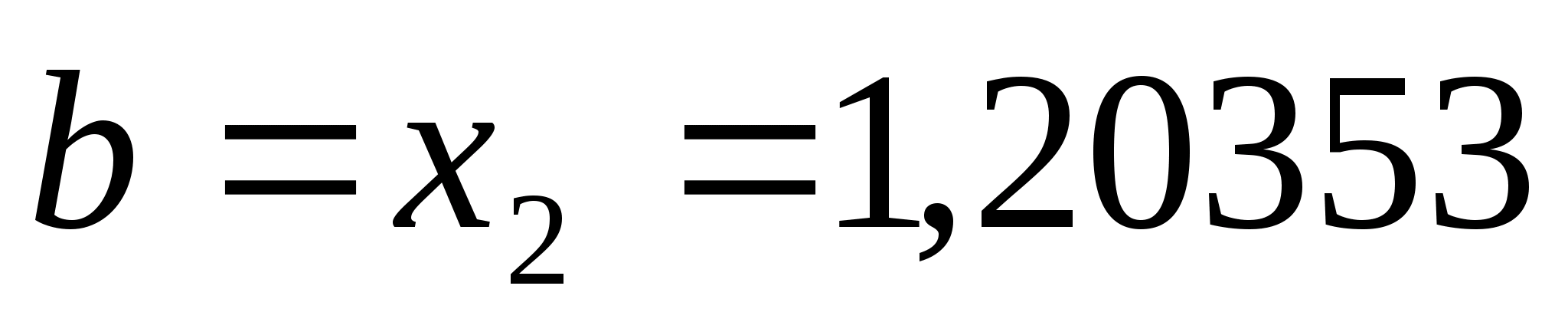 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
 .
Отже продовжуємо процедуру.
.
Отже продовжуємо процедуру.
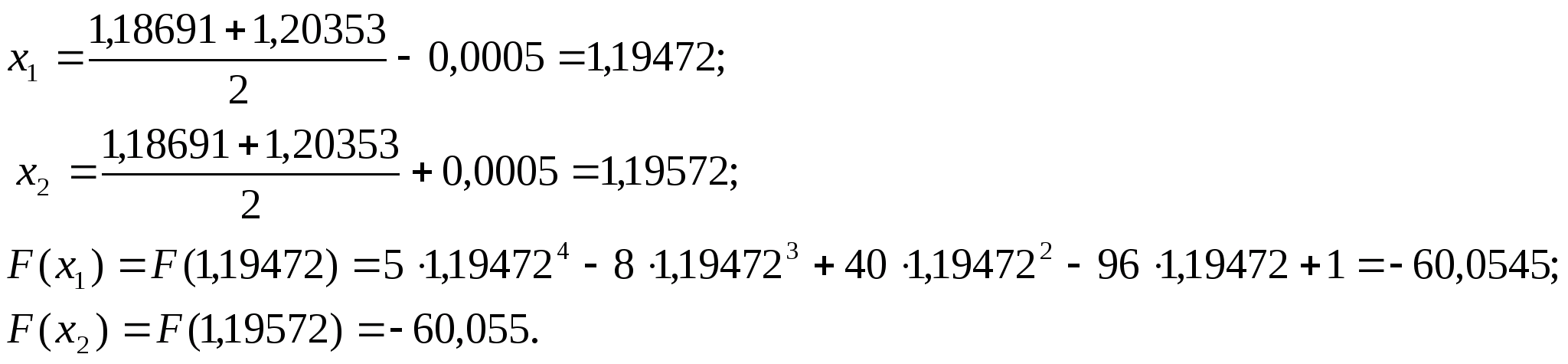
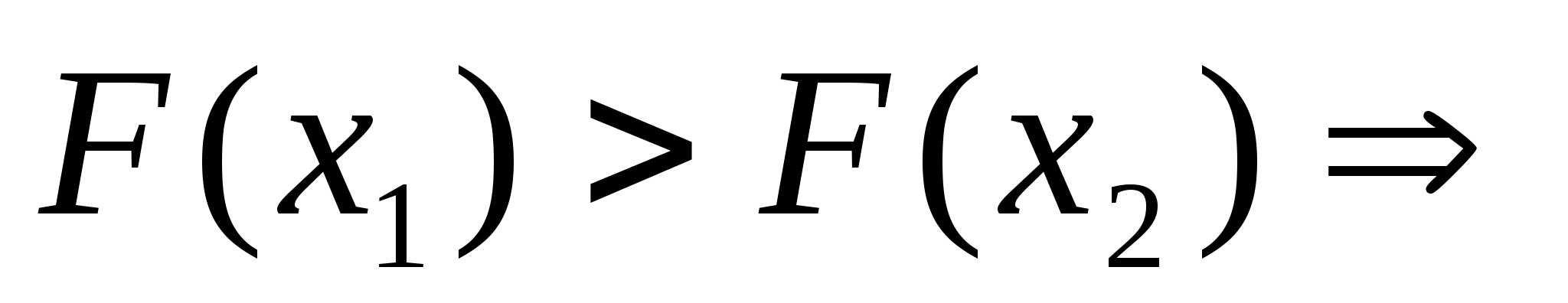 нові межі
відрізка
нові межі
відрізка
 ,
,
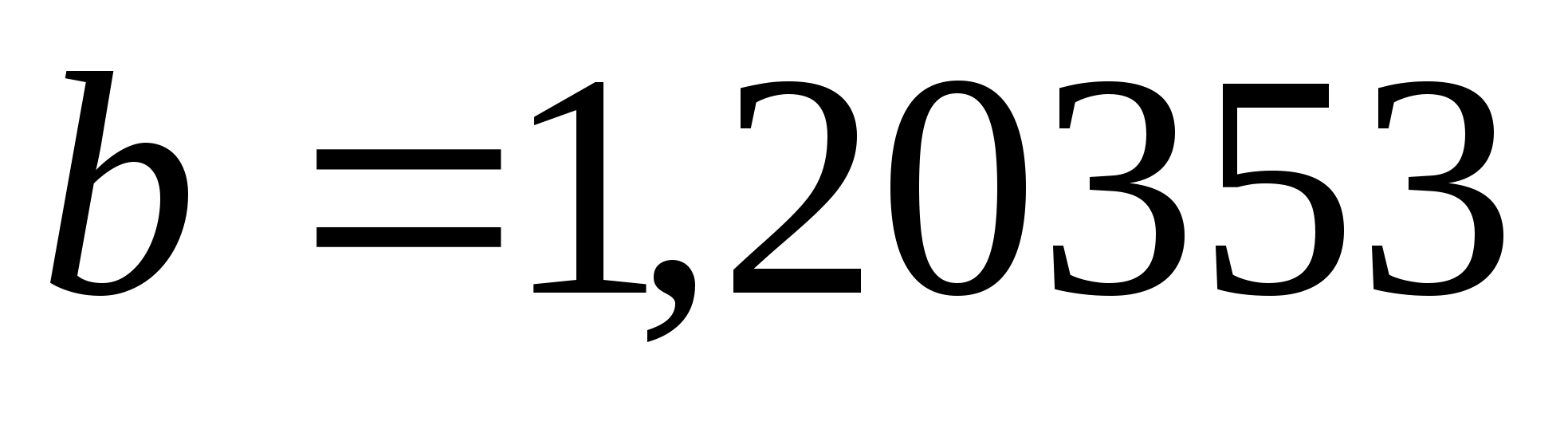 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
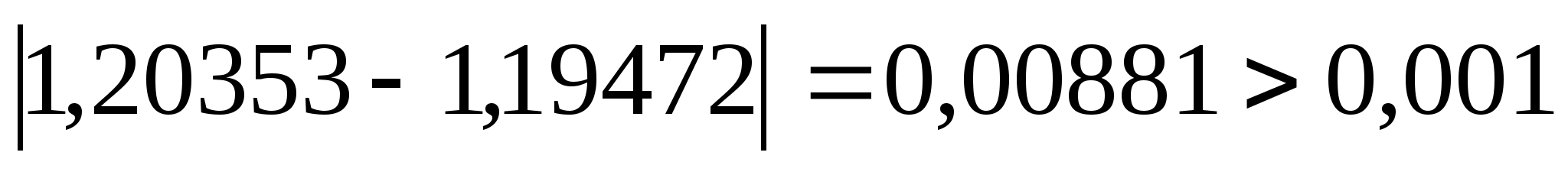 .
Продовжуємо процедуру.
.
Продовжуємо процедуру.
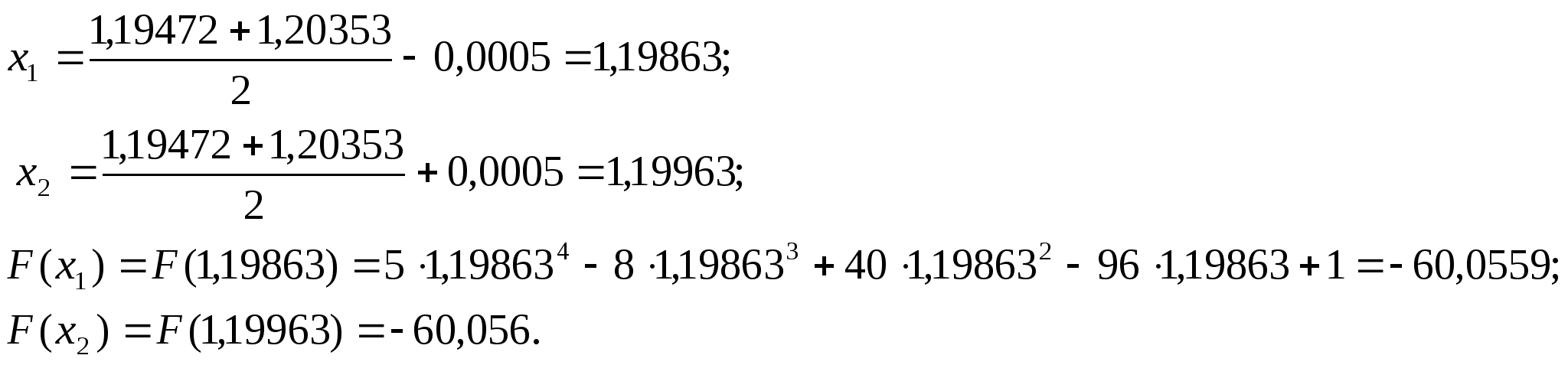
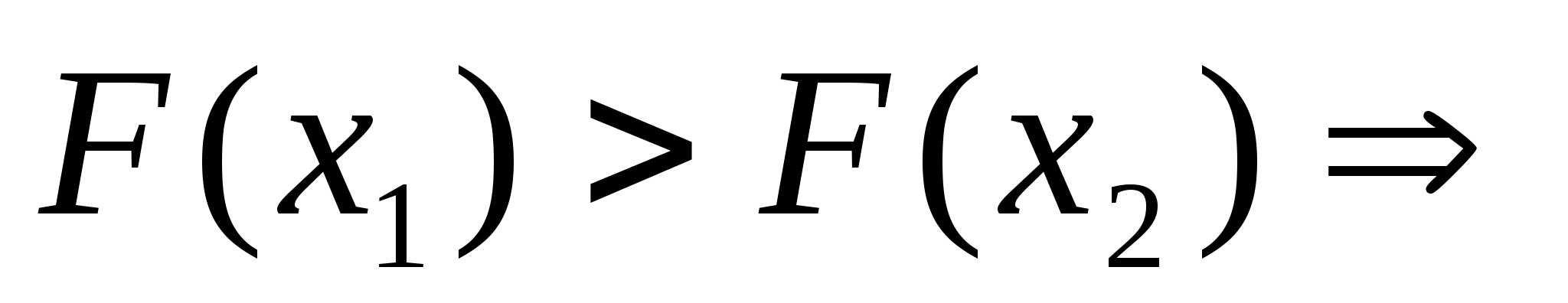 нові межі
відрізка
нові межі
відрізка
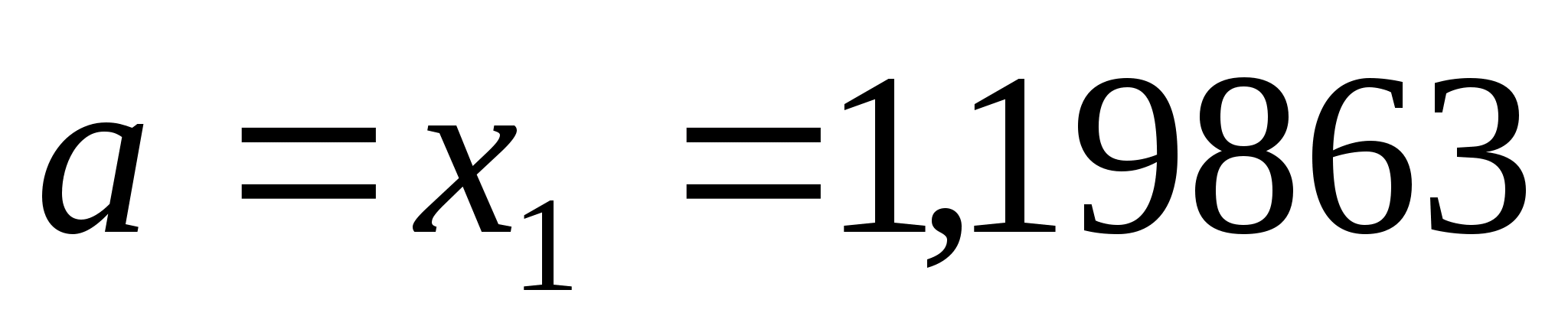 ,
,
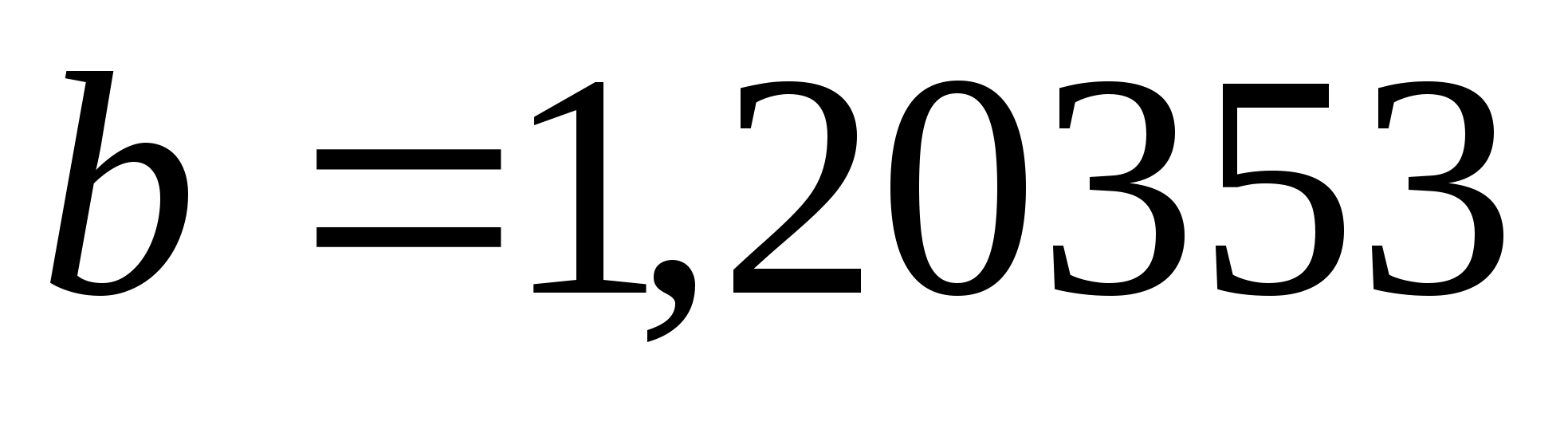 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
 .
Продовжуємо процедуру.
.
Продовжуємо процедуру.
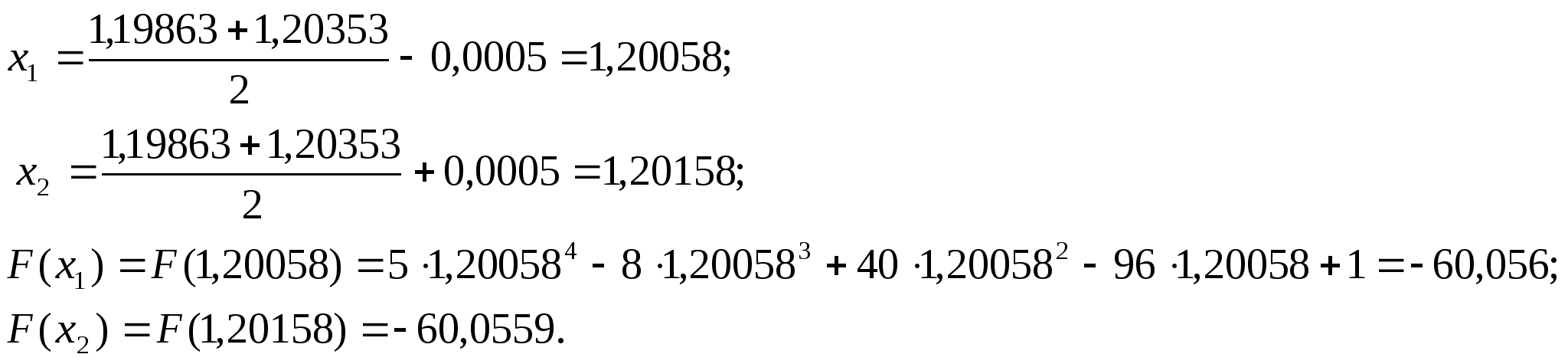
 нові межі
відрізка
нові межі
відрізка
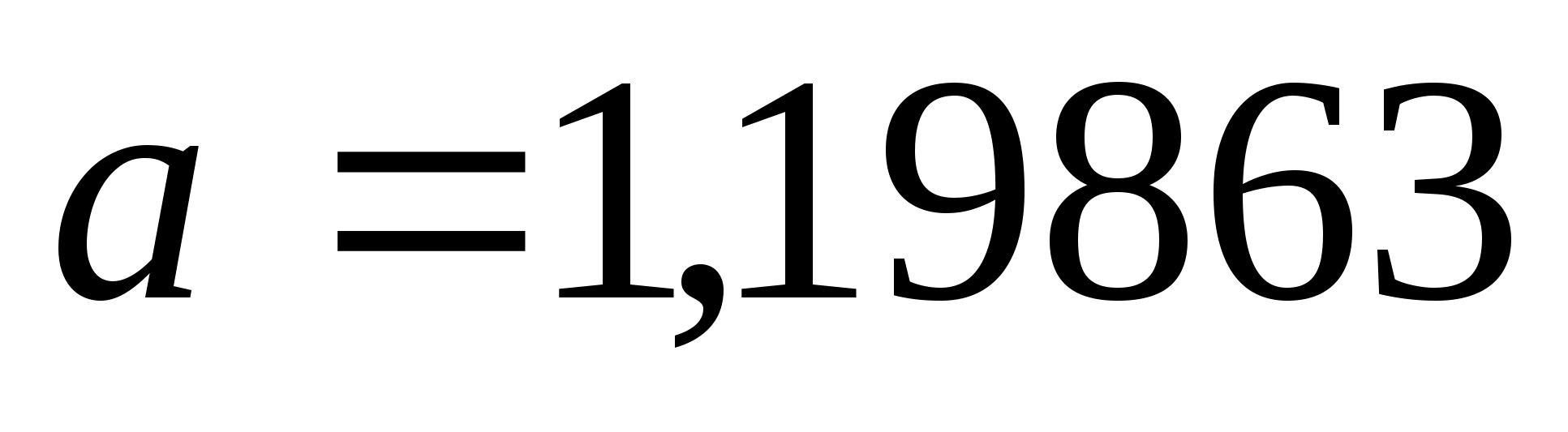 ,
,
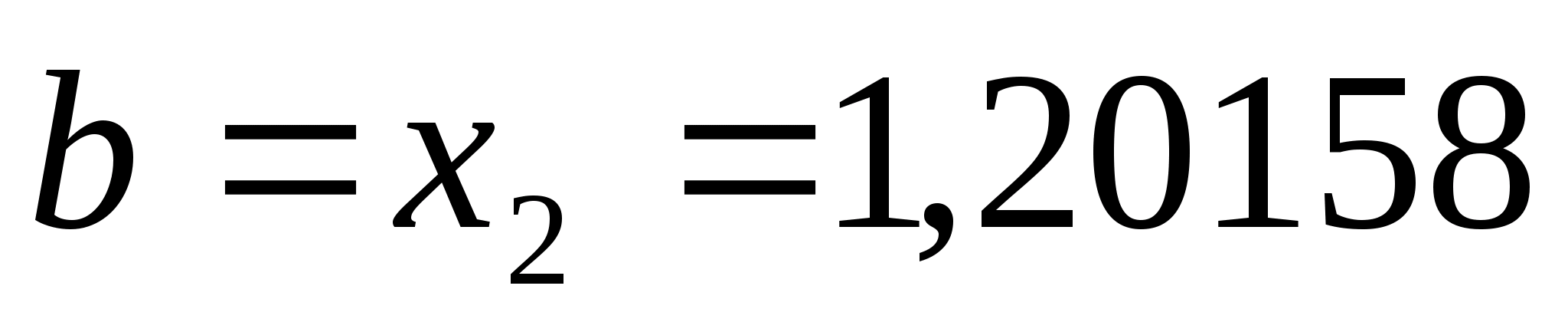 .
Перевіряємо умову зупинки:
.
Перевіряємо умову зупинки:
 .
Продовжуємо процедуру.
.
Продовжуємо процедуру.

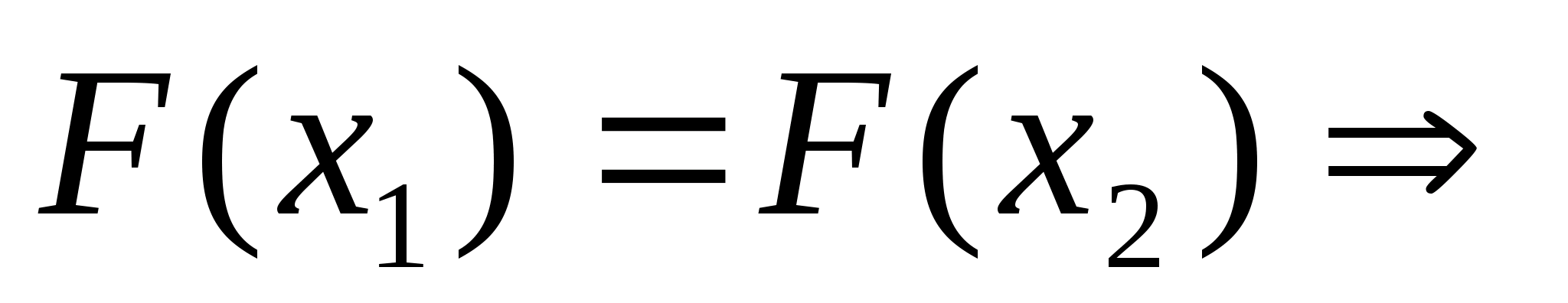 нові межі
відрізка
нові межі
відрізка
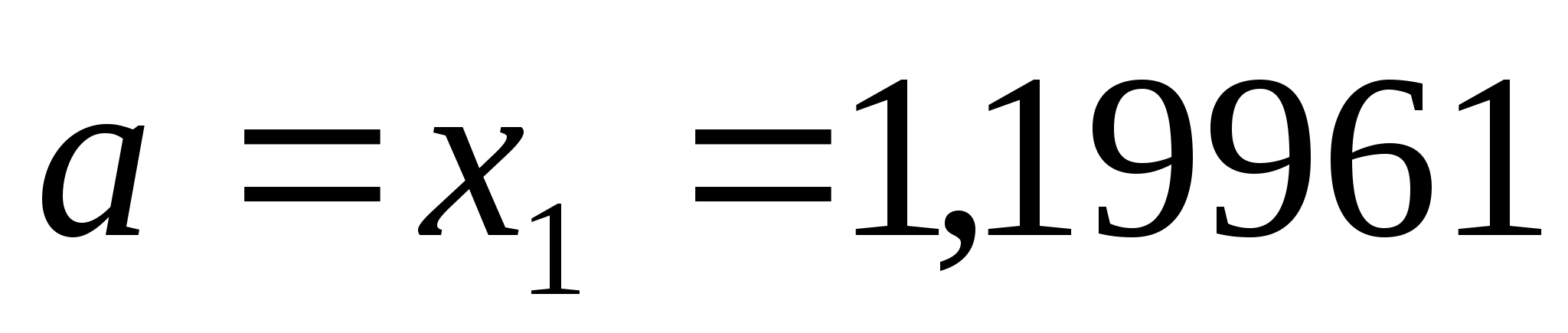 ,
,
 .
.
Перевіряємо
умову зупинки:
 .
Отже в якості точки локального мінімуму
можна наближено прийняти середину
відрізку
.
Отже в якості точки локального мінімуму
можна наближено прийняти середину
відрізку
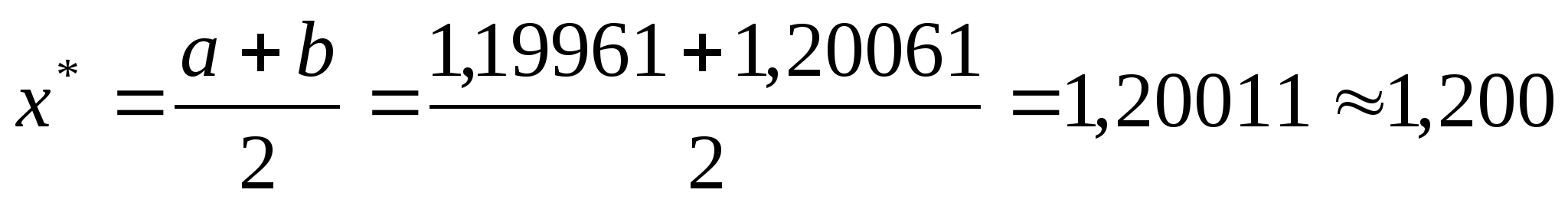 .
Тоді мінімальне значення вихідної
функції буде рівним:
.
Тоді мінімальне значення вихідної
функції буде рівним:
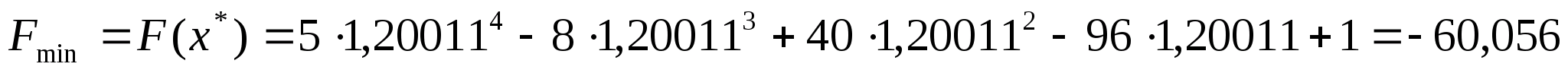 .
.
метод золотого перерізу
На
першій ітерації відрізок
 ділимо двома симетричними відносно
центра точками за формулами:
ділимо двома симетричними відносно
центра точками за формулами:

Обчислюємо значення функції в цих точках:
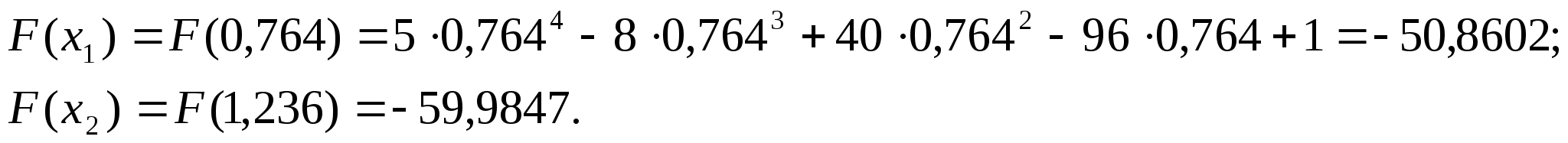
Той
із кінців відрізка, до якого серед знову
поставлених точок ближче опинилась та,
значення функції в якій максимальне,
відкидаємо. Тобто, оскільки
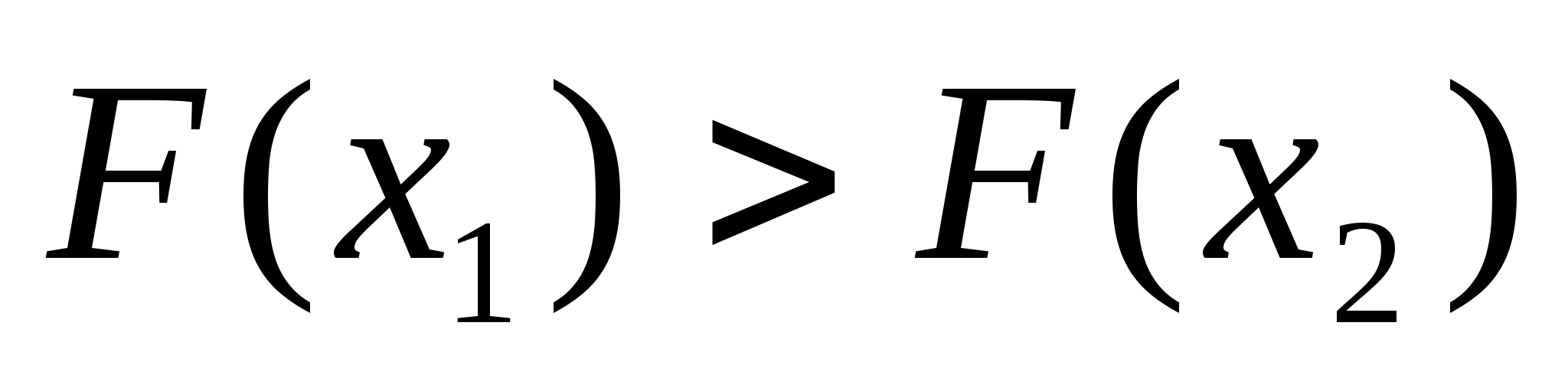 ,
то покладаємо, що
,
то покладаємо, що
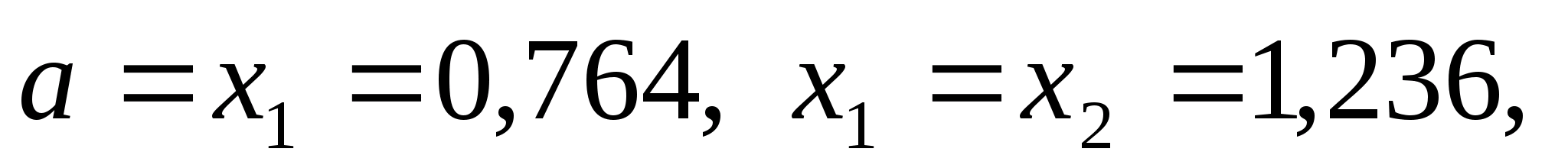
 .
Тепер обчислюємо значення функції в
нових точках:
.
Тепер обчислюємо значення функції в
нових точках:

Так
як і в методі дихотомії процедура буде
продовжуватись до тих пір, поки не буде
виконуватись умова
 .
Отже перевіримо умову зупинки:
.
Отже перевіримо умову зупинки:
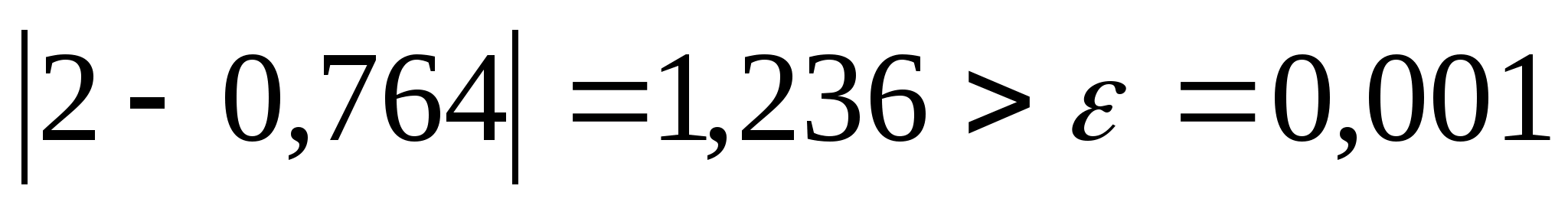 .
Тому знову аналогічно шукаємо нові межі
відрізка. Оскільки
.
Тому знову аналогічно шукаємо нові межі
відрізка. Оскільки
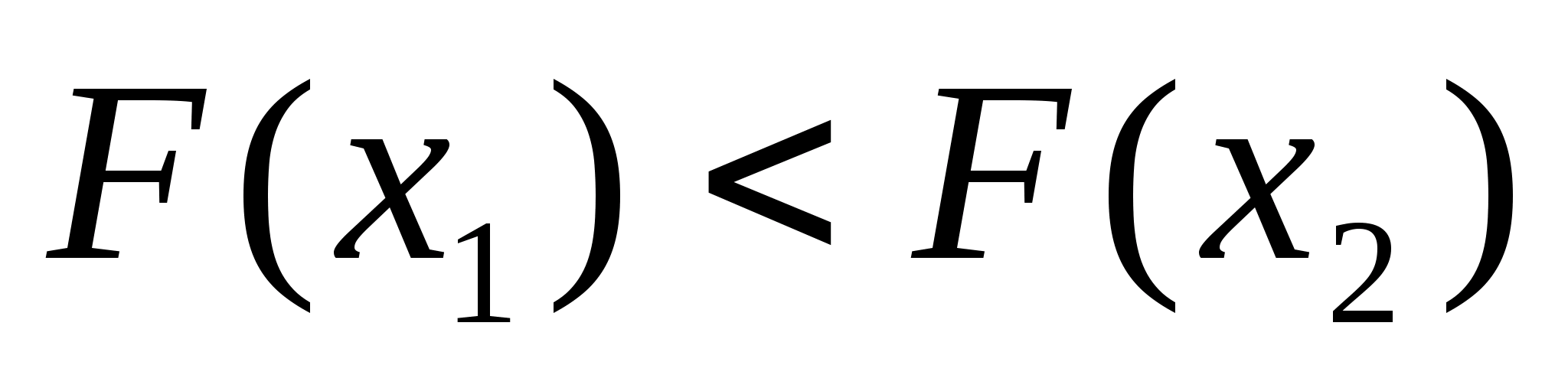 маємо:
маємо:
 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
 ,
тому продовжуємо процедуру.
,
тому продовжуємо процедуру.
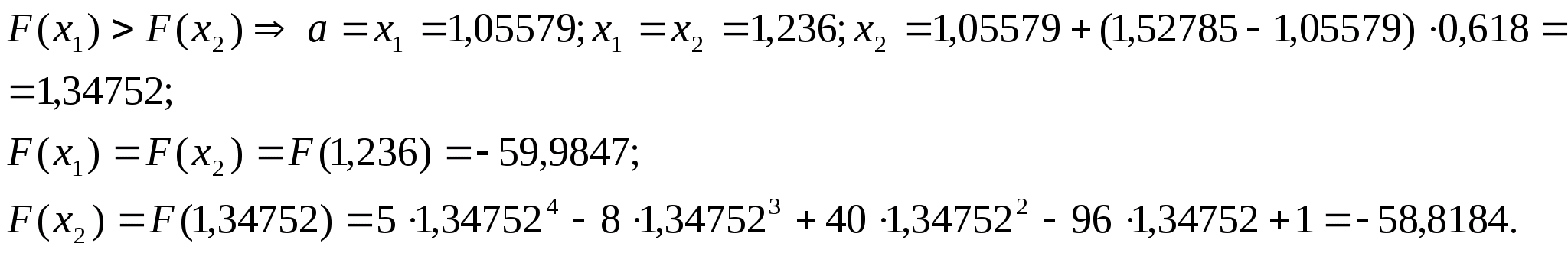
Перевіряємо
умову зупинки:
 ,
тому продовжуємо процедуру.
,
тому продовжуємо процедуру.

Знову
перевіряємо умову зупинки:
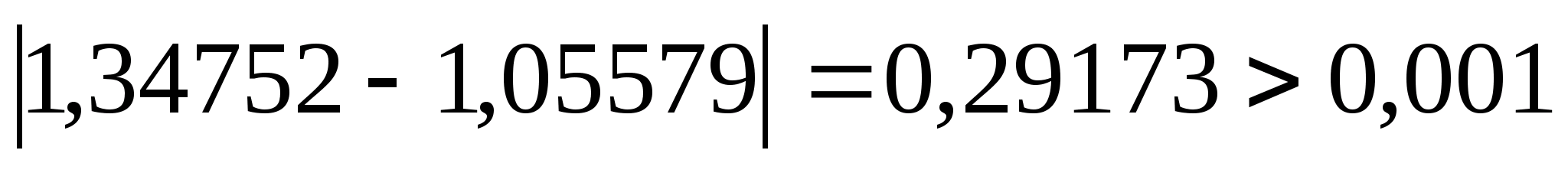 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.
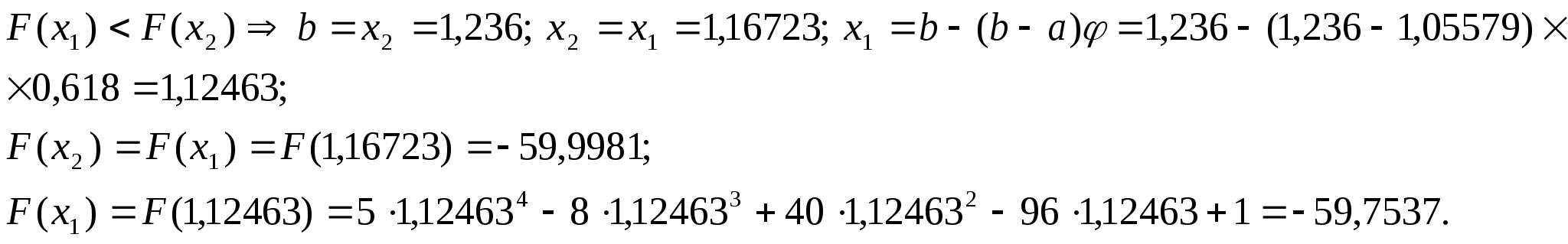
Перевіряємо
умову зупинки:
 ,
тому продовжуємо процедуру.
,
тому продовжуємо процедуру.

Перевіряємо
умову зупинки:
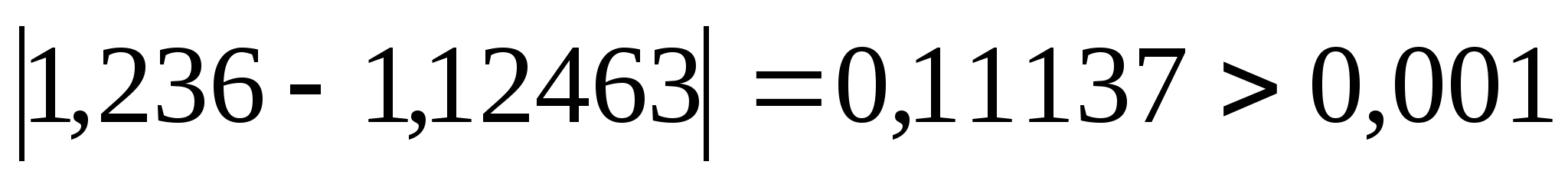 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.

Перевіряємо
умову зупинки:
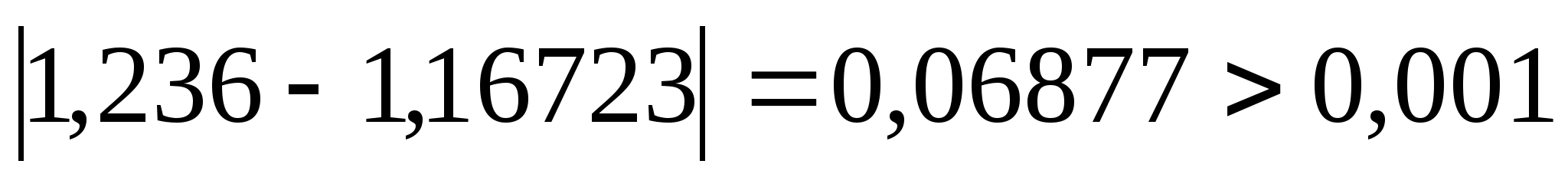 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.
 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
 ,
тому продовжуємо процедуру.
,
тому продовжуємо процедуру.
 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.
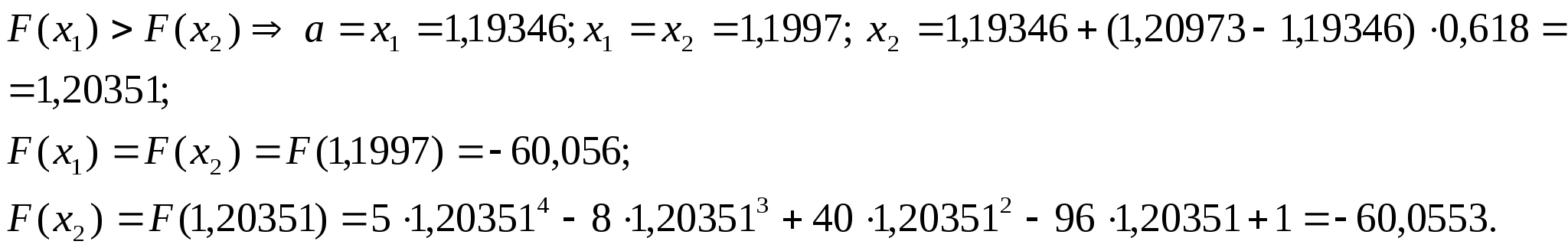 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
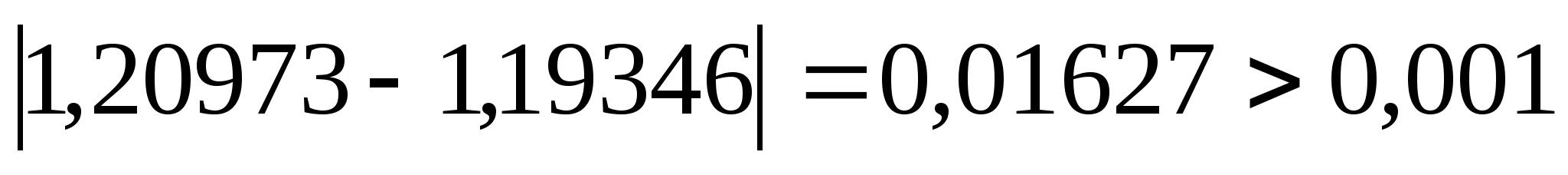 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.
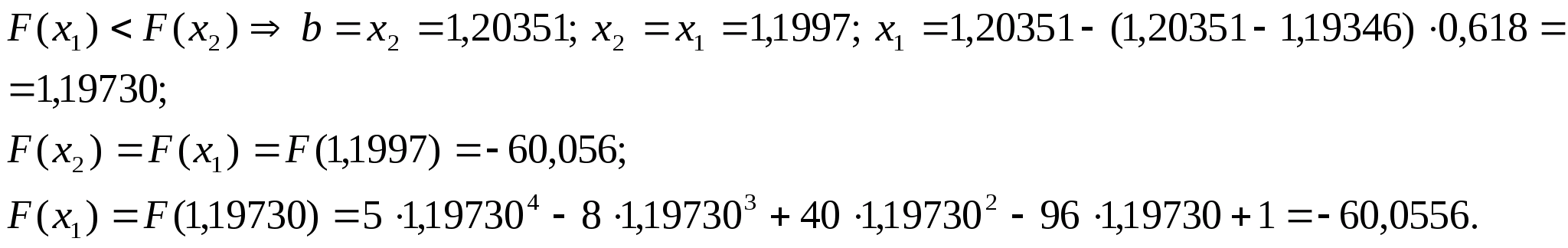 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
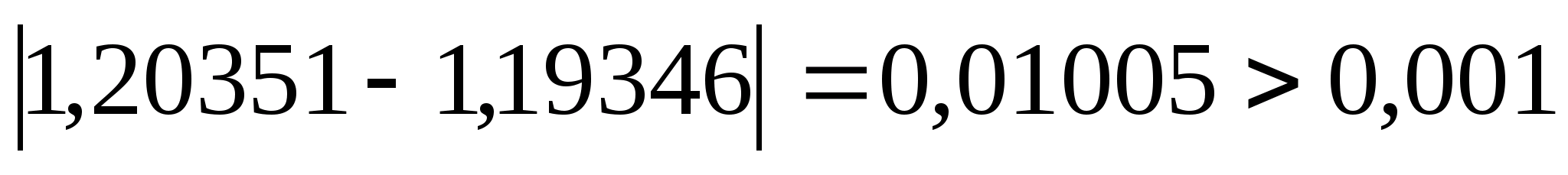 ,
тому продовжуємо процедуру.
,
тому продовжуємо процедуру.
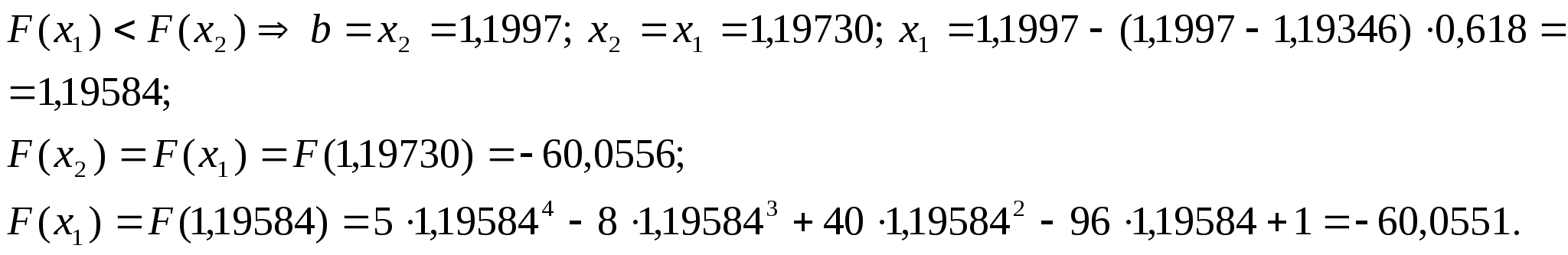 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
 ,
тому продовжуємо процедуру.
,
тому продовжуємо процедуру.
 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.
 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
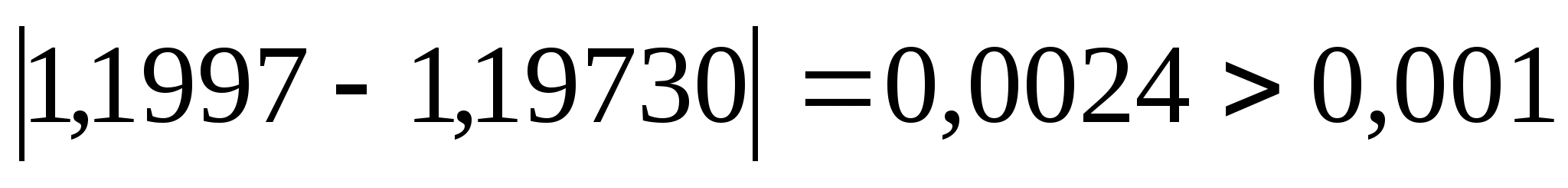 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.
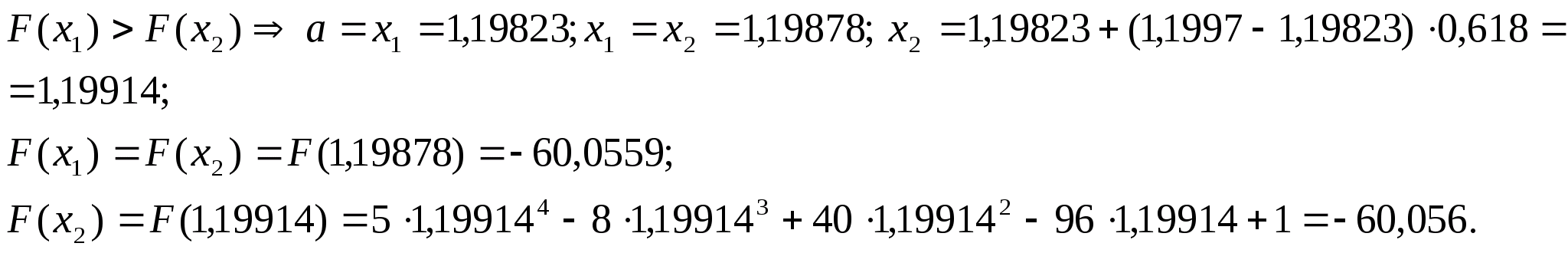 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
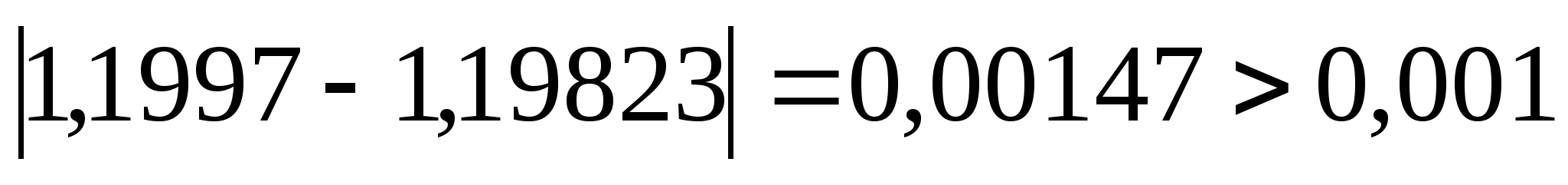 ,
отже продовжуємо процедуру.
,
отже продовжуємо процедуру.
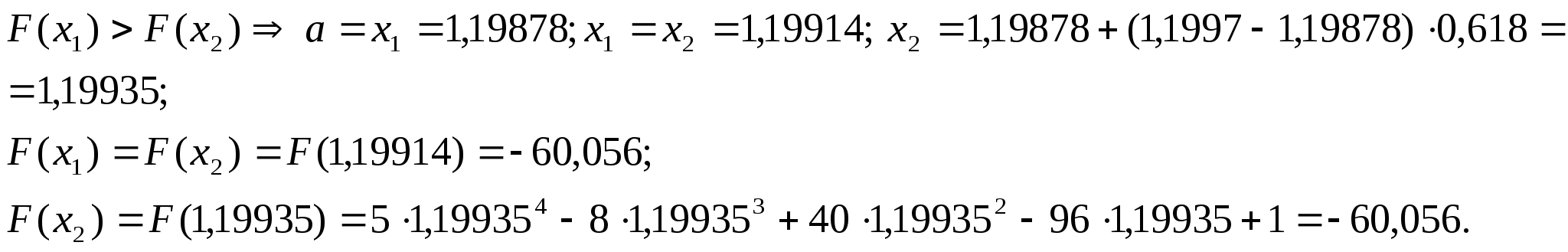 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
 .
Отже за точку локального мінімуму можна
взяти середину відрізку
.
Отже за точку локального мінімуму можна
взяти середину відрізку
 .
При цьому мінімальне значення вихідної
функції буде рівним:
.
При цьому мінімальне значення вихідної
функції буде рівним:
 .
.
Метод
дихотомії побудований таким чином, що
кожний наступний інтервал невизначеності
менше попереднього. Як бачимо, в порівнянні
з методом золотого перерізу цей метод
сходиться значно швидше (тобто через
меншу кількість кроків отримуємо
інтервал невизначеності заданої довжини,
що містить
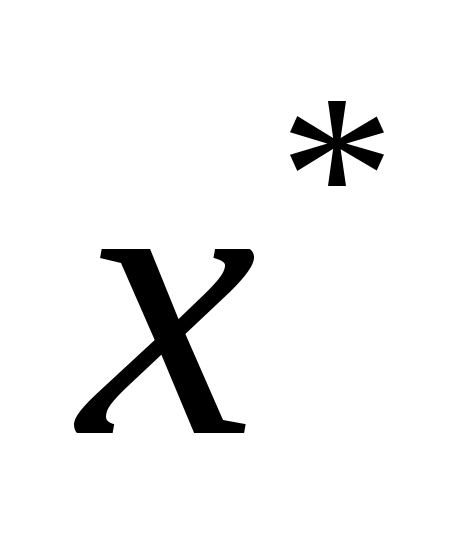 (в
методі дихотомії ми зробили 11 ітерацій,
а в методі золотого перерізу - 16). Крім
того, метод дихотомії потребує вдвічі
менше обчислень, ніж метод золотого
перерізу. Однак мінімальне значення
функції знайдене обома методами
співпадає, тому можемо зробити висновок,
що доцільніше використовувати метод
дихотомії для зменшення затрат часу на
розв’язання задачі.
(в
методі дихотомії ми зробили 11 ітерацій,
а в методі золотого перерізу - 16). Крім
того, метод дихотомії потребує вдвічі
менше обчислень, ніж метод золотого
перерізу. Однак мінімальне значення
функції знайдене обома методами
співпадає, тому можемо зробити висновок,
що доцільніше використовувати метод
дихотомії для зменшення затрат часу на
розв’язання задачі.
метод Фібоначчі
Спочатку
згенеруємо послідовність чисел Фібоначчі:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,
2584, 4181, … . Початкові обрахунки проводяться
в точках:
 ,
де
,
де
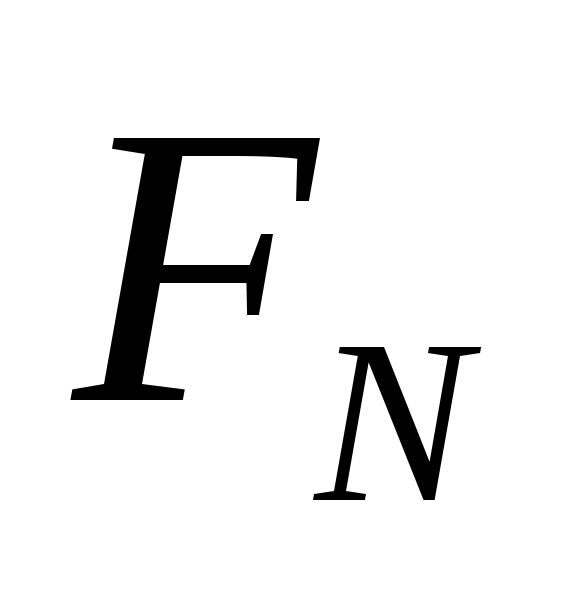 - число Фібоначчі, яке обирається з умови
- число Фібоначчі, яке обирається з умови
 ,
тобто в нашому випадку це 18-те число
Фібоначчі:
,
тобто в нашому випадку це 18-те число
Фібоначчі:
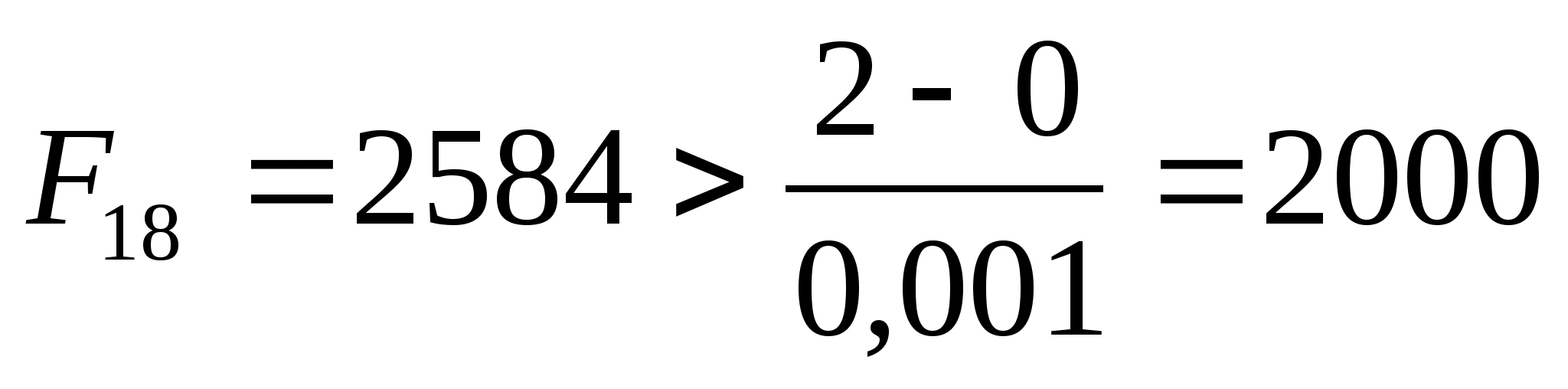 .
Ці точки розташовані симетрично відносно
середини відрізку
.
Ці точки розташовані симетрично відносно
середини відрізку
 .
На кожному кроці точка наступного
обрахунку обирається симетрично відносно
середини відрізка локалізації до точки
уже проведеного обрахунку, що лежить
на цьому відрізку. В силу властивостей
чисел Фібоначчі кількість ітерацій
строго обмежена і дорівнює N=18.
Отже можемо знайти початкові точки
ділення:
.
На кожному кроці точка наступного
обрахунку обирається симетрично відносно
середини відрізка локалізації до точки
уже проведеного обрахунку, що лежить
на цьому відрізку. В силу властивостей
чисел Фібоначчі кількість ітерацій
строго обмежена і дорівнює N=18.
Отже можемо знайти початкові точки
ділення:
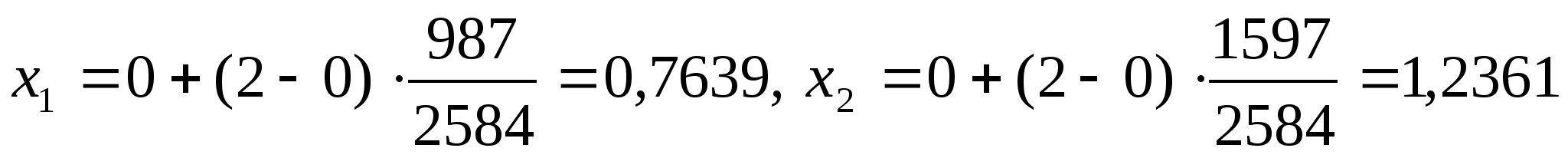 .
Далі обчислюємо значення функції в цих
точках:
.
Далі обчислюємо значення функції в цих
точках:
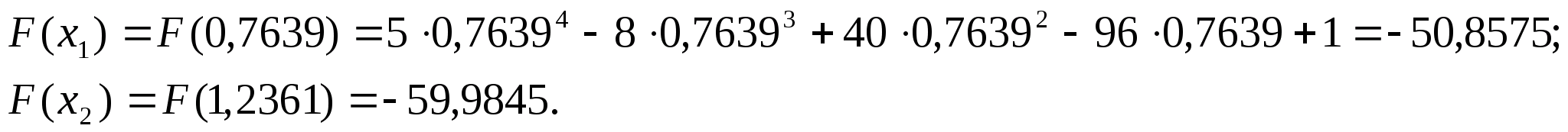
Оскільки
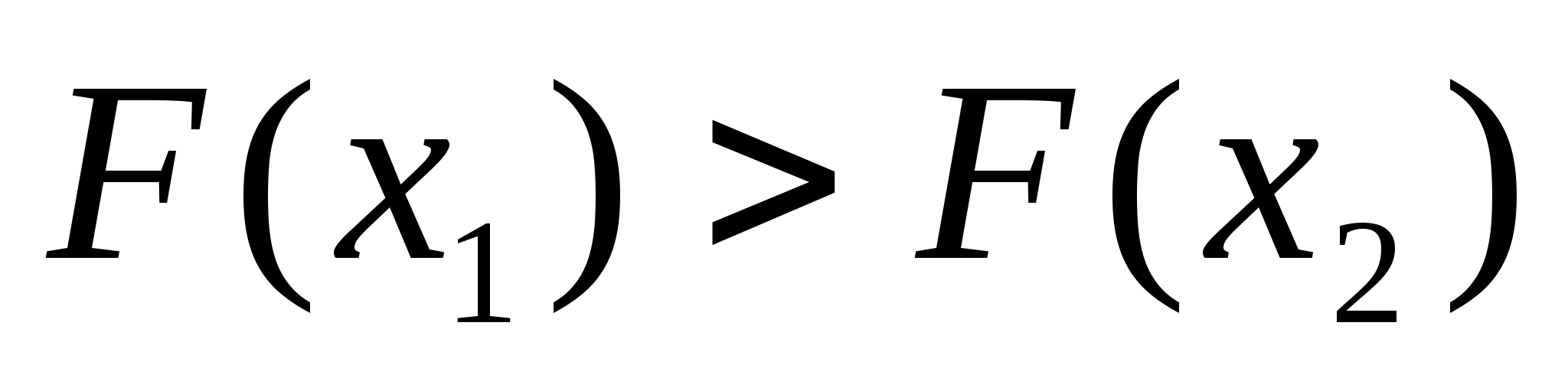 ,
то покладаємо, що N=N-1=18-1=17.
Нові
межі відрізка тепер будуть рівними
,
то покладаємо, що N=N-1=18-1=17.
Нові
межі відрізка тепер будуть рівними
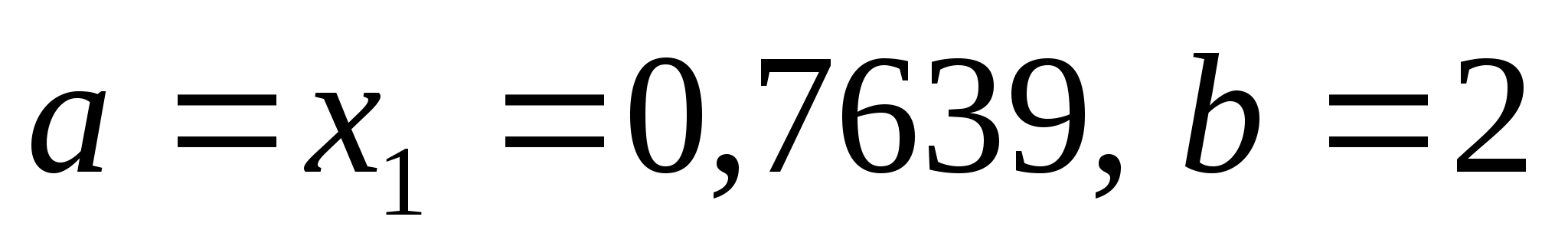 .
Знаходимо нові точки ділення:
.
Знаходимо нові точки ділення:
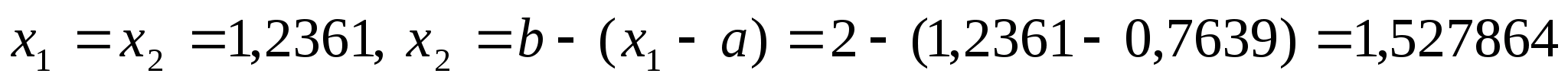 .
Значення функції в цих точках:
.
Значення функції в цих точках:

Оскільки
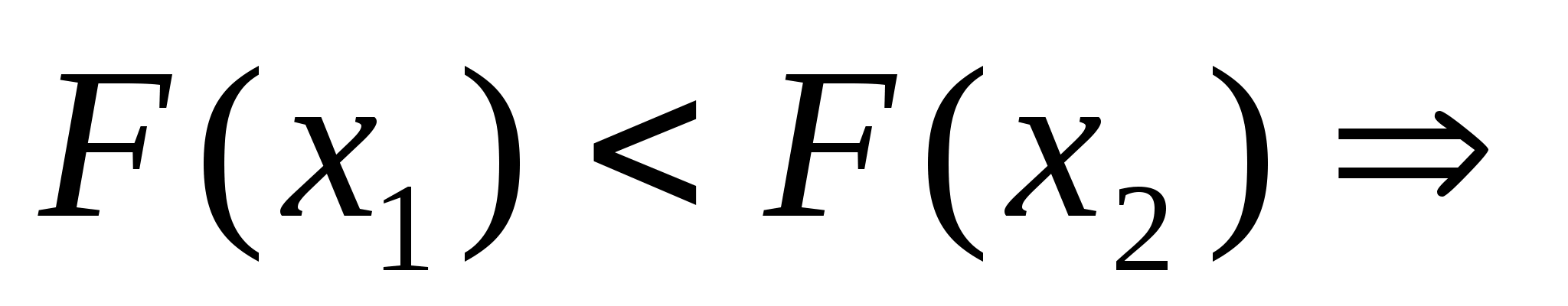 N=16,
нові межі відрізка -
N=16,
нові межі відрізка - .
.

Оскільки
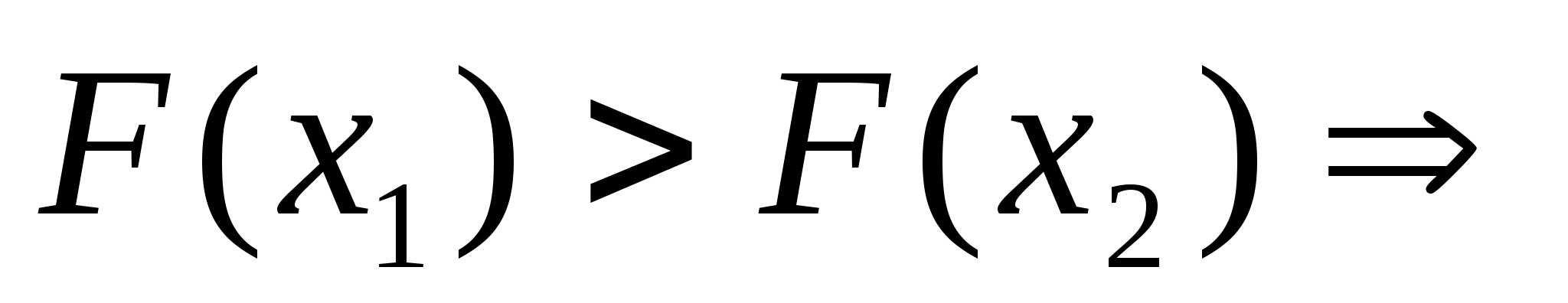 N=15,
нові межі відрізка -
N=15,
нові межі відрізка -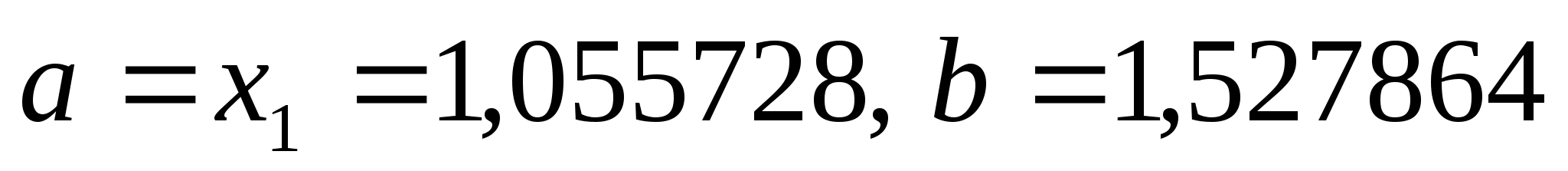 .
.
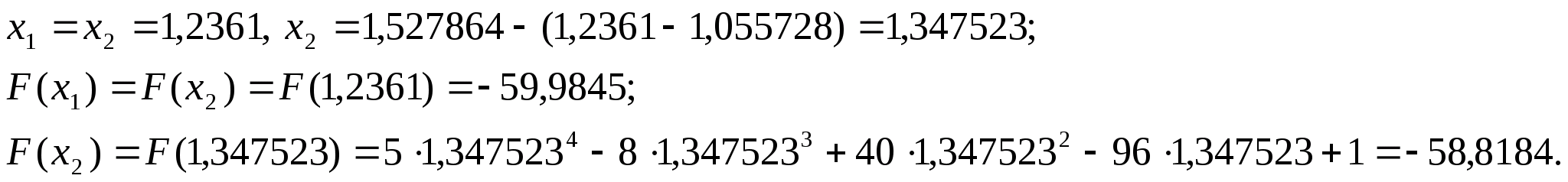
Оскільки
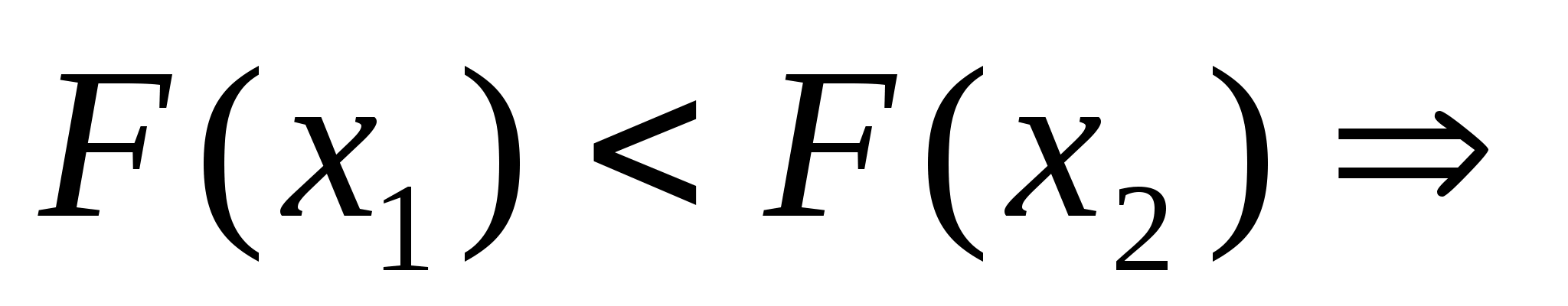 N=14,
нові межі відрізка -
N=14,
нові межі відрізка -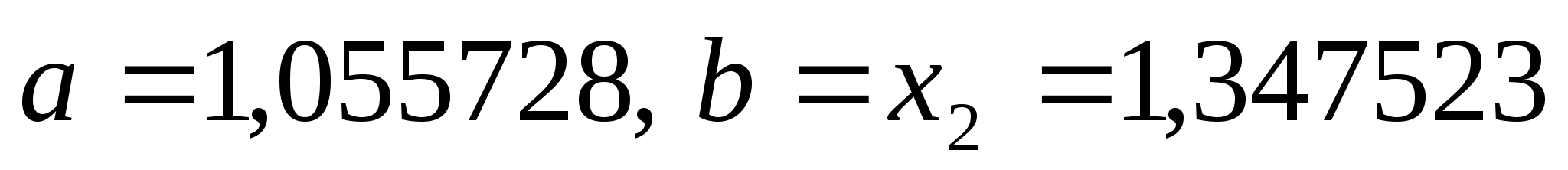 .
.

Оскільки
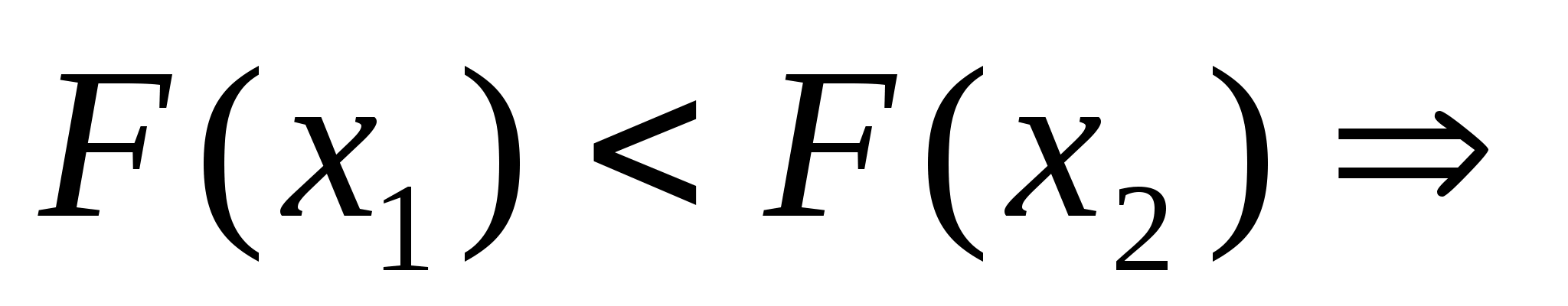 N=13,
нові межі відрізка -
N=13,
нові межі відрізка - .
.
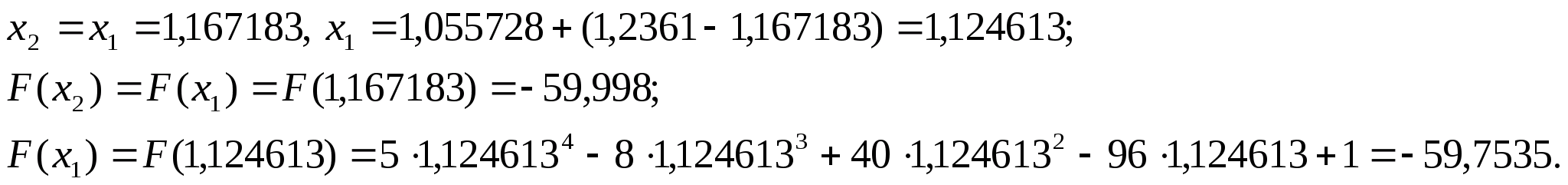
Оскільки
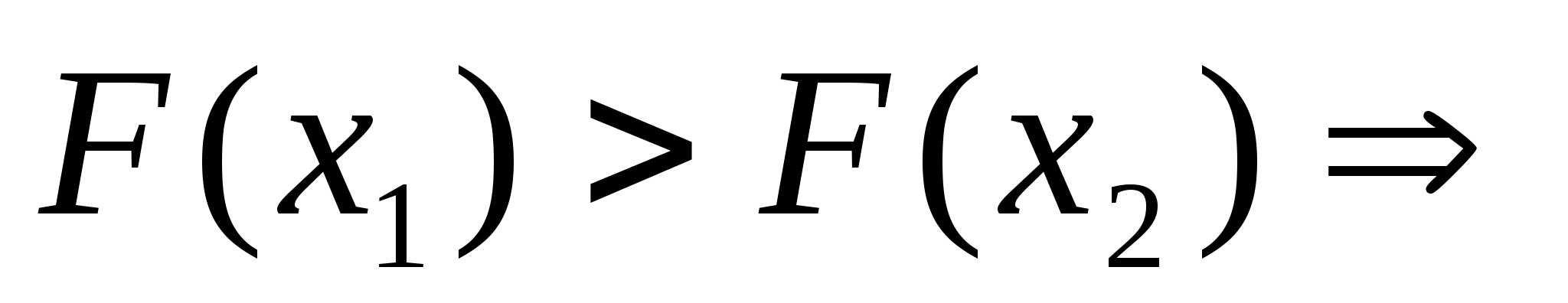 N=12,
нові межі відрізка -
N=12,
нові межі відрізка - .
.

Оскільки
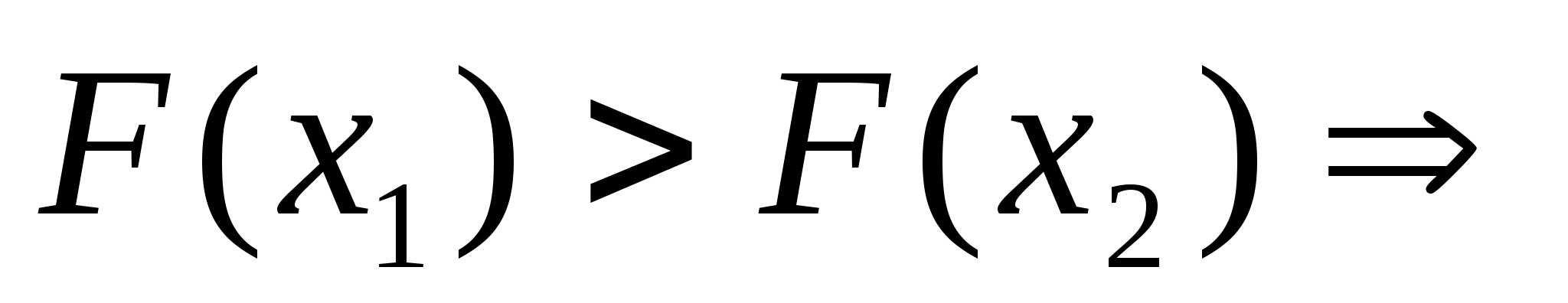 N=11,
нові межі відрізка -
N=11,
нові межі відрізка - .
.
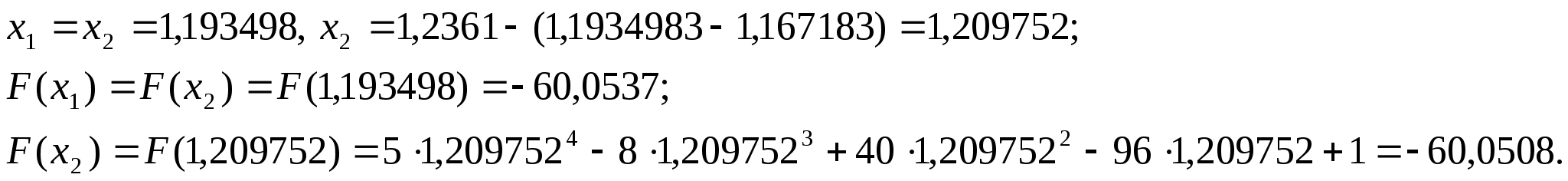
Оскільки
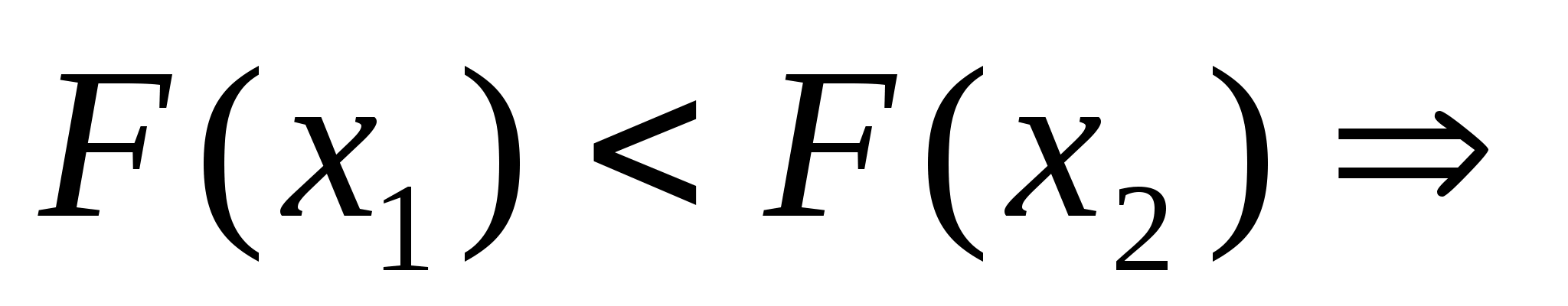 N=10,
нові межі відрізка -
N=10,
нові межі відрізка -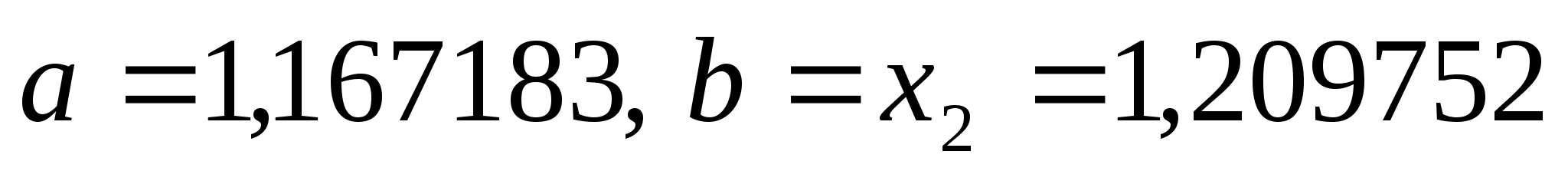 .
.
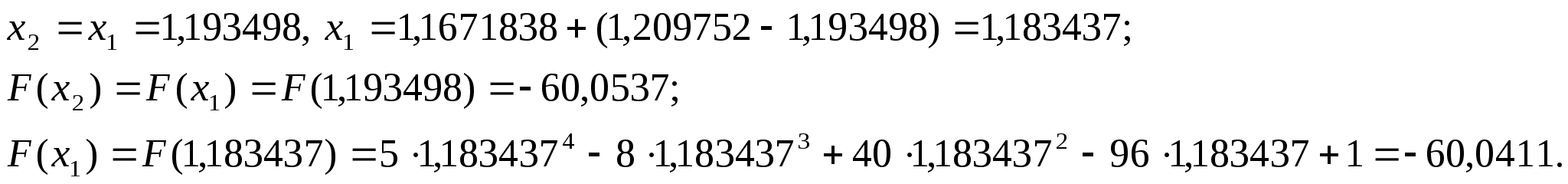
Оскільки
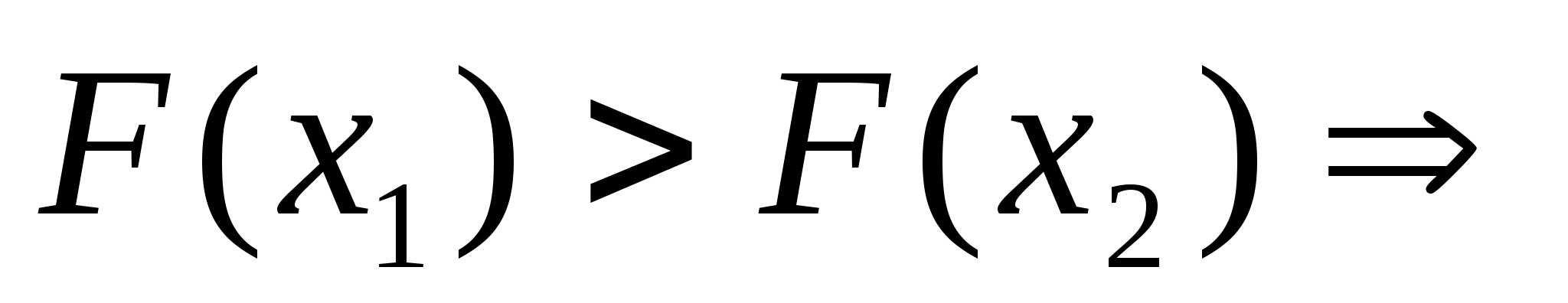 N=9,
нові межі відрізка -
N=9,
нові межі відрізка - .
.
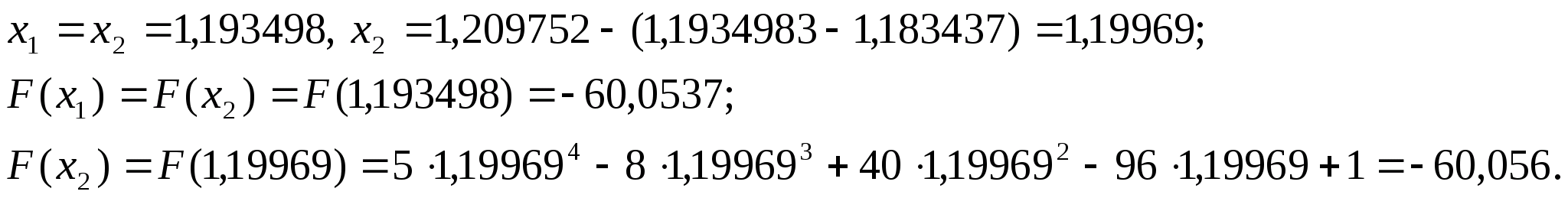
Оскільки
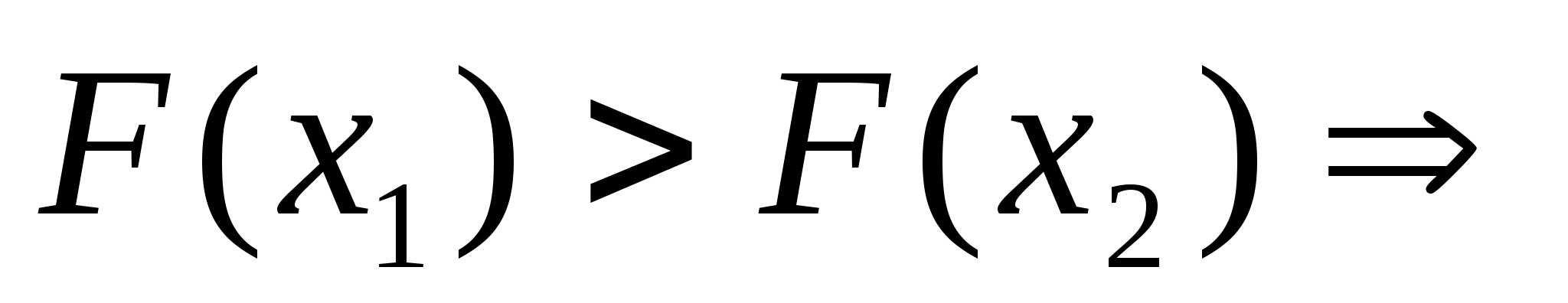 N=8,
нові межі відрізка -
N=8,
нові межі відрізка - .
.

Оскільки
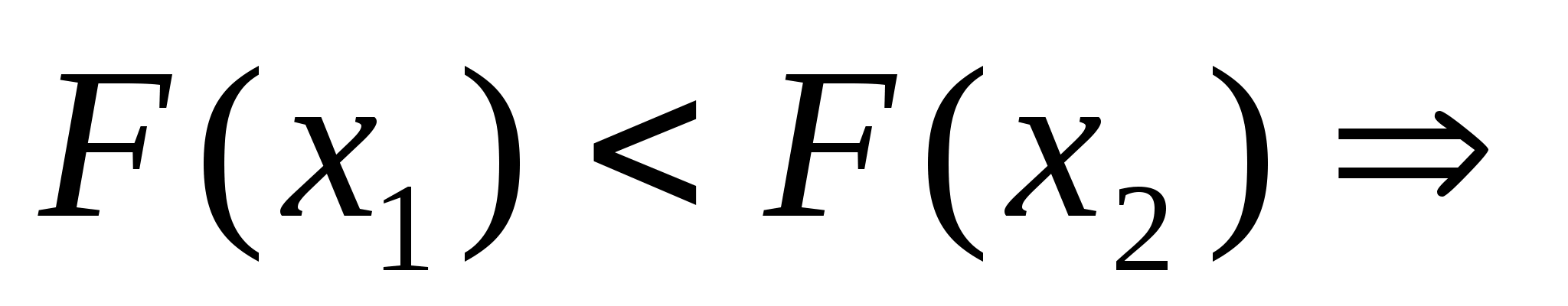 N=7,
нові межі відрізка -
N=7,
нові межі відрізка - .
.
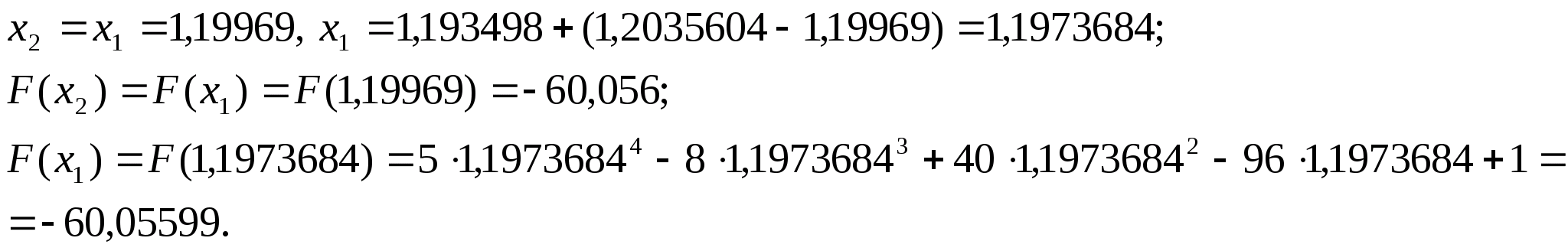
Оскільки
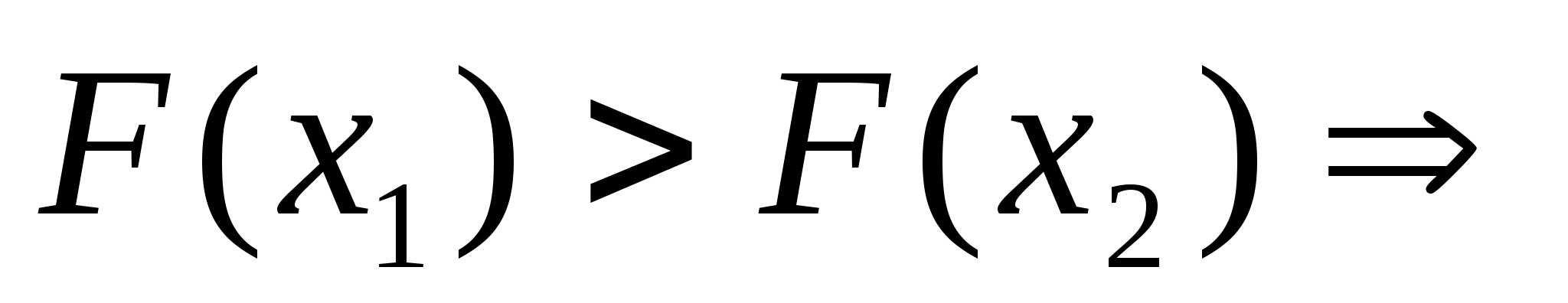 N=6,
нові межі відрізка -
N=6,
нові межі відрізка -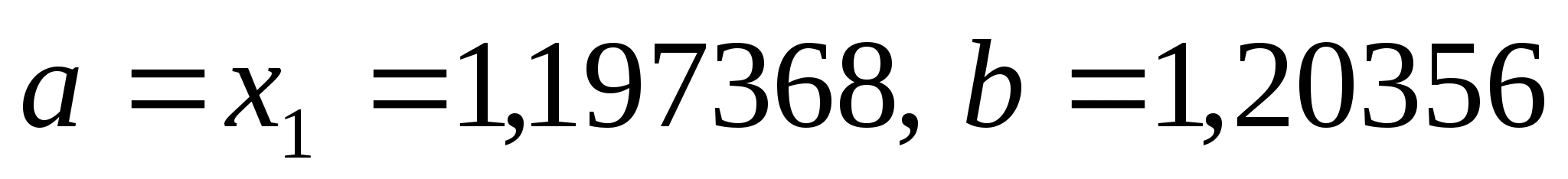 .
.

Оскільки
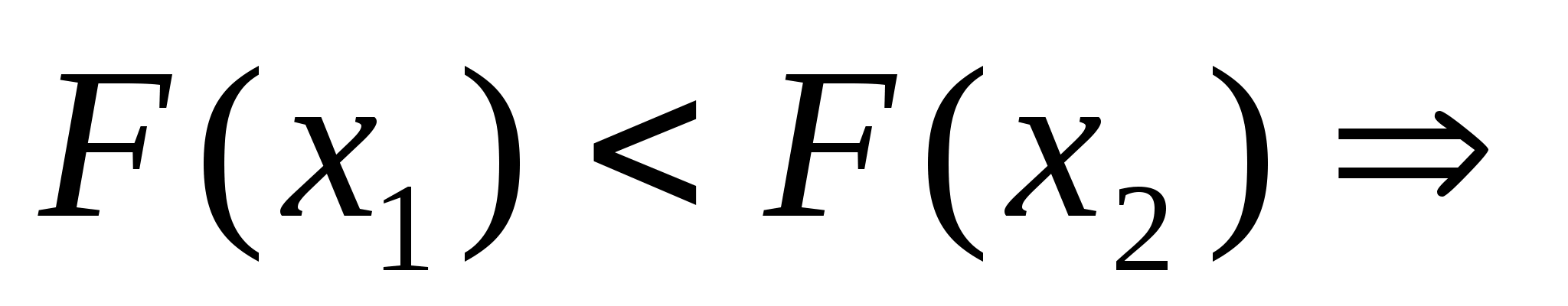 N=5,
нові межі відрізка -
N=5,
нові межі відрізка -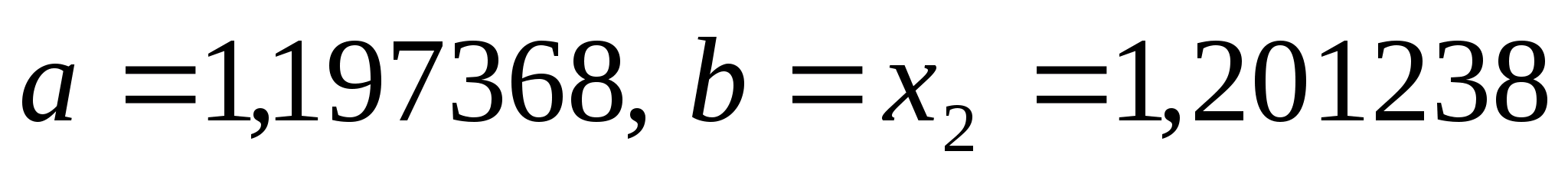 .
.

Оскільки
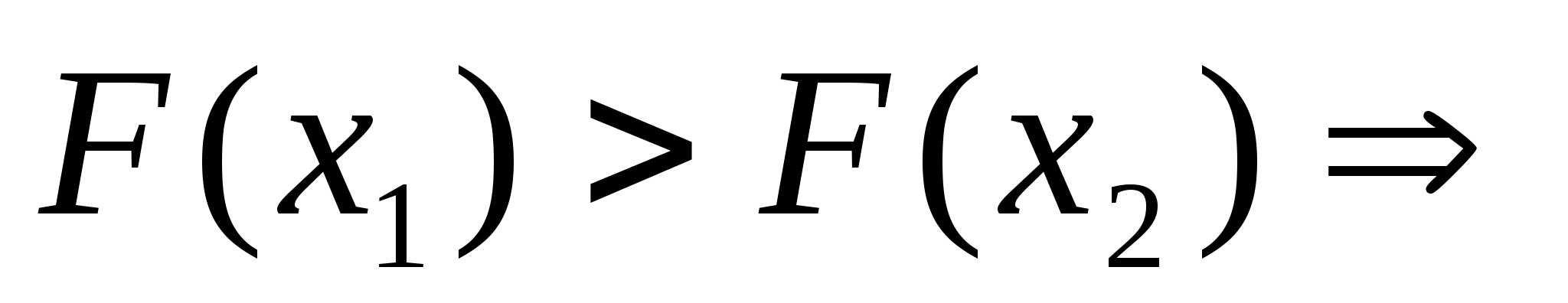 N=4,
нові межі відрізка -
N=4,
нові межі відрізка -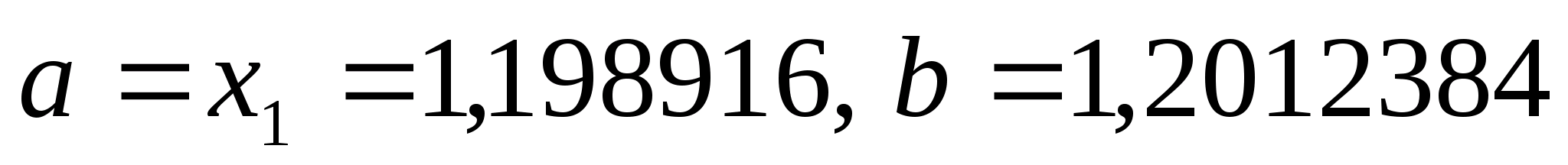 .
.
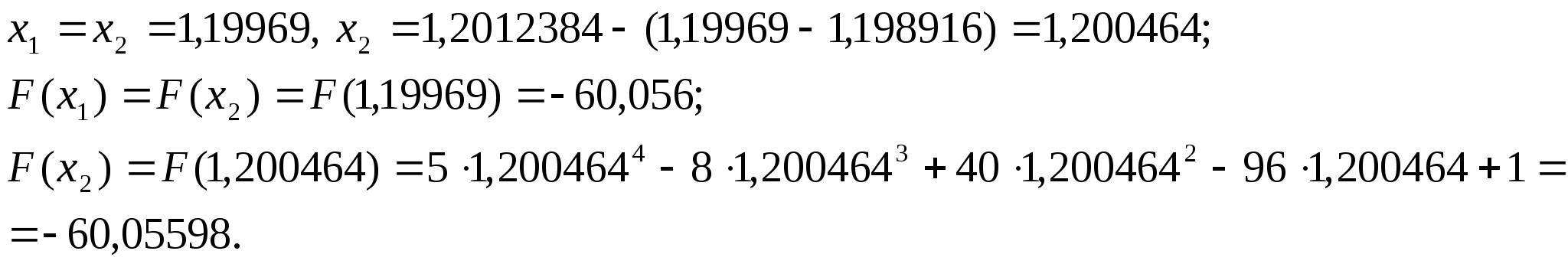
Оскільки
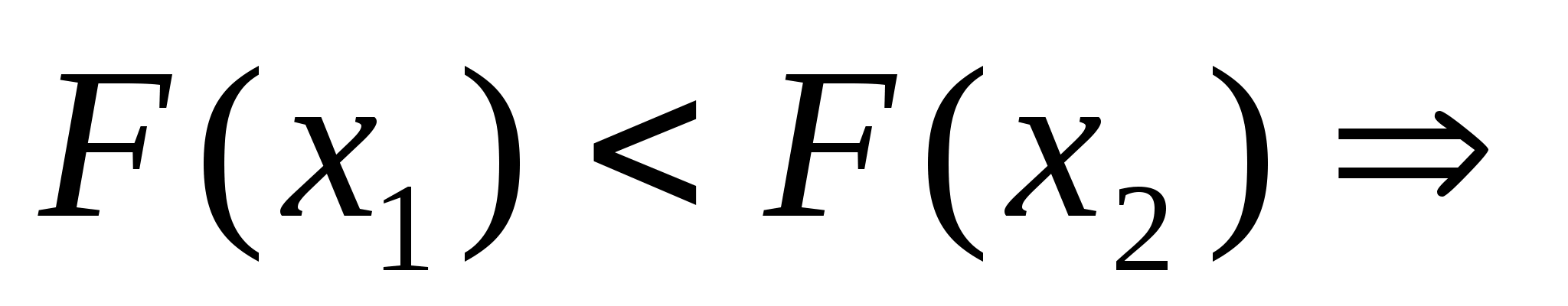 N=3,
нові межі відрізка -
N=3,
нові межі відрізка - .
.

Оскільки
 ,
то локальний мінімум досягається в
точці
,
то локальний мінімум досягається в
точці
 .
При цьому мінімальне значення вихідної
функції буде рівним:
.
При цьому мінімальне значення вихідної
функції буде рівним:
 .
Отже мінімальне значення функції,
знайдене методом дихотомії, методом
золотого перерізу і методом Фібоначчі
співпадають. Однак найбільше ітерацій
було зроблено при розв’занні задачі
методом Фібоначчі.
.
Отже мінімальне значення функції,
знайдене методом дихотомії, методом
золотого перерізу і методом Фібоначчі
співпадають. Однак найбільше ітерацій
було зроблено при розв’занні задачі
методом Фібоначчі.
3. Розв’язання задачі мінімізації за допомогою методу Ньютона і методу найшвидшого спуску
Розв’яжемо
задачу мінімізації для функції
 ,
використовуючи метод
Ньютона.
Це метод другого порядку, який використовує
похідну першого і другого порядку від
цільової функції.
,
використовуючи метод
Ньютона.
Це метод другого порядку, який використовує
похідну першого і другого порядку від
цільової функції.
Перш ніж розв’язувати дану задачу, з’ясуємо чи має вона точку локального мінімуму. Для цього побудуємо матрицю Гессе.
Знайдемо
частинні похідні першого і другого
порядку від функції
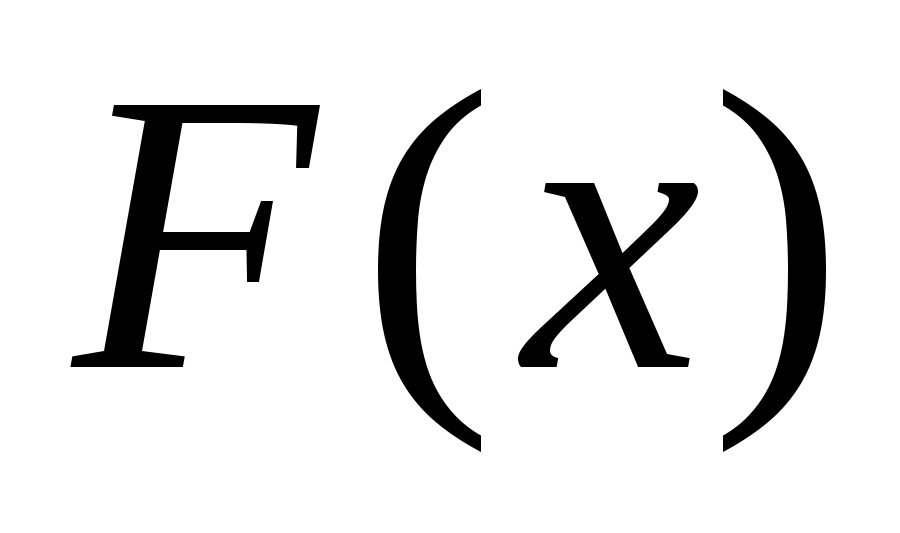 :
:

Отже матриця Гессе матиме вигляд:
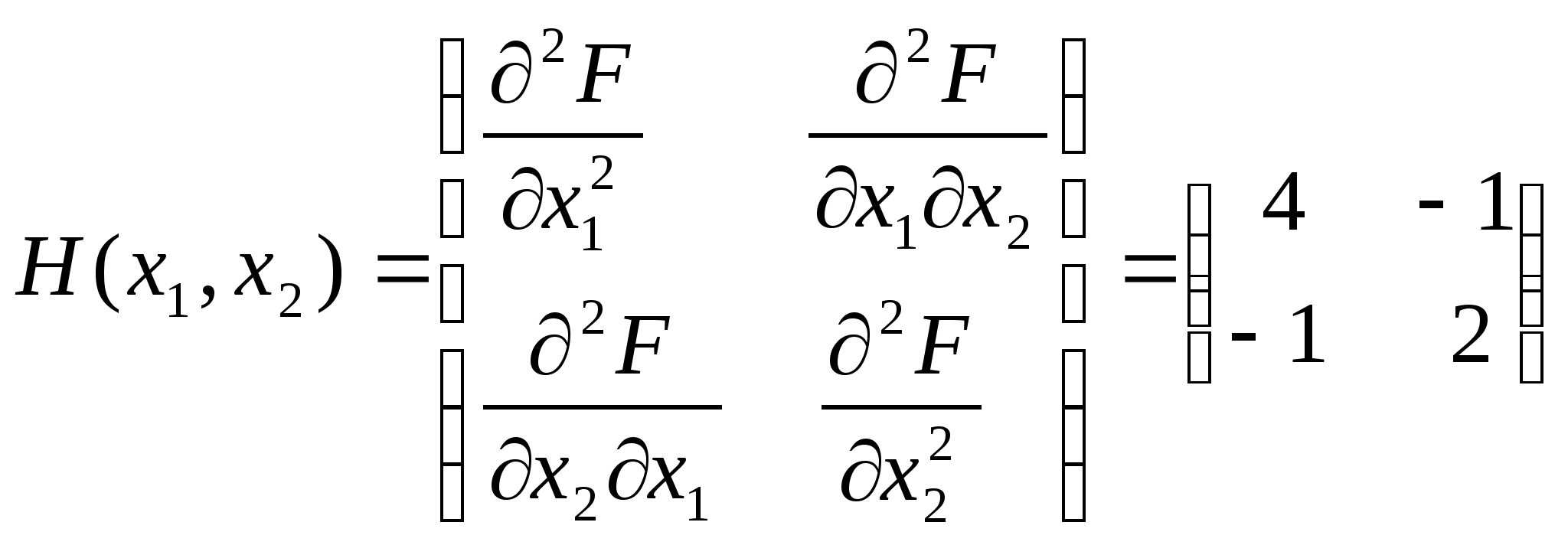 .
А оскільки головні мінори додатні:
.
А оскільки головні мінори додатні:
 ,
то матриця Гессе додатно визначена.
Тобто достатні умови існування локального
мінімуму виконані.
,
то матриця Гессе додатно визначена.
Тобто достатні умови існування локального
мінімуму виконані.
Так
як цільова функція є опуклою, тобто це
задача опуклого програмування, а функція
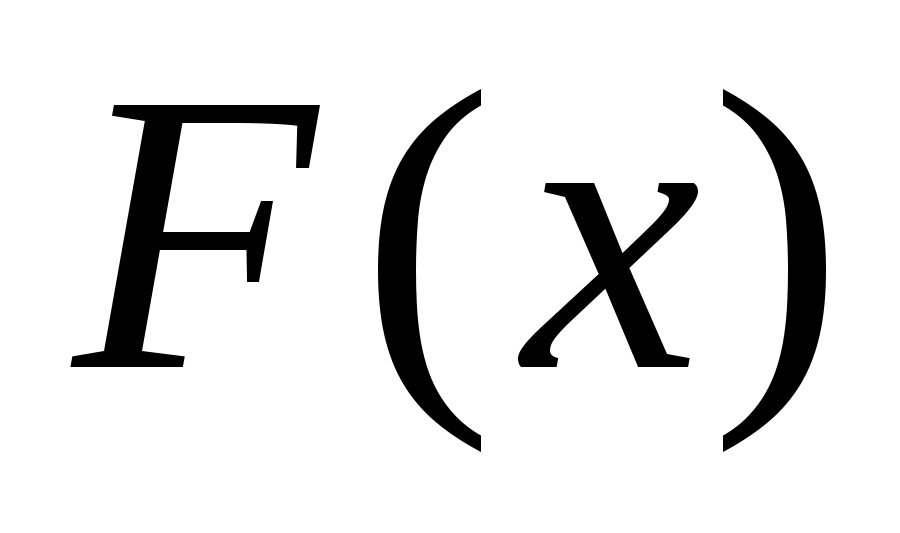 є неперервно диференційованою в Rn
, то якщо точка
є неперервно диференційованою в Rn
, то якщо точка
 є точкою локального екстремуму, то вона
буде і точкою глобального екстремуму
для цієї задачі.
є точкою локального екстремуму, то вона
буде і точкою глобального екстремуму
для цієї задачі.
Отже
можемо застосувати метод Ньютона.
Послідовність точок, яка прямує до точки
мінімуму функції
 згідно цього методу знаходиться за
формулою:
згідно цього методу знаходиться за
формулою:
 ,
де
,
де
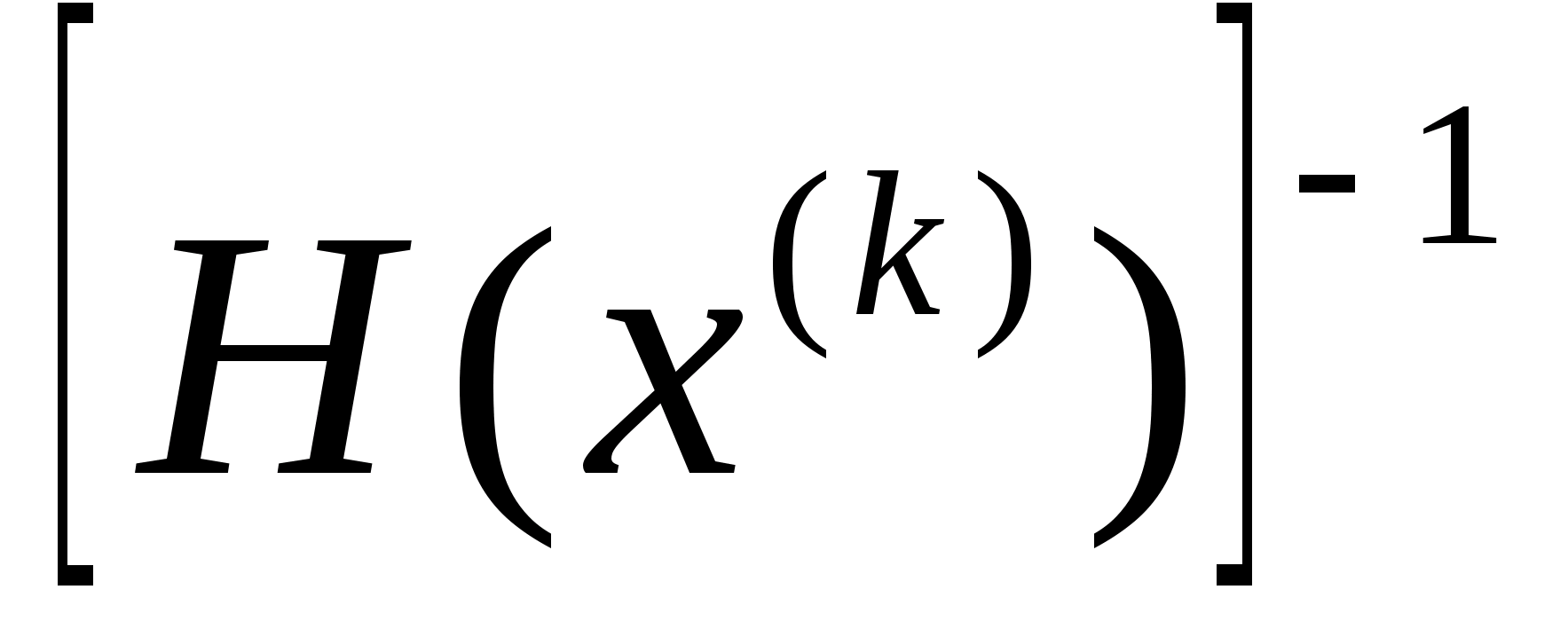 - обернена матриця Гессе.
- обернена матриця Гессе.
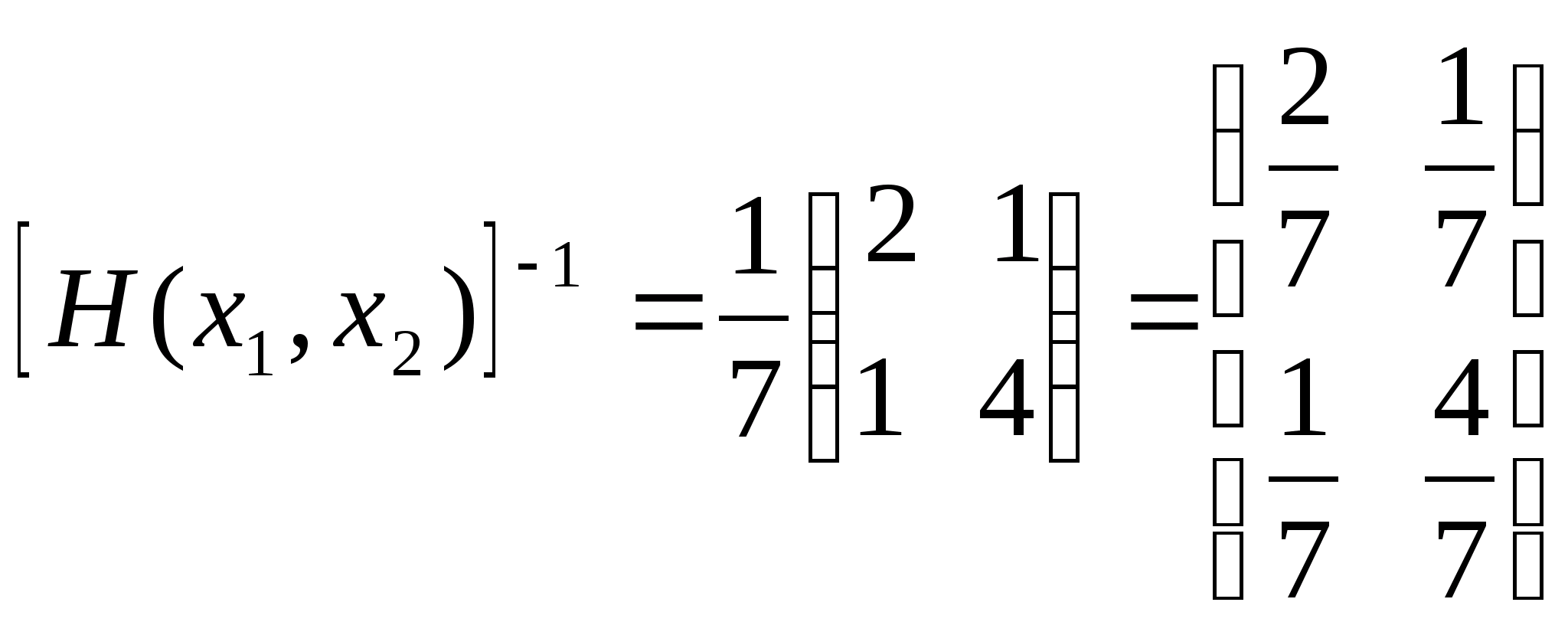 .
.
Обиремо
в допустимій області задачі довільну
точку – початкове наближення. Нехай це
буде точка
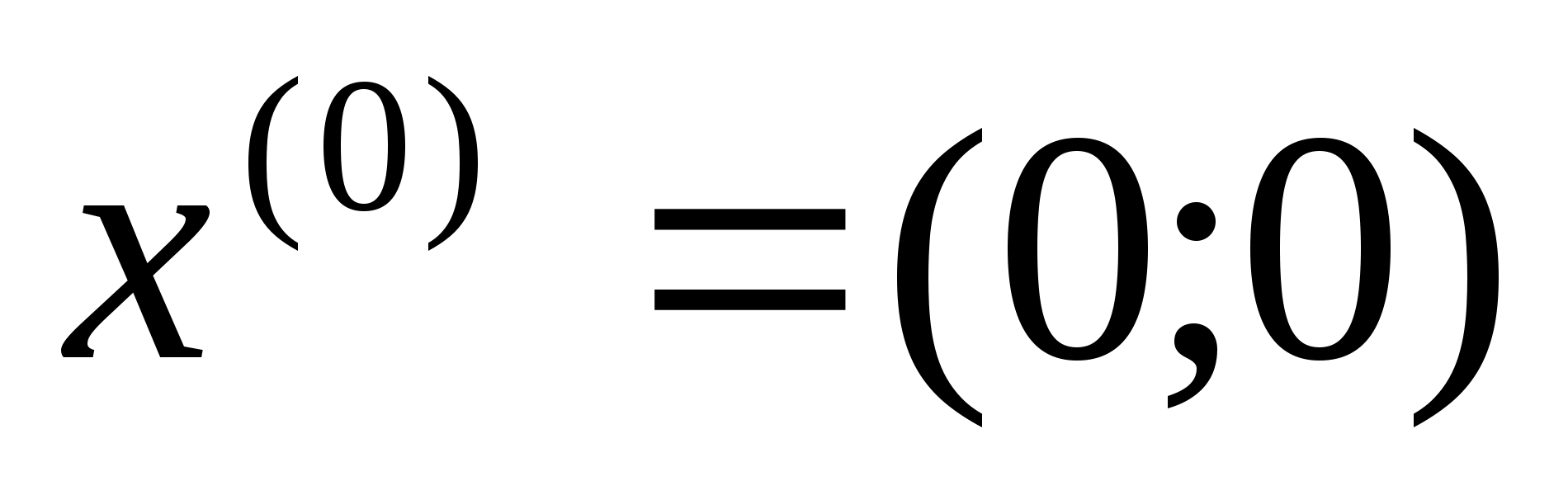 .
.
Знайдемо
градієнт цільової функції: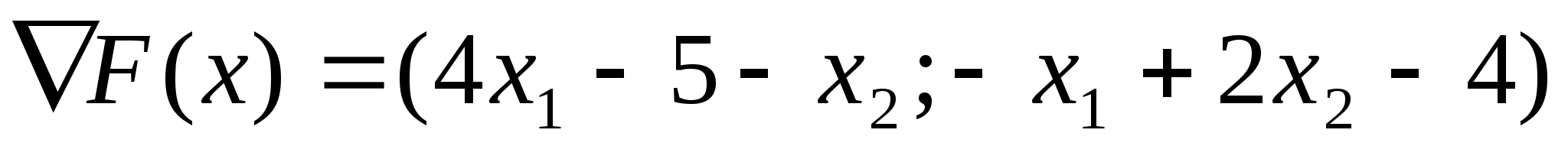 і
обчислимо його в точці
і
обчислимо його в точці
 :
:
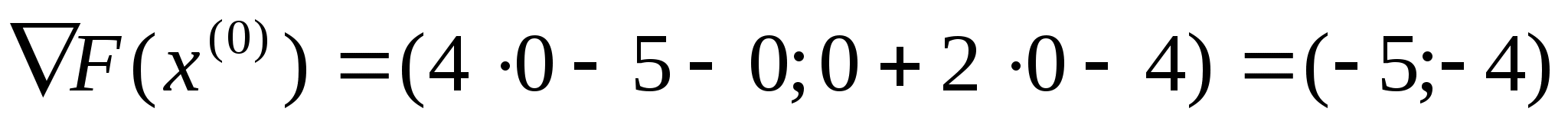 .
.
Знайдемо
наступне наближення до оптимального
розв’язку вихідної задачі:
 і обчислимо градієнт цільової функції
в цій точці:
і обчислимо градієнт цільової функції
в цій точці:
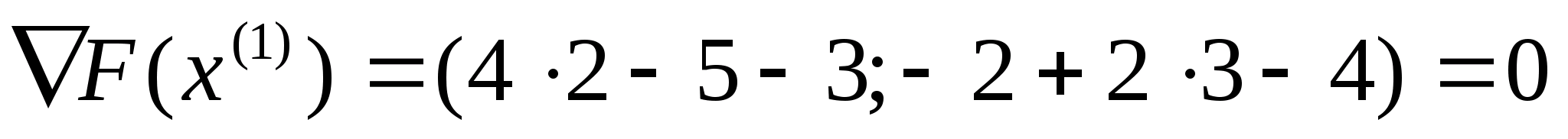 .
Рівність градієнта цільової функції
нулю є необхідною умовою існування
екстремуму функції багатьох змінних.
Тобто оптимальний розв’язок задачі
.
Рівність градієнта цільової функції
нулю є необхідною умовою існування
екстремуму функції багатьох змінних.
Тобто оптимальний розв’язок задачі
 ,
причому
,
причому
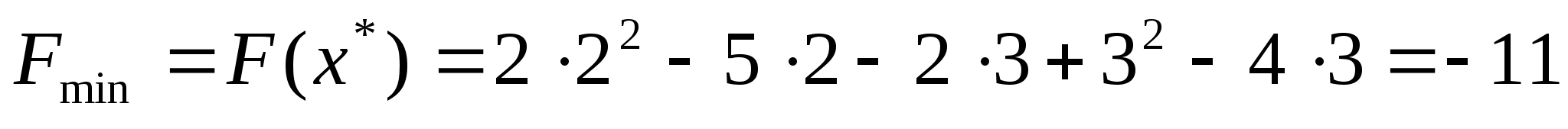 .
.
Тепер
розв’яжемо задачу мінімізації для
функції
 ,
використовуючи метод
найшвидшого спуску.
Цей метод відноситься до градієнтних
методів.
,
використовуючи метод
найшвидшого спуску.
Цей метод відноситься до градієнтних
методів.
За
даним методом будується послідовність
точок
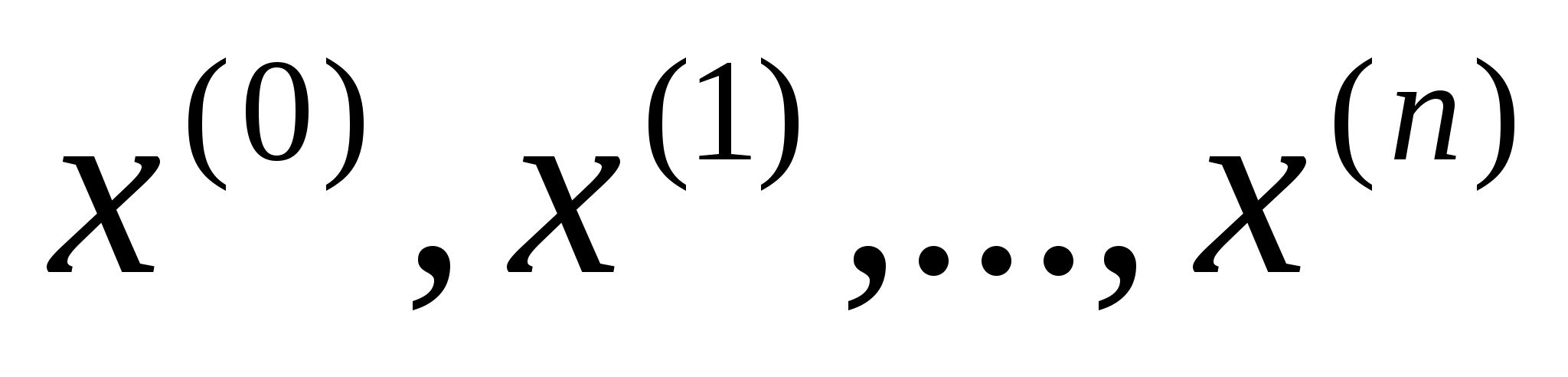 ,
яка прямує до оптимального розв’язку
задачі -
,
яка прямує до оптимального розв’язку
задачі -
 .
Від точки
.
Від точки
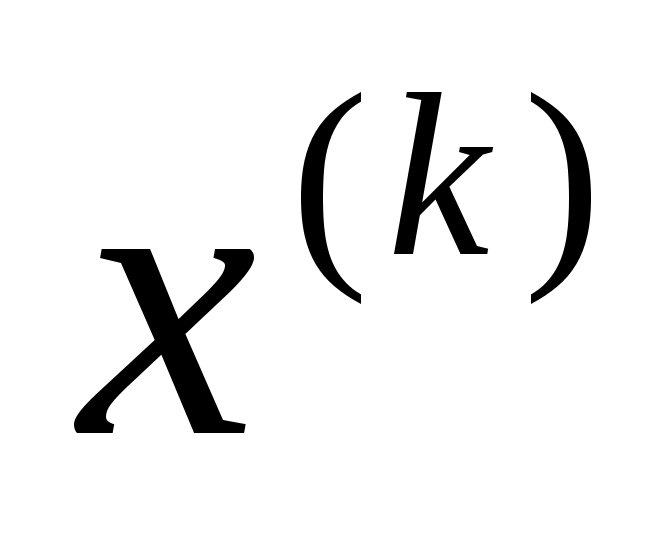 до точки
до точки
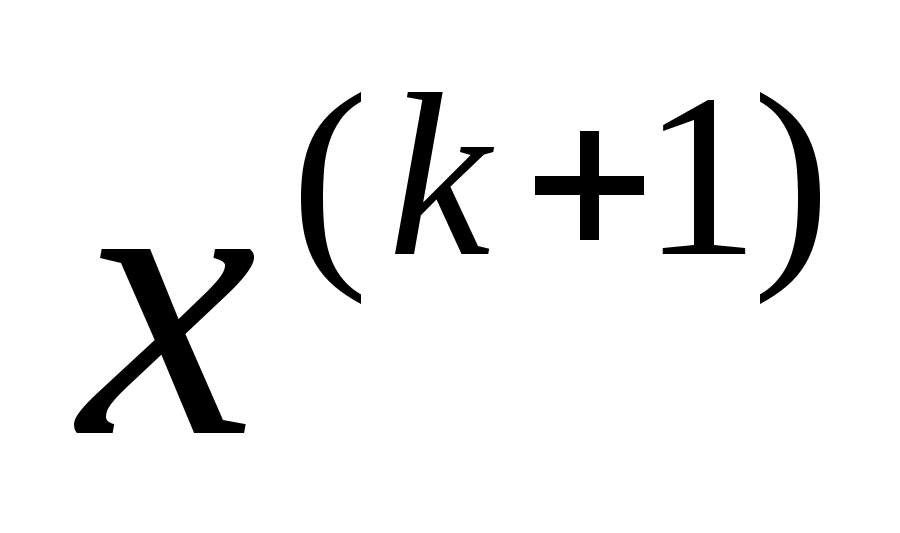 рухаються в напрямі градієнта цільової
функції, обчисленого в точці
рухаються в напрямі градієнта цільової
функції, обчисленого в точці
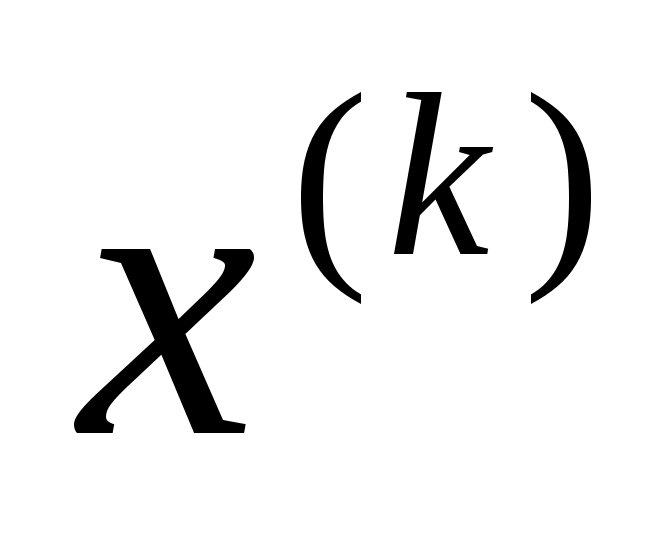 .
.
Широке
застосування цього методу обумовлено
тим, що в напряму антиградієнту —
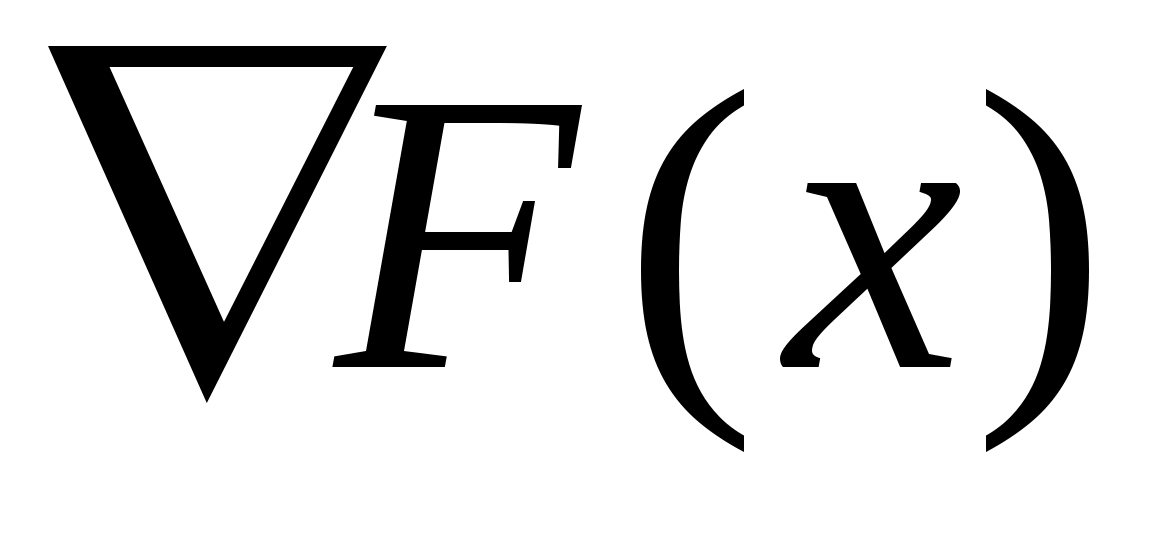 похідна
функції за напрямом досягає найменшого
значення.
похідна
функції за напрямом досягає найменшого
значення.
Алгоритм методу найшвидшого спуску:
Обираємо
довільну початкову точку
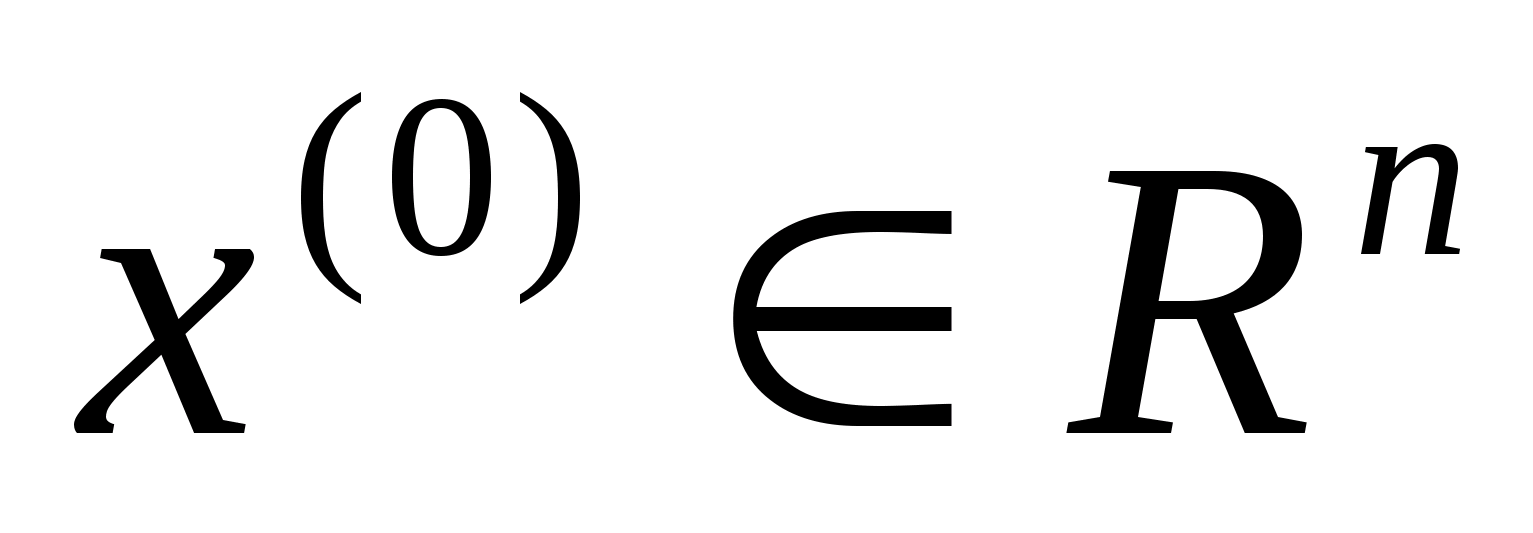 ,
яка називається початковим наближенням
розв’язку задачі
,
яка називається початковим наближенням
розв’язку задачі
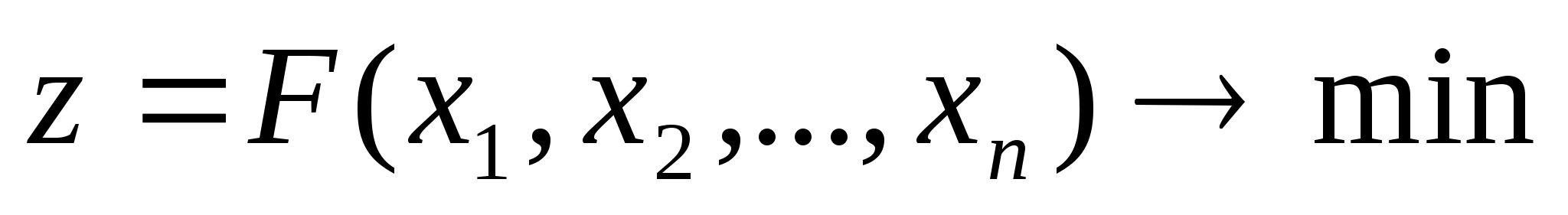 ,
і покладаємо, що
,
і покладаємо, що
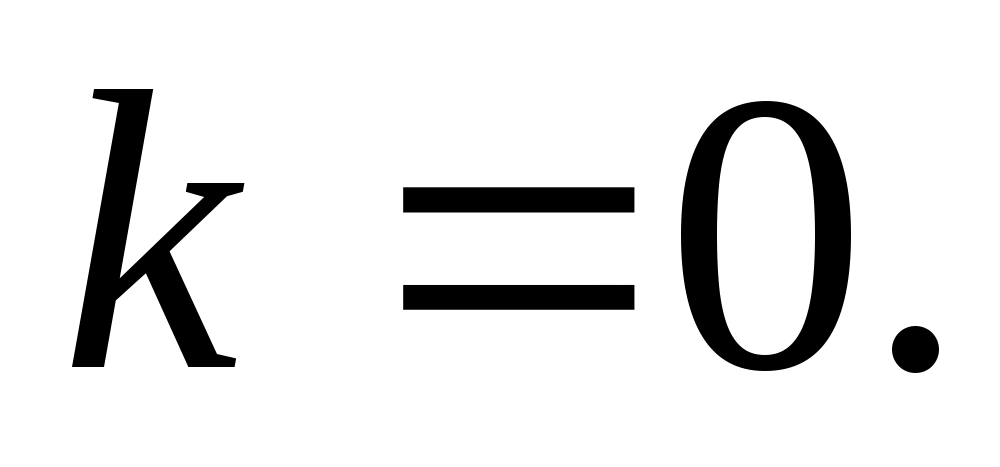 При цьому функція
При цьому функція
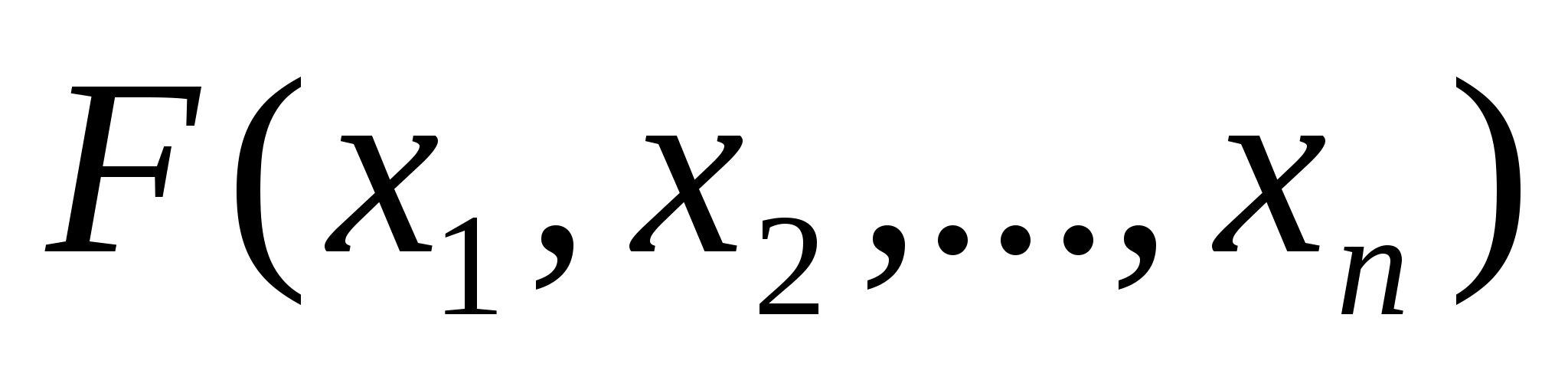 вважається опуклою і неперервно
диференційованою в
вважається опуклою і неперервно
диференційованою в
 .
Також обираємо точність обчислень
.
Також обираємо точність обчислень
 .
.
Обчислюємо
градієнт цільової функції
 .
Якщо
.
Якщо
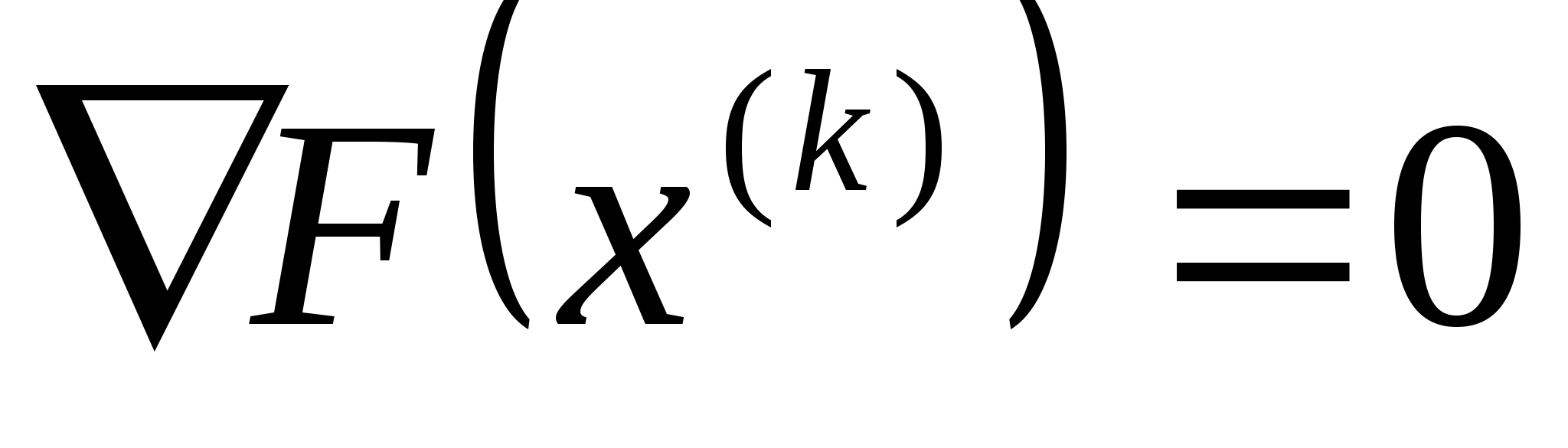 ,
то покладаємо
,
то покладаємо
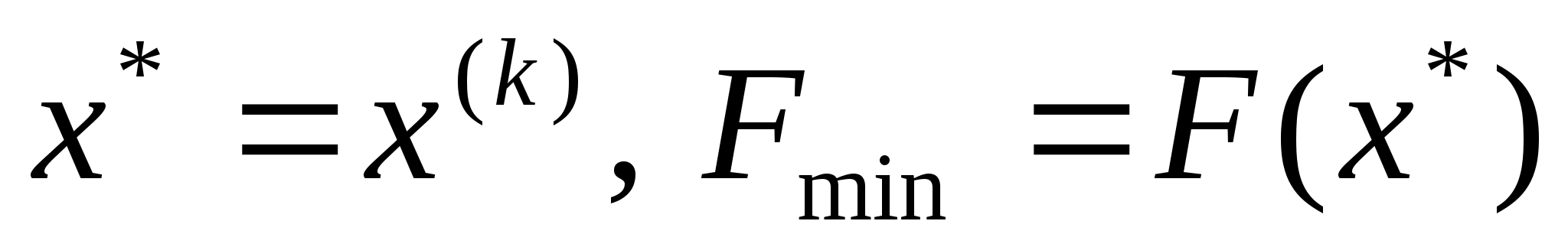 і зупиняємо обчислення, інакше -
переходимо до кроку 3.
і зупиняємо обчислення, інакше -
переходимо до кроку 3.
Шукаємо
наступне наближення за формулою:
 -
для задачі мінімізації, а для задачі
максимізації:
-
для задачі мінімізації, а для задачі
максимізації:
 .
Число
.
Число
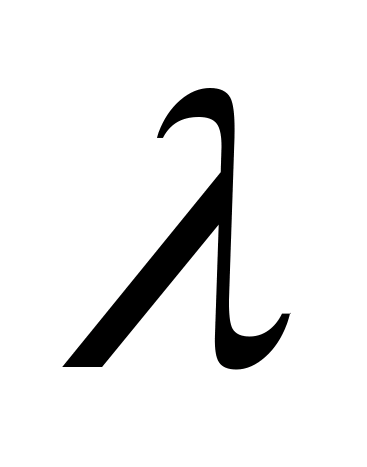 - параметр, який називається довжиною
кроку в точці
- параметр, який називається довжиною
кроку в точці
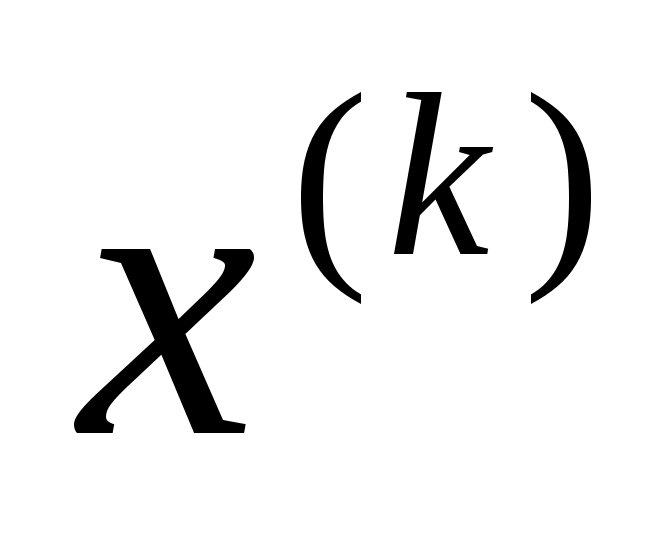 .
Його обирають довільно, однак зазвичай,
параметр
.
Його обирають довільно, однак зазвичай,
параметр
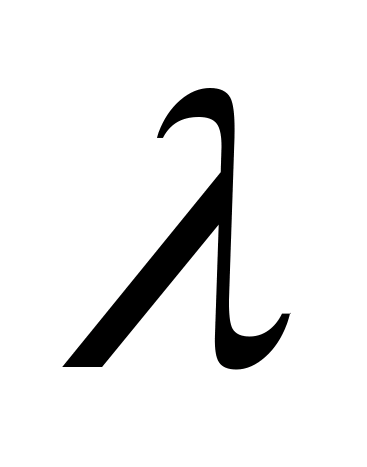 обирається з умови, щоб в точці
обирається з умови, щоб в точці
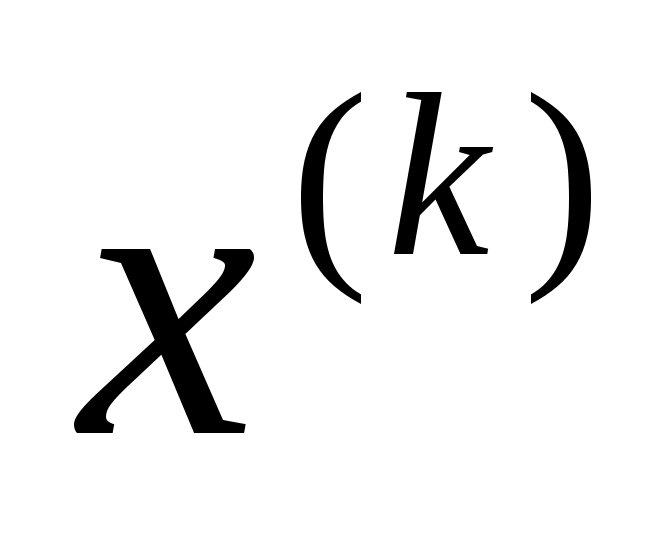 спостерігалося максимальне зменшення
(збільшення) цільової функції
спостерігалося максимальне зменшення
(збільшення) цільової функції
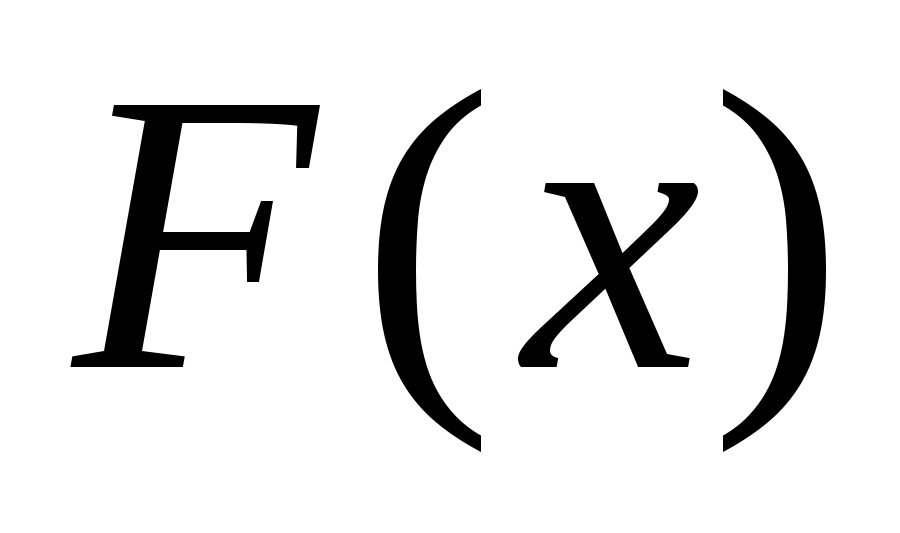 .
.
Перевіряємо
умову зупинки, а саме:
 .
Якщо умова виконана, то покладаємо
.
Якщо умова виконана, то покладаємо
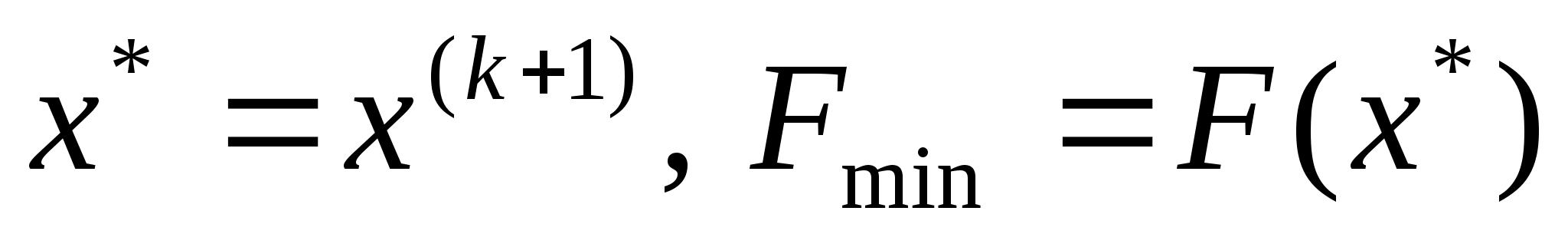 і зупиняємо обчислення, якщо ні, то
переходимо до наступного кроку.
і зупиняємо обчислення, якщо ні, то
переходимо до наступного кроку.
Покладаємо,
що
 і переходимо до кроку 2.
і переходимо до кроку 2.
Тепер перейдемо безпосередньо до нашого прикладу.
Оберемо
спочатку точність обчислень
 .
За початкове наближення як і в методі
Ньютона візьмемо точку
.
За початкове наближення як і в методі
Ньютона візьмемо точку
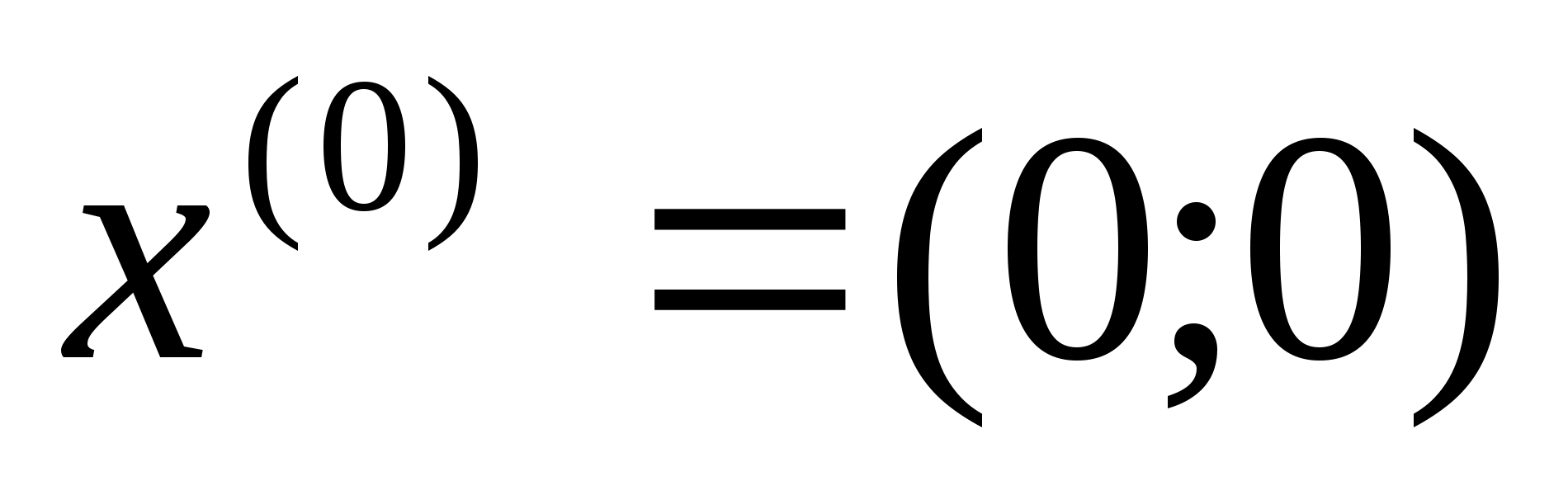 .
З аналізу, проведеного в методі Ньютона,
маємо що цільова функція є опуклою і
неперервно диференційованою в Rn,
отже даний метод застосовувати можна.
.
З аналізу, проведеного в методі Ньютона,
маємо що цільова функція є опуклою і
неперервно диференційованою в Rn,
отже даний метод застосовувати можна.
З
методу Ньютона маємо, що градієнт
цільової функції в точці
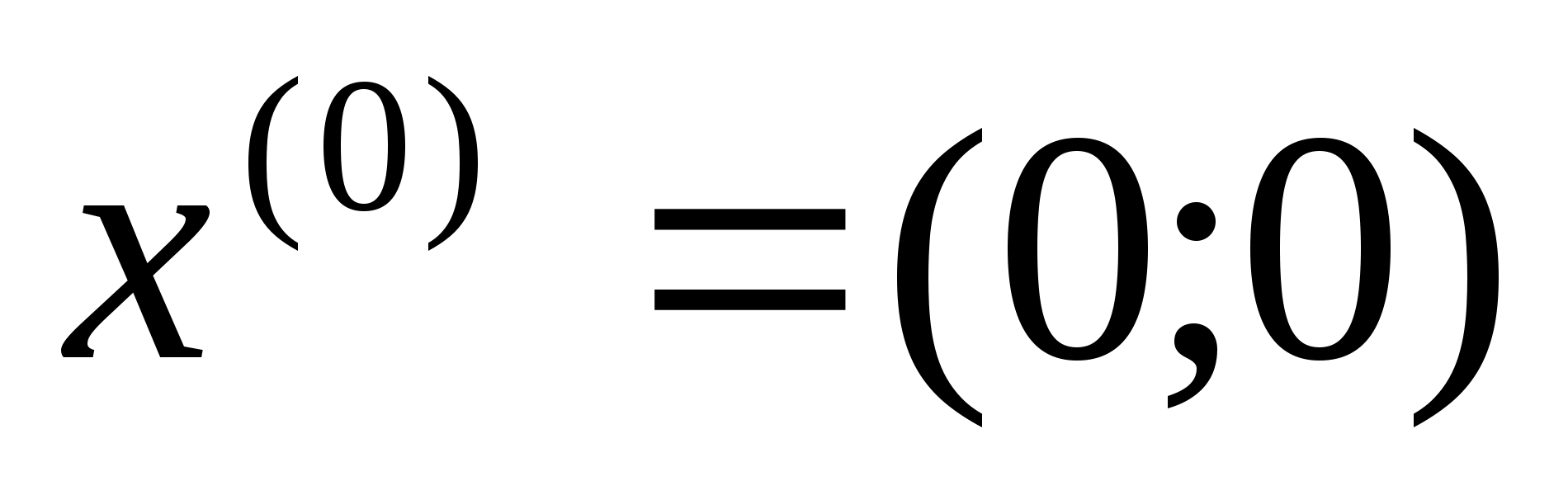 буде рівним
буде рівним
 .
Оскільки
.
Оскільки
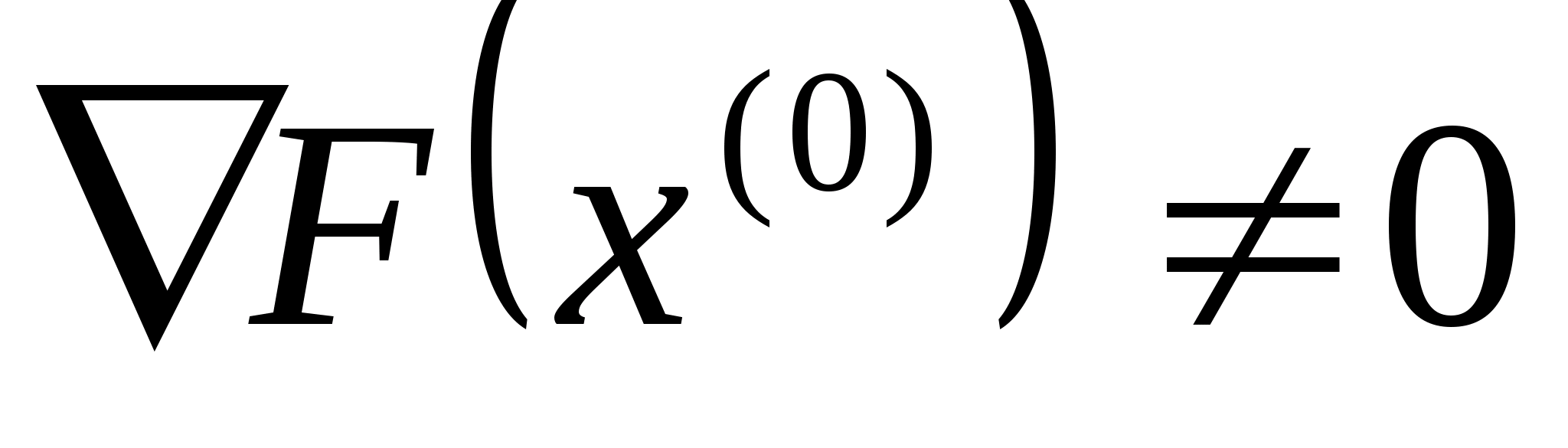 ,
то шукаємо наступне наближення розв’язку
вихідної задачі:
,
то шукаємо наступне наближення розв’язку
вихідної задачі:
 .
.
Знайдемо
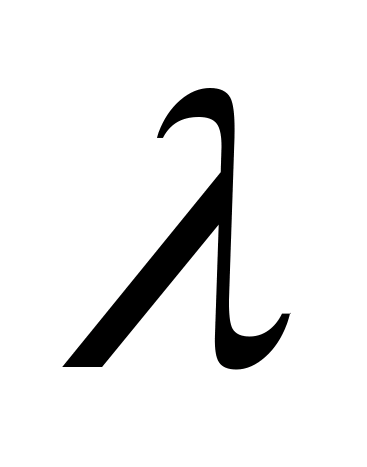 :
:
 .
Оскільки
.
Оскільки
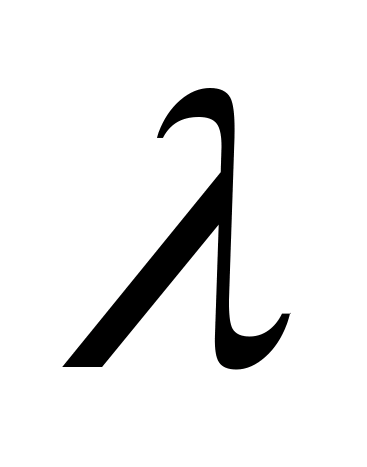 обирається з умови, щоб в точці
обирається з умови, щоб в точці
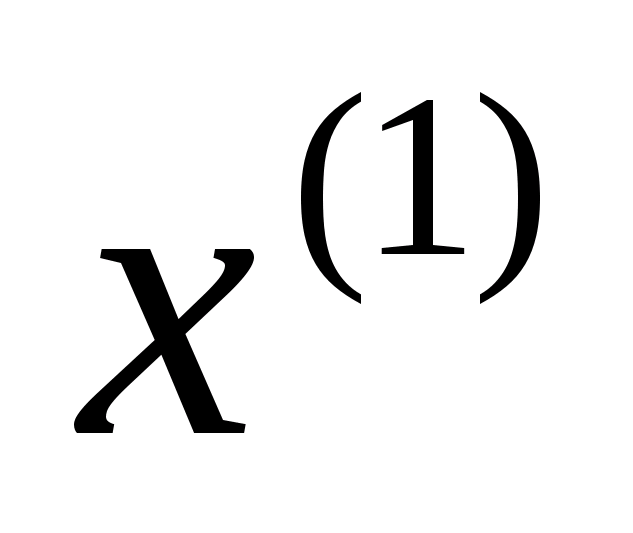 спостерігалося максимальне зменшення
спостерігалося максимальне зменшення
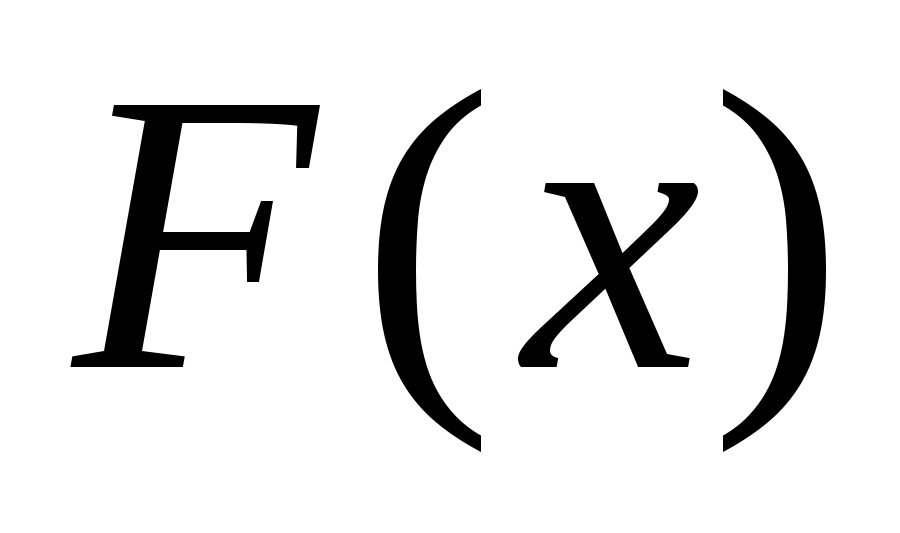 ,
знайдемо похідну від цільової функції
в точці
,
знайдемо похідну від цільової функції
в точці
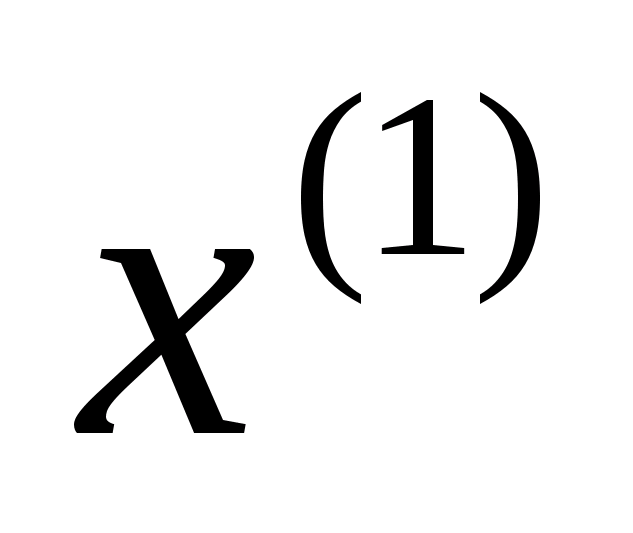 і прирівняємо її до нуля.
і прирівняємо її до нуля.

Отже
можемо тепер знайти координати точки
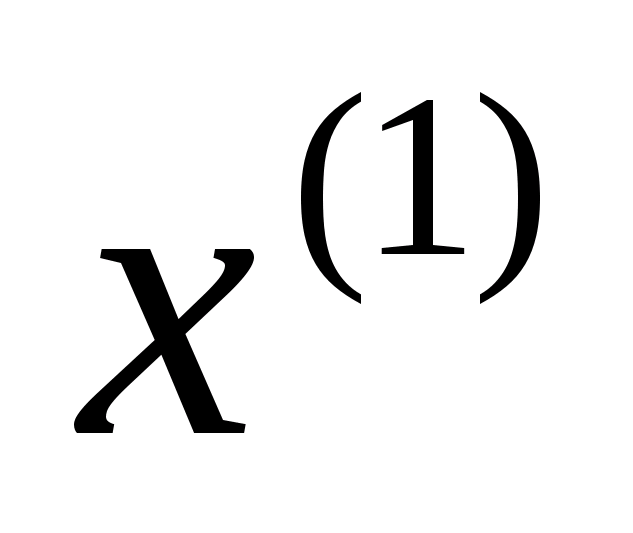 :
:
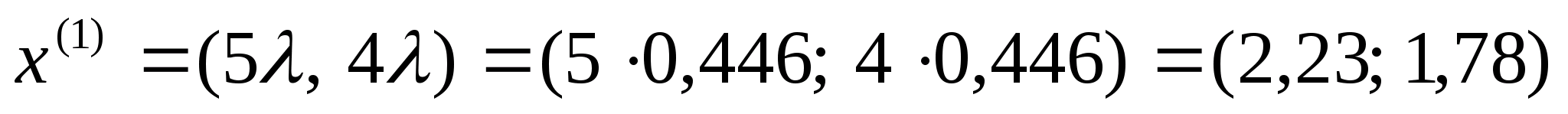 .
Обчислимо значення цільової функції в
цій точці:
.
Обчислимо значення цільової функції в
цій точці:
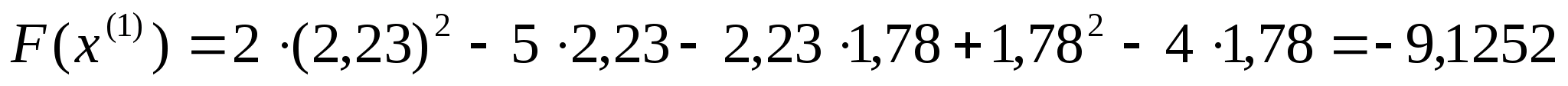 .
.
Перевіряємо умову зупинки:
 отже
шукаємо наступне наближення аналогічним
чином.
отже
шукаємо наступне наближення аналогічним
чином.
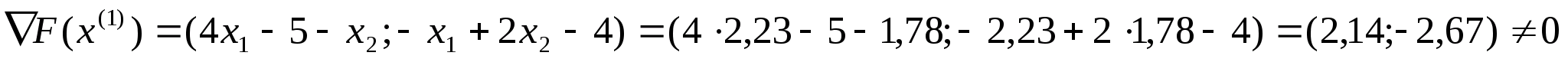

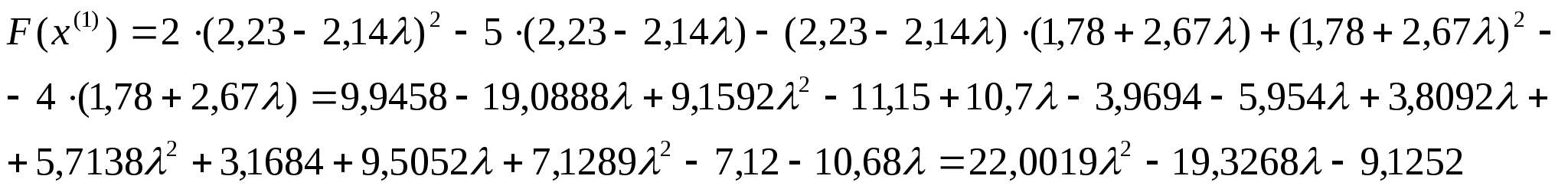
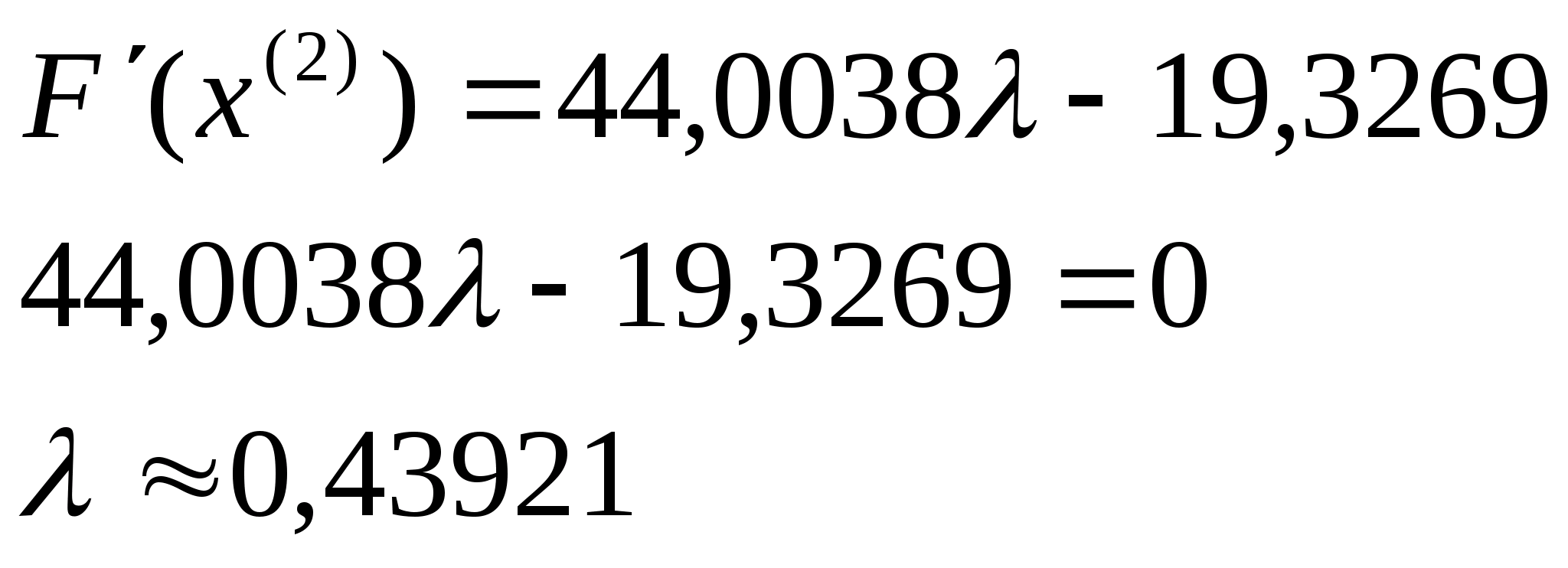
Отже
можемо тепер знайти координати точки
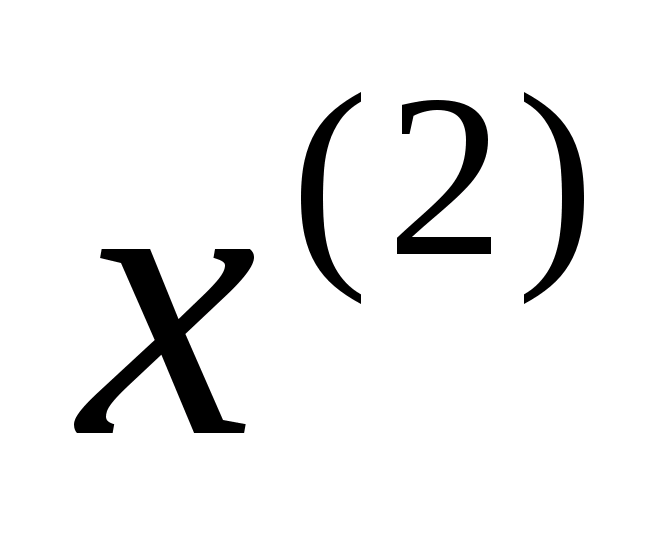 :
:
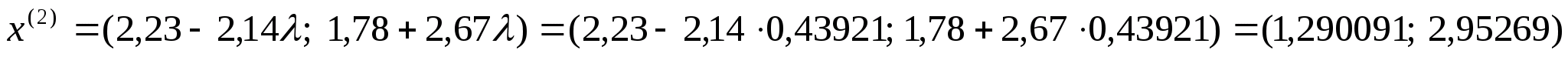 Обчислимо
значення цільової функції в цій точці:
Обчислимо
значення цільової функції в цій точці:
 .
.
Перевіряємо умову зупинки:
 отже
шукаємо наступне наближення:
отже
шукаємо наступне наближення:

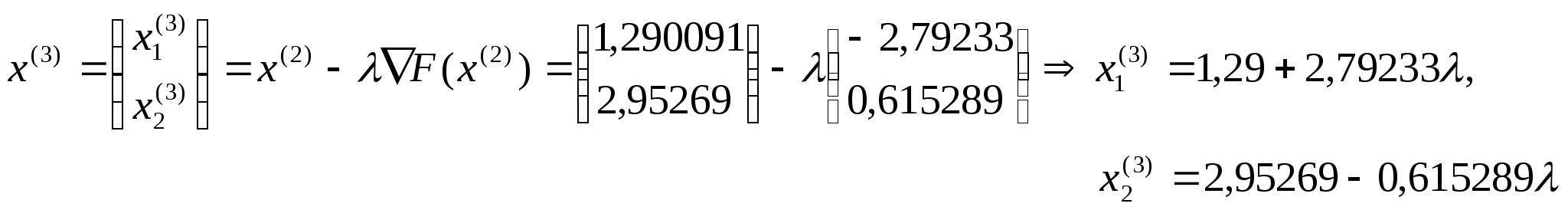
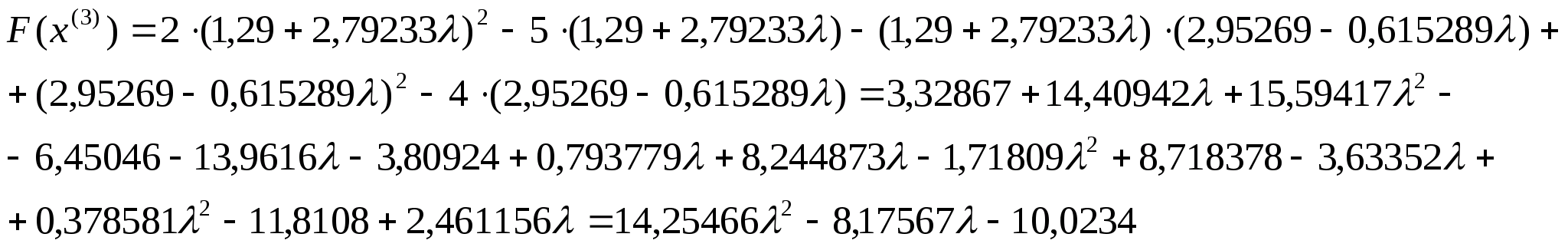

Отже
можемо тепер знайти координати точки
 :
:
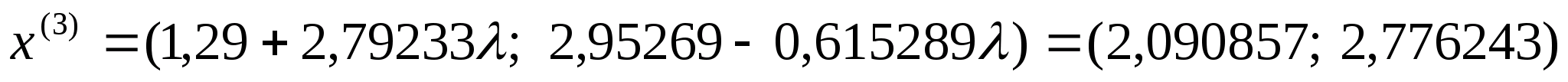 .
.
Обчислимо
значення цільової функції в цій точці:
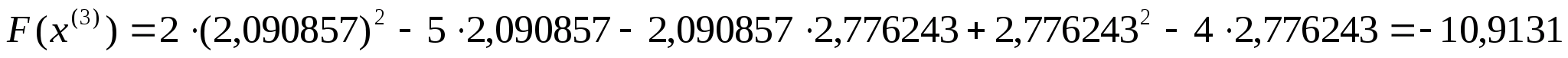 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
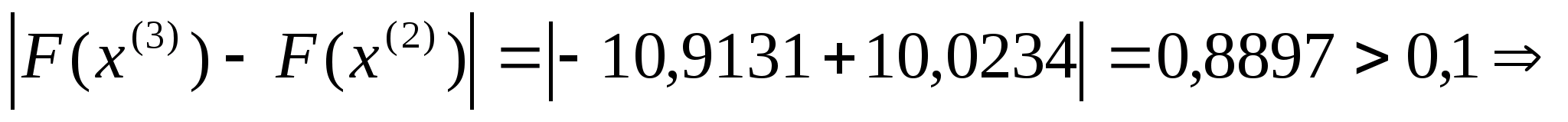 отже
шукаємо наступне наближення:
отже
шукаємо наступне наближення:
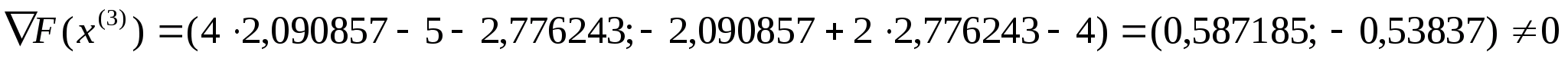

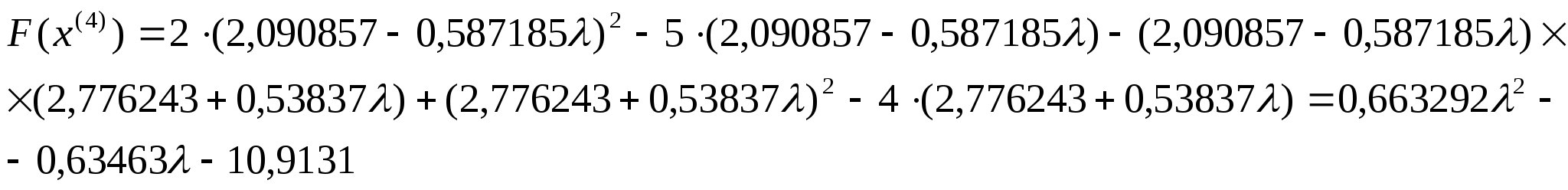

Отже
можемо тепер знайти координати точки
 :
:
 .
.
Обчислимо
значення цільової функції в цій точці:
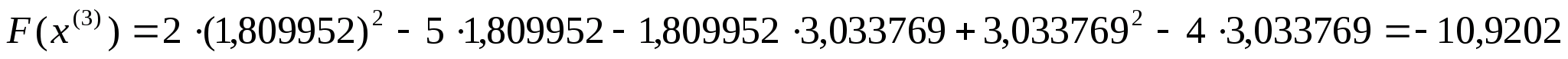 Перевіряємо
умову зупинки:
Перевіряємо
умову зупинки:
 ,
тобто умову зупинки виконано. Отже
,
тобто умову зупинки виконано. Отже
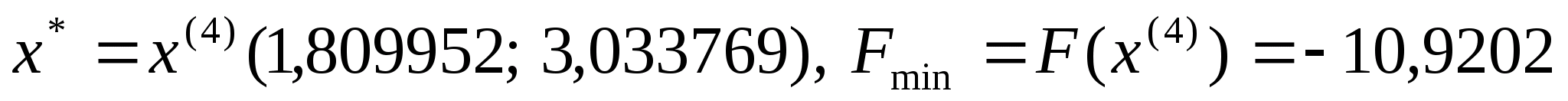 .
.
Як
бачимо, розв’язки задачі, знайдені
обома методами майже однакові, але при
цьому метод Ньютона дав результат вже
на першому кроці ( на відміну від методу
найшвидшого спуску, де довелося робити
4 ітерації). Це пов’язано з тим, що цільова
функція є квадратичною, а отже напрям
спуску
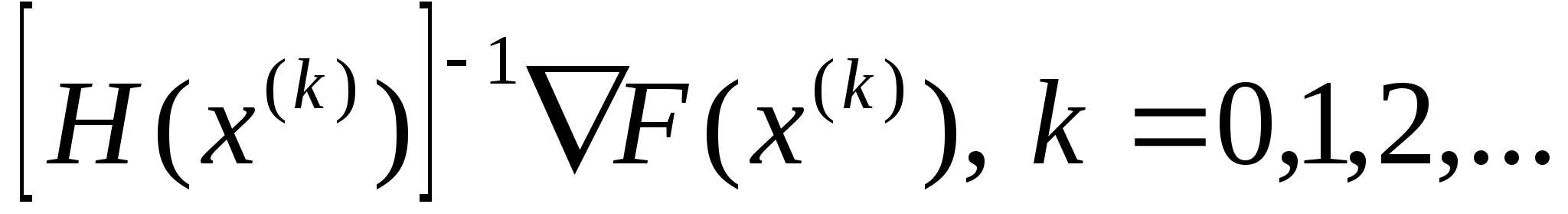 завжди співпадає з напрямом в точку
мінімуму
завжди співпадає з напрямом в точку
мінімуму
 .
Тобто основна перевага методу Ньютона
- швидка збіжність, однак при цьому
суттєвим недоліком є залежність збіжності
від початкового наближення
.
Тобто основна перевага методу Ньютона
- швидка збіжність, однак при цьому
суттєвим недоліком є залежність збіжності
від початкового наближення
 .
Крім того у випадку не квадратичної
цільової функції трудомісткість
ітерації методом Ньютона може виявитись
дуже великою за рахунок необхідності
обчислення матриці других похідних
мінімізуємої функції, що потребує затрат
великої кількості часу.
.
Крім того у випадку не квадратичної
цільової функції трудомісткість
ітерації методом Ньютона може виявитись
дуже великою за рахунок необхідності
обчислення матриці других похідних
мінімізуємої функції, що потребує затрат
великої кількості часу.
Розв’язання задачі умовної оптимізації за допомогою методу Франка-Вулфа і методу штрафних функції
4. Розв’яжемо задачу умовної оптимізації

методом Франка-Вулфа
Функція
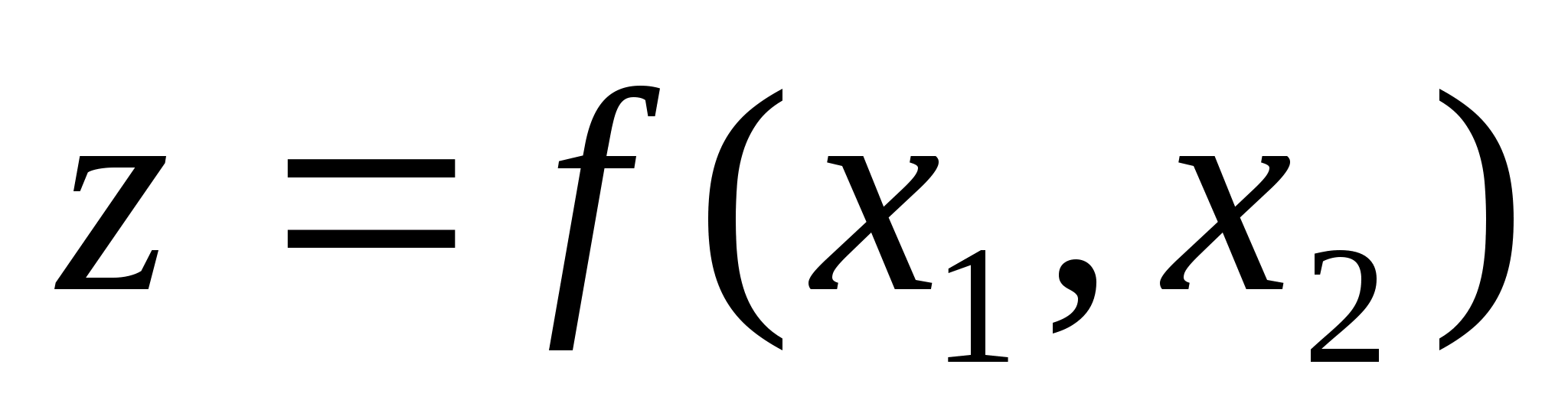 являється вгнутою так як представляє
собою суму лінійної функції (її можна
розглядати як вгнуту) і квадратичної
форми, яка являється від’ємно визначеною
і тому також являється вгнутою. Перевіримо
завдяки матриці Гессе від’ємну
визначеність функції
являється вгнутою так як представляє
собою суму лінійної функції (її можна
розглядати як вгнуту) і квадратичної
форми, яка являється від’ємно визначеною
і тому також являється вгнутою. Перевіримо
завдяки матриці Гессе від’ємну
визначеність функції
 .
Для цього спочатку знайдемо частинні
похідні першого і другого порядку від
функції
.
Для цього спочатку знайдемо частинні
похідні першого і другого порядку від
функції
 :
:
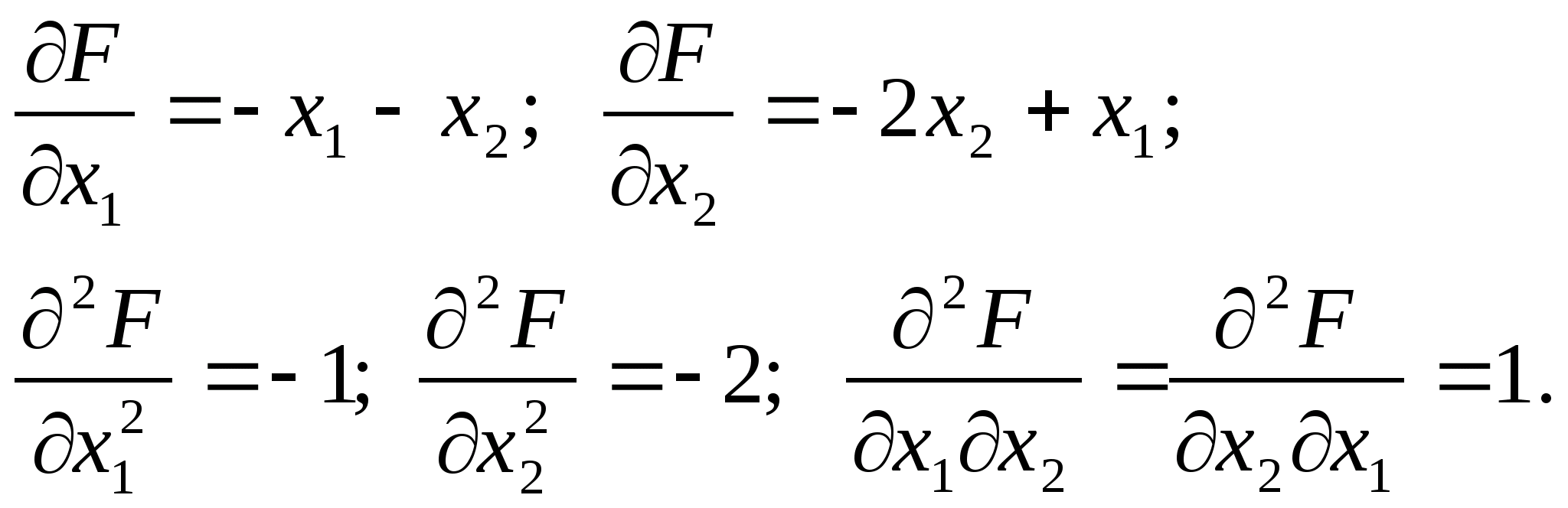
Отже матриця Гессе матиме вигляд:

Головні
мінори : оскільки
в ряді
оскільки
в ряді
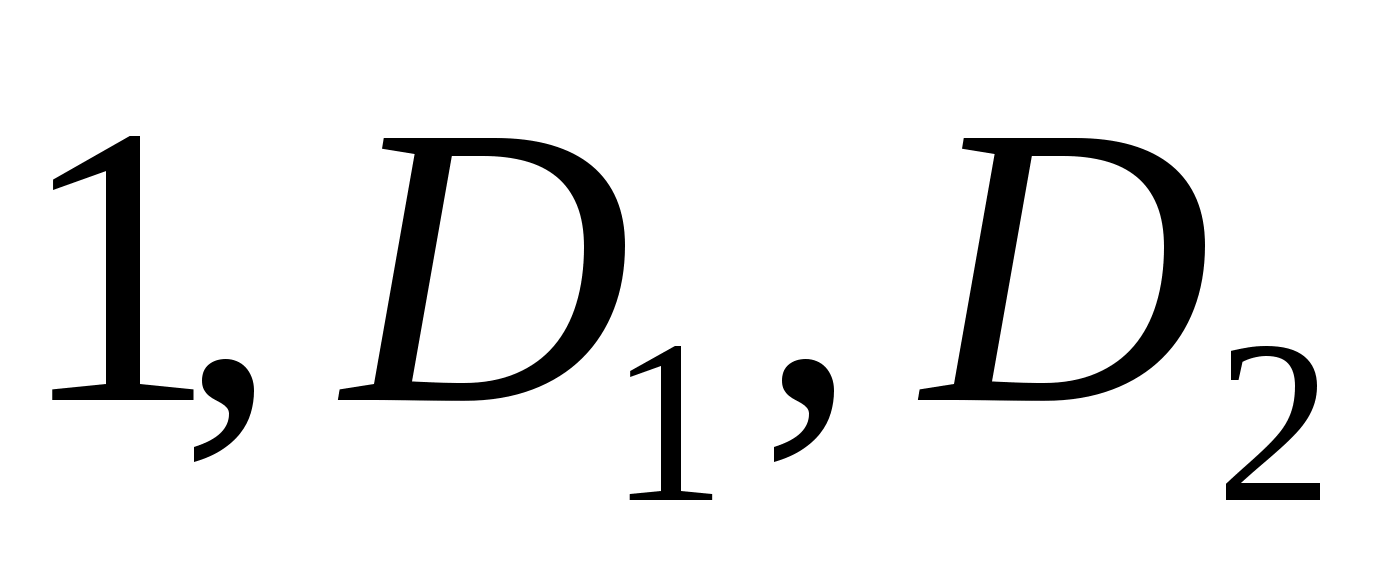 знаки
чергуються, то дана матриця є від’ємно
визначеною, я отже функція
знаки
чергуються, то дана матриця є від’ємно
визначеною, я отже функція
 - вгнута.
- вгнута.
Система обмежень задачі включає тільки лінійні нерівності, які утворюють опуклу множину, отже дана задача є задачею опуклого програмування.
Задачу такого типу можна розв’язувати методом Франка-Вулфа. Цей метод відноситься до групи градієнтних методів.
Розглянемо задачу:

Алгоритм методу Франка-Вулфа:
Спочатку
в допустимій області задачі обирають
довільну точку
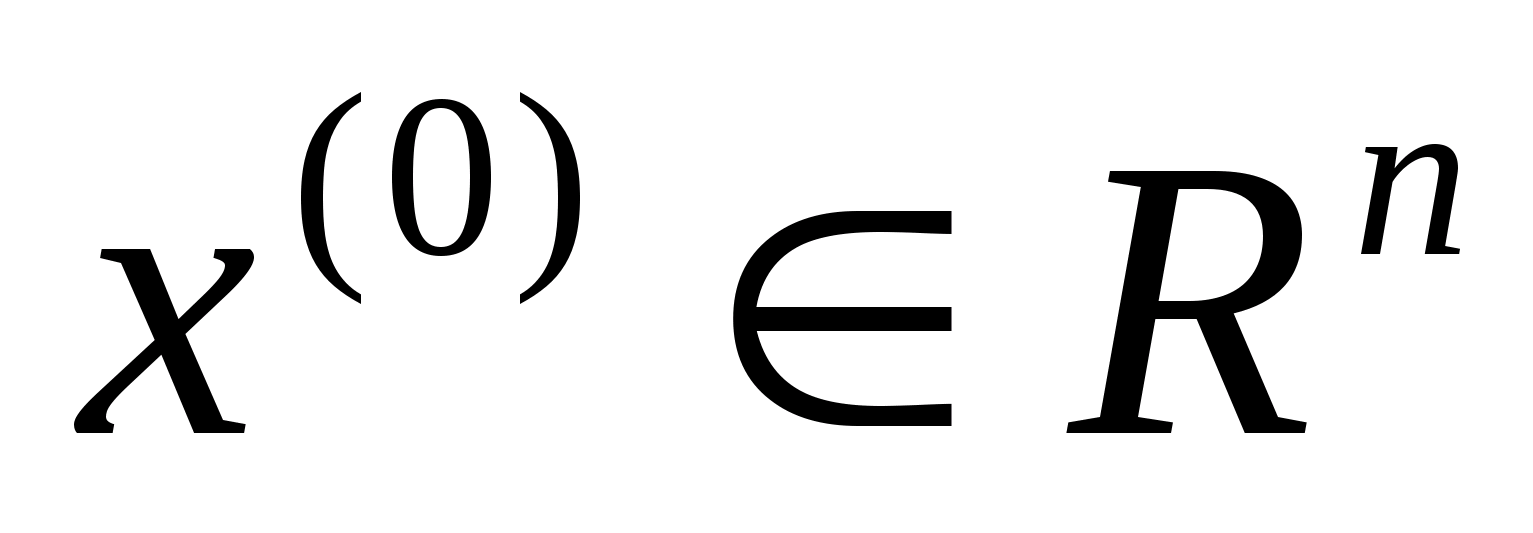 .
Це можна зробити, наприклад, за допомогою
методу штучного базису. Також
обирають точність обчислень
.
Це можна зробити, наприклад, за допомогою
методу штучного базису. Також
обирають точність обчислень
 .
Покладають
.
Покладають
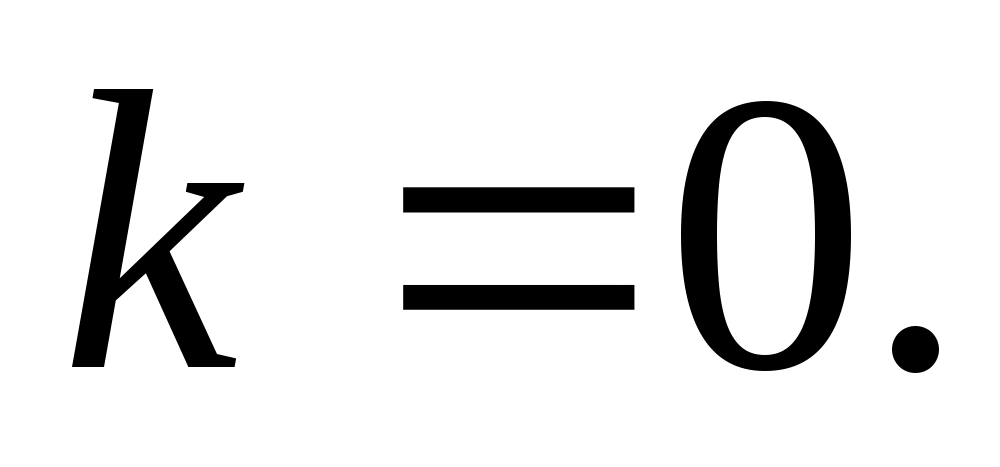
Знаходять
в цій точці градієнт цільової функції
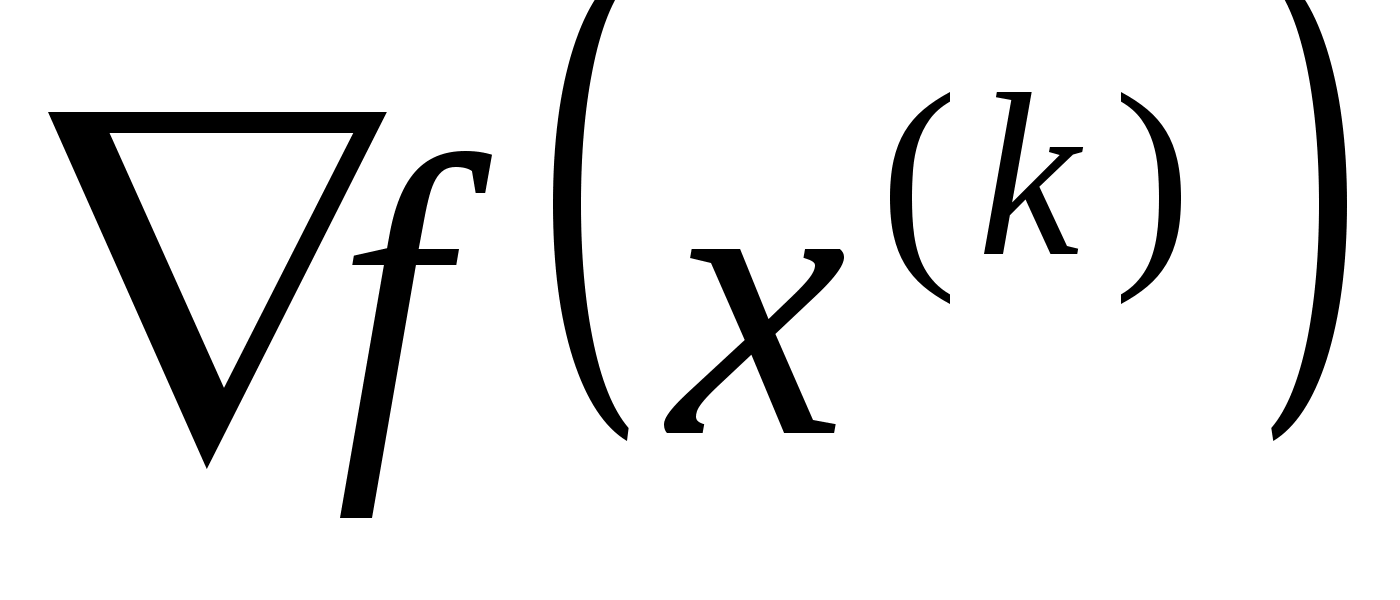 .
.
Будують
функцію
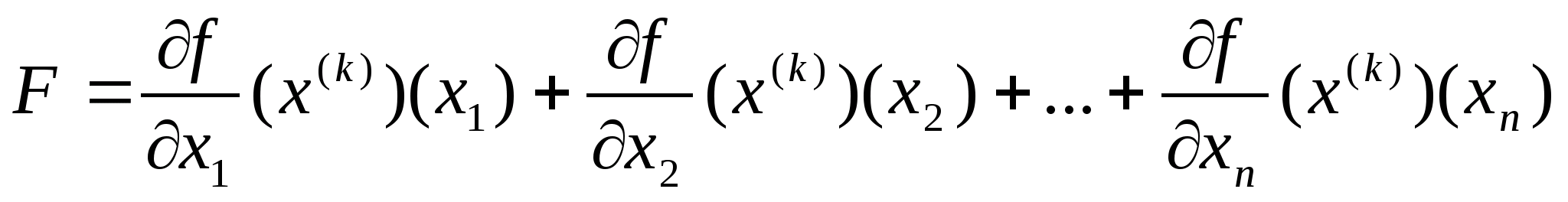 і розв’язують задачу максимізації для
функції
і розв’язують задачу максимізації для
функції
 в області 2-3, тобто таку задачу:
в області 2-3, тобто таку задачу:

Нехай
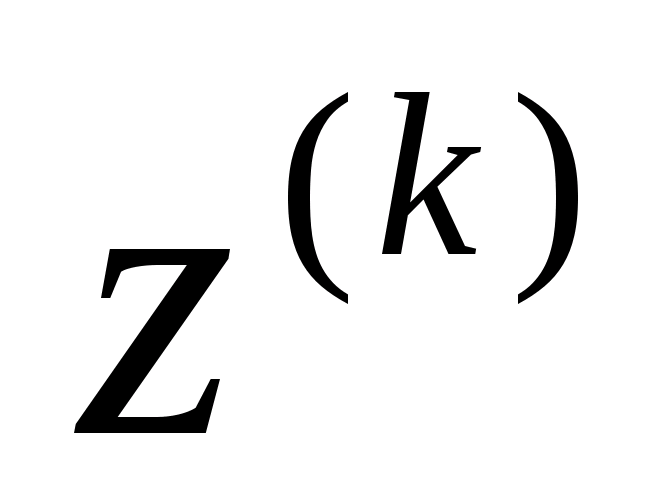 - оптимальний розв’язок задачі 4,2,3.
- оптимальний розв’язок задачі 4,2,3.
Шукаємо
наступне наближення за формулою:
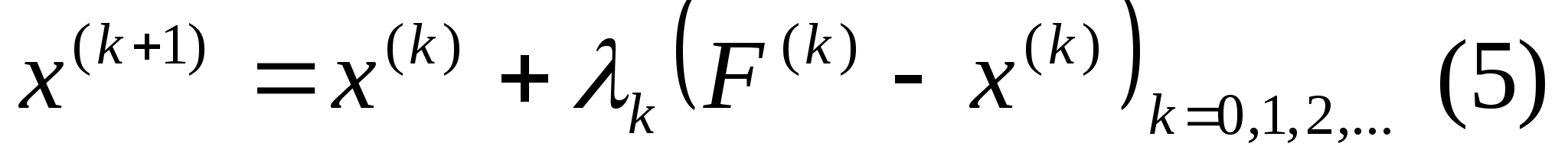 ,
де
,
де
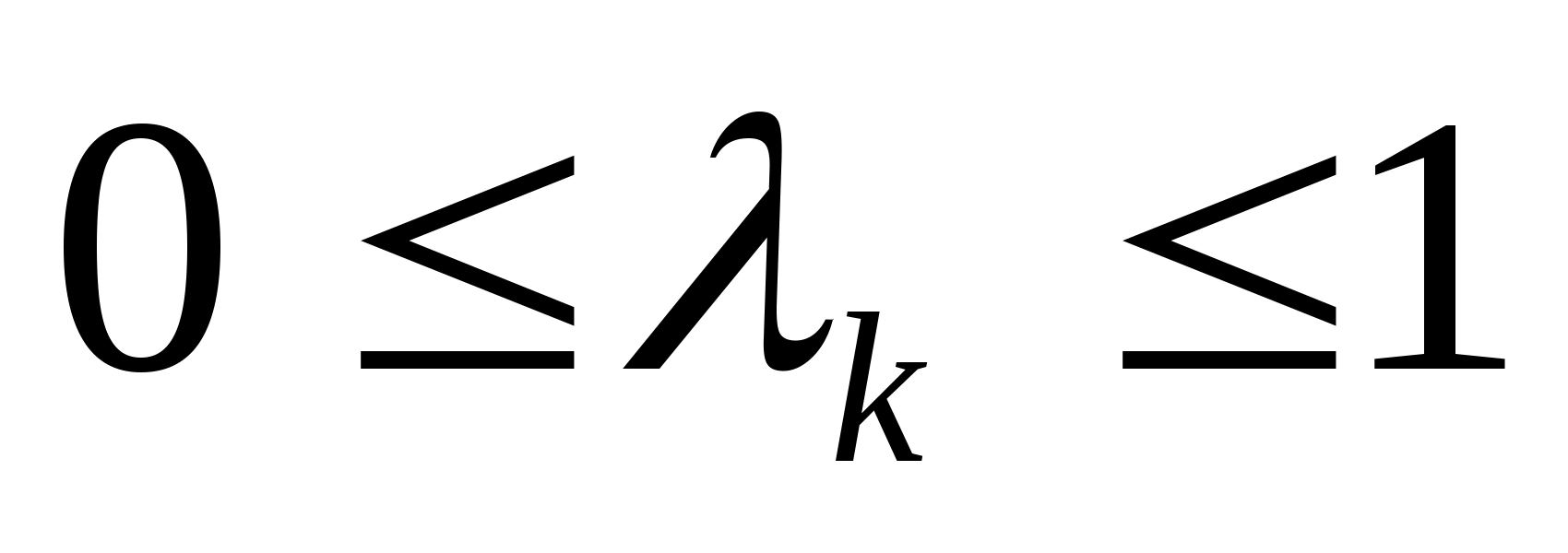 - крок в точці. Його обирають довільно,
однак краще його вибрати так, щоб
- крок в точці. Його обирають довільно,
однак краще його вибрати так, щоб
 при такому значенні
при такому значенні
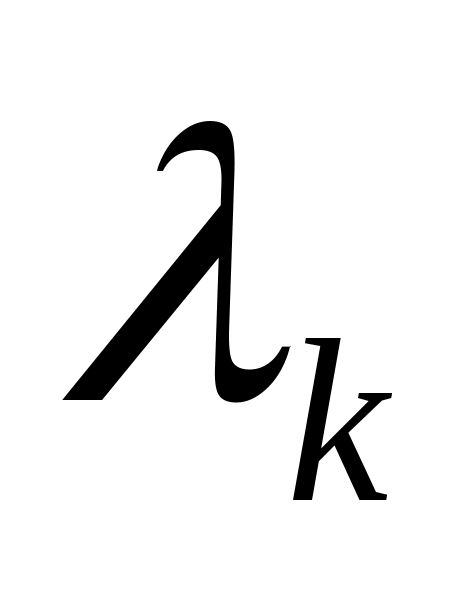 мала найбільше значення. Для цього з
формул 5 знаходять вираз координат
вектора
мала найбільше значення. Для цього з
формул 5 знаходять вираз координат
вектора
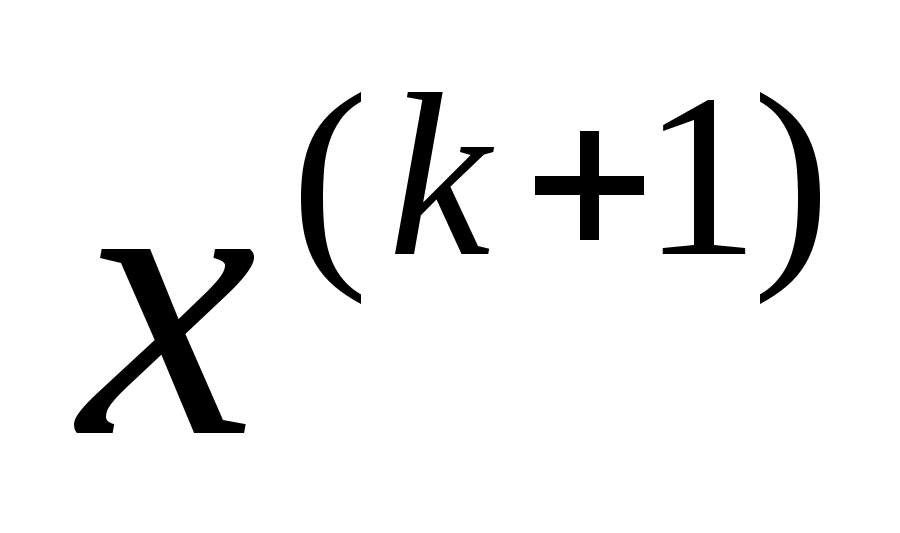 через
через
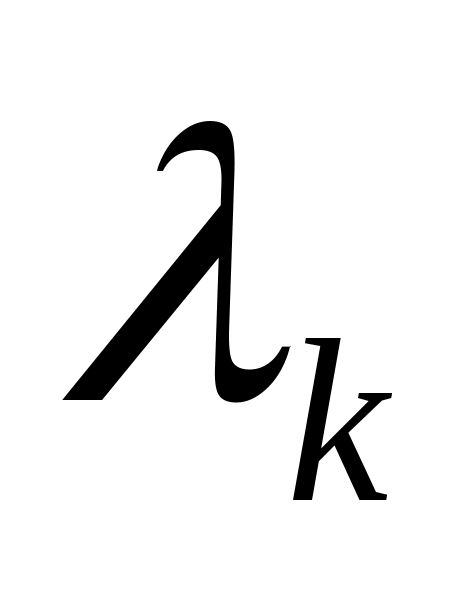 :
:
 і підставляють цей вираз у функцію
і підставляють цей вираз у функцію
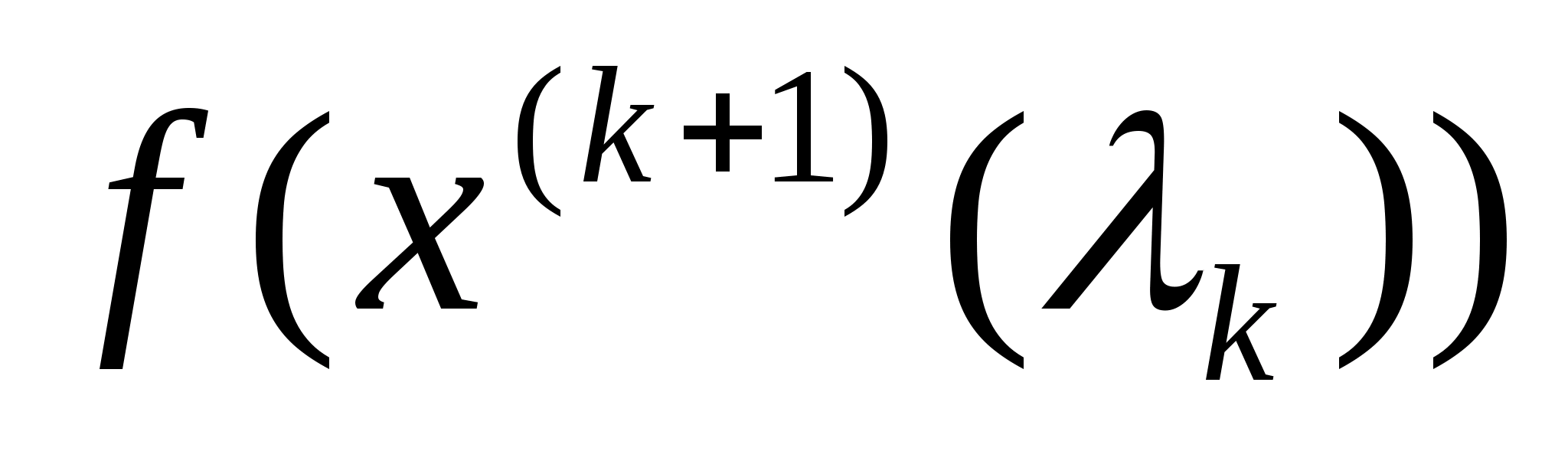 .
Потім розв’язують систему
.
Потім розв’язують систему
 .
За
.
За
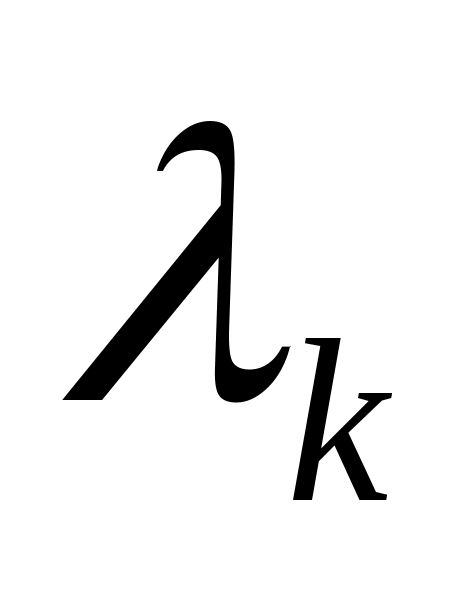 вибирають найменший з коренів цього
рівняння. Якщо цей корінь більше одиниці,
то
вибирають найменший з коренів цього
рівняння. Якщо цей корінь більше одиниці,
то
 .
.
Перевіряють
критерії зупинки:
 ,
,
 .
Якщо дані умови виконались, то покладають
.
Якщо дані умови виконались, то покладають
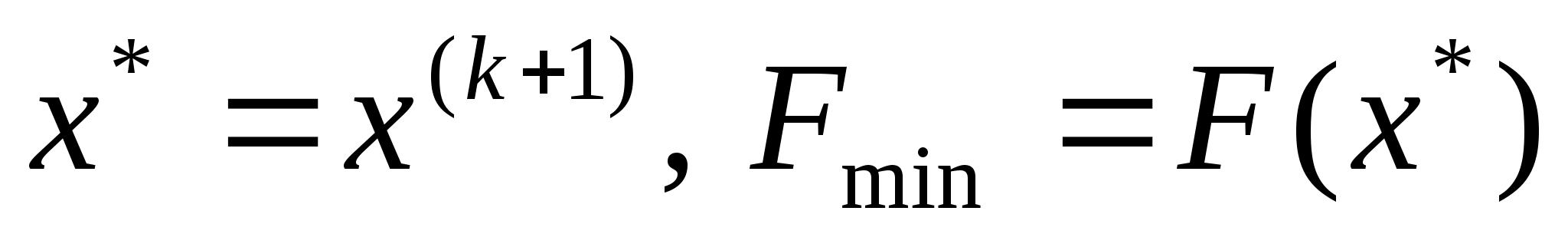 і зупиняють обчислення, якщо ні, то
переходимо до наступного кроку.
і зупиняють обчислення, якщо ні, то
переходимо до наступного кроку.
Покладають,
що
 і переходять до кроку 2.
і переходять до кроку 2.
Тепер
перейдемо безпосередньо до нашої задачі.
За початкове наближення до оптимального
плану задачі обираємо точку
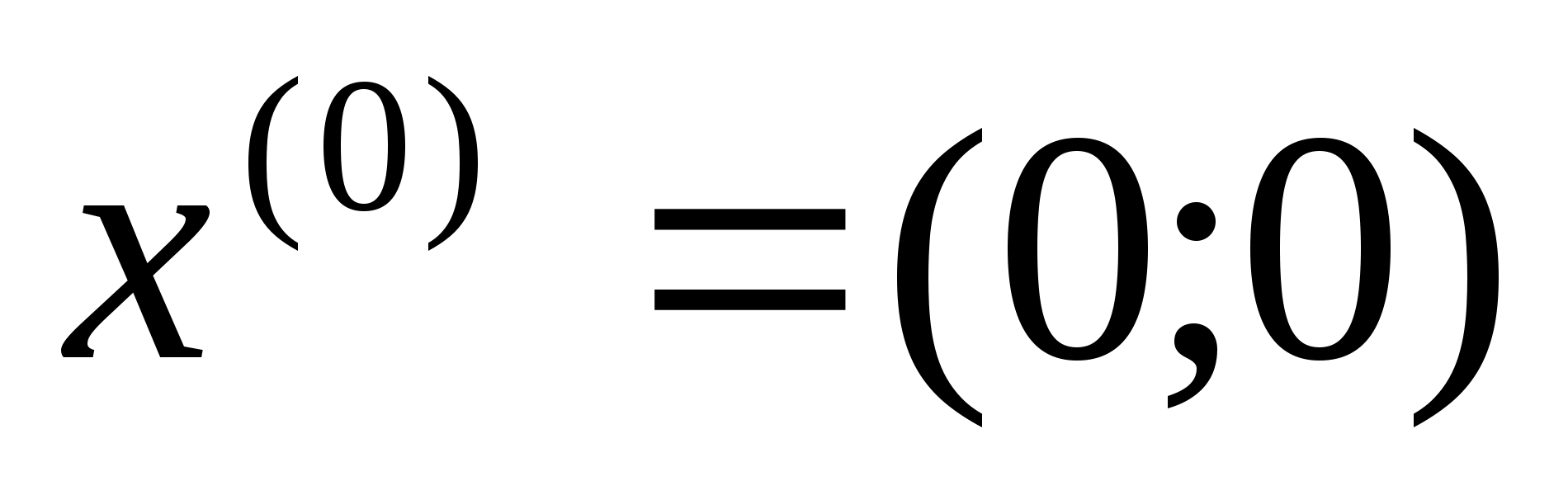 ,
а обчислення будемо проводити з точністю
,
а обчислення будемо проводити з точністю
 ,
,
 .
Градієнт цільової функції в точці
.
Градієнт цільової функції в точці
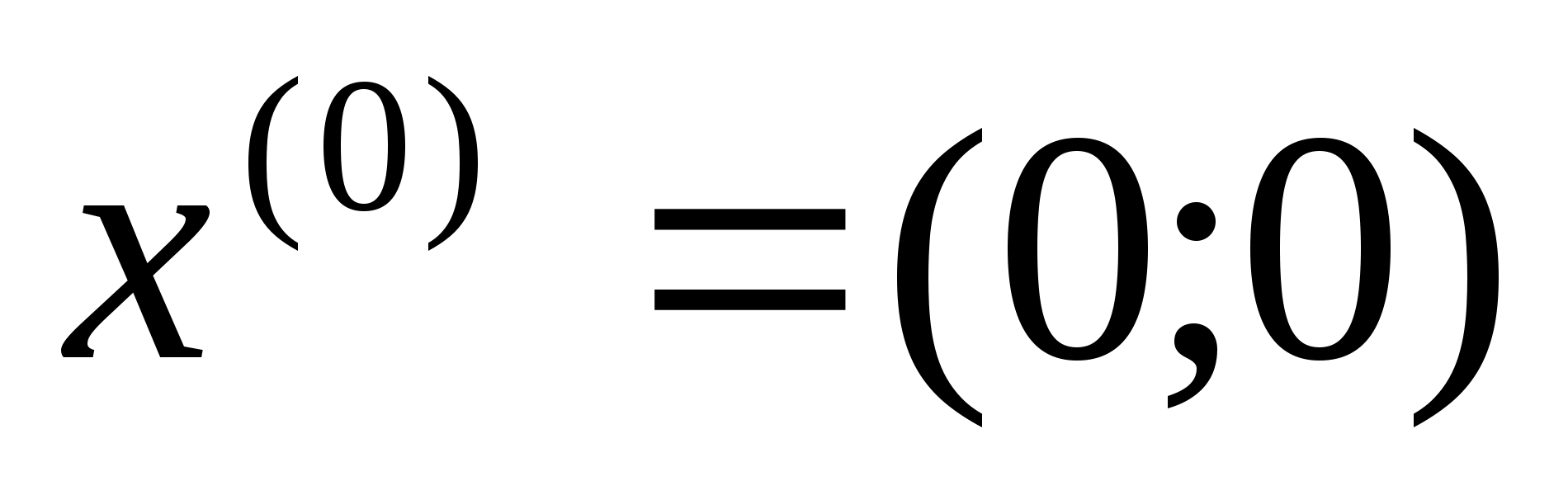
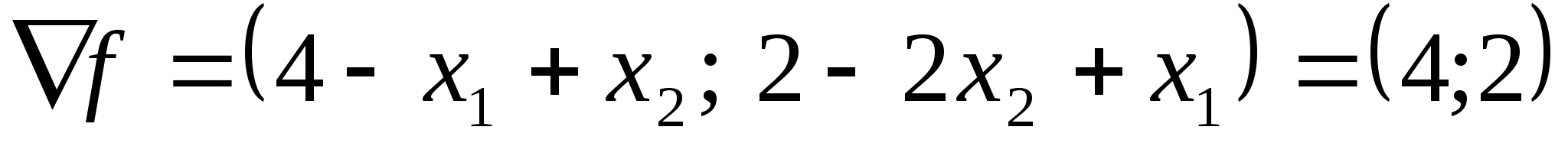 .
.
Розв’яжемо за допомогою симплекс методу задачу:

оптимізаційний одновимірний мінімізація дихотомія ньютон
|
і |
Базис |
Сб |
В |
4 |
2 |
0 |
0 |
|
А1 |
А2 |
А3 |
А4 |
||||
|
1 |
А3 |
0 |
21 |
3 |
7 |
1 |
0 |
|
2 |
А4 |
0 |
1 |
1 |
-1 |
0 |
1 |
|
3 |
|
|
0 |
- 4 |
-2 |
0 |
0 |
|
1 |
А3 |
0 |
18 |
0 |
10 |
1 |
-3 |
|
2 |
А1 |
4 |
1 |
1 |
-1 |
0 |
1 |
|
3 |
|
|
8 |
0 |
-6 |
0 |
4 |
|
1 |
А2 |
2 |
9/5 |
0 |
1 |
1/10 |
-3/10 |
|
2 |
А1 |
4 |
14/5 |
1 |
0 |
1/10 |
7/10 |
|
3 |
|
|
74/5 |
0 |
0 |
3/5 |
11/5 |
Позначимо
через
 оптимальний
розв’язок даної задачі. Отже
оптимальний
розв’язок даної задачі. Отже
 .
Знайдемо новий допустимий розв’язок
вихідної задачі за формулою 5:
.
Знайдемо новий допустимий розв’язок
вихідної задачі за формулою 5:
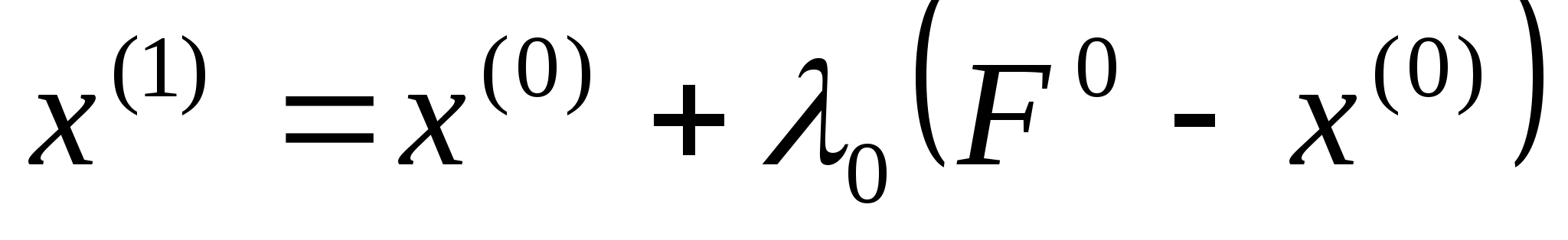


Знайдемо
похідну цієї функції по
 і прирівняємо її до нуля:
і прирівняємо її до нуля:
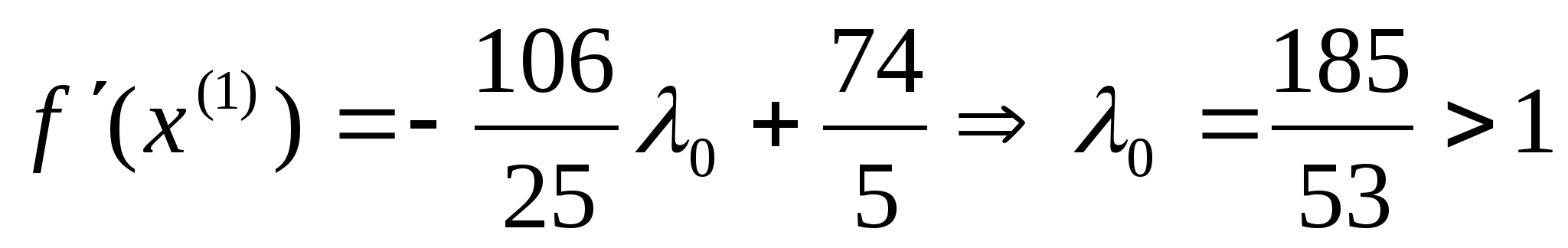 ,
отже покладаємо
,
отже покладаємо
 =1,
таким чином
=1,
таким чином
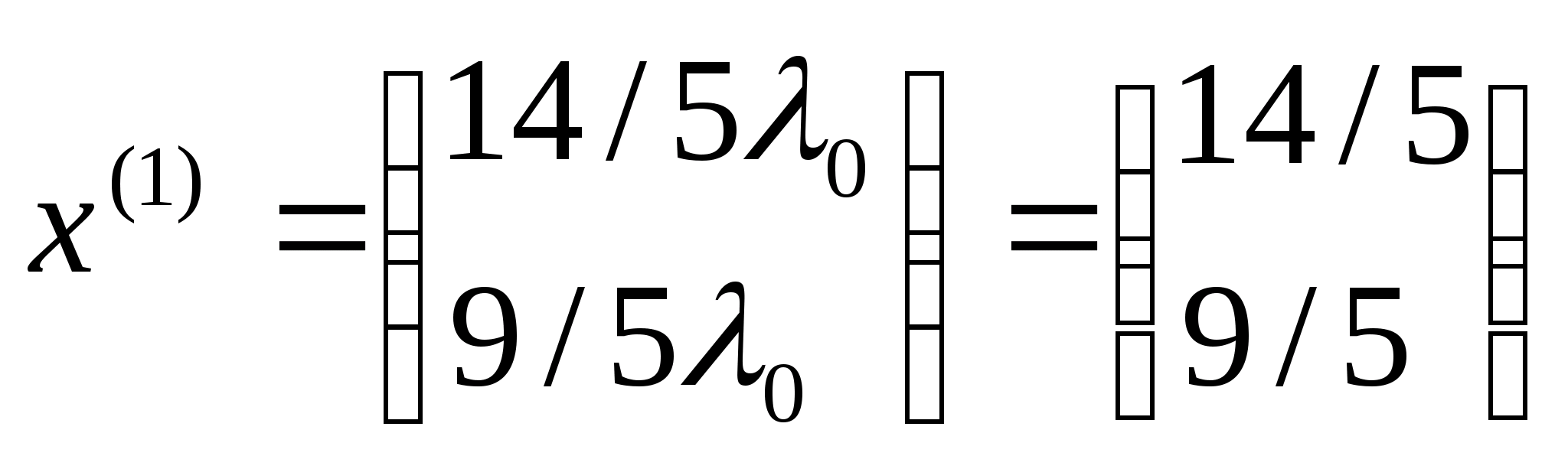 .
Знайдемо значення цільової функції в
цій точці і перевіримо умови зупинки:
.
Знайдемо значення цільової функції в
цій точці і перевіримо умови зупинки:
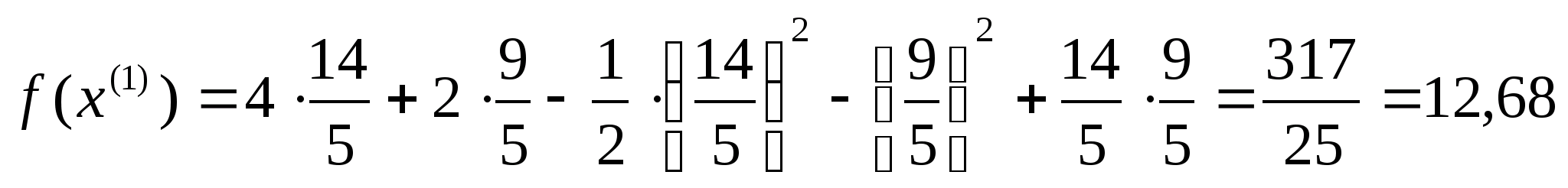
 .
.
Отже
знаходимо нове наближення оптимального
плану вихідної задачі аналогічним
чином. Покладаємо, що
 .
Градієнт цільової функції в точці
.
Градієнт цільової функції в точці
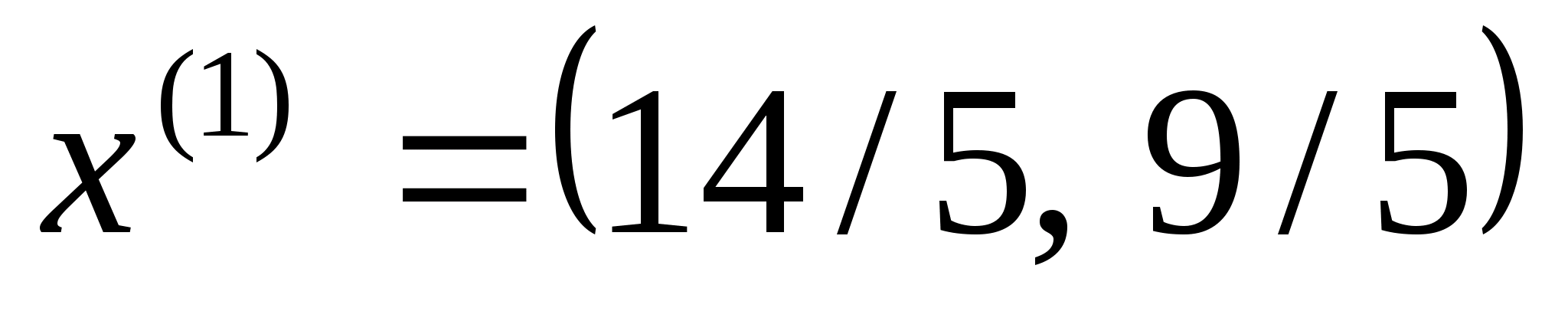 буде рівним:
буде рівним:
 .
.
Знаходимо за допомогою симплекс-методу максимум функції
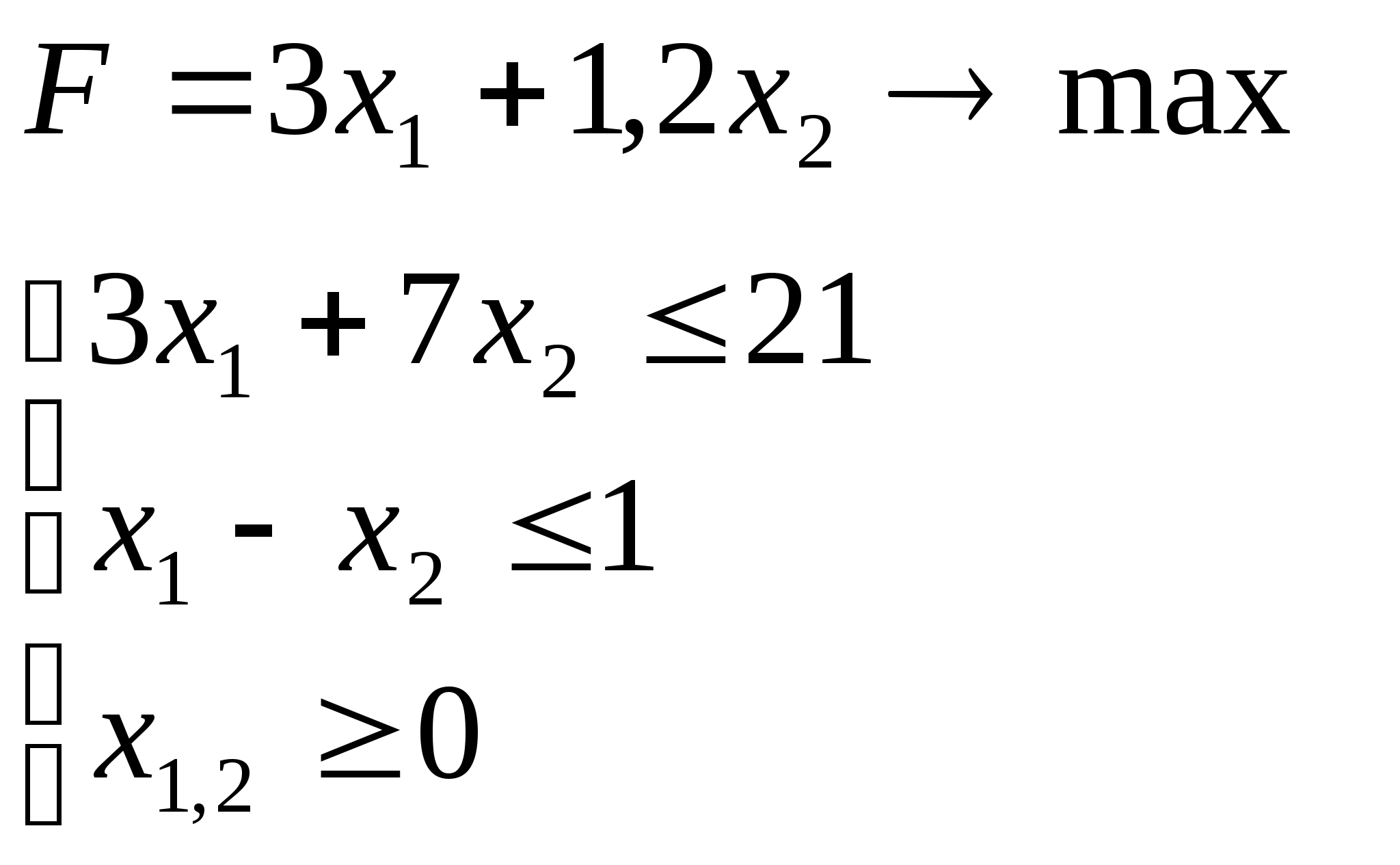
|
і |
Базис |
Сб |
В |
3 |
6/5 |
0 |
0 |
|
А1 |
А2 |
А3 |
А4 |
||||
|
1 |
А3 |
0 |
21 |
3 |
7 |
1 |
0 |
|
2 |
А4 |
0 |
1 |
1 |
-1 |
0 |
1 |
|
3 |
|
|
0 |
- 3 |
-6/5 |
0 |
0 |
|
1 |
А3 |
0 |
18 |
0 |
10 |
1 |
-3 |
|
2 |
А1 |
3 |
1 |
1 |
-1 |
0 |
1 |
|
3 |
|
|
3 |
0 |
-21/5 |
0 |
3 |
|
1 |
А2 |
6/5 |
9/5 |
0 |
1 |
1/10 |
-3/10 |
|
2 |
А1 |
3 |
14/5 |
1 |
0 |
1/10 |
7/10 |
|
3 |
|
|
264/5 |
0 |
0 |
21/50 |
87/50 |
Позначимо
через
 оптимальний
розв’язок даної задачі. Отже
оптимальний
розв’язок даної задачі. Отже
 .
Визначимо тепер
.
Визначимо тепер
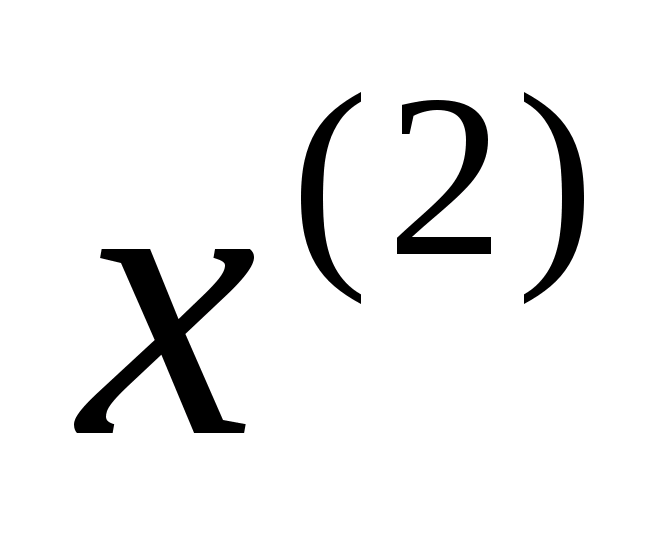 :
:


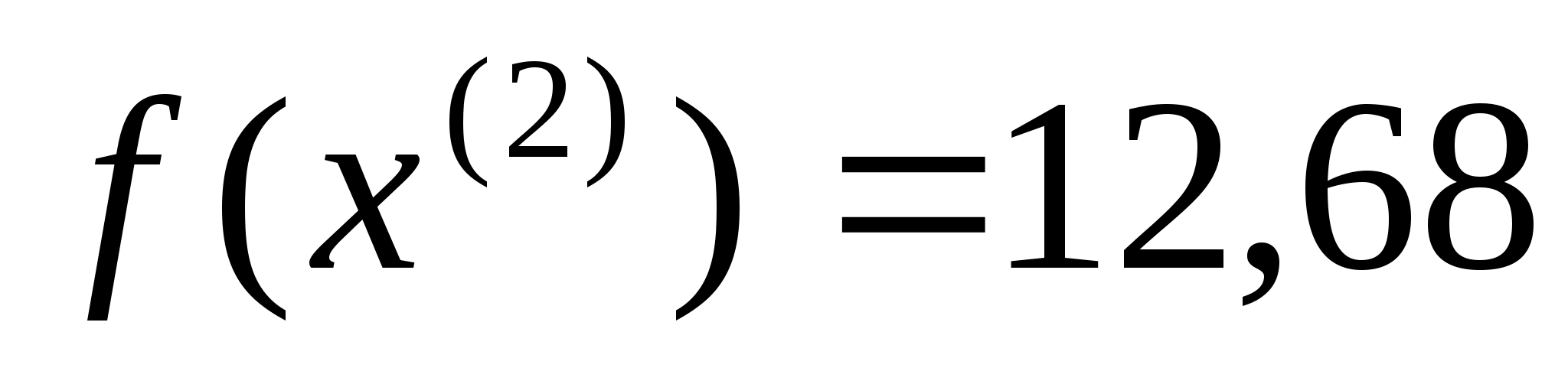
 .
Тобто критерій зупинки виконано. Отже
.
Тобто критерій зупинки виконано. Отже
 являється оптимальним розв’язком
вихідної задачі, тобто
являється оптимальним розв’язком
вихідної задачі, тобто
 .
.
метод штрафних функцій
Цей метод відноситься до групи непрямих методів розв’язання задач нелінійного програмування виду:

Він
зводить задачу з обмеженнями в
послідовність задач безумовної
оптимізації деяких допоміжних функції.
Останні отримуються шляхом модифікації
цільової функції за допомогою
функій-обмежень таким чином, щоб обмеження
в явному вигляді в задачі оптимізації
не фігурували. Це забезпечує можливість
застосування методів безумовної
оптимізації. В загальному випадку
допоміжна функція має вигляд:
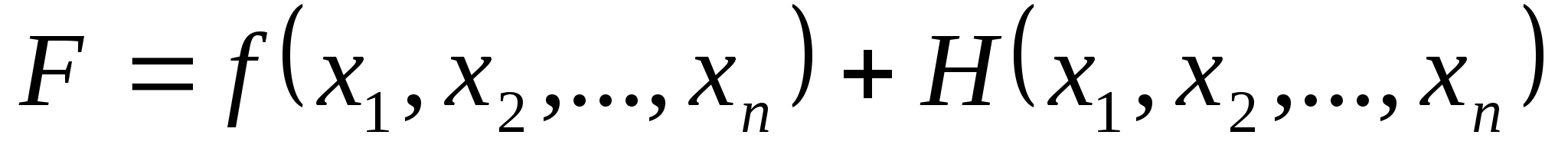 ,
де функція
,
де функція
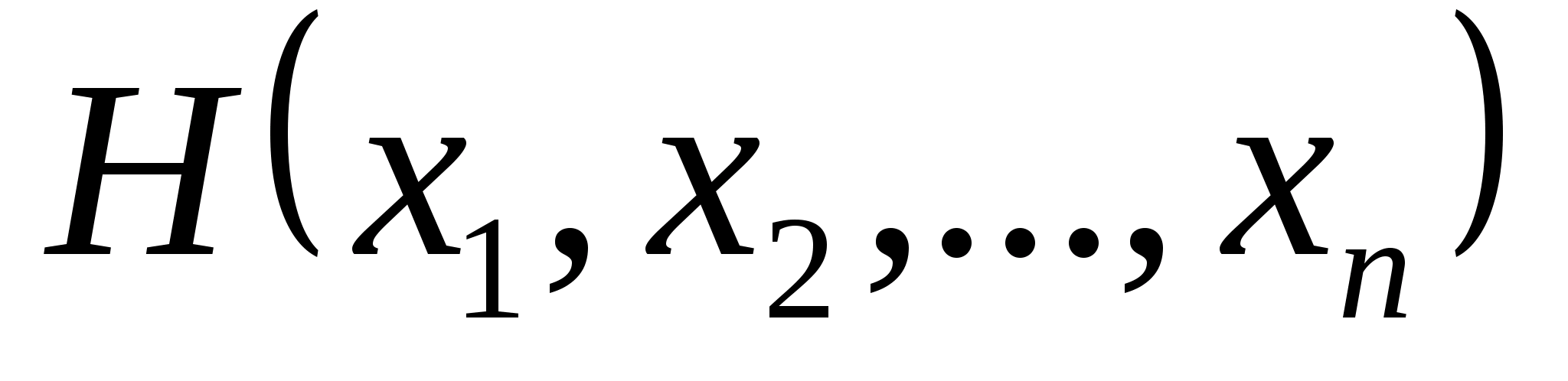 визначається з обмежень вихідної задачі
і називається штрафною функцією.
Необхідно, щоб при порушенні обмеження
вона “штрафувала” функцію Z, тобто
збільшувала її значення. В такому випадку
Z буде знаходитися всередині області
обмежень. Штрафну функцію можна будувати
різними способами. Розглянемо один з
варіантів, коли
визначається з обмежень вихідної задачі
і називається штрафною функцією.
Необхідно, щоб при порушенні обмеження
вона “штрафувала” функцію Z, тобто
збільшувала її значення. В такому випадку
Z буде знаходитися всередині області
обмежень. Штрафну функцію можна будувати
різними способами. Розглянемо один з
варіантів, коли
 ,
де
,
де
 ,
,
 -
параметр штрафної функції.
-
параметр штрафної функції.
Далі
розв’язують задачу мінімізації для
функції
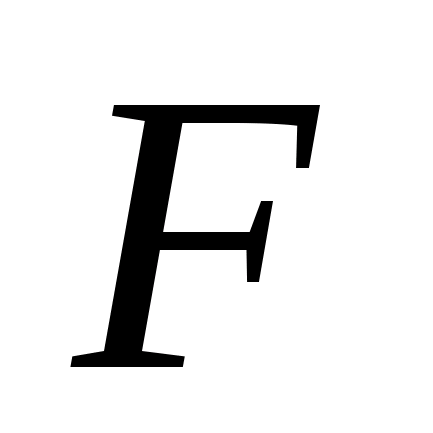 ,
використовуючи один з відомих методів
безумовної оптимізації. Будемо
розв’язувати задачу мінімізації для
,
використовуючи один з відомих методів
безумовної оптимізації. Будемо
розв’язувати задачу мінімізації для
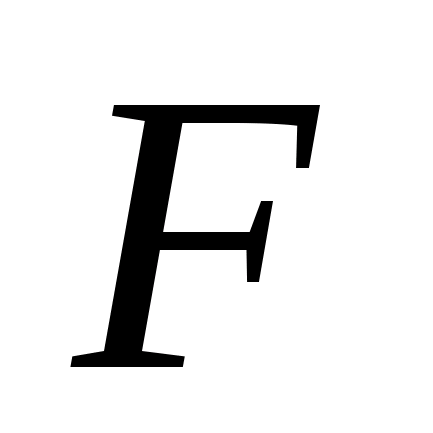 градієнтним методом зі сталим кроком.
Тоді алгоритм
розв’язування задачі буде таким:
градієнтним методом зі сталим кроком.
Тоді алгоритм
розв’язування задачі буде таким:
Обирається
точність обчислень, а в якості початкової
точки
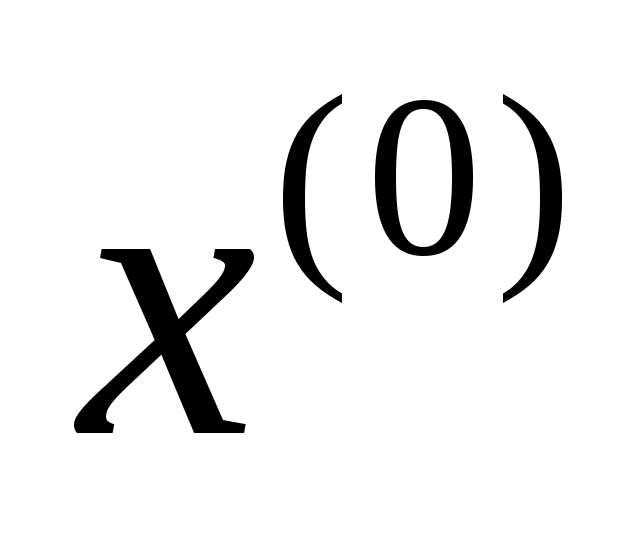 беруть довільну точку, яка належить
допустимій множині задачі. Також
зазначається крок
беруть довільну точку, яка належить
допустимій множині задачі. Також
зазначається крок
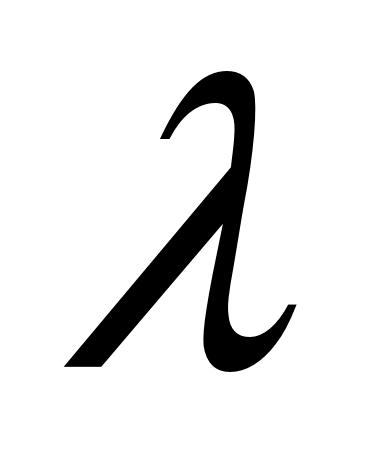 і покладають
і покладають
 .
.
Знаходять
 .
Якщо точка
.
Якщо точка
 належить допустимій множині задачі,
то коефіцієнти
належить допустимій множині задачі,
то коефіцієнти
 будуть рівними нулю, якщо ж не належать,
то вибираємо параметри
будуть рівними нулю, якщо ж не належать,
то вибираємо параметри
 так, щоб точка
так, щоб точка
 належала допустимій множині.
належала допустимій множині.
Перевіряють
чи виконується умова
 .
Якщо не виконується, то переходять до
наступного кроку, якщо виконується ,
то
.
Якщо не виконується, то переходять до
наступного кроку, якщо виконується ,
то
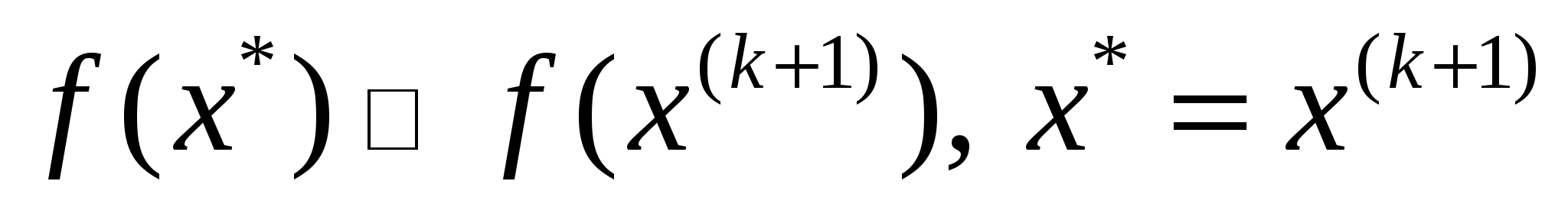 .
.
Покладають,
що
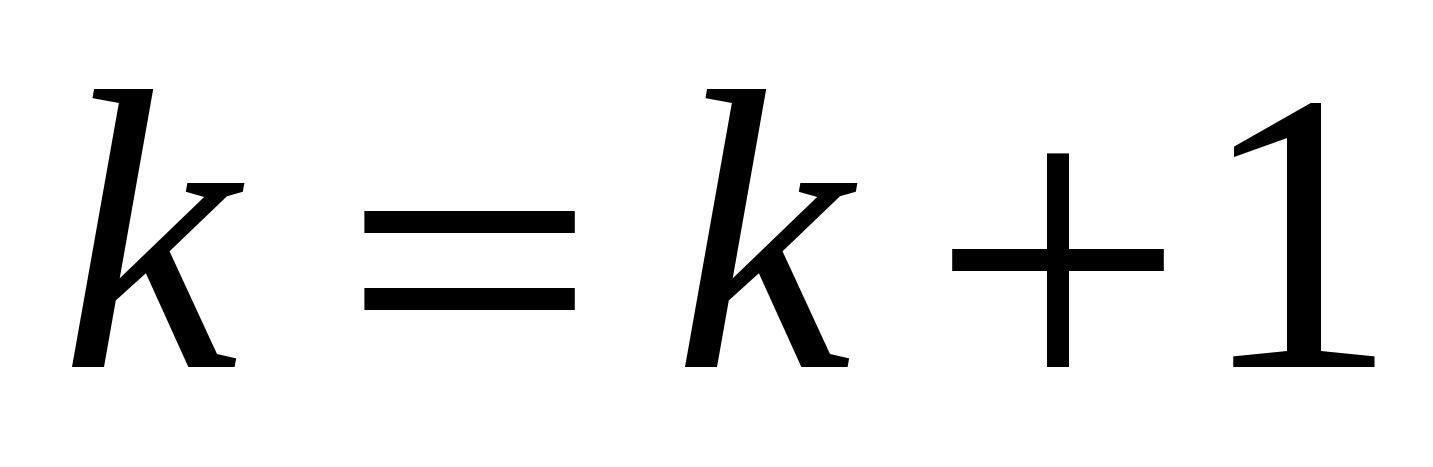 і переходять до кроку 2.
і переходять до кроку 2.
Перейдемо тепер безпосередньо до нашої задачі. Так як ми розглянули алгоритм методу штрафних функцій для випадку пошуку мінімуму функції, то перейдемо від задачі максимізації до задачі мінімізації:

Запишемо
штрафну функцію:
 і
розв’яжемо тепер задачу мінімізації
для цієї функції.
і
розв’яжемо тепер задачу мінімізації
для цієї функції.

За
точність обчислень оберемо
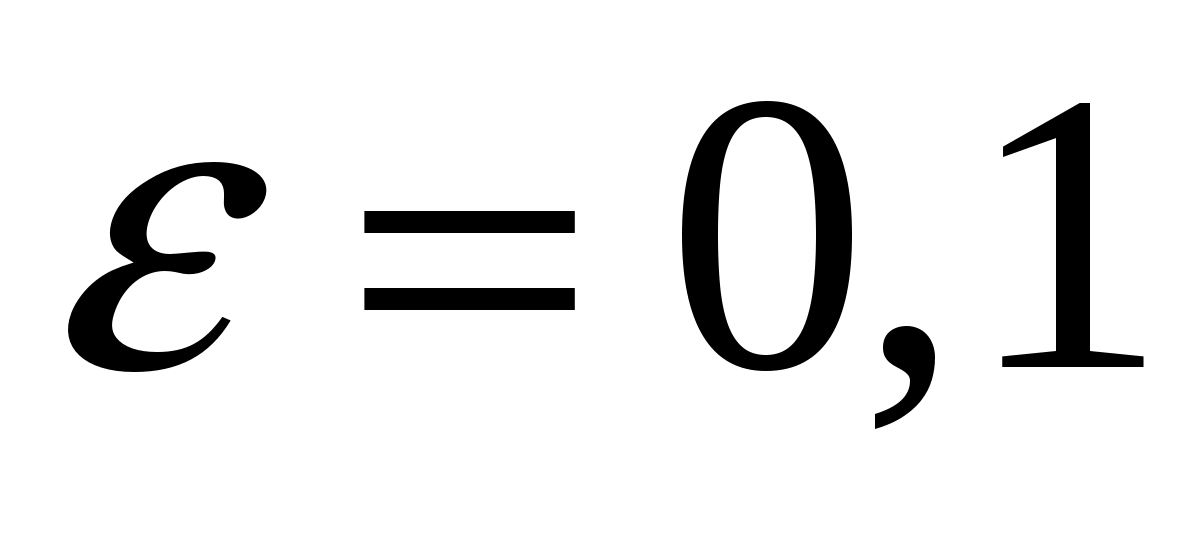 , а крок
, а крок
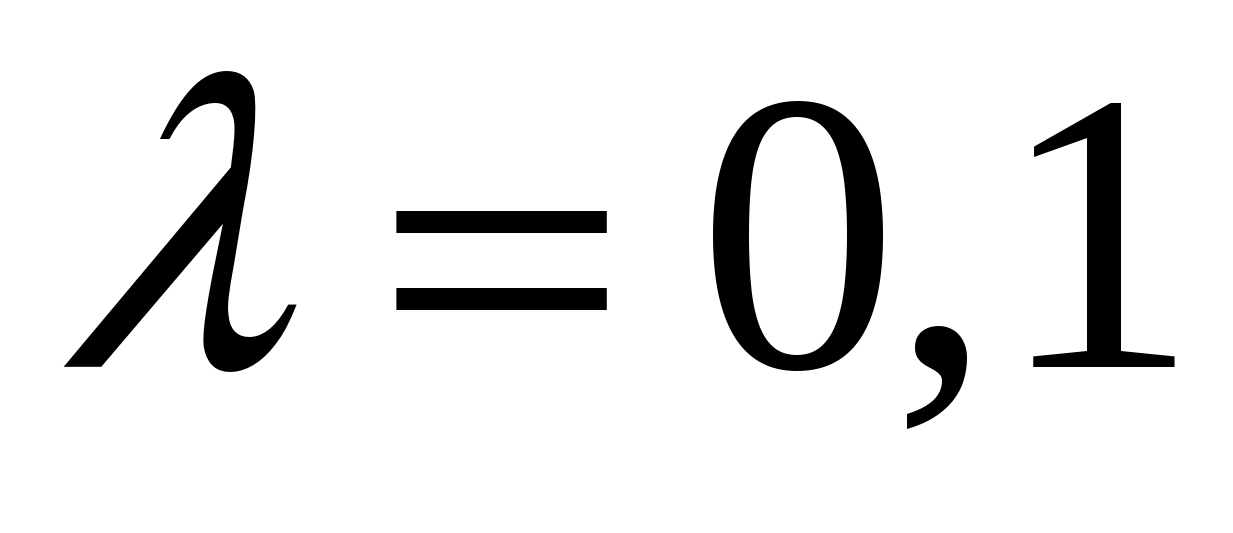 ,
а початкову точку візьмемо таку ж як ми
брали у методі Франка-Вулфа, тобто
,
а початкову точку візьмемо таку ж як ми
брали у методі Франка-Вулфа, тобто
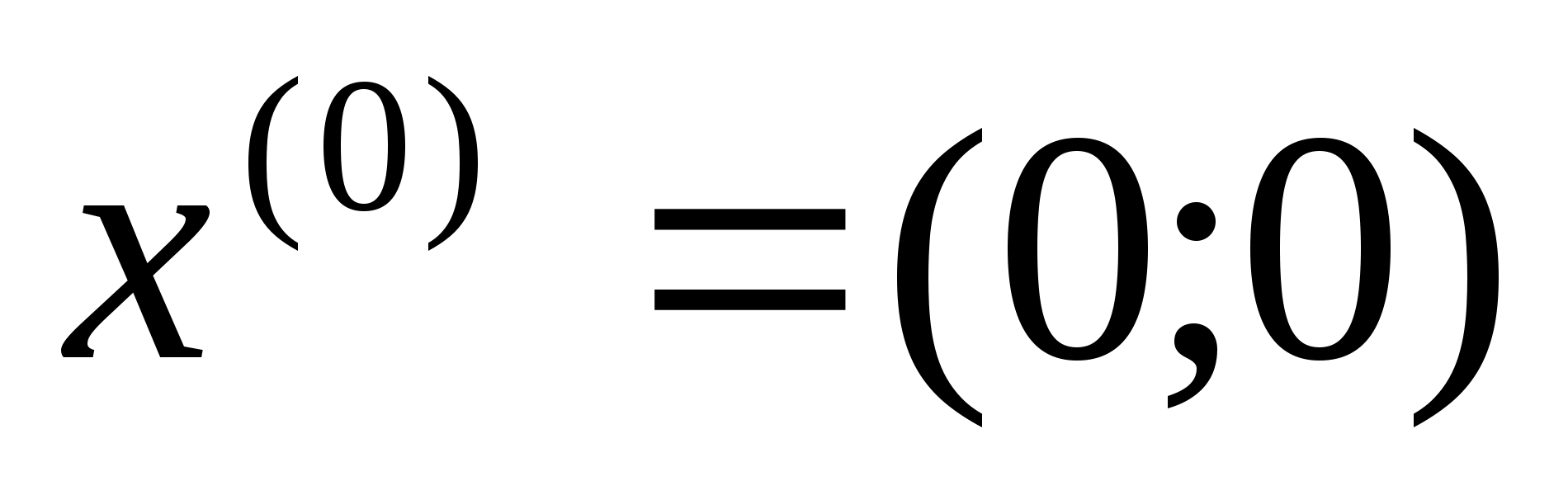 .
Отже
.
Отже

 ;
;
 .
.
Тобто
 ,
,
Точка
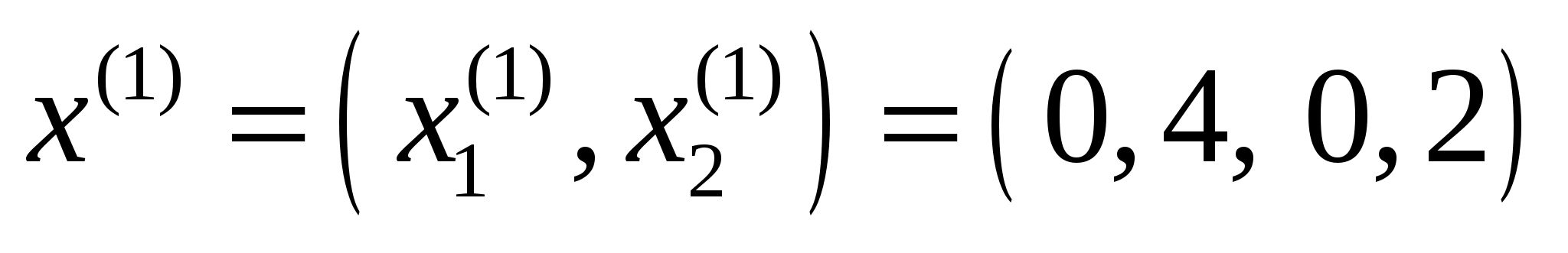 належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі:
належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі:
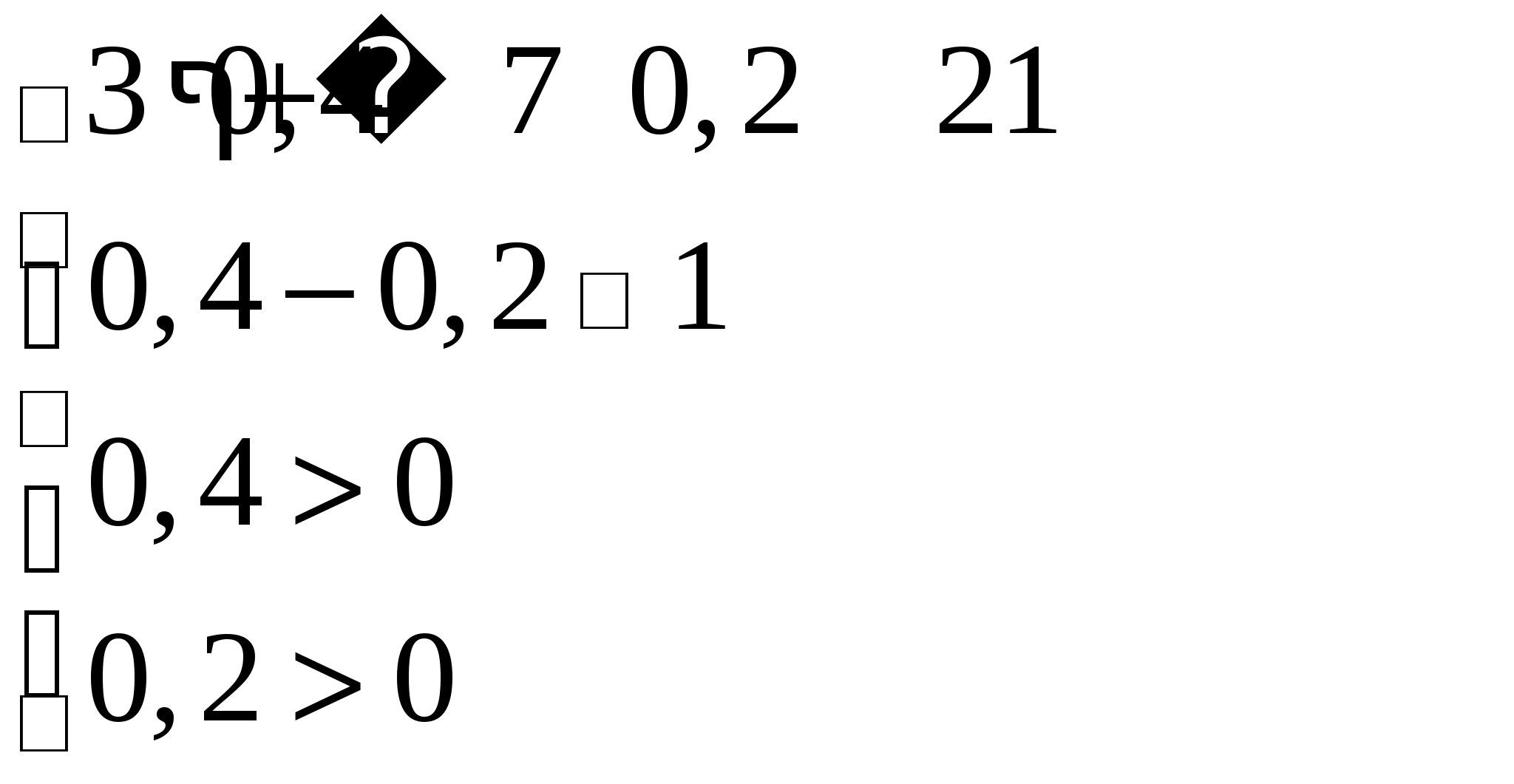
Обчислимо
значення штрафної функції в цій точці:
 .
Перевіримо критерій зупинки:
.
Перевіримо критерій зупинки:
 ,
отже тепер по аналогії шукаємо наступне
наближення до оптимального розв’язку.
,
отже тепер по аналогії шукаємо наступне
наближення до оптимального розв’язку.


Точка
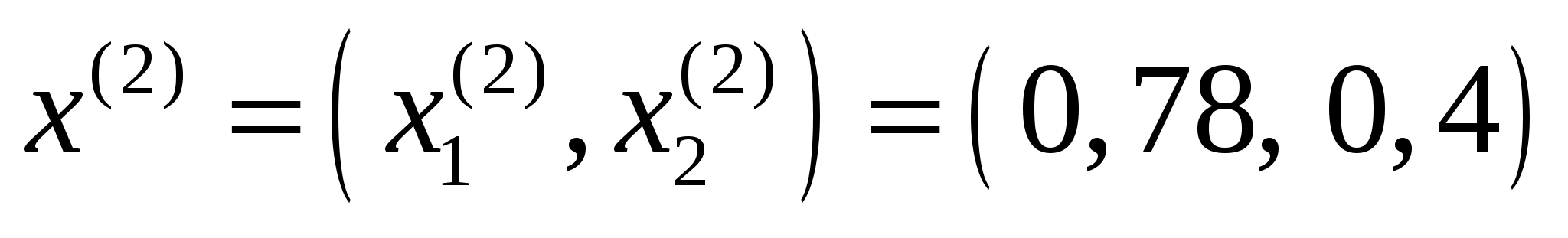 належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі:
належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі:

Обчислимо
значення штрафної функції в цій точці:
 .
Тепер перевіримо критерій зупинки:
.
Тепер перевіримо критерій зупинки:
 ,
отже шукаємо наступне наближення до
оптимального розв’язку.
,
отже шукаємо наступне наближення до
оптимального розв’язку.
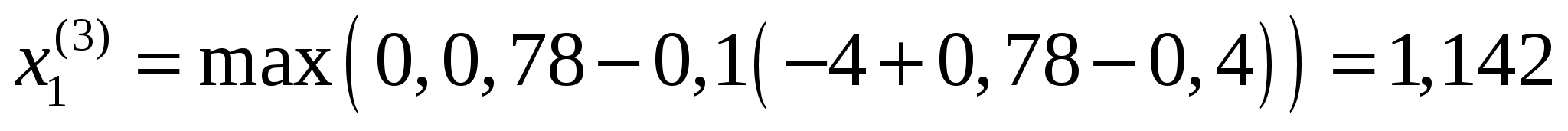

Точка
 належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
Обчислимо
значення штрафної функції в цій точці:
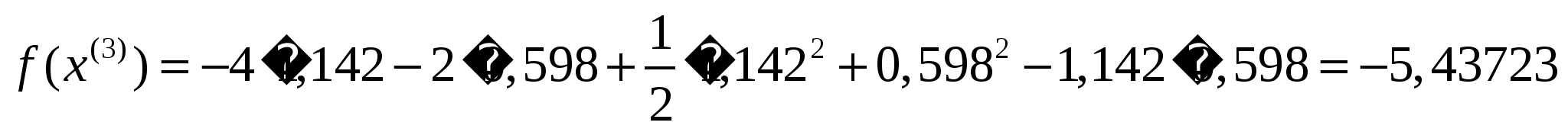 .
.
Тепер перевіримо критерій зупинки:
 ,
отже шукаємо наступне наближення до
оптимального розв’язку.
,
отже шукаємо наступне наближення до
оптимального розв’язку.

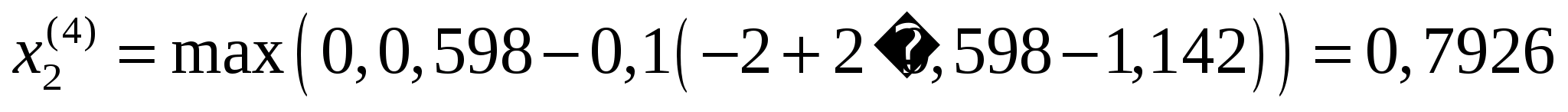
Точка
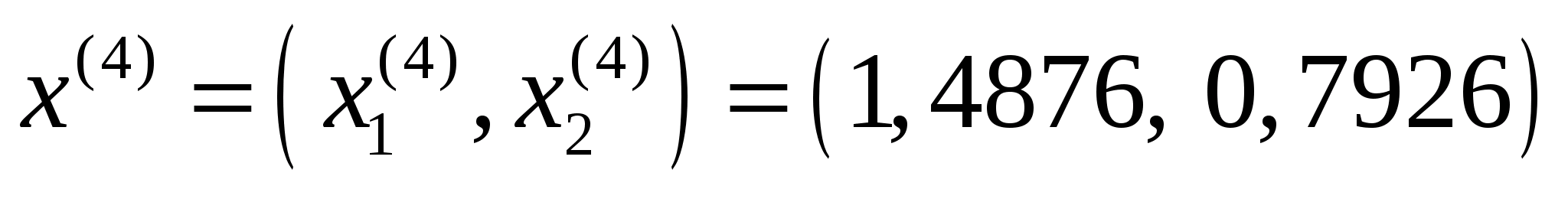 належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
Обчислимо
значення штрафної функції в цій точці:
 .
.
Тепер перевіримо критерій зупинки:
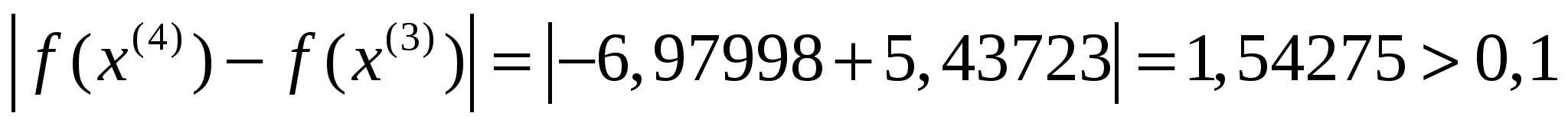 ,
отже шукаємо наступне наближення до
оптимального розв’язку.
,
отже шукаємо наступне наближення до
оптимального розв’язку.
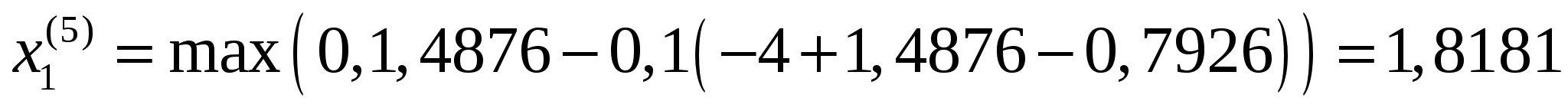

Точка
 належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
Обчислимо
значення штрафної функції в цій точці:
 .
.
Тепер перевіримо критерій зупинки:
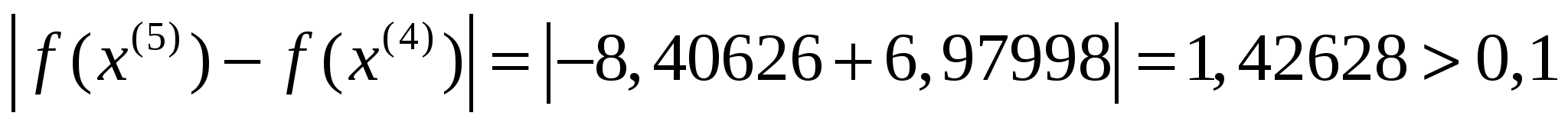 ,
отже шукаємо наступне наближення до
оптимального розв’язку.
,
отже шукаємо наступне наближення до
оптимального розв’язку.
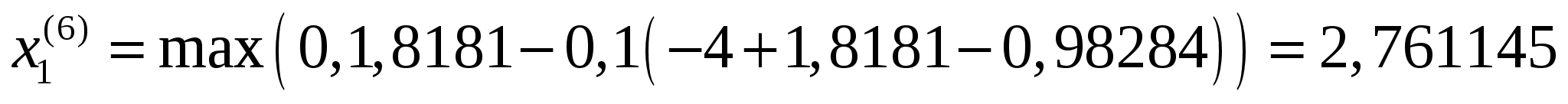
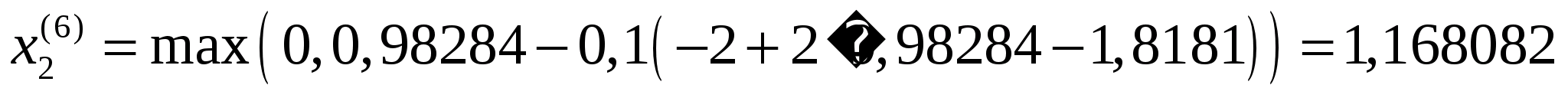
Точка
 належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
належить допустимій множині задачі,
оскільки задовольняє обмеженням задачі.
Обчислимо
значення штрафної функції в цій точці:
 .
.
Тепер перевіримо критерій зупинки:
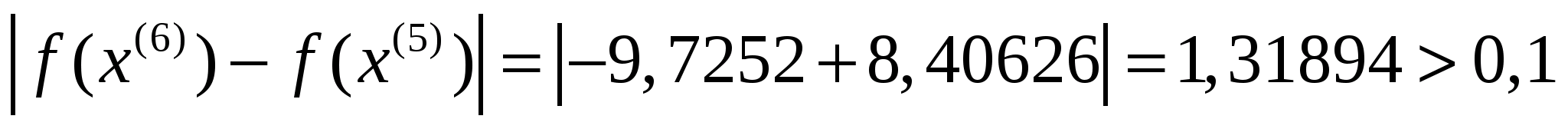 ,
отже шукаємо наступне наближення до
оптимального розв’язку.
,
отже шукаємо наступне наближення до
оптимального розв’язку.


Точка
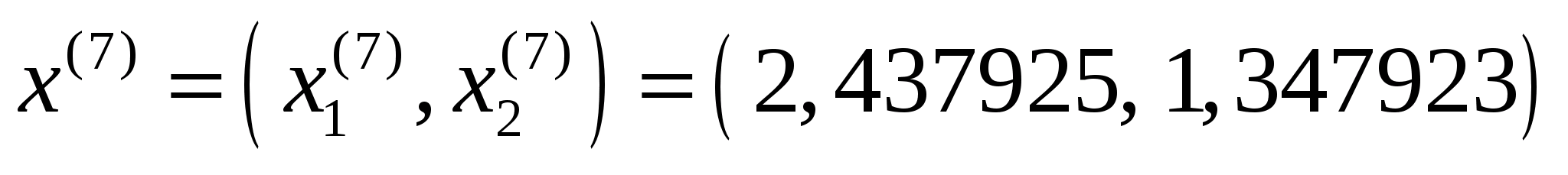 не належить допустимій множині задачі,
оскільки не виконується друге обмеженням
задачі (
не належить допустимій множині задачі,
оскільки не виконується друге обмеженням
задачі ( ),
отже параметр
),
отже параметр
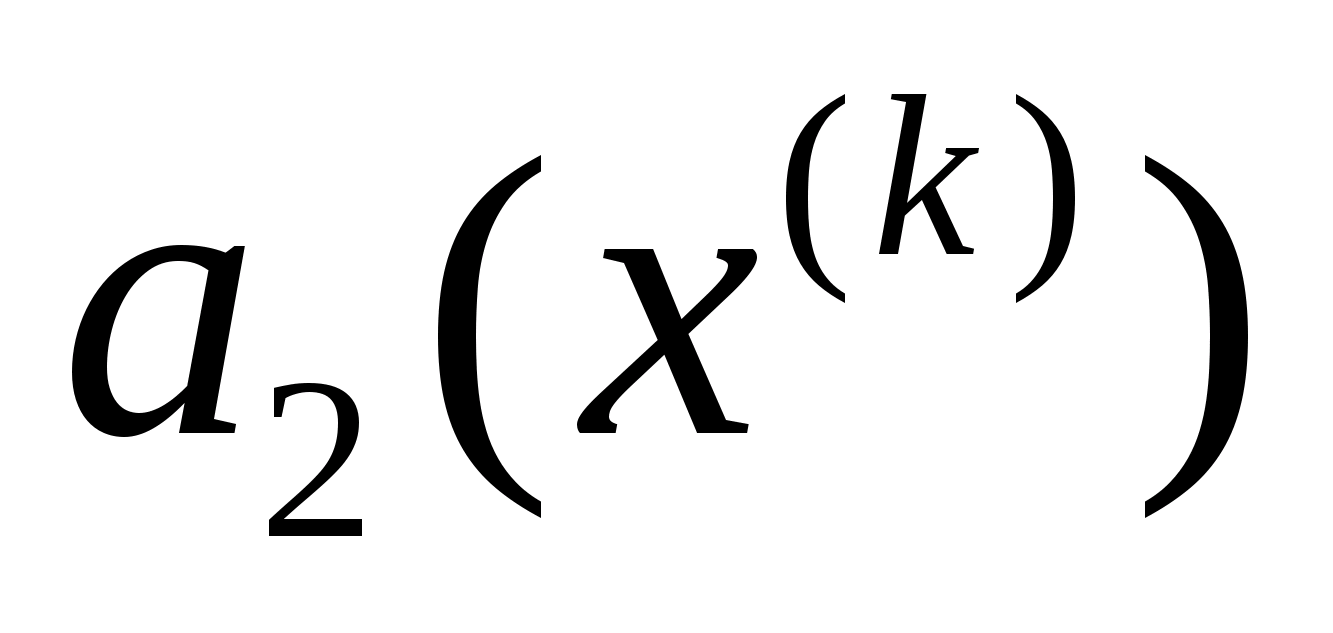 відмінний від нуля. Оберемо його так,
щоб друге обмеження задачі виконувалося.
відмінний від нуля. Оберемо його так,
щоб друге обмеження задачі виконувалося.

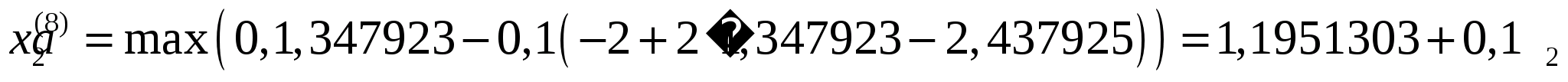
З другого обмеження задачі маємо:
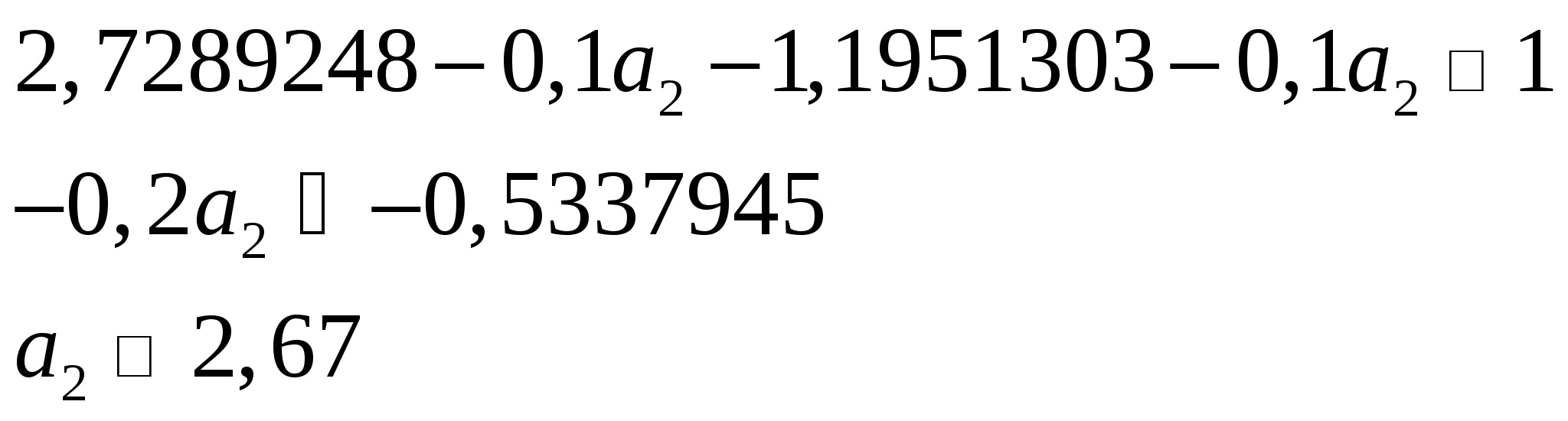
Отже
в якості параметру
 візьмемо
візьмемо
 .
Тоді
.
Тоді
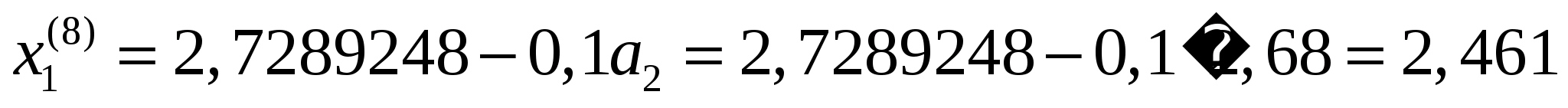

Точка
 належить допустимій множині задачі.
Обчислимо значення штрафної функції в
цій точці:
належить допустимій множині задачі.
Обчислимо значення штрафної функції в
цій точці:
 .
.
І так далі продовжується процес пошуку нового наближення до розв’язку задачі.
Як бачимо, метод штрафних функцій сходиться значно повільніше, ніж метод Франка-Вулфа. Це може бути пов’язано з тим, що початкове наближення знаходиться далеко від мінімуму функції, або ж необхідно обрати більший крок.
5. Розв’язання задачі цілочислового програмування
Розв’яжемо задачу цілочислового програмування
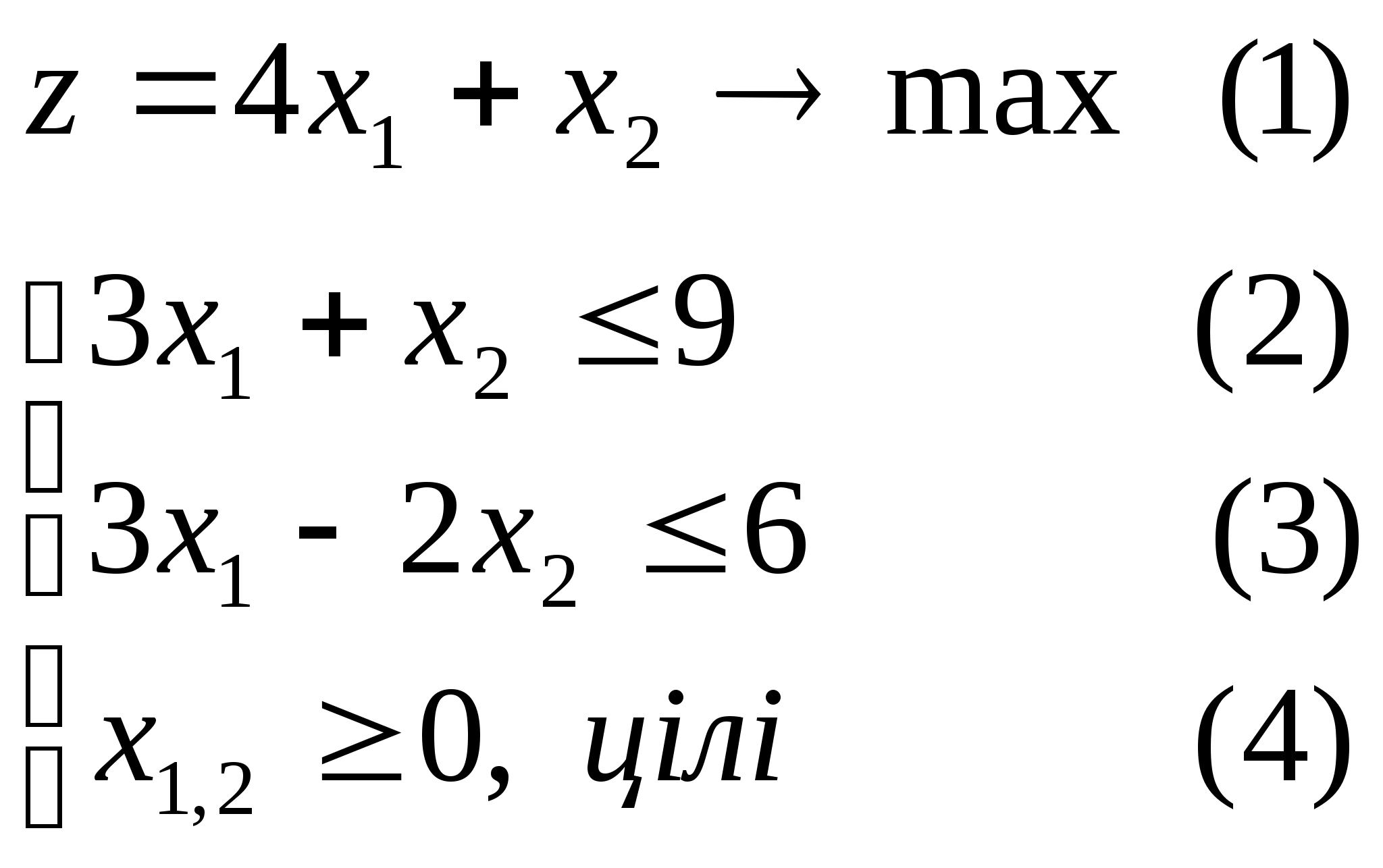
а) графічно:
Оскільки число невідомих задачі дорівнює двом, рішення можна знайти, використовуючи геометричну інтерпретацію заадчі. Для цього, насамперед, побудуємо багатокутник рішення задачі, що складає у визначенні максимальне значення лінійної функції (1) при виконанні умов (2) і (3) (мал. 1). Координати всіх точок побудованого багатокутника рішення ОАВС задовольняють систему лінійних нерівностей 2-3. Разом з тим умові (4), тобто умові цілочисельності змінних, задовольняють координати лише 20 точок, відзначених на мал. 1.
Щоб знайти точку, координати якої визначають рішення вихідної задачі, замінимо багатокутник ОАВС багатокутником, що містить усі припустимі точки з цілочисловими координатами і таким, що координати кожної з вершин є цілими числами. Виходить, якщо знайти точку максимуму функції (1) на отриманому багатокутнику, то координати цієї точки і визначать оптимальний план задачі.
Для
цього побудуємо вектор
 =(4; 1) – градієнт цільової функції і
перпендикуляр до неї – лінію рівня
цільової функції, тобто лінію, в точках
якої цільова функція приймає одне й те
ж значення. Побудовану пряму пересуваємо
в напрямку вектора
=(4; 1) – градієнт цільової функції і
перпендикуляр до неї – лінію рівня
цільової функції, тобто лінію, в точках
якої цільова функція приймає одне й те
ж значення. Побудовану пряму пересуваємо
в напрямку вектора
 доти,
поки вона не пройде через останню
загальну точку її з даним багатокутником.
Координати цієї точки і визначають
оптимальний план, а значення цільової
функції в ній є максимальним.
доти,
поки вона не пройде через останню
загальну точку її з даним багатокутником.
Координати цієї точки і визначають
оптимальний план, а значення цільової
функції в ній є максимальним.
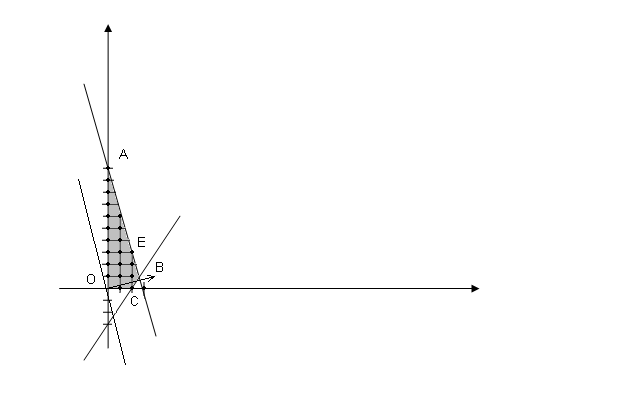
У
даному випадку шуканою є точка Е(2;3),
у якій цільова функція приймає максимальне
значення
 .
Отже, координати точки Е
визначають оптимальний план задачі 1
— 4.
.
Отже, координати точки Е
визначають оптимальний план задачі 1
— 4.
б) методом Гоморі:
Для рішення задачі цілочислового програмування методом Гоморі спочатку визначимо симплекс-методом оптимальний план задачі 1 —3 без умови цілочисельностісті змінних:
|
і |
Базис |
Сб |
В |
4 |
1 |
0 |
0 |
|
А1 |
А2 |
А3 |
А4 |
||||
|
1 |
А3 |
0 |
9 |
3 |
1 |
1 |
0 |
|
2 |
А4 |
0 |
6 |
3 |
-2 |
0 |
1 |
|
3 |
|
|
0 |
- 4 |
-1 |
0 |
0 |
|
1 |
А3 |
0 |
3 |
0 |
3 |
1 |
-1 |
|
2 |
А1 |
4 |
2 |
1 |
-2/3 |
0 |
1/3 |
|
3 |
|
|
8 |
0 |
-11/3 |
0 |
4/3 |
|
1 |
А2 |
1 |
1 |
0 |
1 |
1/3 |
-1/3 |
|
2 |
А1 |
4 |
8/3 |
1 |
0 |
2/9 |
1/9 |
|
3 |
|
|
35/3 |
0 |
0 |
11/9 |
1/9 |
Тобто
оптимальний план буде мати вигляд:
 ,
при цьому
,
при цьому
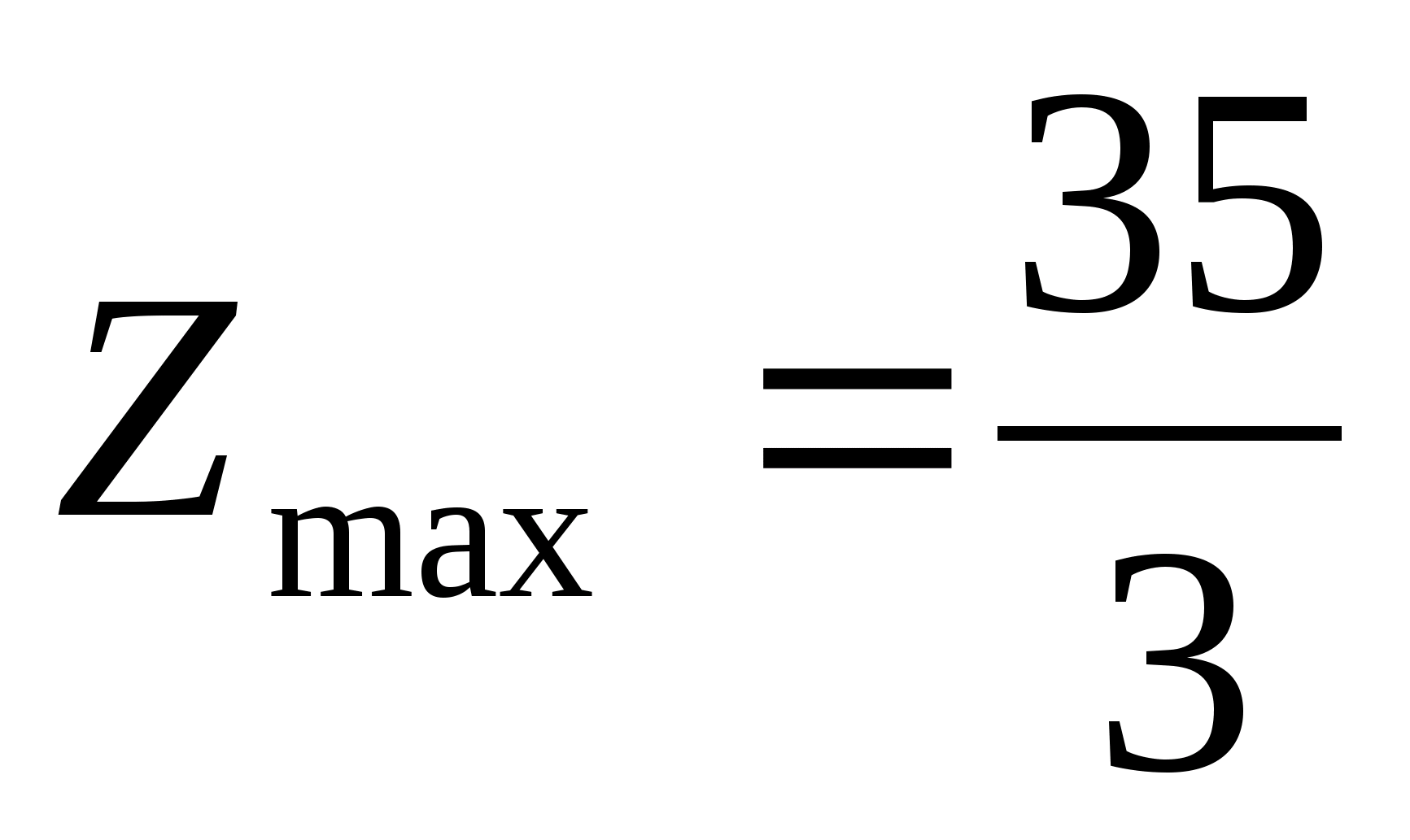 .
Отримане рішення є оптимальним для
задачі лінійного програмування, але
недопустимим для задачі лінійного
цілочислового програмування, оскільки
змінна
.
Отримане рішення є оптимальним для
задачі лінійного програмування, але
недопустимим для задачі лінійного
цілочислового програмування, оскільки
змінна
 приймає дробове значення. Тому будуємо
додаткове обмеження для змінної
приймає дробове значення. Тому будуємо
додаткове обмеження для змінної
 ,
яке є правильним відтинанням, використовуючи
перший алгоритм Гоморі:
,
яке є правильним відтинанням, використовуючи
перший алгоритм Гоморі:
 .
Тобто з останньої симплекс-таблиці
матимемо:
.
Тобто з останньої симплекс-таблиці
матимемо:
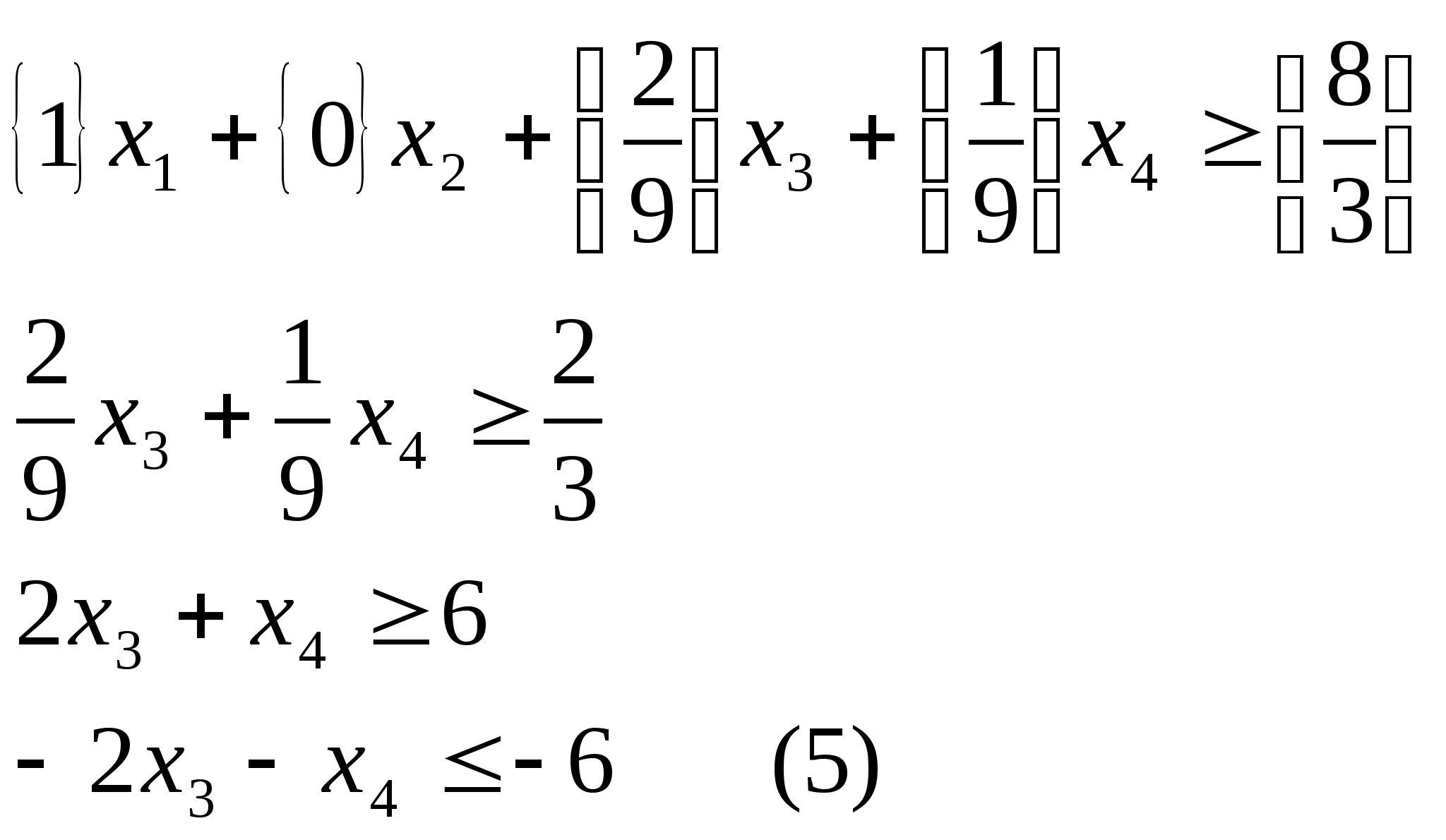
Умову
5 записуємо в канонічній формі:
 і
приєднуємо до останньої симплекс-таблиці
3-ім рядком, при цьому рядок оцінок не
зміниться. Тепер рішення задачі, утвореної
в результаті приєднання додаткового
обмеження, знаходимо за допомогою
двоїстого симплекс-методу.
і
приєднуємо до останньої симплекс-таблиці
3-ім рядком, при цьому рядок оцінок не
зміниться. Тепер рішення задачі, утвореної
в результаті приєднання додаткового
обмеження, знаходимо за допомогою
двоїстого симплекс-методу.
|
і |
Базис |
Сб |
В |
4 |
1 |
0 |
0 |
0 |
|
А1 |
А2 |
А3 |
А4 |
А5 |
||||
|
1 |
А2 |
1 |
1 |
0 |
1 |
1/3 |
-1/3 |
0 |
|
2 |
А1 |
4 |
8/3 |
1 |
0 |
2/9 |
1/9 |
0 |
|
3 |
А5 |
0 |
-6 |
0 |
0 |
-2 |
-1 |
1 |
|
4 |
|
|
35/3 |
0 |
0 |
11/9 |
0 |
0 |
|
1 |
А2 |
1 |
3 |
0 |
1 |
1 |
0 |
-1/3 |
|
2 |
А1 |
4 |
2 |
1 |
0 |
0 |
0 |
1/9 |
|
3 |
А4 |
0 |
6 |
0 |
0 |
2 |
1 |
-1 |
|
4 |
|
|
11 |
0 |
0 |
1 |
0 |
1/9 |
З
останньої симплекс-таблиці видно, що
вихідна задача цілочислового програмування
має оптимальний план Х*
= (2;
3). При цьому плані значення цільової
функції дорівнює:
 .
.
в ) методом Ленг і Дойг
Як
і у випадку знаходження розв’язку
задачі цілочислового програмування за
допомогою методу Гоморі, спочатку
визначаємо симплекс-методом оптимальний
план задачі (1) —(3) без умови цілочисельності
змінних. З попереднього пункту маємо
оптимальне для задачі лінійного
програмування (1-3):
 ,
при цьому
,
при цьому
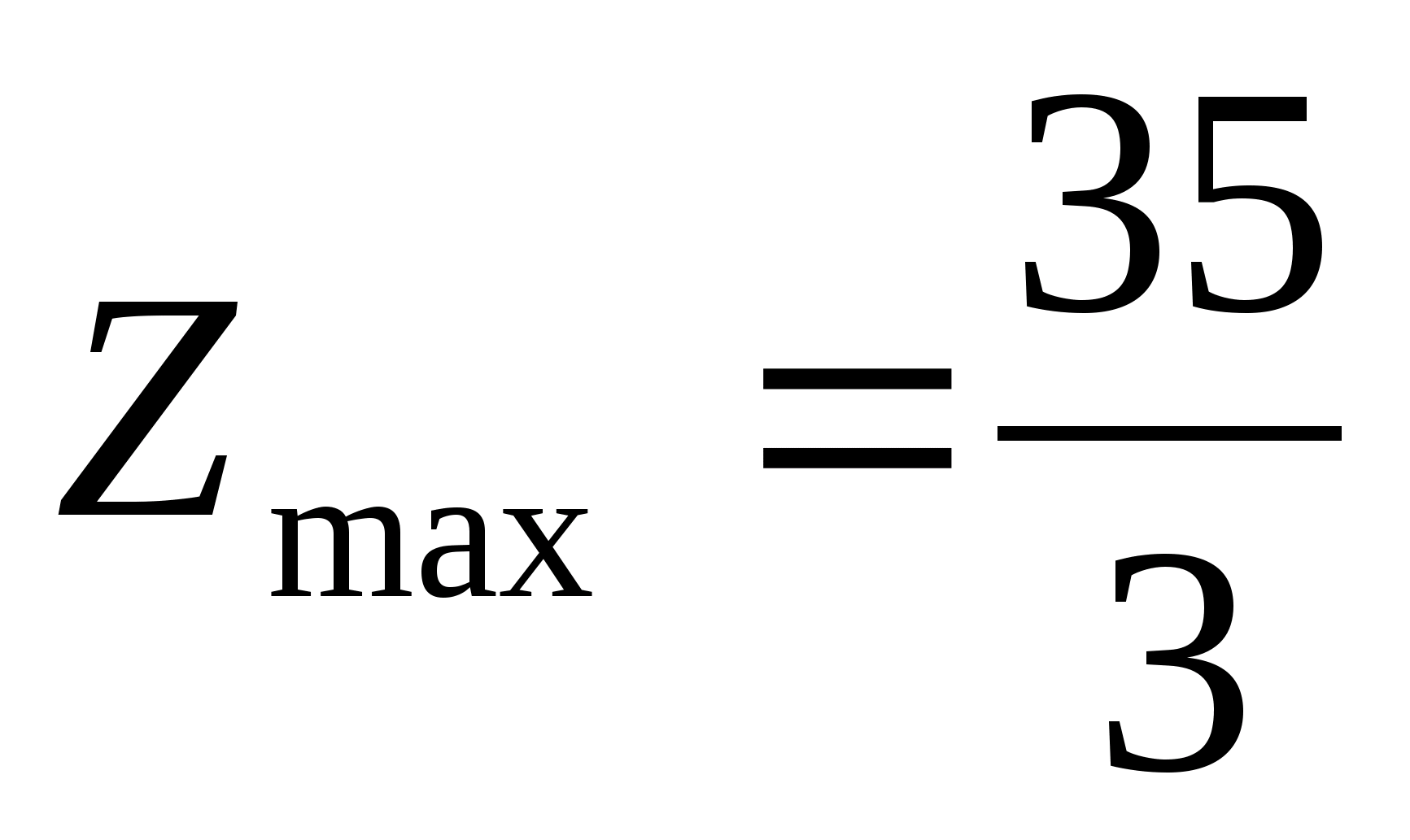 .
.
Оскільки
оптимальне рішення задачі лінійного
програмування 1-3 не задовольняє умові
цілочисельності, метод Ленг і Дойг
заміняє простір рішень задачі лінійного
програмування так, що в кінцевому
результаті отримуємо рішення задачі
цілочислового лінійного програмування.
Для цього спочатку обираємо змінну,
значення якої не є цілочисловим, тобто
 .
Область
.
Область
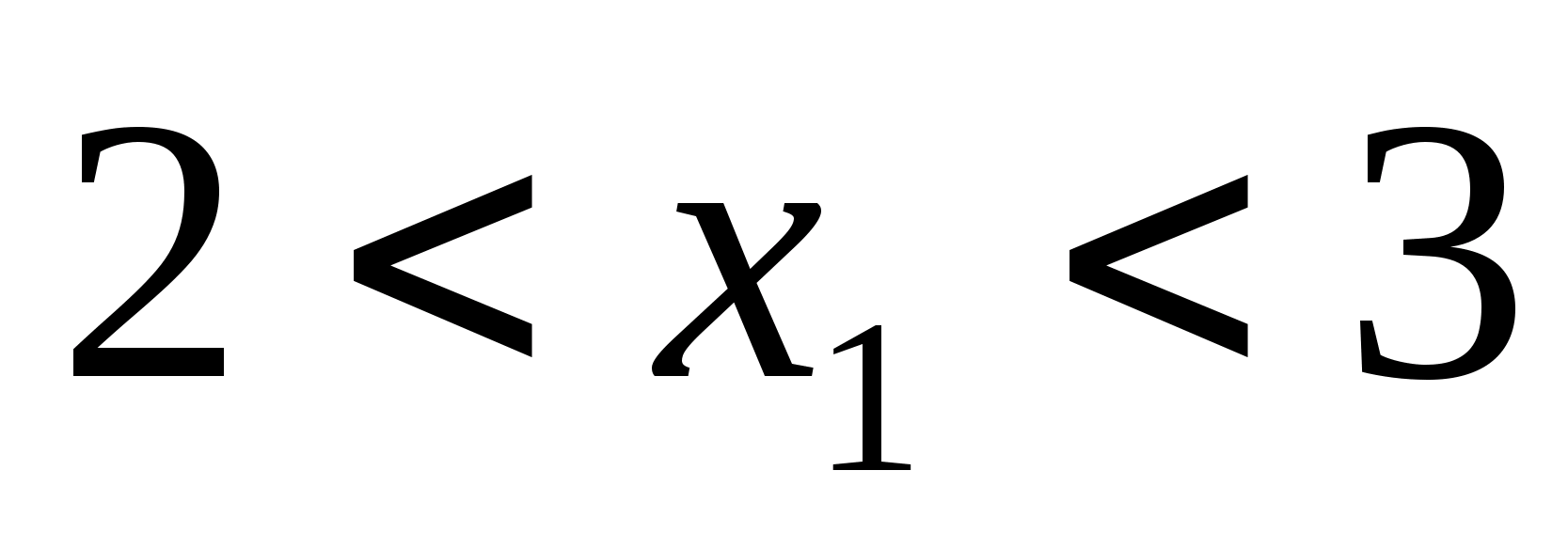 простору допустимих рішень задачі
лінійного програмування не містить
цілочислових значень змінної
простору допустимих рішень задачі
лінійного програмування не містить
цілочислових значень змінної
 ,
тому вона може бути виключена із розгляду,
як безперспективна. Це еквівалентно
заміні вихідної задачі лінійного
програмування 1-3 двома новими задачами
лінійного програмування, котрі
визначаються наступним чином:
,
тому вона може бути виключена із розгляду,
як безперспективна. Це еквівалентно
заміні вихідної задачі лінійного
програмування 1-3 двома новими задачами
лінійного програмування, котрі
визначаються наступним чином:
а) задача 1:

б) задача 2:
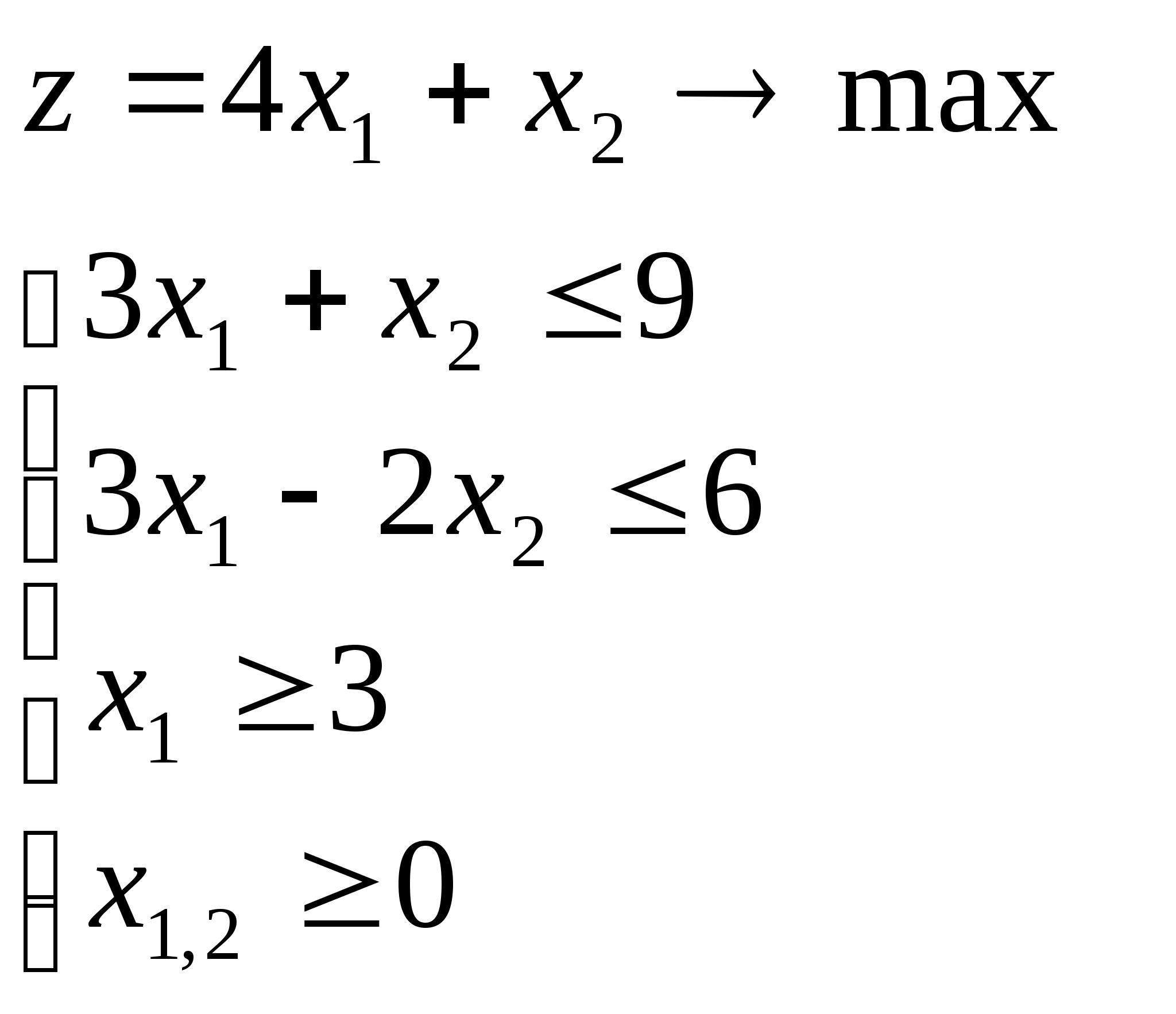
Нові обмеження виключають одна одну, тому задачу 1 і задачу 2 необхідно розглядати як незалежні задачі лінійного програмування. Оптимальне рішення задачі цілочислового програмування знаходиться або в просторі допустимих рішень задачі 1, або задачі 2. Отже обидві звдачі необхідно розв’язати.
Спочатку
розв’яжемо задачу 1. Для цього спочатку
з останньої симплекс-таблиці задачі
1-3 змінну
 виразимо через небазисні невідомі:
виразимо через небазисні невідомі:
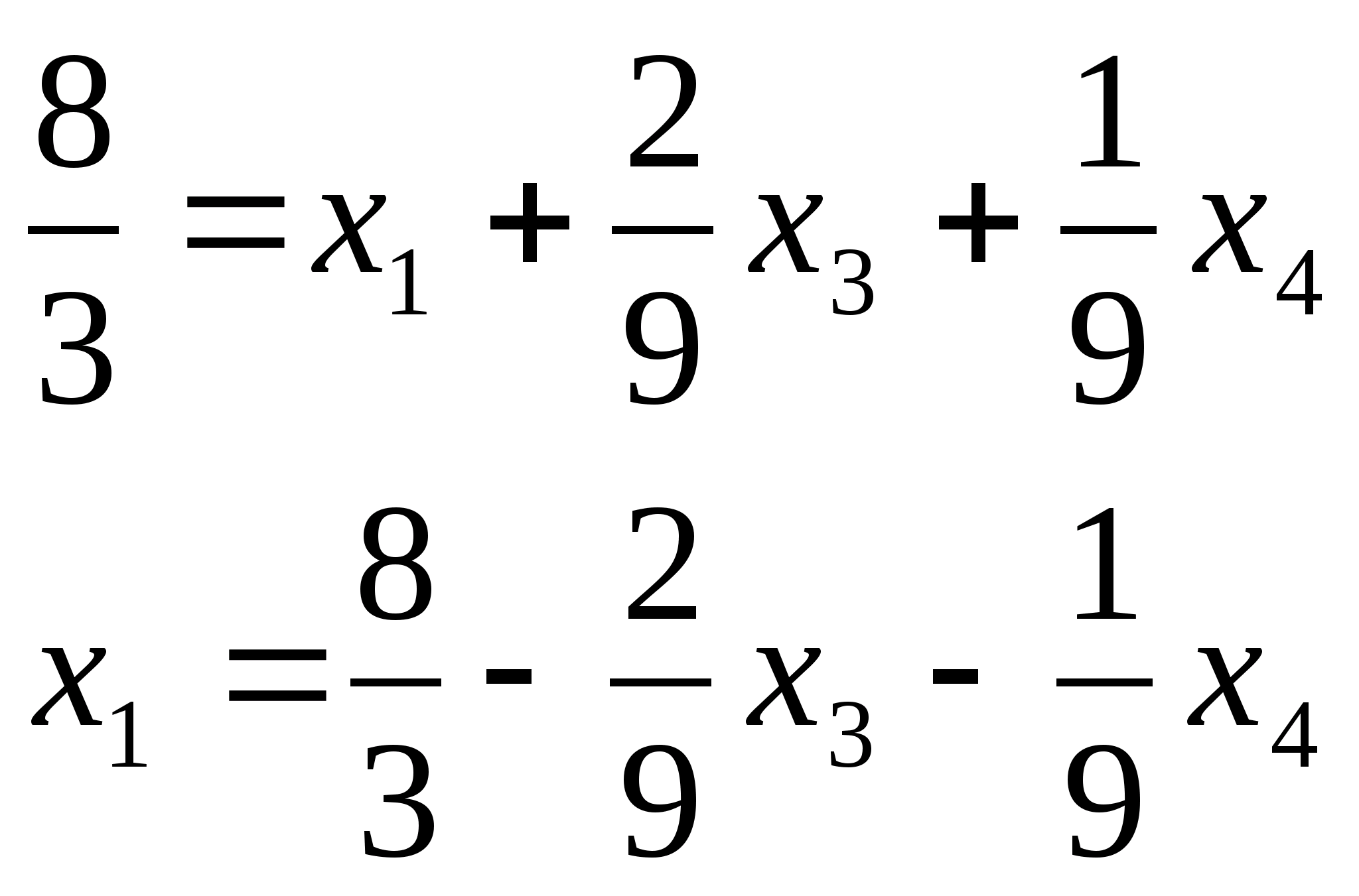
Тепер
нове додаткове обмеження
 запишемо в канонічній формі і допишемо
його до останньої симплекс-таблиці
задачі 1-3:
запишемо в канонічній формі і допишемо
його до останньої симплекс-таблиці
задачі 1-3:

Отже за допомогою двоїстого симплекс-методу можемо розв’язати задачу 1:
|
і |
Базис |
Сб |
В |
4 |
1 |
0 |
0 |
0 |
|
А1 |
А2 |
А3 |
А4 |
А5 |
||||
|
1 |
А2 |
1 |
1 |
0 |
1 |
1/3 |
-1/3 |
0 |
|
2 |
А1 |
4 |
8/3 |
1 |
0 |
2/9 |
1/9 |
0 |
|
3 |
А5 |
0 |
-2/3 |
0 |
0 |
-2/9 |
-1/9 |
1 |
|
4 |
35/3 |
0 |
0 |
11/9 |
0 |
0 |
||
|
1 |
А2 |
1 |
3 |
0 |
1 |
1 |
0 |
-3 |
|
2 |
А1 |
4 |
2 |
1 |
0 |
0 |
0 |
1 |
|
3 |
А4 |
0 |
6 |
0 |
0 |
2 |
1 |
-9 |
|
4 |
11 |
0 |
0 |
1 |
0 |
1 |
Оптимальним
розв’язком задачі 1 буде
 ,
а максимальне значення цільової функції
відповідно -
,
а максимальне значення цільової функції
відповідно -
 .
Оптимальне рішення задачі 1 задовольняє
умову 5, тобто умову цілочисленості.
.
Оптимальне рішення задачі 1 задовольняє
умову 5, тобто умову цілочисленості.
В
цій ситуації ми не можемо оцінити якість
рішення, отриманого при розгляді задачі
1, оскільки розв’язок задачі 2 може
привести до кращого цілочисельного
розв’язку(з більшим значенням цільової
функції). Поки що ми можемо лише сказати,
що значення
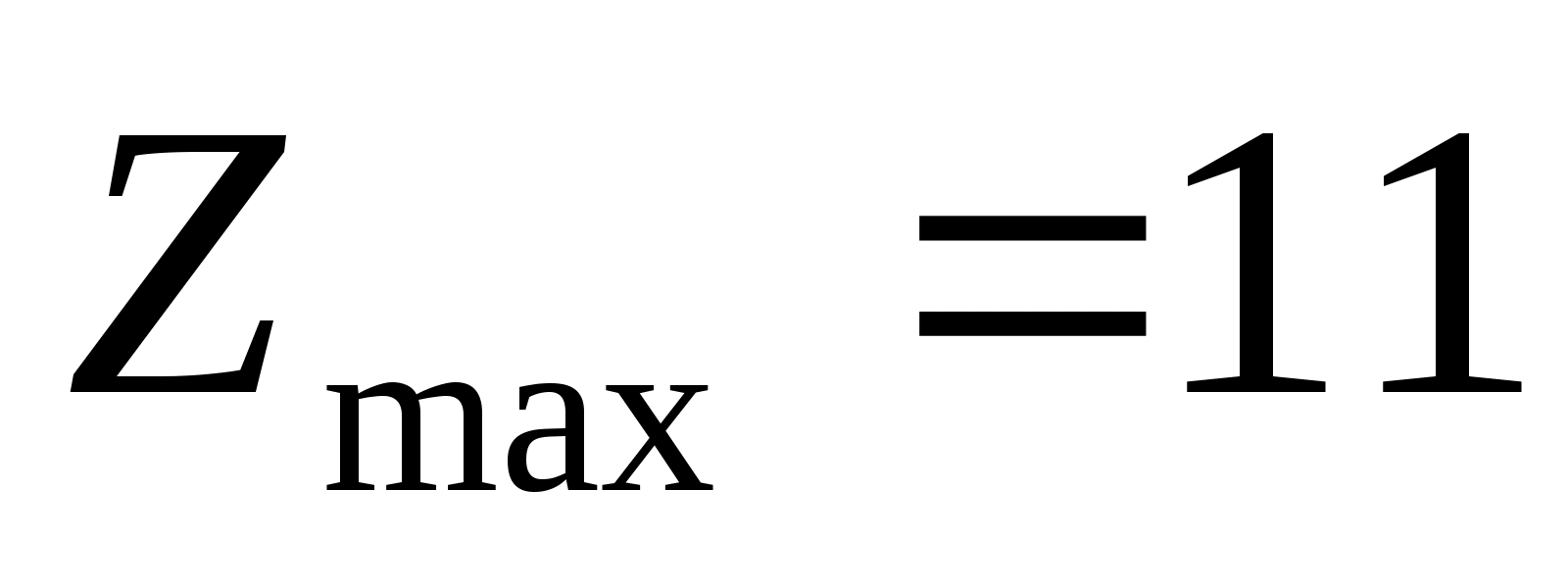 являється нижньою границею максимального
значення цільової функції вихідної
задачі 1-4.
являється нижньою границею максимального
значення цільової функції вихідної
задачі 1-4.
При
значенні нижньої границі
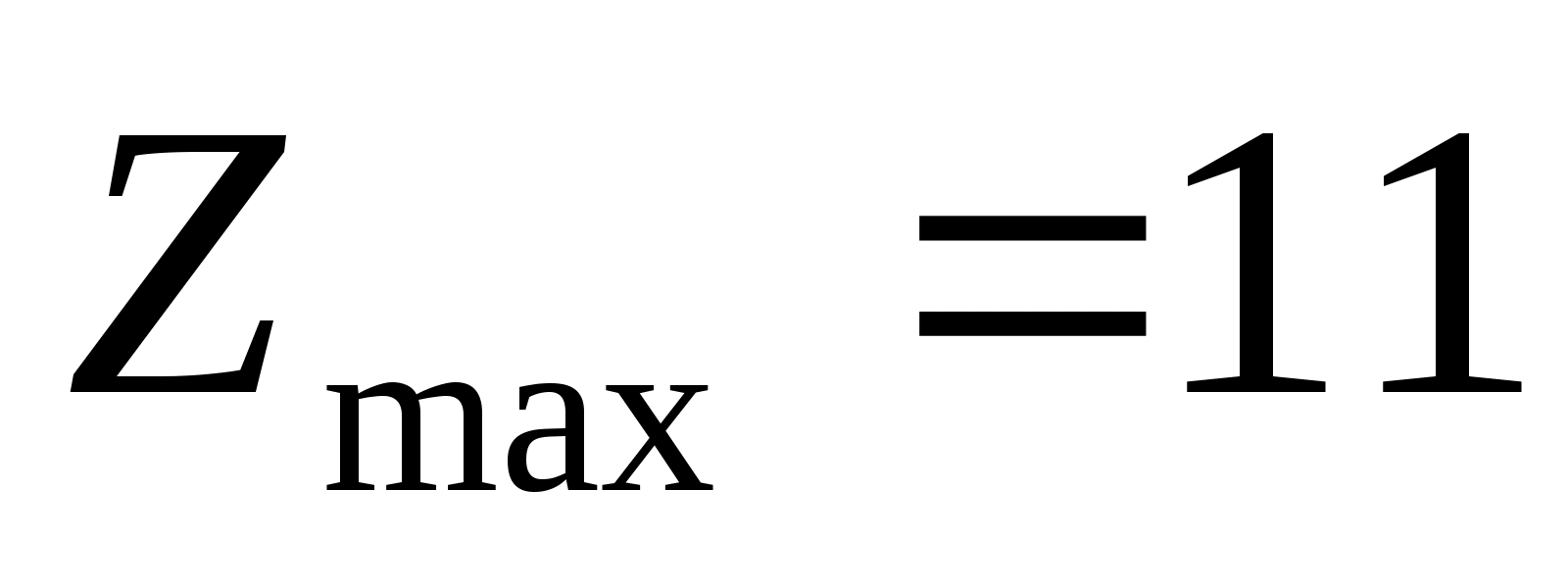 розглянемо задачу 2. Аналогічно до задачі
1 маємо:
розглянемо задачу 2. Аналогічно до задачі
1 маємо:

|
і |
Базис |
Сб |
В |
4 |
1 |
0 |
0 |
0 |
|
А1 |
А2 |
А3 |
А4 |
А6 |
||||
|
1 |
А2 |
1 |
1 |
0 |
1 |
1/3 |
-1/3 |
0 |
|
2 |
А1 |
4 |
8/3 |
1 |
0 |
2/9 |
1/9 |
0 |
|
3 |
А5 |
0 |
-1/3 |
0 |
0 |
2/9 |
1/9 |
1 |
|
4 |
35/3 |
0 |
0 |
11/9 |
0 |
0 |
Оскільки для b=-1/3 в рядку, що йому відповідає немає від’ємних чисел, то задача 2 розв’язку не має.
Отже
оптимальним рішенням задачі лінійного
цілочислового програмування являється
нижня границя, а саме
 ,
при цьому значення цільової функції
,
при цьому значення цільової функції
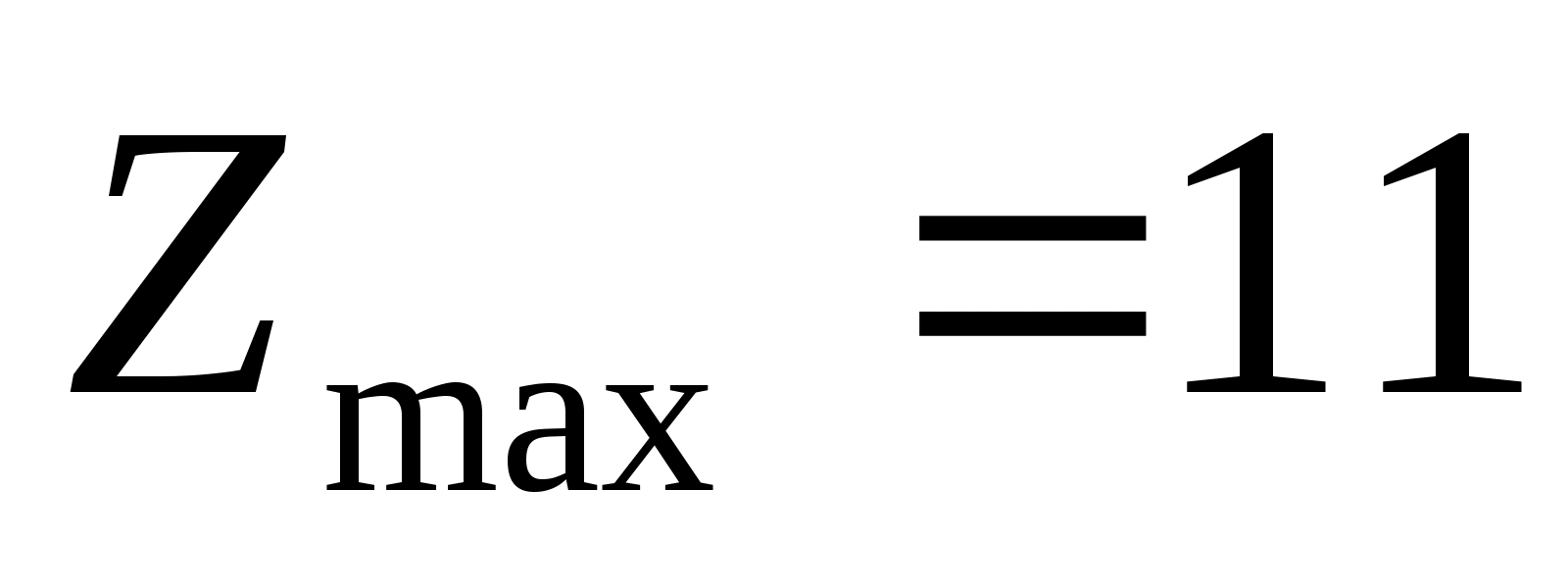 .
.
Як бачимо, розв’язки, отримані трьома способами однакові.
6. Вихідний код програми
Нижче приведемо код програми для знаходження мінімуму фіункції за допомогою методу золотого перерізу і методу Фібоначчі, реалізований в С++. Результат виконання програми виводить в окремий текстовий документ Solution.txt.
Метод золотого перерізу
// zoloto.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <iostream>
#include <cmath>
#include <fstream>
using namespace std;
double g[5]={0};
double a,b;
double E=0;
void Inputkoef()
{
for (int i=0;i<5;i++)
{
cout<<"Enter a value a["<<i+1<<"] : ";
cin>>g[i];
}
}
void Inputotrez()
{
cout<<"Enter the lower limit segment a=";
cin>>a;
cout<<"Enter the upper limit of the interval b=";
cin>>b;
cout<<"enter the calculation accuracy E=";
cin>>E;
}
double f(double x)
{
return (g[0]*pow(x,4)+g[1]*pow(x,3)+g[2]*pow(x,2)+g[3]*x+g[4]);
}
double f(double);
ofstream Out;
int main(int argc, char* argv[])
{
cout<<"function has the form: a1*x^4+a2*x^3+a3*x^2+a4*x+a5->min"<<endl;
Inputkoef();
Inputotrez();
double x,xk,yk,k;
k=0;
xk=a+((3-pow(5,0.5))/2)*(b-a);
yk=a+b-xk;
Out.open("Solution.txt");
cout << "Solution of the golden section method:\n";
Out << "Solution of the golden section method:\n";
cout << "k\ta\tb\tXk\tYk\tF(Xk)\tF(Yk)\n";
Out << "k\ta\tb\tXk\tYk\tF(Xk)\tF(Yk)\n";
do
{
cout << k << "\t" << a << "\t" << b << "\t" << xk << "\t" << yk << "\t" << f(xk) << "\t" << f(yk) << endl;
Out << k << "\t" << a << "\t" << b << "\t" << xk << "\t" << yk << "\t" << f(xk) << "\t" << f(yk) << endl;
if(f(xk)<=f(yk))
{
b=yk;
yk=xk;
xk=a+b-xk;
}
else if(f(xk)>f(yk))
{
a=xk;
xk=yk;
yk=a+b-yk;
}
k++;
}
while (abs(b-a)>E);
cout << k << "\t" << a << "\t" << b << "\t" << xk << "\t" << yk << "\t" << f(xk) << "\t" << f(yk) << endl;
Out << k << "\t" << a << "\t" << b << "\t" << xk << "\t" << yk << "\t" << f(xk) << "\t" << f(yk) << endl;
x=(a+b)/2;
cout<< "x = " << x << "\tf(x) = " << f(x);
Out<< "x = " << x << "\tf(x) = " << f(x);
Out.close();
return 0;
}
Результат виконання програми при введенні даних, що відповідать завданню цієї курсової роботи:

Метод Фібоначчі
// fib.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <iostream>
#include <cmath>
#include <fstream>
using namespace std;
double PoslidovnistFib(double);
double g[5]={0};
double a,b;
double E=0;
void Inputkoef()
{
for (int i=0;i<5;i++)
{
cout<<"Enter a value a["<<i+1<<"] : ";
cin>>g[i];
}
}
void Inputotrez()
{
cout<<"Enter the lower limit segment a=";
cin>>a;
cout<<"Enter the upper limit of the interval b=";
cin>>b;
cout<<"enter the calculation accuracy E=";
cin>>E;
}
double f(double);
double f(double x)
{
return (g[0]*pow(x,4)+g[1]*pow(x,3)+g[2]*pow(x,2)+g[3]*x+g[4]);
};
ofstream Out;
int main(int argc, char* argv[])
{
cout<<"function has the form: a1*x^4+a2*x^3+a3*x^2+a4*x+a5->min"<<endl;
Inputkoef();
Inputotrez();
int d,k=0,p=0;
double eps,x,y,N=-1,kk=1.0;
eps = 0.00001 ;
Out.open("Solution.txt");
cout << "Solution of Fibonachi method:\n";
Out << "Solution of Fibonachi method:\n";
double L0=b-a;
do
{
N++;
}
while (PoslidovnistFib(N)<(abs(L0)/E));
cout << "N = " << N << endl;
Out << "N = " << N << endl;
cout << "k\ta\tb\tXk\tYk\tF(Xk)\tF(Yk)\n";
Out << "k\ta\tb\tXk\tYk\tF(Xk)\tF(Yk)\n";
x=a+(PoslidovnistFib(N-2)/PoslidovnistFib(N))*(b-a);
y=a+(PoslidovnistFib(N-1)/PoslidovnistFib(N))*(b-a);
cout << k << "\t" << a << "\t" << b << "\t" << x << "\t" << y << "\t" << f(x) << "\t" << f(y) << endl;
Out << k << "\t" << a << "\t" << b << "\t" << x << "\t" << y << "\t" << f(x) << "\t" << f(y) << endl;
do
{
if (f(x)<=f(y))
{
b=y;
y=x;
x=a+(PoslidovnistFib(N-k-3)/PoslidovnistFib(N-k-1))*(b-a);
}
else if (f(x)>f(y))
{
a=x;
x=y;
y=a+(PoslidovnistFib(N-k-2)/PoslidovnistFib(N-k-1))*(b-a);
};
k++;
cout << k << "\t" << a << "\t" << b << "\t" << x << "\t" << y << "\t" << f(x) << "\t" << f(y) << endl;
Out << k << "\t" << a << "\t" << b << "\t" << x << "\t" << y << "\t" << f(x) << "\t" << f(y) << endl;
}
while(k!=N-3);
k = 0;
cout << "\tFi(N) = " << PoslidovnistFib << endl;
Out << "\tFi(N) = " << PoslidovnistFib << endl;
do
{
cout << "k = " << k << "\tFi(N-k-1) = " << PoslidovnistFib(N-k-1) << "\tFi(N-k-2) = " << PoslidovnistFib(N-k-2) << "\tFi(N-k-3) = " << PoslidovnistFib(N-k-3) << endl;
Out << "k = " << k << "\tFi(N-k-1) = " << PoslidovnistFib(N-k-1) << "\tFi(N-k-2) = " << PoslidovnistFib(N-k-2) << "\tFi(N-k-3) = " << PoslidovnistFib(N-k-3) << endl;
k++;
}
while(k!=N-3);
y=x+eps;
if (f(x)<=f(y))
{
b=y;
}
if (f(x)>f(y))
{
a=x;
};
x = (b+a)/2;
cout << "x = " << x << "\tf(x) = " << f(x) <<endl;
Out << "x = " << x << "\tf(x) = " << f(x) <<endl;
Out.close();
return 0;
}
double PoslidovnistFib(double n)
{
double f0,fk,p;
f0=1;
fk=1;
for(int i=2;i<=n;i++)
{
p=fk;
fk=fk+f0;
f0=p;
}
if (n<2)
{
fk=1;
}
return fk;
};
Результат виконання рограми:
Solution of Fibonachi method:
N = 17
kabXkYkF(Xk)F(Yk)
0020.7639321.23607-50.8575-59.9845
10.76393221.236071.52786-59.9845-53.5866
20.7639321.527861.055731.23607-58.9696-59.9845
31.055731.527861.236071.34752-59.9845-58.8184
41.055731.347521.167181.23607-59.998-59.9845
51.055731.236071.124611.16718-59.7535-59.998
61.124611.236071.167181.1935-59.998-60.0537
71.167181.236071.19351.20975-60.0537-60.0508
81.167181.209751.183441.1935-60.0411-60.0537
91.183441.209751.19351.19969-60.0537-60.056
101.19351.209751.199691.20356-60.056-60.0553
111.19351.203561.197371.19969-60.0556-60.056
121.197371.203561.199691.20124-60.056-60.0559
131.197371.201241.198921.19969-60.0559-60.056
141.198921.201241.199691.20046-60.056-60.056
Fi(N) = 004112A8
k = 0Fi(N-k-1) = 1597Fi(N-k-2) = 987Fi(N-k-3) = 610
k = 1Fi(N-k-1) = 987Fi(N-k-2) = 610Fi(N-k-3) = 377
k = 2Fi(N-k-1) = 610Fi(N-k-2) = 377Fi(N-k-3) = 233
k = 3Fi(N-k-1) = 377Fi(N-k-2) = 233Fi(N-k-3) = 144
k = 4Fi(N-k-1) = 233Fi(N-k-2) = 144Fi(N-k-3) = 89
k = 5Fi(N-k-1) = 144Fi(N-k-2) = 89Fi(N-k-3) = 55
k = 6Fi(N-k-1) = 89Fi(N-k-2) = 55Fi(N-k-3) = 34
k = 7Fi(N-k-1) = 55Fi(N-k-2) = 34Fi(N-k-3) = 21
k = 8Fi(N-k-1) = 34Fi(N-k-2) = 21Fi(N-k-3) = 13
k = 9Fi(N-k-1) = 21Fi(N-k-2) = 13Fi(N-k-3) = 8
k = 10Fi(N-k-1) = 13Fi(N-k-2) = 8Fi(N-k-3) = 5
k = 11Fi(N-k-1) = 8Fi(N-k-2) = 5Fi(N-k-3) = 3
k = 12Fi(N-k-1) = 5Fi(N-k-2) = 3Fi(N-k-3) = 2
k = 13Fi(N-k-1) = 3Fi(N-k-2) = 2Fi(N-k-3) = 1
x = 1.20046f(x) = -60.056
Список використаної літератури
Таха, Хемди А. Введение в исследование операций, 7-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2005. – 912с.: ил. – Парал. тит. англ.
Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации: учеб. пособие-2-ое изд.-М.:ФИЗМАТЛИТ, 2005
Н.И. Глебов, Ю.А. Кочетов, А.В. Плясунов. Методы оптимизации: учебное пособие. - Новосибирск: Новосибирский государственный университет, 2000. – 105 с.
Васильев Ф.П. Методы оптимизации. – М.: Издательство «Факториал Пресс», 2002. – 824 с.
Волков И.К., Загоруйко Е.А. Исследование операций-М.: МГТУ им. Н.Э. Баумана, 2000
6. Бейко И.В. и др. Методы и алгоритмы решения задач оптимизации. К: Высш.шк., 1983. – 513с
7. Ю. А. Кочетов, А.В. Плясунов. Методы оптимизации: учебное пособие. - Новосибирск: Новосибирский государственный университет, 2000. – 105 с.