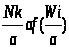Расчет показателей надежности и законов их распределения

Федеральное агентство по образованию (Рособразование)

Архангельский государственный технический университет

Кафедра эксплуатации автомобилей и МЛК

(наименование кафедры)

Расчётно-графическая работа

По дисциплине

Основы теории надежности и диагностики

На тему

Расчет показателей надежности и законов их распределения

Руководитель

Кузнецов Н.И.

Архангельск

2009

Задание

По данным, (они представляют собой ресурсы автомобилей или их агрегатов до капитального ремонта в тысячах километров пробега), необходимо:

- определить среднее арифметическое значение ресурса автомобиля до капитального

ремонта;

- рассчитать среднее квадратическое отклонение ресурса;

- определить коэффициент вариации ресурса;

- построить эмпирический закон распределения ресурса;

- подобрать теоретический закон;

- проверить согласие теоретического и эмпирического законов распределений;

- определить доверительный интервал для математического ожидания ресурса.

1. Расчет параметров экспериментального распределения

Число классов статистического ряда определяем по формуле (11):

,

где N – общее число наблюдений

Принимаем .

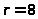Размах выборки для нашего ряда

Значение классового промежутка находим по формуле (12):

Для удобства вычислений принимаем .

Середина классов W – полусумма начала данного класса и начала следующего класса. Середины крайних классов принимаем близкими к наименьшему и наибольшему значениям случайной величины.

Начало Wa и конец Ww класса находим по формулам:

где h-принятая точность измерения случайной величины.

Результаты расчетов сведены в таблицу 1.

Таблица 1 - Cоставление статистического ряда

Границы класса	Середина	Частота
15,09	17,08	16,09	0,00
13,09	15,08	14,09	0,00
11,09	13,08	12,09	0,00
9,09	11,08	10,09	2,00
7,09	9,08	8,09	9,00
5,09	7,08	6,09	16,00
3,09	5,08	4,09	14,00
1,09	3,08	2,09	9,00
Всего			50,00

2. Вычисление среднего арифметического значения и среднего квадратического отклонения

Среднее арифметическое значение случайной величины способом произведений вычисляем по формуле

(13)

где А - условная средняя, середина модального или близкого к нему класса;

S1 - первая сумма,

а - условные отклонения середин классов, выраженные в классовых промежутках,

Среднее квадратическое отклонение определяем по формуле

(14)

где с - сумма взвешенных квадратов центральных отклонений середин классов от средней ряда, выраженная в квадратах классов промежутков,

;

S2 – вторая сумма,

Результаты расчетов сведены в таблицы 2 и 3.

Таблица 2 - Вспомогательные вычисления для определения

W	f	a	fa	fa^2
16,09	0	3,0	0	0
14,09	0	2,0	0	0
12,09	0	1,0	0	0
10,09	2	0,0	0	0
8,09	9	-1,0	-9	9
6,09	16	-2,0	-32	64
4,09	14	-3,0	-42	126
2,09	9	-4,0	-36	144
Всего	50		-119	343

Таблица 3

S1	S2	X	C	Сигма	V
-119	343	5,33	59,78	2,21	0,414

3. Определение вида закона распределения случайной величины

распределение экспериментальный случайный величина

Закон распределения случайной величины определяют в следующей последовательности:

- выравнивают эмпирический ряд одним из теоретических распределений;

- производят оценку различий эмпирического и теоретического распределений по критериям 2 или .

3.1 Экспоненциальный закон распределения

Теоретические частоты для распределения определяют по формуле

,

где - экспоненциальная функция, значения которой табулированы;

- условные отклонения середин классов,

.

Результаты расчетов сведены в таблицу 4, выравнивание статистического ряда по экспоненциальному закону приведено на рисунке 1.

Таблица 4 - Выравнивание статистического ряда по экспоненциальному закону

W	f	W-X	x=Wi/X	ℓ	(Nk/X)*ℓ	f'
16,09	0,00	10,76	3,02	0,026	0,488	0,00
14,09	0,00	8,76	2,64	0,035	0,657	1,00
12,09	0,00	6,76	2,27	0,492	0,657	1,00
10,09	2,00	4,76	1,89	0,077	1,435	1,00
8,09	9,00	2,76	1,52	0,135	2,538	3,00
6,09	16,00	0,76	1,14	0,237	4,445	4,00
4,09	14,00	-1,24	0,77	0,415	7,782	8,00
2,09	9,00	-3,24	0,39	0,733	13,760	14,00
Всего	50,00				31,76	32,00

Рисунок 1 - Выравнивание статистического ряда по экспоненциальному закону распределения

3.1.1 Оценка различий эмпирического и теоретического распределений

Методика оценки различий эмпирического и теоретического распределений для различных законов распределения одна и та же.

Для проверки согласованности теоретического и эмпирического распределений чаще всего используют критерий 2 Пирсона, величину которого рассчитывают по формуле

где 02 – стандартные значения критерия, его значения находят по специальным таблицам в зависимости от числа степеней свободы v;

, – эмпирические и теоретические частоты классов соответственно.

Первичное v1 и вторичное v2 числа степеней свободы определяют по следующим формулам:

; ; .

где r1,r2 - числа классов до и после объединения классов с малыми теоретическими частотами.

Крайние классы с частотой < объединяют с соседними классами ( – минимально допустимая теоретическая частота крайних классов в зависимости от начального числа степеней свободы)

Различия распределений могут считаться случайными, если эмпирический критерий не достигает требуемого порога вероятности . Необходимо ориентироваться на три уровня вероятности: при малой ответственности исследований 1 >= 0,999; при обычной 2 >= 0,99; при большой 3 >= 0,95.

Таблица 5 - Определение различий законов распределения

W1	f	f '	f-f '	(f-f ' )^2	( f-f ' )^2/f '
16,1	0	0,49	-0,49	0,24	0,49
14,1	0	0,66	-0,66	0,43	0,66
12,1	0	0,66	-0,66	0,43	0,66
10,1	2	1,44	0,56	0,32	0,22
8,1	9	2,54	6,46	41,75	16,45
6,1	16	4,44	11,56	133,53	30,04
4,1	14	7,78	6,22	38,66	4,97
2,1	9	13,76	-4,76	22,66	1,65
Всего	50	31,762			55,13

Следовательно, 02: 13,3; 18,5 при  соответственно, 0,99, 0,999

Таким образом, при =0,99 и 0,999 ответственности испытаний 2 больше 02, то есть эмпирическое распределение противоречит экспоненциальному закону распределения.

3.2 Нормальный закон распределения

Таблица 6 - Выравнивание статистического ряда по нормальному закону

Нормальный закон
					Теор частоты
W	f	W-X	x=(W-Ч)/сигма	f(x)	Nkf(x)/сигма	f'
16,09	0,00	10,76	4,87	0,00	0,000	0,00
14,09	0,00	8,76	3,97	0,00	0,007	0,00
12,09	0,00	6,76	3,06	0,00	0,167	0,00
10,09	2,00	4,76	2,15	0,04	1,773	2,00
8,09	9,00	2,76	1,25	0,18	8,277	8,00
6,09	16,00	0,76	0,34	0,38	17,026	17,00
4,09	14,00	-1,24	-0,56	0,34	15,431	15,00
2,09	9,00	-3,24	-1,47	0,14	6,162	6,00
Всего	50,00				48,84	48,00

Рисунок 2 - Выравнивание статистического ряда по нормальному закону распределения

Таблица 7 - Определение различий законов распределения

W1	f	f '	f-f '	(f-f ' )^2	( f-f ' )^2/f '
16,1	0	0,00	0,00	0,00	0,00
14,1	0	0,01	-0,01	0,00	0,01
12,1	0	0,17	-0,17	0,03	0,17
10,1	2	1,77	0,23	0,05	0,03
8,1	9	8,28	0,72	0,52	0,06
6,1	16	17,03	-1,03	1,05	0,06
4,1	14	15,43	-1,43	2,05	0,13
2,1	9	6,16	2,84	8,06	1,31
Всего	50	48,842			1,77

Следовательно, 02:11,1; 15,1; 20,5 при  соответственно 0,95, 0,99, 0,999

Таким образом, при =0,99 и 0,999 ответственности испытаний 2 меньше 02, то есть эмпирическое распределение не противоречит нормальному закону распределения.

3.3 Распределение Вейбула

Таблица 8 - Выравнивание статистического ряда по распределение Вейбула

W	f	Wi /a	x=af (Wi/a)		f'
16,09	0,00	2,74	1,2134	20,636	20,6
14,09	0,00	2,40	1,4715	25,026	25,0
12,09	0,00	2,06	1,5130	25,731	25,7
10,09	2,00	1,72	1,3597	23,124	23,1
8,09	9,00	1,38	1,0791	18,352	18,4
6,09	16,00	1,04	0,7590	12,908	12,9
4,09	14,00	0,70	0,4697	7,988	8,0
2,09	9,00	0,36	0,2495	4,243	4,2
Всего	50,00			138,01	137,90

Рисунок 3 - Выравнивание статистического ряда по распределению Вейбула

Таблица 9 - Определение различий законов распределения

W1	f	f '	f-f '	(f-f ' )^2	( f-f ' )^2/f '
16,1	0	20,6	-20,60	424,36	20,60
14,1	0	25,0	-25,00	625,00	25,00
12,1	0	25,7	-25,70	660,49	25,70
10,1	2	23,1	-21,10	445,21	19,27
8,1	9	18,4	-9,40	88,36	4,80
6,1	16	12,9	3,10	9,61	0,74
4,1	14	8,0	6,00	36,00	4,50
2,1	9	4,2	4,80	23,04	5,49
Всего	50	137,900			106,11

Следовательно, 02: 15,1; 20,5 при  соответственно, 0,99, 0,999

Таким образом, при =0,99 и 0,999 ответственности испытаний 2больше 02, то есть эмпирическое распределение противоречит распределения Вейбула.

Вывод: Эмпирическое распределение соответствует нормальному закону распределения.

4. Определение доверительного интервала для математического ожидания случайной величины

В рассмотренном способе оценки числовых характеристик случайных величин неизвестный параметр определялся одним числом. Такая оценка называется точечной. При оценке надежности машин и оборудования часто требуется не только найти для заданного параметра числовое значение, но и оценить его точность и достоверность. Пусть для параметра X (например, математического ожидания) получена по результатам выборочного обследования точечная оценка этого параметра X.

Требуется определить ошибку замены параметра X его точечной оценкой X. Назначим некоторую вероятность  ( = 0,9) и определим такое значение ошибки  > 0, для которого .

Это равенство означает, что с вероятностью неизвестное значение параметра X попадает в интервал .

Интервал называется доверительным, а  - доверительной вероятностью.

Рассмотрим зависимости, используемые при построении доверительных интервалов для параметров случайной величины, распределенной по нормальному закону.

Для математического ожидания границы доверительного интервала определяют по формуле

,

где t - коэффициент распределения Стьюдента, определяемый по таблицам в зависимости от доверительной вероятности  и числа степеней свободы или размера выборки N -1, ( t= 1,658)

Доверительный интервал для математического ожидания ресурса согласно формуле:

Iβ=(4,812; 5,848)

Вывод:

Таким образом, точное значение ресурса автомобилей или их агрегатов до капитального ремонта с вероятностью 0,99 находится в пределах от 4,812 до 5,848 тыс. км пробега.

Список использованных источников

1. Кузнецов Н. И., Абакумов Н. В. Надежность машин и оборудования: Методические указания и задания к выполнению расчетных работ и задач. - Архангельск: Изд-во АГТУ, 2001. - 36 с.

2. Кузнецов Н. И., Абакумов Н. В. Надежность машин и оборудования: Нормативно справочный материал к выполнению расчетных работ и задач. - Архангельск: Изд-во АГТУ, 2003. - 14 с.