Практическое применение интерполирования гладких функций
Специальность
«Математические методы в экономике»
КУРСОВАЯ РАБОТА
Практическое применение интерполирования гладких функций
2010
Содержание
Введение
1. Постановка задачи интерполяции
1.1 Определение термина интерполяции
1.2 Как выбрать интерполянт
1.3 Полиноминальная интерполяция
1.4 Интерполяционный полином Лагранжа
1.5 Про погрешность полинома
2. Один вид обобщенной интерполяции
2.1 Обобщенная интерполяция
2.2 Важное представление гладкой функции
Заключение
Список использованной литературы
Введение
В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например полученным в ходе некоторого эксперимента. Для вычисления многих функций, оказывается, эффективно приблизить их полиномами или дробно-рациональными функциями. Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.
В нашем случае для более полного раскрытия данной темы подробно рассмотрим для начала само понятие интерполяции, далее интерполирование непосредственно гладкой функции и интерполирование гладкой функции в точке.
Цель работы: изучение интерполирования гладких функций и практическое применение интерполирования функций.
1. Постановка задачи интерполяции
интерполяция погрешность полином
1.1 Определение термина интерполяции
Пусть для функции f(x), определенной на какой - либо части R, известны её значения на некотором конечном множестве точек x>1>, x>2>, …, x>n> [a,b], и в этих точках функция f(x) определена как:
,
Требуется вычислить, хотя бы приближенно, значения при всех x.
Такая задача может возникнуть при проведении различных экспериментов, когда значения искомой функции определяются в дискретные моменты времени, либо в теории приближения, когда сложная функция сравнительно просто вычисляется при некоторых значениях аргумента, для функций заданных таблицей или графически и т.п.
Обычно функцию g(x>i>),
x>i>
[a,b],
,
с помощью которой осуществляется
приближение, находят так, чтобы:
()
Такой способ приближения называют
интерполяцией или интерполированием.
Точки x>1>, x>2>,
…, x>n>
называют узлами интерполяции, если
точка x, в которой вычисляется
f(x), лежит
вне отрезка [a,b],
то употребляют термин экстраполяции.
Функцию g(x>i>),
,
называют интерполянтом.
При этом следует ответить на следующий вопрос.
1.2 Как выбрать интерполянт
Такие функции строятся на основе комбинаций из элементарных функций.
(2)
,
–
фиксированная линейно- независимая
система, а
()
- пока неизвестные параметры.
Математическая постановка задачи
интерполирования заключается в следующем.
Пусть R - пространство
действительных функций, определенных
на отрезке [a,b],
и
- заданная конечная или счетная система
функций из R, такая,
что их любая конечная подсистема является
линейно-независимой. Для данной конечной
совокупности точек x>1>,
x>2>, …, x>n>
(x>i> ≠
x>j> при
i≠j),
принадлежащих отрезку [a,b],
и данной функции f(x)
из R найти функцию φ,
являющуюся линейной комбинацией функций
так, чтобы в заданных точках значения
f и φ совпадали. Другими
словами, определить константы a>1>,
a>2>, …, a>n>
так, чтобы
(3)
()
Совершенно ясно, почему число коэффициентов
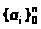должно совпадать с числом узлов
интерполяции x>i>.
Это нужно для того, чтобы матрица системы
была квадратной (т.е. число неизвестных
совпадало бы с числом условий, из которых
находятся эти неизвестные). Кроме того,
для однозначной разрешимости данной
системы (при произвольной правой части)
необходимо и достаточно, чтобы ее
определитель был отличен от нуля, т.е.:
:
Естественно, интерполянт необходимо построить в виде более легкой учетной функции, поэтому за часто берут такие системы как:
{1, х, х2, …, хn}, {1, sinx, cosx, sin2x, cos2x, …, sin(nx), cos(nx)} ,
{1, e x1, e x2, …, e xn} (i R, i≠j (i≠j), nN).
1.3 Полиноминальная интерполяция
Если
являются степенями {1, х, х2,
…, хn},
то говорят об алгебраической интерполяции,
а функцию
называют
интерполяционным полиномом и обозначим
как:
(4)
Если
()
(5),
то можно построить интерполяционный полином степени n и притом только один.
Найдем интерполяционный полином из вида (4). В это время, на основе (5), для нахождения неопределённых коэффициентов используем систему линейных уравнений:
a>0>x>0> + a>1>x>0> + a>2>x>0>2 + …+ a>n>x>0>n= f>0 ,>
a>0>x>0> + a>1>x>1> + a>2>x>1>2 + …+ a>n>x>1>n= f>1 , >(6)
>………………………………………………………….>
a>0>x>0> + a>1>x>n> + a>2>x>n>2 + …+ a>n>x>n>n= f>n ,>
В этом случае определитель системы линейных алгебраических уравнений выглядит так:
.
Этот определитель является определителем Вандермонда и отличен от нуля в случае, когда все узлы x>i> различны. Поскольку матрица системы невырождена, то решение системы существует и единственно.
Единственность интерполяционного полинома можно доказать следующим способом. Предположим, что есть два интерполяционных полинома
L>n> и P>n> H>n> 1 : L>n>> >≠ P>n>.
Из (5) : L>n>(x>i>)
- P>n>(x>i>)
0 и
L>n>(x>i>)
P>n>(x>i>)
().
так, выходит противоречие. Единственность установлена. А так как полином единственный, то у соответствующей системы линейных алгебраических уравнений есть только одно решение.
1.4 Интерполяционный полином Лагранжа
Сейчас перед нами задача, которая состоит из нахождения такого многочлена, степени n, который совпадает с заданной f(x) в точках x>1>, x>2>, …, x>n> [a,b], т.е. чтобы выполнялось равенство
f(x>j>)=L>n>(x>j>) (
).
Чтобы решить эту задачу, введем многочлены степени n, которые в точках при i≠j равны нулю, а в точке при i=j равны единице. Очевидно, что:
>j>H>n>, >j>(x)=A>j>(x-x>0>)(x-x>1>)…(x-x>j>>-1>)(x-x>j>>+1>)…(x-x>n>)=
,
где постоянная А находится из условия >j>(x>j>)=1, тогда
Таким образом, получаем, что
>j>(x)
Получаем, что поставленную задачу решает многочлен
(8)
Многочлен (8) называется интерполяционным многочленом Лагранжа.
Задача 1.
Пусть задана интерполяционная таблица:
|
i |
0 |
1 |
2 |
3 |
|
|
0 |
2 |
3 |
5 |
|
|
1 |
3 |
2 |
5 |
Построить интерполяционный полином Лагранжа.
Решение. Из (8) следует:
Задача 2.
Пользуясь интерполяционной формулой Лагранжа, составить уравнение прямой, проходящей через точки Р>0>(х>0>, у>0>) и Р>1>(х>1>, у>1>), если х>0>=-1, у>0>=-3, х>1>=2, у>1>=4.
Решение. В данном случае многочлен Лагранжа примет вид
.
Уравнение искомой прямой есть
.
1.5 Про погрешность полинома
По строению
().
Но, в общем, это не так и
(
,),
так как интерполирование предполагает
приближенное нахождение:
(
)
И в связи с этим необходимо говорить о
погрешности интерполирования. Заранее
сказав,
разность этого выражения нужно найти.
Замечание 1.
()
чем постоянно записывать равенство,
слагаемое
называют остаточным членом (или
погрешность интерполяции).
Теорема 1.
Если
[a,b] 2
(9)
(
,
),
где
[a,b] в
промежутке беспрерывно n+1
раз объясняет совокупность дифференцируемых
функций.
[a,b] 
[a,b];
Берем любую точку и зафиксируем ее
(,),
рассмотрим вспомогательную функцию:
(10)
,
(
).
- свободный параметр, который открыто
объясняет
().
Значение
берем проходящим через равенство
.
В это время концы
,
будучи точками промежутка, можно
использовать теорему Ролля.
Существует
:
(
)
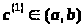Сейчас для этой теоремы берем точки
:
Существует
:
()
Когда закончим этот процесс, то получим следующее:
:
Итак, при t = x из (10) вытекает (9). Что и требовалось доказать.
Следствие 1:
Пусть
.
В то время
(
);
над ними:
.
Задача 3:
С помощью узлов
построить полином
для
этой функции, при:
1)
.
Оценить погрешность полинома;
2) в [a,b] найти максимальную погрешность полинома.
Решение:
1) На основании Следствия 1 в непрерывном виде находим:
2) Использовав второе равенство из
Следствия 1 получаем:
.
Замечание 2:
Полученные с помощью этой формулы
множества полиномов называются полиномами
Чебышева. В отдельных случаях:
В теории приближения функции хорошо
известен следующий факт: если в качестве
узлов интерполяции взять корни полинома
,
то
(
)
В этом случае из Следствия 1 следует, что
.
Если свободная интерполяция находится
в отрезке [a,b],
то с помощью замены
этот отрезок можно заменить на [-1;1]. В
это время точки
(11)
(
,
)
будут однородными с корнями
,
а остаточный член записывается следующим
образом:
.
Последнее неравенство полностью дает оптимальную оценку на отрезке [a,b], т.е. мы оцениваем погрешность интерполяции на отрезке [a,b], чтобы узлы (11) были оптимальными.
2. Один вид обобщенной интерполяции
2.1 Обобщенная интерполяция
Рассмотрим пример интерполяции для
элементов множества
.
Для простоты и краткости возьмем
[a,b]=[-1;1],
.
Пусть точки
и
будут разными между собой. Поставим
такую задачу:
(12)
построить многочлен
,
удовлетворяющий данным условиям. Здесь
«собственный» оператор класса
:
Теорема 2.
Если взять в произвольной форме fC{m;0}, удовлетворяющее условию (12), то существует «обобщенный» интерполяционный полином и он единственен.
Доказательство:
Найдем интерполяционный полином в стандартном виде:
(13)
Затем, учитывая (13) для того, чтобы найти
коэффициенты
(
),
приходим к следующей алгебраической
системе:
(14)
Эту систему упорядочим в матрицу S, являющуюся прямой суммой двух квадратных матриц размерностью m и n+1.
Здесь
Значит, основываясь на фактах линейной алгебры, определяем
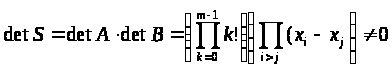
Что и требовалось доказать.
Сейчас поставим перед собой цель записать многочлен G(x) в явном виде. Будет полезно рассмотреть стандартный вид многочлена Лагранжа. Из (13) видно, что
Поэтому имеет место следующее:
(14)
Возьмем параметры из (13):
(15)
Таким образом, из (13), (14), (15) следует, что
(16)
Замечание 3:
Если m=0, C{0;0}
C[-1;1],
(
).
Значит, рассмотрев функцию
в задаче (11) приводится к обычной
интерполяционной задаче, а многочлен
Лагранжа (16) превращается в обычный
интерполяционный многочлен. Таким
образом, задача (11), действительно, в
значении одного определения становится
обобщенной задачей интерполирования.
Сейчас поговорим о погрешности обобщенной интерполяции.
В этом случае
нужно дать оценку побольше. Выше приведены
размышления и следствия, полученные в
целях определения одной системы функций.
.
Теорема 3.
Если
Здесь
Доказательство:
Приняв во внимание (16) получаем
(17)
Следующие приведения к формуле теоремы легко доказываются из (17) и теоремы 1.
Следствие 2.
Пусть
В это время:
2.2 Важное представление гладкой функции
Теорема 4.
Верна следующая связь:
(18)
Вдобавок
(19)
Доказательство:
Пусть
.
По (19) получим
в последовательной форме используем
метод интегрирования по частям, и
изменяем его:
Отсюда выходит следующее неравенство:
(20)
называют
формулой Тейлора с остаточным членом
в интегральной форме.
Возьмем
некоторую функцию
,
чтобы равенство (18) было правильным
.
При рассмотрении второго слагаемого
полинома, достаточно показать что
С(m).
При изучении производной
полезно использовать дифференцирование
интеграла, зависящего от параметра. Эта
формула в математическом анализе очень
известна и определяет следующее:
(21)
здесь
вдобавок
Таким образом, находим в нашем случае необходимый вид:
Значит
.
Замечание 6.
Рассмотрев, оператор
из последнего размышления вытекает
полезное рассуждение:
(22)
Заключение
Мы убедились, что в вычислительной математике существенную роль играет интерполяция функций, значения которой совпадают со значениями заданной функции в некотором числе точек.
В данной курсовой работе рассматривается интерполирование функции полиномами, непосредственно непрерывных функций на отрезке и в точке, определили понятие погрешности интерполяции.
У нас возникла задача о восстановлении непрерывной функции по ее табличным значениям, поэтому в данной работе были приведены конкретные примеры по построению интерполяционного полинома Лагранжа, по оцениванию погрешности интерполяционного полинома.
В нашем случае для более полного раскрытия данной темы подробно проиллюстрировано само понятие интерполяции, далее интерполирование непосредственно гладкой функции и интерполирование гладкой функции в точке.
Список использованной литературы
Н.С.Габбасов. Некоторые применения производной. Наб.Челны, 1998г.
Я.С.Бугров, С.М.Никольский. Дифференциальное и интегральное исчисление. М.: «Наука», 1984г.
С.М.Никольский. Курс математического анализа. М.: «Наука», 1990г.
Л.Д.Кудрявцев. Краткий курс математического анализа. М.: «Наука», 1989г.
И.А.Марон. Дифференциальное и интегральное исчисление. М.: «Наука», 1970г.
А.А.Самарский. Введение в численные методы. М.: «Наука», 1987.
1 Здесь H>n> – это множество всех алгебраических многочленов степени n.
2
На непрерывном отрезке и в точке
обозначили множество функции, имеющей
производную по Тейлору m-го
порядка.
(естественно,
Верно следующее соответствие:
здесь