Теоремы Силова

^{ВВЕДЕНИЕ}

^{Строение абелевых групп во многом определяется строением максимальных р-подгрупп. В теории конечных групп максимальные подгруппы также играют существенную роль. Теорема, доказанная норвежским математиком Л. Силовом в 1872 году, явилась краеугольным камнем теории конечных групп. Она неоднократно обобщалась в разных направлениях как в нашей стране (С. А. Чунихин и др.), так и за рубежом (Ф. Холл и др.). В связи с этой теоремой и в честь ее автора максимальные р-подгруппы конечных (а часто и бесконечных) групп называются силовскими р-подгруппами. Проблема нахождения силовской подгруппы данной группы является важной задачей вычислительной теории групп. Для групп перестановок Уильям Кантор доказал, что силовская p-подгруппа может быть найдена за время, полиномиальное от размера задачи (в данном случае это порядок группы, помноженный на количество порождающих элементов).}

^{Говорят, что группа G действует на множестве М, если для каждых элементов, определен элемент , причем и me=m для всех , ; здесь e — единица группы G. Множество называется орбитой элемента m. Очевидно, орбиты любых двух элементов из М либо совпадают, либо не пересекаются, так что множество М разбивается на непересекающиеся орбиты. Людвиг Силов (норв. Peter Ludvig Mejdell Sylow — фонетически правильней транслитерация «Сюлов»; 1832—1918) — норвежский математик. Автор нескольких работ по теории эллиптических функций и по теории групп. С 1858 по 1898 годы был учителем в школе в городе Фредериксхальд. В 1862 году Силов заменил профессора по теории Галуа в университете Христиании, где он поставил задачу, которая привела к наиболее важному результату его жизни — так называемым теоремам Силова, опубликованным в 1872 году.}

^{ГЛАВА 1. ТЕОРЕМЫ СИЛОВА}

^{Пусть G – конечная группа, а р – простое число, которое делит порядок G. Подгруппы порядка pt называются р-подгруппами. Выделим из порядка группы G примарный делитель по р, то есть | G | = pns , где s не делится на р. Тогда силовской р-подгруппой называется подгруппа G, имеющая порядок pn. Под N(P) понимается нормализатор подгруппы Р в G.}

^{Теорема 1.(первая теорема Силова).}

^{Силовские р-подгруппы существуют.}

^{Доказательство.}

^{Докажем теорему индукцией по порядку G. При |G| = p теорема верна. Пусть теперь |G| > p. Пусть Z(G) - центр группы G. Возможны два случая:}

^{а) p делит |Z|. Тогда в центре существует циклическая группа (как элемент примарного разложения центра), которая нормальна в G. Факторгруппа G по этой циклической группе имеет меньший порядок, чем G, значит, по предположению индукции, в ней существует силовская p-подгруппа. Рассмотрим её прообраз в G. Он и будет нужной нам силовской p-подгруппой G.}

^{б) p не делит |Z|. Тогда рассмотрим разбиение G на классы сопряжённости: (поскольку если элемент лежит в центре, то его класс сопряжённости состоит из него одного). Порядок G делится на p, значит, должен найтись класс K}_>a>^{, порядок которого не делится на p. Соответствующий ему нормализатор имеет порядок pnr, r < s. Значит, по предположению индукции, в нём найдётся силовская p-подгруппа — она и будет искомой.}

^{Теорема 2.(вторая теорема Силова).}

^{Всякая p-подгруппа содержится в некоторой силовской p-подгруппе. Все силовские p-подгруппы сопряжены (т.е. каждая представляется в виде gPg − 1, где g — элемент группы, а P — силовская подгруппа из теоремы 1).}

^{Доказательство}

^{Итак, пусть силовские р-подгруппы в G существуют и Р — одна из них. Пусть, далее, — произвольная р-подгруппа группы G, не обязательно силовская. Заставим действовать левыми сдвигами на множестве левых смежных классов G по Р. Длина любой орбиты относительно делит порядок ,. Таким образом,}

^{где,... — длины орбит. Так как НОД(m,p) = 1, то хотя бы одна орбита имеет длину pki = 1, т. е.}

⁽¹⁾

^{для некоторого элемента. Переписав соотношение (1) в виде, мы приходим к заключению, что}

⁽²⁾

^{(поскольку — группа). В частности, если — силовская р-подгруппа, то | | = |Р|, и из (2) следует, что =.}

^{Теорема 3(третья теорема Силова).}

^{Количество силовских p-подгрупп сравнимо с единицей по модулю p и делит порядок G.}

^{Доказательство.}

^{Рассмотрим несколько более общую ситуацию. Именно, пусть , где , t может делится на p, и пусть - число всех подгрупп порядка в G. Оказывается, что имеет место сравнение , в частности, G содержит подгруппы любого порядка , s=1,2,…,n и .}

^{Рассуждаем следующим образом. Действие левыми сдвигами группы G на себе индуцирует действие G на множестве}

^{всех -элементных подмножеств . Причём . Множество разбивается на G-орбиты , так что}

^,

^{где - стационарная подгруппа некоторого представителя .}

^{Так как , то - объединение нескольких правых смежных классов G по . Поэтому , откуда . В случае имеем . Равенства и эквивалентны. Получаем}

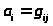^{(- некоторый элемент из G) и, стало быть, - подгруппа порядка . Орбита исчерпывается некоторым числом левых смежных классов группы G по .}

^{Обратно: каждая подгруппа порядка приводит к орбите длины t. Различные подгруппы с приводят к различным орбитам , поскольку из следует , откуда и . Таким образом, имеется взаимно однозначное соответствие между подгруппами порядка и орбитами длины t. Тогда сравнение записывается как}

^{Где следовало бы написать , чтобы подчеркнуть зависимость от G.}

^{Если взять за G циклическую группу порядка , то для неё и поэтому}

^{Так как левые часть сравнений по одному и тому же модулю совпадают, то имеем}

^{А это и даёт искомое сравнение}

^{Получим полезное уточнение теорем Силова.}

^{Теорема 4.}

^{Справедливы следующие утверждения:}

^{1).силовская p-подгруппа P группы G нормальна в G тогда и только тогда, когда}

^{2).конечная группа G порядка является прямым произведением своих силовских - подгрупп в точности тогда, когда все эти подгруппы нормальны в G.}

^{Доказательство.}

^{1).Все силовские подгруппы, отвечающие данному простому делителю р порядка , по второй теореме Силова сопряжены, и если P–одна из них, то}

^{нормальна в G}

^{2).Если - прямое произведение своих силовских подгрупп, то нормальна в G как любой прямой множитель. Значит условие нормальности необходимо.}

^{Пусть теперь нормальна в G, , т.е. . Заметим, что . Стало быть, , а отсюда для любых имеем}

^{Т.е. элементы и перестановочны.}

^{Представим, что единичный элемент записан в виде , где - элемент порядка . Положив и воспользовавшись перестановочностью получим}

^{Но так как а и взаимно просты, то . Это верно при любом j, и, стало быть, равенство возможно лишь при}

^{С другой стороны, каждый элемент порядка , записывается в виде , , . Достаточно положить , где показатели определяются условиями}

^{теорема силов конечная группа}

^,

^{Если теперь - другая запись x в виде произведения -элементов, то в силу перестановочности , с различными нижними индексами будем иметь}

^,

^{что, как было показано выше, влечёт равенства}

^{, т.е. .}

^{Итак, каждый элемент группы G записывается, и притом единственным образом в виде .}

^{Замечание}

^{Нормальная силовская p-подгруппа P группы G характеристична в G, т.е. инвариантна при действии любого автоморфизма . Действительно, , поэтому - силовская р-подгруппа, и, стало быть, , если . Аналоги силовских подгрупп прослеживаются в алгебраических структурах, далёких от конечных групп.}

^{Следствие}

^{Если все делители | G | , кроме 1, после деления на p дают остаток, отличный от единицы, то в G есть единственная силовская p-подгруппа и она является нормальной (и даже характеристической).}

^{Примеры силовских подгрупп.}

^{Пример 1.}

^{Аддитивная группа кольца вычетов разлагается в прямое произведение своих силовских p-подгрупп, которые являются циклическими подгруппами порядков , если n имеет каноническое разложение n=.}

^{Пример 2.}

^{Силовские p-подгруппы симметрических групп. Как мы знаем, Каков максимальный показатель e(n), при котором делит n!? В последовательности 1,2,…,n кратными p будут числа p,2p,…,kp, где , поэтому . Так как , то Удобно разложить n по основанию p: , тогда}

^{Рассмотрим сначала группы , когда n степень p. Пусть в уже найдена силовская p-подгруппа, т.е. подгруппа порядка . Построим по ней в подгруппу порядка . Для этого разобьём переставляемые символы 1,2,…, на последовательные отрезки длины . Если и x – подстановка на символах i-го отрезка, то легко сообразить, что - подстановка на символах (i+1)-го отрезка (сложение по модулю p). Отсюда видно, что подгруппа, порождённая подгруппами , является из прямым произведением, и, стало быть, подгруппа , порожденная подгруппой и элементом с, изоморфна сплетению . Подгруппа - искомая, так как .}

^{Одновременно мы видим, что силовская p-подгруппа в изоморфна последовательному сплетению (…( циклической группы с самой собою m раз.}

^{Теперь пусть n произвольно. Разобьём символы 1,...,n на одноэлементных, р-элементных и т.д. отрезков. На каждом из этих отрезков рассмотрим симметрическую группу – она будет некоторой степени , а в ней возьмём силовскую p-подгруппу, построенную как выше. Так как эти подгруппы действуют на непересекающихся множествах, то их порождение является их прямым произведением, а потому имеет порядок}

^{Следовательно, - силовская p-подгруппа в . Из построения видно, что она изоморфна прямому произведению нескольких последовательных сплетений типа (…(.}

^{Пример 3}

^{Рассмотрим общие линейные группы над конечными полями. Пусть p – простое число, m, n – целые числа и . Покажем, что - силовская p-подгруппа группы . Посчитаем порядки этих групп.}

^{Какие n-ки над полем могут быть первой строкой невырожденной матрицы? Очевидно, любые, кроме нулевой, т. е. штук. Если первая строка выбрана, то в качестве второй строки можно взять любую, не пропорциональную первой; таких строк. Если две первые строки уже выбраны, то в качестве третьей можно взять любую строку, не зависящую линейно от первых двух; это дает возможностей. И так далее. Значит, .}

^{Так как угловые элементы матриц пробегают независимо друг от друга всё поле, а всего угловых мест , то . Из сравнения порядков мы видим, что - силовская p-подгруппа группы .}

^{Нахождение силовской подгруппы.}

^{Проблема нахождения силовской подгруппы данной группы является важной задачей вычислительной теории групп. Для групп перестановок Уильям Кантор доказал, что силовская p-подгруппа может быть найдена за время, полиномиальное от размера задачи (в данном случае это порядок группы, помноженный на количество порождающих элементов).}

^{ГЛАВА 2.РЕШЕНИЕ ЗАДАЧ С ПРИМЕНЕНИЕМ ТЕОРЕМ СИЛОВА}

^{Задача 1.}

^{Докажем, что группа порядка 350 не может быть простой.}

^{Решение}

^{, значит, силовская 5-подгруппа имеет порядок 25. N5 должно делить 14 и сравнимо с 1 по модулю 5. Этим условиям удовлетворяет только единица. Значит, в G одна силовская 5-подгруппа, а значит, она нормальна, и поэтому G не может быть простой.}

^{Задача 2}

^{Найти силовские р-подгруппы в группе всех матриц с определителем 1 над полем из р элементов.}

^{Решение.}

^{Пусть - группа с определителем 1 над полем из р элементов. Из разложения}

^{полной линейной группы в смежные классы по следует, что}

⁽¹⁾

^{Рассматривая как группу автоморфизмов двумерного векторного пространства V над , легко найти порядок . Действительно, действует на множестве пар базисных векторов. Образом может быть любой отличный от нуля вектор (их всего штук), а при всяком выборе образом может быть любой вектор из (таких векторов имеется штук). Стало быть, , что в сочетании с (1) приводит к формуле}

^{По крайней мере две силовские р-подгруппы группы мы находим сразу:}

^{, .}

^{В соответствии с теоремой 3 имеем}

^{а так как}

^{и, следовательно, нормализатор содержит подгруппу}

^{порядка p(p-1), то остаётся единственная возможность}

^.

^{Между группой}

^{и симметрической группой непосредственно устанавливается изоморфизм}

^{(обе группы имеют одинаковое задание образующими и соотношениями). При p>2 группа имеет центр порядка 2. Фактор- группа , которую естественно называть проективной специальной группой(она является группой преобразований проективной прямой ) , играет важную роль в алгебре со времён Галуа. Дело в том, что при p>3 группа простая, и это, наряду с ,- один из самых ранних примеров конечных простых групп.}

^{Задача 3}

^{Описать с помощью теоремы Силова все возможные типы групп порядка pq.}

^{Решение}

^{Пусть р, q — простые числа, р < q. Какой должна быть группа G порядка pq? Силовские р- и д-подгруппы из G, будучи подгруппами простого порядка, являются циклическими. Пусть (а), (b) — соответственно силовские р- и q-подгруппа. По теореме Силова число силовских q-подгрупп в G имеет вид 1+kq и делит pq, поэтому силовская q-подгруппа (b) единственна. В частности, она нормальна в G. Число силовских р-подгрупп имеет вид 1+кр и делит q, поэтому возможны два случая:}

^{а) Силовская р-подгруппа (а) единственна. Тогда она нормальна и, значит,. Так как , то . Таким образом, в этом случае .}

^{б) Имеется q силовских р-подгрупп. Конечно, это возможно лишь при условии . Пусть . Если r=1, то снова ,т. е. . Пусть . Индукцией по х получаем , откуда для всех целых х, у. При х=р, у=1 это дает , кроме того, получаем формулу умножения .}

^{Обратно, легко проверить, что если , , , то эта формула умножения определяет неабелеву группу порядка pq. Наконец, решения сравнения составляют циклическую группу порядка р, поэтому те из них, которые, имеют вид , где r — одно из них. Все эти решения определяют одну и ту же группу, так как замена порождающего а на приводит к замене r на .}

^{Таким образом, с помощью теоремы Силова мы описали все возможные типы групп порядка pq; их оказалось два — абелев и неабелев, причем второй существует только при условии .}

^{ЗАКЛЮЧЕНИЕ}

^{При изучении абелевых групп видно, что их строение во многом определяется строением максимальных р-подгрупп. В теории конечных групп максимальные р-подгруппы также играют существенную роль. В этом курсовой были доказаны теоремы Силова о конечных группах: для каждой степени , делящей порядок группы, существует подгруппа порядка , причем если делит порядок группы, то всякая подгруппа порядка содержится в некоторой подгруппе порядка ; все максимальные р-подгруппы попарно сопряжены в группе, а их число сравнимо с 1 по модулю р. Эта теорема была доказана норвежским математиком Л. Силовом в 1872 году. В связи с этой теоремой и в честь ее автора максимальные р-подгруппы конечных (а часто и бесконечных) групп называются силовскими р-подгруппами.}

^{Из теоремы Силова вытекает, в частности, что силовские р-подгруппы конечной группы — это в точности подгруппы порядка , где — максимальная степень р, делящая порядок группы. Отметим, что если число m делит порядок конечной группы G, но не является степенью простого числа, то в G может и не быть подгрупп порядка m — например, в знакопеременной группе А4 порядка 12 нет подгрупп порядка 6.}

^{В теории групп теоремы Си́лова представляют собой неполный вариант обратной теоремы к теореме Лагранжа и для некоторых делителей порядка группы G гарантируют существование подгрупп такого порядка.}

^{СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ}

^{1. А. И. Кострикин. Введение в алгебру, III часть. М.: Физматлит, 2001.}

^{2. Э. Б. Винберг. Курс алгебры. М.: Факториал-Пресс, 2002.}

^{3. М.И. Каргаполов, Ю.И. Мерзляков. Основы теории групп. М.:Наука, 1982.}