Застосування подвійних інтегралів

Содержание

1. Заміна змінних у подвійному інтегралі. Подвійний інтеграл у полярних координатах

2. Застосування подвійних інтегралів до задач геометрії

3. Застосування подвійних інтегралів до задач механіки

1. Заміна змінних у подвійному інтегралі. Подвійний інтеграл у полярних координатах

Нехай функція неперервна в деякій замкненій і обмеженій області , тоді існує інтеграл

Припустимо, що за допомогою формул

(1)

ми переходимо в інтегралі до нових змінних та . Вважатимемо, що з формул (1) однозначно можна визначити та :

. (2)

Згідно з формулами (2), кожній точці ставиться у відповідність деяка точка на координатній площині з прямокутними координатами і .

Нехай множина всіх точок утворює обмежену замкнену область . Формули (1) називаються формулами перетворення координат, а формули (2) - формулами оберненого перетворення.

Справедлива така теорема.

Теорема. Якщо перетворення (2) переводить замкнену обмежену область в замкнену обмежену область і є взаємно однозначним, і якщо функції (1) мають в області неперервні частинні похідні першого порядку і відмінний від нуля визначник

, (3)

а функція неперервна в області , то справедлива така формула заміни змінних

. (4)

Функціональний визначник називається визначником Якобі або якобіаном.

Таким чином, виконуючи заміну змінних в інтегралі за формулами (1), ми маємо елемент площі в координатах замінити елементом площі в координатах і стару область інтегрування замінити відповідною їй областю .

Розглянемо заміну декартових координат полярними за відомими формулами. Оскільки

То формула (3) набирає вигляду

(4)

де область задана в декартовій системі координат , а - відповідна їй область в полярній системі координат.

У багатьох випадках формулу (4) доцільно застосовувати тоді, коли підінтегральна функція або рівняння границі області містить суму , оскільки ця сума в полярних координатах має досить простий вигляд:

Якщо область (рис.1, а) обмежена променями, які утворюють з полярною віссю кути та і кривими та , то полярні координати області змінюються в межах , (рис.1, б). Тому формулу (4) можна записати у вигляді

(5)

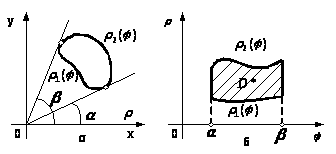
Рисунок 1 - Область: а) ; б)

подвійний інтеграл полярна координата

Якщо область охоплює початок координат, тобто точка є внутрішньою точкою області , то

(6)

де - полярне рівняння межі області .

Приклади

1. Обчислити інтеграл , якщо область - паралелограм,

обмежений прямими (рис.1, а).

Розв’язання

Безпосереднє обчислення цього інтеграла надто громіздке, тому що як в напрямі осі так і в напрямі осі область потрібно спочатку розбити на три області, а потім обчислювати три подвійних інтеграли.

Виконаємо таку заміну змінних: , тоді прямі та в системі переходять в прямі та у системі (рис.1, б), а прямі та відповідно в прямі та .

Таким чином, область (паралелограм) переходить у системі в прямокутник .

Рисунок 2 - Область: а) ; б)

Далі маємо

За формулою (3)

2. У подвійному інтегралі , де - круг, обмежений колом , перейти до полярних координат з полюсом в точці , і обчислити отриманий інтеграл.

Розв’язання

Область зображена на рис.2.

Рівняння, які пов’язують і полярні координати з полюсом у точці , мають вигляд , причому видно, що кут змінюється в межах від до .

Рисунок 3 - Область

Підставивши вирази для і в рівняння кола, отримаємо , звідки або . Ці дві криві на площині при обмежують область , яка є прообразом області при відображенні. Якобіан відображення дорівнює . Підінтегральна функція у нових змінних дорівнює . За формулою (3) маємо

Одержаний подвійний інтеграл за областю зводимо до повторного:

і обчислюємо повторний інтеграл, застосовуючи формулу Ньютона - Лейбніца:

2. Застосування подвійних інтегралів до задач геометрії

1. Площа плоскої фігури. Якщо в площині задана фігура, що має форму обмеженої замкненої області , то площа цієї фігури знаходиться, як відомо, за формулою:

2. Об'єм тіла. Об'єм циліндричного тіла, твірні якого паралельні осі і яке обмежене знизу областю площини , а зверху - поверхнею , де функція неперервна та невід'ємна в області , знаходиться за формулою (2):

3. Площа поверхні. Якщо поверхня , задана рівнянням

(7)

проектується на площину в область (рис.3) і функції , , неперервні в цій області, то площу поверхні знаходять за формулою

(8)

Рисунок 4 - Поверхня

Виведемо цю формулу. Розіб’ємо довільним способом область на частин , які не мають спільних внутрішніх точок і площі яких дорівнюють . У кожній частині візьмемо точку ; на поверхні їй відповідатиме точка , де . Через точку проведемо дотичну площину [3]

На площині виділимо ту її частину, яка проектується на площину в область . Позначимо цю частину дотичної площини через , а її площу - через . Складемо суму

. (9)

Границю суми (9), коли найбільший з діаметрів областей прямує до нуля, назвемо площею поверхні (7), тобто за означенням покладемо

. (10)

Обчислимо цю границю. Оскільки область , яка має площу , проектується в область з площею , то , де - кут між площинами та (рис.3), тому .

Але гострий кут дорівнює куту між віссю і нормаллю до дотичної площини, тобто куту між векторами та . Знайдемо за формулою (4)

Отже,

Підставляючи значення в (10), отримуємо

Під знаком границі маємо інтегральну суму, складену для неперервної в області функції . Ця функція інтегровна в області , тому границя у формулі (10) існує і дорівнює подвійному інтегралу (8).

3. Застосування подвійних інтегралів до задач механіки

1. Маса пластини. Нехай на площині маємо матеріальну пластину, яка має форму обмеженої замкненої області , в кожній точці якої густина визначається неперервною функцією . Маса такої пластини визначається за формулою (1.8):

2. Центр маси пластини. Статичні моменти. Нехай матеріальна пластина в площині має форму області , густина пластини в точці дорівнює , де - неперервна функція в області Розіб'ємо область на частини , виберемо в кожній з них довільну точку і наближено вважатимемо, що маса частини дорівнює , де - площа області . Коли вважати, що кожна з цих мас зосереджена в точці , то пластину можна розглядати як систему цих матеріальних точок. Тоді координати та центра маси пластини наближено визначатимуться рівностями

Щоб знайти точні значення координат, перейдемо в цих формулах до границі при . Тоді інтегральні суми перейдуть у подвійні інтеграли і координати центра маси пластини визначатимуться формулами

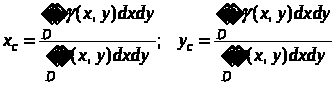. (11)

Величини

(12)

називаються статичними моментами пластини відносно осі та .

Враховуючи формули (8), (11) і (12), координати центра мас можна записати у вигляді

Якщо пластина однорідна, тобто має сталу густину , то у формулах (1.8), (11) і (12) слід покласти .

3. Моменти інерції пластини. Відомо, що момент інерції матеріальної точки відносно деякої осі дорівнює добутку маси точки на квадрат її відстані від цієї осі, а момент інерції системи матеріальних точок відносно однієї і тієї самої осі дорівнює сумі моментів інерції всіх точок системи.

Нехай матеріальна пластина має форму області у площині , а неперервна функція визначає густину в кожній точці цієї пластини. Розіб'ємо область на частини , площі яких дорівнюють , і виберемо в кожній з цих частин довільну точку . Замінимо пластину системою матеріальних точок з масами . Якщо пластину розглядати як систему цих матеріальних точок, то моменти інерції пластини відносно осі та відносно наближено визначатимуться за формулами

Перейшовши до границі в кожній із сум при , отримуємо точні формули для обчислення моментів інерції розглядуваної пластини відносно координатних осей:

. (13)

Знайдемо момент інерції пластини відносно початку координат.

Враховуючи, що момент інерції матеріальної точки з масою відносно початку координат дорівнює , аналогічно отримуємо, що

. (14)