Дослідження топологічного визначення верхніх напівґрат

Курсова робота: Дослідження топологічного визначення верхніх напівґрат

Зміст

Розділ 1

1. Упорядковані множини

2. Ґрати

3. Дистрибутивні ґрати

4. Топологічні простори

Розділ 2

1. Верхні напівґрати

2. Стоуновий простір

Висновок

Список літератури

Розділ 1

1. Упорядковані множини

Визначення: Упорядкованою множиною називається непуста множина, на якої визначене бінарне відношення , що задовольняє для всіх наступним умовам:

1. Рефлективність: .

2. Антисиметричність: якщо й , те .

3. Транзитивність: якщо й , те .

Якщо й , то говорять, що менше або більше , і пишуть або .

Приклади впорядкованих множин:

Множина цілих позитивних чисел, а означає, що ділить .

Множина всіх дійсних функцій на відрізку й

означає, що для .

Визначення: Ланцюгом називається впорядкована множина, на якої для має місце або .

Використовуючи відношення порядку, можна одержати графічне подання будь-якого кінцевого впорядковання множини . Зобразимо кожний елемент множини у вигляді невеликого кружка, розташовуючи вище , якщо . З'єднаємо й відрізком. Отримана фігура називається діаграмою впорядкованої множини .

Приклади діаграм упорядкованих множин:

2. Ґрати

Визначення: Верхньою гранню підмножини в упорядкованій множині називається елемент із , більший або рівний усіх з .

Визначення: Точна верхня грань підмножини впорядкованої множини – це така іі верхня грань, що менше будь-який інший іі верхньої грані. Позначається символом і читається «супремум X».

Відповідно до аксіоми антисиметричності впорядкованої множини, якщо точна верхня грань існує, то вона єдина.

Поняття нижньої грані й точної грані (яка позначається й читається «інфинум»). Також, відповідно до аксіоми антисиметричності впорядкованої множини, якщо точна нижня грань існує, то вона єдина.

Визначення: Ґратами називається впорядкована множина , у якому будь-які два елементи й мають точну нижню грань, позначувану , і точну верхню грань, позначувану .

Приклади ґрат:

1. Будь-який ланцюг є ґратами, тому що збігається з меншим, а з більшим з елементів .

Найбільший елемент, тобто елемент, більшого або рівний кожного елемента впорядкованої множини, позначають , а найменший елемент, тобто меншого або рівний кожного елемента впорядкованої множини, позначають .

На ґратах можна розглядати дві бінарні операції:

- додавання й

- добуток

Ці операції мають наступні властивості:

1. , ідемпотентність

2. , комутативність

3. ,

асоціативність

4. ,

закони поглинання

Теорема. Нехай - множина із двома бінарними операціями , що володіють властивостями (1) – (4). Тоді відношення (або ) є порядком на , а виникаюча впорядкована множина виявляється ґратами, причому:

Доказ.

Рефлективність відносини випливає із властивості (1). Помітимо, що воно є наслідком властивості (4):

Якщо й , тобто й , те в силу властивості (2), одержимо . Це означає, що відношення антисиметричне.

Якщо й , то застосовуючи властивість (3), одержимо: , що доводить транзитивність відносини .

Застосовуючи властивості (3), (1), (2), одержимо:

Отже, і

Якщо й , то використовуючи властивості (1) – (3), маємо:

, тобто

По визначенню верхньої грані переконаємося, що

Із властивостей (2), (4) випливає, що й

Якщо й , то по властивостях (3), (4) одержимо:

Звідси по властивостях (2) і (4) треба, що

, тобто

Таким чином, . :

Нехай ґрати, тоді її найбільший елемент характеризуються одним із властивостей:

2. .

Аналогічно характеризується найменший елемент :

2. .

3. Дистрибутивні ґрати

Визначення: Ґрати називаються дистрибутивної, якщо для виконується:

У будь-яких ґратах тотожності (1) і (2) рівносильні. Доказ цього факту втримується в книзі [1], стор. 24.

Теорема: Ґрати з 0 і 1 є дистрибутивною тоді й тільки тоді, коли вона не містить у

Доказ цього факту можна знайти в книзі [2].

Далі під словом “ґрати” розуміється довільні дистрибутивні ґрати з 0 і 1 (причому ).

Визначення: Непуста множина називається ідеалом у ґратах , якщо виконуються умови:

Визначення: Ідеал у ґратах називається простим, якщо

або .

Ідеал, породжений множиною Н (тобто найменший ідеал, що містить H), буде позначатися (Н]. Якщо Н = {a}, то замість ({a}] будемо писати (a] і називати (a] головним ідеалом.

Позначимо через I(L) множина всіх ідеалів ґрати L. I(L) будемо називати ґратами ідеалів.

Визначення: Ґрати й називаються ізоморфними (позначення: ), якщо існує взаємно однозначне відображення , називане ізоморфізмом, множини на множину , таке, що

4. Топологічні простори

Визначення: Топологічний простір – це непуста множина з деякою системою виділених його підмножин, що задовольняє аксіомам:

Порожня множина й сам простір належить системі : .

Перетинання будь-якого кінцевого числа множин з належить , тобто .

Об'єднання будь-якого сімейства множин з належить , тобто .

Таким чином, топологічний простір – це пари < , >, де - така множина підмножин в , що й замкнуто щодо кінцевих перетинань і довільних об'єднань. Множини з називають відкритими, а їхнього доповнення в замкнутими.

Визначення: Простір називається компактним, якщо в будь-якому його відкритому покритті можна вибрати кінцеве підпокриття.

Визначення: Підмножина простору називається компактним, якщо в будь-якому його відкритому покритті можна вибрати кінцеве підпокриття.

Визначення: Топологічний простір називається - простором, якщо для будь-яких двох різних його крапок існує відкрита множина, що містить рівно одну із цих крапок.

Розділ 2

1. Верхні напівґрати

Визначення: множина називається верхніми напівґратами, якщо sup{a,b} існує для будь-яких елементів a і b.

Визначення: Непуста множина I верхніх напівґрат L називається ідеалом, якщо для будь-яких включення має місце тоді й тільки тоді, коли .

Визначення: Верхні напівґрати називаються дистрибутивної, якщо нерівність ≤ ( , , L) спричиняє існування елементів , таких, що , , і = .(мал.1). Помітимо, що елементи й не обов'язково єдині.

Деякі найпростіші властивості дистрибутивних верхніх напівґрат дає:

Лема 1:

(*). Якщо < , > - довільні напівґрати, то верхні напівґрати дистрибутивна тоді й тільки тоді, коли ґрати дистрибутивна.

(**). Якщо верхні напівґрати дистрибутивна, то для будь-яких існує елемент , такий, що й . Отже, множина є ґратами.

(***). Верхні напівґрати дистрибутивна тоді й тільки тоді, коли множина є дистрибутивними ґратами.

Доказ.

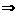(*). < , > - дистрибутивна й , те для елементів , , справедлива рівність :

виходить, напівґрати < , > - дистрибутивна.

< , > - дистрибутивна. Нехай ґрати містять діамант або пентагон (мал.2).

1) Нехай ґрати містять пентагон, . Потрібно знайти такі елементи й , щоб виконувалася рівність . Але множина елементів менших b або c складається з елементів {0,b,c} і їхня нижня границя не дасть a. Одержали протиріччя з тим, що < , > - дистрибутивна. Виходить, наше припущення невірно й ґрати не містять пентагона.

2) Нехай ґрати містять діамант, . Аналогічно, множина елементів менших b або c складається з елементів {0,b,c}, їхня нижня границя не дасть a. Виходить, ґрати не містять діаманта.

Можна зробити висновок, що ґрати дистрибутивна.

(**). Маємо , тому , де (по визначенню дистрибутивних напівґрат). Крім того, є нижньою границею елементів і .

Розглянемо ідеали, що містять елемент і - і . Тоді Ø ,тому що , нижня границя елементів a і b, утримується там.

Покажемо, що I(L) – ґрати, тобто існують точні нижня й верхня грані для будь-яких A і B.

Покажемо, що збігається з перетинанням ідеалів A і B. По-перше, - ідеал. Дійсно, і й По-друге, нехай ідеал і . Тоді , тобто - точна нижня грань ідеалів A і B, тобто .

Тепер покажемо, що збігається з перетинанням всіх ідеалів , що містять A і B. Позначимо . Оскільки для для , те C ідеал. По визначенню C він буде найменшим ідеалом, що містить A і B.

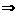(***). Нехай – верхні дистрибутивні напівґрати. Покажемо, що

Нехай , тобто (мал.3), для деяких

Зрозуміло, що . По дистрибутивності, існують такі, що . Т.к. A – ідеал, те, тому що . Аналогічно, . Т.е. . Точно також, . Якщо , то легко показати, що .

Довели, що - ідеал. Очевидно, він є верхньою гранню ідеалів A і B. Якщо C містить A і B, то C буде містити елементи для будь-яких , тобто Тому , оскільки є верхньою гранню ідеалів A і B і втримується в будь-який верхній грані.

Тепер покажемо, що виконується рівність:

. Нехай , де , . , те, звідки й отже . Аналогічно, , виходить,

. Нехай ,де .

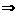
Звідси треба дистрибутивність ґрати .

– дистрибутивні ґрати, . Тепер розглянемо ідеали, утворені цими елементами:

( ,буде нижньою границею для ). Тому , що й доводить дистрибутивність напівґрат . :

2. Стоуновий простір

Визначення: Підмножина верхніх напівґрат називається коідеалом, якщо з нерівності треба й існує нижня границя множини , така, що .

Визначення: Ідеал напівґрати називаються простим, якщо й множина є коідеалом.

Надалі нам буде потрібно лема Цорна, що є еквівалентним твердженням аксіомі вибору.

Лема Цорна. Нехай A – множина й X – непуста підмножина множини P(A). Припустимо, що X має наступну властивість: якщо C – ланцюг в < >, те . Тоді X має максимальний елемент.

Лема 2: Нехай – довільний ідеал і – непустий коідеал дистрибутивних верхніх напівґрат . Якщо , то в напівґратах існує простий ідеал такий, що й .

Доказ.

Нехай X – множина всіх ідеалів в L, що містять I і не пересічних з D. Покажемо, що X задовольняє лемі Цорна.

Нехай C – довільний ланцюг в X і Якщо , те для деяких Нехай для визначеності . Тоді й , тому що - ідеал. Тому . Обернено, нехай , тоді , для якогось Одержуємо , звідки .

Довели, що M – ідеал, мабуть, що містить I і не пересічний з D, тобто . По лемі Цорна X має максимальний елемент, тобто максимальним ідеалом P серед утримуючих I і не пересічних з D.

Покажемо, що P – простій. Для цього досить довести, що L\P є коідеалом. Нехай L\P і . Оскільки , те, інакше в противному випадку по визначенню ідеалу. Отже, . Якщо , то й пересічних з D у силу максимальності P. Одержуємо й для деяких елементів . Існує елемент такий, що й , по визначенню коідеала, отже й для деяких Помітимо, що й не лежать в P, тому що в противному випадку .

Далі, , тому для деяких і . Як і колись . Крім того , тому - нижня грань елементів a і b, що не лежить в P. :

Надалі, через будемо позначати дистрибутивні верхні напівґрати з нулем, через множину всіх простих ідеалів напівґрати .

Множини виду представляють елементи напівґрат у ч.в. множині (тобто ). Зробимо всі такі множини відкритими в деякій топології.

Позначимо через топологічний простір, певний на множині . Простір SpecL будемо називати стоуновим простором напівґрат L.

Лема 3: Для будь-якого ідеалу I напівґрати L покладемо:

Тоді множини виду вичерпують всі відкриті множини в стоуновом просторі SpecL.

Доказ.

Потрібно перевірити виконання аксіом топологічного простору.

1) Розглянемо ідеал, утворений 0. Тоді

але 0 лежить у будь-якому ідеалі, а значить .

2) Візьмемо довільні ідеали й напівґрати й розглянемо

Нехай . Тоді існують елементи a і Звідси треба, що , де L\P – коідеал. По визначенню коідеала існує елемент d такий, що й , виходить, . Так як. , отже, . Одержуємо, що .

Зворотне включення очевидно.

2) Нехай - довільне сімейство ідеалів. Через позначимо множину всіх точних верхніх граней кінцевого числа елементів, що є представниками сімейства . Покажемо, що - ідеал. Нехай , тоді , де для деякого ідеалу . Тоді лежить в ідеалі , отже, і , тобто . Обернено очевидно.

Довели, що - ідеал. Тепер розглянемо довільне об'єднання.

■

Лема 4: Підмножини виду простору можна охарактеризувати як компактні відкриті множини.

Доказ.

Дійсно, якщо сімейство відкритих множин покриває множина , тобто , те Звідси треба, що для деякої кінцевої підмножини , тому . Таким чином, множина компактно.

Нехай відкрита множина r(I) компактно, тоді й можна виділити кінцеве під покриття для деяких .

Покажемо, що I породжується елементом .

Припустимо, що це не так, і в ідеалі I найдеться елемент b не лежачий в. Тоді [b) – коідеал, не пересічний с. По лемі 2 найдеться простий ідеал P утримуючий і не пересічний з [b). Одержуємо, , тому що (тобто ), але , тому що , протиріччя. Отже, компактною відкритою множиною r(I) буде тільки у випадку, якщо - головний ідеал.

Пропозиція 5: Простір є - простором.

Доказ.

Розглянемо два різних простих ідеали й Q. Хоча б один не втримується в іншому. Допустимо для визначеності, що . Тоді r(P) містить Q, але не містить P, тобто SpecL є - простором. :

Теорема 6: Стоуновий простір визначає напівґрати з точністю до ізоморфізму.

Доказ.

Потрібно показати, що двоє напівґрат і ізоморфні тоді й тільки тоді, коли простори й гомеоморфни.

Очевидно, якщо ґрати ізоморфні, то простору, утворені цими напівґратами будуть збігатися.

Нехай і гомеоморфни ( ) і . Тоді a визначає компактна відкрита множина r(a) . Множині r(a) відповідає компактна відкрита множина , з однозначно певним елементом по лемі 4. У такий спосіб одержуємо відображення : , при якому . Покажемо, що - ізоморфізм ґрат. Якщо a,b – різні елементи з , те, отже, , тому й - ін'єкція.

Для довільного відкритій множині відповідає й очевидно, що показує сюрективність .

Нехай a,b – довільні елементи з . Помітимо, що . Відкритій множині при гомеоморфізмі відповідає відкрита множина , а відповідає . Отже, = . Оскільки = , те, тобто

Висновок

алгебра множина грань грата топологічний

Дистрибутивні ґрати є одним з основних алгебраїчних об'єктів. У даній роботі розглянута частково впорядкована множина P(L) простих ідеалів. Вона дає нам багато інформації про дистрибутивні ґрати L, але вона не може її повністю охарактеризувати. Тому, для того, щоб множина P(L) характеризувало ґрати L, необхідно наділити іі більше складною структурою. Стоун [1937] задав на множині P(L) топологію. У цій роботі метод розглянутий у трохи більш загальному виді.

Література

1. Биргкоф Г. Теорія ґрат. – К., 2003.

2. Гретцер Г. Загальна теорія ґрат. – К., 2005

3. Чермних В.В. Півкільця. – К., 1997.