Нахождение минимального остовного дерева алгоритмом Краскала

Содержание

Введение

1. Постановка задачи

2. Методы решения данной проблемы

3. Описание алгоритма Краскала

4. Пример работы алгоритма Краскала

5. Код программы

6. Обзор работы программы

Заключение

Список использованной литературы

Введение

Минимальным остовным деревом (МОД) связного взвешенного графа называется его связный подграф, состоящий из всех вершин исходного дерева и некоторых его ребер, причем сумма весов ребер максимально возможная. Если исходный граф несвязен, то описываемую ниже процедуру можно применять поочередно к каждой его компоненте связности, получая тем самым минимальные остовные деревья для этих компонент.

Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: есть n городов, через которые можно проложить маршрут так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Требуется найти такой маршрут, чтобы стоимость проезда была максимальной.

Эта задача может быть сформулирована в терминах теории графов как задача о нахождении минимального остовного дерева в графе, вершины которого представляют города, рёбра - это пары городов, между которыми есть маршрут, а вес ребра равен стоимости проезда по соответствующему маршруту.

Существует несколько алгоритмов для нахождения минимального остовного дерева. Некоторые наиболее известные из них перечислены ниже:

Алгоритм Прима;

Алгоритм Краскала;

Алгоритм Борувки.

1. Постановка задачи

Пусть имеется связный неориентированный граф G, на ребрах которого задана весовая функция c (e). Связный подграф графа G, являющийся деревом и содержащий все его вершины, называют покрывающим деревом (spanning-tree) этого графа (иногда используют термин остовное дерево или остов). Весом остовного дерева будем считать сумму весов всех его ребер. Тогда возникает задача о нахождении максимального покрывающего дерева, т.е. такого, что его вес наибольший, либо равен весу любого из покрывающих деревьев для данного графа. Будем обозначать наибольшее покрывающее дерево графа G как MAX (G).

2. Методы решения данной проблемы

Остовным деревом графа называется дерево, содержащее все вершмины V графа. Стоимость остовного дерева вычисляется как сумма стоимостей всех ребер.

Идея решения:

Для остовного дерева верно следующее свойство:

Пусть G= (V,E) - свызный граф с заданной функцией стоимости, определенной на множестве ребер. Обозначим через U подмножество множества вершин V. Если (u,v) - такое ребро наибольшей стоимости, что u из U и v из V\U, тогда для графа G существует остовное дерево максимальной стоимости, содержащее ребро (u,v)

На этом свойстве основан алгоритм Прима. В этом алгоритме строится множество вершин U, из которого "вырастает" остовное дерево. Пусть V={1,2,. n}. Сначала U={1}. На каждом шаге алгоритма находится ребро наименьшей стоимости (u,v) такое, что u из U и v из V\U, затем вершина v переносится из множества V\U в множество U. Процесс продолжается до тех пор, пока множество U не станет равным множеству V.

Детали реализации:

Удобно выбрать представление в виде списка дуг.

Допустим, необходимо проложить кабель по территории университета, связав все его здания, так, чтобы из каждого здания кабель по какому-либо пути доходил до любого другого здания. Кроме того, предположим, что надо минимизировать общую длину прокладываемого кабеля. Если рассматривать здания как вершины, а кабели между зданиями как ребра, то эта работа с прокладыванием кабеля превращается в задачу определения каркаса, охватывающего здания территории университета, в котором общая длина проложенного кабеля должна быть минимальной. Такую задачу называют нахождением каркаса минимального веса. В нашей работе длина проложенного кабеля должна быть максимальной.

Определим понятие каркаса более формально. Если дан связный неориентированный граф G= (V, E), то каркас (также называемый остовным или стягивающим деревом) T= (V, E’), где E’E - это связный граф без циклов. Иными словами, каркас неориентированного графа G - это подграф графа G, дерево, содержащее все вершины графа. Понятно, что для того, чтобы T имело тот же набор вершин, что и связный граф G, и чтобы T не имело циклов, оно должно содержать ровно |V|-1 ребро.

Предположим, что для каждого ребра eE существует вес w (e), причем такой вес может выражать, например, цену, длину или время, необходимое для прохода по ребру (в нашем примере - длину кабеля между зданиями). Во взвешенном графе вес подграфа - это сумма весов его ребер. Тогда каркас T максимального веса - это каркас G, в котором вес дерева максимален относительно всех остовных деревьев G.

Если граф G несвязный, он не может иметь остовного дерева, но у него есть остовный лес. Также можно изменить алгоритм нахождения остовного дерева максимального веса, чтобы на выходе получать минимальный остовный лес.

остовное дерево алгоритм краскал

В алгоритме Краскала используется жадный подход к решению задачи, т.е. в любой момент выполнения данных алгоритмов существует множество ребер E’, представляющее подмножество некоторого минимального остовного дерева графа G. На каждом шаге алгоритмов из оставшихся ребер выбирается "лучшее" ребро, обладающее определенными свойствами, и добавляется к формируемому каркасу максимального веса. Одним из важных свойств любого ребра, добавляемого к E’, является его безопасность, т.е. то, что обновленное множество ребер E’ будет продолжать представлять подмножество некоторого минимального остовного дерева.

3. Описание алгоритма Краскала

Алгоритм Краскала может строить дерево одновременно для нескольких компонент связности, которые в процессе решения объединяются в одно связанное дерево.

Полный граф задается списком ребер. Перед работой список ребер сортируется по возрастанию длины. На каждом шаге просматривается список ребер, начиная с ребра, следующего за вошедшим в решение на предыдущем шаге, и к строящемуся поддереву присоединяют то ребро, которое не образует цикла с ребрами, уже включенными в решение.

Алгоритм состоит из следующей последовательности действий:

Создается список ребер R, содержащий длину ребра, номер исходной вершины ребра (i), номер конечной вершины ребра (j), признак включения данного ребра в дерево.

Данный список упорядочивается в порядке возрастания длин ребер.

Просматривается список R и выбирается из него ребро с максимальной длиной, еще не включенное в результирующее дерево и не образующее цикла с уже построенными ребрами.

Если все вершины включены в дерево и количество ребер на единицу меньше количества вершин, то алгоритм свою работу закончил. В противном случае осуществляется возврат к пункту 3.

Или в терминах теории графов:

Дан граф с n вершинами; длины ребер заданы матрицей. Найти остовное дерево максимальной длины.

В задаче Прима-Краскала, которая не кажется особенно простой, жадный алгоритм дает точное оптимальное решение.

Как известно (это легко доказать по индукции), дерево с n вершинами имеет n-1 ребер. Оказывается, каждое ребро нужно выбирать жадно (лишь бы не возникали циклы). То есть n-1 раз выбирать самое короткое ребро из еще не выбранное ребро при условии, что оно не образует цикла с уже выбранными.

А как следить, чтобы новое ребро не образовывало цикла со старыми? Сделать это просто. До построения дерева окрасим каждую вершину i в отличный от других цвет i. При выборе очередного ребра, например (i, j), где i и j имеют разные цвета, вершина j и все, окрашенные в ее цвет (т.е. ранее с ней соединенные) перекрашиваются в цвет i. Таким образом, выбор вершин разного цвета обеспечивает отсутствие циклов. После выбора n-1 ребер все вершины получают один цвет.

Докажем, что описанный алгоритм получает в точности максимальное решение. Для доказательства нам понадобится очень простое утверждение:

Если к дереву добавить ребро, то в дереве появится цикл, содержащий это ребро.

Действительно, пусть добавлено ребро (u, v) - “добавлено” означает, что ребро - новое, что раньше его в дереве не было. Поскольку дерево является связанным графом, то существует цепь C (u, …, v) из нескольких ребер, соединяющая вершины u и v. Добавление ребра (u, v) замыкает цепь, превращая ее в цикл.

Теорема. Алгоритм Прима-Краскала получает максимальное остовное дерево.

Доказательство. Результатом работы алгоритма является набор из n-1 ребер. Они не образуют цикла, ибо на каждом из n-1 шагов соединялись вершины разного цвета, т.е. ранее не связанные. Этот граф связный, потому что после проведения 1-го ребра осталось n-1 разных цветов, …, после проведения (n-1) - го ребра остался один цвет, т.е. одна компонента связности. Итак, полученный набор ребер образует связный граф без циклов, содержащий n-1 ребер и n вершин. Следовательно, граф есть остовное дерево. Осталось доказать, что оно имеет минимальную длину. Пусть {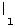, , 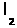…, } ребра остовного дерева в том порядке как их выбирал алгоритм, т.е. ≥. 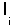Предположим для простоты доказательства, что все ребра сети имеют разную длину, т.е.

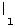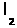>>…> (1)

Если полученное дерево не максимально, то существует другое дерево, заданное набором из n-1 ребер {, , 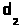…, }, такое что сумма длин больше суммы длин 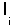. С точностью до обозначений

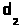>>…> (2)

Может быть 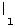=, 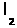= 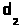и т.д., но так как деревья разные, то в последовательностях (1) и (2) найдется место, где ребра отличаются. Пусть самое левое такое место - k, так, что . Поскольку выбиралось по алгоритму самым большим из не образующих цикла с ребрами 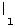, , 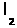…, , то >. Теперь добавим к дереву (2) ребро . В нем появится цикл, содержащий ребро и, может быть, какие-то (или все) ребра 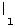, , 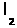…, , но они сами не образуют цикла, поэтому в цикле будет обязательно ребро d из набора , …, , причем d>. Выбросим из полученного графа с одним циклом ребро d. Мы снова получим дерево, но оно будет на d- короче минимального, что невозможно. Полученное противоречие доказывает теорему для сети со всеми разными ребрами.

4. Пример работы алгоритма Краскала

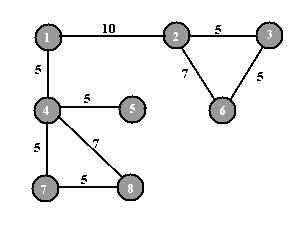
Рисунок 1. Начальный граф

Рисунок 2. Максимальное остовное дерево.

В алгоритме Краскала мы не храним массив used [N]. Вместо этого мы будем на каждой итерации алгоритма проверять, принадлежат ли концы рассматриваемого ребра к разным компонентам связности (и добавлять ребро к каркасу, если это так).

Введем счетчик int counter = 0. Пусть N - количество вершин графа.

Упорядочим список ребер по возрастанию веса.

Если counter == N - 1, закончим выполнение алгоритма.

Проходя по списку ребер, найдем ребро (i, j) такое, что i и j принадлежат разным компонентам связности. Так как список упорядочен по возрастанию веса ребер, мы будем выбирать ребро с максимальным весом, удовлетворяющее условию.

Добавим это ребро в каркас, увеличим на единицу счетчик counter.

Перейдем к шагу 2.

При реализации алгоритма можно использовать систему непересекающихся множеств для проверки того, входят ли две вершины в одну компоненту связности (изначально каждая вершина входит в своё множество, при добавлении ребра в каркас два соответствующих множества объединяются). Также для проверки связности двух вершин можно использовать любой известный алгоритм: поиск в ширину, поиск в глубину или что-либо другое.

5. Код программы

// ---------------------------------------------

#include <stdio. h>

#include <conio. h>

#include <iostream. h>

// -------------------------------------------

typedef int* tint; // указатель на int

void main ()

{ // int max=100; // Максимальный вес ребра

int n; // количество вершин

tint* G; // исходный граф

tint* H; // матрица списка ребер с весом

tint* K; /*матрица, отмечающая принадлежность

вершины компоненте*/

tint* T; // матрица остовного дерева

tint* L; // список ребер с ценами минимального дерева

// -----ввод графа

int max;

cout<<" Maximalno dopustimoe zna4enie vesa rebra = ";

cin>> max;

cout<<"\n Vvedite 4ilo vershin: \n ";

cin>> n;

G=new tint [n];

for (int i=0; i<n; i++)

G [i] =new int [n];

cout<<" Vvedite nignij treugolnik matrici stoimosti: \n ";

for (int i=1; i<n; i++)

for (int j=0; j<i; j++) {

cin>> G [i] [j];

}

for (int i=1; i<n; i++)

for (int j=0; j<i; j++)

G [j] [i] =G [i] [j];

// ---выделение памяти для списка ребер---

int kolreb=0;

for (int i=1; i<n; i++)

for (int j=0; j<i; j++)

if (G [i] [j] <max && G [i] [j]! =0)

kolreb++;

H=new tint [kolreb];

for (int i=0; i<kolreb; i++)

H [i] =new int [3];

// -------------------------------------------

int a=0;

for (int i=1; i<n; i++)

for (int j=0; j<i; j++)

if (G [i] [j] <max && G [i] [j]! =0) {

H [a] [0] =i+1;

H [a] [1] =j+1;

H [a] [2] =G [i] [j];

a++;

}

cout<<endl;

// ----сортировка ребер по возрастанию веса

int f,d,s;

for (int i=0; i<kolreb-1; i++)

for (int j=0; j<kolreb-1; j++)

if (H [j] [2] <H [j+1] [2]) {

f=H [j] [2];

H [j] [2] =H [j+1] [2];

H [j+1] [2] =f;

d=H [j] [0];

H [j] [0] =H [j+1] [0];

H [j+1] [0] =d;

s=H [j] [1];

H [j] [1] =H [j+1] [1];

H [j+1] [1] =s;

}

// вывод ребер отсортированных по возрастанию веса

cout<<"Matrica dostigimosni otsortirovannoe po ubivaniuy: \n ";

for (int i=0; i<kolreb; i++) {

cout<<H [i] [0] <<"-->";

cout<<H [i] [1] <<" = ";

cout<<H [i] [2] <<endl;

cout<<" ";

}

for (int i=0; i<kolreb; i++) {

H [i] [0] - -;

H [i] [1] - -;

}

// матрица для определения компоненты

K=new tint [n];

for (int i=0; i<n; i++)

K [i] =new int [2];

for (int i=0; i<n; i++) {

K [i] [0] =i;

K [i] [1] =0;

}

// ----матрица остовного дерева

T=new tint [n];

for (int i=0; i<n; i++)

T [i] =new int [n];

for (int i=0; i<n; i++)

for (int j=0; j<n; j++)

T [i] [j] =0;

// -присоединение первого ребра

T [H [0] [0]] [H [0] [1]] =H [0] [2];

T [H [0] [1]] [H [0] [0]] =H [0] [2];

K [H [0] [0]] [1] =1;

K [H [0] [1]] [1] =1;

// алгорит соединения ребер без создания цикла:

int m=2; // номер компоненты

for (int i=1; i<kolreb; i++) // пройти по всем ребрам

if (K [H [i] [0]] [1]! =K [H [i] [1]] [1])

// если 2 вершины не из одной компоненты

{

if (K [H [i] [0]] [1] >0 && K [H [i] [1]] [1] >0)

// если обе вершины принадлежат разной компоненте

{

for (int j=0; j<n; j++)

if (K [H [i] [1]] [1] ==K [j] [1])

K [j] [1] =K [H [i] [0]] [1];

K [H [i] [1]] [1] =K [H [i] [0]] [1];

T [H [i] [0]] [H [i] [1]] =H [i] [2];

T [H [i] [1]] [H [i] [0]] =H [i] [2];

}

if ( (K [H [i] [0]] [1] >0 && K [H [i] [1]] [1] ==0)

|| (K [H [i] [0]] [1] ==0 && K [H [i] [1]] [1] >0))

// если одна вершина имеет компоненту а др. нет

{

if (K [H [i] [0]] [1]! =0)

K [H [i] [1]] [1] =K [H [i] [0]] [1];

if (K [H [i] [1]] [1]! =0)

K [H [i] [0]] [1] =K [H [i] [1]] [1];

T [H [i] [0]] [H [i] [1]] =H [i] [2];

T [H [i] [1]] [H [i] [0]] =H [i] [2];

}

if (K [H [i] [0]] [1] ==0 && K [H [i] [1]] [1] ==0)

// если обе вершины не имели компоненты

{

K [H [i] [0]] [1] =m;

K [H [i] [1]] [1] =m;

T [H [i] [0]] [H [i] [1]] =H [i] [2];

T [H [i] [1]] [H [i] [0]] =H [i] [2];

m++;

}

} // конец проверки всех ребер

// ---выделение памяти для списка ребер

kolreb=0;

for (int i=1; i<n; i++)

for (int j=0; j<i; j++)

if (T [i] [j] <max && T [i] [j]! =0)

kolreb++;

L=new tint [kolreb];

for (int i=0; i<kolreb; i++)

L [i] =new int [3];

// ------------------------------------------

// ---вывод ребер

cout<<endl<<" Vivod reber maximalnogo vesa: \n ";

a=0;

for (int i=1; i<n; i++)

for (int j=0; j<i; j++)

if (T [i] [j] <max && T [i] [j]! =0) {

L [a] [0] =i+1;

L [a] [1] =j+1;

L [a] [2] =T [i] [j];

a++;

}

for (int i=0; i<kolreb; i++) {

cout<<L [i] [0] <<"-->";

cout<<L [i] [1] <<" = ";

cout<<L [i] [2] <<"\n ";

}

int b=0;

for (int i=0; i<kolreb; i++)

b+=L [i] [2];

cout<<endl <<" Stoimost dereva = "<<b; // вывод стоимости

getch ();

// return 0;

}

// --------------------------------------------------------------

6. Обзор работы программы

После выполнения программы выводятся ребра максимального веса, и стоимость остовного дерева.

Заключение

В курсовом проекте был разработана программа, реализующая алгоритм Краскала, поиск максимального остовного дерева.

Алгоритм Краскала действительно находит остовный лес максимального веса, поскольку он является частным случаем алгоритма Радо - Эдмондса для графического матроида, где независимые множества - ациклические множества рёбер.

Список использованной литературы

Рыбаков Глеб. Минимальные остовные деревья.

Архангельский А.Я., C++Builder 6. Справочное пособие.

Белов Теория Графов, Москва, "Наука", 1968.

Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергоатомиздат, 1988.

http://rain. ifmo.ru