Теорія і практика обчислення визначників
ТЕОРІЯ І ПРАКТИКА ОБЧИСЛЕННЯ ВИЗНАЧНИКІВ
1. Основні поняття і теореми
Def. Нехай задано квадратну матрицю А n-го порядку з елементами a>ij>, де i визначає номер рядка, j – номер стовпця і при цьому через х>j> позначені стовпці матриці А, тобто
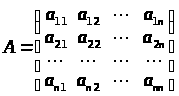 і
і
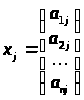 .
.
Визначником (det A) квадратної матриці А зі стовпцями х>j> називається функціонал (х>1>, х>2>, … , х>n>) щодо стовпців цієї матриці, який:
а) лінійний за кожним з аргументів (полілінійний):
теорема обчислення визначник сума
(х>1>, …, х>i1> + х>i2>, … , х>n>) = (х>1>, … , х>i1>, … , х>n>) + (х>1>, … , х>i2>, … , х>n>);
б) абсолютно антисиметричний (антисиметричний по будь-якій парі аргументів): (х>1>, … , х>i>, … , х>j>, … , х>n>) = –(х>1>, … , х>j>, … , х>i>, … , х>n>);
в) підкоряється умові нормування:
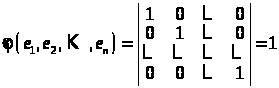 .
.
Тоді, з огляду на загальний вигляд полілінійного антисиметричного функціонала, маємо:

а б
Рис. 1
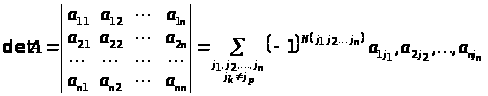 ,
(1)
,
(1)
де N(j>1>
j>2>
… j>n>)
– кількість безладів у перестановці
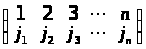 .
.
Говорять, що в перестановці мається безлад, якщо j>k> > j>m> і k < m.
З формули (1)
для визначника другого порядку
одержуємо
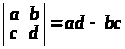 .
.
Визначник третього порядку дорівнює сумі шести (3! = 6) доданків. Для побудови цих доданків зручно скористатися правилом трикутників. Добуток елементів, що розташовані на головній діагоналі, а також добутки елементів, що є вершинами двох трикутників на рис. 1а, беруться з множником +1, а добуток елементів, що розташовані на побічній діагоналі, а також добутки елементів, що є вершинами двох трикутників на мал. 1б, беруться з множником –1, тобто
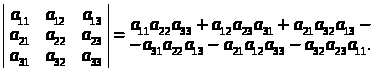
Властивості визначників:
1. det A = det AT. З цієї властивості випливає, що рядки і стовпці визначника рівноправні. У силу цього всі властивості, сформульовані для стовпців, можуть бути сформульовані і для рядків визначника.
2. Якщо один зі стовпців визначника складається з нульових елементів, то визначник дорівнює нулю.
3. Загальний множник у стовпці визначника можна виносити за знак визначника.
4. Якщо у визначнику поміняти два стовпці місцями, то визначник змінить знак.
5. Визначник, що має два рівних стовпці, дорівнює нулю.
6. Якщо стовпці визначника лінійно залежні, то визначник дорівнює нулю.
7.
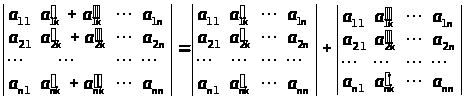 .
.
8. Визначник не зміниться, якщо до стовпця визначника додати лінійну комбінацію інших стовпців.
9. Визначник добутку двох квадратних матриць n-го порядку дорівнює добуткові визначників цих матриць.
Def. Якщо в матриці А порядку n викреслити i-й рядок та j-й стовпець, то елементи, що залишилися, утворять матрицю (n – 1)-го порядку. Її визначник називається мінором (n – 1)-го порядку, додатковим до елемента a>ij> матриці А, і позначається М>ij>, а величина А>ij >= (–1) i + j М>ij> називається алгебраїчним доповненням до елемента a>ij> матриці А.
10.
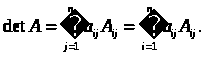 (Розкриття визначника за елементами
j-го стовпця та за елементами i-го рядка).
(Розкриття визначника за елементами
j-го стовпця та за елементами i-го рядка).
11.
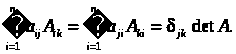
12. (Теорема Лапласа).
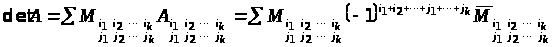 .
.
Тут
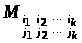 –
мінор, складений з елементів матриці
А, що розташовані на перетині рядків
i>1>,
i>2>,
…, i>k>
і стовпців j>1>,
j>2>,
…, j>k>,
а
–
мінор, складений з елементів матриці
А, що розташовані на перетині рядків
i>1>,
i>2>,
…, i>k>
і стовпців j>1>,
j>2>,
…, j>k>,
а
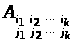 –
алгебраїчне доповнення до цього мінора.
–
алгебраїчне доповнення до цього мінора.
13. (Про зміну елементів визначника).
Якщо
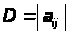 ,
а
,
а
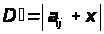 ,
то
,
то
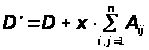 .
.
3. Приклади розв’язування задач
Задача 1. Обчислити
визначник:
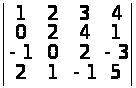 .
.
Розв’язання. I спосіб. Обчислимо визначник розкладанням за елементами (наприклад) третього рядка (властивість 10º):
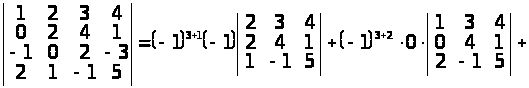
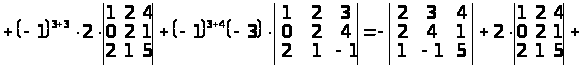
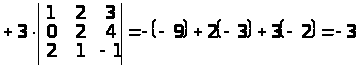 .
.
Визначники третього порядку, що входять до останнього виразу, обчислені за правилом трикутників.
II спосіб. Обчислимо визначник розкладанням за мінорами 2-го порядку (наприклад тими, що розташовані в 1-му і 2-му рядках вихідного визначника, властивість 12º). Усього таких мінорів буде шість (1-й, 2-й стовпці; 1-й, 3-й стовпці; 1-й, 4-й стовпці; 2-й, 3-й стовпці; 2-й, 4-й стовпці; 3-й, 4-й стовпці). Одержимо:
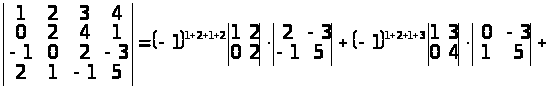
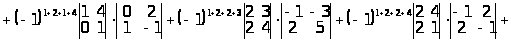
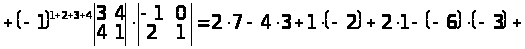
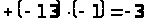 .
.
III спосіб. Обчислимо визначник методом приведення визначника до трикутного вигляду. Для цього скористаємося властивістю 8.
а) 1-й рядок додамо до 3-го рядка;
б) 1-й рядок, помножений на (–2), додамо до 4-го рядка.
При цьому визначник не зміниться.
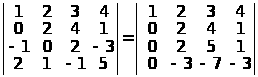
Далі: в) від 1-го рядка віднімемо 2-й рядок;
г) 2-й рядок, помножений на 3, додамо до 4-го рядка, помноженого на 2. При цьому визначник збільшиться вдвічі за рахунок множення 4-го рядка на 2.
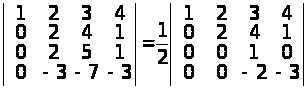 ;
;
д) в останньому визначнику 3-ій рядок помножимо на 2 і додамо до 4-го рядка. Визначник не зміниться. Одержимо:
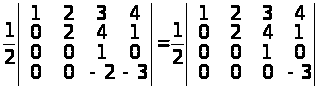 .
.
Визначник матриці трикутного вигляду обчислюється як добуток діагональних елементів. Доходимо висновку, що вихідний визначник дорівнює –3.
Задача 2.
Обчислити визначник:
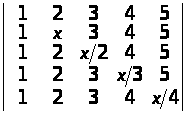 .
.
Рішення. Для обчислення визначника скористаємося методом виділення лінійних множників. Насамперед відзначимо, що вихідний визначник є багаточленом 4-го степеня відносно х. Крім того, при х = 2 перший і другий рядки співпадають, тобто визначник дорівнює нулеві. Отже, х = 2 є коренем багаточлена. Далі зауважуємо, що при х = 6, х = 12, х = 20 перший рядок співпадає з третім, четвертим і п’ятим рядком відповідно. Виходить, ми встановили всі чотири корені полінома, тобто
det А= C(x – 2)(x – 6)(x – 12)(x – 20).
Для знаходження C відзначимо, що у визначник множник х4 входить з коефіцієнтом, який дорівнює 1/24, а в багаточлен, що стоїть в правій частині, – з коефіцієнтом який дорівнює 1. Тоді C = 1/24. У такий спосіб:
det А =
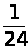 (x
– 2)(x – 6)(x – 12)(x – 20).
(x
– 2)(x – 6)(x – 12)(x – 20).
Задача 3.
Обчислити визначник:
 .
.
Рішення.
Зрозуміло, що вихідний визначник можна
одержати, якщо до всіх елементів
визначника
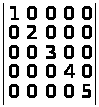 додати х = 4. Тоді скористаємося методом
зміни елементів визначника (властивість
13).
Одержуємо:
додати х = 4. Тоді скористаємося методом
зміни елементів визначника (властивість
13).
Одержуємо:
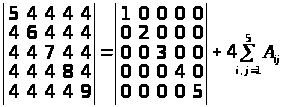 .
.
Визначник діагонального вигляду дорівнює добуткові діагональних елементів (5! = 120). Алгебраїчні доповнення дорівнюють: А>11> = 5! = 120;
А>22> = 3.4.5 = 60; А>33> = 2.4.5 = 40; А>44> = 2.3.5 = 30 і А>55> = 2.3.4 = 24.
Решта А>ij >= 0. Одержуємо: det А = 120 + 4(120 + 60 + 40 + 30 + 24) = 120 + 4.274 = 1216.
Задача 4.
Обчислити визначник n-го порядку
 .
.
Рішення. Розкриємо визначник за елементами 1-го рядка:
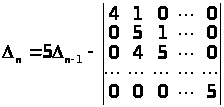 ,
,
а останній визначник розкриємо за елементами 1-го стовпця. Одержуємо:
>n> = 5>n – 1> – 4>n – 2>. (*)
Записане співвідношення називається рекурентним співвідношенням і дозволяє виразити >n >через такі ж визначники більш низького порядку.
З (*) одержуємо:
>n> – >n – 1 >= 4(>n – 1> – >n – 2>) = 42(>n – 2> – >n – 3>) = … = 4n – 2 (>2> – >1>) =
= 4n – 2 (21 – 5) = 4n .
>n> – 4>n – 1> = >n– 1> – 4>n – 2 >= >n– 2> – 4>n – 3> = … = >2> – 4>1> = 21 – 4.5 = 1.
Маємо систему
рівнянь:
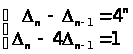 .
Віднімаючи з 1-го рівняння 2-е, одержуємо:
3>n
– 1> = 4n
– 1. У такий спосіб:
.
Віднімаючи з 1-го рівняння 2-е, одержуємо:
3>n
– 1> = 4n
– 1. У такий спосіб:
 .
.
4. Задачі і вправи для самостійного розв’язування
Визначити число безладів у перестановках (за вихідне розташування завжди, якщо немає особливих вказівок, приймається розташування 1, 2, 3, ... у зростаючому порядку):
а) 2, 1, 5, 4, 3; б) 6, 3, 2, 5, 1, 4; в) 7, 5, 6, 4, 1, 3, 2;
г) 2, 1, 7, 9, 8, 6, 3, 5, 4; д) 9, 8, 7, 6, 5, 4, 3, 2, 1.
а) 4; б) 10; в) 18; г) 18; д) 36. ▲
З'ясувати, які з наведених нижче добутків входять у визначники відповідних порядків і, якщо входять, то з яким знаком:
а) а>43>а>21>а>35>а>12>а>54>; б) а>13>а>24>а>23>а>41>а>55>;
в) а>61>а>23>а>45>а>36>а>12>а>54>; г) а>32>а>43>а>14>а>51>а>66>а>25>;
д) а>27>а>36>а>51>а>74>а>25>а>43>а>62>; е) а>33>а>16>а>72>а>27>а>55>а>61>а>44>;
ж) а>12>а>23>а>34 >…а>n–1 n >а>25>а>kk> (1 k n); з) а>12>а>23>а>34 >…а>n-1n>а>n1n>.
а) –; б) не входить у визначник; в) +; г) +; д) не входить у визначник; е) +; ж) не входить у визначник; з) (–1)n. ▲
Вибрати значення i і k так, щоб наступні добутки входили у визначники відповідного порядку із зазначеним знаком:
а) а>1i>а>32>а>4k>а>25>а>53 >з « + »; б) а>62>а>i5>а>33>а>k4>а>46>а>21 >з « – »;
в) а>47>а>63>а>1i>а>55>а>7k>а>24>а>31 >з « + ».
а) i = 1, k = 4; б) i = 5, k = 1; в) i = 6, k = 2. ▲
Користуючись тільки визначенням, знайти члени визначників, які мають у собі множники х4 і х3:
а)
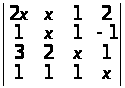 ;
б)
;
б)
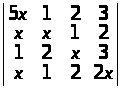 .
.
а) 2х4, –х3; б) 10х4, –5х3. ▲
Знайти члени визначника 4-го порядку а) що містять елемент а>32> і входять у визначник зі знаком « + »; б) що містять елемент а>23 >і входять у визначник зі знаком « – ».
а) а>11>а>24>а>32>а>43>, а>13>а>21>а>32>а>44>, а>14>а>23>а>32>а>41>; б) а>11>а>23>а>32>а>44>, а>12>а>23>а>34>а>41>, а>14>а>23>а>31>а>42>. ▲
Виписати
всі члени визначника 5-го порядку, що
мають вигляд
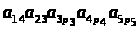 .
Що вийде, якщо з їхньої суми винести
а>14>а>23>
за дужки?
.
Що вийде, якщо з їхньої суми винести
а>14>а>23>
за дужки?
 .
▲
.
▲
Як зміниться визначник n-го порядку, якщо всі його стовпці записати в зворотному порядку? Визначник помножиться на (–1)(n(n–1))/2. ▲
Не розкриваючи визначників, довести, що:
а)
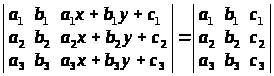 ;
;
б)
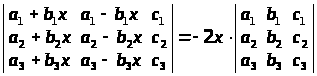 ;
;
в)
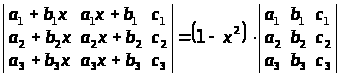 ;
;
г)
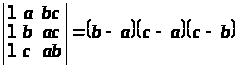 ;
д)
;
д)
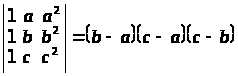 .
.
а) властивості 7, 3; б) властивості 7, 3, 5; в) властивості 7, 3, 5; г) властивість 5;
д) властивість 5. ▲
Знайти
мінори елементів а>13>,
а>24>,
а>43 >визначника
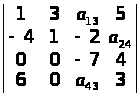 .
.
М>13> = 24; М>24> = – 126; М>43> = 52. ▲
Знайти алгебраїчне доповнення елементів а>14>, а>23>, а>42> визначника
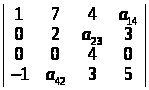 .
.
А>14> = 8; А>23> = 0; А>42> = – 12. ▲
Обчислити
визначник, розкриваючи його по 3-му
рядку
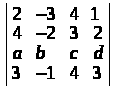 .
.
8a + 15b + 12c – 19d. ▲
Обчислити
визначник, розкриваючи його по 2-му
стовпцю:
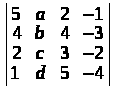 .
.
5a – 5b – 5c + 5d. ▲
Обчислити наступні визначники, знижуючи їхній порядок за допомогою розкладання за елементами деякого рядка або стовпця:
а)
 ;
б)
;
б)
 ;
в)
;
в)
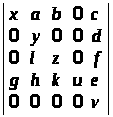 .
.
а) abcd; б) abcd; в) xyzuv. ▲
Обчислити наступні визначники 3-го порядку:
а)
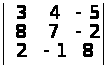 ;
б)
;
б)
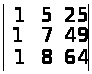 ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
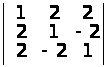 ;
е)
;
е)
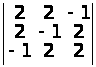 .
.
а) 0; б) 6; в) 0; г) –2; д) –27; е) –27. ▲
Обчислити наступні визначники 3-го порядку:
а)
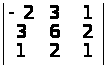 ;
б)
;
б)
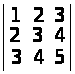 ;
в)
;
в)
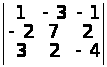 ;
;
г)
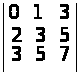 ;
д)
;
д)
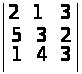 ;
е)
;
е)
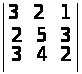 .
.
а) –7; б) 0; в) –1; г) 4; д) 40; е) –3. ▲
Обчислити наступні визначники 3-го порядку:
а)
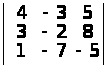 ;
б)
;
б)
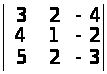 ;
в)
;
в)
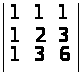 ;
;
г)
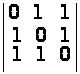 ;
д)
;
д)
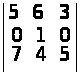 ;
е)
;
е)
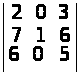 .
.
а) 100; б) –5; в) 1; г) 2; д) 4; е) –8. ▲
Обчислити наступні визначники 3-го порядку:
а)
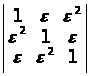 ;
б)
;
б)
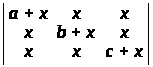 ;
в)
;
в)
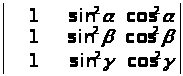 ;
;
г)
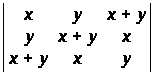 ;
д)
;
д)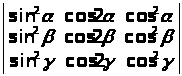 ;
;
е)
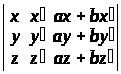 .
.
а) (1 – 3)2; б) abc + x(ab + bc + ac); в) 0; г) –2(x3 + y3); д) 0; е) 0. ▲
Обчислити наступні визначники 4-го порядку:
а)
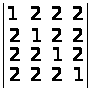 ;
б)
;
б)
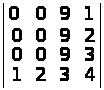 ;
в)
;
в)
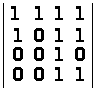 ;
г)
;
г)
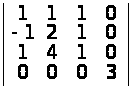 .
.
а) –7; б) 0; в) –1; г) –18. ▲
Обчислити наступні визначники 4-го порядку:
а)
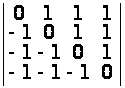 ;
б)
;
б)
 ;
в)
;
в)
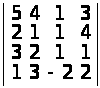 ;
г)
;
г)
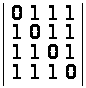 .
.
а) 1; б) –5; в) 0; г) –3. ▲
Обчислити наступні визначники 4-го порядку:
а)
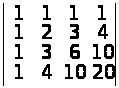 ;
б)
;
б)
 ;
;
в)
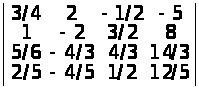 ;
г)
;
г)
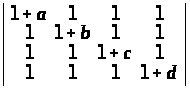 .
.
а) 1; б) 48; в)
1; г)
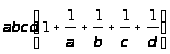 .
▲
.
▲
Обчислити визначники 4-го порядку:
а)
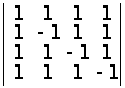 ;
б)
;
б)
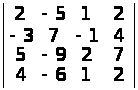 ;
в)
;
в)
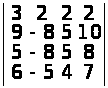 ;
г)
;
г)
 .
.
а) –8; б) –9; в) –6; г) –10. ▲
Обчислити визначники 5-го порядку:
а)
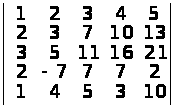 ;
б)
;
б)
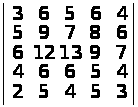 .
а)
52; б) 5. ▲
.
а)
52; б) 5. ▲
Зведенням до трикутного вигляду обчислити визначники:
а)
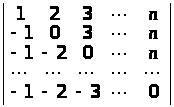 ;
б)
;
б)
 ;
;
в)
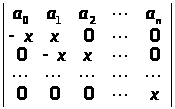 ;
г)
;
г)
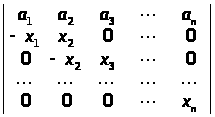 .
.
а)
n!; б) 2n + 1; в) хn(а>0>
+ а>1>
+ … + а>n>);
г)
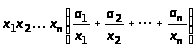 .
▲
.
▲
Обчислити визначники методом виділення лінійних множників:
а)
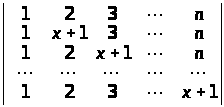 ;
б)
;
б)
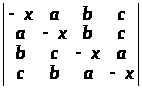 ;
;
в)
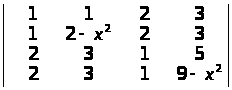 ;
г)
;
г)
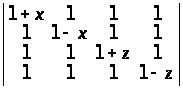 .
.
а) (х – 1)(х – 2)…(х – n +1); б) (x – a – b – c)(x – a + b + c)(x + a – b + c)(x + a + b – c);
в) (х2 – 1)(х2 – 4); г) x2z2, вказівка: визначник не зміниться, якщо 1-й стовпець поміняти місцями з 2-м стовпцем і одночасно 1-й рядок із 2-м рядком; при х = 0 визначник дорівнює 0, аналогічно по z. ▲
Розв’язати рівняння:
а)
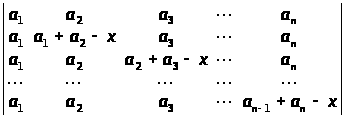 ;
б)
;
б)
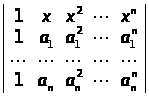 ;
;
в)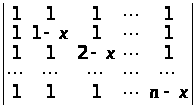 ; г)
; г)
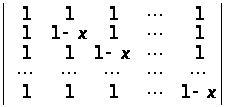 (х
R).
(х
R).
а) х>i >= a>i>, i = 1, 2, … , n – 1; б) х>i >= a>i>, i = 1, 2, … , n; в) х = 0, 1, 2, … , n – 1; г) x = 1. ▲
Використовуючи
метод рекурентних співвідношень,
обчислити визначники: а)
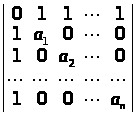 ;
б)
;
б)
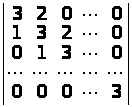 ;
в)
;
в)
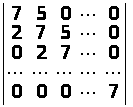 .
.
а)
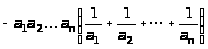 ;
б) 2n
+ 1 –
1; в)
;
б) 2n
+ 1 –
1; в)
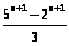 .
▲
.
▲
Обчислити визначники методом представлення їх у вигляді суми визначників:
а)
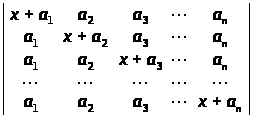 ;
б)
;
б)
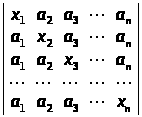 .
.
∆ а) хn + (а>1> + а>2> + … + а>n>)хn – 1; б) вказівка: x>i> (x>i> – a>i> + a>i>),
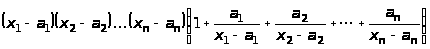 .
▲
.
▲
Обчислити визначники методом зміни елементів визначника:
а)
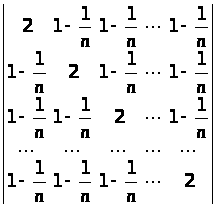 ;
б)
;
б)
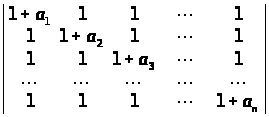 .
.
∆ а)
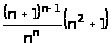 ;
б)
;
б)
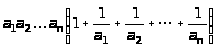 .
▲
.
▲
Обчислити визначники n-го порядку:
а)
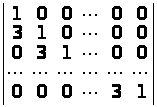 ;
б)
;
б)
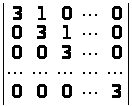 ;
в)
;
в)
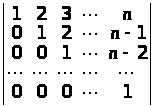 ;
;
г)
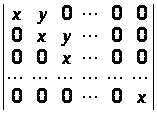 ;
д)
;
д)
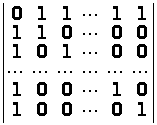 ;
е)
;
е)
 .
.
∆ а) 1; б) 3n; в) 1; г) хn; д) 1 – n; е) (–2)n –1(5n – 2). ▲
Обчислити визначники n-го порядку:
а)
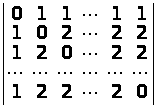 ;
б)
;
б)
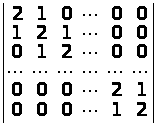 ;
в)
;
в)
 ;
;
г)
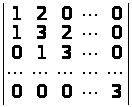 ;
д)
;
д)
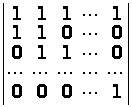 ;
е)
;
е)
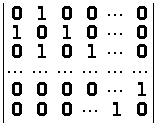 .
.
∆ а) (–2)n –2(1 – n); б) n + 1; в) (–1)n –1(n – 1); г) 1; д) (1 – (–1)n)/2, вказівка:
>n> = 1– >n –1>; е) 0, якщо n = 2k +1; (–1)n/2, якщо n = 2k, k Z; вказівка: >n> = – >n – 2>. ▲
Обчислити визначники n-го порядку:
а)
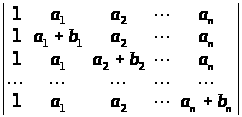 ;
б)
;
б)
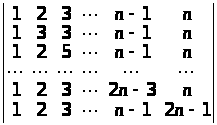 ;
;
в)
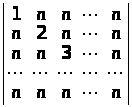 ;
г)
;
г)
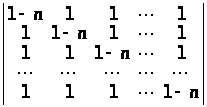 ;
;
д)
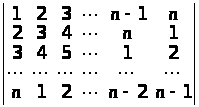 ;
е)
;
е)
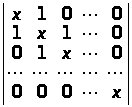 .
.
∆ а) (b>1 >– а>1>)> >(b>2 >– а>2>) … (b>n >– а>n>); б) (n – 1)!; в) (–1)n – 1. n!; г) 0;
д)
(–1)(n(n
–1))/2nn–1(n
+ 1)/2; е)
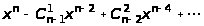 ▲
▲