Теория вероятностей (работа 7)
Контрольная работа
Теория вероятностей
Задача № 1
событие вероятность задача
Опыт – Брошены 2 игральные кости. Образуют ли полную группу событий следующие наборы: А - на обеих костях шестерки, В - ни на одной кости нет шестерки, С - на одной из костей шестерка, на другой – нет. (Указать, образуют ли они в данном опыте полную группу событий).
Решение:
Определение. Полной группой событий называется совокупность всех возможных результатов опыта.
По определению данный опыт является полной группой событий.
Задача № 2.
На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди наудачу взятых 5 ки-нескопов окажется 3 кинескопа Львовского завода.
Решение:
P(A) =

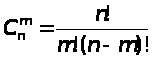



P(A) =

Задача № 3
Имеются изделия четырех сортов, причем число изделий первого сорта – 1, второго сорта - 2, третьего сорта - 3, четвертого сорта - 4. Для контроля наудачу берут 7 изделий. Определить вероятность того, что среди них одно изделие первосортное, одно - второго сорта, два - третьего и три - четвертого сорта.
Решение:
P(A) =

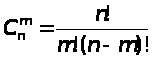
Задача № 4
В мешке смешаны нити, среди которых 30% белых, а остальные красные. Определить вероятность того, что вынутые наудачу две нити будут одного цвета.
Решение:
Вероятность вытягивания белой нити = 30/100 = 0,3,
Вероятность вытягивания красной нити = 70/100 = 0,7,
Вероятность вытягивания двух нитей одного цвета = 0,3*0,7 = 0,21.
Задача № 5
Экспедиция газеты направила газеты в два почтовых отделения. Вероят-ность своевременной доставки газет в каждое из почтовых отделений равна 0,9. Найти вероятность того, что: а) оба почтовых отделения получат газеты вовремя; б) оба почтовых отделения получат газеты с опозданием; в) одно отделение получит газеты вовремя, а второе - с опозданием.
Решение:
а) оба почтовых отделения получат газеты вовремя:
P = 0.9 * 0.9 = 0.81;
б) оба почтовых отделения получат газеты с опозданием:
P = 0.1*0.1 = 0.01;
в) одно отделение получит газеты вовремя, а второе - с опозданием:
P = 0.9*0.1 + 0.1*0.9 = 0.18.
Задача № 6
Вероятности того, что во время работы цифровой электронной машины возникает сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
Решение:
Hi – стоп произошел в i-м узле, i = 1…3;
А – стоп обнаружен.
P(H2) = 0,3
P(H3) = 0,2
P(H3) = 0,5
P(AH2) = 0,8
P(AH3) = 0,9
P(AH3) = 0,9
Формула полной вероятности:
P(A) = P(H2) * P(AH2) + P(H3) * P(AH3) + P(H3) * P(AH3) =
0,3*0,8 + 0,2*0,9 + 0,5*0,9 = 0,24+0,18 +0,45 = 0,87.
Задача № 7
Радиолампа может
принадлежать к одной из трех партий с
вероятностями
 где
где
 .
Вероятности того, что лампа проработает
заданное число часов, равны для этих
партий соответственно 0,1; 0,2; 0,4. Определить
вероятность того, что лампа проработает
заданное число часов.
.
Вероятности того, что лампа проработает
заданное число часов, равны для этих
партий соответственно 0,1; 0,2; 0,4. Определить
вероятность того, что лампа проработает
заданное число часов.
Решение:
Выдвинем гипотезы: Н1 - радиолампа из первой партии, Р(Н1) = 0.25; Н2 - радиолампа из второй партии, Р(Н2) = 0.5; Н3 - радиолампа из третьей партии, Р(Н3) = 0.25. Случайное событие А - лампа проработает заданное число часов.
P(A) = P(H1) * P(AH1) + P(H2) * P(AH2) + P(H3) * P(AH3) = 0,25*0,1 + 0,5*0,2 + 0,5*0,4 = 0,025 + 0,1 + 0,2 = 0,325.
Задача № 8
Вероятность изготовления стандартной детали на автомате равна 0,95. Изготовлена партия в 200 деталей. Найти наиболее вероятное число нестандартных деталей в этой партии. Найти вероятность этого количества нестандартных деталей.
Решение:
Вероятность изготовления нестандартной детали на автомате равна 1 – 0,95 = 0,05.
Наивероятнейшее значение k0 числа наступления события A при проведении n повторных независимых испытаний, удовлетворяющих схеме Бернулли, вычисляется по формуле:
 или
или

Проводится 50 повторных
независимых испытаний с двумя исходами
в каждом. Вероятность появления
нестандартной детали в каждом испытании
постоянна. Значит, схема Бернулли
выполнятся. По формуле
 имеем:
имеем:

Так как число деталей может быть только целым, то наиболее вероятное число нестандартных деталей в этой партии равно 10.
Вероятность, что только первые 10 деталей из 200 будут нестандартные:
0,0510*0,95190 = 5,7*10-18
Теперь нужно посчитать
общее количество комбинаций, в которых
какие-либо 10 деталей из 200 будут
нестандартными, а остальные 190 —
стандартные. Для этого есть стандартная
формула:
 ,
где n = 200 (общее количество), a = 10 (количество
перебираемых элементов), b = 190 (количество
остальных элементов). Итого, возможно
комбинаций:
,
где n = 200 (общее количество), a = 10 (количество
перебираемых элементов), b = 190 (количество
остальных элементов). Итого, возможно
комбинаций:
 ,
,
В результате получаем вероятность для 10 нестандартных деталей:
22451004309013280*5,7*10-18 =0,128.
Задача № 9
Вероятность попадания в цель из орудия при первом выстреле равна 0,1, при втором выстреле равна 0,4, при третьем - 0,7. Предполагается произвести три выстрела. Найти закон распределения, математическое ожидание и дисперсию числа попаданий в цель. Построить функцию распределения. Определить вероятность того, что число попаданий не менее трех.
Решение.
Случайная величина
 - число попаданий в мишень при 3-х
выстрелах, распределена по биномиальному
закону, ее возможные значения 0, 1, 2, 3.
- число попаданий в мишень при 3-х
выстрелах, распределена по биномиальному
закону, ее возможные значения 0, 1, 2, 3.

где
 .
.
 ;
;
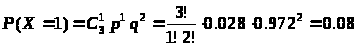 ;
;
 ;
;
 .
.
амнистия законодательство гуманизм
Ряд распределения случайной
величины
 :
:
-

0
1
2
3

0,918
0,08
0,0023
0,00002
 ;
;
 .
.