Численные методы линейной алгебры

Содержание

Введение

1. Метод Гаусса

2. Модификации метода Гаусса

3. Метод прогонки

4. Вычисление определителей

5. Вычисление обратных матриц

6. Итерационные методы

Заключение

Список литературы

Введение

Основной целью реферата является изучение и сравнительный анализ численных методов решения систем линейных алгебраических уравнений, вычисления определителей и обратных матриц; реализация этих методов в виде машинных программ на языке высокого уровня и практическое решение задач на ЭВМ.

В общем случае система линейных алгебраических уравнений имеет вид

(1)

В матричной форме система (1) представляется как

A X = B (2)

где

Чтобы такая система уравнений имела единственное решение, входящие в нее n уравнений должны быть линейно независимыми. Необходимым и достаточным условием этого является неравенство нулю определителя данной системы, т.е. det A  0. Алгоритмы решения систем уравнений такого типа делятся на прямые и итерационные.

1. Метод Гаусса

Данный метод также называется методом последовательного исключения неизвестных. Он относится к группе прямых методов и основан на преобразовании исходной системы к эквивалентной форме с треугольной матрицей коэффициентов.

При использовании метода Гаусса задача решается в два этапа:

1) прямой ход;

2) обратный ход.

Прямой ход заключается в преобразовании системы к треугольному виду.

При обратном ходе производится вычисление значений неизвестных.

Прямой ход метода Гаусса. Для получения расчетных формул прямого хода преобразуем исходную систему (1), заменив элементы b>i> () на a>i,n+1>. В результате система (1) будет иметь следующий вид

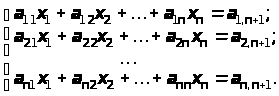
Прямой ход выполняется за (n-1) шагов, причем на каждом шаге из уравнений с номерами k + 1, k + 2, …, n исключается неизвестное x>k>.

На первом шаге сначала первое уравнение делится на a>11 > 0. Получим

(3)

где

Затем из каждого оставшегося уравнения вида

()

вычитается полученное уравнение (3), умноженное на коэффициент a>i1>. В итоге, после выполнения первого шага прямого хода система уравнений примет следующий вид

(4)

где

На втором шаге указанные выше действия повторяются над (n - 1) уравнениями системы (4), всеми кроме первого, с целью исключения переменной x>2>, где

В итоге получим

где

Повторяя шаги прямого хода (n - 1) раз, окончательно получим систему уравнений треугольного вида

(5)

где

При программной реализации прямого хода используется расширенная матрица коэффициентов A

,

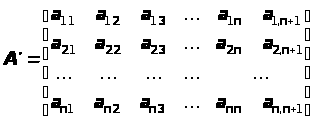для которой элементы имеют следующий смысл

1) - начальные значения;

2) - промежуточные значения;

3) - конечные значения.

Для определения элементов матрицы A на некотором k-ом шаге

()

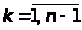используются следующие расчетные формулы

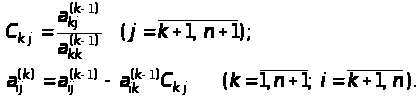
Обратный ход метода Гаусса. После приведения исходной системы уравнений (1) к треугольному виду (5) вычисляются значения корней по следующим формулам

Таким образом, расчетные формулы обратного хода имеют вид

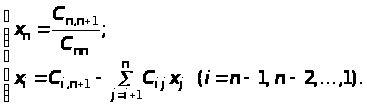
Вычислительная сложность метода Гаусса оценивается как O(n3), причем для реализации прямого хода требуется около арифметических операций, а для обратного – около n2 операций.

2. Модификации метода Гаусса

Метод Гаусса с выбором главного элемента. Основным ограничением метода Гаусса является предположение о том, что все элементы , на которые производится деление на каждом шаге прямого хода, не равны нулю. Эти элементы называются главными элементами и располагаются на главной диагонали матрицы A.

Если на некотором шаге прямого хода главный элемент = 0, то дальнейшее решение системы невозможно. Если главный элемент имеет малое значение, близкое к нулю, то возможен сильный рост погрешности из-за резкого возрастания абсолютной величины получаемых в результате деления коэффициентов. В таких ситуациях метод Гаусса становится неустойчивым.

Исключить возникновение подобных случаев позволяет метод Гаусса с выбором главного элемента.

Идея этого метода состоит в следующем. На некотором k-м шаге прямого хода из уравнений исключается не следующая по номеру переменная x>k>, а такая переменная, коэффициент при которой является наибольшим по абсолютной величине. Этим гарантируется отсутствие деления на нуль и сохранение устойчивости метода.

Если на k-м шаге в качестве главного элемента выбирается , то в матрице A должны быть переставлены местами строки c номерами k и p и столбцы с номерами k и q.

Перестановка строк не влияет на решение, так как соответствует перестановке местами уравнений в системе, но перестановка столбцов означает изменение нумерации переменных. Поэтому информация обо всех переставляемых столбцах должна сохраняться, чтобы после завершения обратного хода можно было бы восстановить исходную нумерацию переменных.

Существуют две более простые модификации метода Гаусса:

- с выбором главного элемента по столбцу;

- с выбором главного элемента по строке.

В первом случае в качестве главного элемента выбирается наибольший по абсолютной величине элемент k-й строки (среди элементов , i = ). Во втором - наибольший по абсолютной величине элемент k-го столбца (среди элементов , i = ). Наибольшее распространение получила первый подход, поскольку здесь не изменяется нумерация переменных.

Следует заметить, что указанные модификации касаются только прямого хода метода Гаусса. Обратный ход выполняется без изменений, но после получения решения может потребоваться восстановить исходную нумерацию переменных.

LU-разложение. В современном математическом обеспечении ЭВМ метод Гаусса реализуется с использованием LU-разложения, под которым понимают представление матрицы коэффициентов A в виде произведения A = LU двух матриц L и U, где L – нижняя треугольная матрица, U - верхняя треугольная матрица

Если LU-разложение получено, то решение исходной системы уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов

L Y = B; (6)

U X = Y (7)

линейный алгебраический уравнение численный

где Y = - вектор вспомогательных переменных.

Такой подход позволяет многократно решать системы линейных уравнений с разными правыми частями B. При этом наиболее трудоемкая часть (LU-разложение матрицы A) выполняется только один раз. Эта процедура соответствует прямому ходу метода Гаусса и имеет оценку трудоемкости O(n3). Дальнейшее решение систем уравнений (6) и (7) может выполняться многократно (для различных B), причем решение каждой из них соответствует обратному ходу метода Гаусса и имеет оценку вычислительной сложности O(n2).

Для получения LU-разложения можно воспользоваться следующим алгоритмом.

1. Для исходной системы (1) выполнить прямой ход метода Гаусса и получить систему уравнений треугольного вида (5).

2. Определить элементы матрицы U по правилу

u>ij> = C>ij> (i = 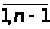; j = )

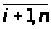3. Вычислить элементы матрицы L по правилам

Расчетные формулы для решения системы (6) имеют следующий вид:

y>1> = b>1> / l>11>;

Расчетные формулы для решения системы (7)

x>n> = y>n>;

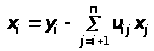(i = n - 1, n - 2, …, 1).

3. Метод прогонки

Метод прогонки представляет собой простой и эффективный алгоритм решения систем линейных алгебраических уравнений с трехдиагональными матрицами коэффициентов следующего вида

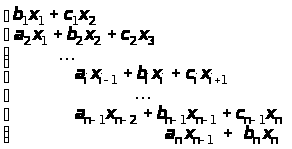
(8)

Системы такого вида часто возникают при решении различных инженерных задач, например, при интерполяции функций сплайнами.

Преобразуем первое уравнение системы (8) к виду x>1> = >1>x>2> + >1>, где

>1 >= -с>1> / b>1> и >1 >= -d>1> / b>1>. Подставим полученное для x>1> выражение во второе уравнение системы (8)

a>2>(>1>x>2> + >1>) + b>2>x>2> + c>2>x>3> = d>2>.

Представим это уравнение в виде x>2> = >2>x>3> + >2>, где >2 >= -с>2> / (b>2> + a>2>>1>) и >2 >= (d>2> - a>2>>1>) / (b>2> + a>2>>1>). Полученное для x>2 >выражение подставим в третье уравнение системы (8) и т.д.

На i-м шаге (1 < i < n) процесса i-е уравнение системы принимает вид

x>i> = >i>x>i+1> + >i>, (9)

где >i >= -с>i> / (b>i> + a>i>>i-1>) и >i >= (d>i> - a>i>>i-1>) / (b>i> + a>i>>i-1>).

На последнем n-м шаге подстановка в последнее уравнение системы (8) выражения x>n>>-1> = >n>>-1>x>n> + >n>>-1> дает уравнение a>n>(>n>>-1>x>n> + >n>>-1>) + b>n>x>n> = d>n>, из которого можно определить значение x>n> = >n> = (d>n> – a>n>>n-1>) / (b>n> + a>n>>n-1>).

Значения остальных неизвестных x>i> (i = n-1, n-2, ..., 1) легко вычисляются по формуле (9).

Таким образом, алгоритм прогонки, подобно методу Гаусса, включает два этапа – прямой ход (прямая прогонка) и обратный ход (обратная прогонка).

Прямой ход метода прогонки состоит в вычислении прогоночных коэффициентов

>i> (i = ) и >i> (i = ).

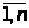При i = 1 эти коэффициенты вычисляются по формулам:

>1 >= -с>1> / >1>; >1 >= -d>1> / >1>; >1> = b>1>.

Для i = используются следующие рекуррентные формулы:

>i >= -с>i> / >i>; >i >= (d>i> - a>i>>i-1>) / >i>; >i> = b>i> + a>i>>i-1>.

Прямая прогонка завершается при i = n:

>n >= (d>n> – a>n>>n-1>) / >n>; >n> = b>n> + a>n>>n-1>.

Обратный ход метода прогонки позволяет вычислить значения неизвестных. Сначала полагают x>n> = >n>. Затем в обратном порядке по формуле (9) определяют значения неизвестных x>n>>-1>, x>n>>-2>, ..., x>1>.

Свойства метода прогонки. Трудоемкость метода прогонки оценивается примерно как 8n арифметических операций, что существенно меньше метода Гаусса. Существование решения системы (8) и его единственность гарантируются при выполнении достаточных условий, задаваемых следующей теоремой.

Теорема [2]. Пусть коэффициенты системы (8) удовлетворяют следующим неравенствам

b>k>a>k>+c>k>; b>k>>a>k>; k = 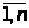, где a>1> = 0; b>n> = 0. Тогда >i>  0 и >i>

1 для всех i =

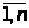
Заметим, что при всех >i>  0 вычисления по формулам прямой прогонки могут быть доведены до конца (ни один из знаменателей не обратится в нуль). Одновременно все коэффициенты >i>, такие, что >i> 1, обеспечивают устойчивость по входным данным этапа обратной прогонки по формуле (9).

4. Вычисление определителей

Идея последовательного исключения переменных, реализованная в методе Гаусса, может быть использована при вычислении определителей. При этом используются следующие свойства определителей:

1) перестановка двух строк или столбцов определителя не изменяет его абсолютной величины, но меняет знак на противоположный;

2) умножение всех элементов одной строки или одного столбца на любое число равносильно умножению определителя на это число;

3) если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на любой общий множитель, то величина определителя не изменится.

Пусть задан определитель

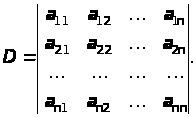
Выберем главный элемент a>11 > 0. Если a>11 >= 0, то выполним перестановку двух строк или столбцов этого определителя, чтобы получить a>11 > 0.

Вынесем главный элемент a>11 >из первой строки за знак определителя

Используя процедуру прямого хода метода Гаусса, преобразуем полученный определитель таким образом, чтобы в первом столбце под единицей были бы все нули. При этом величина определителя не изменится.

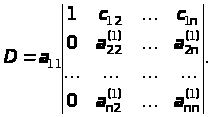
Разложим полученный определитель по элементам первого столбца, что даст понижение его порядка определителя на единицу

Повторим указанную процедуру (n - 1) раз и окончательно получим

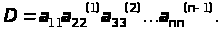
Если при вычислении определителя производилась перестановка строк или столбцов (для выбора главного элемента), то

где s – количество выполненных перестановок.

Таким образом, вычисление определителя detA некоторой матрицы A сводится к выполнению прямого хода метода Гаусса. Абсолютная величина этого определителя равна произведению главных элементов , k = , используемых на каждом шаге прямого хода. Знак определителя зависит от числа перестановок строк и столбцов, выполненных при выборе главных элементов.

Если такие перестановки не производились, то величина определителя также может быть вычислена как произведение диагональных элементов матрицы L, формируемой в процессе LU-разложения исходной матрицы А

5. Вычисление обратных матриц

Обратную матрицу А-1 имеет любая квадратная матрица А, для которой detA  0. Пусть дана матрица А = [a>ij>]>n>>>>n>. Для вычисления элементов обратной матрицы используется соотношение

A A-1 = A-1 A = E,

где E – единичная матрица.

Обозначим обратную матрицу A-1 = X = [x>ij>]>n>>>>n>. Тогда получим

A X = E.

Будем рассматривать столбцы матрицы X как векторы

…

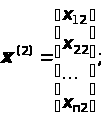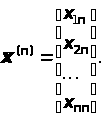
Аналогично выделим столбцы единичной матрицы E

…;

Тогда система линейных уравнений вида

A =

позволяет определить элементы k-го столбца обратной матрицы X = A-1. Всего потребуется решить n таких систем с одинаковой матрицей A, но разными правыми частями для k = . Это можно сделать с использованием LU-разложения матрицы коэффициентов A, либо непосредственно с помощью метода Гаусса.

6. Итерационные методы

При решении систем уравнений высокого порядка с разреженными матрицами коэффициентов, которые характерны для большинства задач автоматизации проектирования сложных систем, наиболее эффективно применение итерационных методов. Такие методы (например, последовательных приближений и Зейделя) позволяют получать значения корней системы с заданной точностью в виде последовательности

некоторых векторов, сходящихся к точному решению X*. Эффективность применения итерационных методов зависит от удачного выбора начального приближения и скорости сходимости процесса вычислений.

Итерационные методы используют особенности разреженных матриц коэффициентов, поскольку ненулевые элементы вычисляются по специальным выражениям по мере необходимости. Поэтому для их реализации требуется меньшее количество вычислительных операций (около n2) и соответствующих затрат машинного времени. Важным преимуществом итерационных методов также является несущественное влияние погрешностей вычислений, так как любое ошибочное приближение может рассматриваться как новый начальный вектор.

Метод последовательных приближений Якоби. Пусть дана система линейных уравнений (1), для которой диагональные элементы

.

Тогда переменную x>1> можно выразить через первое уравнение, 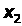- через второе уравнение и т. д.

(10)

где и

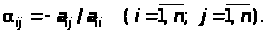
Система (10) называется системой линейных уравнений, приведенной к нормальному виду. Матричная форма записи такой системы представляется как

(11)

где

При решении системы (11) за нулевое приближение корней может быть принят столбец свободных членов, т.е. . Любое k-е приближение ( вычисляется по формуле

Если последовательность приближений ,,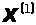, ..., , ... имеет предел , то этот предел является точным решением 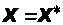системы уравнений (2). Итерационная формула, которая может использоваться при программировании метода Якоби, представляется в обозначениях исходной системы (1) следующим образом

Вычисления продолжаются до тех пор, пока значения 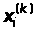не станут достаточно близкими к для всех Формальное условие прекращения итерационного процесса записывается как

(12)

где  - некоторое заданное положительное число, характеризующее точность (погрешность) определения корней системы уравнений.

Итерационный метод Зейделя. Метод Зейделя представляет собой модификацию метода последовательных приближений. При определении значения переменной на некоторой (k+1)-й итерации используются уже вычисленные (k+1)-е приближения неизвестных , , ..., , а также значения полученные на предыдущей k-й итерации.

Пусть дана линейная система уравнений (10). Выбранные начальные приближения корней подставляются в первое уравнение

Для определения полученное значение сразу же подставляется во второе уравнение системы

Аналогично определяются приближения корней 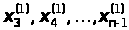. Значение вычисляется с использованием первых приближений всех переменных как

В общем случае получение значений неизвестных по методу Зейделя на некоторой k-ой итерации производится по следующей формуле

При использовании обозначений исходной системы уравнений (1) итерационная формула обычно записывается как

Условие завершения итерационного процесса по методу Зейделя также формулируется в виде соотношения (12). При этом, как правило, процесс сходится к единственному решению быстрее, чем при использовании метода последовательных приближений Якоби.

Условия сходимости итерационных процессов. Пусть дана приведенная к нормальному виду система (11) линейных уравнений. Итерационные процессы последовательных приближений и Зейделя для системы (11) сходятся к единственному решению независимо от выбора начального приближения, если выполняется хотя бы одно из следующих условий

Приведенные соотношения означают, что сумма модулей элементов любой строки или любого столбца матрицы  должна быть меньше единицы.

Таким образом, для сходимости указанных итерационных процессов достаточно, чтобы значения элементов >ij> матрицы  при i  j были небольшими по абсолютной величине. Можно показать, что для линейной системы вида (2) итерационные процессы последовательных приближений и Зейделя сходятся к точному решению X, если для всех уравнений системы модули диагональных коэффициентов удовлетворяют условиям

и по крайней мере для одного из уравнений выполняется соотношение

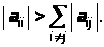
Линейную систему (2) можно заменить такой эквивалентной системой нормального вида (11), которая удовлетворяет условиям сходимости итерационных процессов. Для этого используются следующие элементарные преобразования:

    перестановка двух строк или столбцов;

    умножение всех элементов какой-либо строки на одно и то же число, отличное от нуля;

    сложение элементов какой-либо строки с соответствующими элементами другой строки, умноженными на одно и то же число.

В качестве примера рассмотрим метод [1] приведения линейной системы к виду, удобному для итераций. Система уравнений AX = B умножается на матрицу D = A-1 - , где  = [>ij>] - матрица с малыми по модулю элементами. В результате получается эквивалентная система уравнений

(A-1 - ) A X = D B

или в нормальном виде

X =  +  X,

где  =  A и  = D B. Если значения >ij > достаточно малы, то очевидно, что полученная система вида (9) удовлетворяет условиям сходимости, поскольку умножение на матрицу D эквивалентно совокупности элементарных преобразований над уравнениями системы.

Заключение

Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.

Список литературы

    Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.

    Васильев, Ф.П. Численные методы решения экстремальных задач. [Текст] Ф.П. Васильев – М.: Наука, 2002. C. 415.

    Симанков, В.С. Основы функционального программирования [Текст] В.С. Симанков, Т.Т. Зангиев, И.В. Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.

    Калиткин, Н.Н. Численные методы. [Электронный ресурс] Н.Н. Калиткин. – М.: Питер, 2001. С. 504.

    Кнут, Д.Э. Искусство программирования. Основные алгоритмы [Текст] Д.Э. Кнут. – М.: Вильямс, 2007. Т.1.– 712 с.