Исследование метода простой итерации и метода Ньютона для решения систем двух нелинейных алгебраических уравнений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра экономической информатики
Курсовая работа
по дисциплине «Численные методы»
на тему: «Исследование метода простой итерации и метода Ньютона для решения систем двух нелинейных алгебраических уравнений»
Выполнил
Студент: Обухова Т.С.
Факультет ФБ
Группа ФБИ-72
Преподаватель: Сарычева О.М.
Новосибирск
2009
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Постановка задачи. Математическое описание методов
Метод простой итерации
Метод Ньютона
Описание программного обеспечения
Описание тестовых задач
Анализ результатов, выводы
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Очень часто в различных областях экономики приходится встречаться с математическими задачами, для которых не удается найти решение классическими методами или решения выражены громоздкими формулами, которые не приемлемы для практического использования. Поэтому большое значение приобрели численные методы. В большинстве случаев численные методы являются приближенными, так как с их помощью обычно решаются задачи, аппроксимирующие исходные. В ряде случаев численный метод строится на базе бесконечного процесса, который в пределе сводится к искомому решению. Однако реально предельный переход не удается осуществить, и процесс, прерванный на некотором шаге, дает приближенное решение. Кроме того, источниками погрешности являются несоответствие математической модели изучаемому реальному явлению и погрешность исходных данных.
Решение систем нелинейных алгебраических уравнений – одна из сложных и до конца не решенных задач. Даже о расположении и существовании корней систем нелинейных уравнений почти ничего нельзя сказать. Большинство методов решения систем нелинейных уравнений сходятся к решению, если начальное приближение достаточно близко к нему, и могут вообще не давать решения при произвольном выборе начального приближения. Условия и скорость сходимости каждого итерационного процесса существенно зависят от свойств уравнений, то есть от свойств матрицы системы, и от выбора начальных приближений.
Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения решения, называется итерационным. Итерационные методы дают возможность найти решение системы как предел бесконечного вычислительного процесса, позволяющего по уже найденным приближениям к решению построить следующее, более точное приближение. Плюсом таких методов является самоисправляемость и простота реализации на ЭВМ. В точных методах ошибка в вычислениях приводит к накопленной ошибке в результате, а в случае сходящегося итерационного процесса ошибка в каком-либо приближении исправляется в последующих итерациях, и такое исправление требует, как правило, только нескольких лишних шагов единообразных вычислений. Для начала вычислений итерационных методом требуется знание одного или нескольких начальных приближений к решению.
В данной курсовой работе необходимо рассмотреть два из множества существующих итерационных методов - метод простой итерации и метод Ньютона (классический) для решения систем линейных алгебраических уравнений.
1 Постановка задачи. Математическое описание методов
При
определенных условиях ЭО в установившемся
режиме описывается системой нелинейных
АУ вида . Если при этом входной сигнал
известен, то для определения соответствующего
значения
необходимо решить систему нелинейных
АУ вида:
(1)
Которая в нашем случае представляет собой систему из двух нелинейных уравнений с двумя неизвестными вида:
(2)
Обобщенный алгоритм решения системы (1) определяется формулой
,
где:
G – вектор-функция размерности n, которая определяется способом построения итерационного процесса;
p – количество предыдущих точек значений X, используемых в данном итерационном процессе.
Если в итерационном процессе используется только одна предыдущая точка (p=1), то
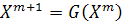
Рассмотрим подробнее два таких метода – метод простой итерации и метод Ньютона.
1.1 Метод простой итерации
Пусть дана система (2), корни которой требуется найти с заданной точностью.
Предположим,
что система допускает лишь изолированные
корни. Число этих корней и их приближенные
значения можно установить, построив
кривые
и
и определив координаты их точек
пересечения (либо из существующих
представлений о функционировании
экономического объекта).
Для применения метода итераций система (2) приводится к виду
(3)
Функции
и
называются итерирующими. Алгоритм
решения задается формулами:
(n=0,
1, 2, …),
где
- некоторое начальное приближение.
Для приведения системы (2) к виду (3) используем следующий прием. Положим
(
).
(4)
Коэффициенты
найдем как приближенные решения следующей
системы уравнений:
Характеристики метода:
1. Сходимость.
Локальная, то есть метод сходится при выборе начальных приближений достаточно близко к точному решению. Насколько близко необходимо выбирать начальное приближение, исследуем в практической части.
2. Выбор начального приближения
Начальные значения переменных должны выбираться близко к точным.
3. Скорость сходимости линейная.
4. Критерий окончания итераций.
Определяется по формуле:
,
1.2 Метод Ньютона
Пусть дана система (2). Согласно методу Ньютона последовательные приближения вычисляются по формулам
Где
,
,
а якобиан
Характеристики метода:
1. Сходимость.
Локальная, то есть метод сходится при выборе начальных приближений достаточно близко к точному решению. Насколько близко необходимо выбирать начальное приближение, исследуем в практической части.
2. Выбор начального приближения
Начальные значения переменных должны выбираться близко к точным.
3. Скорость сходимости квадратичная.
4. Критерий окончания итераций.
Аналогично методу простой итерации:
,
2 Описание программного обеспечения
метод итерация ньютон нелинейное уравнение
Программное обеспечение представлено в виде двух основных модулей – mpi2.m (метод простой итерации) и kmn2.m (классический метод Ньютона) и трех вспомогательных модулей – funF.m (матрица системы), funJ.m (матрица Якоби для системы), head.m (головная программа).
Головная программа – модуль head.m
Используемые переменные:
x0 – вектор начальных приближений;
edop – допустимая ошибка вычислений;
Текст программы:
Исходная система уравнений – модуль funF.m
Входные параметры:
x – вектор - текущее приближение к решению;
Выходные параметры:
F – вектор значений функции, полученных в точке x
Текст программы:
function [F]=funF(x)
F=[
;
];
В векторе содержатся функции F>1> и F>2> по строкам.
Матрица Якоби – модуль funJ.m
Входные параметры:
x – вектор - текущее приближение к решению;
Выходные параметры:
J – матрица Якоби, полученная в точке x
Текст программы:
function[j]=funJ(x)
j=[
;
];
В матрице содержатся частные производные функций F>1> и F>2 >по x>1> и x>2.>
Метод простой итерации – модуль mpi2.m
Входные параметры:
x0 – вектор начальных приближений;
edop – допустимая ошибка вычислений;
Используемые переменные:
F – вектор функции, полученный в некоторой точке;
J – матрица Якоби, вычисленная от начальных условий;
dx - вектор ошибки на каждом шаге итерационного процесса;
alpha, beta, gamma, delta – параметры используемые для приведения системы (2) к виду (3);
nf, ndx – нормы вектора функции и вектора ошибки соответственно;
x - вектор решения системы на каждом шаге итерационного процесса.
Выходные параметры:
xout – матрица размерности n×2 значений решения системы, составленная по строкам из решений на m-ном шаге;
dxout – матрица размерности n×2 значений ошибки решения, составленная по строкам из ошибок на m-ном шаге;
mout – вектор, составленный из номеров итераций на каждом шаге.
Текст программы:
Классический метод Ньютона – модуль mpi2.m
Входные параметры:
x0 – вектор начальных приближений;
edop – допустимая ошибка вычислений;
Используемые переменные:
F – вектор функции, полученный в некоторой точке;
J – матрица Якоби, вычисленная в некоторой точке;
dx - вектор ошибки на каждом шаге итерационного процесса
delta – вектор промежуточных значений, используемых для расчета dx
nf, ndx – нормы вектора функции и вектора ошибки соответственно;
x - вектор решения системы на каждом шаге итерационного процесса.
Выходные параметры:
xout – матрица размерности n×2 значений решения системы, составленная по строкам из решений на m-ном шаге;
dxout – матрица размерности n×2 значений ошибки решения, составленная по строкам из ошибок на m-ном шаге;
mout – вектор, составленный из номеров итераций на каждом шаге.
Текст программы:
3 Описание тестовых задач
В данной работе спроектированы программа, реализующие методы простой итерации и Ньютона применительно к решению систем нелинейных уравнений. Для проверки предлагается решение системы уравнений с последующим исследованием рассматриваемых методов на её примере. При этом исследуется влияние вектора начального приближения к решению и значения допустимой ошибки на сходимость методов и число итераций.
1.
Решение системы
обеими методами, графики решений и
ошибок при начальных условиях
:
Как и следовало ожидать, метод Ньютона сошелся на две итерации быстрее благодаря квадратичной скорости сходимости.
2.
При начальных условиях
- начальные условия отстоят от точного
решения примерно на 0,5.
Метод Ньютона опять сошелся быстрее на две итерации, общее число итерации каждого метода по сравнению с предыдущим решением увеличилось на единицу, поэтому можно сделать вывод, что разница между точным решением и начальным приближением 0,5 несущественно повлияла на сходимость.
3.
При начальных условиях
- начальные условия отстоят от точного
решения примерно на 2.
Результаты вычислений показывают, что при отстоянии начального приближения от точного значения на 2 количество итераций в методе простой итерации значительно возросло, в то время как число итерации метода Ньютона увеличилось всего на 1.
4.
Для проверки времени счета введем в
модули методов новую переменную t,
определяющую время счета, и возьмем
начальные приближение, очень далекие
от точного решения
- начальные условия отстоят от точного
решения примерно на 37.
Время в MatLab выводится в формате год/месяц/день/часы/минуты/секунды, то есть метод простой итерации сошелся за 0,015 секунд, а метод Ньютона за время менее 0,00009 секунд (не отображается); число итераций метода простой итерации возросло на 200, метода Ньютона – на единицу. Так как из теории известно, что если метод Ньютона не сходится за 6-7 итераций, то он не сойдется вообще, попытаемся найти такое начальное приближение, при котором этот метод уже не сойдется.
При начальных условиях x0=[1000;500]; edop=0.01 метод итераций сходится уже более чем за минуту и 44 тысячи итераций, а метод Ньютона – за неотображаемое время и 15 итераций. Таким образом, метод итераций хоть и сходится, но требует неадекватных эффективности вычислительных затрат, а метод Ньютона, несмотря на теорию о его несходимости при количестве итераций больше 6-7, сходится, и очень быстро.
Возьмем начальные условия x0=[10000000000; 1500000000], edop=0.01 и решим систему методом Ньютона.
t =0 0 0 0 0 0.0160
То есть метод сошелся за 0,016 секунд, выполнив при этом 35 итераций, и все еще сходится.
Увеличивая начальное приближения до величины порядка 1040, мы все еще получаем сходимость, при количестве итераций порядка 130.
4 Анализ результатов, выводы
Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального приближения подробно представлена в предыдущем пункте. Проанализировав полученные результаты, можно сказать, что при достаточном удалении от точного решения количество итераций и время счета обоих методов, безусловно, возрастает, но в случае метода простой итерации количество итерации возрастает геометрически относительно метода Ньютона. Мы попытались определить границы сходимости метода Ньютона, но многократные расчеты при достаточно больших начальных приближениях (порядка 1040) не смогли дать ответа на этот вопрос – точное решение достигалось за очень малое (в сравнении со степенью приближений) число итераций – порядка 130.
Сравнив методы по времени счета и количеству итераций при различной точности (в данной работе наглядно не представлено), можно сделать вывод, что метод Ньютона и по этому параметру эффективней метода простой итерации – при допустимой ошибке 10-14 метод простой итерации сошелся за 235 итераций и 0,016 секунд, а метод Ньютона – за 7 итераций и неотобразимо малое время.
Таким образом, сделаем общий вывод: метод Ньютона на порядок эффективней метода простой итерации по таким параметрам, как время счета и число итераций при выборе начального приближения, достаточно далекого от точного решения или при достаточно высокой точности вычислений.
ЗАКЛЮЧЕНИЕ
При выполнении данной работы были рассмотрены теоретически и практически основные характеристики методов простой итерации и Ньютона для решения систем двух нелинейных уравнений.
Мы получили следующие результаты:
метод простой итерации проще в реализации, чем метод Ньютона – он не требует, в частности, расчета матрицы Якоби на каждом шаге;
методы сходятся за небольшое количество итераций, если начальное приближение взято близко к точному решению;
при отдалении начального приближения от точного решения, скорость сходимости и число итераций методов отличаются на порядки, метод Ньютона сходится за гораздо меньшее время и число итераций;
при очень сильном отдалении от начального решения применение метода простой итерации нецелесообразно ввиду очень больших вычислительных затрат;
при уменьшении допустимой ошибки вычислительные затраты метода простой итерации значительно больше, чем метода Ньютона, но не так велики, как при увеличении начальных приближений на тот же порядок – то есть изменение точности имеет меньшее влияние на параметры сходимости, чем изменение начального приближения;
Метод Ньютона для решения систем двух нелинейных уравнений оказался более эффективным, чем метод простой итерации по всем рассматриваемым параметрам.
Нам не удалось определить мерность начального приближения, необходимого для того, чтобы метод Ньютона не сошелся.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах.–М.: Наука, 1972. – 368 с.
Сарычева О.М. Численные методы в экономике: Конспект лекций /НГТУ –Новосибирск, 1995. – 65 с.
Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. – М.:Мир, 1975. – 558 с.