Дослідження функцій гіпергеометричного рівняння
Курсова робота з математики
«Дослідження функцій гіпергеометричного рівняння»
Введення
У зв'язку із широким розвитком чисельних методів і зростанням ролі чисельного експерименту у великому ступені підвищився інтерес до спеціальних функцій. Це пов'язане із двома обставинами. По-перше, при розробці математичної моделі фізичного явища для з'ясування відносної ролі окремих ефектів вихідну задачу часто доводиться спрощувати для того, щоб можна було одержати рішення в легко аналізованій аналітичній формі. По-друге, при рішенні складних задач на ЕОМ зручно використовувати спрощені задачі для вибору надійних і економічних обчислювальних алгоритмів. Дуже рідко при цьому можна обмежитися задачами, що приводять до елементарних функцій. Крім того, знання спеціальних функцій необхідно для розуміння багатьох важливих питань теоретичної й практичної фізики.
Найбільше часто вживаними функціями є так звані спеціальні функції математичної фізики: класичні ортогональні поліноми (поліноми Якоби, Лагерра, Ермита), циліндричні, сферичні й гіпергеометричні. Теорії цих функцій і їхніх додатків присвячений цілий ряд досліджень.
1. Гіпергеометричне рівняння
1.1 Визначення гіпергеометричного ряду
Гіпергеометричним рядом називається статечної ряд виду

де z – комплексна змінна,
 ,
,
 ,
,
 - параметри, які можуть приймати будь-які
речовинні або комплексні значення (
- параметри, які можуть приймати будь-які
речовинні або комплексні значення (
 0,-1,-2,…),і символ
0,-1,-2,…),і символ
 позначає величину
позначає величину
 =
=
 =1
=1
Якщо
 й
й
 – нуль або ціле негативне число, ряд
обривається на кінцевому числі членів,
і сума його являє собою поліном відносно
z. За винятком цього випадку, радіус
збіжності гіпергеометричного ряду
рівняється одиниці, у чому легко
переконатися за допомогою ознаки
збіжності Даламбера: думаючи
– нуль або ціле негативне число, ряд
обривається на кінцевому числі членів,
і сума його являє собою поліном відносно
z. За винятком цього випадку, радіус
збіжності гіпергеометричного ряду
рівняється одиниці, у чому легко
переконатися за допомогою ознаки
збіжності Даламбера: думаючи

 zk
zk
маємо
 =
=

 ,
,
коли k
 , тому гіпергеометричний ряд сходиться
при
, тому гіпергеометричний ряд сходиться
при
 <1
і розходиться при
<1
і розходиться при
 >1.
>1.
Сума ряду
F( ,
,
 ,
,
 ,z)
=
,z)
=
 ,
,
 <1 (1.1)
<1 (1.1)
називається гіпергеометричною функцією.
Дане визначення гіпергеометричної
функції придатне лише для значень z, що
належать колу збіжності, однак надалі
буде показано, що існує функція
комплексного змінного z, регулярна в
площині з розрізом (1,
 )
яка при
)
яка при
 <1
збігається з F(
<1
збігається з F( ,
,
 ,
,
 ,z).
Ця функція є аналітичним продовженням
F(
,z).
Ця функція є аналітичним продовженням
F( ,
,
 ,
,
 ,z)
у розрізану площину й позначається тим
же символом.
,z)
у розрізану площину й позначається тим
же символом.
Щоб виконати аналітичне продовження
припустимо спочатку що R( )>R(
)>R( )>0 і скористаємося інтегральним
поданням
)>0 і скористаємося інтегральним
поданням
 (1.2)
(1.2)
k=0,1,2,..
Підставляючи (1.2) в (1.1) знаходимо
F( ,
,
 ,
,
 ,z)
=
,z)
=
 =
=
=
=

причому законність зміни порядку інтегрування й підсумовування випливає з абсолютної збіжності.
Дійсно, при R( )>R(
)>R( ) >0 і
) >0 і
 <1
<1




 =
=
= F(
F( , R(
, R( ),R(
),R( ),
), )
)
На підставі відомого біноминального розкладання
 =(1-tz)-a(1.3)
=(1-tz)-a(1.3)
0 t
t 1,
1, <1
<1
тому для F( ,
,
 ,
,
 ,z) виходить
подання
,z) виходить
подання
F( ,
,
 ,
,
 ,z)=
,z)=
 (1.4)
(1.4)
R( )>R(
)>R( ) >0 і
) >0 і
 <1
<1
Покажемо, що інтеграл у правій
частині останньої рівності зберігає
зміст і представляє регулярну функцію
комплексного змінного z у площині з
розрізом (1,
 ).
).
Для z приналежні області
 ,
,
 (R – довільно велике,
(R – довільно велике,
 і
і
 довільно малі позитивні числа), і 0 < t
< 1 підінтегральне вираження є регулярна
функція z і безперервна функція t ; тому
досить показати що інтеграл сходиться
рівномірно в розглянутій області. Доказ
треба з оцінки
довільно малі позитивні числа), і 0 < t
< 1 підінтегральне вираження є регулярна
функція z і безперервна функція t ; тому
досить показати що інтеграл сходиться
рівномірно в розглянутій області. Доказ
треба з оцінки

(М – верхня границя модуля функції (1-tz)-a, безперервної в замкнутій області
 ,
,
 ,
0
,
0 t
t
 1)
1)
що показує, збіжність інтеграла
буде при R( )>R(
)>R( ) >0 інтеграл
) >0 інтеграл
 сходиться
сходиться
Таким чином, умова
 <1
в (1.4) може бути відкинуто, і шукане
аналітичне продовження гіпергеометричної
функції в розрізану площину дається
формулою
<1
в (1.4) може бути відкинуто, і шукане
аналітичне продовження гіпергеометричної
функції в розрізану площину дається
формулою
F( ,
,
 ,
,
 ,z)=
,z)=
 (1.5)
(1.5)
R( )>R(
)>R( ) >0;
) >0;

У загальному випадку, коли
параметри мають довільні значення,
аналітичне продовження F( ,
,
 ,
,
 ,z)
площина з розміром (1,
,z)
площина з розміром (1,
 )
може бути отримане у формі контурного
інтеграла, до якого приводить підсумовування
ряду (1.1) за допомогою теорії відрахувань.
)
може бути отримане у формі контурного
інтеграла, до якого приводить підсумовування
ряду (1.1) за допомогою теорії відрахувань.
Більше елементарний метод продовження, що не дає, однак, можливість одержати в явній формі загальне аналітичне вираження гіпергеометричної функції, полягає у використанні рекурентного співвідношення (1.6)
 F(
F( ,
,
 ,
,
 ,z)
=
,z)
=
 +
+

справедливість якого може бути встановлена підстановкою в нього ряду (1.1). Після підстановки й приведення подібних членів коефіцієнт при zk у правій частині (1.6) буде

 +
+ -
-
 = =
= = {
{
 -
-
 -
- }= =
}= = (
(



Шляхом повторного застосування
цієї тотожності можна представити
функцію F( ,
,
 ,
,
 ,z)
з довільними параметрами (
,z)
з довільними параметрами (
 0,-1,-2,…)у вигляді суми
0,-1,-2,…)у вигляді суми
F( ,
,
 ,
,
 ,z)=
,z)=
 F(
F( +s,
+s,
 +p,
+p,
 +2p,
z) (1.7)
+2p,
z) (1.7)
де р – ціле позитивне число
 (
( ,
,
 ,
,
 ,z)
– поліном відносно z. Якщо вибрати число
р досить більшим, так, щоб R(
,z)
– поліном відносно z. Якщо вибрати число
р досить більшим, так, щоб R( )>-p і R(
)>-p і R( -
- )>-p, то аналітичне продовження кожної
з функцій F(
)>-p, то аналітичне продовження кожної
з функцій F( +s,
+s,
 +p,
+p,
 +2p,
z) може бути виконане по формулі (1.5).
Підставляючи отримані вираження в (1.7)
одержимо функцію, регулярну в площині
з розрізом (1,
+2p,
z) може бути виконане по формулі (1.5).
Підставляючи отримані вираження в (1.7)
одержимо функцію, регулярну в площині
з розрізом (1,
 ),
що при
),
що при
 <1
збігається із сумою гіпергеометричного
ряду (1.1) і, отже, є шуканим аналітичним
продовженням.
<1
збігається із сумою гіпергеометричного
ряду (1.1) і, отже, є шуканим аналітичним
продовженням.
Гіпергеометрична функція F( ,
,
 ,
,
 ,z)
відіграє важливу роль в аналізі і його
додатках. Введення цієї функції дає
можливість одержати рішення багатьох
цікавих проблем теоретичного й прикладного
характеру, до яких, зокрема, ставиться
задача конформного відображення
трикутника, обмеженого пересічними
прямими або дугами окружностей, різні
задачі квантової механіки й так далі.
,z)
відіграє важливу роль в аналізі і його
додатках. Введення цієї функції дає
можливість одержати рішення багатьох
цікавих проблем теоретичного й прикладного
характеру, до яких, зокрема, ставиться
задача конформного відображення
трикутника, обмеженого пересічними
прямими або дугами окружностей, різні
задачі квантової механіки й так далі.
Велика кількість спеціальних
функцій може бути виражене через функцію
F( ,
,
 ,
,
 ,z),
що дозволяє розглядати теорію цих
функцій як відповідні спеціальні випадки
загальної теорії, даної в справжньому
пункті.
,z),
що дозволяє розглядати теорію цих
функцій як відповідні спеціальні випадки
загальної теорії, даної в справжньому
пункті.
1.2 Елементарні властивості гіпергеометричної функції
У справжньому розділі ми розглянемо деякі властивості гіпергеометричної функції, які безпосередньо випливають із її визначення за допомогою ряду (1.1).
1. Беручи до уваги, що члени ряду
не змінюються при перестановці параметрів
 і
і
 маємо співвідношення симетрії
маємо співвідношення симетрії
F( ,
,
 ,
,
 ,z)=
F(
,z)=
F( ,
, ,
, ,z), (2.1)
,z), (2.1)
2. Диференціюючи розглянутий ряд по членне, знаходимо
 F(
F( ,
,
 ,
,
 ,z)=
,z)= =
= =
=
= =
= F(
F( +1,
+1,
 +1,
+1,
 +1,z)
+1,z)
Таким чином,
 F(
F( ,
,
 ,
,
 ,z)=
,z)=
 F(
F( +1,
+1,
 +1,
+1,
 +1,z)
(2.2)
+1,z)
(2.2)
3. Повторне застосування цієї формули приводить до рівностей
 F(
F( ,
,
 ,
,
 ,z)=
,z)=
 F(
F( +m,
+m,
 +m,
+m,
 +m,z)
(2.3)
+m,z)
(2.3)
m=1,2,...
Покладемо надалі для скорочення запису
F( ,
,
 ,
,
 ,z)=
F,
,z)=
F,
F(
 1,
1,
 ,
,
 ,z)=
F(
,z)=
F(
 1),
1),
F( ,
,

 1,
1,
 ,z)=
F(
,z)=
F(
 1),
1),
F( ,
,
 ,
,

 1,z)=
F(
1,z)=
F(
 1).
1).
Функції F(
 1), F(
1), F(
 1), F(
1), F(
 1) називаються суміжними з F.
1) називаються суміжними з F.
4. Ми покажемо, що F і будь-які дві суміжні функції зв'язані між собою рекурентним співвідношенням з коефіцієнтами, що є лінійними функціями змінного z. Як основні співвідношення цього типу можуть бути обрані рівності (2.4), (2.5), (2.6) відповідно.
( -
- -
- )F+
)F+ (1-z)F(
(1-z)F( +1)-(
+1)-( -
-
 )F(
)F( -1)=0,
-1)=0,
( -
- -1)F+
-1)F+ F(
F( +1)-(
+1)-( - 1)F(
- 1)F( -1)=0,
-1)=0,
 (1-z)F-
(1-z)F- F(
F( -1)+(
-1)+( -
-
 )F(
)F( +1)=0.
+1)=0.
Підставляючи ряд (1.1) в (2.4) маємо (2.4)
( -
- -
- )F+
)F+ (1-z)F(
(1-z)F( +1)-(
+1)-( -
-
 )F(
)F( -1)=
-1)=
=( -
- -
- )
) +
+ (1-z)
(1-z) -(
-( -
-
 )
) =
=
= {(
{( -
- -
- )
) +
+
 -(
-( -
-
 )
) -
-

 }zk=
}zk=
= {(
{( -
- -
- )(
)( +k-1)+(
+k-1)+( +k)(
+k)( +k-1)-(
+k-1)-( -
- )(
)( -1)
-1)
( -k-1)k} zk=0,
-k-1)k} zk=0,
тому що
z
= =
=
 =
= (
( +1)...(
+1)...(
 +k-1)
+k-1)
 =(
=( +1)...(
+1)...(
 +k-1)(
+k-1)(
 +k)
+k)
 =(
=( -1)
-1)
 (
( +1)...(
+1)...(
 +k-2)
+k-2)
 =
= (
( +1)…(
+1)…( +k-2)
+k-2)
 =(
=( +1)…(
+1)…( +k-2)(
+k-2)( +k-1)
+k-1)
 =(
=( -1)
-1) (
( +1).......(
+1).......(
 +k-3)
+k-3)
Формули (2.5) і (2.6) доводяться аналогічним способом:
( -
- -
- )F+
)F+ F (
F ( +1)-(
+1)-( - 1)F(
- 1)F( -1)=
-1)=
= { (
{ ( -
- -1)
-1)
 +
+
 -(
-( - 1)
- 1) =
=
=
 {
{ -
- -1 +
-1 + + k-(
+ k-( +k-1)}zk=0,
+k-1)}zk=0,
 (1-z)F-
(1-z)F- F (
F ( -1)+(
-1)+( -
-
 )zF(
)zF( +1)=
+1)=
= {
{

 -
-
 -
-
 +(
+( -
-
 )
)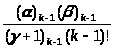 }zk
}zk
=
 {
{ (
( + k -1)(
+ k -1)( + k-1)-
+ k-1)-
 (
( + k -1)k-
+ k -1)k- (
( -1)(
-1)( + k-1)
+ k-1)
+( -
- )
) k}zk=0,
k}zk=0,
З (2.4)-(2.6) і властивості симетрії (2.1) треба три інших рівності:
( -
- -
- )F+
)F+ (1-z)F(
(1-z)F( +1)-(
+1)-( -
-
 )F(
)F( -1)=0, (2.7)
-1)=0, (2.7)
( -
- -1)F+
-1)F+ F (
F ( -1)-(
-1)-( - 1)F(
- 1)F( -1)=0, (2.8)
-1)=0, (2.8)
 (1-z)F-
(1-z)F- F (
F ( -1)+(
-1)+( -
-
 )zF(
)zF( +1)=0. (2.9)
+1)=0. (2.9)
( -
- -
- )F+
)F+ (1-z)F(
(1-z)F( +1)-(
+1)-( -
-
 )F(
)F( -1)=
-1)=
= {(
{( -
- -
- )
) +
+
 -
-
 -(
-( -
-
 )
) } zk =
} zk =
=
 {(
{( -
- -
- )(
)( +k-1)+
+k-1)+ (
( + k -1)(
+ k -1)( +k)-
+k)- (
( +k-1)k -(
+k-1)k -( -
- )(
)( -
-
1)}zk=0,
( -
- -1)F+
-1)F+ F (
F ( -1)-(
-1)-( - 1)F(
- 1)F( -1)=
-1)=
= {(
{( -
- -1)
-1)
 +
+
 -(
-( - 1)
- 1)
 }
zk =
}
zk =
=
 {
{ -
- -1+
-1+ (
(
 +
k )-
+
k )-
 (
( +k-1)}zk=0,
+k-1)}zk=0,
 (1-z)F-
(1-z)F- F (
F ( -1)+(
-1)+( -
-
 )zF(
)zF( +1)=
+1)=
= {
{
 -
-
 -
-
 +(
+( -
-
 )
)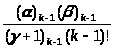 } zk
} zk
=
 {
{ (
( +k-1)(
+k-1)(
 +k-1)-
+k-1)- k(
k( +k-1)-
+k-1)-
 (
( +k-1)(
+k-1)( -1)+k
-1)+k
( -
- )}zk=0.
)}zk=0.
Інші рекурентні співвідношення виходять із (2.4) - (2.9) шляхом виключення з відповідної пари формул загальної суміжної функції. Наприклад, комбінуючи (2.5) і (2.8) або (2.6) і (2.9) одержуємо
( -
- )F-
)F- F (
F ( +1)+
+1)+ F(
F( +1)=0 (2.10)
+1)=0 (2.10)
( -
- )(1-z)F+(
)(1-z)F+( -
- )F (
)F ( -1)-(
-1)-(
 -
- )F(
)F( -1)=0 (2.11)
-1)=0 (2.11)
і так далі
( -
- )F-
)F- F (
F ( +1)+
+1)+ F(
F( +1)=
+1)=
= {(
{( -
- )
) +
+
 +
+
 } zk=
} zk=
=
 {
{ -
- -
- (
( +k)+
+k)+
 (
(
 +k)}
zk =0.
+k)}
zk =0.
( -
- )(1-z)F+(
)(1-z)F+( -
- )F (
)F ( -1)-(
-1)-( -
- )F(
)F( -1)=
-1)=
= {(
{( -
- )
) -(
-( -
- )
) +(
+( -
- )
) -(
-( -
-
 )
) } zk=
} zk=
=
 {(
{( -
- )(
)( +k-1)(
+k-1)( +k-1)-(
+k-1)-( -
- )(
)( +k-1)k+(
+k-1)k+( -
- )(
)( -1)(
-1)( +k-1)-
+k-1)-
( -
- )(
)( +k-1)(
+k-1)( -1)}zk=0.
-1)}zk=0.
Крім розповсюджених рекурентних
співвідношень існують аналогічні
співвідношення, що зв'язують гіпергеометричну
функцію виду F( ,
,
 ,
,
 ,z)
з який – або парою родинних функцій
виду F(
,z)
з який – або парою родинних функцій
виду F( +1,
+1,
 +m,
+m,
 +n,z),
де l,m,n – довільні цілі числа.
+n,z),
де l,m,n – довільні цілі числа.
Найпростішими рекурентними співвідношеннями цього типу є
F( ,
,
 ,
,
 ,z)-F(
,z)-F( ,
,
 ,
,
 -1,z)=
-1,z)=
 F(
F( +1,
+1,
 +1,
+1,
 +1,z)
(2.12)
+1,z)
(2.12)
F( ,
,
 +1,
+1,
 ,z)-
F(
,z)-
F( ,
,
 ,
,
 ,z)=
,z)=
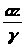 F(
F( +1,
+1,
 +1,
+1,
 +1,z)
(2.13)
+1,z)
(2.13)
F( ,
,
 +1,
+1,
 +1,z)-
F(
+1,z)-
F( ,
,
 ,
,
 ,z)=
,z)=
 F(
F( +1,
+1,
 +1,
+1,
 +2,z)(2.14)
+2,z)(2.14)
F( -1,
-1,
 +1,
+1,
 ,z)-
F(
,z)-
F( ,
,
 ,
,
 ,z)=
,z)=
 F(
F( ,
,
 +1,
+1,
 +1,z)
(2.15)
+1,z)
(2.15)
До даного класу ставляться також рівність (1.6)
Формули (2.12) і (2.15) доводяться підстановкою в них ряду (1.1) або виводяться на основі вже відомих рекурентних співвідношень для суміжних функцій.
1.3 Гіпергеометричне рівняння
Помітимо, що гіпергеометрична
функція u= F( ,
,
 ,
,
 ,z)
є інтегралом лінійного диференціального
рівняння
,z)
є інтегралом лінійного диференціального
рівняння
z(1-z)
 +[
+[
 -(
-( +
+ +1)]
+1)]
 -
-
 u=0 (2.16)
u=0 (2.16)
регулярним в околиці крапки z=0.
Рівняння (2.16) називається гіпергеометричним і включає, як окремі випадки, багато диференціальних рівнянь, що зустрічаються в додатках.
Якщо привести це рівняння до
стандартної форми, розділивши його на
коефіцієнт при другій похідній, то
коефіцієнти отриманого рівняння будуть
регулярними функціями змінного z в
області 0< <1 <1, наявними при z=0 полюс першого
порядку або звичайну крапку, залежно
від значень параметрів
<1 <1, наявними при z=0 полюс першого
порядку або звичайну крапку, залежно
від значень параметрів
 ,
,
 ,
,
 .
.
Із загальної теорії лінійних диференціальних рівнянь треба, що в такому випадку розглянуте рівняння повинне мати приватне рішення виду
u=zs
 zk (2.17)
zk (2.17)
де s – належне обране число,
 0, статечної ряд сходиться при
0, статечної ряд сходиться при
 <1
<1
u=
 zk+s
zk+s
 =
=
 (k+s)zk+s-1
(k+s)zk+s-1

 =
=
 (k+s)(k+s-1)zk+s-2
(k+s)(k+s-1)zk+s-2
Підставляючи (2.17) у рівняння (2.16) знаходимо
z(1-z)
 (
( zk+s
zk+s +[
+[
 -(
-( +
+ +1)z]
+1)z]
 (
( zk+s
zk+s -
-


 zk+s=0,
zk+s=0,
z(1-z) (
( zk+s-1(k+s)(k+s-1))+[
zk+s-1(k+s)(k+s-1))+[ -(
-( +
+ +1)z]
+1)z] (
( zk+s-1(k+s))-
zk+s-1(k+s))-



zk+s=
= (
( zk+s-1(k+s)(k+s-1))-
zk+s-1(k+s)(k+s-1))- (
( zk+s(k+s)(k+s-1))+
zk+s(k+s)(k+s-1))+ (
( zk+s-1
zk+s-1 (k+s))-
(k+s))-
-
 zk+s(
zk+s( +
+ +1)(k+s))-
+1)(k+s))-

 zk+s
zk+s
 =
=
=
 zk+s-1(k+s)(k+s-1+
zk+s-1(k+s)(k+s-1+ )-
)-
 zk+s(s+k+
zk+s(s+k+ )(s+k+
)(s+k+ )=0,
)=0,
звідки для визначення показника
s і
 виходить система рівнянь
виходить система рівнянь

 s(s-1-)=0,
s(s-1-)=0,
 (s+k)(s+k-1+
(s+k)(s+k-1+ ) -
) -
 (s+k-1+
(s+k-1+ )(s+k-1+
)(s+k-1+ )=0,
)=0,
k=1,2,...,
перше з яких дає s=0 або s=1-
Припустимо, що

 0,-1,-2,…і
виберемо s=0
0,-1,-2,…і
виберемо s=0
Тоді для обчислення коефіцієнтів
 одержимо рекурентне співвідношення
одержимо рекурентне співвідношення
 =
=
 k=1,2,…,
k=1,2,…,
звідки, якщо прийняти
 =1,
треба
=1,
треба
 =
= k=0,1,2,…,
k=0,1,2,…,
де для скорочення запису уведене позначення
 =
= (
( +1)…(
+1)…( +k-1),
+k-1),
 =1,k=1,2,…,
=1,k=1,2,…,
У такий спосіб перше приватне
рішення рівняння (2.16) при

 0,-1,-2,…буде
0,-1,-2,…буде
u= = F(
= F( ,
,
 ,
,
 ,z)=
,z)=

 zk,
zk,
 <1
(2.18)
<1
(2.18)
Аналогічно, вибираючи s=1- одержуємо в припущенні, що
одержуємо в припущенні, що

 2,3,4,…
2,3,4,…
 =
=
 k=1,2,…,
k=1,2,…,
звідки, якщо взяти
 =1
знаходимо
=1
знаходимо
 =
=
k=0,1,2,...,
Таким чином, при

 2,3,4,…рівняння
(2.16) має друге приватне рішення
2,3,4,…рівняння
(2.16) має друге приватне рішення
u= =
=


 =
= F(1-
F(1- +
+ ,1-
,1- +
+ ,2-
,2- ,z), (2.19)
,z), (2.19)
 <1,
<1,
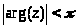
Якщо
 не є цілим числом (
не є цілим числом (
 0,
0, 1,
1,
 2,…),те
обоє рішення (2.18-2.19) існують одночасно
й лінійно незалежні між собою, так, що
загальне рішення рівняння (2.17) може бути
представлене у формі
2,…),те
обоє рішення (2.18-2.19) існують одночасно
й лінійно незалежні між собою, так, що
загальне рішення рівняння (2.17) може бути
представлене у формі
u=A F( ,
,
 ,
,
 ,z)+B
,z)+B F(1-
F(1- +
+ ,1-
,1- +
+
 ,2-
,2-
 ,z),
(2.20)
,z),
(2.20)
де А и В довільні постійні
 <1,
<1,
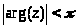
2. Подання різних функцій через гіпергеометричну
Гіпергеометрична функція F( ,
,
 ,
,
 ,z)
приводиться до полінома, коли
,z)
приводиться до полінома, коли
 =0,-1,-2,…або
=0,-1,-2,…або
 =0,-1,-2.
Наприклад,
=0,-1,-2.
Наприклад,
F( , 0,
, 0,
 ,z)=
,z)=

 zk=
zk= =1,
=1,
тому що
 =0(0+1)(0+2)…....(0+k-1)=0.
=0(0+1)(0+2)…....(0+k-1)=0.
F( , -2,
, -2,
 ,z)=
,z)=

 zk=
zk= z0+
z0+ z+
z+ z2 =
z2 =
=1-2 z+
z+ z2,
z2,
тому що
 =1,
=1,
 =-2,
=-2,
 =(-2)(-1)=2,
=(-2)(-1)=2,
 =(-2)(-1)0=0,
=(-2)(-1)0=0,
 =(-2)(-1)01=0
=(-2)(-1)01=0
і так далі.
Перетворення
F( ,
,
 ,
,
 ,z)=(1-z
,z)=(1-z F(
F( -
- ,
, -
- ,
,
 ,z)
,z)
 -
- =0
=0
 =
=
показує, що гіпергеометрична
функція при
 -
- =0,-1,-2,…або
=0,-1,-2,…або
 -
- =0,-1,-2,…виражається через алгебраїчні
функції. Зокрема,
=0,-1,-2,…виражається через алгебраїчні
функції. Зокрема,
F( ,
,
 ,
,
 ,z)=
(1-z
,z)=
(1-z ,
,
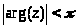 (3.1)
(3.1)
Надаючи параметрам
 ,
,
 спеціальні значення, знаходимо
спеціальні значення, знаходимо
(1-z)v= F(-v, 1, 1,z)
(1-z = F(
= F( , 1, 1,z (3.2)
, 1, 1,z (3.2)
(1-z)n= F(-n,
 ,
,
 ,z)
,z)
n=0,1,2,...
Щоб одержати подання логарифмічної функції, скористаємося розкладанням
ln(1-z)= -

 =-z
=-z

 <1
<1
звідки треба
ln(1-z)=-zF(1,1,2,z)
 (3.3)
(3.3)
Аналогічним образом виводяться формули для зворотних кругових функцій:
arctg z=zF( ,1,
,1,
 ,-z2)
,-z2)
 (3.4)
(3.4)
arcsin z=zF( ,
, ,
,
 ,z2)
,z2)

arctg z= (-1)k
(-1)k =z
=z
 =z
=z
 =
=
=z
 =z
=z

 =z
=z
 =zF(
=zF( ,1,
,1,
 ,-z2),
,-z2),
тому що
 =1*2*…*k=k!
=1*2*…*k=k!
arcsinz=z+
 =z[1+
=z[1+
 ]=
]=
=z[1+
 ]=z[1+
]=z[1+
 ]=z[1+
]=z[1+
 ]=
]=
=z[1+
 ]=z[1+
]=z[1+
 =zF(
=zF( ,
, ,
, ,z2)...
,z2)...
3. Вироджена гіпергеометрична функція
Поряд з гіпергеометричною
функцією F( ,
, ,
, ,z), важливу роль у теорії спеціальних
функцій грає так звана Вироджена
гіпергеометрична функція F(
,z), важливу роль у теорії спеціальних
функцій грає так звана Вироджена
гіпергеометрична функція F( ,
,
 ,z).
,z).
Щоб визначити цю функцію, помітимо, що статечної ряд

де z – комплексне змінне,
 і
і
 -
параметри, які можуть приймати будь-які
речовинні або комплексні значення, крім
-
параметри, які можуть приймати будь-які
речовинні або комплексні значення, крім
 =0,-1,-2,…і
символ
=0,-1,-2,…і
символ
 позначає величину
позначає величину
 =
=
 =1
=1
сходиться при будь-яких кінцевих z.
Тому що, якщо позначити через
 загальний член ряду, те
загальний член ряду, те
 =
=
 0, коли k
0, коли k
 .
.
Вироджена гіпергеометрична
функція F( ,
,
 ,z)
визначається як сума розглянутого ряду
,z)
визначається як сума розглянутого ряду
F( ,
,
 ,z)=
,z)=
 ,
,

 0,-1,-2,…,
0,-1,-2,…, <
< (4.1)
(4.1)
З даного визначення випливає,
що F( ,
,
 ,z)
функція комплексного змінного z.
,z)
функція комплексного змінного z.
Якщо покласти
f( ,
,
 ,z)=
,z)=
 F(
F( ,
,
 ,z)=
,z)=
 ,
(4.2)
,
(4.2)
те f( ,
,
 ,z)
при фіксованому z буде цілою функцією
від
,z)
при фіксованому z буде цілою функцією
від
 і
і
 .
Дійсно, члени ряду (6.2) є цілими функціями
цих змінних, і ряд сходиться рівномірно
в області
.
Дійсно, члени ряду (6.2) є цілими функціями
цих змінних, і ряд сходиться рівномірно
в області
 <A,
<A,
 <C.
<C.
Думаючи
 ,
маємо для досить більших k
,
маємо для досить більших k
 =
=


Звідси треба, що при заданому z
функція F( ,
,
 ,z)
,z)
представляє цілую
функцію
 й мероморфну функцію
й мероморфну функцію
 із простими полюсами в крапках
із простими полюсами в крапках
 =0,-1,-2,…
=0,-1,-2,…
Функція F( ,
, ,z) досить часто зустрічається в аналізі,
причому головне її значення полягає в
тому, що багато спеціальних функцій
можуть розглядатися як її окремі випадки,
що значною мірою полегшує побудову
теорії цих функцій і надає їй загальний
і компактний характер.
,z) досить часто зустрічається в аналізі,
причому головне її значення полягає в
тому, що багато спеціальних функцій
можуть розглядатися як її окремі випадки,
що значною мірою полегшує побудову
теорії цих функцій і надає їй загальний
і компактний характер.
Зв'язок функції F( ,
, ,z) з гіпергеометричною функцією дається
співвідношенням
,z) з гіпергеометричною функцією дається
співвідношенням
F (
( ,
, ,z)=lim F(
,z)=lim F( ,
, ,
, ,
, ) (4.3)
) (4.3)
З визначення виродженої гіпергеометричної функції безпосередньо випливають рівності
 F(
F( ,
, ,z)=
,z)=
 F(
F( +1,
+1, +1,z) (4.4)
+1,z) (4.4)
 F(
F( ,
, ,z)=
,z)=
 F(
F( +m,
+m, +m,z) m=1,2,... (4.5)
+m,z) m=1,2,... (4.5)
і рекурентні співвідношення
( -
- -1)F+
-1)F+ F (
F ( +1)-(
+1)-( -1)F(
-1)F( -1)=0 (4.6)
-1)=0 (4.6)
 F-
F- F(
F( -1)-zF(
-1)-zF( +1)=0 (4.7)
+1)=0 (4.7)
( -1+z)F+(
-1+z)F+( -
- )F(
)F( -1)-(
-1)-(
 -1)F(
-1)F( -1)=0 (4.8)
-1)=0 (4.8)
 (
( +z)F-
+z)F-
 F(
F( +1)-(
+1)-(
 -
-
 )zF(
)zF( +1)=0 (4.9)
+1)=0 (4.9)
( -
- )F(
)F( -1)+(2
-1)+(2 -
- +z)F-
+z)F- F(
F( +1)=0 (4.10)
+1)=0 (4.10)
 (
( -1)F(
-1)F( -1)-
-1)-
 (
( -1+z)F+(
-1+z)F+( -
- )zF(
)zF( +1)=0 (4.11)
+1)=0 (4.11)
єднальну функцію F F(
F( ,
, ,z) із двома будь-якими суміжними функціями
,z) із двома будь-якими суміжними функціями
F(
 1)
1)
 F(
F(
 1,
1, ,z) і F(
,z) і F(
 1)
1)
 F(
F( ,
,
 1,z)
1,z)
Формули (4.6) і (4.7) доводяться шляхом підстановки ряду (4.1) інші рекурентні співвідношення виходять із них у результаті простих алгебраїчних операцій.
( -
- -1)F+
-1)F+ F (
F ( +1)-(
+1)-( -1)F(
-1)F( -1)=
-1)=
= {(
{( -
- -1)
-1)
 +
+
 -(
-( -1)
-1)
 }zk=
}zk=
=
 {
{ -
- -1+
-1+ (
( +k)-
+k)-
 (
( +k-1)} zk=
+k-1)} zk=
=

 {
{ -
- -1+
-1+ +k-
+k-
 -k+1)}
zk=0
-k+1)}
zk=0
 F-
F- F(
F( -1)-zF(
-1)-zF( +1)=
+1)=
= {
{
 -
-
 -
- } zk=
} zk=
=
 {
{ (
( +k-1)-
+k-1)- (
(
 -1)-k
-1)-k } zk=
} zk=
=

 {
{
 +
+ k-
k- -
-
 -
- -k
-k } zk=0.
} zk=0.
Повторне застосування рекурентних
формул приводить до лінійних співвідношень,
що зв'язують функцію F( ,
, ,z) з родинними функціями F(
,z) з родинними функціями F( +m,
+m, +n,z), де m,n- задані цілі числа. Прикладами
подібних співвідношень можуть служити
рівності:
+n,z), де m,n- задані цілі числа. Прикладами
подібних співвідношень можуть служити
рівності:
F( ,
, ,z) = F(
,z) = F( +1,
+1, ,z)-
,z)-
 F(
F( +1,
+1, +1,z) (4.12)
+1,z) (4.12)
F( ,
, ,z)=
,z)=
 F(
F( ,
, +1,z) +
+1,z) +
 F(
F( +1,
+1, +1,z) (4.13)
+1,z) (4.13)
4. Диференціальне рівняння для виродженої гіпергеометричної функції. Вироджена гіпергеометрична функція другого роду
Покажемо, що вироджена гіпергеометрична функція є приватним рішенням диференціального рівняння
z
 +(
+( -z)
-z)
 -
- u=0 (5.1)
u=0 (5.1)
де

 0,-1,-2,…
0,-1,-2,…
u=F( ,
, ,z)=
,z)=
 zk
zk
 =
=
 zk-1
zk-1

 =
=
 zk-2
zk-2
Дійсно, позначаючи ліву частину
рівняння l(u) і полога u=
 =
F(
=
F( ,
, ,z), маємо
,z), маємо
l( ) =
) =

 zk-2+(
zk-2+( -z)
-z)

 zk-1-
zk-1-

 zk=
zk=
=[
 -
- ]+
]+
 [k
[k +
+
 -k-
-k- ]
] 0.
0.
Щоб одержати друге лінійне
незалежне рішення розглянутого рівняння,
припустимо, що
 ,
і виконаємо підстановку
,
і виконаємо підстановку
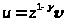 .
.
Рівняння (5.1) перетвориться тоді в рівняння того ж виду
z
 +(
+( -z)
-z)
 -
-
 =0
=0
с новими значеннями параметрів
 =1+
=1+ ,
,
 =2-
=2- . Звідси треба, що при
. Звідси треба, що при

 2,3,…функція
також є рішенням рівняння (5.1).
2,3,…функція
також є рішенням рівняння (5.1).
Якщо

 0,
0,
 1,
1,
 2,…обоє
рішення (
2,…обоє
рішення ( ) мають сенс і лінійно незалежні між
собою, тому загальний інтеграл рівняння
(5.1) може бути представлений у вигляді
) мають сенс і лінійно незалежні між
собою, тому загальний інтеграл рівняння
(5.1) може бути представлений у вигляді
u= F( ,
, ,z)+B
,z)+B F(1+
F(1+ -
- ,2-
,2- ,z) (при
,z) (при
 =1
u=
=1
u=
 )
(5.2)
)
(5.2)

 0,
0,
 1,
1,
 2,…
2,…
Щоб одержати вираження загального
інтеграла у формі, придатної для будь-яких
значень (крім
 =0,-1,-2,…),
краще увести вироджену гіпергеометричну
функцію другого роду
=0,-1,-2,…),
краще увести вироджену гіпергеометричну
функцію другого роду
G ,
, ,z)=
,z)= F(
F( ,
, ,z)+
,z)+

 F(1+
F(1+ -
- ,2-
,2- ,z)(5.3)
,z)(5.3)

 0,
0,
 1,
1,
 2,…
2,…
Формула (5.3) визначає функцію G ,
, ,z) для будь-яких
,z) для будь-яких
 ,
відмінних від цілого числа. Покажемо,
що при
,
відмінних від цілого числа. Покажемо,
що при

 n+1
(n=0,1,2,…)права частина (5.3) прагнути до
певної межі. Для доказу замінимо
гіпергеометричні функції відповідними
рядами й скористаємося співвідношенням
теорії Г-Функції. Тоді одержимо (5.4)
n+1
(n=0,1,2,…)права частина (5.3) прагнути до
певної межі. Для доказу замінимо
гіпергеометричні функції відповідними
рядами й скористаємося співвідношенням
теорії Г-Функції. Тоді одержимо (5.4)
G ,
, ,z)=
,z)= [
[

 -
-

 ]=
]=
= (
( )
)
Ми маємо
 =
=

 =
=


n=0,1,2,…
=


 =
=

 =
=
=

 ,
,
тому вираження в правій частині
(5.4) при

 n+1
приймає невизначений вид і прагне до
межі, значення якого може бути знайдене
за правилом Лопиталя. Відповідно до
цього результату покладемо
n+1
приймає невизначений вид і прагне до
межі, значення якого може бути знайдене
за правилом Лопиталя. Відповідно до
цього результату покладемо
G( ,
, ,z)=
,z)=
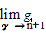 G
G ,
, ,z)= (-1)n+1[
,z)= (-1)n+1[ ] (5.5)
] (5.5)
n=0,1,2,…
Виконавши обчислення, знаходимо:
 =
=
 [
[ ],
],
 =
=
 [
[ ]+
]+
+
 ,
,
звідки для G( ,n+1,z) виходить явне вираження у формі
ряду (5.6)
,n+1,z) виходить явне вираження у формі
ряду (5.6)
G( ,n+1,z)=
,n+1,z)=


 [
[ ]+
]+
+
 ,
,
n=0,1,2,…,
 0,-1,-2,…,
0,-1,-2,…,
Тут
 -
логарифмічна похідна Г-Функція, і для
випадку n=0 порожня сума
-
логарифмічна похідна Г-Функція, і для
випадку n=0 порожня сума
 приймається
рівної 0.
приймається
рівної 0.
Якщо
 =-m
(m=0,1,2,…),те граничний перехід
=-m
(m=0,1,2,…),те граничний перехід

 n+1
(n=0,1,2…)у формулі (5.3) приводить до вираження
n+1
(n=0,1,2…)у формулі (5.3) приводить до вираження
G(-m,n+1,z)=
 F(-m,n+1,z), (5.7)
F(-m,n+1,z), (5.7)
m=0,1,2,... , n=0,1,2,...
З (5.3) безпосередньо треба, що Вироджена гіпергеометрична функція другого роду задовольняє функціональному співвідношенню
G( ,
, ,z)=
,z)=
 G(
G( -
- +1,2-
+1,2- ,z),
,z),
 (5.8)
(5.8)
На підставі цієї формули можна
визначити функцію G( ,
, ,z) при
,z) при
 ,
рівному нулю або цілому негативному
числу, за допомогою рівності
,
рівному нулю або цілому негативному
числу, за допомогою рівності
G( ,1-n,z)=
,1-n,z)=
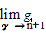 G(
G( ,
, ,z)= zn G(
,z)= zn G( +n,n+1,z) (5.9)
+n,n+1,z) (5.9)
n=1,2,…,
Таким чином, функція має сенс
при будь-яких значеннях її параметрів.
З донного визначення випливає, що G( ,
, ,z) регулярна функція від z у площині з
розрізом (-
,z) регулярна функція від z у площині з
розрізом (- ,0) і ціла функція
,0) і ціла функція
 й
й
 .
.
Покажемо, що функція G( ,
, ,z) є рішенням диференціального рівняння
(5.1).
,z) є рішенням диференціального рівняння
(5.1).
При

 0,
0,
 1,
1,
 2,…доказ
треба безпосередньо з (5.3). Для цілих
2,…доказ
треба безпосередньо з (5.3). Для цілих
 необхідний результат може бути
обґрунтований шляхом застосування
принципу аналітичного продовження.
необхідний результат може бути
обґрунтований шляхом застосування
принципу аналітичного продовження.
Якщо

 0,
0,
 1,
1,
 2,…інтеграли
F(
2,…інтеграли
F( ,
, ,z) і G(
,z) і G( ,
, ,z) лінійно незалежні між собою, у чому
легко переконатися, склавши вронскиан
цієї пари рішень.
,z) лінійно незалежні між собою, у чому
легко переконатися, склавши вронскиан
цієї пари рішень.
З (5.1) треба W{F,G}=C ez. Порівнюючи обидві частини цієї
рівності при z
ez. Порівнюючи обидві частини цієї
рівності при z 0, знаходимо
0, знаходимо
C=
W{ F( ,
, ,z),G(
,z),G( ,
, ,z)}= -
,z)}= -

 ez (5.10)
ez (5.10)

 0,
-1, -2,…,
0,
-1, -2,…,
Загальний інтеграл рівняння (7.1) у цьому випадку може бути представлений у формі
u = AF( ,
, ,z)+BG(
,z)+BG( ,
, ,z) (5.11)
,z) (5.11)
 ,
,
 0, -1, -2,…,
0, -1, -2,…,
Функція G( ,
, ,z) володіє рядом властивостей, аналогічних
властивостям функції F(
,z) володіє рядом властивостей, аналогічних
властивостям функції F( ,
, ,z). Так, наприклад, мають місце формули
диференціювання:
,z). Так, наприклад, мають місце формули
диференціювання:
 G(
G( ,
, ,z)= -
,z)= -
 G(
G( +1,
+1, +1,z)
+1,z)
 G(
G( ,
, ,z)= (-1)m
,z)= (-1)m G(
G( +m,
+m, +m,z) (5.12)
+m,z) (5.12)
m=1,2,...
рекурентні співвідношення:
G- G(
G( +1)-G(
+1)-G( -1)=0, (5.13)
-1)=0, (5.13)
( -
- )G+G(
)G+G( -1) -zG(
-1) -zG( +1)=0, (5.14)
+1)=0, (5.14)
( -1+z)G - G(
-1+z)G - G( -1)+(
-1)+(
 -
- +1)G(
+1)G( -1)=0, (5.15)
-1)=0, (5.15)
( +z)G+
+z)G+ (
( -
- -1)G(
-1)G( +1)-zG(
+1)-zG( +1)=0, (5.16)
+1)=0, (5.16)
G( -1)+(2
-1)+(2 -
- +z)G +
+z)G +
 (
(
 -
- +1)G(
+1)G( +1)=0, (5.17)
+1)=0, (5.17)
( -
- -1)G(
-1)G( -1)- (
-1)- ( -1+z)G + zG(
-1+z)G + zG( +1)=0, (5.18)
+1)=0, (5.18)
G G(
G( ,
, ,z), G(
,z), G(
 1)
1)
 G(
G(
 1,
1, ,z), G(
,z), G(
 1)
1)
 G(
G( ,
,
 1,z)
1,z)
і так далі.
Справедливість цих формул випливає з визначення функції G і відповідних властивостей функції F.
5. Подання різних функцій через вироджені гіпергеометричні функції
Як ми вже відзначали, багато
елементарних і спеціальних функцій, що
зустрічаються в аналізі, можуть бути
вироджені через функцію F( ,
, ,z).
,z).
Ми маємо, наприклад,
1) F( ,
, ,z)=
,z)=
 =
=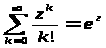
тому що

F(1,2,z)=
 =
= ,
,
тому що


3) F(-2,1,z)=

Висновок
Курсова робота присвячена дослідженню гіпергеометричних функцій. Можна зробити висновок:
Гіпергеометричні функції застосовуються в різних розділах математичного аналізу, зокрема, при рішенні диференціальних рівнянь і при розгляді інших спеціальних функцій.
За допомогою гіпергеометричних функцій виражаються не тільки сферичні, еліптичні, але й ряд інших, у тому числі й елементарні функції.
У роботі розглянуті визначення гіпергеометричного ряду й гіпергеометричної функції, доведені деякі елементарні властивості гіпергеометричної функції, функціональні й спеціальні функціональні співвідношення, подання різних функцій через гіпергеометричну, вироджену функція 1 і 2 роди, диференціальне рівняння для виродженої гіпергеометричної функції і його інтеграли, подання різних функцій через вироджені гіпергеометричні функції.
Література
1. Балк М.Б. Математичний аналіз: теорія аналітичних функцій. – К., 2000
2. Гурвиц А.І., Теорія функцій. – К., 2004
3. Евграфов М.О. Аналітичні функції. – К., 2003
4. Лебедєв І.І. Спеціальні функції і їхні додатки. – К., 2000
5. Маркушевич. М.М. Введення в теорію аналітичних функцій. – К., 1999
6. Смирнов В.И. Курс вищої математики тім 3,4. – К., 2005
7. Уиттекер І, Ватсон У. Курс сучасного аналізу тім 1,2. – К., 2000
8. Фихтенгольд К. Курс диференціального й інтегрального вирахування. – К., 2004
9. Фильчаков М. Довідник по вищій математиці. – К., 2000