Общий курс высшей математики
Академия труда и социальных отношений
Курганский филиал
Социально-экономический факультет
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Общий курс высшей математики»
Студент гр. ЗМб 1338
Ст. преподаватель
Курган – 2009
Задание 03
В ромбе ABCD
известны координаты вершин А и С и
тангенс внутреннего угла С. Найти
уравнения диагоналей и сторон, координаты
двух других вершин, а также площадь
этого ромба, если А(4,2), С(16;18),
.
Сделать чертеж.
Решение:
Зная координаты вершин А и С запишем уравнение диагонали АС как уравнение прямой, проходящей через две заданные точки:
12(y-2)=16(x-4);
12y-24=16х-64
16х-12у-40=0 /:4
4х-3у-10=0 – уравнение диагонали А С в форме общего уравнения прямой.
Перепишем это уравнение в форме уравнения прямой с угловым коэффициентом:
-3y=-10-4х;
3y=4x-10;
y=
откуда k
А С=
Так как в ромбе диагонали взаимно перпендикулярны, то угловой коэффициент диагонали BD будет равен
К>В>>D>
=
Само же уравнение диагонали BD найдем как уравнение прямой, проходящей через заданную точку в направлении, определяемом угловым коэффициентом К>BD>>.>
В качестве «заданной точки» возьмем точку Е пересечения диагоналей ромба, которая лежит на середине отрезка АС, вследствие чего:
Е (10;10)
Итак, уравнение диагонали BD запишем в виде
у – yE= К>В>>D>> >(x-xE)
y-10=
(x-10);
y-10=x+
/
4
4у-40=-3х+30
3х+4у-70=0 – уравнение диагонали BD
Чтобы найти уравнение сторон ромба, надо определить только угловые коэффициенты К>АВ> = К>CD> и К>ВС> = К>AD> прямых, на которых эти стороны лежат, ибо точки, через которые эти прямые проходят, известны – это вершины А и С ромба.
Для определения указанных угловых
коэффициентов воспользуемся формулой
,
позволяющей вычислять тангенс угла φ
между двумя заданными прямыми по их
угловым коэффициентам К>1>
и К>2>; при
этом угол φ отсчитывается против часовой
стрелки от прямой у = К>1>х
+ b>1>
до прямой у = К>2>х
+ b>2>.
Формула оказывается удобной, потому
что уравнение диагонали АС уже найдено
(и, следовательно, известен ее угловой
коэффициент К>АС>),
а положение сторон ромба относительно
этой диагонали однозначно определяется
внутренними углами А и С, которые равны
между собой и для которых по условию
известен их тангенс (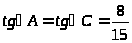
).
Так диагонали ромба делят его
углы пополам, то, положив
из формулы
для
тангенса двойного угла при
найдем tg
φ:
Положим z
= tg
φ;
тогда
,
тогда
15
2z
= 8 (1-z2)
30z=8-8z2
8z2+30z-8=0 /:2
4z2+15z-4=0
D=152-4
4
(-4)= 225+64=289
z>1>=
;
z>2=>
Но т.к. угол в ромбе φ
всегда острый корень z>2>=-4
отбрасываем и получаем в итоге, что tg
φ
=
Угол φ является углом между прямыми ВС и АС, с одной стороны, и прямыми АС и CD – с другой (см. чертеж).
Потому в первом случае по формуле
имеем
откуда при
то получим
4(
)=1+
;
=
/3
16-12 K>BC>=3+4K>BC>>;>
16 K>BC>=13;
K>BC>=
Во втором случае по формуле
имеем
=
;
При К>АС>
=
получим:
;
4(KcD-)=1+KcD;
4KcD-
=1+
KcD
/
3;
12KcD-16=3+4KcD;
8KcD =19
KcD=
Так как противоположные стороны ромба параллельны, то тем самым мы определили угловые коэффициенты всех его сторон.
К>CD>
= K>AB>>
>=
;
K>BC>
= K>AD>
=
.
Зная теперь эти угловые коэффициенты и координаты вершин А и С, по уже использовавшимся выше формулам найдем уравнения прямых АВ, CD, BC и AD.
Уравнение АВ: у – уA = K>A> >B> (х – хA),
у -2 =
(х-4) /8;
8у-16=19х-76;
19 х-8 у-60=0.
Уравнение CD: у – у>C>= К>CD>(х – x>C>)
у -18=
(
х-16) /
8;
8у -144=19х-304;
19 х-8 у-160=0.
Уравнение ВС: у – у>C>= К>BC>> >( х x>C>);
у -18=(
х - 16);
у - 18=
х – 13 /
16;
16у -288 = 13х - 208;
13х -16 у +80=0
Уравнение AD: у – уA = КA>D>( х -xA);
у -2=(
х -4);
у -2=
х -
/16;
16у -32= 13х-52;
13х-16у-20=0
Вершины ромба являются точками пересечения его соответствующих сторон. Поэтому их координаты найдем путем совместного решения уравнений этих сторон.
19х -8у -60 = 0 /
(-2)
13х -16у +80= 0
-38х+16у+120=0
13х-16у+80=0
-25х = - 200
х = 8
13
8 -16у+80=0
104-16у+80=0
16у=184
у=11,5 т.В (8;11,5)
Для вершины D:
1
9х
-8у +-160 = 0 /
(-2)
1
3x
- 16 y
– 20 = 0
-38х + 16у +320 = 0
13x - 16 y – 20 = 0
-25х = - 300
х=12
13
12 - 16у-20 = 0
156 -16 у-20=0
16у – 136
у=8,5 т.D (12;8,5)
Координаты этих точек удовлетворяют ранее найденному уравнению 3х + 4у - 70 = 0 диагонали BD, что подтверждает их правильность.
Площадь ромба вычислим по формуле S = ½ d>1>d>2>, где d>1> и d>2> – диагонали ромба.
Полагая d>1> = |АС|, а d>2> = |BD|, длины этих диагоналей найдем как расстояния между соответствующими противоположными вершинами ромба:
d>1>
=
d>2>
=
В итоге площадь ромба будет равна
S
=
∙ 20 ∙ 5 = 50 кв.ед.
Ответ:
АС: 4х - 3у - 10 = 0;
BD: 3х + 4у - 70= 0;
АВ: 19х -8у -60 = 0;
CD:19 х -8у - 160 = 0;
ВС: 13х -16у + 80 = 0;
AD: 13х -16у – 20=0;
В (8;11,5);
D (12; 8,5);
S = 50 кв.ед.
Задание 27
Найти предел
а)
Решение:
а) Функция, предел которой при х→ 2 требуется найти, представляет собой частное двух функций. Однако применить теорему о пределе частного в данном случае нельзя, так как предел функции, стоящей в знаменателе, при х→ 2 равен нулю.
Преобразуем данную функцию,
умножив числитель и знаменатель дроби,
находящейся под знаком предела, на
выражение
,
сопряженное знаменателю. Параллельно
разложим квадратный трехчлен в числителе
на линейные множители:
=
=
=
=
=
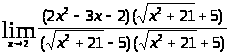2 х 2 - 3 х - 2=0
D=3
2 -42>(->2)=9+16=25
х1 =
=
=2;
х2 =
=
=
-
=
=
=
=
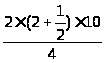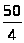=12,5
Ответ: 12,5
б)
Умножим числитель и знаменатель дроби, стоящей под знаком предела, на выражение, сопряженное к знаменателю:
=
=
=
=
=
+
=
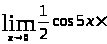
Найдем каждый сомножитель.
=
=
=
=
+
)=(
=1+1=2.
Предел
есть первый замечательный предел.
Таким образом.
после замены t=3x
будет равен
=3
Аналогично
=5
Получим
=
1
В итоге получим:
Ответ:
в)
Преобразуем основание данной функции:
Ведем новую переменную t=
,
тогда
t (4x-1) = 2
4xt – t = 2
4xt =2 + t
x=
x=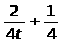
Заметим, что предел функции t при x → ∞ равен нулю т.е t → 0 при x → ∞. Следовательно
=
=
=
=
Воспользуемся теоремой о пределе произведения, следствием теоремы о пределе сложной функции, вторым замечательным пределом получим.
Ответ:
г)
Представим выражение под знаком предела в виде
=
=
=
=
=
Найдем значение каждого предела:
=
=1
=
- ln
e
следствие из второго замечательного
предела.
=3
=3
1=3
В итоге получим
=1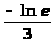
=
=
Ответ:
Задание 50
Найти производную функции
а)
Решение:
при решении будем применять правила дифференцирования частного произведения и сложной функции.
=
=
=
=
б)
+
+
=
+=
=
+=
+
в)
Решение:
г)
=
=
=
-
=
-
=
-
-
=-
=
=
Задание 73
Вычислить приближенное значение
функции f
(x)
= ln
в точке x1
заменив приращение функции в точке х>0>
= 0 ее дифференциалом. Если известно a=8;
b=13;
c=21;x1=0.013
Решение:
Если приращение аргумента ∆х = х>1> – х>0> достаточно мало по абсолютной величине, то приращение функции ∆f = f (x>1>) – f (x>0>) приближенно равно дифференциалу функции df. Поэтому справедлива формула
f (x>0> + >∆>x) ≈ f (x>0>) + f / (x>0>) >∆>x.
Для вычисления приближенного
значения функции у = ln
в точке х>1>
= 0,013 вычислим производную этой функции
в точке х>0>
= 0:
f /
(x)
=
=
=
=
=
f /
(x)
= f
/ (0) =
=
=-1
Подставив в формулу получим; f
(0,013)
=-0,013
Ответ: -0,013
Задание 96
Исследовать функцию
и построить ее график.
Решение
1. Область определения данной функции – вся числовая ось, то есть интервал (-∞; +∞), так как выражение
f (x)
=
в правой части аналитического задания функции имеет смысл при любом действительном х.
2. Как элементарная функция, данная функция является непрерывной в каждой точке своей области определения, то есть в каждой точке числовой оси.
3. Найдем все асимптоты графика данной функции.
Вертикальных асимптот график данной функции у = f (x) не имеет, поскольку последняя непрерывна на всей числовой оси формула
Для отыскания наклонной асимптоты при х→ +∞ вычислим следующие два предела k = lim y/x и b = lim (y – kx)
Если оба они существуют и конечны, то прямая у = kx + b является наклонной асимптотой при х→+∞ графика функции у = f (x)
Прежде чем обращаться к вычислению указанных пределов, напомним тождество √х2 = |х| (1), из которого следует, что при x > 0 √х2 = х ,
а при х < 0 √х2 = -х или х = -√х2 (2)
Приступая к вычислению первого предела, разделим числитель и знаменатель дроби на х2, затем воспользуемся равенством (1) и основными свойствами предела:
k=
=
=
=
=
=
=
=0
Для вычисления второго предела разделим числитель и знаменатель дроби на х и, действуя далее аналогично тому, как и при вычислении первого предела, получим:
b =(y
– kx)= y
== 
=
=
=
=3
Следовательно, прямая у = 3 является наклонной асимптотой графика данной функции при х→+∞ (поскольку угловой коэффициент k этой прямой равен нулю, то такую наклонную асимптоту называют также горизонтальной при х→+∞.
Для отыскания наклонной асимптоты при х→ -∞ вычислим пределы k>1> = lim y/x и b>1> = lim (y – kx)
Если оба они существуют и конечны, то прямая y = k>1>x + b>1> является наклонной асимптотой при х→-∞
Для вычисления этих пределов используем те же приемы, что и выше, учитывая только на сей раз вместо равенства (1) равенство (2). Теперь, в частности, для отрицательных значений аргумента имеем:
=
=-
=-
и следовательно, k>1>
= 0, b>1>
= -3, то есть наклонной (горизонтальной)
асимптотой при х→-∞ на сей раз является
прямая у = -3
4. Найдем точки пересечения графика данной функции с осями координат и установим участки ее знакопостоянства.
Для отыскания абсцисс точек
пересечения графика с осью ОХ решим
уравнение
=0
Его единственным решением,
очевидно, является х =
Причем, в силу положительности знаменателя
при любом х
ясно, что f(x)>0
при х>
f(x)<0при
х <
Таким образом, точка А (;
0) является единственной точкой пересечения
графика функции с осью ОХ, а для х
из интервалов (-∞;
)
и (;
+∞) соответствующие точки графика
функции расположены, соответственно,
ниже и выше оси абсцисс.
Точка пересечения графика функции
у = f
(x)
с осью ОУ – это всегда точка (0; f(0)),
если только нуль входит в область
определения функции. В нашем случае: f
(0) =
=
=-
=-2,24
такой точкой является В(0;-2,24).
5. Приступим теперь к отысканию точек экстремума данной функции и участков ее монотонности.
Вычислим сначала ее производную:
у=
=
=
=
=
=
=
Решая уравнение у/ = 0, получим единственный корень производной:
5(3+х) = 0 х=-3
Таким образом, необходимое условие экстремума выполняется лишь в точке х = -3. Эта точка разбивает ось абсцисс на два интервала (-∞;-3) и (-3; +∞) знакопостоянства производной.
Для определения знака производной в каждом интервале (пользуясь ее непрерывностью) определим знак производной в одной какой-либо точке каждого интервала. Так как
f/(-1)
=
<
0 и f/(2)
=
=
>0
то заключаем, что функция убывает на интервале (-∞;-3) и возрастает на интервале (-3; +∞), и значит точка х = -3 является точкой минимума данной функции.
Значение функции в этой точке (то есть минимум функции) равно
f (-3) =
=
=-
=-3,74
С (-3;-3,74)
6. Наконец, обратимся к исследованию данной функции на выпуклость, вогнутость и существование точек перегиба.
С этой целью найдем производную второго порядка данной функции:
у=(у)//==
=
=
=
=
=
=
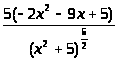
Решим затем уравнение у// = 0, эквивалентное квадратному уравнению:
его корни: х>1> = -5; х>2> = 0,5 , которые разбивают область определения функции на три интервала знакопостоянства второй производной: (-∞; -5), (-5; 0.5), (0.5; +∞).
Для определения знака производной второго порядка в каждом из этих интервалов определим ее знак в какой-либо точке соответствующего интервала:
f//(-6)
=
=
=
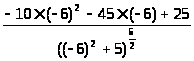< 0
f//(0)
=
=
> 0
f//(2)
=
=
=
< 0
Из полученных неравенств вытекает, что график функции является вогнутым на интервале (-5; 0.5), и выпуклым на интервалах (-∞; -5) и (0.5; +∞) и значит точки D (-5; f(-5)) и Е (0.5; f(0.5)), являются точками перегиба графика данной функции. Осталось найти ординаты этих точек:
f (-5)
=
=
= 
≈-3,65
f (0.5) =
=
=
≈ -1,53
Точки D(-5;-3,65) и E(0,5; -1,53)
Учитывая результаты полного исследования, соединим непрерывной кривой все ранее отмеченные точки предварительного чертежа так, чтобы эта кривая слева и справа неограниченно приближалась к асимптотам у=-3 и у=3
Список использованной литературы:
1 Данко. П.Е. Попов А.Г., Кожевникова Т.Я., Высшая математика в упражнениях и задачах. Учебное пособие для вузов.М.: ОНИКС 21век, 2002.- 304 с.
2 Кремер Н.Ш. Высшая математика для экономистов: учебник для студентов вузов по экономическим специальностям. М.: ЮНИТИ-ДАНА, 2007.-479 с.
3 Коломогоров А..Н., Абрамов А..М., Дудницын Ю.П.. Ивлев Б.М., Шварцбурд С.И. Алгебра и начала анализа:Учебник .М.: Просвещение, 1993.-320 с.
4 Кудрявцев Л.Д. курс математического анализа: Учебник для студентов вузов. М.: высшая школа, 1989.-352 с.