Общее понятие определённого интеграла, его геометрический и механический смысл

Кафедра: Высшая математика

Реферат

по дисциплине Высшая математика

Тема: «Общее понятие определённого интеграла, его геометрический и механический смысл. Необходимое условие интегрируемости»

Тольятти, 2008.

Содержание

Введение

Задачи, приводящие к понятию определенного интеграла

Определенный интеграл как предел интегральной суммы

Связь между определенным и неопределенным интегралами. Формула Ньютона-Лейбница

Свойства определенного интеграла

Геометрический смысл определенного интеграла

Механический смысл определенного интеграла

Необходимое условие интегрируемости

Список использованной литературы

Введение

Интеграл (от лат. integer – целый), одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой – измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т.п. Соответственно с этим различают неопределенные и определённые интегралы, вычисление которых является задачей интегрального исчисления.

Определенный интеграл – одно из основных понятий математического анализа – является мощным средством исследования в математике, физике, механике и других дисциплинах.

Задачи, приводящие к понятию определенного интеграла

Задача о пройденном пути.

Пусть известен закон изменения мгновенной скорости v = v(t). Определим путь, пройденный при движении точки за промежуток времени от t = α до t = β. Движение в общем случае предполагается неравномерным.

Поступим следующим образом.

1). Разобьем весь промежуток времени на n произвольных интервалов

t_>0 >= α < t_>1>< t_>2 >< … < t_>i>_>-1 >< t_>i> < … t_>n>_>-1 >< t_>n> = β,

где t_>i> – t_>i>_>-1> = Δt_>i>. На произвольном участке [t_>i>_>-1>, t_>i>] будем считать движение близким к равномерному с постоянной скоростью v = v(τ_>i>), t_>i>_>-1> ≤ τ_>i> ≤ t_>i>. Тогда за время Δt_>i> пройденный путь приближенно равен s_>i> = v(τ_>i>)Δt_>i>. Результат справедлив для каждого интервала (i = 1, 2, …, n).

2). Если указанные интервалы достаточно малы, то весь путь приближенно равен сумме:

Эта формула тем точнее, чем мельче разбиение данного промежутка времени.

3). Для получения точной формулы пути перейдем к пределу, увеличивая число дроблений (n→∞) и бесконечно измельчая сами интервалы. Обозначим λ = Δt_>i>, тогда

Задача о количестве вещества, вступившего в реакцию.

Пусть скорость химического превращения некоторого вещества, участвующего в химической реакции, есть функция времени v = v(t). Найти количество m вступившего в реакцию вещества за промежуток времени от t_>0> до T. Проделаем последовательно те же операции, что и при решении предыдущей задачи. В результате получим:

Работа переменной силы.

Пусть материальная точка под действием постоянной силы F перемещается по направлению этой силы. Если пройденный путь равен s, то, как известно из курса физики, работа Р этой силы F вычисляется по формуле: Р = F_>S>.

Пусть теперь материальная точка движется по оси Ох от точки А(а) до точки B(b) (b>a) под действием переменной силы, направленной по Ох и являющейся функцией от х: F = f(x).

Для нахождения работы Р в этом случае разобьем отрезок [a; b] точками a = x_>0><x_>1><…<x_>n> = b на n частичных отрезков и положим: Δx_>i> = x_>i> – x_>i>_>-1>, i = 1, 2, ..., n. Наибольшую из этих разностей обозначим через λ = maxΔx_>i>. Если эти отрезки достаточно малы, то без большой ошибки на каждом из них силу F можно считать постоянной (равной f(τ_>i>)), что дает приближенное выражение для работы

,

где τ_>i> – одна из точек сегмента [x_>i>_>-1>, x_>i>]. Отсюда:

Задачи о площади криволинейной трапеции.

Пусть на промежутке [a; b] задана функция f(x)≥0. Криволинейной трапецией называется плоская фигура, ограниченная указанной кривой y=f(x), прямыми x=a, x=b и осью Оx. (рис. 1). Для вычисления ее площади проделаем несколько операций.

Рис. 1.

1). Разобьем промежуток [a; b] произвольными точками x_>0>=a<x_>1><x_>2><…<x_>i>_>-1><x_>i><…<x_>n>=b на n частей. Положим Δx_>i> = x_>i> – x_>i>_>-1>, то есть Δx_>i> есть длина i-го частичного отрезка, а наибольшую из этих длин обозначим λ, (λ=max Δx_>i>).

2). На каждом отрезке [x_>i>_>-1>, x_>i>] возьмем по произвольной точке c_>i>,

x_>i>_>-1><c_>i>< x_>i> и вычислим f(c_>i>). Построим прямоугольник с основанием [x_>i>_>-1>, x_>i>] и высотой f(c_>i>). Его площадь равна S_>i>=f(c_>i>)( x_>i> – x_>i>_>-1>). Проделаем это для каждого i = 1, 2, …, n.

3). Площадь всей заштрихованной ступенчатой фигуры, составленной из прямоугольников, равна сумме

Площадь S криволинейной трапеции будет приближенно равна площади ступенчатой фигуры:

Чем мельче отрезки деления, тем точнее полученная фигура “отображает” криволинейную трапецию.

4). За площадь криволинейной трапеции принимают предел, к которому стремятся площади ступенчатых фигур, когда длины отрезков деления стремятся к нулю, а их число неограниченно увеличивается (n→∞). Таким образом,

Определенный интеграл как предел интегральной суммы

Естественный ход решения каждой из рассмотренных конкретных задач позволяет установить ту математическую операцию, с выполнением которой связано получение ответа во всех вопросах такого же характера.

Пусть на отрезке [a, b] задана непрерывная функция y=f(x).

1). Заданный отрезок разделим на n промежутков (равных или неравных) точками

a=x_>0><x_>1><x_>2><…<x_>n>_>-1><x_>n>=b,

причем для всякого индекса i, принимающего целые значения от 1 до n, имеет место соотношение x_>i>_>-1><x_>i>. Выразим длину каждого из этих частичных промежутков:

x_>1> - x_>0> = Δx_>1>, x_>2> – x_>1> = Δx_>2>, ..., x_>n> – x_>n>_>-1> = Δx_>n>.

При этом обозначим длину наибольшего из них через λ.

2). В каждом из этих промежутков выберем произвольное число ξ_>i> так, что x_>i>_>-1>≤ ξ_>i> ≤ x_>i>., и по каждому такому числу определим соответствующее значение функции f(ξ_>i>). Вычислим для каждого промежутка произведение f(ξ_>i>)Δx_>i>.

3). Составим сумму таких произведений по всем n промежуткам заданного отрезка:

f(ξ_>1>)Δx_>1>+ f(ξ_>2>)Δx_>2>+ f(ξ_>3>)Δx_>3>+...+ f(ξ_>n>)Δx_>n>= .

Такая сумма называется интегральной суммой.

Построение интегральной суммы состоит в произвольном делении заданного отрезка [a, b] на частичные и произвольном выборе числа ξ_>i> на каждом отрезке.

4). Выполняется дробление каждого из имеющихся отрезков на более мелкие так, что длина наибольшего из них безгранично уменьшается (λ→0). При этом интегральная сумма становится переменной величиной, имеющей конечный предел, если заданная функция непрерывна, а отрезок [a, b] конечен.

Этот предел называется определенным интегралом от функции f(x) на отрезке [a, b].

Соответствующее математическое выражение таково:

lim = λ→0

Знак ∫, представляющий растянутую S (начальную букву латинского слова «Summa»), символизирует здесь бесконечное увеличение числа слагаемых интегральной суммы. Буквы a и b, указывающие границы отрезка, на котором выполняется суммирование, называются пределами интегрирования.

Таким образом, определенным интегралом функции от f(x) в границах от a до b называется предел интегральной суммы вида

при условии, что длина наибольшего частичного отрезка стремится к нулю.

Выясним теперь возможность непосредственного использования операции, которая привела к понятию определенного интеграла, для решения соответствующих задач. Ограничимся при этом двумя примерами на вычисление площадей.

Пример 1.

Вычислить площадь, заключенную между прямой y=x, осью Ox и прямой x=1.

Решение. Так как данная прямая пересекается с Ox в начале координат, то отрезок интегрирования здесь будет [0, 1].

1). Разбиением этого отрезка на n равных между собой частей получим точки деления с абсциссами:

2). В каждом из полученных n отрезков выберем правые концы, т.е.

Так как f(x) = x, то

и слагаемые интегральной суммы выразятся в виде

где i – номер элементарного отрезка и принимает значения от 1 до n.

3). Интегральная сумма выразится в виде

(здесь применена формула n членов арифметической прогрессии).

4). Находим предел этой суммы при n → ∞:

Таким образом, искомая площадь равна 1/2 кв.ед. Проведенное вычисление, явно невыгодное из-за своей громоздкости, знакомит с операцией, составляющей сущность определенного интеграла.

Пример 2.

Вычислить площадь, ограниченную параболой y=x², осью Ox и прямой x=1.

Решение.

1). Разбивая отрезок интегрирования [0, 1] на n равных частей, получим такие же абсциссы точек деления, как в примере 1.

2). В каждом из частичных отрезков выберем снова правые концы:

Так как f(x) = x², то

и слагаемые интегральной суммы выразятся в виде

3). Интегральная сумма

Помещенная в скобках сумма квадратов первых n чисел натурального ряда может быть преобразована по формуле, доказываемой в элементарной алгебре:

Отсюда

4). Переход к пределу интегральной суммы при n → ∞ дает S = 1/3. Таким образом, искомая площадь равна 1/3 кв.ед.

Выполненное в этих двух примерах непосредственное вычисление определенных интегралов как пределов интегральных сумм

и

оказалось возможным только благодаря простой структуре операции суммирования, да и то оно потребовало проведения сложных подсчетов. Надо отметить, что такие приемы вычисления (здесь применен способ Архимеда) существовали до появления понятия интеграла.

Поэтому естественным развитием понятия определенного интеграла является выбор целесообразного способа его вычисления. Такой способ, оказывается, дает операция интегрирования ввиду наличия связи между определенным интегралом и интегралом неопределенным.

Связь между определенным и неопределенным интегралами. Формула Ньютона-Лейбница

Рассмотрим криволинейную трапецию (рис. 2), у которой правая граничная прямая не зафиксирована. Площадь этой трапеции измеряется переменной величиной, зависящей от положения ее правой границы х. Пусть это будет некоторая функция Φ(х). Тогда справедлива следующая теорема.

Рис. 2

Теорема. Функция Φ(х), выражающая площадь переменной криволинейной трапеции (с подвижной правой стороной), является первообразной для функции y = f(х), графиком которой является кривая, ограничивающая эту же трапецию сверху.

По смыслу определения первообразной запись

Φ(х) = ∫f(х)dx

будет оправдана, если мы докажем, что

Φ'(х) = f(х).

Доказательство. Дадим начальному значению х приращение Δх. Тогда функция, выражающая площадь криволинейной трапеции, получит приращение

ΔΦ(х) = пл. хММ_>1>х_>1>,.

Это приращение площади (рис. 2) больше площади прямоугольника хМNх_>1>, равной f(х)Δх, и меньше площади прямоугольника xN_>1>M_>1>x_>1>, равной

f(х+ Δх)Δх, т.е. f(х)Δх < ΔΦ(х) < f(х+ Δх)Δх.

Деление всех членов неравенств на Δх > 0 дает

f(х) < < f(х+ Δх).

Если теперь ввести условие Δх → 0, то в силу непрерывности функции

у= f(х)

Таким образом, отношение заключено между двумя переменными, имеющими общий предел при Δх → 0. Но из этого следует,

что ,

т.е. Φ'(х) = f(х).

Этим доказано, что функция Φ(х), выражающая площадь криволинейной трапеции, является первообразной для f(х).

Выражение этой функции возможно в двоякой форме.

Исходя из того, что рассмотренная ранее задача о площади криволинейной трапеции (с фиксированными границами) получает свое разрешение с помощью определенного интеграла, можно записать

пл. aABb =

Вместе с тем эта же площадь может быть выражена как частное значение функции Φ(х) при x = b, и тогда

Φ(b) = (1)

Аналогично площадь криволинейной трапеции (рис. 2) с переменной правой границей х выражается в виде

Φ(х) = (2)

Этот интеграл оказывается функцией от верхнего предела.

С другой стороны, если Φ(х), выражающая площадь aAMx, является первообразной для функции f(х), то можно представить ее в виде Φ(х)=F(х)+C, где F(х) – некоторая первообразная для той же функции.

Приравнивая первые части равенств (1) и (2), получаем

= F(х) + C.

Для определения постоянной С используем то, что при х = а трапеция превращается в отрезок, и ее площадь оказывается равной нулю, т.е.

Φ(а) = F(а) + C = 0,

а отсюда С = − F(а) и, следовательно,

Φ(х) = = F(х) − F(а).

Давая аргументу х значение фиксированного верхнего предела, т.е. при x = b, мы получаем выражение определенного интеграла через значения первообразной в виде следующей формулы:

Это – формула Ньютона-Лейбница. Она связывает определенный интеграл с неопределенным.

Для вычисления определенного интеграла эта формула обычно записывается в виде

где знак служит символическим обозначением разности между значениями первообразной функции F(b) и F(а).

Пример 1.

Пример 2.

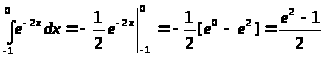
Пример 3.

Таким образом, формула Ньютона-Лейбница используется для вычисления определенного интеграла так:

1). Находится первообразная для данной подынтегральной функции.

2). Вычисляются частные значения первообразной подстановкой значений x = a и x = b, где b – верхний и a – нижний пределы интегрирования.

3). Определяется разность частных значений первообразной F(b) – F(а).

Свойства определенного интеграла

Доопределим понятие определенного интеграла при a ≥ b следующими равенствами:

Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

1). Если функция интегрируема на [a; b], то она интегрируема на

любом отрезке [x_>1>; x_>2>] [a; b].

2). Для любых a, b и c

3). Интеграл обладает свойством линейности: для любых функций f(x) и g(x) и любой постоянной A

4). Если f(x) и g(x) интегрируемы на [a; b], то f(x) · g(x) также интегрируема на этом отрезке.

5). Если f(x) – периодическая функция с периодом T, то для любого a

Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).

1). Если f(x) ≥ g(x), то

2). В частности, если f(x) ≥ 0, то

3). Если f(x) ≥ 0 для любого х  [a; b] и существует х_>0>  [a; b] такое, что f(x_>0>)>0, причем f(x) непрерывна в х_>0> то

4). |f(x)| интегрируема на [a; b], причем

5). Если на отрезке [a; b] m ≤ f(x) ≤ M, то

Геометрический смысл определенного интеграла

Понятие определенного интеграла введено таким образом, что в случае, когда функция y = f(x) неотрицательна на отрезке [a; b], где a < b,

численно равен площади S под кривой y = f(x) на [a; b] (рис. 3).

Рис. 3

Действительно, при стремлении к нулю ломаная (рис. 4) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.

Рис. 4

Учитывая сказанное, можно указать значения некоторых интегралов, используя известные планиметрические формулы для площадей плоских фигур. Например,

и т.д.

(Первый из интегралов – площадь квадрата со стороной единичной длины; второй – площадь прямоугольного треугольника, оба катета которого единичной длины; третий – площадь четверти круга единичного радиуса).

Механический смысл определенного интеграла

Пусть материальная точка М перемещается под действием силы , направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х – абсцисса движущейся точки М.

Найдем работу А силы по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (a < b). Для этого отрезок [a; b] точками а = х_>0>, х_>1>, ..., b = х_>n> (х_>0>< х_>1><...< х_>n>) разобьем на n частичных отрезков [х_>0>; х_>1>], [х_>1>; х_>2>], ..., [х_>n>_>-1>; х_>n>]. Сила, действующая на отрезке [х_>i>_>-1>; х_>i>], меняется от точки к точке. Но если длина отрезка Δх_>i> = х_>i> – х_>i>_>-1> достаточно мала, то сила на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = c_>i> [х_>i>_>-1>; х_>i>]. Поэтому работа, совершенная этой силой на отрезке [х_>i>_>-1>; х_>i>], равна произведению F(c_>i>)∙Δх_>i>. (Как работа постоянной силы F(c_>i>) на участке [х_>i>_>-1>; х_>i>]).

Приближенное значение работы А силы на всем отрезке [a; b] есть

Это приближенное равенство тем точнее, чем меньше длина Δх_>i>. Поэтому за точное значение работы А принимается предел суммы при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

.

Итак, работа переменной силы , величина которой есть непрерывная функция F = F(x), действующая на отрезке [a; b], равна определенному интегралу от величины F(x) силы, взятому по отрезу [a; b].

В этом состоит механический смысл определенного интеграла.

Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t = a до t = b, равен определенному интегралу от скорости v(t):

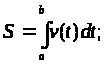
масса т неоднородного стержня на отрезке [a; b] равна определенному интегралу от плотности

γ(х):

Необходимое условие интегрируемости

Теорема. Если функция y = f(x) непрерывна на отрезке [a; b], то она интегрируема на этом отрезке.

Приведем пример нахождения определенного интеграла на основании определения.

Пример 1. Вычислить

Решение. Запишем выражение для интегральной суммы, предполагая, что все отрезки [х_>i>_>-1>; х_>i>] разбиения имеют одинаковую длину Δх_>i>, равную 1/n, где n – число отрезков разбиения, причем для каждого из отрезков [х_>i>_>-1>; х_>i>] разбиения точка ξ_>i> совпадает с правым концом этого отрезка, т.е.

ξ_>i> = х_>i> = ,

где i=1, 2, ..., n. (В силу интегрируемости функции у = х², выбор такого «специального» способа разбиения отрезка интегрирования на части и точек ξ_>1>, ξ_>2>, ..., ξ_>п> на отрезках разбиения не повлияет на искомый предел интегральной суммы). Тогда

Известно, что сумма квадратов чисел натурального ряда равна

Следовательно,

Анализ приведенного примера показывает, что успешное решение поставленной задачи оказалось возможным благодаря тому, что интегральную сумму удалось привести к виду, удобному для нахождения предела. Однако такая возможность существует далеко не всегда, поэтому долгое время задача интегрирования конкретных функций оставалась задачей чрезвычайно сложной. Установление связи между определенным и неопределенным интегралами позволило разработать эффективный метод вычисления определенного интеграла.

Список использованной литературы

1). Баврин И.И. Высшая математика. Учебник для педагогических институтов. Москва: Просвещение, 1993 год, 319 стр.

2). Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридма М.Н. Высшая математика для экономистов. Москва: Юнити, 2000 год, 271 стр.

3). Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики. Москва: Высшая школа, 1972 год, 480 стр.