Основная теорема алгебры (работа 2)

Федеральное агентство по образованию Российской Федерации

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО

Кафедра компьютерной алгебры и теории чисел

Основная теорема алгебры

Курсовая работа

студента 1 курса 121 группы механико-математического факультета

Батура Ирина Сергеевна

Научный руководитель Е.В. КОРОБЧЕНКО, ассистент

Зав. кафедрой В.Н.КУЗНЕЦОВ, д.т.н., профессор

САРАТОВ

2009 год

СОДЕРЖАНИЕ

1. Введение

2. Основные определения, используемые в курсовой работе

3. Элементы теории пределов для комплексных чисел

4. Доказательство основной теоремы

5. Список используемой литературы

1. ВВЕДЕНИЕ

Данная работа посвящена Основной теореме Алгебры, изучению существования корней в поле . Как предположение эта теорема впервые встречается у немецкого математика Питера Роуте(1617г.). Д’Аламбер первым в 1746г. опубликовал доказательство этой теоремы. Его доказательство основывалось на лемме. Доказательство это было бы совершенно строгим, если бы Д’Аламбер мог доказать, что-то на комплексной плоскости значение модуля многочлена достигает наименьшего значения. Во второй половине 18 века появляются доказательства Эйлера, Лапласа, Лагранжа и других. Во всех этих доказательствах предполагается заранее, что какие-то "идеальные" корни многочлена существуют, а затем доказывается, что, по крайней мере, один из них является комплексным числом. Со времен доказательства теоремы в алгебре было открыто очень много нового, поэтому сегодня "основной" эту теорему назвать уже нельзя: это название теперь является историческим.

Целью моей работы является выявления, что поле комплексных чисел алгебраически замкнуто. Для доказательства Основной теоремы Алгебры я использовала ряд лемм: лемма Даламбера и лемма о достижении точной нижней грани значений.

При написании работы мною была использована следующая литература: Д.К.Фадеев "Лекции по алгебре", Л.Д.Кудрявцев "Курс математического анализа". А.Г.Курош "Курс высшей алгебры".

2. Основные определения, используемые в курсовой работе

Множества, удовлетворяющие требованиям:1-операция сложения,2-операция умножения,3-связь операций сложения и умножения, и содержащие хотя бы один элемент, отличный от нуля, называется полями.

Множество комплексных чисел можно определить как множество упорядоченных пар действительных чисел, , , в котором введены операции сложения и умножения согласно следующему определению:

В результате этого определения множество указанных пар превращается в поле, т.е. удовлетворяет условиям 1,2,3. Полученное таким образом поле, называется полем комплексных чисел.

Последовательность комплексных чисел - это функция, определенная на множестве натуральных чисел и имеющая своими значениями комплексные числа.

Последовательность называется подпоследовательностью , если для любого k существует такое натуральное , что =, причем Б тогда и только тогда, когда .

Комплексное число – расширение множества вещественных чисел, обычно обозначается. Любое комплексное число может быть представлено как формальная сумма , где x и y— вещественные числа, i— мнимая единица, то есть число, удовлетворяющее уравнению .

Вещественное число (действительное число) – любое положительное число, отрицательное число или нуль.

Функция – 1) Зависимая переменная величина; 2) Соответствие между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение величины y (зависимой переменной или функции в значении 1).

Теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность.

Последовательность называется ограниченной на множестве Е, если существует такая постоянная М>0, что для всех и всех выполняется неравенства

Последовательность сходится к функции f равномерно на множестве Е, если для любого существует такой номер , что если , то для всех выполняется неравенство. Последовательность называется равномерно сходящейся на множестве Е, если существует функция f, к которой она равномерно сходится на Е.

3. Элементы теории пределов для комплексных чисел

В моей работе полиномы рассматриваются только над полями и как функции от комплексной или вещественной переменной, так что моя работа является скорее главой математического анализа, а не алгебры, хотя теорема о существовании корня у любого отличного от константы полинома с комплексными коэффициентами (т.е. установление алгебраической замкнутости поля ) носит название основной теоремы алгебры.

Определение: Пусть задана последовательность комплексных чисел . Число называется ее пределом, если для любого действительного числа существует такой номер , что при выполняется неравенство . В этом случае пишут lim , а=lim, b=lim. Предельное соотношение lim=c равносильно соотношению , ибо

max

Последовательность такая, что R, при некотором R, называется ограниченной.

Для вещественных переменных известная теорема Больцано-Вейерштрасса: из любой ограниченной последовательности можно извлечь сходящуюся подпоследовательность. То же самое верно и для последовательностей, составленных из комплексных чисел.

Действительно, пусть ограниченная последовательность, т.е. , тогда , так что есть ограниченная последовательность вещественных чисел. Из нее можно выбрать сходящуюся подпоследовательность . Рассмотрим соответствующую подпоследовательность мнимых частей . Она ограничена, и из нее можно извлечь сходящуюся подпоследовательность .

Соответствующая подпоследовательность комплексных чисел имеет сходящиеся последовательности вещественных и мнимых частей и, следовательно, сходятся, и ее предел равен .

4. Доказательство основной теоремы

Прежде чем приступить к формальному доказательству, наметим его идею. Пусть -полином, рассматриваемый как функция от комплексной переменной .Представим себе "график" функции , считая , что значения изображаются на горизонтальной плоскости, перпендикулярной к плоскости чертежа, а значения откладываются вверх в направлении оси . Мы установим, что являются непрерывными функциями от на всей плоскости комплексной переменной. Функция от комплексной переменной называется непрерывной в точке , если достаточно близким к значениями соответствует сколь угодно близкие к значения .В более точных терминах - для любого найдется такое , что , как только .

Непрерывность дает основания представлять себе график в виде непрерывной поверхности, накрывающей плоскость , и местами доходящей до этой плоскости. Собственно говоря, нам и нужно доказать, что существует такое значение , в котором , и, тем самым, , т.е. что поверхность доходит до плоскости в точке . Мы докажем, что если дана точка на поверхности ,которая расположена выше плоскости , то в ее окрестности найдется точка поверхности расположенная ниже данной точки. Тогда останется только доказать, что на поверхности существует самая низкая точка, скажем, при . Она не может находиться выше плоскости , ибо тогда она была бы самой низкой точкой. Следовательно, и , следовательно , т.е. корень полинома .

Теперь приступим к доказательству основной теоремы, разбив это доказательство на цепочку лемм.

Лемма 1. Дан полином c нулевым свободным членом.

Тогда для любого найдется такое , что , как только .

Доказательство: Пусть . Тогда

Положим

Если

то

что и требовалось доказать.

Лемма 2. Полином есть непрерывная функция во всех точках плоскости комплексной переменной.

Доказательство: Пусть дан полином и точка _>.> Расположим полином по степеням

,

Тогда так что

Правая часть есть полином от _> >с нулевым свободным членом.

По лемме 1 для любого найдется такое, что как только что и требовалось доказать.

Лемма 3. Модуль полинома есть непрерывная функция.

Доказательство: Из неравенства следует, что для данного то , которое "обслуживает" , подходит и для . Действительно, при имеем

Лемма 4. (о возрастании модуля полинома). Если -полином, отличный от константы, то для любого М>0 существует такое R>0, что M,как только .

Это означает, что любая горизонтальная плоскость отрезает от поверхности конечный кусок, накрывающий часть круга |z|≤R.

Доказательство: Пусть

где полином от c нулевым свободным членом.

В силу леммы 1 для найдется такое , что при , будет . Модуль может быть сделан сколь угодно большим, именно, при будет . Возьмем Тогда при будет

и так что

Лемма 5. Точная нижняя грань значений достигается, т.е. существует такое, что при всех .

Доказательство: Обозначим точную нижнюю грань через . Возьмем последовательностью стремящихся к сверху. Каждая из этих чисел не является нижней гранью значений , ибо -точная нижняя грань. Поэтому найдутся такие, что . Воспользуемся теперь леммой о возрастании модуля. Для найдем такое , что при будет 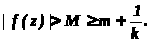Отсюда следует, что при все . Последовательностью _> >оказалась ограниченной, и из нее можно извлечь сходящуюся подпоследовательность _> >. Пусть ее предел равен . Тогда в силу непрерывности . Кроме того, . Поэтому Итак , что и требовалось доказать.

Лемма 6. (Лемма Даламбера). Пусть полином отличный от константы, и пусть . Тогда найдется такая точка, что

Геометрический смысл этой леммы: если на поверхности дана точка, находящаяся выше плоскости , то на ней найдется другая точка, расположенная ниже первой.

Доказательство: Расположим полином по степеням

Тогда Идея доказательства состоит в том, чтобы за счет первого отличного от нуля слагаемого "откусить кусочек" от , а влияние дальнейших слагаемых сделать незначительным. Пусть – первое отличное от нуля слагаемое после , так что (если k>1). Такое слагаемое имеется, так как не константа. Тогда

+

+( +…+ ))=

= c_>0 >(1+ +).

Здесь

=

есть полином от с нулевым свободным членом. По лемме 1 для = найдется такое ,что ||<, как только ||<. Положим =() и . Тогда

.

Выберем так, что . Для этого нужно взять . Далее, положим , т.е. возьмем . При таком выборе будет . Теперь положим

при и . Тогда и

||=.

Лемма доказана.

Заметим, что с тем же успехом мы могли бы взять при так что при k>1 (т.е. в случае, когда -корень кратности полинома )имеется k направлений спуска по поверхности . Они разделяются направлениями подъема при

Действительно, в этих направлениях

и

Так что если есть корень производной кратности , то поверхность в окрестности точки "гофрирована" так, что на ней имеется "долин" cпуска, раздельных "хребтами" подъема.

Теорема: Полином с комплексными коэффициентами, отличный от постоянной, имеет по меньше мере один комплексный корень (т.е. поле , комплексных чисел алгебраически замкнуто).

Доказательство: Пусть - данный полином, отличный от константы. Пусть, далее, и - точка, в которой ; Она существует по лемме 5. Тогда ибо иначе, согласно лемме 6, нашлась бы такая точка что невозможно.

СПИСОК ЛИТЕРАТУРЫ

Д.К.Фадеев Лекции по алгебре. - СПб.: Изд-во "Лань", 2007. - 416с.

Л.Д.Кудрявцев Курс математического анализа. – М.: Изд-во "Высш. Школа", 1981г. – 687с.

А.Г.Курош Курс высшей алгебры. – М.: Изд-во "Наука", 1971 г. – 431с.