Математические вычисления
ОБРАЗОВАТЕЛЬНЫЙ КОНСОРЦИУМ
СРЕДНЕРУССКИЙ УНИВЕРСИТЕТ
НОУ ВПО ТУЛЬСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ И БИЗНЕСА
Контрольная работа
по курсу «Математика»
Выполнил студент В.В.Тюрин
Тула 2010
1. Задача 1
Для заданных двух множеств найти
произведения
и
,
изобразить их графически и найти
пересечение
,
Решение
1.Определяем мощность декартового произведения:
2.Записываем декартовы произведения в виде явного перечисления:
3.Определяем пересечение множеств:
{Ø}
4.Изображаем элементы декартовых произведений АхВ и ВхА в виде точек декартовой плоскости (рис.1). Произведениями множеств являются
совокупности точек, обозначенные разными символами.
Рис. 1. Прямое A x B и обратного B x A произведения двух точечных множеств
Очевидно, что их пересечение пусто, что и соответствует аналитическому решению.
2. Задача 2
Вычислить предел функции с использованием основных теорем
Решение
3. Задача 3
Раскрытие неопределенности вида
и
с использованием правила Лопиталя
Решение
Неопределенность
4. Задача 4
Найти производную простой функции
Решение
Итак,
5. Задача 5
Найти наибольшее и наименьшее значение функции на интервале
Решение
1. Находим первую производную заданной функции
2. Определяем критические точки первого рода:
или
,
Отсюда
,
3. Подвергаем эти точки
дополнительному исследованию в табличной
форме (таблица 1), учитывая, что заданная
функция определена на участке
числовой оси:
Таблица 1
|
|
-1,2 |
( |
0 |
( |
1 |
( |
2,5 |
|
Знак
|
- |
|
+ |
|
- |
||
|
Величина
|
32,88 |
|
-6 |
|
-1 |
|
244 |
|
Экстремум |
m |
M |
)
)
)
Итак,
В данном случае один из глобальных экстремумов совпадает с одним из локальных экстремумов.
6. Задача 6
Вычислить
неопределенный интеграл методом
подстановки
Решение
Выполним подстановку:
Продифференцируем обе части уравнения:
=
7. Задача 7
Вычислить неопределенный интеграл от рациональной дроби
Решение
1. Найдем производную знаменателя:
2. Выделим в числителе выражение
,
для этого умножим знаменатель на 2 и
умножим дробь на
,
чтобы значение дроби не изменилось, и
вынесем
за знак интеграла.
3. Запишем число
,
как
,
получим:
4. Разлагаем подынтегральное выражение на сумму элементарных дробей:
5. Вычислим интеграл
,
для этого выражение
внесем
под знак дифференциала. Интеграл
принимает табличный вид:
6. Вычислим интеграл
,
для этого выделим в знаменателе полный
квадрат.
Интеграл принимает табличный вид:
7. Записываем решение:
8. Задача 8
Вычислить определенный интеграл методом интегрирования по частям
Решение
9. Задача 9
По заданным координатам вершинам А, В, С треугольника определить его длины сторон, углы и площадь
А(-5; -5; 3);В(-4; 1; 1);С(1; 4; 0)
Решение
1. Записываем стороны треугольника в форме линейных разложений векторов и строим векторную схему треугольника (рис.1):
Рис. 2 Схема треугольника
2 Вычисляем длины сторон:
3. Определяем углы треугольника,
следовательно,
=23.3o
следовательно,
25,4о
Угол
по формуле
.
Следовательно,
,
4. Проверяем достоверность вычисления углов треугольника
следовательно, все расчеты выполнены правильно.
5. Вычисляем площадь треугольника:
10. Задача 10
Найти для заданной матрицы
присоединенную
и обратную
матрицы
Решение
Вычисляем определитель матрицы
Итак, матрица неособенная и для
нее существует обратная матрица
.
2. Вычисляем для всех элементов
матрицы
алгебраические дополнения:
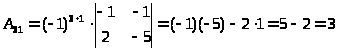
3. Записываем присоединенную матрицу:
4. Вычисляем обратную матрицу
5. Проверяем достоверность вычисления обратной матрицы, умножая ее на исходную матрицу
=
Получили единичную матрицу, следовательно, задача решена верно.
11. Задача 11
Найти произведения
и
квадратных матриц
и
Решение
Обе перемножаемые матрицы третьего порядка, поэтому умножение их всегда возможно по обычному правилу:
Находим прямое произведение матриц (умножение слева направо)
2. Находим обратное произведение матриц (умножение справа налево)
12. Задача 12
Найти произведение
прямоугольных матриц
Решение
1. Сопоставляя размеры заданных матриц
,
устанавливаем, что эти прямоугольные матрицы можно перемножать, при этом результирующая матрица будет иметь размеры 3х1:
2. Находим прямое произведение матриц (умножение слева направо)
13. Задача 13
Решить систему линейных уравнений методами Гаусса, Крамера и в матричной форме
Решение
1. Решаем систему методом Крамера, учитывая, что в общем случае, решение методом Крамера имеет вид:
то есть решение сводится к вычислению четырех определителей третьего порядка.
2. Вычисляем определитель системы:
так как определитель системы
,
следовательно, система имеет решение
и при этом одно.
3. Вычисляем остальные определители:
4. Вычисляем значения неизвестных:
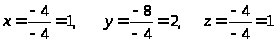
Итак, решение системы имеет вид: (1, 2, 1).
2. Решение в матричной форме.
В общем случае решение СЛАУ в матричной форме имеет вид:
.
1. Записываем компоненты заданной СЛАУ в явном виде:
,
,
2. Вычисляем определитель матрицы
:
Итак, матрица
неособенная и для нее существует обратная
матрица
.
3. Вычисляем алгебраические дополнения для всех элементов матрицы:
4. Записываем присоединенную матрицу в явном виде:
5. Вычисляем обратную матрицу
:
6. Проверяем достоверность вычисления обратной матрицы по условию:
Следовательно, обратная матрица вычислена верно.
7. Решаем заданную систему уравнений:
или
(1,
2, 1).
3. Метод Гаусса
1. Запишем СЛАУ в виде матрицы, расширенной за счет элементов правой части ее:
Первую строку оставляем без изменения. Умножаем элементы первой строки на (-3) и прибавляем к соответствующим элементам второй строки. Получим:
Затем умножаем элементы первой строки на (-2) и прибавляем к соответствующим элементам третьей строки.
Умножаем элементы третьей строки на (-2) и прибавляем к соответствующим элементам второй строки.
Первую и вторую строки оставляем без изменения. Умножаем элементы второй строки на 3 и прибавляем к соответствующим элементам третьей строки. Получим:
Вычисляем значения переменных СЛАУ снизу вверх:
Итак, решение системы уравнений имеет вид:
,
,
или в краткой форме: (1,2,1).
14. Задача 14
Определить число элементарных событий и простых соединений
Сколько есть двузначных чисел, у которых обе цифры четные?
Решение
Всего четных цифр 4 (2,4,6,8), значит
существует 4 способа выбора первой цифры
двузначного числа и 4 способа выбора
второй цифры. Так как выбор цифр
осуществляется одновременно, по правилу
произведения вычислим количество
двузначных чисел, у которых обе цифры
четные:
15. Задача 15
Вычислить вероятность события по классической схеме
Имеется 6 билетов в театр, 4 из которых на места первого ряда. Какова вероятность того, что из 3 наудачу выбранных билета 2 окажутся на места первого ряда?
Решение
1. Определяем общее количество способов, которыми можно взять 3 билета из 6.
2. Определяем количество способов взять три билета, в том числе два на места первого ряда и один на другой ряд:
3. Вероятность искомого события:
16. Задача 16
Вычислить вероятность события с использованием теорем сложения и умножения.
Охотник выстрелил три раза по удаляющейся мишени. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что он попал в цель все три раза.
Решение
Пусть
P(A) – вероятность попадания 3 раза,
P(B) – вероятность попадания в 1-й раз,
P(C) – вероятность попадания во 2-й раз,
P(D) – вероятность попадания в 3-й раз.
Тогда
P(B)=0,8
P(C)= P(B)-0,1=0,8-0,1=0,7
P(D)= P(C)-0,1=0,7-0,1=0,6
P(A)=P(B) ∙P(C) ∙P(D)=0,8∙0,7∙0,6=0,336
17. Задача 17
Вычисление вероятности повторных независимых испытаний
Определить вероятность того, что в семье, имеющей 5 детей, будет не более трех девочек. Вероятность рождения мальчиков и девочек считаем одинаковой.
Решение
Используем формулу Я. Бернулли:
1. Определяем исходные данные для формулы Бернулли:
n=5, k=3, p=0,5, q=1-0,5=0,5
2. Вычисление вероятности искомого события:
18. Задача 18
Найти законы распределения
случайных величин
и
,
если законы распределения случайных
величин
и
имеют вид
|
|
0 |
2 |
4 |
6 |
||||
|
|
0,1 |
0,2 |
0,3 |
0,4 |
||||
|
|
3 |
5 |
7 |
9 |
|
|
0,3 |
0,2 |
0,2 |
0,3 |
Решение
Вычисления производим в табличной форме на основании определения разности и произведения случайных величин.
1. Вычисляем промежуточные величины для вычисления распределения переменной величины Z=Х-Y (разности двух случайных величин), используя табл.2.
Таблица 2.
-
3
5
7
9
0.3
0.2
0.2
0.3
0
0.1
-3 0.03
-5 0.02
-7 0.02
-9 0.03
2
0.2
-1 0.06
-3 0.04
-5 0.04
-7 0.06
4
0.3
1 0.09
-1 0.06
-3 0.06
-5 0.09
6
0.4
3 0.12
1 0.08
-1 0.08
-3 0.12
2. Записываем закон распределения случайной величины Z=X-Y в табл.3.
Таблица 3
-
-9
-7
-5
-3
-1
1
3
0.03
0.08
0.15
0.25
0.2
0.17
0.12
Проверяем достоверность вычислений:
0.03+0.08+0.15+0.25+0.2+0.17+0.12=1.0
4. Вычисляем промежуточные
величины для вычисления распределения
случайной величины
(произведения тех же случайных величин),
используя табл.4.
Таблица 4
|
|
|
3 |
5 |
7 |
9 |
|
|
0.3 |
0.2 |
0.2 |
0.3 |
|
|
0 |
0.1 |
0 0.03 |
0 0.02 |
0 0.02 |
0 0.03 |
|
2 |
0.2 |
6 0.06 |
10 0.04 |
14 0.04 |
18 0.06 |
|
4 |
0.3 |
12 0.09 |
20 0.06 |
28 0.06 |
36 0.09 |
|
6 |
0.4 |
18 0.12 |
90 0.08 |
42 0.08 |
54 0.12 |
5. Записываем закон распределения
случайной величины
в табл. 5.
Таблица 5
|
|
0 |
6 |
10 |
12 |
14 |
18 |
20 |
28 |
36 |
42 |
54 |
90 |
|
|
0.1 |
0.06 |
0.04 |
0.09 |
0.04 |
0.18 |
0.06 |
0.06 |
0.09 |
0.08 |
0.12 |
0.08 |
6. Проверяем достоверность вычислений:
0=1.0+0.06+0.04+0.09+0.04+0.18+0.06+0.06+0.09+0.08+0.12+0.08=1.0
19. Задача 19
Вычислить основные характеристики вариационного ряда
Таблица 6
|
|
25 |
29 |
33 |
37 |
41 |
Итого |
|
|
16 |
8 |
19 |
10 |
7 |
60 |
Решение
1. Вычисления производим в табличной форме (табл.7).
Таблица 7
-
№№
1
25
16
625
400
10000
2
29
8
841
232
6728
3
33
19
1089
627
20691
4
37
10
1369
370
13690
5
41
7
1681
287
11767
Итого
60
6505
1916
62876
Среднее
-
-
93,42
31,93
1047,93
2. По итоговым данным табл.7, получаем:
- среднюю производительность
труда
3. Вычисляем характеристики вариации:
- дисперсию
- среднее квадратическое отклонение
- коэффициент вариации
4. Результаты вычислений иллюстрирует график рис.3.
Р ис. 3. Результаты вычислений
20. Задача 20
Найти линейное уравнение регрессии с построением эмпирической и теоретической линий регрессии и оценить тесноту связи для следующих статистических данных
Таблица 8
|
|
103 |
108 |
102 |
111 |
95 |
109 |
118 |
123 |
|
|
106 |
103 |
108 |
102 |
111 |
91 |
109 |
118 |
Решение
1. Решение производим в форме табл. 9 на основании системы нормальными уравнениями метода наименьших квадратов для линейной двухпараметрической регрессии:
.
Таблица 9
|
№№ |
|
|
|
|
|
|
1 |
103 |
106 |
10609 |
11236 |
10918 |
|
2 |
108 |
103 |
11664 |
10609 |
11124 |
|
3 |
102 |
108 |
10404 |
11664 |
11016 |
|
4 |
111 |
102 |
12321 |
10404 |
11322 |
|
5 |
95 |
111 |
9025 |
12321 |
10545 |
|
6 |
109 |
91 |
11881 |
8281 |
9919 |
|
7 |
118 |
109 |
13924 |
11881 |
12862 |
|
8 |
123 |
118 |
15129 |
13924 |
14514 |
|
Итого |
869 |
848 |
94957 |
90320 |
92220 |
|
Среднее |
108,63 |
106 |
11870 |
11290 |
11528 |
2. Подставляя итоговые числа сумм в уравнения метода наименьших квадратов, получаем алгебраическую систему двух уравнений с двумя неизвестными вида:
Отсюда получаем:
,
а из первого уравнения
3. Записываем корреляционное уравнение
4. Вычисляем коэффициент корреляции уравнения, используя итоговые данные табл.9
Линейный коэффициент корреляционного
показывает, что зависимость между
параметрами
и
слабая.
5. Графически результаты вычислений
показаны на рис.4 в виде точек исходной
статистической совокупности, соединенных
серой линией и графика регрессионной
зависимости
(сплошная черная линия).
Рис. 4. Результаты вычислений